Introduction

Nanofluids are well-known materials used in a variety of technical, commercial, and scientific fields that combine innovative thermal applications. The physical qualities of nanofluids herald some energetic applications in engine cooling, solar water heating, automated operation, astronomical and safety, physiological and automated operation, magnetic retention, solar issues, cooling devices, nuclear heating and the devices, etc. The nanoparticles are typically thought to be tiny metallic particles less than 100 nm in size. In the field of diligence and research, the transmission of energy is more compensated in nanofluids than in conventional viscous liquids. The pioneer researcher to pay direct attention to the thermal perspective of nanofluids was Choi [1]. Batool et al. [2] investigated the effects of lid-driven cavity on micropolar nanofluids with heat and mass transfer. Said et al. [3] studied the impact of surface injection on nanofluids with interfacial nanolayers and Lorentz force due to orthogonal permeable sheet. Chu et al. [4] designed the study for calculating the influence of different geometry of time-depended hybrid nanofluid with magnetic field. Algehyne et al. [5] analyzed the Cattaneo–Christov double diffusion effects on stretched hybrid nanofluids of GO-Ag/kerosene oil and GO-Ag/water.

The process of heat transfer is in which some amount of heat transfers from high- to low-temperature region. It appears when a body has different temperature with respect to its surroundings to equate body temperature with its surroundings. Fluid flows and heat transport Maxwell nanofluid have many applications in cooling devices, food heating, energy converters, solar, heat exchangers, microelectronics, ventilation systems in buildings, and cooling devices. Chatterjeeet al. [6] inspected the consequences of Reynolds number and Nusselt number on a circular rotating cylinder. Maleki et al. [7] analyzed the impression of thermal conductivity on hybrid nanoparticles in different directions. Hanif [8] estimated the influence of heat transfer on layer flow in Maxwell fluid. Baiet al. [9] examined the heat transfer flow of time-dependent Maxwell fluid near the stagnation point. Liu et al. [10] investigated the flow of Maxwell fluid with magnetic field and heat transfer by using fast method. Rashidi et al. [11] explored the effect of thermophoresis on time-dependent hybrid nanoparticles in the presence of thermal radiation due to the stretched plate.

Magnetohydrodynamics has a long and distinguished history among theories of many fluid mechanics. This theory of magnetohydrodynamics has made it very popular among researchers to deepen their research in pure and applied mathematics. There are several approaches to the study of (MHD) flow in both engineering and business. In liquid metals fluid, metal turning, cooling in nuclear reactors, and glass blowing aerodynamics. In industrial applications play the most significant functions. The MHD flow has become the focus of interest for many researchers in the field of physiological fluid, blood pump devices, and blood plasma due to its several vital uses in industry. Various industrial and engineering concerns were found through the study of MHD flows, including MHD pumps, blood flow measurements, plasma research, and metallurgical phenomena. MHD flows are important in a variety of fields, including cosmic fluid dynamics, geophysics, solar physics, and astrophysics. In the magnetosphere, chemical engineering industries, stellar and planetary systems, and electronics, MHD free convection flow has key applications and benefits. The magnetohydrodynamic MHD flow of nanofluid in thermophoresis and chemical diffusion over a vertical sheet is explored by [12]. Akbar et al. [13] studied the inspiration of MHD and thermal radiation on Maxwell fluid over a stretching sheet. According to their observation, the elasticity number causes an enhancement in the heat transfer rate from the stretching sheet by increasing the magnetic parameter. Hayat et al. [14] worked on rotating Maxwell fluid in a porous medium and obtained an analytical solution for unsteady MHD fluid. Kumaria et al. [15] observed the MHD mixed convection stagnation-point flow of an upper convected Maxwell fluid.

Another intriguing area of study connected to the microscopic convection of various liquids is bioconvection. Smaller density microorganisms float, which is the basis of the bioconvection process. The nonuniform instability structure is usually to blame for the swimming of microorganisms in the top region. The movement of the microorganisms is frequently observed at the fluid’s upper layer of surface. The process of bioconvection plays an essential role in the field of bioengineering and biotechnological sciences with significant applications such as polymer coating, building structures, micro-systems, enzymes, biofuels, transportation processes, and oil recovery. Kuznetsov [16] was pioneer to discover the process of bioconvection in nanofluid. Muhammad [17] discussed the influence of bioconvection on Jeffrey nanofluid with magnetic flux in the occurrence of swimming microorganisms. Bhatti et al. [18] investigated the impact of bioconvection and magnetic field on Williamson nonliquids with motile microorganisms due to permeable surface. Mandal et al. [19] explored the swimming of motile microorganisms in the stratification of electrically conducting nanofluid through radiative stretched cylinder. This investigation investigates the purposes of bioconvective transport in Maxwell nanofluid flow in the presence of motile microorganisms and activation energy. Moreover, the improved relations of nonlinear thermal features are used to revise the thermal analysis. The acquired system of PDEs is converted into a system of nonlinear-coupled ODEs by using famous similarity techniques. A numerical treatment of the system of ODEs is achieved by using the shooting method and comparing the obtained numerical results with the bvp4c code in MATLAB and the ND solve code in Mathematica. The numerical results are discussed for different parameters shown in the solution.

Mathematical analysis

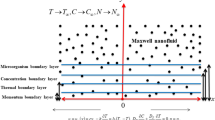
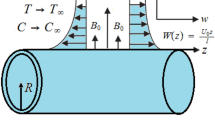
Consider the two-dimensional and steady flow of a Maxwell nanofluid with heat transfer past over the radially stretching surface. The features of Brownian motion and thermophoresis are also discussed. Nonlinear thermal radiation is taken as function of temperature and chemical reaction as a function of concentration. The components of velocity \(u\) and \(v\) are measured in the position abscissa and ordinate, respectively. The associated equations for the flow model are given as (Fig. 1):

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0, $$
(1)
$$ \begin{aligned} u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} + \lambda_{1} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v\frac{{\partial^{2} u}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right) & = \nu \frac{\partial }{\partial y}\left( {\frac{\partial u}{{\partial y}}} \right) - \frac{{\sigma^{ * } B_{0}^{2} }}{{\rho_{{\text{f}}} }}\left( {u + \lambda_{1} v\frac{\partial u}{{\partial y}}} \right) \\ & \quad + \frac{g}{{\rho_{{\text{f}}} }}\left[ \begin{gathered} \left( {1 - C_{{\text{f}}} } \right)\rho_{{\text{f}}} \beta \left( {T - T_{\infty } } \right) \hfill \\ - \left( {\rho_{{\text{p}}} - \rho_{{\text{f}}} } \right)\left( {C - C_{\infty } } \right) \hfill \\ - \left( {n - n_{\infty } } \right)\gamma \left( {\rho_{{\text{m}}} - \rho_{{\text{f}}} } \right) \hfill \\ \end{gathered} \right], \\ \end{aligned} $$
(2)
$$ u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha_{{\text{f}}} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\left( {\rho c} \right)_{{\text{p}}} }}{{\left( {\rho c} \right)_{{\text{f}}} }}\left( {D_{{\text{B}}} \frac{\partial C}{{\partial y}}\frac{\partial T}{{\partial y}} + \frac{{D_{{\text{T}}} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right) + \frac{{16\sigma^{*} }}{{3\left( {\rho c} \right)_{{\text{f}}} k^{*} }}\frac{\partial }{\partial y}\left( {T^{3} \frac{\partial T}{{\partial y}}} \right), $$
(3)
$$ u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D_{{\text{B}}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{{\text{T}}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - k_{{\text{c}}} (C - C_{\infty } )\left( {\frac{T}{{T_{\infty } }}} \right)^{n} \exp \left( { - \frac{{E_{{\text{a}}} }}{kT}} \right), $$
(4)
$$ u\frac{\partial N}{{\partial x}} + v\frac{\partial N}{{\partial y}} + \frac{{bW_{{\text{c}}} }}{{\left( {C_{{\text{w}}} - C_{\infty } } \right)}}\left[ {\frac{\partial }{\partial y}\left( {N\frac{\partial C}{{\partial y}}} \right)} \right] = D_{{\text{m}}} \left( {\frac{{\partial^{2} N}}{{\partial y^{2} }}} \right), $$
(5)
Fig. 1
figure 1

Flow problem geometry

Full size image

Governing model is subjected to boundary conditions:

$$ u = u_{{\text{w}}} \left( x \right) = ax,\;v = 0,\; - k\frac{\partial T}{{\partial y}} = h_{{\text{f}}} \left( {T_{{\text{w}}} - T} \right),\;D_{{\text{B}}} \frac{\partial C}{{\partial y}} + \frac{{D_{{\text{T}}} }}{{T_{\infty } }}\frac{\partial T}{{\partial y}} = 0\;{\text{at}}\;y = 0, $$
$$ u \to 0,\;T \to T_{\infty } ,\;C \to C_{\infty } \;{\text{as}}\;y \to \infty , $$

Similarity transformation

Let us describe following similarity functions to transformed set of PDEs in to dimensionless ODEs:

$$ u = axf^{\prime}(\eta ),\;v = - \sqrt {a\nu } \;f(\eta ),\;\eta = \sqrt {\frac{a}{\nu }} y, $$
(6)
$$ \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }},\;\phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{{\text{w}}} - C_{\infty } }},\;\chi (\eta ) = \frac{{N - N_{\infty } }}{{N_{{\text{w}}} - N_{\infty } }}. $$
(7)
$$ f^{\prime\prime\prime} + \left( {1 + {\text{Ha}}\Gamma } \right)ff^{\prime\prime} + \Gamma \left( {2ff^{\prime}f^{\prime\prime} - f^{2} f^{\prime\prime\prime}} \right) - {\text{Ha}}f^{\prime} - f^{{\prime}{2}} + \Lambda \left( {\theta - R_{{\text{b}}} \phi - R_{{\text{c}}} \chi } \right) = 0 $$
(8)
$$ \begin{aligned} & \left( {1 + \frac{4}{3}R_{{\text{d}}} \left( {1 + \left( {\theta_{w} - 1} \right)\theta } \right)^{3} } \right)\theta^{\prime\prime} + \left( {4R_{{\text{d}}} \left( {\theta_{{\text{w}}} - 1} \right)\left( {1 + \left( {\theta_{{\text{w}}} - 1} \right)\theta } \right)^{2} \theta^{{\prime}{2}} } \right) \\ & \quad + \Pr f\theta^{\prime} + \Pr N_{{\text{t}}} \theta^{{\prime}{2}} + \Pr N_{{\text{b}}} \theta^{\prime}f^{\prime} = 0 \\ \end{aligned} $$
(9)
$$ \phi^{\prime\prime} + \Pr {\text{Le}}f\phi^{\prime} + \frac{{N_{{\text{t}}} }}{{N_{{\text{b}}} }}\theta^{\prime\prime} - \Pr {\text{Le}}\sigma \left( {1 + \delta \theta } \right)^{\text{n}} \exp \left( { - \frac{E}{1 + \delta \theta }} \right)\phi = 0, $$
(10)
$$ \chi^{\prime\prime} + L_{{\text{b}}} f\chi^{\prime} - {\text{Pe}}\left[ {\phi^{\prime\prime}\left( {\chi + \Omega } \right) + \chi^{\prime}\phi^{\prime}} \right] = 0, $$
(11)

After applying the transformation similarly, the boundary conditions are transformed as follows

$$ f(0) = 0,\;f^{\prime}(0) = 1,\;\theta^{\prime}(0) = - \gamma \left( {1 - \theta \left( 0 \right)} \right),\;N_{{\text{b}}} \theta^{\prime}(0) + N_{{\text{t}}} \phi^{\prime}(0) = 0,\;\chi (0) = 1, $$
(12)
$$ f^{\prime} \to 0,\;\theta \to 0,\;\phi \to 0,\;\chi \to 0\;{\text{as}}\;\eta \to \infty , $$
(13)

The physical quantities describe as:

$$ C_{{\text{f}}} = \frac{{\tau_{{\text{w}}} }}{{\rho U_{{\text{w}}}^{2} }},\;{\text{Nu}}_{{\text{x}}} = \frac{{xq_{{\text{w}}} }}{{k(T_{{\text{w}}} - T_{\infty } )}},\;{\text{Sh}}_{{\text{x}}} = \frac{{xq_{{\text{m}}} }}{{D_{{\text{B}}} (C_{{\text{w}}} - C_{\infty } )}},\;{\text{Nn}}_{{\text{x}}} = \frac{{xq_{{\text{m}}} }}{{D_{{\text{n}}} (N_{{\text{w}}} - N_{\infty } )}} $$
(14)
$$C_{\text{f}} {{\text{Re}}_{\text{x}}^{1/2}}= - f^{\prime\prime}(0),\;{\text{Nu}}_{\text{x}} \;{\text{Re}}_{\text{x}}^{1/2}= - \theta^{\prime}(0),\;{\text{Sh}}_{\text{x}} \;{\text{Re}}_{\text{x}}^{1/2}= - \phi^{\prime}(0),{\text{Nn}}_{\text{x}} \;{\text{Re}}_{\text{x}}^{1/2}= - \chi^{\prime}(0)$$
(15)

where \({\text{Re}}_{{\text{x}}}^{1/2}\) = \(U_{{\text{w}}} {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x \upsilon }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\upsilon $}}\) is Reynolds number.

Numerical treatment

As couple of Eqs. (8–11) with the associated boundary conditions Eqs. (12–13) is coupled and nonlinear, so approximate solution cannot be found directly. For this we use the numerical technique, i.e., the shooting method to find the approximate solution. By making use of these technique, we convert system of higher-order ODEs into set of first-order ODEs.

$$ \left. {\begin{array}{*{20}l} {y_{1}^{\prime } = y_{2} } \hfill \\ {y_{2}^{\prime } = y_{3} } \hfill \\ {y_{3}^{\prime } = \frac{1}{{(1 - \beta y_{1}^{2} )}}\left[ {M^{2} y_{2} - (1 + M\beta )y_{1} y_{3} - 2\beta y_{1} y_{2} y_{3} - \lambda (y_{4} - N_{{\text{c}}} y_{6} - N_{{\text{r}}} y_{8} )} \right]} \hfill \\ {y_{4}^{\prime } = y_{5} } \hfill \\ {y_{5}^{\prime } = - \frac{{\Pr \left( {y_{1} y_{4} + N_{{\text{t}}} y_{5}^{2} + N_{{\text{b}}} y_{5} y_{7} } \right) + 4R_{{\text{d}}} \left( {\theta_{{\text{w}}} - 1} \right)\left( {1 + \left( {\theta_{{\text{w}}} - 1} \right)y_{4} } \right)^{2} y_{5}^{2} }}{{1 + \frac{4}{3}R_{{\text{d}}} \left( {1 + \left( {\theta_{{\text{w}}} - 1} \right)y_{4} } \right)^{3} }}} \hfill \\ {y_{6}^{\prime } = y_{7} } \hfill \\ {y_{7}^{\prime } = \Pr {\text{Le}}\sigma (1 + \delta )^{n} \exp \left( {\frac{ - E}{{1 + \delta z_{4} }}} \right)y_{6} - \left( {\frac{{N_{{\text{t}}} }}{{N_{{\text{b}}} }}} \right)y_{5}^{\prime } - \Pr {\text{Le}}y_{1} y_{7} } \hfill \\ {y_{8}^{\prime } = y_{9} } \hfill \\ {y_{9}^{\prime } = {\text{Pe}}\left[ {y_{7}^{\prime } \left( {y_{8} + \delta_{1} } \right) + y_{9} y_{7} } \right] - L_{{\text{b}}} y_{1} y_{9} } \hfill \\ \end{array} } \right\} $$
(16)

The set of model boundary conditions are described as in form of dimensionless form:

$$ y_{1} \left( 0 \right) = 0,\;y_{2} \left( 0 \right) = 1,\;y_{5} \left( 0 \right) = - \gamma \left( {1 - y_{4} \left( 0 \right)} \right),\;N_{{\text{b}}} y_{5} \left( 0 \right) + N_{{\text{t}}} y_{7} \left( 0 \right) = 0,\;y_{8} \left( 0 \right) = 1, $$
(17)
$$ y_{2} \left( \infty \right) \to 0,\;y_{4} \left( \infty \right) \to 0,\;y_{6} \left( \infty \right) \to 0,\;y_{8} \left( \infty \right) \to 0,\;y_{10} \left( \infty \right) \to 0. $$
(18)

Results and discussion

In the current section explain the impact of prominent parameters involved in this study. Choose the guess as.

\(L_{{\text{b}}} = 1.0,\;R_{{\text{d}}} = 0.5,\;{\text{Le}} = {\text{Pe}} = 2.0,\;N_{{\text{t}}} = 0.3,\;N_{{\text{b}}} = 0.2,\;\Pr = 1.0,\;R_{{\text{c}}} = R_{{\text{b}}} = 0.2,\;\Lambda = 0.2,\;{\text{Ha}} = 0.5,\;\Gamma = 0.2.\) Figure 2a–d determines to explore the outcome of Hartmann number \({\text{Ha}}\) on the velocity profile \(f^{\prime}\left( \eta \right)\), temperature function \(\theta \left( \eta \right)\), concentration profile \(\phi \left( \eta \right)\), and germs density \(\chi \left( \eta \right)\). Figure 2a illustrates that the improving values of Hartman number produces hindrance in the velocity function \(f^{\prime}\left( \eta \right)\). The \(f^{\prime}\left( \eta \right)\) acquires a peak with extending Ha at = 1.5. Temperature, concentration, and microorganism distributions were improved by boosting values of Ha (Fig. 2b–d). Hartman number includes Lorentz forces that are resistive forces. As \({\text{Ha}}\) increased, the Lorentz force also increased, producing a decrease in liquid flow velocity as well as an increase in temperature, concentration, and microorganisms. Figure 3 symbolizes the influence of Deborah number \(\Gamma\) on velocity distribution. In the rise of Deborah number \(\Gamma\), the fluid velocity distribution \(f^{\prime}\left( \eta \right)\) dropped. Deborah number influences the viscoelastic fluid’s velocity profile, impacting the extent of elastic response and deformation timescale in flow behavior. The velocity distribution \(f^{\prime}\left( \eta \right)\), temperature field \(\theta \left( \eta \right)\), concentration field \(\phi \left( \eta \right)\), and microorganism density profile \(\chi \left( \eta \right)\) are demonstrated in Fig. 4a–d under the influence of mixed bioconvection parameter \(\Lambda\). Figure 4a noticeably predicts that by boosting up the parameter \(\Lambda\), the velocity field is retarded. Observation shows that in case of stationary plate as related to moving plate, the declining profile is governing. Actually the buoyant forces increased due to mixed convection which in turn consequences in drop of the velocity field. Figure 4b predicts the effect of \(\Lambda\) on temperature distribution \(\theta \left( \eta \right)\) of nanoparticles with the variation in parameter \(\Lambda\). The heat transfer rate is heightened. However, this enrichment is comparatively deliberate for geometry. Mixed convection alters temperature profiles by combining forced and natural convection, impacting heat transfer rates and distributions in various systems. We note that the concentration field linearly rises for greater values of \(\Lambda\) in Fig. 4c. Mixed convection alters concentration profiles by combining forced and natural convection effects, impacting heat and mass transfer, enhancing, or suppressing boundary layer growth. Figure 4d describes the collision of mixed convection parameter \(\Lambda\) on the density field of microorganism. The intensifying values of parameter \(\Lambda\) turn microorganism density profile far extreme, comparatively deliberate, while the wedge is stationary. Mixed convection affects the spatial distribution of microorganisms due to variations in density, impacting their physical profile within a given environment. Figure 5a expresses the velocity profile \(f^{\prime}\left( \eta \right)\) for buoyancy number \(R_{{\text{b}}}\) and Rayleigh parameter \(R_{{\text{c}}}\). It is detected that by enhancing the value of \(R_{{\text{b}}}\), the velocity profile is retarded. It can be defensible substantially as the existence of buoyancy forces consequences in reduction of velocity. The buoyancy number affects the velocity profile by altering fluid motion, influencing flow patterns, and determining the intensity of buoyancy-driven convection in the physical system. The behaviors of the bioconvection Rayleigh parameter on the velocity field are shown in Fig. 5b. Rayleigh parameter influences fluid flow. Higher values result in a more parabolic velocity profile, indicating increased stability and reduced disturbances in viscous flow systems. When values of \(R_{{\text{c}}}\) rise, velocity is seen to decrease. Actually, because of bioconvection, which causes a rise in velocity, the buoyant force is recognized to have higher values. Influence of thermal radiation \(R_{{\text{d}}}\) on the temperature function is shown in Fig. 6. Radiation is essentially solar energy, which has a strong enriching effect on temperature. Increasing the radiation parameter raises the temperature. Figure 7 establishes to examine the comportment of thermophoresis parameter for the curves of \(\theta \left( \eta \right)\) and \(\phi \left( \eta \right)\). The larger thermophoresis constraint results in boosting up the curves of \(\theta \left( \eta \right)\) and \(\phi \left( \eta \right)\). The superior thermophoresis parameter results to improve the thermal conductivity of liquid. A mixture of nanoparticles in regular base liquids is formed permitting to recent technology. This physical conduct is because of the passage of tiny particles from hottest region to coldest region isolated from sheet. The influence of the Biot number on the temperature profile and concentration distribution is seen in Fig. 8. The improvement causes a significant increase in the rate of convective heat transfer. As a result of the increase in intense convective heat transfer, the profiles for fluid temperature and nanoparticle concentration climb. The dimensionless Biot number, which is related to the coefficient of heat transfer, increases temperature and nanoparticle concentration. Figure 9 shows how the Prandtl number affects the temperature field and the concentration field. Because of the improvement, nanoparticle temperatures decrease. The concentration of nanoparticles across the entire field decreases as causes do. Prandtl number is defined as the relationship between a fluid’s thermal conductivity and thermal diffusivity. As a result, the highest thermal diffusivity results from the smallest Prandtl number, while the temperature and thickness of the boundary layer are reduced. The description for significance of Brownian motion parameter \(N_{{\text{b}}}\) Lewis number \({\text{Le}}\) and activation energy \(E\) on concentration field of nanoparticles is explored in Fig. 10a–c. By enhancing the parameter \(N_{{\text{b}}}\) concentration profile declines. Usually, this Brownian parameter \(N_{{\text{b}}}\) exists because of the participation of nanoparticles. The Brownian parameter influences fluid concentration profiles by inducing random particle motion, impacting diffusion rates, and altering spatial distribution in dynamic systems. By holding the other parameters constant, Fig. 10b illustrates how the Lewis number \({\text{Le}}\) effects the concentration field. \({\text{Le}}\) is made stronger, which reduces the concentration field. As a result, the diffusivity of concentration decreases for leading values of \({\text{Le}}\). Lewis number influences fluid concentration profiles by affecting the relative rates of heat and mass transfer, crucial in combustion, and chemical processes. Figure 10c shows how activation energy \(E\) affects the volumetric concentration field. The value of activation energy is thought to be increased to optimize the concentration profile. Lower temperature and higher activation lead to a slower pace of reaction, which enriches the concentration of solutes. Figure 11a–c represents the effects of parameter \(\Omega\) called microorganism concentration difference, Peclet number \({\text{Pe}}\), and bioconvected Lewis number \(L_{{\text{b}}}\) on swimming germs density profile \(\chi \left( \eta \right)\). By enhancing the values of \(\Omega\), germs density profile is retarded. From Fig. 11b, it is demonstrated that within the increment in bioconvected Peclet number \({\text{Pe}}\), \(\chi \left( \eta \right)\) is retarded. Here the extreme rapidity of cell swimming’s enriched by raising the value of \({\text{Pe}}\). This advanced rapidity of cell swimming is accountable in the lesser performance of \(\chi \left( \eta \right)\). Bioconvective Peclet influences microbial density profiles, shaping the spatial distribution of microorganisms in physical environments. Figure 11c examines the microorganism profile when the bioconvected Lewis number was present. As the Lewis number rises, the impeding behavior of is seen. The reason for the slowing down of behavior is the fragile diffusivity of microorganisms. The instance of strengthening is delayed as a result of the reduced diffusivity. The definitions of emerging parameters involved in this study are shown in Table 1. The influence of prominent parameters on involved profiles is deliberated in Tables 2–5.

Fig. 2
figure 2

a–d Influence of \({\text{Ha}}\) over \(f^{\prime}\left( \eta \right)\), \(\theta \left( \eta \right)\), \(\phi \left( \eta \right)\) and \(\chi \left( \eta \right)\)

Full size image
Fig. 3
figure 3

Deviation of \(\Gamma\) over \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 4
figure 4

a–d Influence of \(\Lambda\) over \(f^{\prime}\left( \eta \right)\), \(\theta \left( \eta \right)\), \(\phi \left( \eta \right)\) and \(\chi \left( \eta \right)\)

Full size image
Fig. 5
figure 5

a–b Effects of \(R_{{\text{b}}}\) and \(R_{{\text{c}}}\) over \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 6
figure 6

Effects of \(R_{{\text{d}}}\) over \(\theta \left( \eta \right)\)

Full size image
Fig. 7
figure 7

a–b Effects of \(N_{{\text{t}}}\) over \(\theta \left( \eta \right)\) and \(\phi \left( \eta \right)\)

Full size image
Fig. 8
figure 8

a–b Effects of \(Bi\) over \(\theta \left( \eta \right)\) and \(\phi \left( \eta \right)\)

Full size image
Fig. 9
figure 9

a–b Effects of \({\text{Pr}}\) over \(\theta \left( \eta \right)\) and \(\phi \left( \eta \right)\)

Full size image
Fig. 10
figure 10

a–c Distribution of \(\phi \left( \eta \right)\) for various values of Nb, \({\text{Le}}\) and \(E\)

Full size image
Fig. 11
figure 11

a–c Distribution of \(\chi \left( \eta \right)\) for \(\Omega\), \({\text{Pe}}\) and Lb

Full size image
Table 1 Input parameters to carry out the solution of governing equations
Full size table
Table 2 Numerical treatment of \(- f^{\prime\prime}(0)\), for various values of emerging parameters \(\Gamma ,\) \({\text{Ha}},\) \(\Lambda ,\) \(R_{{\text{b}}}\) and \(R_{{\text{c}}} .\) Using bvp4c in MATLAB and ND solve code in wolfram Mathematica 11 for well settlement
Full size table
Table 3 Numerical treatment for \(- \theta^{\prime}(0)\) local for several values of \({\text{Ha,}}\) \(\Lambda ,\) \(\Pr ,N_{{\text{b}}} ,\) \(R_{{\text{b}}} ,\) \(R_{{\text{c}}} ,\) \({\text{Le}}\), \(N_{{\text{t}}} ,\) and \(R_{{\text{d}}} .\) Using bvp4c in MATLAB and ND solve code in wolfram Mathematica 11 for well settlement
Full size table
Table 4 Numerical treatment for \(\phi^{\prime}(0)\) for various values of \({\text{Ha}},\) \(\Lambda ,\) \(N_{{\text{t}}} ,{\text{Le}}\), \(\Pr\),\(R_{{\text{b}}} ,\) \(R_{{\text{c}}} ,\) \(N_{{\text{b}}}\) and \(R_{{\text{d}}} .\) Using bvp4c in MATLAB and ND solve code in wolfram Mathematica 11 for well settlement
Full size table
Table 5 Numerical treatment for motile germs density \(- \chi ^{\prime}(0)\) using bvp4c in MATLAB and ND solve code in wolfram Mathematica 11 for well settlement
Full size table

Conclusions

We have presented the numerical study of steady Maxwell nanofluid flow and heat transfer of viscous, incompressible, laminar, and two-dimensional fluid over a stretched surface with motile germs and activation energy. The current investigation is carried out in the presence of nonlinear thermal radiation, thermophoresis, and convective boundary condition. The special effects of emerging parameters on nondimensional velocity \(f{\prime}\) and dimensionless temperature \(\theta \), concentration \(\phi \), and density profile are presented in the form of tables and graphs. The core results of this work are as follows:

  • Velocity field \(f{\prime}\) increases by enlarging Maxwell parameter and decreases by enlarging magnetics parameter.

  • Significance declined is noted in velocity profile for growing value of buoyancy number \(R_{{\text{b}}}\) and Rayleigh parameter \(R_{{\text{c}}}\)

  • Temperature field \(\theta \) increases with an increase in thermal radiation.

  • Increase of Prandtl number \({\text{Pr}}\) causes decrease in temperature field and volumetric concentration field.

  • Energy field and volumetric concentration function increase by enlarging thermophoresis parameter \(N_{{\text{t}}}\).

  • Temperature and concentration profile both decreases for increasing value of Biot number.

  • For higher values of Lewis number \({\text{Le}}\) and chemical reaction parameter, concentration field \(\phi \) shows decreasing behavior.

  • The density field of swimming motile microorganisms progressively lessens as growth in the value of the bioconvective Lewis number \(L_{{\text{b}}}\) and Peclet number \({\text{Pe}}\).

Future research directions

The present analysis can be protracted by using the inspiration of.

  • Cattaneo–Christov heat flux model

  • Hybrid nanoparticles

  • Viscous dispersion

  • Engine oil base fluid

  • Sink/source

  • Taking different types of nanoparticles.