Performance improvement of air separation unit for an iron-steel industry using enhanced exergy analysis

Abstract

In this study, the thermodynamic performance of a real operating three-stage turbo/centrifugal type main air compressor for the air separation unit in an iron-steel industry was evaluated using both conventional and enhanced exergy analyses. Furthermore, the interaction and the potential for improvement of system components at two different airflow rates, 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹, were investigated under real operating conditions. The results indicated that the conventional exergy analysis of the system yields efficiency rates of approximately 21.3% and 25.0% for these airflow rates, respectively. It was found that implementing operating conditions proposed by the enhanced exergy analysis could increase the system’s exergy efficiency to about 40.8% and 80.7%, respectively. The primary causes of exergy destruction in the compressor are generally attributed to frictions occurring in the impeller, diffuser, and volute, as well as shock waves and air circulation during the compression process. It was observed that system efficiency could potentially increase to 80.7% with improvements in compressors and pump. The study also determined that enhanced exergy analysis is beneficial for identifying losses in system components and is seen as a tool that complements conventional exergy analysis.

Introduction

Air, vital for all living things, is composed of 20.9% oxygen, 78.1% nitrogen, 0.9% argon, and other components, volumetrically. Gases that are consistently present in air and maintain a stable concentration are separated using methods such as cryogenic distillation, adsorption, and membrane techniques [1]. These gases find diverse applications. For instance, oxygen is crucial in medical applications and various industrial processes, including metallurgy, glass production, ammonia synthesis, oxy-fuel combustion, and gasification. Nitrogen plays a significant role in the chemical and petroleum industries, while argon is used as an inert shielding gas in welding and electronics such as light bulb [2]. In the iron and steel industry, oxygen, nitrogen, and argon are predominantly separated through cryogenic distillation to achieve the high quantities and purity required. Air separation units (ASUs) are categorized into two types based on their compression systems: internal and external. In the internal system, oxygen and nitrogen are initially produced in the liquid phase. They are pressurized using integrated compression pumps, passed through the main heat exchanger, and delivered as gases to consumers. Conversely, in the external compression system, oxygen and nitrogen are also produced in the liquid phase but are passed through the main heat exchanger without pressurization, at production pressure, and then sent to oxygen and nitrogen compressors as gases. Post-compression, these gases are supplied to consumers such as Blast Furnaces and basic oxygen furnaces (BOF). In both systems, air is supplied by a multi-stage turbo/centrifugal type main air compressor (MAC). This equipment, while energy-intensive, is a major factor in exergy destruction in cryogenic ASUs [3]. Therefore, conducting energy and exergy analyses is crucial. These thermodynamic analysis methods provide valuable insights for improving efficiencies in such equipment.

In the field of cryogenic ASUs, numerous studies have been conducted, each contributing unique insights. Wagner et al. [4] focused on the energy and exergy analysis of a scroll compressor, developing a computer code to analyze energy and the mechanisms of exergy destruction within this compressor. Their analysis identified major destructions in the engine, including friction, mixing, heat transfer, and compression. Cornelissen and Hirs [5] examined the energy-saving potential of the cryogenic ASU process through exergy analysis. Their results indicated that over half of the exergy destruction occurred in the liquefaction unit, which re-liquefies the final products, with almost one-third occurring in the air compression unit. They identified the use of compressors and, to a lesser extent, turbines, as the primary causes of exergy destruction, proposing improvements that could save a quarter of the exergy destruction. Van der Ham and Kjelstrup [6] investigated a differently designed cryogenic ASU plant, comparing two and three column systems. They found that adding a third column to the distillation section reduced exergy damage by 31%, and overall, the three-column design was 12% more efficient in term of exergy conservation compared to the two-column design. Ural [7] conducted a comprehensive energy and exergy analysis of an ASU using a process simulator program. This study established a simulation model for an ASU producing gas/liquid oxygen, nitrogen, and argon, and it calculated the energy and exergy efficiencies of the system. Hnydiuk-Stefan and Skladzien [8] examined the thermal, energy, exergy, and economic analyzes of a power plant with two columns of cryogenic oxygen units operating in an oxy-combustion process with coal. They provided a thorough assessment of these various aspects. Singla and Chowdhury [9] developed a process for a cryogenic ASU, conducting both exergy and economic analyses. Their study determined the optimal parameters for achieving high exergy efficiency with low capital and operating expenditures. Rong et al. [10] proposed a cascade system for enhancing the compressor’s operating condition in ASUs through inlet air cooling and dehumidification. They built a thermodynamic model to assess the impact of air dehumidification and cooling on compressor performance in a 60,000 Nm³ h⁻¹ scale ASU. Their model predicted a reduction of about 5% in total compression power and an increase of about 5% in the isothermal efficiency of the air compressor. Mehrpooya et al. [11] introduced two novel ASU processes: a three-column cryogenic ASU and an integrated process combining a cryogenic ASU with combined-cycle power plants and LNG regasification, without external refrigeration. The first process showed a reduction in specific energy consumption of high purity nitrogen, oxygen, and argon by 18.7%, 13%, and 12%, respectively, compared to conventional processes. The second process demonstrated improvements in specific energy consumptions and exergy efficiency by 33% and 16%, respectively, compared to the first process. Lastly, Saedi [12] investigated a cryogenic process for producing neon in a recovery column alongside nitrogen and liquid oxygen from a two-column ASU. The study reported mole fractions of neon, nitrogen, and oxygen as 0.2%, 98.8%, and 74.5%, respectively.

The traditional exergy analysis method often falls short in pinpointing areas for improvement in systems, due to its limited capability in assessing the interactions between system components. As a result, many researchers have expanded beyond conventional exergy analysis to apply enhanced exergy analysis to various compressed air energy storage (CAES) systems [13,14,15,16,17]. CAES, a system that stores energy in the form of compressed air for later use, typically involves air compression and expansion. The standard CAES system employs gas turbine technology, where during the charging process, air is compressed and stored, and during the discharge process, compressed air is mixed with fossil fuels, burned in a combustion chamber, then expanded in a turbine to generate power. Wang et al. [18] investigated a 2 MW underwater CAES system using both conventional and enhanced exergy analyses, marking a first in this field. Similarly, Ebrahimi et al. [19] utilized enhanced exergy analysis to gain detailed insights into the Toronto Island underwater CAES plant. Their enhanced exergy analysis prioritized improvements in the heat exchanger, followed by the turbine and compressor. Zhang et al. [20] performed an enhanced exergy analysis of both low-temperature compressed CO₂-CAES and standard low-temperature CAES systems, comparing the two. Yang et al. [21] thoroughly investigated a thermal CAES system integrated with an ejector-assisted superheated Kalina cycle, using enhanced exergy analysis. Güleryüz and Ozen [22] applied both conventional and advanced exergy and exergoeconomic analysis to a 10 MW advanced adiabatic CAES system. Tian et al. [23] performed conventional and enhanced exergy analyses on real, unavoidable, and hybrid thermodynamic cycles based on the actual engineering of a 300 MW adiabatic CAES power plant. This approach has led to the rapid rise in the use of enhanced exergy analysis methods [24, 25]. By splitting exergy destruction into avoidable, unavoidable, endogenous, and exogenous parts, enhanced exergy analysis provides researchers with clearer guidance on which system components require focus [26, 27].

This study’s focus is on a system that differs from conventional CAES systems. The primary purpose of this system is to supply the main compressed air required for the ASU, operational without the need for storage. In the literature, there are notable instances where enhanced exergy analysis has been applied to ASU systems. Specifically, Zonouz and Mehrpooya [28] conducted enhanced exergy and exergoeconomic analyses on an integrated cryogenic ASU, combined with an oxy-fuel CO₂ power cycle and LNG evaporation process. Their results revealed that the endogenous part of exergy destruction was greater than the exogenous part. Tesch et al. [29] introduced a novel concept integrating LNG into the cryogenic ASU process for regasification in industrial applications. They evaluated two integration options, using both traditional and enhanced exergy analyses. These studies highlight the importance of enhanced exergy analysis in identifying areas for improvement and optimizing the efficiency of ASU systems.

The main objective of this study, setting it apart from existing literature, is to obtain more accurate results in exergy destruction analysis. This involves not just evaluating exergy destruction within individual system components using conventional exergy analysis, but also examining the interactions between these components under various working conditions. This research applies both conventional and enhanced exergy analyses to a real operating three-stage turbo/centrifugal type MAC system in the iron-steel industry’s ASU for the first time. Additionally, this is the first instance of utilizing these two exergy analysis methods together to analyze and evaluate multi-stage turbo/ centrifugal compressors. The approach broadens the scope of these analyses, making them applicable not only to centrifugal compressors used in power generation, chemical, ecological plants, ASUs, and petrochemical plants, but also to axial and reciprocating compressors that operate on multistage compression principles. This comprehensive analysis enables the identification of components within the system that suffer from performance degradation, thereby preventing excessive time and cost losses, or focusing on optimizing only the inefficient components. The study examined a compressor with an operating range of 168,000 Nm³h⁻¹–252,000 Nm³h⁻¹ and a nominal capacity of 240,000 Nm³h⁻¹. Analyses were conducted specifically for capacities of 210,000 Nm³h⁻¹ and 240,000 Nm³h⁻¹, in line with the consumption needs of BOF and Blast Furnaces for ASU products. Notably, the MAC’s turn-down rate is not frequently altered due to these consumption requirements. To the best of the author’s knowledge, no previous research has focused on the enhanced exergy analysis and assessment of a multi-stage turbo/ centrifugal type MAC system used in the iron-steel industry for ASU.

System description

Air separation units (ASUs) play a crucial role in iron-steel industry, particularly for processes in blast furnaces and an oxygen converters, as well as in the basic oxygen furnace (BOF) for steel processing. These operations require high purity and large quantities of oxygen. ASUs are designed to produce not only oxygen but also nitrogen and argon gases at high purity levels. To achieve this, ASUs cool the air to boiling temperatures, enabling the separation of these gases in their liquid phase. The process begins with atmospheric air being filtered to remove particles up to 5 μm in size. Following this, the air undergoes two main processes before entering the three-stage Main Air Compressor (MAC) system of the ASU, as shown schematically in Fig. 1. These processes are: (i) compression and (ii) cooling under constant pressure. The compression process involves three stages, named Compressor1, Compressor2, and Compressor3, based on the airflow sequence. These stages are indirectly driven by an electric motor, which rotates a shaft. This shaft, in turn, rotates a bull gear that transmits torque to pinion gears connected to the impellers. In addition, the cooling process incorporates two intercoolers, named Cooler1 and Cooler2, also based on the airflow sequence. Therefore, this study specifically focuses on analyzing the MAC system in the ASU of an iron-steel industry, highlighting its critical role and operational intricacies.

Fig. 1

Flowchart of the three-stage MAC system for the ASU of an iron-steel industry

In Fig. 1, the process begins as air flows from the filters directly into the first stage of the compressor (Compressor1). This flow occurs after the air passes through the inlet guide valve, which is where the compressor’s capacity is adjusted. In the first stage, the impellers increase both the kinetic energy and static pressure of the air. During this process, the air’s temperature also rises due to energy losses. The diffuser then converts this acquired kinetic energy into static pressure. Consequently, the air exits the first stage at a pressure of approximately 1.29 bar(g) and a temperature of 98 °C. Next, the air, now at a high temperature, is cooled using a counter-flow shell and tube-type heat exchanger (Cooler1). In this heat exchanger, water is used in a closed cycle to theoretically cool the air back to its initial temperature at the first stage’s air inlet. During this cooling process, the air undergoes a stage change, and its specific volume decreases. This change brings the air closer to an isothermal condition, thereby reducing the energy consumption required for the next compression stage.

As shown in Fig. 1, the air, now at a lower temperature after the first stage, moves on to the second stage of the compressor (Compressor2). Similar to the first stage, the kinetic energy, static pressure, and temperature of the air are increased with the assistance of the impeller. A diffuser is then used to convert this enhanced kinetic energy into static pressure. The air exits the second stage at approximately 3.01 bar(g) at 96 °C. Subsequently, the air enters a counter-flow shell and tube-type heat exchanger (Cooler2), where it is again cooled using water. This cooling process decreases the air’s specific volume, bringing its state closer to an isothermal change and thus reducing the energy consumption required for the third stage (Compressor3). In the final compression stage, the air reaches the third level. As in the previous two stages, the impellers increase the air’s kinetic energy and static pressure, and the temperature rises due to energy losses. The air is then compressed by the diffuser. Finally, it exits the system with a pressure of 4.85 bar(g) and a temperature of 90 °C.

Following the third stage of compression, unlike the previous stages, there is no counter-flow shell and tube-type heat exchanger. This is because the air is directed to an Air Cooling Tower. Consequently, there is no need for additional cooler in this final stage.

Conventional exergy analysis

To conduct the exergetic analysis and performance assessment of the three-stage MAC system in the ASU, this study makes several assumptions: (i) No chemical reaction occurs in the MAC system, as the compositions of process air and water remain unchanged throughout the system. (ii) The potential and kinetic energies, along with exergy exchanges, are considered negligible. (iii) The dead state values for water are assumed to be 2 °C and 101.325 kPa, and for air, they are 6.6 °C and 98.1 kPa. (iv) The MAC system’s nominal working capacity is set at 22,000 kW. The analysis uses real data collected on 25 November 2021 from the Distributed Control System (DCS) program, aligning with the components and measurement points indicated on the flow diagram in Fig. 1. To analyze the system’s exergy, the flow rate measured in Nm³ by the DCS system is first converted into mass flow rate. This conversion involves initially changing the flow rate from Nm³ to m³ as follows:

$$ \frac{{1.013 \times \dot{V}_{{{\text{nominal}}}} }}{273.15} = \frac{{0.981 \times \dot{V}_{{{\text{standard}}}} }}{{\left( {273.15 + 15} \right)}} $$

(1)

Then, the density is determined based on the air’s parameters in the dead state, and the system’s mass flow rate (in m³ s⁻¹) is calculated by multiplying this density with the flow rate. Once the mass flow rate is established, the mass balance equation of the system can be expressed as follows:

$$ \sum {\dot{\text{m}}}_{{\text{in,k}}} { = }\sum {\dot{\text{m}}}_{{\text{out,k}}} $$

(2)

The unit exergy rate of the system is expressed as follows:

$$ \dot{E}_{{\text{j}}} = \dot{m}_{{\text{j}}} \psi_{{\text{j}}} $$

(3)

where ${\dot{E}}_{j}$ represents the unit exergy rate at the jth location (in kW), and ${\psi }_{j}$ denotes the specific flow exergy (in kJ kg⁻¹), which is calculated as follows:

$$ \psi_{{\text{j}}} = \left[ {\left( {h_{{\text{j}}} - h_{0} } \right) - T_{0} \left( {s_{{\text{j}}} - s_{0} } \right)} \right] $$

(4)

where ${h}_{0}$, ${T}_{0}$, and ${s}_{0}$ denote the specific enthalpy (kJ kg⁻¹), temperature (K), and specific entropy (k kg⁻¹ K⁻¹) at the reference state, respectively. It should be noted that the chemical exergy is disregarded in the solution of the exergy balance equations, since the system under consideration does not involve any change in steam composition throughout the process. The exergy efficiency of the system is then determined by the ratio of the difference in component’s inlet and outlet exergy (${\dot{E}}_{{\text{P}},{\text{k}}}$) to the energy required for the component’s operation (${\dot{E}}_{{\text{F}},{\text{k}}}$):

$$ \varepsilon = \frac{{\dot{E}_{{\text{P,k}}} }}{{\dot{E}_{{\text{F,k}}} }} $$

(5)

For the conventional exergy analysis, the equations representing the exergy destruction and efficiency of each component in the MAC system, based on Eqs. (2)-(5), are listed in Table 1. The energy consumption values for ${\dot{W}}_{Comp.}$ and ${\dot{W}}_{Pump}$ have been obtained from the active energy meter of the equipment.

Table 1 Equations expressing the exergy destruction and exergy efficiency of the three-stage MAC system and its components

Enhanced exergy analysis

The conventional exergy analysis cannot accurately evaluate a particular system as it ignores the interdependencies of system components and technological constraints. The enhanced exergy analysis splits the exergy destruction rate into unavoidable (${\dot{E}}_{{\text{D}}}^{{\text{UN}}}$), avoidable (${\dot{E}}_{{\text{D}}}^{{\text{AV}}}$), endogenous (${\dot{E}}_{{\text{D}}}^{{\text{EN}}}$), and exog $\dot{E}_{{\text{D,k}}} = \dot{E}_{{\text{D,k}}}^{{{\text{EN}}}} + \dot{E}_{{\text{D,k}}}^{{{\text{EX}}}}$ enous (${\dot{E}}_{{\text{D}}}^{{\text{EX}}}$) parts. The splitting of exergy destruction into its components is clearly demonstrated in Fig. 2.

Fig. 2

Splitting of the exergy destruction into its components

To evaluate the improvement potential of the kth component in the system, the system’s exergy destruction (${\dot{E}}_{{\text{D}},{\text{k}}}$) of the component is split into endogenous (${\dot{E}}_{{\text{D}},{\text{k}}}^{{\text{EN}}}$) and exogenous (${\dot{E}}_{{\text{D}},{\text{k}}}^{{\text{EX}}}$) parts. This can be expressed as follows:

$${\dot{E}}_{{\text{D}},{\text{k}}} = {\dot{E}}_{{\text{D}},{\text{k}}}^{{\text{EN}}} + {\dot{E}}_{{\text{D}},{\text{k}}}^{{\text{EX}}}$$

(6)

The exogenous part represents the external aspect of exergy destruction in component k, caused by irreversibilities occurring in other components of the system, excluding the kth component. This can be expressed using Eq. (7). This division enables engineers to estimate the exergy destruction occurring due to the kth component, while simultaneously optimizing the operation of the system by considering other components. This information is crucial in deciding whether to focus on the evaluated k component or other components in the system to effectively enhance overall performance [30].

$$ \dot{E}_{{\text{D,k}}}^{{{\text{EX}}}} = \dot{E}_{{\text{D,k}}} - \dot{E}_{{\text{D,k}}}^{{{\text{EN}}}} $$

(7)

The results of this discretization process offer more insight into the interactions between components. However, accurately determining the endogenous exergy destruction part for a component is a significant challenge in enhanced exergy analysis. The precision of this part directly impacts the analysis results. In this process for the three-stage MAC system, the engineering (graphical) method [31] was used for more accurate outcomes, instead of relying on the pure state of the working fluids. When calculating the endogenous part, it is crucial to consider that the kth component operates under real conditions, while all other components are assumed to operate under ideal conditions (with irreversibilities neglected).

Only a portion of the exergy destruction rate in the system’s component can be mitigated. The part of exergy destruction that cannot be reduced due to technological limitations, such as material availability, cost, and production methods, is categorized as the unavoidable (${\dot{E}}_{D}^{UN}$) part. This aspect is futther explained in the subsequent sections.

$$ \dot{E}_{{\text{D,k}}}^{{{\text{UN}}}} = \dot{E}_{{\text{P,k}}}^{{{\text{real}}}} \left( {\frac{{\dot{E}_{{\text{D}}} }}{{\dot{E}_{{\text{P}}} }}} \right)_{{\text{k}}}^{{{\text{UN}}}} $$

(8)

As illustrated in Fig. 2, the remaining portion represents the avoidable (${\dot{E}}_{{\text{D}}}^{{\text{AV}}}$) part of exergy destruction, as stated as follows:

$$ \dot{E}_{{\text{D,k}}} = \dot{E}_{{\text{D,k}}}^{{{\text{AV}}}} + \dot{E}_{{\text{D,k}}}^{{{\text{UN}}}} $$

(9)

Splitting the exergy destruction of component k in the MAC system into unavoidable (${\dot{E}}_{{\text{D}}}^{{\text{UN}}}$) and avoidable (${\dot{E}}_{{\text{D}}}^{{\text{AV}}}$) is crucial for realistically assessing a component’s potential to improve thermodynamic efficiency [32]. To calculate the unavoidable exergy destruction in two different capacities, as detailed in Table 2, the exergy destruction rate of component ${\left(\frac{{\dot{E}}_{D}}{{\dot{E}}_{P}}\right)}_{{\text{k}}}^{{\text{UN}}}$ is determined. The isentropic assumptions for the MAC process, particularly under critical operation temperature conditions, are based on operational experience. These include the assumption that that the inlet temperatures of Compressor2 and Compressor3 match the inlet temperature of Compressor1 due to complete stage cooling. These isentropic assumptions align closely with those in Dragan’s work [33]. The notable difference between the theoretical and unavoidable isentropic efficiencies in compressors arises because the compressor outlet temperature under theoretical conditions is lower than the normal operating value, and higher than the normal operating value under unavoidable conditions. The discrepancy in unavoidable isentropic efficiencies of compressors is attributed to varying working conditions such as pressure ratio and acceptable temperature values. In essence, when energy is transferred to the fluid as pressure and kinetic energy, the temperature should not rise, which encompasses theoretical conditions. However, any problems originating from the equipment or the general system cause this energy to convert into heat, creating unavoidable conditions. Additionally, the performance maps of the MAC are illustrated in Figs. 3(a) and (b).

Table 2 Assumptions for the theoretical and unavoidable operating conditions of the MAC system at flow rates of 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹

Fig. 3

MAC system performance maps: a flow-discharge pressure map, b flow-coupling power map [34]

To better understand the relationship between the components of the system, the exergy destruction is divided into endogenous ($\dot{E}_{{\text{D}}}^{{{\text{EN}}}}$), exogenous ($\dot{E}_{{\text{D}}}^{{{\text{EX}}}}$), avoidable ($\dot{E}_{{\text{D}}}^{{{\text{AV}}}}$) and unavoidable ($\dot{E}_{{\text{D}}}^{{{\text{UN}}}}$) parts. Subsequently, as illustrated in Fig. 2, these are further examined in four distinct categories: avoidable/ endogenous ($\dot{E}_{{\text{D,k}}}^{{\text{AV,EN}}}$), avoidable/ exogenous ($\dot{E}_{{\text{D,k}}}^{{\text{AV,EX}}}$), unavoidable/ endogenous ($\dot{E}_{{\text{D,k}}}^{{\text{UN,EN}}}$), and unavoidable/ exogenous ($\dot{E}_{{\text{D,k}}}^{{\text{UN,EX}}}$). The calculation of these categories is performed by subtracting values between the specified groups [32]. The determination of the avoidable exergy destruction for each component aids in developing effective strategies to optimize energy consumption within the process. Therefore, the calculation of the unavoidable part of the endogenous exergy destruction rate for the kth component in the system can be achieved as follow.

$$ \dot{E}_{{\text{D,k}}}^{{\text{UN,EN}}} = \dot{E}_{{\text{P,k}}}^{{{\text{EN}}}} \left( {\frac{{\dot{E}_{{\text{D}}} }}{{\dot{E}_{{\text{P}}} }}} \right)_{{\text{k}}}^{{{\text{UN}}}} $$

(10)

The irreversibility associated with the k component in this system, which arises from technological and economic limitations, is a significant aspect of its operation. Equation 11) is utilized for calculating this parameter. It is assumed that the kth component operates under unavoidable conditions due to these limitations, while other components in the system are considered to be operating under ideal conditions.

$$ \dot{E}_{{\text{D,k}}}^{{\text{UN,EX}}} = \dot{E}_{{\text{D,k}}}^{{{\text{UN}}}} - \dot{E}_{{\text{D,k}}}^{{\text{UN,EN}}} $$

(11)

Based on the calculated value of $\dot{E}_{{\text{D,k}}}^{{\text{UN,EN}}}$, the endogenous and exogenous parts of the avoidable exergy destruction for component k can, respectively, be calculated as follows.

$$ \dot{E}_{{\text{D,k}}}^{{\text{AV,EN}}} = \dot{E}_{{\text{D,k}}}^{{{\text{EN}}}} - \dot{E}_{{\text{D,k}}}^{{\text{UN,EN}}} $$

(12)

$$ \dot{E}_{D,k}^{AV,EX} = \dot{E}_{D,k}^{EX} - \dot{E}_{D,k}^{UN,EX} $$

(13)

By increasing the efficiency and structural optimization of a system component, it is possible to prevent these exergy destruction parts. The values $\dot{E}_{{\text{D,k}}}^{{\text{UN,EN}}}$, $\dot{E}_{{\text{D,k}}}^{{\text{UN,EX}}}$, $\dot{E}_{{\text{D,k}}}^{{\text{AV,EN}}}$. and $\dot{E}_{{\text{D,k}}}^{{\text{AV,EX}}}$. are the main indicators obtained from the enhanced exergy analysis. This analysis provides more useful information compared to traditional methods, thereby aiding designers iroving the energy efficiency of a process knowingly. Enhanced exergy analysis is a strategic method for evaluating energy systems. The effectiveness of enhanced exergy analysis can be determined by the modified exergy efficiency, as calculated by [32]

$$ \varepsilon_{{{\text{modified}}}} = \frac{{\dot{E}_{{\text{P,k}}} }}{{\dot{E}_{{\text{F,k}}} - \dot{E}_{{\text{D,k}}}^{{{\text{UN}}}} - \dot{E}_{{\text{D,k}}}^{{\text{AV,EX}}} }} $$

(14)

While the study meticulously analyzes the exergetic performance of the MAC system using both conventional and enhanced exergy analyses, several inherent limitations and shortcomings must be acknowledged. Firstly, the analysis assumes a constant composition of process air and water throughout the system, which may not accurately reflect real-world variations and chemical reactions that could affect the system’s performance. Secondly, the potential and kinetic energies, along with exergy exchanges, are considered negligible, potentially overlooking significant factors in a dynamic industrial environment. Furthermore, the study relies on specific dead state values for water and air, which, while standardized, may not accurately represent local environmental conditions. The use of real data from the distributed control system (DCS) provides a robust basis for analysis; however, this data is limited to specific operational conditions and may not capture the full range of variations and anomalies encountered in practical scenarios. Additionally, the precision of the endogenous part of exergy destruction in enhanced exergy analysis poses a challenge, as it heavily influences the results and is difficult to determine accurately. Finally, while the study provides valuable insights into the exergy efficiency of the MAC system, it does not fully address the technological and economic constraints that limit practical applications, such as material availability, cost, and production methods. These factors are critical in realistically assessing the potential for improvements in thermodynamic efficiency and the practical implementation of optimization strategies.

Results and discussion

In this study, the thermodynamic performance of turbo/centrifugal type MAC system in the ASU of the iron-steel industry has been meticulously examined for two different airflow rates: 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹. As shown schematically in Fig. 1, actual data from the MAC system’s measurement points were collected under these two different airflow conditions, utilizing the Distributed Control System (DCS) program. The temperature, pressure, and mass flow rate values at these points for the specified airflow rates are listed in Table 3 and 4, respectively. Additionally, specifications of the devices measuring these parameters at the measurement points are provided in Appendix 1. It is noted that the measuring points on the same pipeline (2–3; 4–5; 6–7; 8–9) exhibit different values from each other. This variation is attributed to changes in air temperature due to heat transfer from the surroundings and air pressure variations in the system caused by friction loss in the pipeline. Furthermore, the maximum pressure ratio of the stages is 2.3, which does not exceed the industrial standard of 3.0 [35, 36]. The electricity consumption of the compressor is also continuously monitored through this system. It was determined that the electricity consumption of the compressor is 17,958 kW and 18,985 kW for airflow rates of 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹, respectively. Consequently, when the measured values in Table 3 and 4 are applied to the equations listed in Table 1, the unit exergy rate for each measured point in the MAC system is calculated (as shown in the last column of Table 3 and 4).

Table 3 Measurement points’ values for the MAC system at a flow rate of 210,000 Nm³ h⁻¹

Table 4 Measurement points’ values for the MAC system at a flow rate of 240,000 Nm³ h⁻¹

The conventional exergy analysis results for the MAC system are presented in Fig. 4, detailing two district airflow rates of 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹. For the airflow rate of 210,000 Nm³ h⁻¹, as indicated in Fig. 4(c), the total exergy input into the system is 17,958.00 kW. Of this, 1,635.82 kW (9.1%) accounts for exergy loss, and 15,501.44 kW (86.3%) is due to the exergy destruction in the components, resulting in a net exergy output of 820.74 kW, which is 4.6% of the total incoming exergy. According to Figs. 4(a) and (b), the most efficient components at this airflow rate are Cooler1 with 96.5% efficiency, followed by Cooler2 at 92.6%, and Compressor3 at 21.4%. On the other hand, the components with the highest exergy destruction are Compressor1 with 50.6% (7.8 MW), Compressor2 with 28.2% (4.4 MW), and Compressor3 with 18.4% (2.9 MW), indicating Compressor1 as the top priority for improvement.

Fig. 4

Results of the conventional exergy analysis for the MAC at flow rates of 210.000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹: a compressors (stages), b cooling system, and c overall system

In contrast, at an airflow rate of 240,000 Nm³ h⁻¹, as seen in Fig. 4(c), the system receives 18,985 kW of exergy, with 2,017.24 kW (10.6%) lost and 15,840.68 kW (83.4%) destroyed component-related processes. The system generates 1,127.08 kW of exergy, constituting 5.9% of the total input. Figure 4(a) and (b) reveals the highest exergy destruction again occurs in Compressor1 at 51.1% (8.1 MW), followed by Compressor2 at 28.3% (4.5 MW), and Compressor3 at 18.5% (2.9 MW). The top three most efficient equipments at this higher airflow rate are Cooler1 and Cooler2, both at 94.2%, and the Pump at 38.8%, as shown in Fig. 4(b). These figures illustrate that although the power drawn by the system increases, the component-related exergy destruction rate does not escalate proportionally with the increased airflow rate. is the system shows a rise of 339 kW in exergy destruction and 381 kW in exergy loss for an additional 1,027 kW of power, suggesting that the system operates more effectively at the higher airflow rate.

So far, the conventional exergy analysis conducted has proven insufficient in identifying the specific reasons for exergy destructions within the system. To accurately determine whether the exergy destruction in a component is due to the component itself or the operation of other components, as well as to identify potential areas for improvement, enhanced exergy analysis is essential. Relying solely on the results of the conventional exergy analysis for making changes could lead to inefficient use of time and resources. For the enhanced exergy analysis of the MAC system at two different airflow rates, the assumptions regarding theoretical and unavoidable conditions, as outlined in Table 2, are employed. These include the isentropic and mechanical loss percentages of the system, as well as the temperature and pressure losses of the coolant and the mechanical and shaft losses of the electric motor. Operating the system under these theoretical and unavoidable conditions is critical to ensure the accuracy and effectiveness of the enhanced exergy analysis.

When applying enhanced exergy analysis to the MAC system of the ASU in an iron-steel industry for both airflow rates, the exergy destruction of the system components is split into endogenous, exogenous, unavoidable, and avoidable parts, with further detailed analysis. Consequently, the results of this enhanced exergy analysis for airflow rates of 210,000 Nm³/h and 240,000 Nm³/h are given in Figs. 5 and 6, respectively. This approach provides a comprehensive understanding of how each component contributes to the overall exergy destruction and identifies potential areas for improvement within the system.

Fig. 5

Results of the enhanced exergy analysis for the MAC system at a flow rate of 210,000 Nm³ h⁻¹: a compressors (stages), and b cooling system

Fig. 6

Results of the enhanced exergy analysis for the MAC system at a flow rate of 240,000 Nm³ h⁻¹: a compressors (stages); b cooling system

According to the data presented in Fig. 5, of the total exergy destruction (15,501.44 kW) in the MAC system operating at an airflow rate of 210,000Nm³ h⁻¹, 11,201.39 kW (72.3%) is attributed to endogenous factors. In contrast, the remaining 4,300.05 kW (27.7%) is due to exogenous factors influenced by other components in the system. Notably, maintenance or revision interventions on Compressors 1, 2, and 3 can significantly reduce the endogenous exergy destruction rates, which are 6,729.76 kW, 2,983.50 kW, and 1,206.37 kW respectively, thereby enhancing the system’s efficiency (refer to column 2 of Fig. 5(a)). A large portion of this equipment’s exergy destruction is linked to their technology aspects. However, the exogenous exergy destruction in Compressor3, positioned at end of the process, is higher than its endogenous exergy destruction, primarily due to the exergy destructions in Compressors 1 and 2. The presence of exogenous exergy destruction in components like Cooler1, Cooler2, and Pump (as shown in Fig. 5(b)) is attributed to the selection of coolers with large capacities. These coolers are chosen not only to mitigate the temperature rise caused by the compression process but also to address issues related to contamination and wear in the heat exchanger.

In reference to column 8 of Figs. 5(a) and (b), a critical aspect in the further splitting process of component-related exergy destruction rate in the MAC system is the avoidable-endogenous part ($\dot{E}_{{\text{D,k}}}^{{\text{AV,EN}}}$). Specifically, Compressor1 stands out with the highest value in this category at 5,101.51 kW. It is followed by Compressor2 at 1,707.65 kW and Compressor3 at 762.00 kW. These results indicate that these three components should be prioritized for improvement. Furthermore, as observed in Fig. 5, all the unavoidable exergy destruction in the system, attributed to technological and economic constraints, is a result of endogenous exergy destruction caused by the interactions between the components during the process. The compressors, which suffer the most from unavoidable-endogenous exergy destruction, are significantly affected by the exergy destruction of the coolers. Therefore, reducing the temperature of the water from the Cooling Tower, that is, the water drawn by the pump, could be a beneficial strategy. Lastly, the analysis suggests that all endogenous exergy destruction in the system, influenced by factors such as the working environment and condition, can potentially be made avoidable through calculated interventions.

Figure 6 displays the results of the enhanced exergy analysis for the MAC system operating at an airflow rate of 240,000 Nm³ h⁻¹. According to the data in Fig. 6, 63.1% (10,076.81 kW) of the total exergy destruction (15,840.67 kW) within the system is attributed to endogenous causes, while the remaining 36.4% (5,763.86 kW) results from the impact on other components. As shown in column 2 of Fig. 6(a), retrofit applications to Compressors 1, 2, and 3 can reduce their endogenous exergy destruction rates, which are 6,560.5 kW, 2,585.79 kW, and 688.04 kW, respectively. This portion of exergy destruction arises from the components themselves. The endogenous exergy destructions in the compressors are mainly caused by friction losses during power transmission from the shaft to the compressor gears, the loss of air in the volume as the impeller imparts kinetic energy to the air, and the pressure drops in the air within the system.

Figure 6 shows that, in the entire system, 4,583.99 kW (28.9%) of the system’s total exergy destruction (15,840.67 kW) is avoidable, while the remaining 71.1% (11,256.69 kW) is unavoidable. This indicates that there is a significant potential for improvement, amounting to 28.9%. As depicted in columns 4 and 5 of Fig. 6(a), Compressor1 has the highest rate of avoidable exergy destruction at 2,524.39 kW. It is traced by the Compressor2 with 1,182.71 kW, and Compressor3 with 706.20 kW. Consequently, a large portion of the exergy destruction in all components is unavoidable, primarily due to technological and economic constraints. It is noted in column 8 of Fig. 6 that the endogenous exergy destruction caused by the components themselves is largely avoidable for all compressors. Specifically, the highest avoidable part of endogenous exergy destruction is observed in the Compressors 1, 2, and 3 with 4,966.82 kW, 1,018.76 kW, and 595.00 kW, respectively. This analysis suggests that the exergy destruction rate in other components like the Pump, and Coolers 1 and 2, can be reduced through technological improvements in the compressors.

When comparing the system states for airflow rates of 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹ as presented in Figs. 5 and 6, respectively, it is observed that with an increase in airflow rate by 2.2% from the former’s exergy destruction value, the latter’s value rises to 15,840.67 kW. An increase in airflow rate results in a decrease in the endogenous exergy destruction of all equipment. For example, the endogenous exergy destruction of Compressor1 decreases from its initial value of 6,729.76 kW to 6,560.51 kW at the higher airflow rate. Conversely, the exogenous exergy destruction increases with the higher airflow rate. This pattern is also evident in avoidable exergy destruction. For example, the avoidable exergy destruction of Compressor1 decreases from 2,973.52 kW to 2,524.39 kW. This decrease is attributed to the increase in air outlet temperature due to inefficiency in the compressor impeller during compression at higher airflow rates. As the airflow rate increases, a portion of the avoidable exergy destruction transitions into the unavoidable category.

Regarding to the data presented in Figs. 5 and 6, for avoidable-endogenous exergy destruction, the value in the initial case exceeds that in the subsequent case for all equipment, except for Coolers 1 and 2. A notable observation is evident for Coolers and Compressor2. For instance, the avoidable parts of the endogenous exergy destruction rate for Coolers 1 and 2 increases from 15.42 kW to 21.96 kW and from 38.50 kW to 41.22 kW, respectively, with the increase in airflow rate. This rise is attributed to the coolers’ capacity selection, which becomes more significant with higher airflow. The substantial decrease in the Compressor2’s exergy destruction is linked to its lower efficiency compared to other compressors and the corresponding increase in inflow and exergy input in the system. In contrast, there is a marked reduction in the Pump’s exergy destruction, which is primarily due to the increased cooling requirement caused by the airflow and the temperature rise in the Cooling Tower. As the airflow rate rises, the effect of the exergy destruction caused by the two coolers on the compressors intensifies, thereby reducing the avoidable part of the endogenous in the compressors.

Examining Figs. 5 and 6, a notable observation for the airflow rates of 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹ is that the values of avoidable-endogenous exergy destruction for Compressor1 are negative, being − 2,127.99 kW and − 2,442.44 kW, respectively. Additionally, at the airflow rate of 240,000 Nm³ h⁻¹, similar negative values are seen for Coolier2 and Pump, with − 17.90 kW and − 33.57 kW, respectively. Among these, Cooler2 has the smallest absolute value of avoidable-endogenous exergy destruction. Consequently, the optimization process should prioritize Cooler2. Despite the fact that the avoidable-endogenous exergy destruction rate in Compressor1 is higher than that of all other components, the absolute value of avoidable-exogenous exergy destruction in Compressor1 is significantly greater than that in Coolier2 and Pump. This indicates that exergy destruction in Compressor1 is more sensitive to the optimization of other components in the system.

In Fig. 7, the comparison of the system’s exergy efficiency for two different exergy analysis methods and two different airflow rates is presented for the MAC system. For this comparison, conventional exergy analysis was calculated in accordance with Eq. (4), while enhanced exergy analysis followed Eq. (14). The overall exergy analysis of the system incorporated the sum of product exergy and fuel exergy for each component, as applied to Eq. (4). When calculating the overall enhanced exergy efficiency of the system, product exergy, fuel exergy, unavoidable and avoidable exergy destructions of all components were collectively considered and applied to Eq. (14). As observed in Fig. 7, the system’s exergy efficiency at an airflow rate of 240,000Nm³ h⁻¹ is 25%, which is higher than the 21.3% efficiency at 210,000 Nm³ h⁻¹. This indicates that a higher airflow rate contributes to greater system exergy efficiency. Post maintenance and revision operations on the system components, the overall efficiency for the MAC system increases from 21.3% to 40.8% at 210,000 Nm³ h⁻¹, and from 25% to 80.7% at 240,000 Nm³ h⁻¹. Operating under enhanced exergy conditions could lead to an increase in exergy efficiency by 92% for 210,000 Nm³ h⁻¹ and by 222% for 240,000 Nm³ h⁻¹. Figure 7 also demonstrates that higher airflow rates offer more room for improvements in the system. Comparing data obtained from the two different analysis methods reveals that the exergy efficiency of the compressors improves as they approach the working capacity of the electric motor, which nominal capacity is 22,000 kW.

Fig. 7

Comparison of conventional and enhanced exergy analyses in terms of exergy efficiency for the MAC system, illustrated at airflow rates of 210,000 Nm³ h⁻¹ (in blue) and 240,000 Nm³ h.⁻¹ (in red)

Figure 8 illustrates the exergy efficiency of the MAC system components at an airflow rate of 210,000 Nm³ h⁻¹, comparing both conventional and enhanced exergy analysis methods. From this figure, it is evident that the exergy yields for the enhanced exergy analysis are consistently higher than those from the conventional analysis. The most significant difference is observed in Compressor3, with respective efficiencies of 21.4% and 50.6%, suggesting that Compressor3 offers the greatest potential for optimization among all components. Compressor2 and Pump also show notable differences. Additionally, at this airflow rate, the modified exergy efficiencies of Compressors 1, 2 and 3 are 14.86%, 34.05%, and 50.6%, respectively. As seen in Fig. 8, while the exergy efficiencies of Coolers 1 and 2 are the highest, the Pump exhibits the lowest efficiency. Figure 9 presents the variation in exergy efficiency for the system components at a higher airflow rate of 240,000Nm³ h⁻¹. Here, the disparity in exergy efficiencies between the two analyses is most pronounced in the Pump, showing 38.8% and 99.9% efficiencies. This significant difference is attributed to the reduction in air outlet temperature from the compressor, resulting from improvements in Compressor1, Compressor2, and Compressor3. Following these, Compressor3 and Compressor2 exhibit notable differences. At 240,000 Nm³ h⁻¹, the modified exergy efficiencies of Compressors 1, 2, and 3 are determined to be 18.81%, 36.96%, and 60.63%, respectively. This analysis highlights that higher airflow rates lead to more substantial improvements in the system, particularly in the compressor components.

Fig. 8

Variation in exergy efficiency of the MAC system components at an airflow rate of 210,000 Nm³ h.⁻¹

Fig. 9

Change in exergy efficiency of the MAC system components at an airflow rate of 240,000 Nm³ h.⁻¹

Figure 10 depicts the change in the modified exergy efficiency of the MAC system at the airflow rates of 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹. From this figure, it is apparent that the increase in airflow rate results in the most significant exergy efficiency improvement in the Pump, attributed to the enhanced cooling requirement due to higher airflow and the increased temperature in the Cooling Tower. Consequently, the exergy efficiencies of the Pump and Coolers 1 and 2 reach their maximum at 99.9%. However, the exergy efficiencies of the coolers remain unchanged. As shown in Fig. 10, the modified exergy efficiency for the compressors increases with the higher airflow rate. Specifically, for Compressor1, the efficiency rises from 14.8 to 18.8%, for Compressor2 from 34.0 to 36.9%, and for Compressor3 from 50.6 to 60.6% when the airflow rate increases from 210,000 Nm³ h⁻¹ to 240,000 Nm³ h⁻¹.

Fig. 10

Variation in modified exergy efficiency of the MAC system components at airflow rates of 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹, as evaluated by enhanced exergy analysis

As demonstrated in this study, applying enhanced exergy analysis to the system effectively reveals the causes of exergy destruction within equipment. This analysis guides users to make informed decisions for maintenance and revision of components. Typically, compressor manufacturers recommend an overhaul of these compressors every 5 years for efficient operation. Although this process is crucial, it often requires significant budgets due to high system parts and labor costs. By adopting the approach presented in this study, compressor revision specialists, manufacturers, system process engineers, and energy experts can easily pinpoint inefficiencies within specific system components and their causes. This method not only prevents excessive time and cost losses but also allows focusing on just the inefficient components needing chance. Moreover, inefficiencies identified by process engineers in an ongoing system study can be addressed earlier than the scheduled overhaul, depending on the system’s criticality and severity of the issue. This proactive approach helps in reducing exergy destructions and enhancing system efficiency. The data and methodology obtained from this study are applicable not only to centrifugal compressors used in power generation, chemical, ecological plants, ASUs, and petrochemical plants but also to multi-stage axial and reciprocating compressors in various other industries.

Conclusions

The Air separation unit (ASU), crucial for boosting production in the iron-steel industries globally, is the centerpiece of this study, which focuses on the thermodynamic performance of a three-stage Main Air Compressor (MAC) system and its components. This study encompasses both conventional and enhanced exergy analyses of the three-stage MAC at its most intensive working flow rates of 210,000 Nm³ h⁻¹ and 240,000 Nm³ h⁻¹. The enhanced exergy analysis, especially pertinent for this high-energy-consuming compressor, is utilized to discem the interplay among components and to pinpoint areas for enhancement. Additionally, this analysis enriches the comprehension of exergy destruction splitting process, thereby illuminating the interactions between system components and unveiling opportunities for improvement, consequently aiding in the optimization of the entire system. The outcomes of both conventional and enhanced exergy analyses are elaborated in a comparative manner for the two distinct capacities. Consequently, the study yielded the following key findings:

• At 210,000 Nm³ h⁻¹, the electricity consumption of the compressor was 17,958 kW, while at 240,000 Nm³ h⁻¹, it was 18,985 kW. These values highlight the system’s energy use under different operational conditions.

• The maximum pressure ratio of the stages was found to be 2.3, remaining within the industrial standard of 3.0. This suggests the system operates within acceptable pressure limits.

• The total exergy input for the system at 210,000 Nm³ h⁻¹ was 17,958 kW, with a net exergy output of 820.74 kW. At the higher airflow rate of 240,000 Nm³ h⁻¹, the system received 18,985 kW of exergy, with a net output of 1,127.08 kW. Comparatively, this shows an increase in both input and output at the higher rate.

• Enhanced exergy analysis revealed that endogenous factors accounted for 72.3% of exergy destruction at 210,000 Nm³ h⁻¹, whereas at 240,000 Nm³ h⁻¹, it was 63.1%. This indicates a shift in the source of exergy destruction with airflow variation.

• The highest avoidable exergy destruction was observed in Compressor1, indicating it as a primary target for improvements. This component showed significant potential for reducing energy wastage.

• Higher airflow rates lead to more substantial improvements, especially in compressor components. This suggests a correlation between airflow rate and system efficiency.

• The enhanced exergy analysis suggested that operating the system under theoretical and unavoidable conditions is crucial for accuracy and effectiveness. This highlights the importance of optimal operating conditions for energy efficiency.

• The effectiveness of enhanced exergy analysis in identifying inefficiencies and guiding maintenance decisions. It underscores the importance of this analytical approach for system optimization and cost-effective operations.

This study acts as a guide for compressor revision experts, manufacturers, system process engineers and energy specialists, providing insights into conducting exergy and efficiency assessments to boost system efficiency, not just in centrifugal compressors but also in other types of multi-stage compression systems. This study empowers these professionals to conduct analyses at the component level and to forecast the potential enhancements and productivity increases that can be achieved before and after system revisions.

Appendix 1

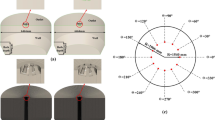
The measurement points at the inlet and outlet of the compressor stages, as well as those at the cooling water supply lines, are depicted in Fig. 1. Temperature and pressure are continuously monitored at these points. The temperature measurement devices used are known as PT100s, and the pressure measurement devices are referred to as transmitters, with their technical properties listed in Table 

Table 5 Technical properties of temperature and pressure measuring devices

5. Figure 

Fig. 11

Connection of a temperature and b pressure measuring devices to the system

11 shows the photographs illustrating how these measuring instruments are connected to the system.