Skip to main content
SpringerLink
Log in

Thermal study of Darcy–Forchheimer hybrid nanofluid flow inside a permeable channel by VIM: features of heating source and magnetic field

  • Published:
Journal of Thermal Analysis and Calorimetry Aims and scope Submit manuscript

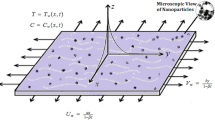
Abstract

The nanofluids extensively contribute to cope the new heat transport challenges facing by the engineering systems and industries including paint, ceramics, chemical, aerodynamics, electronics, and medical sciences, etc. Thus, the innovations in new nanoliquid models can be disregarded in light of broad applications spectrum. Therefore, the current work concerns with the thermal process of hybrid nanoliquid by adding the important physical phenomenon. The flow of bionanofluid is taken inside a uniform expanding/contracting channel. To increase the model novelty, the significant influence of Lorentz forces, porous media, and heating source is added in the problem formulation. The resultant bionanofluid model is then analyzed via VIM (variational iteration method) and provided a deep discussion. It is inspected that unvarying expansion/contraction in the range of \(\alpha = \, {1.0,2.0,3.0,4.0}\) and \(\alpha =-1.0,-2.0,-3.0,-4.0\), the bionanofluid attained maximum velocity about the central portion and in rest of the part it declines. However, due to increased viscosity of hybrid nanofluid, it reduced rapidly than conventional nanofluid. By increasing the permeability from 0.1 to 0.4, a rapid decrease in the fluid movement is observed. Further, the heat transmission progress reduced against the porous medium and Lorentz forces. The heat generation effects boosted the heating performance of the hybrid nanofluid. Moreover, the skin friction and heat transport rate are also discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data availability

The data that support the findings of this study are available within the article.

Abbreviations

\(\widetilde{u}, \widetilde{v}\) :

Velocity components

\(\widetilde{P}\) :

Pressure

\({\rho }_\text{b}\) :

Fluid density

\({\rho }_\text{hbnf}\) :

Density of hybrid nanofluid

\({k}_\text{b}\) :

Thermal conductivity of the basic fluid

\({k}_\text{hbnf}\) :

Thermal conductivity of hybrid nanofluid

\({\mu }_\text{b}\) :

Dynamic of basic fluid

\({\mu }_\text{hbnf}\) :

Dynamic viscosity of hybrid nanofluid

\(\widetilde{T}\) :

Fluid temperature

\({\sigma }_\text{b}\) :

Electrical conductivity of basic fluid

\({\sigma }_\text{hbnf}\) :

Electrical conductivity of hybrid nanofluid

\({\phi }_{1}, {\phi }_{2}\) :

Nanoparticles mass concentration

\(M\) :

Hartmann number

\({D}_\text{a}\) :

Darcy number

\({F}_\text{r}\) :

Forchheimer number

\({R}_\text{e1}\) :

Reynolds number

\({P}_\text{r}\) :

Prandtl number

\(Q\) :

Heat generation number

\({C}_\text{Fl}\) :

Skin friction at the lower plate

\({C}_\text{Fu}\) :

Skin friction at the upper plate

\({N}_\text{ul}\) :

Nusselt number at the lower plate

\({N}_\text{up}\) :

Nusselt number at the upper plate

References

  1. Ali B, Jubair S, Al-Essa LA, Mahmood Z, Al-Bossly A, Alduais FS. Boundary layer and heat transfer analysis of mixed convective nanofluid flow capturing the aspects of nanoparticles over a needle. Mater Today Commun. 2023;35. https://doi.org/10.1016/j.mtcomm.2023.106253.

  2. Bilal A, Duraihem FZ, Sidra J, Alqahtani H, Yagoob B. Analysis of Interparticle spacing and nanoparticle radius on the radiative alumina based nanofluid flow subject to irregular heat source/sink over a spinning disk. Material Today Commun. 2023. https://doi.org/10.1016/j.mtcomm.2023.106729.

    Article  Google Scholar 

  3. Ali B, Mishra NK, Rafique K, Jubair S, Zafar M, Eldin SM. Mixed convective flow of hybrid nanofluid over a heated stretching disk with zero-mass flux using the modified Buongiorno model. Alexandria Eng J. 2023;83–96.

  4. Mustafa M, Mushtaq A, Hayat T, Ahmad B. Nonlinear radiation heat transfer effects in the natural convective boundary layer flow of nanofluid past a vertical plate: a numerical study. PLoS ONE. 2014;9. https://doi.org/10.1371/journal.pone.0103946.

  5. Hosseinzadeh K, Amiri AJ, Ardahaie SS, Ganji DD. Effect of variable lorentz forces on nanofluid flow in movable parallel plates utilizing analytical method. Case Stud Thermal Eng. 2017;10. 595–10.

  6. Adnan. Heat transfer inspection in [(ZnO-MWCNTs)/water-EG(50:50)]hnf with thermal radiation ray and convective condition over a Riga surface. Waves Random Complex Media. 2022. https://doi.org/10.1080/17455030.2022.2119300.

  7. Alharbi KAM, Adnan, A. M. Galal. Novel magneto-radiative thermal featuring in SWCNT–MWCNT/C2H6O2–H2O under hydrogen bonding. Int J Mod Phys B. 2023. https://doi.org/10.1142/S0217979224500176.

  8. Rafique k, Mahmood Z, Alqahtani H, Eldin SM. Various nanoparticle shapes and quadratic velocity impacts on entropy generation and MHD flow over a stretching sheet with joule heating. Alexandria Eng J. 2023. vol. 71.147–59.

  9. Bilal A, Jubair S, Fathima D, Akhter A, Khadija K, Zafar M. MHD flow of nanofluid over moving slender needle with nanoparticles aggregation and viscous dissipation effects. Sci Prog. 2023. https://doi.org/10.1177/00368504231176151.

    Article  Google Scholar 

  10. Mishra NK, Adnan, Sarfraz G, Bani-Fwaz MZ, Eldin SM. Dynamics of Corcione nanoliquid on a convectively radiated surface using Al2O3 nanoparticles. J Thermal Anal Calorimetry. 2023. https://doi.org/10.1007/s10973-023-12448-y.

  11. Bhatti MM, Sait SM, Ellahi R, Sheremet MA, Oztop H. Thermal analysis and entropy generation of magnetic Eyring-Powell nanofluid with viscous dissipation in a wavy asymmetric channel. Int J Numer Methods Heat Fluid Flow. 2023;33:1609–36.

  12. Zhang L, Tariq N, Bhatti MM. Study of nonlinear quadratic convection on magnetized viscous fluid flow over a non-Darcian circular elastic surface via spectral approach. J Taibah Univ Sci. 2023. https://doi.org/10.1080/16583655.2023.2183702.

    Article  Google Scholar 

  13. Kumar NM, Adnan, Sohail MU, Hassan AM. Thermal analysis of radiated (aluminum oxide)/water through a magnet based geometry subject to Cattaneo-Christov and Corcione’s Models. Case Stud Thermal Eng. 2023;49. https://doi.org/10.1016/j.csite.2023.103390.

  14. Nidhish NM, Adnan, Rahman KU, Fwaz MZB. Investigation of blood flow characteristics saturated by graphene/CuO hybrid nanoparticles under quadratic radiation using VIM: study for expanding/contracting channel. Sci Rep. 2023;13. https://doi.org/10.1038/s41598-023-35695-3.

  15. Madhukesh JK, Ramesh GK, Roopa GS, Prasannakumara BC, Shah NA, Yook SJ. 3D flow of hybrid nanomaterial through a circular cylinder: saddle and nodal point aspects. Mathematics. 2022;10. https://doi.org/10.3390/math10071185.

  16. Gowda RJP, Rauf A, Kumar RN, Prasannakumara BC, Shehzad SA. Slip flow of Casson–Maxwell nanofluid confined through stretchable disks. Ind J Phys. 2022; 96:2041–49.

  17. Kumar RN, Suresha S, Gowda RJP, Megalamani SB, Prasannakumara BC. Exploring the impact of magnetic dipole on the radiative nanofluid flow over a stretching sheet by means of KKL model. Pramana. 2021;95. https://doi.org/10.1007/s12043-021-02212-y.

  18. Murtaza S, Kumam P, Ahmad KZ, Ramzan M, Ali I, Saeed A. Computational simulation of unsteady squeezing hybrid nanofluid flow through a horizontal channel comprised of metallic nanoparticles. J Nanofluids. 2023;12:1327–34.

  19. Khan N, Ali F, Ahmad Z, Murtaza S, Ganie AH, Khan I, Eldin SM. A time fractional model of a Maxwell nanofluid through a channel flow with applications in grease. Sci Rep. 2023;13. https://doi.org/10.1038/s41598-023-31567-y.

  20. Ali F, Ahmad Z, Arif M, Khan I, Nisar K. a time fractional model of generalized couette flow of couple stress nanofluid with heat and mass transfer: applications in engine oil. IEEE Access. 2020. https://doi.org/10.1109/ACCESS.2020.3013701.

    Article  PubMed  Google Scholar 

  21. Bano A, Dawood A, Rida, Saira F, Malik A, Alkholief M, Ahmad HMA, Ahmad Z, Bazighifan O. Enhancing catalytic activity of gold nanoparticles in a standard redox reaction by investigating the impact of AuNPs size, temperature and reductant concentrations. Sci Rep. 2023;13. https://doi.org/10.1038/s41598-023-38234-2.

  22. Murtaza S, Zubair A, Ali IE, Akhtar Z, Tchier F, Ahmad H, Yao SW. Analysis and numerical simulation of fractal-fractional order non-linear couple stress nanofluid with cadmium telluride nanoparticles. J King Saud Univ Sci. 2023;35. https://doi.org/10.1016/j.jksus.2023.102618.

  23. Hasin F, Ahmad Z, Ali F, Khan N, Khan I, Eldin SM. Impact of nanoparticles on vegetable oil as a cutting fluid with fractional ramped analysis. Sci Rep. 2023. https://doi.org/10.1038/s41598-023-34344-z.

    Article  PubMed  PubMed Central  Google Scholar 

  24. Sharma A, Dubewar AV. MHD flow between two parallel plates under the influence of inclined magnetic field by finite difference method. Int J Innov Technol Explor Eng. 2019;8. https://doi.org/10.35940/ijitee.L3643.1081219.

  25. Abbas W, Magdy MM. Heat and mass transfer analysis of nanofluid flow based on Cu, Al2O3, and TiO2 over a moving rotating plate and impact of various nanoparticle shapes. Math Probl Eng. 2020. https://doi.org/10.1155/2020/9606382.

    Article  Google Scholar 

  26. Ali K, Ahmad A, Ahmad S, Nisar KS, Ahmad S. Peristaltic pumping of MHD flow through a porous channel: biomedical engineering application. Waves Random Complex Media. 2023. https://doi.org/10.1080/17455030.2023.2168085.

    Article  Google Scholar 

  27. Zhang X, Yang D, Kashif A, Faridi AA, Ahmad S, Jamshed W, Raezah AA, El Din SM. Successive over relaxation (SOR) methodology for convective triply diffusive magnetic flowing via a porous horizontal plate with diverse irreversibilities. Ain Shams Eng J. 2023;14. https://doi.org/10.1016/j.asej.2023.102137.

  28. Zainal NA, Nazar R, Naganthran K, Pop I. Stability analysis of MHD hybrid nanofluid flow over a stretching/shrinking sheet with quadratic velocity. Alexandria Eng J. 2020;60. 915–26.

  29. Akbar S, Hussain A. The Influences of squeezed inviscid flow between parallel plates. Math Probl Eng. 2021. https://doi.org/10.1155/2021/6647708.

    Article  Google Scholar 

  30. Mishra NK, Khalid AMA, Rahman KU, Adnan A, Eldin SM, Fwaz MZB. Investigation of improved heat transport featuring in dissipative ternary nanofluid over a stretched wavy cylinder under thermal slip. Case Stud Thermal Eng. 2023;48. https://doi.org/10.1016/j.csite.2023.103130.

  31. Ahmad S, Ashraf M, Ali K. Simulation of thermal radiation in a micropolar fluid flow through a porous medium between channel walls. J Thermal Anal Calorimetry. 2021;941–53.

  32. AL-Zahrani AA, Adnan A, Mahmood I, Khaleeq RU, Mutasem ZBF, Tag-Eldin E. Analytical study of (Ag–graphene)/blood hybrid nanofluid influenced by (platelets-cylindrical)nanoparticles and joule heating via VIM. ACS Omega. 2023;8:19926–38.

  33. Kashif A, Ahmad S, Nisar KS, Faridi AA, Ashraf M. Simulation analysis of MHD hybrid CuAl2O3/H2O nanofluid flow with heat generation through a porous media. Int J Energy Res. 2021. https://doi.org/10.1002/er.7016.

    Article  Google Scholar 

  34. Noor AAM, Shafie S, Admon MA. Heat and mass transfer on MHD squeezing flow of Jeffrey nanofluid in horizontal channel through permeable medium. PLOS One. 2021;16. https://doi.org/10.1371/journal.pone.0250402.

  35. Hussain A, Alshbool MH, Abdussattar A, Rehman A, Ahmad H, Nofal T, Khan MR. A computational model for hybrid nanofluid flow on a rotating surface in the existence of convective condition. Case Stud Thermal Eng. 2021;26. https://doi.org/10.1016/j.csite.2021.101089.

  36. Waqas H, Farooq U, Naseem R, Hussain S, Alghamdi M. Impact of MHD radiative flow of hybrid nanofluid over a rotating disk. Case Stud Thermal Eng. 2021;26. https://doi.org/10.1016/j.csite.2021.101015.

  37. Ahammad NA, Badruddin IA, Kamangar S, Khaleed HMT, Saleel CS, Mahila TMI. Heat transfer and entropy in a vertical porous plate subjected to suction velocity and MHD. Entropy. 2021. https://doi.org/10.3390/e23081069.

    Article  PubMed  PubMed Central  Google Scholar 

  38. Adnan A, Abbas W, Sayed ME, Mutasem ZBF. Numerical investigation of non-transient comparative heat transport mechanism in ternary nanofluid under various physical constraints. AIMS Math. 2023;8:15932–49.

  39. Abdullah MR, Khawatreh SA. Unsteady MHD flow and heat transfer through porous medium between parallel plates with periodic magnetic field and constant pressure gradient. Int J Eng Res Technol. 2021;14:782–87

  40. Rashad AM, Nafe MA, Eisa DA. Heat Generation and Thermal Radiation Impacts on Flow of Magnetic Eyring–Powell Hybrid Nanofluid in a Porous Medium. Arab J Sci Eng. 2022. vol. 48. 939–52.

  41. Abdulkhaliq KAM, Adnan A, Akgul A. Investigation of Williamson nanofluid in a convectively heated peristaltic channel and magnetic field via method of moments. AIP Adv. 2023;13. https://doi.org/10.1063/5.0141498.

  42. Yaseen M, Rawat SK, Shafiq A, Kumar M, Nonlaopon K. Analysis of heat transfer of mono and hybrid nanofluid flow between two parallel plates in a darcy porous medium with thermal radiation and heat generation/absorption. Symmetry. 2022. https://doi.org/10.3390/sym14091943.

    Article  Google Scholar 

  43. Alhowaity A, Bilal M, Hamam H, Alqarni MM, Mukdasai K, Aatif A. Non-Fourier energy transmission in power-law hybrid nanofluid flow over a moving sheet. Sci Rep. 2022. https://doi.org/10.1038/s41598-022-14720-x.

    Article  PubMed  PubMed Central  Google Scholar 

  44. Muhammad B, Ali A, Hejazi HA, Mahmuod SR. Numerical study of an electrically conducting hybrid nanofluid over a linearly extended sheet. J Appl Math Mech. 2022. https://doi.org/10.1002/zamm.202200227.

    Article  Google Scholar 

  45. Alqahtani AM, Bilal M, Usman M, Alsenani TR, Samy RM, Ali A. Heat and mass transfer through MHD Darcy Forchheimer Casson hybrid nanofluid flow across an exponential stretching sheet. J Appl Math Mech. 2023. https://doi.org/10.1002/zamm.202200213.

    Article  Google Scholar 

  46. Haq I, Bilal M, Ahammad NA, Ghoneim ME, Weera W. Mixed convection nanofluid flow with heat source and chemical reaction over an inclined irregular surface. ACS Omega. 2022;30477–85.

  47. Abbas N, Shatanawi W, Shatnawi TAM. Transportation of nanomaterial Maxwell fuid fow with thermal slip under the efect of Soret-Dufour and second-order slips: nonlinear stretching. Sci Rep. 2023. https://doi.org/10.1038/s41598-022-25600-9.

    Article  PubMed  PubMed Central  Google Scholar 

  48. Zeighami LAF, Federico V. Efective forchheimer coefcient for layered porous media. Transp Porous Media. 2022. https://doi.org/10.1007/s11242-022-01815-2.

    Article  Google Scholar 

  49. Elbashbeshy EMA, Asker HG. Fluid flow over a vertical stretching surface within a porous medium filled by a nanofluid containing gyrotactic microorganisms. Eur Phys J Plus. 2022. https://doi.org/10.1140/epjp/s13360-022-02682-y.

    Article  Google Scholar 

  50. Adnan A, Alharbi KAM, Bani-Fwaz MZ, Eldin SM, Yassen MF. Numerical heat performance of TiO2/Glycerin under nanoparticles aggregation and nonlinear radiative heat flux in dilating/squeezing channel. Case Stud Therm Eng. 2023;41. https://doi.org/10.1016/j.csite.2022.102568.

  51. Nadeem A, Adnan A, Sayed ME. Heat transport mechanism in glycerin-titania nanofluid over a permeable slanted surface by considering nanoparticles aggregation and Cattaneo Christov thermal flux. Sci Prog. 2023. https://doi.org/10.1177/00368504231180032.

    Article  PubMed  PubMed Central  Google Scholar 

  52. Kumar RN, Gowda RJP, Alam MM, Ahmad I, Mahrous YM, Gorji MR, Prasannakumara BC. Inspection of convective heat transfer and KKL correlation for simulation of nanofluid flow over a curved stretching sheet. Int Commun Heat Mass Transf. 2021. https://doi.org/10.1016/j.icheatmasstransfer.2021.105445.

    Article  Google Scholar 

  53. Kumar RSV, Alhadhrami A, Gowda RJP, Kumar RN, Prasannakumara BC. Exploration of arrhenius activation energy on hybrid nanofluid flow over a curved stretchable surface. ZAMM. 2021. https://doi.org/10.1002/zamm.202100035.

    Article  Google Scholar 

  54. Rekha MB, Sarris IE, Madhukesh JK, Prasannakumara BC. Activation energy impact on flow of aa7072-aa7075/water-based hybrid nanofluid through a cone, wedge and plate. Micromachines. 2022;13. https://doi.org/10.3390/mi13020302.

  55. Saeed A, Tassaddiq A, Khan A, Jawad M, Deebani W, Shah Z, Islam S. Darcy–Forchheimer MHD hybrid nanofluid flow and heat transfer analysis over a porous stretching cylinder. Coatings. 2020;10. https://doi.org/10.3390/coatings10040391.

  56. Majdalani J, Zhou C, Dawson CA. Two-dimensional viscous flow between slowly expanding or contracting walls with weak permeability. J Biomech. 2002;35:1399–03.

  57. Shi QH, Hamid A, Khan MI, Kumar RN, Gowda RJP, Prasannakumara BC, Shah NA, Khan SU, Chung JD. Numerical study of bio-convection flow of magneto-cross nanofluid containing gyrotactic microorganisms with activation energy. Sci Rep. 2021. https://doi.org/10.1038/s41598-021-95587-2.

    Article  PubMed  PubMed Central  Google Scholar 

Download references

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through large group Research Project under grant number RGP2/16/44.

Author information

Authors and Affiliations

  1. Department of Mathematics, Mohi-ud-Din Islamic University, Nerian Sharif, 12080, AJ&K, Pakistan

    Khaleeq ur Rahman &  Adnan

  2. Basic Science Department, College of Science and Theoretical Studies, Saudi Electronic University, 11673, Riyadh, Saudi Arabia

    Nidhish Kumar Mishra

  3. Department of Chemistry, College of Science, King Khalid University, P. O. Box 9004, 61413, Abha, Saudi Arabia

    Mutasem Z. Bani-Fwaz

Authors
  1. Khaleeq ur Rahman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Adnan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nidhish Kumar Mishra
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mutasem Z. Bani-Fwaz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Adnan.

Ethics declarations

Conflict of interest

There is no financial/competing interest regarding the publication of this work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahman, K.u., Adnan, Mishra, N.K. et al. Thermal study of Darcy–Forchheimer hybrid nanofluid flow inside a permeable channel by VIM: features of heating source and magnetic field. J Therm Anal Calorim 148, 14385–14403 (2023). https://doi.org/10.1007/s10973-023-12611-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10973-023-12611-5

Keywords

Search

Navigation