Introduction

The classical theory for solid state transformations developed by Kolmogorov [1] and, independently, by Johnson and Mehl [2], and Avrami [3] (KJMA theory) is strictly valid for polymorphic transformations, under isothermal conditions, and processes governed by random nucleation and non-decelerated growth of crystals, which, in addition, must share a common orientation [4, 5].

This theory correlates the actual transformed fraction, \(X\), with an extended transformed fraction, \({X}^{*}\), that is calculated as the transformed fraction that would occur if any impingement between growing crystals is neglected. In isothermal conditions, assuming power laws for nucleation rate and linear crystal growth, this extended fraction is expressed as follows:

$$X^{ * } = (kt)^{\rm{n}}$$
(1)

where \(k\) is a frequency factor, \(t\) is the time from the onset of the process, and \(n\) is the Avrami exponent.

The requirement of non-decelerated growth and common orientation is needed to avoid the artifacts due to overgrowth and phantom nuclei (virtual nuclei that statistically would appear in an already transformed region). These phantom nuclei grow faster than the crystal in which they appear, and they can overcome the surface of that crystal, statistically leading to an artificial overgrowth [4, 6, 7]. In a similar way, overgrowth can occur in processes with anisotropic growth when the crystal orientation is different between crystals. KJMA theory considers geometrical impingement only as the overlapped regions between growing crystals. However, as extended fraction allows crystals to cross each other, the growth beyond the intersected crystal is not blocked [4]. Therefore, Kolmogorov originally obtained two solutions for the Avrami exponent: \(n=3\), for saturation of nucleation sites at \(t=0\) and interface controlled growth (constant linear growth) and \(n=4\), for constant nucleation rate and interface controlled growth [8].

The key concept in the classical KJMA theory is thus the definition of the extended transformed fraction \({X}^{*}\), which corresponds to the theoretical transformed fraction in the absence of geometrical impingement. This magnitude continuously increases beyond 1 but is related to the actual transformed fraction, \(X\), statistically as follows:

$$\frac{\rm{d}X}{\rm{d}{X}^{*}}=1-X$$
(2)

which leads to:

$$X=1-\text{exp}\left(-{X}^{*}\right)$$
(3)

These relations are valid whether the regime is isothermal or non-isothermal. The calculation of \({X}^{*}\) is easy once the laws governing the rate of nucleation and growth are assumed, and the overlapping between transformed regions is neglected:

$${X}^{*}\left(t\right)=\underset{{t}_{0}}{\overset{t}{\int }}I\left(T,\tau \right)V\left(\tau ,t\right)\rm{d}\tau$$
(4)

where \(I\left(T,\tau \right)=\text{d}N/\text{d}\tau\) is the nucleation rate (\(N\left(\tau \right)\), number of nuclei per unit volume at time \(\tau\)), which depends on the temperature, \(T\) and \(V\left(\tau ,t\right)\), the volume, at time \(t\), of the transformed region nucleated at time \(\tau\). This volume can be calculated as follows:

$$V\left( {\tau ,t} \right) = \frac{{4\pi }}{3}\left[ {r^{*} \left( \tau \right) + \int\limits_{\tau }^{t} {u\left( {t',T} \right)\rm{d}t'} } \right]^{3}$$
(5)

In the equation above, the transformed regions are considered spherical with \({r}^{*}\) the critical radius of the nuclei (\({r}^{*}\ll\) and can be neglected) and \(u\left( {t^{\prime},T} \right) = \frac{\text{d}r}{{\text{d}t^{\prime}}}\) the linear growth rate. Assumed a constant nucleation rate and an interface controlled growth, both \(I\left(t,T\right)=\mathrm{d}N/\mathrm{d}t={I}_{0}\left(T\right)\) and \(u\left(t,T\right)={u}_{0}\left(T\right)\) are only dependent on temperature. For isothermal regimes, Eq. (1) is obtained with \(n=4\).

In case of non-isothermal conditions, for constant nucleation rate and interface controlled growth processes, both quantities are assumed to follow an Arrhenius like behavior: \(I\left(T\right)={{I}_{0}e}^{-\frac{{Q}_{\rm{n}}}{{\rm{k}}_{\rm{B}}\rm{T}}}\) and \(u\left(T\right)={u}_{0}{e}^{-\frac{{Q}_{\rm{g}}}{{\rm{k}}_{\rm{B}}\rm{T}}}\). Therefore, Eq. (5) can be written for a constant heating rate, \(\beta =\text{d}T/\text{d}t\), as follows:

$$X^{*} \left( t \right) = C\int\limits_{{T_{0} }}^{T} {\exp \left( { - \frac{{Q_{\rm n} }}{{k_{\rm{B}} \theta }}} \right)\left[ {\int\limits_{\theta }^{T} {\exp \left( { - \frac{{Q_{\rm{g}} }}{{k_{\rm{B}} T'}}} \right)\rm{d}T'} } \right]} ^{3} \rm{d}\theta$$
(6)

With \(C={4\pi I}_{0}{{u}_{0}}^{3}/3{\beta }^{4}\), \({Q}_{\rm{n}}\) and \({Q}_{\rm{g}}\) are the corresponding activation energies for nucleation and growth of the new phase, and \({k}_{\rm{B}}\) is the Boltzmann constant. Despite the KJMA theory was developed for isothermal processes, non-isothermal regimes present many advantages like shorter time and enhancement of signal to noise ratio with respect to isothermal experiments and, therefore, many attempts to extend KJMA to non-isothermal conditions are found in the literature [9,10,11,12]. Some of the authors [12] already proposed an extension to non-isothermal regimes of KJMA analysis based on previous works of Nakamura [11]. However, Nakamura’s approximation is based on a generalization in Eq. (1) to calculate \({X}^{*}\left(T\right)\) by integrating Arrhenius like frequency factors. For constant heating rate, this leads to:

$$X^{*} \left( T \right) = \frac{1}{{\beta ^{\rm n} }}\left[ {\int\limits_{{T_{0} }}^{T} {k_{0}^{'} \exp \left( { - \frac{{Q'}}{{k_{\rm{B}} \rm{T}'}}} \right)\text{d}T'} } \right]^{n}$$
(7)

where \({k}_{0}^{^{\prime}}\) is an effective frequency factor, and Q′ is the effective activation energy. This approximation, when compared to Eq. (6), implies the relationship:

$$\left[ {\int\limits_{{T_{0} }}^{T} {k_{0}^{'} \exp \left( { - \frac{{Q'}}{{k_{\rm B} T'}}} \right)\text{d}T'} } \right]^{n} \sim C\int\limits_{{T_{0} }}^{T} {\exp \left( { - \frac{{Q_{\rm{n}} }}{{k_{\rm{B}} \theta }}} \right)} \left[ {\int\limits_{\theta }^{T} {\exp \left( { - \frac{{Q_{\rm{g}} }}{{k_{\rm{B}} T'}}} \right)\text{d}T'} } \right]^{3} \text{d}\theta$$
(8)

As will be shown below, volume melting is driven by thermally activated nucleation processes and negligible activation energy for growth, thus \({Q}_{\rm{g}}\sim 0\) implies:

$$\left[ {\int\limits_{{T_{0} }}^{T} {k_{0}^{'} \exp \left( { - \frac{{Q'}}{{k_{\rm{B}} \rm{T}'}}} \right)\text{d}T'} } \right]^{n} \sim C\int\limits_{{T_{0} }}^{T} {\exp \left( { - \frac{{Q_{\rm{n}} }}{{k_{\rm{B}} \theta }}} \right)\left( {T - \theta } \right)^{3} \text{d}\theta }$$
(9)

However, numerical analysis of such approximation, when \(Q^{\prime} = Q_{\rm{n}}\) , leads to \(n\sim 1\), instead of expected \(n=4\) value from KJMA theory (corresponding to constant nucleation rate and interface controlled growth). This difference can be understood when instantaneous growth approximation is valid:

$$\int\limits_{{T_{0} }}^{T} {k_{0} '\exp \left( { - \frac{{Q'}}{{k_{\rm{B}} \rm{T}'}}} \right)\text{d}T'\sim C'\int\limits_{{T_{0} }}^{T} {\exp \left( { - \frac{{Q_{\rm{n}} }}{{k_{\rm{B}} \theta }}} \right)\text{d}\theta } }$$
(10)

where \(C^{\prime} = I_{0} V_{0} /\beta\) and \({V}_{0}\) are the final volume of the nuclei. Instantaneous growth thus leads to \(n=1\) in the frame of KJMA. Actually, lower values of \(n\) are expected due to overgrowth artifact as instantaneous growth departs from KJMA premises (phantom nuclei overlapped with already formed crystals) [6].

In this work, we propose a different approach to extend KJMA theory to non-isothermal regimes for interface controlled processes with a constant nucleation rate. The present approach leads to a simple analysis of the temperature dependence of transformed fraction from which it is possible to obtain the activation energy. We applied the developed approximation to the volume melting process of pure metals (indium and lead) and of a eutectic bulk metallic glass (BMG) composition studied by differential scanning calorimetry.

Experimental

Pure indium and lead standards for calorimetry from Perkin-Elmer company were used in this study along with a bulk metallic glass (BMG) composition, Fe70B5C5Si3Al5Ga2P10, obtained in amorphous state by melt spinning [13]. Differential scanning calorimetry (DSC) experiments were performed in a Perkin-Elmer DSC7 for In and Pb standards (up to 1073 K and heating rates up to 80 K min−1) and in a TA Instruments SDT Q600 (for temperatures above 1073 K and heating rates up to 20 K min−1). Thermal inertia in both calorimeters was calibrated taken the onset of melting as a constant value. X-ray diffraction was performed at room temperature in a Philips PW 1820 diffractometer using Co Kα wavelength.

Extension of classical nucleation and growth kinetics to non-isothermal regimes

Previously, [12, 14], we have proposed that the following approximation is valid for the type of integrals appearing in Eq. (6):

$$\Sigma_{0} = \int\limits_{0}^{T} {e^{{ - \frac{\rm Q}{{\rm k_{\text{B}} \uptheta }}}} \text{d}\theta \sim a_{0} \left( {T - T^{\prime}_{0} } \right)e^{{ - \frac{{\rm Q^{^{\prime}} }}{{\rm k_{\text{B}} \rm T}}}} }$$
(11)

where \(a_{0} = \frac{{k_{0} ^{\prime}}}{{k_{0} }}\) with \(k_{0} ^{\prime}\) and \({k}_{0}\), the effective and actual frequency factors, respectively, and \({Q}^{^{\prime}}\) an effective activation energy that fulfills \(Q^{\prime}\sim Q\). Although optimum approximation for the full range is obtained [14] for \(T_{0} ^{\prime} = T_{\rm{pk}} /2\) , (where \({T}_{pk}\) is the peak temperature) the use of \({T}_{0}^{^{\prime}}=0\) does not significantly affect the quality of the approximation.

The goodness of this approximation to \({\Sigma }_{0}\) is shown in Fig. 1, using \(T_{0} ^{\prime} = 0\) , and compared to the approximation \(\Sigma_{0} \sim \frac{{k_{\text{B}} T^{2} }}{Q^{\prime\prime}}e^{{ - \frac{\rm Q^{\prime\prime}}{{\rm k_{\text{B}} \rm T}}}}\) found in the literature [15]. In order to do such comparison, we represent in Fig. 1\(\text{ln}\left({\Sigma }_{0}\right)-\eta \text{ln}\left(T\right)\) vs. \({T}^{-1}\), with \(\eta =1\) for our approximation and \(\eta =2\) for that of Fischer et al. In both cases, a linearity is predicted. Results are presented for three different values of \(Q=\) 0.1, 1 and 10 eV/at, in a temperature range from 0–2000 K and indicating the resulting values of Q′ and Q′′ from the linear fitting of the corresponding curves. In the latter case, two values of Q″ can be obtained, from the slope and from the intercept, labeled as \({Q}_{\mathrm{slope}}\) and \({Q}_{\mathrm{intercept}}\), respectively. In both approximations, linearity is well fulfilled in the complete temperature range and effective values of the activation energy deviates less than 2% from the actual value (except for \({Q}_{\mathrm{intercept}}\), although this can be solved by considering a temperature dependent prefactor [15]).

Fig. 1
figure 1

Linearity predicted by the approximation \({\Sigma }_{0}\sim {\mathrm{a}}_{0}{\mathrm{Te}}^{-\frac{{\mathrm{Q}}^{\mathrm{^{\prime}}}}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}}\) is proposed in Eq. (11) (symbols) for \(\mathrm{Q}=\) 0.1, 1 and 10 eV/at, along with the linearity predicted by the approximation \(\Sigma_{0} \sim \frac{{k_{B} T^{2} }}{{Q^{\prime\prime}}}e^{{ - \frac{{\rm Q^{\prime\prime}}}{{\rm{k}_{\rm{B}} \rm{T}}}}}\) (lines). Effective values of activation energy from the corresponding linear fitting are shown. In the case of \(Q^{\prime\prime}\), two different values can be obtained from the slope, \({\mathrm{Q}}_{\mathrm{slope}}\), and from the intercept, \({\mathrm{Q}}_{\mathrm{intercept}}\)

Full size image

Therefore, assuming Eq. (11) and for experiments performed at a constant heating rate, β, it is possible to write:

$${X}^{*}\left(T\right)=C{{a}_{0}}^{3}\underset{{T}_{0}}{\overset{T}{\int }}{e}^{-\frac{{\text{Q}}_{\text{n}}}{{\text{k}}_{\text{B}}\uptheta }}{\left({e}^{-\frac{{\text{Q}}_{\text{g}}}{{\text{k}}_{\text{B}}\text{T}}}T-{e}^{-\frac{{\text{Q}}_{\text{g}}}{{\text{k}}_{\text{B}}\uptheta }}\theta \right)}^{3}\text{d}\theta$$
(12)

Developing the power of the parenthesis in the previous expression yields:

$${X}^{*}\left(T\right)=C{{a}_{0}}^{3}\left({T}^{3}{e}^{-\frac{3{\rm{Q}}_{\rm{g}}}{{\rm{k}}_{\rm{B}}\rm{T}}}\underset{{T}_{0}}{\overset{T}{\int }}{e}^{-\frac{{\rm{Q}}_{\rm{n}}}{{\rm{k}}_{\rm{B}}\theta }}\text{d}\theta -3{T}^{2}{e}^{-\frac{2{\rm{Q}}_{\rm{g}}}{{\rm{k}}_{\rm{B}}\rm{T}}}\underset{{T}_{0}}{\overset{T}{\int }}\theta {e}^{-\frac{{\rm{Q}}_{\rm{n}}+{\rm{Q}}_{\rm{g}}}{{\rm{k}}_{\rm{B}}\theta }}\text{d}\theta +3T{e}^{-\frac{{\rm{Q}}_{\rm{g}}}{{\rm{k}}_{\rm{B}}\rm{T}}}\underset{{T}_{0}}{\overset{T}{\int }}{\theta }^{2}{e}^{-\frac{{\rm{Q}}_{\rm{n}}+2{\rm{Q}}_{\rm{g}}}{{\rm{k}}_{\rm{B}}\theta }}\text{d}\theta -\underset{{T}_{0}}{\overset{T}{\int }}{\theta }^{3}{e}^{-\frac{{\rm{Q}}_{\rm{n}}+3{\rm{Q}}_{\rm{g}}}{{\rm{k}}_{\rm{B}}\theta }}\text{d}\theta \right)$$
(13)

Analogously to Eq. (11), we will simplify the new integrals in a general way to:

$${\Sigma }_{\alpha }=\underset{0}{\overset{T}{\int }}{\theta }^{\upalpha }{e}^{-\frac{\rm{Q}}{{\rm{k}}_{\rm{B}}\uptheta }}\text{d}\theta \sim {a}_{\alpha }{T}^{\alpha +1}{e}^{-\frac{{\rm Q}^{^{\prime}}}{{\rm k}_{\rm B}\rm T}}$$
(14)

In order to appreciate the goodness of the proposed approximation, Fig. 2(a) shows the plot of \(\text{ln}\left({\Sigma }_{\upalpha }\right)-\left(\upalpha +1\right)\text{ln}\left(T\right)\) vs. \(1/T\) for theoretical curves with \(Q=\) 0.1, 1 and 10 eV, respectively, in a temperature range extended from room temperature to 2000 K. We can observe that the fitted intercept of straight lines at \(1/T\to\) 0 (i.e., the prefactor \({a}_{\alpha }\)) is slightly dependent on α but this dependence even decreases as \(Q\) increases.

Fig. 2
figure 2

a Linearity predicted by the approximation proposed in Eq. (14) for different values of activation energy and exponent α. b Deviation of effective activation energy, \(Q^{\prime}\) with respect to the actual one, \(\mathrm{\it{Q}}\), and c ratio between the effective and actual frequency factors, \({\mathrm{a}}_{\mathrm{\alpha }}\), both as a function of the temperature from the derivative of (a). Horizontal lines in (c) correspond to \(\frac{1}{\alpha +1}\) values

Full size image

Despite the apparently good linearity in the whole range (for \(Q=0.1\), \({r}^{2}>0.9992\) and \(\varepsilon_{Q} = \left( {Q^{\prime} - Q} \right)/Q < 0.5 \%\) ; for \(Q=1\), \({r}^{2}>0.99992\) and \({\varepsilon }_{Q}\sim 1 \%\) and for \(Q=10\), \({r}^{2}>0.99999\) and \({\varepsilon }_{Q}<2 \%\)), it is worth mentioning that we are interested in applying the approximation in a limited range of temperatures in which the process develops. Therefore, Fig. 2b shows the difference between the local apparent activation energy, \({Q}^{^{\prime}}\)(obtained from the partial derivative of Fig. 2a with respect to \(1/T\), i.e., we assume local value of the parameters \({Q}^{^{\prime}}\) and \({a}_{\alpha }\), neglecting their temperature dependence in the vicinity of the temperature of interest), and the actual one, \(Q\), for \(Q=\) 0.1, 1 and 10 eV. Figure 2c shows the estimated local values of \({a}_{\alpha }\). It can be observed that in the range of interest, overestimation of \(Q\) is below 0.15 eV. The absolute deviation increases with activation energy but the relative one decreases. Moreover, the dependence on α increases as \(Q\) decreases. In fact, we can write \({\Sigma }_{\alpha }\), without any approximation as follows:

$${\Sigma }_{\alpha }=\underset{0}{\overset{T}{\int }}{\theta }^{\alpha }{e}^{-\frac{\rm{Q}}{{\rm{k}}_{\rm{B}}\theta }}\text{d}\theta =\frac{1}{\alpha +1}{T}^{\upalpha +1}{e}^{-\frac{\rm{Q}}{{\rm{k}}_{\rm{B}}\rm{T}}}-\frac{\rm{Q}}{{\rm{k}}_{\rm{B}}\left(\alpha +1\right)}{\Sigma }_{\alpha -1}$$
(15)

where it is clear that \({a}_{\alpha }\sim {\left(1+\alpha \right)}^{-1}\) when \(Q\sim 0\). Figure 2c shows that we can incorporate the second term of the right hand of Eq. (15) into the effective prefactor \({a}_{\alpha }<{\left(1+\alpha \right)}^{-1}\) once we assume the approximation proposed in Eq. (14).

Therefore, assuming the validity of approximation proposed in Eq. (14), neglecting the low limit value (\({T}_{0}\to 0\)) and taking \({C}_{1}=\frac{4\pi {I}_{0}{{u}_{0}}^{3}}{3{\beta }^{4}}{{a}_{0}}^{3}\), it is possible to write:

$${X}^{*}\left(T\right)={C}_{1}{T}^{4}{e}^{-\frac{{\rm{Q}}_{\rm{n}}+3{\rm{Q}}_{\rm{g}}}{{\rm{k}}_{\rm{B}}\rm{T}}}\left\{{a}_{0}-3{a}_{1}+3{a}_{2}-{a}_{3}\right\}$$
(16)

Finally, taking logarithm to both sides of the equation and regrouping:

$$\text{ln}\left[{X}^{*}\left(T\right)/{T}^{4}\right]=-\frac{3{Q}_{\text{g}}+{Q}_{\text{n}}}{{k}_{\text{B}}}\frac{1}{T}+\text{ln}\left({C}_{1}\left\{{a}_{0}-3{a}_{1}+3{a}_{2}-{a}_{3}\right\}\right)$$
(17)

This allows us to propose a representation of \(\text{ln}\left({X}^{*}\right)-4\text{ln}T={\text{ln}}\left(-{\text{ln}}\left(1-X\right)\right)-4\text{ln}T\) versus \(1/T\) from which we would obtain information on the activation energy for a given temperature as the slope of the representation. However, as \(\left\{{a}_{0}-3{a}_{1}+3{a}_{2}-{a}_{3}\right\}\sim 0\) (see Fig. 2c), the intercept may fluctuate depending on the value of \(Q\) and the temperature range, preventing further analysis on the frequency factor.

Results

Application to melting process of pure metals

The onset of the melting process of pure elements is generally used as the standard measurement to calibrate calorimeters. This choice is based on the non-thermally activated character of surface melting as the surface energy between solid and vapor is larger than the sum of the surface energies between solid and liquid and liquid and vapor [16]. Therefore, a liquid layer is formed between the solid and the vapor as soon as the liquid becomes thermodynamically stable. However, volume melting is thermally activated, and it can be analyzed once heating rates used are fast enough to allow volume melting to be the leading process in the melting [17].

Whereas Eq. (16) is an approximation to the transformed fraction of volume melting, surface melting could be described as a nucleation site saturated, interface controlled growth. Taking \(Q=0\), the extended transformed fraction for surface melting should be:

$${X}_{S}^{*}\left(t\right)\sim \frac{4\pi }{3}\frac{{N}_{S}{{u}_{S}}^{3}}{{\beta }^{3}}{\left(T-{T}_{m}\right)}^{3}$$
(18)

With \({N}_{S}\) the number of nuclei at surface, \({u}_{S}\) the linear growth of these nuclei and \({T}_{m}\) the melting temperature. This power dependence (which can be overestimated as surface nucleation is not random) grows much slower than the exponential dependence predicted by Eq. (16). The effect of the heating rate is important, taking the full width at half maximum as indicative of the temperature span, \(\Delta T\sim \left(T-{T}_{m}\right)\), the ratio \({\left(\Delta T/\beta \right)}^{3}\) decreases ~ 95% in the melting processes of indium and lead when \(\beta\) increases from 5 to 80 K min−1.

Figure 3 shows the DSC scans at different heating rates along with the corresponding plots derived from Eq. (17) for melting of pure indium and lead. These plots have been limited to the transformation range from \(0.1<X<0.9\) to avoid artifact effects from the baseline selection.

Fig. 3
figure 3

Heat flow measured by DSC at different heating rates for pure indium (a) and lead (b) standards, and corresponding \(\mathrm{ln}\left({\mathrm{X}}^{*}/{\mathrm{T}}^{4}\right)\) vs. \(1/\mathrm{T}\) plots (c) and (d)

Full size image

Application to melting process of a bulk metallic glass

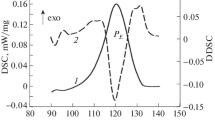
DSC scan recorded at 20 K min−1 for Fe70B5C5Si3Al5Ga2P10 BMG sample is shown in Fig. 4. Several processes, already analyzed in Ref. [13], are observed: glass transition (\({T}_{\rm{g}}=\) 760 K), crystallization (onset at \({T}_{\rm{x}}=\) 809 K), after which residual amorphous phase remains, and secondary crystallization or recrystallization processes (broad peaks around 900 K) leading to the crystalline phases that finally melt (onset at \({T}_{\rm{m}}=\) 1248 K). Melting appears as a single peak process, indicative of the eutectic character of the composition.

Fig. 4
figure 4

DSC scan at 20 K min−1 for as-cast amorphous Fe70B5C5Si3Al5Ga2P10 BMG sample showing the glass transition (\({T}_{\rm{g}}\)), the onset of crystallization (\({T}_{\rm{x}}\)) and the onset of melting (\({T}_{\rm{m}}\))

Full size image

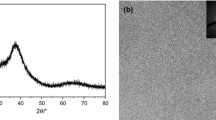
Figure 5 shows the XRD pattern of the BMG composition heated at 975 K for 1 h. The annealed sample presents the following crystalline phases: (i) ordered fcc Fe3Si with \(a=\) 0.5708 ± 0.0011 nm, (ii) a phase with a (Fe, Ni)3P-like tetragonal structure (space group: I-4) (ref. JCPDS 14–212), (iii) a phase with an Fe3NiN-like cubic structure, space group Pm3m, with a lattice parameter of \(a=\) 0.3787 ± 0.0010 nm (ref. JCPDS 9–318), (iv) a third fcc phase with lattice parameter \(a=\) 0.3543 ± 0.0018 nm, (v) tetragonal Fe2B phase (space group I-42 m) and (vi) orthorhombic Fe7C3 phase (space group Pnma). Phases (ii) and (iii) were previously found in these alloys in a previous stage of crystallization [13] and in alloys with similar compositions [18]. The large number of phases is coherent with the Gibbs rule applied to the eutectic point of such a multicomponent alloy as the one studied here.

Fig. 5
figure 5

XRD patterns using CoKα wavelength on BMG sample after being heated up to975 K for 1 h

Full size image

Figure 6a shows the melting process of BMG sample at different heating rates for the BMG sample. The equipment used for high temperatures is limited to a maximum of 20 K min−1 above 1273 K. Therefore, the values of \(\beta\) used here are 7.5, 10, 15 and 20 K min−1. Analogously to what is found for pure elements, as heating rate increases, the melting process extends to higher temperatures (although onset temperature is the same). Application of Eq. (17) leads to the plot shown in Fig. 6b.

Fig. 6
figure 6

a DSC scans at different heating rates for melting process of the BMG sample; b corresponding \(\mathrm{ln}\left({X}^{*}/{T}^{4}\right)\) vs. \(1/T\) plots

Full size image

Discussion

Figures 3c, 3d and 6b show that the linearity predicted by Eq. (17) worsens as β increases. This is due to the broader temperature range affected during the melting and the dependence of \(Q\) with \(T\). In fact, we can obtain the local value of Q′(T) from the slope of \(ln\left({X}^{*}/{T}^{4}\right)\) vs. \(1/T\) plots. The corresponding values are shown in Fig. 7a and b for indium and lead, respectively, and in Fig. 8a for the BMG sample.

Fig. 7
figure 7

Local effective activation energy for different heating rates as a function of temperature corresponding to pure indium (a) and pure lead (b). Corresponding linear correlation between \(1/\sqrt {Q^{\prime}}\) and temperature expected for nucleation-driven processes (c). Error bars (similar to the size of the symbols) are calculated as three times the standard deviation of fitted slope in Fig. 3c and d

Full size image
Fig. 8
figure 8

Local effective activation energy for different heating rates as a function of temperature corresponding to the BMG sample (a) and corresponding linear correlation between \(1/\sqrt {Q^{\prime}}\) and temperature expected for nucleation-driven processes (b). Error bars (similar to the size of the symbols) are calculated as three times the standard deviation of fitted slope in Fig. 6b

Full size image

A general decay of Q′ with temperature is observed, which can be explained by the leading role of nucleation activation energy in volume melting processes [17]. In fact, \({Q}_{\rm{g}}\ll {Q}_{\rm{n}}\) and the temperature dependence of the nucleation activation energy depends on departure of the temperature from the onset temperature as [19, 20]:

$$Q_{\rm{n}} = \frac{{4\eta^{3} \sigma^{3} T_{\rm{m}}^{2} }}{{27k_{\rm{B}} \Delta h_{\rm{m}}^{2} \left( {T - T_{\rm{m}} } \right)^{2} }}$$
(19)

where η is the surface area (for spherical nuclei: \(\eta =\sqrt[3]{36{\pi }^{2}{{v}_{l}^{2}}}\) with \({v}_{l}\) the liquid atomic volume), \(\sigma\) is the surface energy between the liquid nucleus and the surrounding solid phase, \({T}_{\rm{m}}\) is the melting point (temperature at which free energies of bulk liquid and solid are equal), and \({\Delta h}_{\rm{m}}\) is the heat of melting per atom to obtain \({Q}_{\rm{n}}\) in eV/at.

In order to confirm the leading role of thermally activated nucleation of liquid into the volume of the sample, Figs. 7c and 8b show \(1/\sqrt{Q}\) as a function of \(T\) for the pure metals and the BMG samples, respectively. The expected straight line is observed for the average values derived from the linear fittings of Figs. 3c, 3d and 6b. Symbols correspond to the temperatures at which the local values coincide with the average ones. Moreover, the values of \(1/\sqrt {Q^{\prime}\left( T \right)}\) obtained from the derivative of \(ln\left({X}^{*}/{T}^{4}\right)\) vs. \(1/T\) coherently describe a linear behavior particularly at higher heating rates and advanced transformed fractions, which is in agreement with the expected enhancement of volume melting contribution with respect to a non-thermally activated surface melting process. From the linear fitting of the plot of \(1/\sqrt {Q^{\prime}\left( T \right)}\) vs. \(T\) and once the other parameters are estimated, it is possible to obtain a value for α. Results are collected in Table 1.

Table 1 Kinetics parameters of melting for the different samples studied here
Full size table

Estimated value of surface energy is much larger in the case of the eutectic high temperature melting of BMG, \(\sigma \sim 70\) mJ m−2, than for the case of indium and lead, for which, \(\sigma \sim 10\) mJ m−2. This parameter can be related to the surface energy of solid phases, \({\sigma }_{\rm{sol}}\), as \(\sigma=f\cdot {\sigma }_{\rm{sol}}\), [21] where \(f\sim 0.05-0.1\). The values of \({\sigma }_{sol}\) for indium and lead are 630 and 560 mJ m−2, respectively [23], leading to values of σ ~30–60 and 20–40 mJ m−2, which are higher than the one estimated here (σ ~ 10 mJ m−2).

Concerning BMG samples, a value of surface tension of liquid \({\sigma }_{\rm{liq}}\)~1700 mJ m−2 has been reported for a similar composition, Fe57.75Ni19.25Mo10C5B8, to the one studied here [24]. Taking into account that \({\sigma }_{\rm{sol}}\sim 1.2{\sigma }_{\rm{liq}}\) [23], σ~100–200 mJ m−2. In general, our values are below the low limit values (about >  ~ 50%). We have to take into account that theoretical surface energy between liquid and crystal corresponds to a liquid nucleus into the core of a crystal, i.e., homogeneous nucleation. However, crystal boundaries must provide numerous randomly distributed heterogeneous nucleation sites with a reduced value of σ, which could be the explanation of the systematically lower values we obtain from our analysis.

Conclusions

The approximation here proposed to extent classical nucleation and growth theory to non-isothermal regimes, for processes characterized by constant nucleation rate and interface controlled growth, allows us to obtain the activation energy and its temperature dependence. Application of this approach to the melting process of different metallic substances is coherent with the expected volume nucleation-driven transformation and allows us to obtain the interface energy between the liquid nucleus and the solid. The obtained values, although of the same order of the expected ones, are systematically reduced which can be due to the heterogeneous character of nucleation, preferentially occurring in the crystalline boundaries.