Introduction

Nowadays, one of the most participate scientific and technological challenge is the study of promising materials with tunable properties suitable for different applications. In this scenario, layered double hydroxides (LDHs) play a role of leading actors owing to their 2D layered structure and the possibility of building them (fine tuning their specific properties) by combining different cations and anions.

The structure of LDHs can be derived from that of brucite, Mg(OH)2, consisting of layers of Mg2+ cations octahedrally coordinated with six hydroxide anions; in an LDH, the replacement of a fraction of the Mg2+ ions with a trivalent cation occurs, thus leading to a positive charge on the surface, which necessitates a balancing anion at the interlayer. These M2+/N3+(OH)6 octahedra (where M and N are bivalent and trivalent metals, respectively) form 2D sheets via edge sharing and may be connected sheet to sheet by hydrogen bridge bonding between the hydroxide groups. As the structure, LDHs similarly to hydrotalcite belong to the space group R \(\overline{3}\) m-h [1]. LDHs are used in a wide range of applications [2], including catalysis [3], energy conversion and storage [4, 5], remediation [6, 7], electrochemical and drugs delivery purposes [8, 9].

Furthermore, only a deep knowledge of the LDH chemical physical properties can allow to plan and set up the better compound for each scope. Just for this purpose in this work will be studied a Mg–Al LDHs as far as the structure, the thermal behavior and the biocompatibility are concerned.

The investigated compound is MgAl-CO3; a carbonate LDH material whose carbonate groups are located between adjacent layers, has been previously used for the removal of sulfate from wastewater [10] and remediation [6], demonstrating to provide a good performance when used with a galvanic plant polluted water. Since Mg–Al-based LDHs also find use in drug delivery and biomedical imaging [9, 11], the knowledge of the antibacterial activity seems to assume, like for bioactive glasses [12, 13], a crucial importance and needs to be further investigated. On the other hand, some of these LDHs may intercalate suitable molecules and a thermal treatment of the so-obtained precursor materials may convert them into very promising oxides or composites [14, 15]. The thermal activation of a LDH by calcination in a wide temperature range that usually is between 300 and 500 °C causes the release of water due to condensation of hydroxyl groups resulting in the formation a mixed metal oxides [16, 17]. Therefore, the knowledge of their thermal behavior is also of paramount importance to select the most appropriate temperature for the thermal treatment [18]. Furthermore, the knowledge of the decomposition step upon heating is fundamental in plan the better compound for the specific usage in surgical equipment and devices. In addition, in recent years the thermal behavior study and the assessment of thermal stability have become crucial issues in the characterization of different classes of materials and nanocomposites via the use of thermal analysis techniques. As a matter of fact, in the last one or two decades these aspects were particularly developed for glasses [19,20,21], organic–inorganic hybrids [22,23,24,25,26], ceramic and geopolymer materials [27, 28], nanocomposites [29, 30], polysiloxanes [31], analgesics and antibiotics [32] and coordination compounds [33,34,35,36].

So, as a continuation of this research, the aim of this study is to investigate the thermal behavior of MgAl-CO3 prepared via hydrothermal synthesis and characterized by means of several techniques (inductively coupled plasma atomic emission spectroscopy, ICP-AES), Fourier transform infrared spectroscopy (FT-IR), X-ray powder diffraction (XRPD), field emission scanning electron microscopy (FESEM), Kirby–Bauer test). This end was achieved also through thermogravimetry (TG) and differential thermal analysis (DTA), focusing mainly our attention on the potential reversible characteristics of dehydration and the very promising results derived by an isoconversional kinetic analysis of this process.

Experimental

Synthesis

The achievement of the desired LDH stoichiometry and morphology (depending from the perspective of usage) is just a matter of the right combination of different factors: synthesis procedures, pH of the reaction, type of reagents, solvents, temperature and reaction duration. Based on our previous experiences and on the literature [18], the compound has been synthesized by choosing a hydrothermal pathway at 180 °C for 1 h, which leads to a more nanostructured product with respect to the one synthesized for the study reported in [18], and dried overnight at low temperature (80 °C).

To prepare the MgAl-CO3 LDH, as described by [37], the reagents Al(NO3)3·9H2O (98.8% purity, supplied by VWR CHEMICALS, Leuven, Belgium), Mg(NO3)2·9H2O (98.9% purity, supplied by VWR CHEMICALS, Leuven, Belgium) and urea (99.8 mass% purity, supplied by CARLO ERBA, Milan, Italy) were used. After dissolution of the due amount of the reagents depending on the desired Mg/Al ratio, the reaction was carried out in a Teflon vessel autoclave at 180 °C for 1 h. The obtained white compound was separated from the solution by centrifugation at 7000 rpm for 10 min, repeatedly washed with water and dried in an oven at 60 °C for 24 h. The chemical analyses were performed by inductively coupled plasma atomic emission spectroscopy (ICP-AES) after dissolution of the sample in a concentrated nitric acid solution. A final Mg/Al molar ratio of 2.4 was then obtained for the material investigated.

Characterization

All the samples were characterized by means of several techniques. The ICP-AES measurements were performed using an axially viewed Varian (Springvale, Australia) Vista PRO. The sample introduction system consisted of a glass concentric K-style pneumatic nebulizer (Varian) jointed to a glass cyclonic spray chamber (Varian). In order to compensate for non-spectral interferences, the online internal standardization (4 μg mL−1 Lu standard solution) was applied. All details of the ICP-AES operating parameters are available in a previous study [6]. XRPD patterns were collected to identify the eventual crystalline phase using a X’Pert MPD (Philips, Almelo, Netherland) X-ray powder diffractometers equipped with a Cu anticathode with Cu Kα1 radiation (λ = 1.5406 Å). The indexing of the obtained diffraction data was performed by comparison of signals with those available in the literature [38] and refined with the Rietveld method, while the lattice parameters of the phases were calculated using the LATCON program [39]. A ZEISS SUPRA 40 V model of the field emission scanning electron microscope (FESEM) was used, where the sample was analyzed by applying an acceleration voltage of 5 kV for 50 s. FT-IR spectra were collected in the usual wavelength range from 4000 to 600 cm−1 using a Spectrum 65 FT-IR Spectrometer (PerkinElmer, Waltham, MA, USA) equipped with a KBr beam splitter and a DTGS detector by using an ATR accessory with a diamond crystal. TG/DTA analysis was performed using a LabsysEvo 1600–Setaram; about 20 mg of sample was placed in an open alumina crucible and heated under a flowing Ar atmosphere at 60 mL min‒1 from 30 to 1250 °C at 5 °C min‒1 (for the thermal behavior study) and at five different heating rates (1, 3, 5, 7 and 9 °C min‒1) for computing kinetics analysis. To check the occurrence of a possible interaction between the solid reactant or the solid product and the gaseous product, four different TG experiments have been carried out using different sample masses (about 5, 10, 15 and 20 mg) under a heating rate of 5 °C min-1 in a flowing Ar atmosphere at 60 mL min‒1 from ambient temperature to 320 °C.

Antibacterial activity

To evaluate the antibacterial properties of the material, a Kirby–Bauer test was performed as it was recently made for glass hybrid materials [40, 41]. Gram-negative bacteria (−), namely Escherichia coli (ATCC 25,922) and Pseudomonas aeruginosa (ATCC27853), and gram-positive bacteria ( +), as Staphylococcus aureus (ATCC 25,923) and Enterococcus faecalis (ATTC29212), were growth in the absence and presence of the sample.

Hundred milligrams of powder sample was radiated by UV light for 1 h for sterilization. A bacterial suspension of 109 CFU mL–1 was obtained by diluting pellet strains in distilled saline water (0.9% NaCl). Then, E. coli was plated on TBX (Tryptone Bile X-Gluc) Medium (Liofilchem, Italy), while S. aureus was plated on Baird-Parker agar (Liofilchem, Italy), P. aeruginosa on Pseudomonas CN agar and, finally, E. faecalis on Slanetz Bartley agar base. Except for E. faecalis, all media were sterilized up to 120 °C for 15 min. After the occurrence of the sterilization process, a CN pseudomonas supplement was added to Pseudomonas CN agar after cooling up to 45 °C. Finally, the powders were placed in the middle of Petri dishes, and then E. coli plates were incubated at 44 °C for 24 h, S. aureus at 36 °C for 24 h and E. faecalis and P. aeruginosa plates at 36 °C for 48 h.

The diameter of inhibition halos (IDs) in relation to the Petri plate diameter (PPD) (6 cm) was calculated. Four measurements were carried out for each specimen to obtain the mean standard deviation. Data are expressed as bacterial viability (BV) (expressed as %) according to Eq. (1):

$$BV = \frac{{\left( {PPD - IDs} \right)}}{PPD} \times 100$$
(1)

100% BV represents the bacteria viability without samples. The bacterial plating process is shown in Fig. S1 (Supplementary Material).

Theoretical background of kinetic analysis

The reaction rate of each degradation step is expressed by the basic kinetic equation using the following form:

$${\text{d}}\alpha /{\text{d}}t = k\left( T \right) \, \cdot f\left( \alpha \right)$$
(2)

where α is the degree of conversion defined as the fractional area of the corresponding DTA or DSC peak associated with the investigated process. Furthermore, k and f are temperature and conversion functions, respectively, where k(T) is a temperature function that may assume different forms (like that of Hartcourt and Esson [42]). The k(T) function is often expressed by the Arrhenius equation (lnk(T) = lnAk‒E/RT), where Ak and E are the pre-exponential factor and the activation energy, respectively. After some rearrangements, the left-hand side of Eq. (1), being the heating rate β equal to dT/dt, becomes:

$${\text{d}}\alpha /{\text{d}}t = {\text{ d}}T/{\text{d}}t\cdot{\text{ d}}\alpha /{\text{d}}T = \beta \cdot{\text{ d}}\alpha /{\text{d}}T$$
(3)

and, after separating both α and T variables, it yields:

$${\text{d}}\alpha /f(\alpha ) \, = \, (A_{\rm k} /\beta ) \, \cdot \, \exp \left( { - E/RT} \right){\text{d}}T$$
(4)

By integrating both hand sides of Eq. (4), Eq. (5) can be obtained:

$$\int_{0}^{\alpha } {{\text{d}}\alpha } /f\left( \alpha \right) \, = \, \int_{0}^{T} {\left( {A_{\rm k} /\beta } \right)} \, \cdot \, \exp \left( { - E/RT} \right){\text{d}}T$$
(5)

The temperature integral in Eq. (5) has no exact but approximate solutions. The so-called integral isoconversional methods can be obtained using the well-known Doyle’s approximation [43], based on the general equation:

$$\ln \left( {\beta /T_{\alpha } ^{a} } \right) \, = f\left( {1/T\alpha } \right)$$
(6)

where at each given degree of conversion a single value of activation energy E is determined from the slope of the linear regression line of Eq. (6) according to the least square method, being a = 2 for the Kissinger–Akahira–Sunose (KAS) method [44]. The integral isoconversional methods can be considered correct only on assuming that the E values are practically constant over the almost whole range of α values (E depends formally only on the temperature [45,46,47]).

By contrast, when activation energy varies by more than 20% of the average value, incremental isoconversional methods represent a valuable compromise between the differential (too sensitive toward the experimental noise [48]) and integral ones (not able to handle the conversion dependence of the E values). The incremental isoconversional methods proposed by Simon and co-workers [43, 46] have the advantage that prior to the calculation no transformation can be made on the experimental data, and the objective function (to be minimized) has a physically meaning and is statistically well-grounded. At each given value of α, the values of activation energy and pre-exponential factor are obtained from the slope and intercept of the regression line reported in Eq. (7):

$$\ln \left[ {\beta /\left( {T_{{\rm i} + 1} - T_{\rm i}} \right)} \right] \, = \, - \, \ln \left( A \right) \, - \, \left( {E/R} \right) \, \cdot \, 2/\left( {T_{{\rm i} + 1} + T_{\rm i}} \right)$$
(7)

where A = [g(αi+1) ‒ g (αi)]/Ak, being g(αi+1) and g(αi) the values of the integral model function g(α) for two conversion levels αi and αi+1 corresponding to temperatures Ti and Ti+1, respectively [45]. The detailed procedure for kinetic analysis adopted in this study has been summarized for the sake of clarity in Fig. S2 (Supplementary Material).

On the other hand, the estimated reaction time can be easily predicted isothermally by summing all the Δti time intervals according to Eq. (8) [49]:

$$t_{\alpha } = \, \Sigma_{\rm i} \Delta t_{\rm i} = \, \Sigma_{\rm i} A_{\rm i} \cdot\exp \left( { - E{}_{\rm i}/RT} \right)$$
(8)

where Ai and Ei are the Arrhenius pair related to the corresponding degree of conversion α.

Results and discussion

Structural (XRDP) and morphological (FESEM) analysis

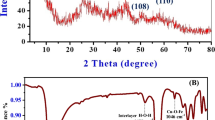
Figure 1 displays the diffraction patterns of the compound; owing to the synthesis pathway chosen, the carbonate LDH (prepared hydrothermally) is clearly highly crystalline, showing the typical symmetric (003) (006) (110) (113) and asymmetric (015) (018) reflections. The crystal structure was determined by Rietveld refinement with the assistance of the FullProf software package [50], and the cell parameters have been calculated giving the following results: a = 0.3044(34) nm, c = 2.2712(1) nm, Vcell = 0.1823(1) nm3.

Fig. 1
figure 1

XRPD patterns of MgAl-CO3

Full size image

The hydroxide layer thickness is approximately evaluated 0.24 nm [51], so the interlayer regions thickness can be estimated 0.51 nm. Figure 2 shows the FT-IR spectrum for the compound, which reveals a high amount of interlayered carbonate. The absorption band due to the vibrational modes of the very symmetric interlayer carbonate results in a single large band at 1347 cm−1, partially overlapped to a slight shoulder at 1440 cm−1 typical for the asymmetric environment of an intercalated carbonate anion.

Fig. 2
figure 2

FT-IR spectra of MgAl-CO3

Full size image

Further concerning the carbonate signals, going toward the lower wave numbers there are the two absorption bands at 865 and 835 cm−1. The signals at the lowest frequency can be attributed to the cation oxygen bonds vibrations. At 3410 cm−1, there is the broad adsorption band related to the stretching of the OH groups in coordination with the cations [52], followed by the hydrogen bending in the water molecules bonded with carbonate anions in the interlayer at 2979 cm−1. Finally, the angular deformation of the water in the interlayer is responsible for the small narrow signal at 1576 cm−1.

The FESEM image in Fig. 3 shows the micrographic appearance demonstrating that the morphology develops into a microcrystalline flower like structure, as typical in the hydrotalcite-based compounds prepared via a urea assisted hydrothermal synthesis.

Fig. 3
figure 3

FESEM images of MgAl-CO3

Full size image

The 3D architecture of the compound is the preferred one for different fields of use, due to a high exchanged surface available [53]. The thickness of the constituent lamellae was estimated between 10 and 20 nm.

Thermal behavior study

The TG and DTA curves of MgAl-CO3 are shown in Fig. 4. Taking into account that the Mg/Al molar ratio is equal to 2.4, the thermal behavior of this material is quite different from that of a MgAl-CO3 (denoted as material 2) reported in the literature [18], probably because of a different Mg/Al ratio (equal to 4 for material 2).

Fig. 4
figure 4

TG/DTA curves of MgAl-CO3 (Mg/Al molar ratio = 2.4) at 5 °C min‒1 under Ar atmosphere (60 mL min‒1) after baseline corrections (a) and DTA curves before and after baseline correction (bold and solid lines, respectively)

Full size image

In particular, Fig. 4a displays the TG and DTA curves after baseline corrections, where Fig. 4b shows DTA raw data (bold line) and the blank curve (dashed line) and the corrected DTA curve (solid line) after a point-by-point subtraction procedure, according to the recommendations for collecting experimental thermal analysis data available in the review published in 2014 by the ICTAC kinetic Project Committee [54]. Two distinct endothermic processes are evident in both TG and DTA curves. No mass loss is observed up to 100 °C (while a sudden mass loss of about 3–4% by mass is detected for material 2 for water physically adsorbed). A small mass loss is found between 100 and 140 °C, associated with a weakly intense, and broad DTA peak is ascribed to the release of water chemically bound to the material. For the sake of comparison, material 2 showed a single step of mass loss (about 12–13% by mass) attributed to the loss of chemically bound water in a wider range 70–250 °C. As far as MgAl-CO3 is concerned, once this process is ended, a noticeable mass loss (about 10% by mass) takes place up to 270 °C, with a strong almost symmetrical DTA peak, attributed to evolution of water bound with stronger bonds to the material. In this regard, the occurrence of dehydroxylation due to condensation of hydroxyl groups of the inner layers cannot be excluded, although this process usually takes place in a wider temperature range and ends at higher temperature (> 500 °C) [55].

It is worth noting that more usually the shape and position of a TG curve may vary with the sample mass and the thickness of the sample particle layer [56]. It should be stressed that the sample mass may affect the TG curves depending on the type of reaction considered [55]. Figure 5 shows four TG curves carried out with different sample sizes (ranging from about 5 to 20 mg).

Fig. 5
figure 5

Effect of sample mass on the TG curves at a heating rate of 5 K min−1 under a flowing Ar atmosphere (60 mL min−1). Sample size of about: 5 mg (——), 10 mg (― ―), 15 mg (‒ ‒) and 20 mg (· · ·)

Full size image

A systematic shift toward higher temperature is evident with increasing the sample size for each of the two processes accompanied by the evolution of water differently bound to the material. This behavior is attributed to a significant interaction between the vapor product in each process (water) and either the corresponding solid reactant or the solid product, like it was found for the thermal dehydration of calcium oxalate monohydrate [55].

Kinetic analysis of dehydration and decomposition

According to the scheme reported in Fig. S2, the kinetic analysis of both dehydration and decomposition was performed by processing DTA data related to both processes and determining the degree of conversion a from the fractional area. To this end, the original DTA curves at the five different heating rates from 1 to 9 °C min−1 (Fig. S3a, Supplementary Materials) were corrected for the baseline drift and the corresponding a vs. T curves were constructed (Fig. S3b).

Once the isoconversional temperatures were determined for both the two steps, the activation energy is calculated at each given degree of conversion from the slopes of the KAS and incremental isoconversional Simon equations (according to Eqs. 6 and 7, respectively). The isoconversional dependence of activation energy of both processes is reported in Fig. 6 (plots a and b, respectively).

Fig. 6
figure 6

Isoconversional E vs. α plots related to the first (a) and second (b) degradation steps of MgAl-CO3

Full size image

Activation energy for the first step shows in Fig. 6a a slight decreasing trend (from 83 to 72 kJ mol−1), although practical constant values can be considered (within the estimated uncertainties expressed as error bars) and an average value of (69 ± 10) kJ mol−1 can be evaluated in the range 0.1 < a < 0.9. These values are higher than that of the molar evaporation enthalpy of pure water at 100 °C (40.65 kJ mol−1, as recalculated from [57]), thus demonstrating that a significant interaction takes place between water bound to the material and the material itself, as indicated by the results of the thermal behavior study (temperature shift with increasing the sample size). The corresponding dependence of pre-exponential factor is determined for both the first and second steps from the conversion dependence of activation energy of dehydration using the incremental isoconversional method (Eq. (8)), and the values are reported in Fig. S4 (plots a and b, Supplementary Material) with the associated uncertainties as error bars.

As it is currently recognized by several authors [45, 47], neither the activation energy nor the pre-exponential factor can be considered alone as a stability parameter. However, using both the Arrhenius pair mean values derived by the incremental isoconversional Simon method (Eq. (7)), reasonable reaction time values are obtained according to Eq. (8) at 90, 120 and 150 °C. These values are reported in Table 1 along with those extrapolated outside the experimental temperature range at 25 and 37 °C (value corresponding to the temperature of human body). Just for the sake of example, it was possible to reasonably predict that 50% of water (which is a very small amount) is released from the LDH material tested at 37 °C in about 5 days (4 days and 14 h) and at 25 °C in 13 days and 10 h.

Table 1 Estimated and extrapoled reaction time values at fixed constant temperatures for given degree of conversions using isoconversional Arrhenius kinetic parameters related to the first step derived by the incremental isoconversional method (Eq. (8))
Full size table

A similar decreasing trend is observed in Fig. 6b for the E vs. a plot related to the second step with values ranging from 121 to 98 kJ mol−1 and also in this case almost constant values can be considered within the estimated uncertainties and a mean value of (106 ± 7) kJ mol−1 can be estimated in the range of a between 0.1 and 0.9. The dependence of pre-exponential factor is calculated through Eq. (8) from the conversion dependence of activation energy related to the second step using the incremental isoconversional method and the corresponding values reported in Fig. S3b (Supplementary Material) with the associated uncertainties as error bars. From the Arrhenius pair determined by the Simon method for the second step, extremely high reaction time values were calculated using Eq. (8). Reaction time values of step 2 listed in Table 2 ranged from 10 to 40 times higher than those related to the first step resulting in a significant and probably unrealistic prediction of high stability: about 100 and more than 500 years to reach 50% of degradation at 37 and 25 °C, respectively. This overestimation of stability can be reasonably predicted also by considering that extrapolation outside the temperature range explored could be taken into account with care, since for reliable results kinetic parameters related to step 2 should hold for low temperatures, which are outside the measured range. In other words, the larger is the difference between measured and estimated temperature, the worse are prediction of stability made using kinetic parameters of decomposition.

Table 2 Estimated and extrapoled reaction time values at fixed constant temperatures for given degree of conversions using isoconversional Arrhenius kinetic parameters related to the second step derived by the incremental isoconversional method (Eq. (8))
Full size table

Antimicrobial analysis

The antimicrobial properties of this material were investigated to check its potential ability to inhibit the growth of the pathogenic bacterial strains, according to Kirby–Bauer method: the zone in which no growth has occurred is called inhibition halo. Also, according to Kirby–Bauer method, the bacterium is defined as resistant (R) if the diameter of the inhibition halo is equal to or less than 17 mm; intermediate (I) if the diameter is between 18 and 22 mm; sensitive (S) if it is equal to or greater than 23 mm. As observed from representative image of petri plate (Fig. 7), no inhibition halo was observed and 100% of bacterial viability was observed for the MgAl-CO3 tested with four different strains. The bacterial resistance to the synthesized material could be explained by the inability of the material to release metal ions at toxic concentration. Indeed, many authors support the idea that metal ions at higher concentration have a negative effect on the microbial growth [58, 59].

Fig. 7
figure 7

Representative images of the sample with respect to the control

Full size image

Conclusions

The thermal behavior and the antibacterial properties of the layered MgAl-CO3, synthesized were analyzed along with its structural and morphological characteristics with XRPD and FESEM measurements, respectively. The compound has been synthesized via a co-precipitation route (direct method) followed by an hydrothermal treatment, and a partially disordered structure was observed, which is characterized by the presence of crystallites with a nanoscopic size. The antibacterial tests carried out in this study demonstrated the inability of the layered MgAl-CO3 to inhibit the growth of the pathogenic bacterial strains, according to the Kirby–Bauer method. The results of the thermal behavior study, through the TG and DTA experiments revealed that a noticeable interaction takes place between water (in the vapor phase) and MgAl-CO3 in both processes. Kinetic analysis of both steps (according to either isoconversional integral and incremental isoconversional methods) provides almost constant values of activation energy, whose mean values in the range 0.1 < a < 0.9 are: E1 = (66 ± 9) kJ mol‒1; E2 = (106 ± 7) kJ mol‒1. Finally, reaction times were reasonably predicted by extrapolation at 25 and 37 °C using kinetic parameters of the first step and can be used for assessment of thermal stability. Conversely, the same procedure adopted by using the kinetic parameters related to the second step seems to provide almost unrealistic reaction time values.