Introduction

Non-equilibrium thermodynamics are often of significance in transport of heat and mass in chemically reactive systems [1, 2]. Most specifically, the thermal diffusion of mass (Soret effect) and the transport of energy through diffusion of chemical species (Dufour effect) become noticeable in the presence of strong thermal and concentration gradients [2]. Such situations are frequently encountered in chemical reactors. In porous media, a common manifestation of non-equilibrium thermodynamics is through local thermodynamic non-equilibria, which include local thermal non-equilibrium [3, 4]. Thus, porous thermochemical systems can involve Soret and Dufour effects and also feature local thermal non-equilibrium. The former has been already the topic of a large number of investigations, e.g. [5,6,7], and the latter has been confirmed in a few recent studies [8,9,10]. Nevertheless, comprehensive non-equilibrium analyses of chemically reactive porous media that take into account all the preceding effects are rare. Resolving this issue is the primary objective of the present work.

Surface reactions in general and catalytic reactions in particular are essential in a wide range of chemical reactors. In such reactors, the catalyst might be deposited on the surfaces embedded in a porous medium. This is, perhaps, the reason for the existence of a series of studies on heat and mass transfer from a flat surface covered with porous material. A concise survey of these studies is put forward in the followings. Postelnicu [11] conducted an analysis of natural convection of heat and mass from the surface of a vertical flat plate embedded in saturated porous media. Soret and Dufour effects were considered in this work, and two-dimensional governing equations were solved numerically through employing a similarity solution [11]. Constant wall temperature and concentration were implemented as boundary conditions, and a magnetic field was also applied [11]. It was argued that by intensifying the magnetic field, the local Nusselt and Sherwood numbers would increase [11]. This work was then extended to the cases with homogeneous chemical reactions with varying reaction order and Darcian flow in porous media, [12]. Later, Postelnicu [13] investigated the same problem under a stagnation-point flow and added transpiration of mass to the flat plate. The effects of variable viscosity on the natural convection of heat and mass from a vertical, flat plate covered by porous materials were investigated by Afify [5]. Similar to the work of Postelnicu [11, 12], the influences of a magnetic field as well as the effects of Soret and Dufour numbers were taken into account [5]. However, Afify considered a non-Darcian flow with temperature-dependent viscosity [5]. In another work, the effects of viscoelastic fluid were also included in the problem by Hayat et al. [14].

Chamkha and Ben-Nakhi [6] took two major steps in the analysis of magnetohydrodynamic (MHD) convection from a flat plate embedded in porous media with Soret and Dufour effects. These authors [6] introduced the added influences of forced convection through examining mixed convection and also included thermal radiation by employing Rosseland approximation. They reported that the local Nusselt and Sherwood numbers decreased in the presence of a magnetic field for the free and mixed convection regimes. However, Nusselt and Sherwood numbers decrease and then increased forming minima as the mixed convection parameter was increased from free convection regime to the forced convection regime [6]. The existence of thermal radiation was reported to reduce the local Nusselt number and to increase the local Sherwood number particularly when there is fluid suction through the flat surface [6]. A similar configuration was analysed by Tsai and Huang [15], who extended the classical Hiemenz flow through porous media to heat and mass transferring cases with Soret and Dufour effect. These authors also considered the effects of heat of reaction and thermal radiation and non-uniform wall temperature and concentration [15]. It was concluded that for some mixtures (e.g. hydrogen-air) with the low and medium molecular weights, the Soret and Dufour effects are significant and hence should be taken into consideration [15]. Mohammad Hemmat et al. [16, 17] considered the problem of mixed convection inside lid-driven cavities filled with nanofluids. They reported a comprehensive dataset on fluid flow and heat transfer in different configurations including square, rectangular, triangular and trapezoidal with varying governing parameters such as Rayleigh number, Hartmann number, Richardson number and solid volume fraction [16, 17]. Other related works can be found in the literature, see, for example, [18,19,20,21] and references therein.

In the work of Prasad et al. [22], Soret and Dufour effects were included in the magnetohydrodynamic free convection analysis of a vertical plate embedded in porous media. Nonlinear and viscous effects were considered in the momentum transfer, while the wall temperature and concentration were assumed constant [22]. It was concluded that increasing Soret number and decreasing Dufour number intensify the local rate of heat transfer (local Nusselt number) on the surface of the plate with the opposite effect upon mass transfer rate (i.e. local Sherwood number) [22]. More recently, Mabood et al. [23] considered the problem of MHD forced convection of heat and mass transfer in a chemically reactive flow impinging on a flat plate. This analysis did not include Soret and Dufour effects but considered transpiration of mass from the surface of flat plate [23]. Amongst other findings, Mabood et al. demonstrated the significance of mass transpiration upon the transport of heat and mass [23]. In a recent work of Reddy and Chamkha [24], Soret and Dufour effects as well as thermal radiation were considered in the problem of MHD forced convection on a flat plate covered with a porous medium [24]. This investigation also included unsteady and temperature-dependent heat generation and considered two types of nanofluids [24]. It is worth mentioning that the general literature on impinging flows upon stretching surfaces with chemical reactions and Soret and Dufour effect is rather wide (see for example [23, 25,26,27]). However, as the focus of the current work is on the curved surfaces embedded in porous media, non-porous configurations are not discussed here.

A few points are well reflected by the preceding survey of the literature. First, the problem of combined heat and mass transfer by natural convection and by the inclusion of Soret and Dufour effects is well studied [6, 15, 22,23,24]. However, the same under forced convection has received less attention. Second, MHD effects have been investigated extensively, e.g. [22,23,24], and influences of thermal radiation and mass transpiration have been also considered [6]. Third, almost all investigated cases have been concerned with flows impinging on a flat plate and curved surfaces have remained unexplored. Importantly, few recent works on curved surfaces in porous media did not consider stagnation flows [28, 29]. Fourth, all the existing works have assumed that local thermal equilibrium (LTE) holds within the porous medium and local thermal non-equilibrium (LTNE) effects have been totally ignored. The current work aims at releasing the restrictive assumptions stated in the last two points. In practice, the surfaces in contact with porous media can be curved. This introduces a new level of complexity to the analysis of transport phenomena, which is still largely unexplored. Further, recent works in other configurations showed that forced convection in porous media with chemically reactive flows is most likely to violate the assumption of LTE [9, 30, 31]. Consequently, analysis of these flows demands an LTNE approach. Given this, the proceeding part of this work develops an LTNE model of forced convection of heat and mass over a cylinder with non-uniform suction/injection of fluid. This is then complemented by an evaluation of entropy generation. It is noted that while there are few studies on entropy generation in stagnation flows on stretching surfaces, e.g. [32]. The equivalent problem in porous media that includes Soret and Dufour effects does not currently exist.

Theoretical and numerical methods

Problem configuration, assumptions and governing equations

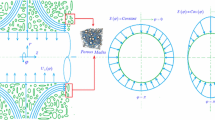
Figure 1 depicts schematically the problem under investigation. This includes a cylinder with radius a centred at r = 0 covered with a layer of catalyst and embedded in a porous medium. The surface of the cylinder can include uniform or non-uniform transpiration with prescribed circumferential distributions, while the temperature of the external surface of the cylinder is maintained constant. An external axisymmetric radial stagnation-point flow of strain rate of \(\bar{k}\) impinges on the cylinder. Due to the non-uniformity of transpiration, the flow configuration around the cylinder can be highly un-axisymmetric. The following assumptions are made through this work.

Fig. 1
figure 1

Schematic view of a stationary cylinder under radial stagnation flow of nanofluid in porous media

Full size image

  • The flow is steady, incompressible and laminar.

  • The cylinder is assumed to be infinitely long.

  • A zeroth-order, temperature-independent, catalytic reaction [33,34,35] takes place on the external surface of the cylinder.

  • Thermal diffusion of chemical species (Soret effect) and transport of energy through mass diffusion (Dufour effect) are considered.

  • The porous medium is homogenous, isotropic and under local thermal non-equilibrium (LTNE).

  • The radiation heat transfer, gravitational effects and viscous dissipation of the kinetic energy of the flow are ignored.

  • Physical properties such as porosity, specific heat, density and thermal conductivity are assumed to be constant, and hence, the thermal dispersion effects are negligible.

  • A moderate range of pore-scale Reynolds number is considered in the porous medium, and therefore, the nonlinear effects in momentum transfer are negligibly small.

It should be noted that a zeroth-order surface chemical reaction is a fair representation of many catalytic reactions [36] and is therefore of practical significance.

The governing equations and boundary conditions, in the cylindrical coordinate system shown in Fig. 1, can be summarised as follows.

The continuity of mass reads,

$$\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0$$
(1)

The transport of momentum in the radial direction is

$$\frac{1}{{\varepsilon^{2} }}\left( {u\frac{\partial u}{\partial r} + w\frac{\partial u}{\partial z}} \right) = - \frac{1}{\rho }\frac{\partial p}{\partial r} + \frac{\upsilon }{\varepsilon }\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r} - \frac{u}{{r^{2} }} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }} } \right) - \frac{\upsilon }{{k_{1} }}u$$
(2)

while in the axial direction it takes the form of

$$\frac{1}{{\varepsilon^{2} }}\left( {u\frac{\partial w}{\partial r} + w\frac{\partial w}{\partial z}} \right) = - \frac{1}{\rho }\frac{\partial p}{\partial z} + \frac{\upsilon }{\varepsilon }\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} w}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }} } \right) - \frac{\upsilon }{{k_{1} }}w.$$
(3)

The transport of thermal energy in the fluid phase is expressed by:

$$\begin{aligned} u\frac{{\partial T_{\text{f}} }}{\partial r} + w\frac{{\partial T_{\text{f}} }}{\partial z} &= \alpha_{\text{f}} \left( {\frac{{\partial^{2} T_{\text{f}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{\text{f}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{\text{f}} }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T_{\text{f}} }}{{\partial z^{2} }} } \right) + \frac{{h_{\text{sf}} \cdot a_{\text{sf}} }}{{\rho \cdot C_{\text{p}} }}\left( {T_{\text{s}} - T_{\text{f}} } \right) \\ & + \frac{{D k_{\text{T}} }}{{C_{s} \cdot C_{\text{p}} }}\left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} C}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} C}}{{\partial z^{2} }} } \right) \\ \end{aligned}$$
(4)

The last term on the left-hand side of this equation represents the Dufour effect [33, 34].

Further, the transport of thermal energy in the solid phase of the porous medium can be written as

$$k_{\text{s}} \left( {\frac{{\partial^{2} T_{\text{s}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{\text{s}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{\text{s}} }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T_{\text{s}} }}{{\partial z^{2} }} } \right) - h_{\text{sf}} \cdot a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right) = 0.$$
(5)

Mass transfer of chemical species is governed by the following advective–diffusive model, which considers the thermal diffusion of mass (Soret effect) in addition to the classical Fickian diffusion of species [14, 32]:

$$u\frac{\partial C}{\partial r} + w\frac{\partial C}{\partial z} = D\left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} C}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} C}}{{\partial z^{2} }} } \right) + \frac{{D k_{\text{T}} }}{{ T_{\text{m}} }}\left( {\frac{{\partial^{2} T_{\text{f}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{\text{f}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{\text{f}} }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T_{\text{f}} }}{{\partial z^{2} }} } \right).$$
(6)

In Eqs. (4–6), the subscripts “f” and “s” refer to the fluid and solid properties, respectively. The velocity boundary conditions of the momentum equations are as follows:

$$r = a:\quad w = 0,\quad u = - U_{0} \left( \varphi \right)$$
(7)
$$r = \infty : \quad w = 2\bar{k}z,\quad u = - \bar{k}\left( {r - \frac{{a^{2} }}{r}} \right)$$
(8)

Also, the two boundary conditions with respect to φ (angular coordinate) are expressed by

$$u\left( {r,0} \right) = u\left( {r,2\pi } \right),\quad \frac{{\partial u\left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial u\left( {r,2\pi } \right)}}{\partial \varphi }$$
(9)

Equation (7) denotes the no-slip conditions on the external surface of the cylinder. Further, Eq. (8) indicates that the viscous flow solution approaches, in a manner analogous to the Hiemenz flow, the potential flow solution as \(r \to \infty\) [37,38,39]. This can be verified by starting from the continuity equation in the followings. \(- \frac{1}{r}\frac{{\partial \left( {ru} \right)}}{\partial r} = \frac{\partial w}{\partial z}\) Constant \(= 2\bar{k}z\) and integrating in r and z directions with boundary conditions, w = 0 when z = 0 and u = − U0(φ) when r = a.

The boundary condition for the transport of thermal energy is given by

$$\begin{aligned} r = a: \quad T_{\text{f}} = & T_{\text{w}} = {\text{Constant}}, \\ {\text{T}}_{s} = & T_{\text{w}} = {\text{Constant}} \\ r = \infty :\quad T_{\text{f}} = & T_{\infty } \\ {\text{T}}_{s} = & T_{\infty } \\ \end{aligned}$$
(10)

and the two boundary conditions with respect to the angular coordinate, φ, are

$$\begin{aligned} &T_{\text{f}} \left( {r,0} \right) = T_{\text{f}} \left( {r,2\pi } \right),\quad T_{\text{s}} \left( {r,0} \right) = T_{\text{s}} \left( {r,2\pi } \right) \hfill \\ & \frac{{\partial T_{\text{f}} \left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial T_{\text{f}} \left( {r,2\pi } \right)}}{\partial \varphi },\quad \frac{{\partial T_{\text{s}} \left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial T_{\text{s}} \left( {r,2\pi } \right)}}{\partial \varphi } \hfill \\ \end{aligned}$$
(11)

in which Tw is the cylinder surface temperature and T∞ is the freestream temperature.

The boundary condition for the transport of mass is given by

$$\begin{aligned} & r = a: \quad \frac{\partial C}{\partial r} = - \frac{{k_{\text{R}} }}{D} = {\text{Constant}}, \\ & r = \infty :\quad C \to C_{\infty } \\ \end{aligned}$$
(12)

in which D is the molecular diffusion coefficient and kR is the kinetic constant for a zeroth-order chemical reaction [28, 29]. Further, C∞ is the freestream concentration. The two boundary conditions with respect to angular coordinate, φ, are

$$\begin{aligned} & C\left( {r,0} \right) = C\left( {r,2\pi } \right) \\ & \frac{{\partial C\left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial C\left( {r,2\pi } \right)}}{\partial \varphi }. \\ \end{aligned}$$
(13)

Self-similar solutions

A reduction of the governing Eqs. (1–6) is developed through applying the following similarity transformations.

$$u = - \frac{{\bar{k} \cdot a}}{\sqrt \eta }f\left( {\eta ,\varphi } \right),\quad w = \left[ {2\bar{k}f^{{\prime }} \left( {\eta ,\varphi } \right)} \right]z, \quad p = \rho_{\text{f}} \bar{k}^{2} a^{2} P,$$
(14)

where \(\eta = \left( {\frac{r}{a}} \right)^{2}\) is the dimensionless radial variable. It is important to note that it has been already demonstrated that Eq. (3) has a negligible contribution with the flow field [40]. Hence, this equation is discarded in the similarity solution. Transformations (14) satisfy the two-dimensional version of Eq. (1) automatically, and their substitution into Eqs. (2) and (3) leads to the following system of coupled differential equations.

$$\varepsilon^{2} \left[ {\eta f^{\prime \prime \prime } + f^{\prime \prime } + \frac{1}{4\eta }\frac{{\partial^{2} f^{\prime } }}{{\partial \varphi^{2} }}} \right] + Re\left[ {1 + ff^{\prime } - \left( {f^{\prime } } \right)^{2} } \right] + \varepsilon^{2} \cdot \lambda \left[ {1 - f^{\prime } } \right] = 0$$
(15)
$$P - P_{0} = - \frac{1}{{2\varepsilon^{2} }}\left( {\frac{{f^{2} }}{\eta }} \right) - \frac{1}{\varepsilon }\left[ {\left( {\frac{{f^{\prime \prime \prime } }}{Re} - \frac{1}{4Re}\mathop \smallint \limits_{1}^{\eta } \frac{1}{{\eta^{2} }}\frac{{\partial^{2} f}}{{\partial \varphi^{2} }}{\text{d}}\eta } \right) + \frac{\lambda }{Re}\mathop \smallint \limits_{1}^{\eta } \frac{f}{\eta }{\text{d}}\eta } \right] - 2\left[ {\frac{1}{{\varepsilon^{2} }} + \frac{\lambda }{Re}} \right]\left( {\frac{z}{a}} \right)^{2} ,$$
(16)

in which \(Re = \frac{{\bar{k} \cdot a^{2} }}{2\upsilon }\) is the freestream Reynolds number, \(\lambda = \frac{{a^{2} }}{{4k_{1} }}\) is referred to as permeability parameter, and prime indicates differentiation with respect to η. Considering Eqs. (6), (7) and (8), the boundary conditions for Eqs. (14) and (15) are written as

$$\eta = 1:\quad f^{{\prime }} \left( {1,\varphi } \right) = 0,\quad f\left( {1,\varphi } \right) = S\left( \varphi \right),$$
(17)
$$\eta \to \infty : \quad f^{{\prime }} \left( {\infty ,\varphi } \right) = 1,$$
(18)
$$f\left( {\eta ,0} \right) = f\left( {\eta ,2\pi } \right) , \frac{{\partial f\left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial f\left( {\eta ,2\pi } \right)}}{\partial \varphi },$$
(19)

in which \(S\left( \varphi \right) = \frac{{U_{0} \left( \varphi \right)}}{{\bar{k} \cdot a}}\) is the transpiration rate function. Note that Eqs. (15) and (16) are the complete form of Eqs. (10) and (12) in Ref. [40].

To non-dimensionalise the energy Eq. (4), the following transformation is introduced [40, 41],

$$\theta_{\text{f}} \left( {\eta ,\varphi } \right) = \frac{{T_{f} \left( {\eta ,\varphi } \right) - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}.$$
(20)

Substitution of Eqs. (14) and (20) into Eq. (4) and ignoring the small dissipation terms yields

$$\eta \theta _{\text{f}}^{{\prime \prime }} + \theta_{\text{f}}^{{\prime }} + \frac{1}{4\eta }\frac{{\partial^{2} \theta_{\text{f}} }}{{\partial \varphi^{2} }} + Re \cdot Pr \cdot \left( {f \cdot \theta_{\text{f}}^{{\prime }} } \right) + Bi\left( {\theta_{\text{s}} - \theta_{\text{f}} } \right) + Df \cdot Pr\left[ {\eta \phi^{{\prime \prime }} + \phi^{{\prime }} + \frac{1}{4\eta }\frac{{\partial^{2} \phi }}{{\partial \varphi^{2} }}} \right] = 0$$
(21)

in which \(Bi = \frac{{h_{\text{sf}} a_{\text{sf}} \cdot a}}{{4k_{\text{f}} }}\) is the Biot number and \(Df = \frac{{D \cdot k_{\text{T}} }}{{C_{\text{s}} \cdot C_{\text{p}} }}\frac{{C_{\infty } }}{{\left( {T_{\text{w}} - T_{\infty } } \right)\upsilon }}\) is the Dufour number and the boundary conditions reduce to:

$$\eta = 1:\quad \theta_{\text{f}} \left( {1,\varphi } \right) = 1$$
(22a)
$$\eta \to \infty : \quad \theta_{f} \left( {\infty ,\varphi } \right) = 0$$
(22b)
$$\theta_{\text{f}} \left( {\eta ,0} \right) = \theta_{\text{f}} \left( {\eta ,2\pi } \right),\; \frac{{\partial \theta_{\text{f}} \left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial \theta_{\text{f}} \left( {\eta ,2\pi } \right)}}{\partial \varphi }.$$
(23)

Substitution of Eqs. (14) and (20) into Eq. (5) yields

$$\eta \theta_{\text{s}}^{\prime \prime } + \theta_{\text{s}}^{\prime } + \frac{1}{4\eta }\frac{{\partial^{2} \theta_{\text{s}} }}{{\partial \varphi^{2} }} - Bi \cdot \gamma \left( {\theta_{\text{s}} - \theta_{\text{f}} } \right) = 0,$$
(24)

in which \(\gamma = \frac{{k_{\text{f}} }}{{k_{\text{s}} }}\) is the modified conductivity ratio, while the boundary conditions reduce to:

$$\eta = 1:\quad \theta_{\text{s}} \left( {1,\varphi } \right) = 1$$
(25a)
$$\eta \to \infty :\quad \theta_{\text{s}} \left( {\infty ,\varphi } \right) = 0$$
(25b)
$$\theta_{\text{s}} \left( {\eta ,0} \right) = \theta_{\text{s}} \left( {\eta ,2\pi } \right),\quad \frac{{\partial \theta_{\text{s}} \left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial \theta_{\text{s}} \left( {\eta ,2\pi } \right)}}{\partial \varphi }.$$
(26a,b)

To transform the mass transport Eq. (6) into a dimensionless form, the following transformation is introduced,

$$\phi \left( {\eta ,\varphi } \right) = \frac{{C\left( {\eta ,\varphi } \right) - C_{\infty } }}{{C_{\infty } }}.$$
(27)

Substitution of Eqs. (14) and (20) into Eq. (6) results in

$$Pr\left[ {\eta \phi^{{\prime \prime }} + \phi^{{\prime }} + \frac{1}{4\eta }\frac{{\partial^{2} \phi }}{{\partial \varphi^{2} }}} \right] + Sr \cdot Sc\left[ {\eta \theta_{\text{f}}^{{\prime \prime }} + \theta _{\text{f}}^{{\prime }} + \frac{1}{4\eta }\frac{{\partial^{2} \theta_{\text{f}} }}{{\partial \varphi^{2} }}} \right] + Re \cdot Pr \cdot Sc\left( {f \cdot \phi^{{\prime }} } \right) = 0$$
(28)

in which \(Sc = \frac{\upsilon }{D}\) is the Schmidt number and \(Sr = \frac{{D \cdot k_{\text{T}} }}{{T_{\text{m}} }}\frac{{\left( {T_{\text{w}} - T_{\infty } } \right)}}{{C_{\infty } \cdot \alpha }}\) is the Soret number, while the boundary conditions reduce to:

$$\eta = 1: \quad \phi^{{\prime }} \left( {1,\varphi } \right) = - \gamma^{*}$$
(29a)
$$\eta \to \infty :\quad \phi \left( {\infty ,\varphi } \right) = 0$$
(29b)

where, \(\gamma^{*} = \frac{{k_{R} \cdot a}}{2D}\frac{1}{{C_{\infty } }}\) is the Damköhler number.

$$\phi \left( {\eta ,0} \right) = \phi \left( {\eta ,2\pi } \right) , \frac{{\partial \phi \left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial \phi \left( {\eta ,2\pi } \right)}}{\partial \varphi }.$$
(30a,b)

Equations (15), (21), (24) and (28), together with the boundary conditions (17–19), (22–23), (25–26), (29) and (30), are solved numerically using an implicit, iterative tri-diagonal finite difference method similar to that discussed in Ref. [42].

Nusselt and Sherwood numbers

For the current problem with isothermal boundaries, the local heat convection coefficient and rate of heat transfer for fluid phase are defined as

$$h = \frac{{q_{\text{w}} }}{{T_{\text{w}} - T_{\infty } }} = \frac{{ - k_{\text{f}} \left( {\frac{{\partial T_{\text{f}} }}{\partial r}} \right)_{r = a} }}{{T_{\text{w}} - T_{\infty } }} = - \frac{{2k_{\text{f}} }}{a}\frac{{\partial \theta_{\text{f}} \left( {1,\varphi } \right)}}{\partial \eta },$$
(31)

and

$$q_{\text{w}} = - \frac{{2k_{\text{f}} }}{a}\frac{{\partial \theta_{\text{f}} \left( {1,\varphi } \right)}}{\partial \eta }T_{\text{w}} - T_{\infty } .$$
(32)

Hence, Nusselt number on the surface of the cylinder can be written as

$$Nu = \frac{h \cdot a}{{2k_{f} }} = - \theta ^{{\prime }} \left( {1,\varphi } \right).$$
(33)

Similarly, the local mass transfer coefficient and rate of mass transfer are defined as

$$k_{\text{m}} = \frac{{q_{\text{m}} }}{{C_{\text{w}} - C_{\infty } }} = \frac{{ - D\left( {\frac{\partial C}{\partial r}} \right)_{r = a} }}{{C_{\text{w}} - C_{\infty } }} = - \frac{2D}{a}\frac{{\partial \phi \left( {1,\varphi } \right)}}{\partial \eta }.$$
(34)

and

$$q_{\text{m}} = - \frac{2D}{a}\frac{{\partial \phi \left( {1,\varphi } \right)}}{\partial \eta }C_{\text{w}} - C_{\infty } .$$
(35)

Hence, Sherwood number can be expressed as

$$Sh = \frac{{k_{\text{m}} \cdot a}}{2D} = - \phi^{{\prime }} \left( {1,\varphi } \right).$$
(36)

Entropy generation

Considering the assumption stated in Sect. 3.1, the volumetric rate of local entropy generation in the problem is given by [41, 43]:

$$\begin{aligned} \dot{S}_{\text{gen}}^{\prime \prime \prime } & = \dot{S}_{\text{f}}^{\prime \prime \prime } + \dot{S}_{\text{T}}^{\prime \prime \prime } + \dot{S}_{\text{D}}^{\prime \prime \prime } \\ \dot{S}_{\text{f}}^{\prime \prime \prime } & = \frac{2\mu }{{T_{\infty } }}\left[ {\left( {\frac{\partial u}{\partial r}} \right)^{2} + \left( {\frac{u}{r}} \right)^{2} + \left( {\frac{\partial w}{\partial z}} \right)^{2} } \right] + \frac{\mu }{{T_{\infty } }}\left[ {\left( {\frac{1}{r}\frac{\partial w}{\partial \varphi }} \right)^{2} + \left( {\frac{\partial w}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{\partial u}{\partial \varphi }} \right)^{2} } \right] + \frac{\mu }{{k_{1} T_{\infty } }}\left[ {u^{2} + w^{2} } \right] \\ \dot{S}_{\text{T}}^{\prime \prime \prime } & = \frac{{k_{\text{f}} }}{{T_{\text{f}}^{2} }}\left[ {\left( {\frac{{\partial T_{\text{f}} }}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{{\partial T_{\text{f}} }}{\partial \varphi }} \right)^{2} } \right] + \frac{{k_{\text{s}} }}{{T_{\text{s}}^{2} }}\left[ {\left( {\frac{{\partial T_{\text{s}} }}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{{\partial T_{\text{s}} }}{\partial \varphi }} \right)^{2} } \right] + h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right)\left[ {\frac{1}{{T_{\text{f}} }} - \frac{1}{{T_{\text{s}} }}} \right] \\ \dot{S}_{\text{D}}^{\prime \prime \prime } & = \frac{{R_{\text{g}} \cdot D}}{C}\left[ {\left( {\frac{\partial C}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{\partial C}{\partial \varphi }} \right)^{2} } \right] + \frac{{R_{\text{g}} \cdot D}}{{T_{\text{f}} }}\left[ {\frac{\partial C}{\partial r}\frac{{\partial T_{f} }}{\partial r} - \frac{1}{{r^{2} }}\frac{\partial C}{\partial \varphi }\frac{{\partial T_{\text{f}} }}{\partial \varphi }} \right]. \\ \end{aligned}$$
(37)

Using the similarly variables given in Eqs. (14) and (37), the local entropy generation reduces to

$$\begin{aligned} \dot{S}_{\text{T}}^{\prime \prime \prime } = & \frac{{4k_{\text{f}} .\left( {T_{\text{w}} - T_{\infty } } \right)^{2} }}{{a^{2} \cdot T_{\text{f}}^{2} }}\left[ {\eta \theta_{\text{f}}^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{{\partial \theta_{\text{f}} }}{\partial \varphi }} \right)^{2} } \right] + \frac{{4k_{\text{s}} \cdot \left( {T_{\text{w}} - T_{\infty } } \right)^{2} }}{{a^{2} \cdot T_{\text{s}}^{2} }}\left[ {\eta \theta _{\text{s}}^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{{\partial \theta_{\text{s}} }}{\partial \varphi }} \right)^{2} } \right] \\ & + \frac{{\bar{k} \cdot a^{3} \cdot a_{\text{sf}} \cdot h_{\text{sf}} \cdot T_{\infty } }}{{8k_{\text{f}} \cdot \left( {T_{\text{w}} - T_{\infty } } \right)\upsilon }}\left( {\theta_{\text{f}} - \theta_{\text{s}} } \right)\left[ {\frac{1}{{\varLambda \theta_{\text{f}} + 1}} - \frac{1}{{\varLambda \theta_{\text{s}} + 1}}} \right], \\ \dot{S}_{\text{f}}^{\prime \prime \prime } = & \frac{{4\bar{k}^{2} \cdot \mu }}{{T_{\infty } }}\left\{ {\left[ {\eta f^{\prime \prime 2} + 4f^{\prime 2} + \left( {\frac{f}{\eta }} \right)^{2} - 2\frac{{ff^{\prime } }}{\eta } + \frac{1}{\eta }\left( {\frac{{\partial f^{\prime } }}{\partial \varphi }} \right)^{2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial f}{\partial \varphi }} \right)^{2} } \right] + \frac{{a^{2} }}{{4k_{1} }}\left[ {\left( {\frac{f}{\eta }} \right)^{2} + 4f^{\prime 2} } \right]} \right\}, \\ \dot{S}_{\text{D}}^{\prime \prime \prime } = & \frac{{R_{\text{g}} \cdot D \cdot C_{\infty } }}{{k_{\text{f}} }}\frac{{\bar{k} \cdot a^{2} \cdot T_{\infty }^{2} }}{{2\left( {T_{\text{w}} - T_{\infty } } \right)^{2} \upsilon }}\frac{1}{{\left( {\phi + 1} \right)}}\left[ {\eta \phi^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial \phi }{\partial \varphi }} \right)^{2} } \right] \\ & + \frac{{R_{\text{g}} \cdot D \cdot C_{\infty } }}{{k_{\text{f}} }}\frac{{\bar{k} \cdot a^{2} \cdot T_{\infty } }}{{2\left( {T_{\text{w}} - T_{\infty } } \right)\upsilon }}\frac{1}{{\left( {\frac{{T_{\text{w}} - T_{\infty } }}{{T_{\infty } }}\theta_{f} + 1} \right)}}\left[ {\eta \cdot \phi ^{\prime } \cdot \theta^{\prime }_{f} - \frac{1}{{4\eta^{2} }}\left( {\frac{\partial \phi }{\partial \varphi }} \right)\left( {\frac{{\partial \theta_{\text{f}} }}{\partial \varphi }} \right)} \right], \\ \end{aligned}$$
(38)

in which \(N_{\text{GT}} = \frac{{\dot{S}_{\text{T}}^{{{\prime \prime \prime }}} }}{{\dot{S}_{0}^{{{\prime \prime \prime }}} }},\;N_{\text{GF}} = \frac{{\dot{S}_{\text{f}}^{{{\prime \prime \prime }}} }}{{\dot{S}_{0}^{{{\prime \prime \prime }}} }},N_{\text{GD}} = \frac{{\dot{S}_{\text{D}}^{{{\prime \prime \prime }}} }}{{\dot{S}_{0}^{{{\prime \prime \prime }}} }}\)and \(\dot{S}_{0}^{\prime \prime \prime } = \frac{{8k_{\text{f}} \cdot \left( {T_{\text{w}} - T_{\infty } } \right)^{2} \upsilon }}{{\bar{k} \cdot a^{4} \cdot T_{\infty }^{2} }}\) are the non-dimensional entropy generations due to heat transfer, fluid friction, mass transfer and the characteristic entropy generation rate, respectively. The dimensionless form of the volumetric rate of local entropy generation (NGT, NGF, NGD) can be written as follows.

$$\begin{aligned} N_{\text{GT}} = & \frac{\text{Re}}{{\left( {\varLambda \theta_{f} + 1} \right)^{2} }}\left[ {\eta \theta_{\text{f}}^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{{\partial \theta_{\text{f}} }}{\partial \varphi }} \right)^{2} } \right] + \frac{Re}{{\gamma \cdot \left( {\varLambda \theta_{\text{s}} + 1} \right)^{2} }}\left[ {\eta \theta_{\text{s}}^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{{\partial \theta_{\text{s}} }}{\partial \varphi }} \right)^{2} } \right] \\ & + \frac{Bi \cdot Re}{\varLambda }\left( {\theta_{\text{f}} - \theta_{\text{s}} } \right)\left[ {\frac{1}{{\varLambda \theta_{\text{f}} + 1}} - \frac{1}{{\varLambda \theta_{\text{s}} + 1}}} \right], \\ N_{\text{GF}} = & \frac{Re \cdot Br}{\varLambda }\left\{ {\left[ {\eta f^{\prime \prime 2} + 4f^{\prime 2} + \left( {\frac{f}{\eta }} \right)^{2} - 2\frac{{f^{\prime } }}{\eta } + \frac{1}{\eta }\left( {\frac{{\partial f^{\prime } }}{\partial \varphi }} \right)^{2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial f}{\partial \varphi }} \right)^{2} } \right] + \lambda \left[ {\left( {\frac{f}{\eta }} \right)^{2} + 4f^{\prime 2} } \right]} \right\}, \\ N_{\text{GD}} = & \frac{Re \cdot \delta }{{\varLambda^{2} \cdot \left( {\phi + 1} \right)}}\left[ {\eta \phi^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial \phi }{\partial \varphi }} \right)^{2} } \right] + \frac{Re \cdot \delta }{{\varLambda \cdot \left( {\varLambda \theta_{\text{f}} + 1} \right)}}\left[ {\eta \cdot \phi^{\prime } \cdot \theta_{\text{f}}^{\prime } - \frac{1}{{4\eta^{2} }}\left( {\frac{\partial \phi }{\partial \varphi }} \right)\left( {\frac{{\partial \theta_{\text{f}} }}{\partial \varphi }} \right)} \right], \\ \end{aligned}$$
(39)

where \(\varLambda = \frac{{\left( {T_{\text{w}} - T_{\infty } } \right)}}{{T_{\infty } }}\) is the dimensionless temperature difference, \(\delta = \frac{{R_{\text{g}} \cdot D \cdot C_{\infty } }}{{k_{\text{f}} }}\) is the diffusive constant parameter, and \(Br = \frac{{\mu \left( {\bar{k} \cdot a} \right)^{2} }}{{k_{\text{f}} \left( {T_{\text{w}} - T_{\infty } } \right)}}\) is the Brinkman number. The Bejan number, defined as the ratio of entropy generation due to heat transfer to the total entropy generation, is used to facilitate understanding of the mechanisms of entropy generation. Bejan number for the current problem is expressed as

$$Be = \frac{{N_{\text{GT}} + N_{\text{GD}} }}{{N_{\text{GF}} + N_{\text{GT}} + N_{\text{GD}} }}.$$
(40)

Grid independency and validation

To ensure about the grid independency of the numerical simulations, the surface-averaged values of Nusselt, Sherwood and Bejan numbers were calculated for mesh sizes of 51 × 18, 102 × 36, 204 × 72, 408 × 144 and 819 × 288. Table 1 shows that there are no considerable changes in these quantities for the (η, φ) mesh sizes of (204 × 72), (408 × 144) and (8169 × 288). Thus, a (408 × 144) grid in η − φ directions was used for the computational domain reported in the present work. A non-uniform grid was applied in η-direction to capture the sharp gradients around the external surface of the cylinder, and a uniform mesh was implemented in φ direction. The computational domain extends over φmax = 360° and ηmax = 15. In this expression, ηmax corresponds to η → ∞, which for all investigated cases is located outside the momentum, thermal and concentration boundary layers. As the convergence criterion in the numerical simulations, when the difference between the two consecutive iterations became less than 10−7, the iterative process was terminated. On the basis of the implemented numerical scheme, the numerical error estimated to be of O(∆η)2 [41, 42].

Table 1 Grid independence study at \(Df = 1.0,\; Bi = 0.1,\; Sr = 0.5,\;Re = 5.0,\;\lambda = 10,\; Sc = 0.1\)
Full size table

Tables 2 and 3 show that in the limit of very large porosity and permeability (no porous material) and in the absence of mass transfer, the numerical solutions developed in Sect. 2 reproduce the results of Wang [44] and Gorla [45] for stagnation flow over a cylinder. Further, although not shown here, it was confirmed that in the limit of large Biot numbers the current LTNE results reduce to the LTE results reported in Ref. [40].

Table 2 Comparison between the present work and the results of Wang [44] in the limit of very large porosity and permeability
Full size table
Table 3 Comparison between the present work and the results of Gorla [45] in the limit of very large porosity and permeability
Full size table

Results and discussion

Temperature, concentration and entropy generation fields

In the current problem, the flow field is the result of interactions between the stagnation flow and the transpiration from the surface of the cylinder. Since the fluid was assumed to have constant density, the heat and mass transfer do not influence the flow and hence the hydrodynamics discussed in Ref. [40] remain unaltered. Nonetheless, because of the importance of the flow field it is briefly discussed here. Figure 2 shows the dimensionless radial velocity field (f) when the non-uniform transpiration, shown in Fig. 1, is in place. It is clear from this figure that in the regions of 0° ≲ φ ≲ 135° there exists a low velocity region, whereas in the rest of the cylinder circumference there is a strong flow towards the centre. Transpiration of mass in the form of blowing and it is interaction with the impinging flow has resulted in the radially stagnant flow in the first quarter of the cylinder cross section. In other parts, however, suction of mass is in the direction of the impinging flow, which results in a uniform flow towards the centre of the sphere. Figure 2 further indicates that the extent of low-speed region is dependent upon the Reynolds number of the external flow and in general increases as the Reynolds number becomes smaller. It will be later shown that the state of the flow around the cylinder greatly influences the transport.

Fig. 2
figure 2

Non-dimensional radial velocity (f) for different values of Reynolds numbers for \(\varepsilon = 0.9,\;\lambda = 10\)

Full size image

Figures 3–5 depict the solid and fluid dimensionless temperature fields within the porous medium and under varying parameters and for non-uniform transpiration. The influences of Biot number are shown in Fig. 3. It is clear from this figure that for low values of Biot number there are significant differences between the temperature distributions in the fluid and solid phases. Nonetheless, as the numerical value of Biot number increases, these differences diminish and for high Biot number (i.e. Bi = 100) the two temperature distributions are very similar. The influences of non-uniform transpiration are completely noticeable in Fig. 3. At low values of Biot number, there is a nearly uniform circumferential temperate distribution in the solid phase. Yet, this is clearly not the case in the fluid phase, in which there is a strong heat transfer in the region of the circumference with fluid blowing (see Fig. 1). In other regions, however, the thickness of thermal boundary layer is generally low. As Biot number increases, the temperature distribution within the solid phase becomes increasingly more non-uniform and variations become limited to small area near the surface of the cylinder. This is to be expected as the strong heat exchanges between the solid and fluid phases at high values of Biot number hinder diffusion of heat away from the hot surface of the cylinder. In the limit of high Biot number, the extracted heat from the solid phase causes an increase in the thickness of the thermal boundary layer. This can be readily verified in Fig. 3a through comparing the high-temperature region at the back of the cylinder (90° < φ < 360°) for different values of Biot number.

Fig. 3
figure 3

Effects of Biot number on aθf(η, φ), bθs(η, φ), \(Df = 1.0,\; Sr = 0.5,\;Re = 10,\;Sc = 0.1,\;\lambda = 10\)

Full size image

Figure 4 shows the effects of Dufour number on the temperature field within the porous medium. Increasing Dufour number strengthens the thermal energy received by the fluid phase due to the diffusion of mass. It is therefore not surprising that at high Dufour numbers the region of hot fluid within 0 < φ < 90° has been extended. Interestingly, however, this has little effects upon the temperature distribution in the solid phase. Reynolds number appears to have a pronounced effect on the temperature field (see Fig. 5). At low values of Reynolds number, representing a gentle impinging flow, Fig. 5a shows that the fluid temperature, in almost the entire investigated domain, has been influenced. However, as the flow impingement becomes stronger, two noticeable events happen. First, thickness of the thermal boundary layer in the region of 90° < φ < 360° decreases. This is due to the well-known effect of flow velocity on the boundary layer thickness, which in this case is further intensified by the action of mass suction. Second, in the region of 0° < φ < 90° the heat transfer is significantly enhanced, and thus, a larger volume of the fluid phase in this part of the domain becomes hot. This is caused by the interactions between the high momentum impinging flow and the blowing of the fluid from the surface of the cylinder. These two opposing flows tend to generate thick hydrodynamic and thermal boundary layers. Thus, a large volume of fluid can almost reach thermal equilibrium with the surface of the cylinder. As indicated in Fig. 5b, the effects of thermal equilibrium are much less significant on the solid phase. This results in distinctively different solid and fluid temperature distributions at high Reynolds numbers.

Fig. 4
figure 4

Effects of Dufour number on aθf(η, φ), bθs(η, φ), \(Bi = 0.1,\;Sr = 0.5,\;Re = 5.0,\; Sc = 0.1,\;\lambda = 10\)

Full size image
Fig. 5
figure 5

Effects of Reynolds number on aθf(η, φ), bθs(η, φ), \(Df = 1.0,\;Bi = 0.1,\;Sr = 0.5,\;Sc = 0.1,\;\lambda = 10\)

Full size image

Figure 6 illustrates the influences of Damköhler and Schmidt numbers upon the concentration field. Figure 6a clearly shows that increasing Damköhler number results in significant intensification of the concentration field. This is to be expected as the chemical kinetics of the surface are stronger at higher Damköhler numbers. At low values of Schmidt number, which can be viewed as large mass diffusivity, the concentration filed is fairly uniform. This is due to the fact that at this limit the mass transfer is diffusion dominated, and therefore, the hydrodynamic non-uniformities have rather insignificant effects. However, as the Schmidt number grows in value and thus the mass diffusivity becomes relatively smaller than the kinematic viscosity, the concentration field becomes increasingly more affected by the flow field. Figure 6a and b demonstrates the effects of non-uniform transpiration upon the concentration field. Most noticeably, thickening of the concentration boundary layer for the part of the circumference with blowing transpiration is evident in these figures.

Fig. 6
figure 6

Variations of ϕ(η, φ) for different values of a Damköhler number, b Schmidt number, \(Df = 1.0,\;Bi = 0.1,\;Sr = 0.5,\;Re = 10,\;Sc = 0.1,\;\lambda = 10\)

Full size image

The spatial distributions of Bejan number with varying Brinkman number and permeability parameter are shown in Fig. 7. Part a of this figure shows that at low Brinkman numbers the numerical value of Bejan number is relatively high for most of the domain. Brinkman number is proportional to the square of the flow strain rate, and thus, low Brinkman number indicates a low momentum impinging flow. This allows for the development of thick thermal and concentration boundary layers and renders higher values of Bejan number. Figure 7a shows that as the value of Brinkman increases, the region with finite value of Bejan number becomes increasingly small and ultimately it becomes limited to a narrow region close to the surface of the cylinder. As already discussed, the existence of blowing around the first quarter of the cylinder circumference thickens the boundary layers and enlargers the region of finite Bejan number. Figure 7b demonstrates the pronounced effect of the permeability parameter on Bejan number. With high permeability of the porous medium (low values of permeability parameter), the transfer processes take place more conveniently and therefore a large fraction of the investigated area experiences temperature and concentration gradients. This results in finite values of Bejan number for most of the domain. Increasing the permeability parameter, or decreasing the permeability of the porous medium, affects Bejan number in two different ways. First, it hinders the transfer processes within the porous medium and limits the temperature and concentration gradients to a region close to the cylinder walls. Second, it boosts the frictional loss and consequently increases the entropy generation through fluid flow mechanism. Both of these tend to reduce Bejan number and result in very low values of this parameter at large value of permeability parameter.

Fig. 7
figure 7

Variation of \({\text{Be}}\left( {\eta ,\varphi } \right)\) for different values of a Brinkman number, b Permeability parameter, \(Df = 1.0,\;\gamma^{*} = 1.0,\; \varLambda = 1.2,\; Sr = 0.5,\,Re = 10,\;Sc = 0.1,\;\lambda = 10\)

Full size image

The thermal and flow entropy generations have been further investigated as shown in Fig. 8. The distributions of flow entropy for different values of Brinkman number are shown in Fig. 8a. It is inferred from this figure that by increasing the strain rate of the impinging flow (increasing Brinkman number) the average value of flow entropy generation increases. Nonetheless, this increase is not uniform and features a complex structure, particularly for large Brinkman number. This behaviour stems from the complicated two-dimensional nature of the flow field in the current problem. Despite its apparent complexity, suppression of the flow entropy generation within the region experiencing blowing of mass is clear. This is due to the slow motion of the fluid in this region (see Fig. 2), which reduces the frictional entropy generation. The influences of Biot number upon the thermal entropy generation are shown in Fig. 8b. This figure indicates that regardless of the value of Biot number, there is little thermal entropy generation in the region of the domain with blowing. This can be explained by noting that, as shown in Figs. 2–5, the slow flow in this region is almost isothermal and thus does not include strong temperature gradients and thermal entropy generation. Figure 8b further shows that increasing the Biot number and the resultant increase in the heat exchanges between the fluid and solid phases widen the region with finite thermal entropy generation. Tables 2–5 provide the numerical values of the average Bejan number for different values of the pertinent parameters. In particular, Table 4 shows that by increasing Reynolds number the value of Bejan number increases substantially. This is consistent with the behaviour observed in Fig. 5, in which increasing Reynolds number results in thinner thermal boundary layers and thus more intense thermal gradients. Also Table 4 shows that enhancing the permeability parameter reduces Bejan number. Significant increases in the flow friction at lower values of permeability of the porous medium and the subsequent increase in the flow irreversibility are the reason of this behaviour.

Fig. 8
figure 8

a Variation of NGF for different values of Brinkman number, b Variation of NGT for different values of Biot number, \(Df = 1.0,\; \gamma^{*} = 1.0,\; \varLambda = 1.2,\; Sr = 0.5,\;Re = 10,\; Sc = 0.1,\;\lambda = 10\)

Full size image
Table 4 Effects of the Reynolds number and permeability parameter on average Nusselt, Sherwood and Bejan numbers, \(Df = 1.0,\;Bi = 0.1,\;Sr = 0.5,\;Re = 5.0,\;Sc = 0.1,\;\lambda = 10\)
Full size table

Nusselt and Sherwood numbers

The circumferential distributions of Sherwood and Nusselt numbers are depicted in Figs. 9–12. Figure 9 shows the angular variations of Sherwood number for different values of Reynolds number and permeability parameter. The strong effect of Reynolds number on the distribution of Sherwood number is evident in Fig. 9a. For low values of Reynolds number, the distribution is more and less uniform with an increase at around 0°/360°. This is because in the non-uniform transpiration case shown in Fig. 1, 0° is a singular point in which transpiration changes from suction to blowing. Thus, this point effectively provides a stagnation spot in the flow where the boundary layers start to develop. As a result, the values of Sherwood and Nusselt number are generally quite high at this point and then drop φ increase. This statement remains correct for all graphs in Figs. 9–12. As reflected in Fig. 9a and further quantified in Table 4, on average, increasing the Reynolds number boosts the value of Sherwood number on the cylinder. This observation is in keeping with the physical anticipation, which correlates Sherwood number with Reynolds number in forced convection problems. Figure 9b reflects the effects of permeability parameter on the distribution of Sherwood number. In general, permeability appears to have a modest effect on the Sherwood number (also see Table 4). This is particularly the case at around 0° and 360° for which there is a sharp increase in Sherwood number. Further, it seems that Sherwood number varies only within a specific range of permeability parameter. For instance, increasing the permeability parameter from 1000 to 5000 in Fig. 9b results in almost no increase in Sherwood number.

Fig. 9
figure 9

Variation of Sh for different values of a Reynolds number, b Permeability parameter, \(Df = 1.0,\;Bi = 0.1,\; Sr = 0.5,\;Re = 5.0,\;Sc = 0.1,\;\lambda = 10\)

Full size image

Figure 10a reveals a strong positive correlation between Damköhler number and Sherwood number. This correlation appears to be nearly linear, in which increasing Damköhler number from 1 to 4 increases the Sherwood number by almost four times. It should be noted that due to the implementation of a zeroth-order surface reaction in the current problem, increases in Damköhler number can be viewed as increasing the surface mass flux. This intensifies the radial gradient of the concentration and through Eq. (34) enhances the mass convection coefficient and Sherwood number. Figure 10b shows that the effect of Soret number on Sherwood number varies with the sign of Soret number. In general, Soret number can be either positive or negative [46,47,48]. It is clear in Fig. 11b that for positive values of Soret number increasing this parameter results in the reduction of Sherwood number in a large fraction of the circumference. However, this trend is reversed for negative values of Soret number. Interestingly, for values of φ close to 0° (or 360°) Sherwood number becomes independent of Soret number. This is due to the small thickness of the concentration boundary layer and hence the high strength of the primary mass transfer process in this region, which overrules the secondary influences of Soret effect.

Fig. 10
figure 10

Variation of Sh for different values of aγ*, b Soret number, \(Df = 1.0,\;Bi = 0.1,\;Sr = 0.5,\;Re = 5.0,\;Sc = 0.1,\;\lambda = 10\)

Full size image
Fig. 11
figure 11

Variation of Nu for different values of a permeability parameter, b Biot number, \(Df = 1.0,\;Bi = 0.1,\;Sr = 0.5,\;Re = 1.0,\;Sc = 0.1,\;\lambda = 10\)

Full size image

Figure 11 illustrates the effects of permeability parameter and Biot number on the numerical value of Nusselt number. Similar to that discussed with respect to Sherwood number in Fig. 9, Nusselt number appears to be rather insensitive to the changes in the permeability of the porous medium (see Fig. 11a).Yet, Biot number does have noticeable effects upon the Nusselt number. For φ ≲8 0°, increasing Biot number results in an increase in Nusselt number. However, in the rest of the circumference the numerical value of Nusselt number decreases through increasing Biot number. This behaviour is consistent with that observed in Fig. 3 on the temperature field of the fluid phase. Figure 3a shows that for 0° ≲ φ ≲ 80°, which coincides with the blowing transpiration, the thickness of thermal boundary layer decreases by increasing the Biot number. This causes an increase in the radial temperature gradient and thus enhances the Nusselt number. In the rest of the circumference, increasing Biot number thickens the thermal boundary layer and therefore the value of Nusselt number decreases. Table 5 shows that the surface-averaged value of Nusselt number decreases by increasing Biot number. The extent of this reduction is quite considerable, rendering Biot number an important factor influencing the overall rate of heat transfer.

Table 5 Effects of the Biot number and modify conductivity ratio on the average Nusselt, Sherwood and Bejan numbers \(Df = 1.0,\; Bi = 0.1,\;Sr = 0.5,\;Re = 5.0,\;Sc = 0.1,\;\lambda = 10\)
Full size table

Figure 12 demonstrates the very significant effects of Reynolds number on Nusselt number. As expected, there exists a strong positive correlation between Reynolds number and Nusselt number, which becomes particularly noticeable for Re > 10 (see also Table 4). Figure 12b shows that increasing Dufour number results in the reduction of Nusselt number. This finding can be confirmed by noting that in Fig. 4 the thickness of thermal boundary layer increases as Dufour number increases. Dufour effect represents diffusion of mass contributing to the diffusion of thermal energy (see Eq. 4). Hence, strengthening Dufour effect is analogous to increasing the thermal conductivity of the fluid, which results in thickening the thermal boundary layer. At the same time, it increases the share of diffusion in the heat transfer process, while does not alter the advection mechanism and thus reduces the value of Nusselt number. Table 6 includes the numerical values of Nusselt number for different values of Dufour number. The important point in this table is the sensitivity of the non-dimensional parameters upon changes in Dufour and Soret numbers. For example, changing Dufour number from 0.5 to 0.7 results in 6.5% variation in Nusselt number. Further, Table 7 shows that increasing Prandtl number leads to a significant increase in Nusselt and Sherwood numbers. This table also shows that the average Nusselt number decreases significantly through increasing Schmidt number, while this results in an increase in Sherwood number. The strong dependency of Nusselt number on Schmitt number is because of the relatively large value of Dufour number (Df = 1 in Table 7.

Fig. 12
figure 12

Variation of Nu for different values of a Reynolds number, b Dufour number, \(Df = 1.0,\;Bi = 0.1,\;Sr = 0.5,\;Re = 1.0,\;Sc = 0.1,\;\lambda = 10\)

Full size image
Table 6 Effects of the Dufour and Soret numbers on the average Nusselt, Sherwood and Bejan numbers, \(Df = 1.0,\;Bi = 0.1,\;Sr = 0.5,\;Re = 5.0,\;Sc = 0.1,\;\lambda = 10\)
Full size table
Table 7 Effects of the Prandtl and Schmidt numbers on the average Nusselt, Sherwood and Bejan numbers, \(Df = 1.0,\;Bi = 0.1,\,Sr = 0.5,\;Re = 5.0,\;Sc = 0.1,\;\lambda = 10\)
Full size table

The preceding analyses have consistently reflected the strong effects of transpiration on the different characteristics of the system under investigation. Table 8 reports the results of a more systematic study on these effects in which the average Nusselt, Sherwood and Bejan numbers have been calculated for two different types of transpiration and for different values of Reynolds number. It is clear from Table 8 that the numerical values of all these dimensionless numbers are smaller in the case of non-uniform transpiration in comparison with those under uniform transpiration. The difference increases with increasing Reynolds number and becomes quite significant for Re ≥ 1. This is particularly true for the average Nusselt number, for which changes in the type of transpiration can alter the numerical values by a few folds. The trend can be explained by noting the strong influences of transpiration upon the thickness of the thermal and concentration boundary layers as shown in Figs. 4–7. It is well known that convection coefficients and therefore Nusselt and Sherwood number are directly affected by changes in the boundary layer thicknesses. Transpiration in the form and blowing and suction of fluid change these thicknesses and either help or hinder the transport process. In the non-uniform transportation case, the overall effect is to thicken the boundary layers and therefore to decrease Nusselt, Sherwood and Bejan numbers.

Table 8 Effects of the transpiration function on the average Nusselt, Sherwood and Bejan numbers when \(Df = 1.0,\; Bi = 0.1,\;Sr = 0.5,\;Re = 5.0,\;Sc = 0.1,\;\lambda = 10\)
Full size table

Conclusions

A set of semi-similar solutions were developed for the problem of forced convection of heat and mass from the surface of a cylinder embedded in porous media and subject to a stagnation flow. The problem includes zeroth-order chemical reactions on the surface of the cylinder as well as a non-uniform transpiration and an impinging flow. The conducted analyses considered the non-equilibrium thermodynamics including the local thermal non-equilibrium in the porous medium and coupled heat and mass transfer through Soret and Dufour effects. To the best of authors’ knowledge, none of these have been investigated in the curved surfaces embedded in porous media. The major findings of this study can be summarised as follows:

  • It was shown that the numerical value of Biot number can considerably influence the temperature fields of the fluid and solid phases in the porous medium and thus affect the average Nusselt number. This clearly reflects the importance of considering local thermal non-equilibrium in the problem under investigation.

  • Variation of Dufour number appears to have considerable effects on the fluid temperature but does not noticeably change the temperature of the solid phase of the porous medium.

  • Changes in Reynolds number strongly affect the fluid temperature. However, they have much limited influences upon the temperature of the solid phase. Also, increases in Brinkman number enhance Bejan number in a highly non-uniform way.

  • It was shown that small variations in Soret and Dufour numbers can lead to noticeable changes in Nusselt and Sherwood numbers. This reflects the significance of these secondary mechanisms of transport and also highlights the importance of predicting the temperature and concentration fields accurately.

  • Non-uniform transpiration has a strong effect upon the temperature and concentration fields and hence majorly influences the average Nusselt, Sherwood and Bejan numbers. Further, the circumferential distribution of Sherwood and Nusselt numbers is shown to be highly sensitive to transpiration on the surface of the cylinder.

It follows that consideration of non-equilibrium thermodynamics and particularly local thermal non-equilibrium is an important necessity in the analysis of the porous thermochemical systems such as that investigated in this study.