Thermal behavior of natural dolomite

Abstract

The thermodynamic analysis of the thermal decomposition reaction of carbonates showed that the temperatures of thermal stability of dolomite and magnesium carbonate are very similar. Kinetics of isothermal and non-isothermal decompositions of natural dolomite in air atmosphere were investigated. Under the examined conditions, dolomite decomposed in a one-stage process. The final solid products of dolomite’s decomposition were calcium and magnesium oxides. The average value of isoconversional apparent activation energy of non-isothermal decomposition was 205.60 kJ mol⁻¹. The kinetics of decomposition can be described by the power-law model P2/3 with ln(A) = 20.98 for the extent of reaction α < 0.77 and by two-dimensional diffusion model D2 with ln(A) = 21.12 for α > 0.77.

Introduction

Naturally occurring dolomite—a double carbonate of Ca and Mg—CaMg(CO₃)₂ is typically sedimentary rock associated with calcite, widely scattered in nature. Its theoretical composition is 30.41 % CaO, 21.86 % MgO and 47.73 % CO₂. Dolomites are composed of dolomite and variable amounts of calcite. Divalent Fe can replace Mg²⁺ in dolomite to form solid solutions toward ankerite. Other dolomites include those bearing manganese, zinc, lead, strontium, as well as cobalt and nickel [1].

Dolomite is an important material in various industries such as metallurgy, the production of paper, glass, fertilizer, cement, concrete, functional construction material, and pharmaceutical industries [2]. The dolomite-based sorbents are used in low temperatures to reduce the emission of pollutants such as carbon, sulfur and nitrogen oxides, hydrogen chloride, and fluoride [1, 3, 4]. The applications of dolomite depend on its physicochemical, structural, and thermodynamic properties.

Knowledge of kinetics thermal decomposition of minerals is very important for the calcination process in industrial production. The kinetics of the thermal decomposition of dolomite has been studied owing to their technical importance and theoretical interest. Many researches have studied the kinetics of the calcination of natural and synthetic dolomites [2, 3, 5–28]. A great variability exists in the reports on subject reaction products and values of kinetic parameters of decomposition. The comparison of published data is difficult due to varied concentrations of impurities in the carbonate rocks, a wide range of used experimental conditions of decomposition (different atmospheres, the prevailing CO₂ pressure, sample mass, particle size and other) as well as different kinetic models being implemented in various studies.

Depending on the experimental conditions, the thermal decomposition can proceed in one endothermic step in air, nitrogen atmosphere, or at CO₂ pressure of less than 150 mm Hg according to equation (the dolomite has a loss of mass of 47.73 %) [2, 3, 5, 11, 16, 19–21, 25]:

$$ {\text{CaMg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} \, \Leftrightarrow {\text{CaO }} + {\text{ MgO }} + {\text{ 2CO}}_{ 2} $$

(I)

Porous oxides are formed in the course of the dolomite’s decomposition with the change of molar volumes ranging from 62.94 cm³ mol⁻¹ for CaMg(CO₃)₂ to 16.92 cm³ mol⁻¹ for CaO and 11.26 cm³ mol⁻¹ for MgO [3]. After calcinations, the resultant oxides have lower molar volumes, larger surface areas, and greater porosities than carbonates. The calcinations of carbonate entails the formation of an oxide having a pseudo-lattice of the normal cubic lattice of the oxide [3]. The single-stage decomposition of natural dolomite in the air was reported by Engler [11, 13] but for a synthetic-ordered dolomite, the decomposition occurred in two stages [11]. In the two-stage process, the thermal decomposition of dolomite proceeds as follows:

$$ {\text{CaMg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} \Leftrightarrow \,{\text{CaCO}}_{ 3} + {\text{ MgO }} + {\text{ CO}}_{ 2} $$

(II)

$$ {\text{CaCO}}_{ 3} \Leftrightarrow {\text{CaO }} + {\text{CO}}_{ 2} $$

(III)

The mass loss is 23.87 % in the first stage and 43.97 % in the second stage of calcium carbonate decomposition [7–9, 11, 13]. The second stage of decomposition is reversible. The extent of the reversibility depends on the temperature [9].

Engler et al. [13] based on in situ XRD analysis of dolomite’s decomposition in air concluded that the process between 973 and 1,023 K is as follows:

$$ 2 {\text{CaMg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} \Leftrightarrow {\text{CaCO}}_{ 3} + {\text{ CaO }} + {\text{ 2MgO }} + {\text{ 3CO}}_{ 2} $$

(IV)

At the latter temperature, the two reactions appear to occur simultaneously as (I) and (III). These reactions end simultaneously at 1,058 K.

The following mechanism has been proposed as “a more accurate representation of the decomposition” with the primary dissociation into individual carbonates followed by immediate decomposition to magnesite [1]:

$$ {\text{CaMg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} \Leftrightarrow {\text{MgCO}}_{ 3} + {\text{ CaCO}}_{ 3} $$

(V)

$$ {\text{MgCO}}_{ 3} \Leftrightarrow {\text{MgO }} + {\text{ CO}}_{ 2} $$

(VI)

However, magnesium carbonate is difficult to isolate. It has also been suggested that in the initial step, both CaO and MgO are formed. The formed CaO undergoes an exchange reaction with unreacted dolomite [9].

Samtani et al. reported [9] that the first stage of dolomite’s decomposition in the atmosphere of carbon dioxide occurs by a formation of an unstable magnesium carbonate which decomposes immediately to the magnesium oxide and calcium carbonate (half-burnt dolomite). The second stage of dolomite’s decomposition involves the reversible dissociation of calcium carbonate to calcium oxide which is a highly reactive. Subsequently, calcium oxide probably undergoes carbonation and hydroxylation with carbon dioxide and moisture from air.

Caceres [16] suggested that severe grinding of dolomite causes mechanically induced crystal structure’s distortion and the existence of two different Mg forms namely Mg-I and Mg-II. Decomposition of Mg-II takes place at temperatures lower than 893 K, whereas temperatures greater than 993 K are required for the decomposition of Mg-I.

Structurally deformed dolomite crystallites developed due to mechanical treatment decompose in two stages at a higher and lower CO₂ partial pressure [12]. Bercina et al. [8] reported that DTG curves in nitrogen atmosphere of quarry dolomites show two peaks (not perfectly resolved) at 1,023 and 1,073 K and that the MgO formation is not completed when the CaCO₃ decomposition starts. These authors reported that mixed oxides of Ca and Mg did not form as a consequence of the calcination. According to Barcina et al. [8], a smaller size of magnesium with respect to calcium atoms facilitates the magnesium mobility, and thus the formation of carbon dioxide associated to magnesium oxide is kinetically favored against the formation of CO₂ associated to calcium dioxide.

Britton [23] suggested that in the vacuum, the loss of CO₂ occurs at advancing interface by the direct decomposition of the dolomite leading to the formation of a solid solution (Ca, Mg)O, which subsequently breaks up into crystallites of CaO and MgO or by the break-up of the dolomite into crystallites of CaCO₃ and MgCO₃, which then decompose to oxide.

Hashimoto et al. proposed a solid solution, noted Ca_1−xMg_xCO₃, as a final reaction of half-decomposition of dolomite [17].

Since the proportion of MgCO₃ to CaCO₃ differs in the species of dolomite, the dissociation temperature and the rate of decomposition are also different and are difficult to predict.

The second stage of decomposition is more complex. XRD studies of the solid phase have shown that dolomite, calcium carbonate, magnesium oxide, and calcium oxide are present simultaneously.

The formation of CaCO₃, CaO, and MgO accompanies dolomite’s decomposition. The calcium carbonate begins to decompose even though dolomite is still present [7, 13]. Thus, many reactions appear to occur simultaneously. It testifies that the transformation during this stage involves multiple overlapping reactions rather than a single process. The rate of the overall transformation process involves consecutive and competing reactions.

The decomposition mechanism of dolomite is the source of many controversies. There is no agreement between these studies concerning the kinetic model, the influence of CO₂ pressure, and the rate-controlling step [14].

Gallai et al. [14] studied the mechanisms of growth of MgO and CaCO₃ during the dolomite partial decomposition under CO₂ pressure of 0.02–0.5 atm. They reported that the decomposition rate is limited by the diffusion of Mg from CaCO₃/MgO interface to MgO/CO₂ interface. Fine particles of MgO are formed at the surface of the initial dolomite needles. MgO grows with an external development, while the calcium carbonate develops inward at the dolomite phase. Growths of MgO and CaCO₃ can be controlled by the diffusion of magnesium through the MgO-phase surface.

Criado and Ortega [18] identified the reaction mechanism of dolomite’s decomposition in vacuum as a first-order process (F1 model) with activation energy of 146.3 kJ mol⁻¹ and pre-exponential factor A being equal to 1.3 10⁶ min⁻¹.

The influence of macrokinetic parameters on the value of activation energy is low [7]. The impurities could function as catalysts owing to their influence in the crystalline structure [1].

L`vov [15] reported the theoretical value of activation energy of dolomite’s decomposition as being equal to 234 kJ mol⁻¹. The authors concentrated on the effect of self-cooling and the partial transfer of the energy released in the condensation of low-volatility product to the reactant on measured values of E parameter. A.W. Searcy who studied dolomite’s decomposition in high vacuum obtained the energy of activation as being equal to 195 ± 1 kJ mol⁻¹ [28].

Samtani et al. [21] reported that dolomite decomposes in an atmosphere of nitrogen via a zero-order mechanism. The energy of activation for the decomposition of dolomite was 175.05 kJ mol⁻¹. In addition, the ln A-value for dolomite’s decomposition was estimated as 18.76 min⁻¹. Others [9] argued that the second stage of decomposition is reversible. The calcium oxide can be re-carbonated in CO₂ to form calcium carbonate.

Hartmann et al. [3] described the apparent kinetic parameters of the dolomite’s decomposition in air in the equation

$$ \frac{{\rm d}\alpha }{{\rm d}t} = A \cdot \exp \left( { - \frac{E}{RT}} \right)(1 - \alpha )^{\text{n}} $$

(1)

with pre-exponential factor A being equal to 0.1628·10⁸ ± 297 s⁻¹; the order of reaction n = 0.4043 + 0.02; and the activation energy, E = 190.67 + 0.515 kJ mol⁻¹.

There is a great disparity regarding the apparent activation energy with the values ranging between 146 and 440 kJ mol⁻¹ in different studies. This reflects the high complexity of the decomposition reaction. The controversies and conflicting data of the published studies of dolomite’s decomposition prompted us to analyze the thermodynamics and kinetics of this process.

Experimental

The starting material was a natural dolomite from the Zelatowa mine (Poland) containing 14.37 mass  % MgO, 33.70 % CaO, 3.37 % Fe₂O₃, 0.11 % Al₂O₃, 0.32 % MnO and 0.55 % SiO₂ with a particle size of ≤0.25 mm. This was studied under isothermal conditions in temperatures ranging from 923 to 953 K and non-isothermal conditions in air atmosphere at different heating rates ranging from 2.5 to 15 deg min⁻¹. Simultaneous recordings of thermogravimetric (TG), derivative thermogravimetric (DTG), and differential thermoanalytical (DTA) curves were obtained on a Hungarian Derivatograph MOM—PC. The thermoanalytic diagrams were recorded for the sample mass of dolomite—20 mg in temperatures ranging from room temperature to 1,273 K.

A method of the X-ray diffraction XRD was used in the investigation of dolomite calcinations products. The samples used in the study were prepared in a manner similar to that used in the thermogravimetry method. After drying, the samples (approximate mass of 10 g) were heated in a muffle furnace under air atmosphere for two hours at a temperature of 923 K. The phase composition was analyzed by the XRD method.

The samples of calcined dolomite were cooled and then put into a diffractometer. The measurements were obtained with Philips PW 1710 diffractometer, with a copper anode lamp Kα1 = 1.54060 and Kα2 = 1.54438, in an angle range of two theta from 25° to 55°, with electric parameters being 40 kV and 35 mA.

The dolomite used in our study was analyzed by the X-ray fluorescence spectrometer PHILIPS PW 1480.

The thermodynamics of chemical equilibrium of the analyzed carbonates

The kinetic analysis of these complicated reactions in a solid state is often a very difficult task, and knowledge of the thermodynamic functions of reactions may be very helpful. The approach to equilibrium in the solid is often a slow process, and it is important to be aware of the kinetics of structural and phase transformations. The knowledge of the temperatures at which solids lose their thermodynamic stability is useful for the analysis of the kinetics of thermal decompositions.

The diagram below has been plotted using the base data [29] and illustrates the energetics of carbonates—products reactions under equilibrium conditions (Fig. 1).

Fig. 1

Dependence of reactants’ Gibbs energy on temperature

The graph illustrates that dolomite is thermodynamically stable up to the temperature of 588.6 K in which the Gibbs energy curves of reactants intersect and

$$ {\text{G}}\left( {\text{T}} \right)_{{({\text{CaCO}_{3}} + {\text{MgO}} + {\text{CO}_{2}})}} < {\text{ G}}\left( {\text{T}} \right)_{{({\text{CaMg}}\left( {\text{CO}_{3}} \right) }{_{2})}} $$

The second intersect occurs at 1,118.9 K. The calcium carbonate is a stable phase between 588.6 and 1,118.9 K. In higher temperature, CaCO₃ decomposes to CaO. Magnesium carbonate MgCO₃ does not show a stable phase within the analyzed temperature range (the sum of CaCO₃ and MgCO₃ Gibbs energies is higher than dolomite Gibbs energy).

The thermodynamic analysis of carbonates decomposition revealed the following equilibrium temperatures:

$$ {\text{MgCO}}_{ 3} \Leftrightarrow {\text{MgO }} + {\text{ CO}}_{ 2}\,\,5 8 4. 3 {\text{ K}} $$

(IV)

$$ {\text{CaMg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} \Leftrightarrow \,\,{\text{CaCO}}_{ 3} + {\text{ MgO }} + {\text{ CO}}_{ 2}\,5 8 8. 6 {\text{ K}} $$

(II)

$$ {\text{CaMg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} \Leftrightarrow {\text{MgCO}}_{ 3} + {\text{ CaCO}}_{ 3}\,\,60 5.0{\text{ K}} $$

(V)

$$ {\text{CaMg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} \Leftrightarrow {\text{MgO }} + {\text{ CaO }} + {\text{ 2CO}}_{ 2}\,\,8 1 1. 3 {\text{ K}} $$

(I)

$$ {\text{CaCO}}_{ 3} \Leftrightarrow {\text{CaO }} + {\text{ CO}}_{ 2}\,1 1 1 8. 9 {\text{ K}} $$

(III)

The above analysis shows that under equilibrium conditions, the dolomite will decompose to solids: calcium carbonate and magnesium oxide (in the temperature above 588.6 K); and then to two oxides (above 811.3 K). In the temperature above 1118.9 K, calcium carbonate will decompose into calcium oxide. All the above reactions are endoenergetic having positive enthalpies.

Within the analyzed temperature range, the enthalpy of the first reaction is 2.4 times higher than the second one. Also the enthalpy of the third reaction is 1.4 times higher than the second one. Further, the entropies of all the above reactions are positive. The temperature increase favors the spontaneity of the processes. The second reaction (II) has the highest entropy.

The equilibrium constant quotient for the reaction (III) at 273.15 K is as follows:

$$ K = \frac{{{a}_{\text{eq(CaO)}} \cdot {a}_{{{\text{eq(CO}}_{ 2} )}} }}{{{a}_{{{\text{eq(CaCO}}_{ 3} )}} }} \approx {a}_{{{\text{eq(CO}}_{ 2} )}} \approx \frac{{{P}_{{{\text{eq(CO}}_{ 2} )}} }}{{{P}^{\text{o}} }} $$

(2)

where ${\text{P}}_{{{\text{eq(CO}}_{ 2} )}}$ is an equilibrium pressure of CO₂, and P ^o is a standard pressure, since the activities, a _eq(i) of the solid are nearly equal to unity. If the equilibrium constant is greater than unity, then the equilibrium activities of the products will be greater than those of the reactants. From the Gibbs energies of formation G ^o_i

$$ K_{\text{P}} = \exp \left( {\frac{{ - \Delta_{\text{r}} {G}}}{RT}} \right) $$

(3)

This equilibrium constant is highly temperature dependent and increases with rising temperature. The equilibrium pressures of CO₂ at different temperatures were calculated based on the values of the equilibrium constants for all reactions of carbonates decomposition. The logarithms of CO₂ pressure at equilibrium with different oxides and carbonates depending on temperature are shown in Fig. 2.

Fig. 2

Dependence of ${\text{ln}}\left( {P_{{{\text{CO}}_{2} }} } \right)$ on temperature

Figure 2 shows that the equilibrium pressures of CO₂ in the decomposition reactions (II), (IV), and (V) reach the atmospheric pressure (exactly 1 atm) $\left( {P_{{{\text{CO}}_{2} }} /P^{\circ } \, = \,1;\,\ln P_{{{\text{CO}}_{2} }} \, = \,0} \right)$ at very close temperatures. The decomposition of MgCO ^(s)₃ ocurrs at the lowest temperature. At this temperature, the dolomite is still stable, and MgCO₃ is not present in the system. The dolomite’s decomposition into two carbonates (CaCO₃ and MgCO₃) requires slightly higher temperature than that required for decomposition into CaCO₃ and MgO. The decomposition of CaCO₃ begins at temperature significantly higher than that for dolomite.

The proximity of temperatures of decomposition under equilibrium conditions may explain the high variability of results in the published studies analyzing dolomite’s decomposition in real conditions, other than equilibrium. The differences may result from the temperature gradient between the sample crucible and the furnace wall, the different temperatures within the sample itself, and the presence of diffusion resistance.

Results

Analysis of solid reactants

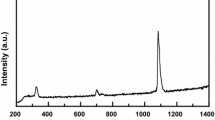
The X-ray diffraction XRD and spectrometry of X-ray fluorescence were used in the identification of solids. The diffraction patterns are illustrated in Fig. 3.

Fig. 3

The diffraction patterns of natural dolomite at 293 and 923 K, D dolomite, C calcium carbonate, P magnesium oxide

The Fig. 3 illustrates dolomite’s diffraction pattern at ambient temperature. The main peaks correspond to the dolomite phase; however, other peaks can be seen for calcium carbonate or magnesium oxide phase. The peaks of magnesium oxide partially overlap with calcium carbonate peaks. Therefore, it is impossible to determine with certainty the presence of MgO in the dolomite sample by this method.

At the temperature of 923 K, we can see a significant reduction in the peaks corresponding to the dolomite phase. At the same time, we note an increase in the peaks corresponding to calcium carbonate and magnesium oxide. The decrease of dolomite phase at 923 K based on the peak height can be estimated as 35 %.

The XRF analysis of the composition of natural dolomite showed the following results (mass/ %): MgO—14.37; Al₂O₃—0.11; SiO₂—0.55; CaO—33.70; MnO—0.32; Fe₂O₃—3.37; ZnO—0.40.

Isothermal investigations

Isothermal decomposition of dolomite was studied in temperatures ranging from 923 to 953 K. The observed mass loss was close to the theoretical value of 47.73 %.

The extents of reaction calculated from the losses of mass over time are presented in Fig. 4. The observed mass loss was close to the theoretical value of 47.73 %. The isothermal decomposition of dolomite was studied in temperatures ranging from 923 to 953 K. The dolomite’s decomposition occurs in a single stage which is a continuous and a slow process. At the temperature of 923 K, the complete decomposition takes 7 h and 25 min. The degree of dolomite conversion (α) was calculated based on the mass reduction measured at a given time and after the complete conversion, as illustrated in Fig. 4.

Fig. 4

Exemplary reaction profiles of dolomite’s decomposition

The kinetics of thermal decomposition can be adequately described using a simple equation:

$$ \frac{{\rm d}\alpha }{{\rm d}\tau } = k(T)f(\alpha ) $$

(4)

where α is the extent of conversion and τ the time. The dependence of the process rate on the temperature T is represented by the rate constant k(T). The dependence on the extent of conversion is defined by the reaction model, f(α) [24]. The temperature dependence may be described by Arrhenius equation:

$$ k\left( {T} \right) \, = {\text{ A exp}}\left( { - E/{RT}} \right) $$

(5)

and

$$ \frac{{{\text{d}}\alpha }}{{{\text{d}}\tau }} = {A}\exp \left( { - \frac{E}{RT}} \right){f{\text{(}}\alpha )} $$

(6)

When the temperature changes are linear with time, τ, then the heating rate, β, is described by the following equation:

$$ \beta = {\text{d}}{T}/{\text{d}}\tau $$

(7)

Substituting the function

$$ g(\alpha ) = \int\limits_{0}^{\alpha } {\frac{\text{d}\alpha }{f(\alpha )}} $$

(8)

we obtained the following equation:

$$ {g}\left( \alpha \right) = \frac{A}{\beta }\int\limits_{{{T}_{\text{i}} }}^{{{T}_{\text{f}} }} {\exp \left( { - \frac{E}{RT}} \right)} {\text{d}}{T} $$

(9)

The integral does not have an analytic solution, but many approximations were used in resolving this equation [30, 31, 33]. This equation substituted with g(α) suitable for a given reaction model is generally used to describe the kinetics of thermal decomposition of solids.

The kinetic curves in Fig. 4 are not straight lines as in the case of the zero-order reaction of dolomite’s decomposition in nitrogen studied by Samtani et al. [21].

The “kinetic curves” in Fig. 4 show that the isothermal decomposition process has a moderate decelerating character. It is not a first-order reaction as has been assumed for the decomposition in vacuum [18]. The dependence of ln(dα/dt) versus time is not linear. These kinetic curves can be best described by the power-law P2/3 model. The function g(α) = α ^3/2 was calculated based on the experimental data α (τ) for four different temperatures. The reaction rate constants k(T) were calculated based on the Eqs. (4) and (8).

The graph of dependence ln k = f(1/T) was used to assign the value of kinetic parameters of isothermal decomposition of dolomite. The value of energy activation E was equal to 184.69 kJ mol⁻¹ (model P2/3). The pre-exponential factor A was 6.27·10⁷ min⁻¹(lnA = 17.95). The correlation coefficient was calculated as R ² = 0.9995. Similar values of kinetic parameters were obtained based on the R1 model where g(α) = α: E = 184.43 kJ mol⁻¹ and lnA = 17.82 A = 5.47·10⁷ min⁻¹. In this case, the correlation coefficient was worse and equaled R ² = 0.9988. These values of kinetic parameters are similar to the values proposed by Samtani et al. [21] for the non-isothermal decomposition of dolomite in nitrogen atmosphere (E = 175.05 kJ mol⁻¹ lnA = 18.76).

Non-isothermal investigations

The published literature regarding the kinetic of the non-isothermal dolomite’s decomposition differs significantly. The previously conducted studies were based on different kinetic models which resulted in different kinetics parameters. This prompted us to perform our study. The results of the thermogravimetric investigations are presented in Figs. 5–7.

Fig. 5

TG curves of dolomite non-isothermal decomposition

Fig. 6

DTG curves of dolomite non-isothermal decomposition

Fig. 7

The comparison of the experimental and calculated reaction rates at the heating rate of 10 K min⁻¹

The results of non-isothermal thermogravimetric investigations of dry natural dolomite (Fig. 5) show a single-stage decrease of sample mass associated with the removal of carbon dioxide on the TG curves. One-stage decomposition under experimental conditions also indicates a single endothermic asymmetric peak on the DTA curves. At the heating rate of 15 deg min⁻¹, the dolomite’s decomposition starts at the temperature of 823 K and ends at 1,134 K. The mass loss in the temperature range of 588.5–811.1 K was less than 1 %. This suggests that the rate of dolomite’s decomposition to calcium carbonate and magnesium oxide was unremarkable in these temperatures.

In our study, we have used the procedure postulated by Dallimore [26] to recognize the kinetic mechanism of decomposition. We followed the changes of the initialT _i and final temperature T _f of the decomposition on the TG curves. We recognized the diffuse character of T _i changes and the sharp character ofT _f changes. The observed T _i and T _f changes are consistent with the R2-3 and D1-4 mechanisms. These findings also correspond to the analysis of the half-width on the differential plot of dα/dT = f(T) or DTG = f(T).

The ratio of the half-widths of the derivative peaks was ≫1. The half-way point was chosen on the perpendicular line drawn between the initial (T _i) and the final temperature (T _f) at the minimum of peaks.

Based on the α values at the maximal rate of decomposition ((dα/dT)–α plots or DTG-curves) the D2 model appears to be the best (dα/dT)_max is for α _max = 0.8−0.9 [26]. For the R2, D4 models −α _max ranges between 0.7 and 0.8. The decline of f(α) curve with the increasing degree of conversion has been observed in the model D2 and at a slower rate for model P2/3.

Illustrative DTG-curves of dolomite’s decomposition are shown in the Fig. 6.

Figure 6 shows that the temperature of peak minimum increases, whereas the peak height decreases in relation to increasing heating rate.

The apparent activation energy of non-isothermal decomposition was calculated based on model-free methods [24]. At first, the value of apparent activation energy was calculated from the temperatures of DTG peaks’ minimum at different heating rates using Kissinger’s method.

At the peak minimum,

$$ \frac{{{\text{d}}^{2} \alpha }}{{{\text{d}}{t}^{2} }} = \left[ {\frac{E\beta }{{{RT}_{\text{m}}^{ 2} }}{{\text{Af}}^{\prime}}\left( {\alpha_{\text{m}} } \right)\exp \left( { - \frac{E}{{{RT}_{\text{m}} }}} \right)} \right]\left( {\frac{{{\text{d}}\alpha }}{\text{d}{t}}} \right)_{\text{m}} = 0 $$

(10)

where ${f^{\prime}}(\alpha ) = \frac{{\rm d}f\left( \alpha \right)}{{\rm d}\alpha }$ and the subscript m describes the values obtained at the maximal reaction rate. After the rearrangements of the above Eq. (10), we obtained the Kissinger’s equation:

$$ \ln \left( {\frac{\beta }{{{{T}}_{{m,i}}^{ 2} }}} \right) = \ln \left( { - \frac{\text{AR}}{E}{{\text{f}}^{\prime}}(\alpha_{{m}} )} \right) - \frac{E}{{{{RT}}_{{m,i}} }} $$

(11)

The index i is introduced to denote various temperature programs, and i identifies an individual heating rate.

The left-hand side this equation was plotted against 1/T _m. The slope of the straight line was used to estimate of the activation energy.

The value of activation energy calculated by this method was equal to 222.28 kJ mol⁻¹. However, the strict independence of f′(α _m) on β is accomplished only for a first-order kinetic model (F1) [24], and this value ought to be treated as approximate.

The apparent activation energy was also determined by the isoconversional method recommended by ICTAC Kinetic Committee [24]. This method assumes that the reaction rate for a constant extent of conversion is only a function of temperature.

The isoconversional integral method of Coats–Redfern [30] modified by Burnham [32] using the dependence

$$ \ln \left( {\frac{{{\text{g(}}\alpha )}}{{{T}^{ 2} }}} \right) = \ln \left[ {\frac{\text{AR}}{\beta E}\left( {1 - \frac{{2{RT}}}{E}} \right)} \right] - \frac{E}{RT} $$

(12)

gives the following relation:

$$ \ln \frac{{\beta_{i} }}{{{T}_{{\alpha ,{\text{i}}}}^{2} \left( {1 - \frac{{2{RT}}}{{E_{\alpha } }}} \right)}} = \ln \left( {\frac{AR}{{E_{\alpha } }}} \right) - \ln g\left( \alpha \right) - \frac{{E_{\alpha } }}{{{RT}_{\alpha } }} $$

(13)

The left-hand side was plotted versus 1/T _α at the fixed extents of conversion for all heating rates. This is straight line dependence with E _α/R slope. Based on the graph (after sequence approaches), we calculated the values of apparent activation energies for particular degrees of conversion. Isoconversional values of activation energies for all conversion extents, E _α , are almost constant. The average value of apparent activation energy E ₀, determined by an isoconversional method was equal 205.60 kJ mol⁻¹. The value of the isoconversional activation energy was slightly lower than the value determined from the minimum DTG peak by Kissinger’s method and also lower than the theoretical value of the activation energy of the dolomite’s decomposition (234 kJ mol⁻¹) reported by L’vov [15].

For the reaction models (D2 and P2/3) identified in the isothermal investigations, we determined the values of pre-exponential factors based on the following equation:

$$ A = \frac{{ - \beta E_{0} }}{{{{RT}}_{ \hbox{max} }^{ 2} {\text{f}}^{\prime}\left( {\alpha_{\hbox{max} } } \right)}}\exp \left( {\frac{{E_{\rm o} }}{{{{RT}}_{ \hbox{max} } }}} \right) $$

(14)

where the subscript max denotes the values related to the maximum of the differential kinetic curve [24]. For the P2/3 model, the function f(α) equals 2/3 α ^−1/2 and the derivative of the function f′(α) equals −1/3 α ^(−3/2). For the D2 model, f(α) = [−ln(1−α)]⁻¹, and f′(α) = −(1−α)⁻¹[−ln(1−α)]⁻². For the model P2/3, the pre-exponential factor, A, for α at the maximum decomposition rate and the average activation energy E ₀ = 205.60 kJ mol⁻¹ was equal 3.48·10⁹ min⁻¹ (lnA = 21.97). For the model D2, the calculated pre-exponential factor A was equal 8.21·10⁸ (lnA = 20.53).

The values of kinetic parameters were subsequently used to calculate reaction rate. The results were compared with our experimental values of reaction rates. The differences between the calculated and the measured reaction rates were significant. This supports the kinetic complexity of the decomposition process.

Our reaction rates calculated based on the above kinetic parameters differed significantly from the experimental values. The deviation of values supports the complexity of the decomposition process. This can be potentially explained by the formation of oxide layers on the surface of the unreacted dolomite.

The appearance of MgO on the surface of dolomite needles was suggested by Gallai et al. [14] who studied the mechanism of dolomite’s decomposition in CO₂ atmosphere.

Due to the significant difference between the calculated and the experimental reaction rates, the pre-exponential factors were fitted by the numerical method for an average isoconversional activation energy E = 205.60 kJ mol⁻¹.

The P2/3 model with lnA = 20.98 (A = 1.29·10⁹) was the best for the conversion degree <0.77. For α > 0.77, the best model was D2 with lnA = 21.12 (A = 1.49·10⁹). The exemplary comparison of the calculated and the experimental reaction rates at the heating rate of 10 deg min⁻¹ is presented in Fig. 7.

Figure 7 illustrates that the kinetic equations determined by the numerical method well describe the experimental results for particular ranges of conversion.

Conclusions

• 1. From the analysis of thermodynamics, during decomposition reactions, results show that the sequence of reactions under equilibrium conditions ought to be the following:

  $$ {\text{CaMg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} \Leftrightarrow {\text{CaCO}}_{ 3} + {\text{ MgO }} + {\text{ CO}}_{ 2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{above 588}}. 5 {\text{ K}} $$

  (I)
  $$ {\text{CaMg}}\left( {{\text{CO}}_{ 3} } \right)_{ 2} \Leftrightarrow {\text{MgO }} + {\text{ CaO }} + {\text{ 2CO}}_{ 2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{above 8}}0 1. 1 {\text{ K}} $$

  (II)
  $$ {\text{CaCO}}_{ 3} \Leftrightarrow {\text{CaO }} + {\text{ CO}}_{ 2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{above 1118}}. 8 {\text{ K}} $$

  (III)

• 2. Isothermal decomposition of dolomite from Zelatowa mine (Poland) at the temperatures ranging from 923 to 953 K to solid CaO and MgO is one-step process and can be described by power-law P2/3 kinetic model with kinetic parameters E = 184.69 kJ mol⁻¹ and A = 6.27·10⁷ min⁻¹(lnA = 17.95).

• 3. Non-isothermal decomposition of dolomite occurs at heating rates ranging from 2.5 to 15 deg min⁻¹ at the temperatures ranging from 916.5 K (at heating rate of 2.5 deg min⁻¹) to 1,134 K (at 15 deg min⁻¹), and it is complex one-stage process.

• 4. Final solid products of decomposition are calcium and magnesium oxides.

• 5. The average value of apparent activation energy of non-isothermal decomposition E ₀, determined by model-free isoconversional method was equal 205.60 kJ mol⁻¹.

• 6. Kinetics of non-isothermal dolomite’s decomposition can be described by P2/3 model for α < 0.77 and D2 model for α > 0.77.

• 7. Pre-exponential factor, A for P2/3 model was equal 1.29·10⁹ min⁻¹ (lnA = 20.98) for α < 0.77 and 1.49·10⁹ min⁻¹ (lnA = 21.12) for D2 model and α > 0.77.