In situ measurement of neutron temperature for the extended k₀ NAA at FRM II

Abstract

The neutron temperature at different irradiation positions in the research reactor FRM II was measured using thermometer labels together with lutetium standards. This was the first time to measure the local temperature at the irradiation positions with this combination. The simplified Westcott formalism was used to calculate the neutron temperature using Lu and g(T_n) factors from different data sources. The results showed agreement between neutron temperature according to the Lu method and the temperature showed on the labels. They can be used as a reliable alternative to determine the neutron temperature instead of using Lu standards in the extended k₀ NAA.

Introduction

k₀ NAA was introduced in 1980s based on the Høgdahl convention [1, 2]. This is a convenient idea for multi element NAA because only one comparator is enough to calculate the local neutron flux. Later, in the 1990s, this method was modified by using the Westcott convention with consideration of the influence of the neutron temperature, so that the analysis of some non-1/v nuclides with the k₀ NAA approach became possible [3, 4]. To unify the two conventions, at least for the non-1/v isotopes, an extended Høgdahl formalism retaining flux parameters f and α and adding the neutron temperature effected by means of g(T_n) was developed a few years ago [5]. However, the determination of the local neutron temperature at the irradiation position becomes unavoidable. Lutetium is usually used as a temperature monitor, because the thermal neutron-capture cross section of the reaction ¹⁷⁶Lu(n,γ)¹⁷⁷Lu varies with the neutron temperature very strongly.

In most cases, the activity of ¹⁷⁷Lu is measured and the local neutron temperature T_n is determined from the g factor originally introduced to correct the neutron cross section σ for different temperatures. Then, the neutron temperature determined in this way is used for the calculation of the g factor and thus the concentration of other non-1/v nuclides. The g(T_n) factors available in the literature were calculated from the σ(E) values and can be dated back to the 1960s and 1970s [3, 6]. The last updates using the evaluated neutron data libraries ENDF/B-VI, VII were published in 1999 and 2015 [7, 8]. Because the σ(E) values were calculated using different sources, e.g. ENDF or experimental data from technical reports, significant differences in g(T_n) values can be found for Lu and also for other non-1/v nuclides over the last 50 years. These lead to different neutron temperatures determined by using Lu standards.

Attempts to measure the temperature were made in other ways too, e.g. assuming that the neutron temperature is equal to the Maxwellian temperature of the medium surrounding the irradiation position. Monte Carlo simulation was also used to calculate the local neutron temperature [9]. Some tried to use temperature readings of the inlet and outlet of the reactor moderator instead of measuring Lu at small reactors [10]. None of these was performed in the irradiation positions directly. In addition, the method of moderator temperature readings is not suitable for large reactors like FRM II with the thermal power of 20 MW and numerous internal equipment surrounding the core, unless the moderator temperature can be measured very close to the irradiation position.

Earlier, thermometer labels were successfully used at FRM II to measure the local temperature in high-dose gamma fields. The goal of this work was to use them to measure the temperature at the irradiation positions in situ. The labels record the maximum temperature on the samples or in the irradiation capsules during the whole irradiation procedure. The idea was to find out whether this temperature is in agreement with the one determined using Lu activation.

Contrary to other k₀ values determined experimentally, the recommended k₀ values of ¹⁷⁷Lu were calculated based on theoretical parameters. Only a few determinations of the Lu k₀ values have been carried out [11]. The main obstacles are the accurate determination of the neutron temperature and the different g(T_n) factors. The independent way to measure the local temperature could offer a possibility to determine the real k₀ values of Lu.

Theory

We start from the k₀ method modified with the Westcott formalism. Neglecting the neutron self-shielding, the mass fraction ρ of an unknown element is calculated by the following formula according to the common notation of the k₀ method [12]:

$$\rho = \frac{{\left( {\frac{{N_{\text{p}} }}{{SDCWt_{m} }}} \right)}}{{\left( {\frac{{N_{\text{p}} }}{{SDCwt_{m} }}} \right)^{*} }}\frac{1}{{k_{0} }}\frac{{g(T_{n} )^{*} + r\sqrt {T_{n} /T_{0} } s_{0}^{*} (\alpha )}}{{g(T_{n} ) + r\sqrt {T_{n} /T_{0} } s_{0} (\alpha )}}\frac{{\varepsilon_{\text{p}}^{*} }}{{\varepsilon_{\text{p}} }},$$

(1)

where N_p is the net peak area, S = 1 − exp(− λt_irr) with the decay constant λ and the irradiation time t_irr, D = exp(− λt_d) with the decay time t_d, C = [1 − exp(− λt_m)]/λt_m with the measuring time, W and w are sample and monitor masses, g(T_n) is the Westcott’s g factor, T_n is the neutron temperature, r is the modified spectral index, $s_{0}$ is the modified reduced resonance integral, α is the neutron spectrum shape parameter, ε_p is the full-energy peak efficiency.

By definition, the epithermal neutron spectral index r introduced by Westcott is equal to 0 for a pure Maxwellian neutron spectrum [3]. On the other hand, van Sluijs et al. tried to replace the Westcott formalism with the conventional k₀ NAA parameters in the extended version of the modified Høgdahl convention [5]:

$$\rho = \frac{{\left( {\frac{{N_{\text{p}} }}{{SDCWt_{m} }}} \right)}}{{\left( {\frac{{N_{\text{p}} }}{{SDCwt_{m} }}} \right)^{*} }}\frac{1}{{k_{0} }}\frac{{1 + Q_{0}^{*} (\alpha )/f}}{{g(T_{n} ) + Q_{0} (\alpha )/f}}\frac{{\varepsilon_{\text{p}}^{*} }}{{\varepsilon_{\text{p}} }},$$

(2)

where gold (*) is used as co-irradiated monitor and ¹⁹⁷Au is treated as a 1/v-nuclide, f is the thermal to epi-thermal flux ratio, $Q_{0} (\alpha )$ is the resonance integral to thermal neutron cross section ratio.

For a modern reactor like FRM II with a very well-thermalized neutron spectrum, i.e. with high f values (> 3000) in most irradiation positions [13], the ratio of $Q_{0} (\alpha )/f$ is less than 0.5% both for Au and Lu. Thus, according to both conventions, the above equations can be simplified to the one below using only the g(T_n) factor instead of the epithermal correction factor:

$$\rho = \frac{{\left( {\frac{{N_{\text{p}} }}{{SDCWt_{m} }}} \right)}}{{\left( {\frac{{N_{\text{p}} }}{{SDCwt_{m} }}} \right)^{*} }}\frac{1}{{k_{0} }}\frac{1}{{g(T_{n} )}}\frac{{\varepsilon_{\text{p}}^{*} }}{{\varepsilon_{\text{p}} }}.$$

(3)

Determining the neutron temperature T_n using a Lu monitor with a known mass W, g(T_n) can be expressed as:

$$g(T_{n} ) = \frac{{\left( {\frac{{N_{\text{p}} }}{{SDCW\rho t_{m} }}} \right)}}{{\left( {\frac{{N_{\text{p}} }}{{SDCwt_{m} }}} \right)^{*} }}\frac{1}{{k_{0} }}\frac{{\varepsilon_{\text{p}}^{*} }}{{\varepsilon_{\text{p}} }}.$$

(4)

The main advantage of the high f values is that the uncertainties of other relevant parameters such as $Q_{0} (\alpha )$, $\overline{E}_{\text{r}}$ (effective resonance energy) or $s_{0} (\alpha )$ have negligible influence on the g(T_n) calculation making the determination of g(T_n) and T_n simpler and more precise.

Figure 1 shows the Westcott g(T_n) factors which were used in k₀ NAA and mentioned in the literature [2, 11]. They were calculated by different authors [3, 6,7,8] with different input data and algorithms. The data of Holden show a significant discrepancy to others of about 3%. The temperature range between 20 and 80 °C is the design temperature range of the FRM II. The data points can be fitted with a linear regression for all groups. In a recent work, van Sluijs proposed a fitting of the g(T_n) factors with a second-degree polynomial [14]. However, the difference is less than 0.1% within the temperature range considered here. The linear expression for the temperature T_n as a function of g(T_n) is written in Eq. 5 and the coefficients of the linear approximations used in this work are given in Table 1.

Fig. 1

g(T_n) factors of ¹⁷⁶Lu from different data sources [3, 6,7,8]

Table 1 The coefficients of the linear approximations used for the temperature calculation

$$T_{n} \;(^\circ {\text{C}}) \, = ag + b.$$

(5)

Experimental

Sample preparation

For the determination of the neutron temperature at FRM II, Lu standards were prepared using a 1000 mg/L (± 0.5%) certified ICP standard solution CertiPUR^®, manufactured by Merck. For each standard sample, 200 µL aliquot was pipetted onto 0.1 mm thick round filter paper (Ø16 mm) with a polyethylene foil on the backside directly on a balance. The certified element concentration of Lu was (989 ± 5) µg/g. After drying, the filter papers were enclosed in PE bags. Additionally, Lu–Al standard foils (IRMM-sp96091, 0.1% Lu) and Au–Al foils (IRMM-530R, 0.1003 ± 0.0012%) with a thickness of 0.1 mm were punched to disk shapes with the same diameter as the Lu-standards and packed in PE bags too.

Thermochromic substances change colour due to thermally induced chemical reaction or phase transformation, when a certain threshold temperature has been exceeded. This procedure can be either irreversible and used for one-time monitoring of the temperature or reversible and are suitable for multiple use. There are many commercial products for a wide range of applications with different designs from strip to clock shape stickers [15]. For this work, 5-level labels from company RS with 2 successive temperature ranges (40–54 °C and 60–82 °C) in steps of 3 to 6 °C were chosen. The labels indicate the temperatures by changing from white/grey to black permanently. Each label has a diameter of 14 mm, somewhat smaller than the standards. According to the information of the manufacturer, most irreversible labels usually go through a permanent change in less than 1 min and the temperature tolerance is ± 1 °C. Thermal crayons with different melting points were also used as reference. However, the temperature step of 10 °C is much larger than that of the labels. Small pieces of crayons were packed into PE-bags for irradiation. Standards, comparators, thermometer labels, and crayons were packed together in the irradiation capsule.

Irradiation

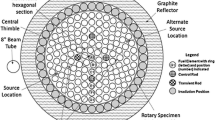
The research reactor FRM II has a compact hollow cylinder core of about 1.3 m in length, 24 cm in diameter with a single fuel element of highly enriched uranium located in the centre of the moderator tank filled with heavy water.

The temperature was measured in four irradiation positions (a “fishing” position and 3 rabbit channels) with different neutron fluxes and f values from 3300 to 6500. The irradiation durations were from 10 min to 1 h. The burn-up effect could be neglected due to the short irradiation time, although the thermal neutron cross sections of ¹⁷⁶Lu and ¹⁷⁷Lu are large (2100 barn, and 1000 barn). The radiation resistance of the used thermometer labels was proven up to 4 GGy gamma dose at the gamma-ray irradiation facility at FRM II. The dose values collected in the irradiation positions were estimated to be lower.

The “fishing” position (JBE70) is located in a vertical channel and filled with the reactor pool water. The Al-sample container has a wall thickness of 1 mm. It has direct thermal contact to the surrounding light water. This is a good condition for the temperature measurements, because a thermal equilibrium between the samples and the pool water can be reached quickly. The rabbit system (RPA) at FRM II consists of two groups with a total of six irradiation tubes mounted directly in the moderator behind the cold neutron source. The tubes are made of AlMg3 and have good thermal contact with the heavy water.

Gamma counting

All Au and Lu standards were measured at 25 cm with two HPGe detectors with relative efficiencies of 27–34%. The gamma counting was carried out using Genie 2000 (Mirion) spectroscopy software. The activity of ¹⁷⁷Lu was determined using the main gamma-line at 208 keV and the gold comparator at 412 keV line of ¹⁹⁸Au. The dead time of each counting and the uncertainties of counting statistic at the relevant gamma energies were less than 1% and 0.5%, respectively. Thus, the pile-up effect and the random coincidence effect could be neglected. The full-energy peak efficiencies at 25 cm from the detectors were calibrated by measuring a fresh standard of QCY48 from Eckert & Ziegler, a multiple radionuclide standard solution, which was pipetted on a filter paper (Whatman type 1001) with a diameter of 16 mm. All Lu standards, Au monitors, and the QCY48 standard had exactly the same geometry and were measured at the same distance, so any systematic errors could be minimized: only one efficiency curve was used, and a calculation for the solid angles was not necessary.

Results

Temperatures

The g factors were calculated according to Eq. 4 using data from the k₀ library [12]. The neutron temperatures were determined by means of Eq. 5 with different g(T_n) factors and are shown in Table 2 for 4 different irradiation positions with different irradiation durations. The values are averages of several measurements. The statistical and the total uncertainties are given in brackets for the Lu method. The neutron temperatures were between 35 and 51 °C calculated with the g(T_n) factors of Gryntakis, Westcott and van Sluijs, while the values of Holden were 8–9 °C lower. The Lu standards made with the ICP-standard solution and the LuAl–alloy showed the same results. For each irradiation position, the discrepancies between the four different values of the Lu method stem from the differences of the g(T_n) factors.

Table 2 Irradiation conditions and temperatures measured in 4 irradiation positions

The temperature labels showed a temperature range between 40 °C (in two rabbit positions RPA2, 5) and 54 °C (in the fishing positions JBE70). The results of the thermal crayons (melt or not) covered this range too. Figure 2 shows the temperature labels and standards after the irradiation in the position RPA3, where the temperature was between 46 and 49 °C.

Fig. 2

Thermometer labels and standards after irradiation in the rabbit system

The temperature in the moderator tank is monitored by the reactor control system continuously. The temperature sensors showed a temperature range between 34 °C at the heat exchanger and 64 °C in 30 cm from the reactor core with a temperature fluctuation less than 2 °C during the irradiation periods. The reactor pool water surrounding the moderator tank was 37 °C. The temperature values measured in the irradiation channels were in this temperature range of the reactor control system.

Uncertainties

The g factor calculated with Eq. 4 is the key parameter for the temperature determination using the Lu standard and the simplified extended Høgdahl convention. The uncertainty of the activities of Au and Lu includes the uncertainties of net peak areas N_p (< 0.5%) and sample weights W (< 0.1%), All other uncertainties related to the irradiation and the gamma counting such as the uncertainties of the time factors were not taken into account. These give a statistical uncertainty of about 0.7% for the calculation of the g factor.

Furthermore, the main contributions for the systematic uncertainty are the uncertainties of the concentration ρ of the standards (1.2% for Au and 0.5% for Lu) and the efficiency ratio. If the same efficiency curve is used, the efficiencies at 412 keV of Au und 208 keV of Lu are correlated. According the approach of Smodiš an uncertainty propagation factor of ca. 0.4 can be found for the ratio of the two energies [16]. The certificate of the QCY-standard gives 2.3% uncertainty of the activities used for the efficiency calibration. Thus, the uncertainty of this efficiency ratio is estimated to be 1%. The uncertainty of the experimentally determined g factor can be given with a simple propagation formula:

$$\frac{\Delta g}{g} = \sqrt {\left( {\frac{\Delta \rho }{\rho }} \right)_{\text{Au}}^{2} + \left( {\frac{\Delta \rho }{\rho }} \right)_{\text{Lu}}^{2} + \left( {\frac{{\Delta N_{\text{p}} }}{{N_{\text{p}} }}} \right)_{\text{Au}}^{2} + \left( {\frac{{\Delta N_{\text{p}} }}{{N_{\text{p}} }}} \right)_{\text{Lu}}^{2} + \left( {\frac{\Delta W}{W}} \right)_{\text{Au}}^{2} + \left( {\frac{\Delta W}{W}} \right)_{\text{Lu}}^{2} + \left( {\frac{{\Delta \varepsilon_{\text{p}} }}{{\varepsilon_{\text{p}} }}} \right)^{2} } = 1.8\% .$$

(6)

In addition, each calculation of the g(T_n) factors has its uncertainty, which can be estimated to be 2%. The uncertainty of the recommended k₀ value of ¹⁷⁷Lu is not given in the k₀ database. By definition, the k₀ value is the product of θ (the isotope abundance), σ₀ (the cross section at a neutron velocity of 2200 m s⁻¹) and e_γ (the absolute gamma-intensity) and these have uncertainties of 0.8%, 2.4% and 4% given in [4] for the 208 keV line. Combining these in quadrature, k₀ has an uncertainty of 4.7%. If all the uncertainties are taken into account, the total uncertainty of the Lu method is 5.4%.

The uncertainty of the temperature can be calculated with

$$\Delta T_{n} = a\Delta g$$

(7)

where a is the slope in the Eq. 5.

According to the data sheet of the thermometer label, the tolerance of the sensitivity is ± 1 °C from 29 to 99 °C [17]. However, the thermometer labels have discrete levels of 3 °C and 6 °C. The uncertainty is estimated to be ± 1.5 °C for the range 1 (40 to 49 °C) and ± 3 °C for the higher temperature levels. Compared to the results of the Lu method, the labels can likely give the temperature values more precisely.

Discussion

The highest temperature of 54 °C was measured in the “fishing” position (JBE70) filled with the light water. According to an MCNP calculation, the neutron absorption by the light water in this channel creates an additional thermal power of ca. 1 kW during the reactor operation. Due to this heating effect, the sample temperature must be higher than the temperature of the heavy water surrounding it. The temperature in the RPA3 position was found to be higher than at other rabbit system positions. This can be explained by the fact that this position is placed above the others and a thermal gradient exits.

Table 2 shows good agreement between the label temperatures and the Lu temperatures calculated with the g(T_n) factors by Gryntakis, Westcott and van Sluijs, considering the uncertainties of the temperatures calculated by the Lu method. As shown in Fig. 1, the difference between these three g(T_n) calculations is lower than 0.8%, although the first two data sources are already 50 years old. Holden’s g(T_n) factors are significantly higher than the others. Hence, the temperature values calculated with them are significantly lower. Those temperatures lower than the pool water temperature of 37 °C are obviously unrealistic.

On the other hand, the comparison between the Lu method and the measurement using thermometer labels can only partially evaluate which g(T_n) factors are the best. In k₀ NAA, the temperature determination using Lu is also directly dependent on the accuracy of the k₀ value. Until now, the recommended k₀ value of ¹⁷⁷Lu was calculated with nuclear data dated back to the 1980s and is not yet verified sufficiently; its uncertainty is estimated to be 4.7%. The neutron temperature T_n, g(T_n) factors and the k₀ value are in a circular dependence. The results show only that the combination of the Holden’s g(T_n) factors and the recommended k₀ value of ¹⁷⁷Lu is not suitable for the temperature determination.

The Lu method is sensitive due to the very steep slope of the g(T_n) factor lines (Fig. 1). As shown above, the measurement of Lu can bring only an uncertainty below 2% to the result, this corresponds to ca. 5 °C. The uncertainty of the k₀ value is the biggest error source in the whole calculation chain. It is much greater than the total uncertainty stemming from the experiment. Together with the uncertainty of the g(T_n) factor, the total uncertainty of the Lu method is about 15 °C for the temperature determination. This covers almost the same the temperature range in this work.

In the extended version of the modified Høgdahl convention (Eq. 2) and in the Eq. 4 derived directly from this algorithm, the g factor of Au has been neglected until now. Although this value is very small and not strongly dependent on the temperature, it can increase the g factor of Lu calculated with Eq. 4 about 0.5%. This corresponds to a temperature increase of about 1.5 °C in the temperature range from 40 to 55 °C. However, for the calculation of the Lu concentration in the k₀ NAA, this influence is quite small.

The results show that the temperature from the labels is systematically higher than the one from the Lu method. The reasons might be the irradiation effect on the labels and the errors of the g(T_n) factors and the k₀ value of Lu. Considering the uncertainties of each method, the temperature from the labels is closer to the local neutron temperature.

The irradiation duration plays a role in the temperature determination using the label method due to the heat transfer. The irradiation of 10 min was a test for the lower limit at our reactor. The label method will not be accurate for very short irradiations. On the other hand, very short irradiations are normally not used for the determination of non-1/v nuclides in practice. Furthermore, the property and the volume of the real samples could also influence the heat transfer within the sample container.

The goal of this work was to investigate whether the temperature measured by using the thermometer labels instead of the Lu standards can be used for the extended k₀ NAA. We can treat the co-irradiated Lu standards as “unknown samples” and determine the Lu concentration with the label temperature in each irradiation using the Eq. 3 with the recommended k₀ value. The deviations from the certified concentration are normalized to 1 and given in Fig. 3. Depending on the different g(T_n) factors, the deviations are less than 2.5% and 5% (Holden) from the certified value. All the results in Fig. 3 are lower than the certified value which could mean a systematic error or indicate a smaller k₀ value of ¹⁷⁷Lu. A further investigation is needed to clarify it.

Fig. 3

The deviations of the determined Lu concentrations from the certified value

Generally, this method with the labels could create an error of maximum 3% for the Lu determination with the recommended k₀ value and much smaller for the other non-1/v nuclides which are not very sensitive to the temperature like ¹⁷⁶Lu. For comparison, e.g. the data of van Sluijs 2015 show that the g factors vary by 6.9% for ¹⁵¹Eu and 4.7% for ¹⁶⁸Yb, but 32% for ¹⁷⁶Lu in the temperature range from 20 to 100 °C. Even an error of 10 °C for the temperature determination would lead to an error less than 1% for the concentration determination of Eu and Yb.

Conclusions

The temperature distribution in a big reactor with diverse facilities in the moderator tank is complex. A difference of about 15 °C was found between the irradiation positions at FRM II. The neutron temperatures as determined with the Lu method and the thermometer labels are in good agreement, if the recommended k₀ value of ¹⁷⁷Lu and the g(T_n) factors of Gryntakis, Westcott and van Sluijs are used. All three g(T_n) factors for ¹⁷⁶Lu can be confidently used for the neutron temperature determination and also for the Lu determination in the extended k₀ NAA. The difference between them is less than 0.8% (ca. 2 °C) in the temperature range from 20 to 100 °C. The g(T_n) factors by Holden gave up to 10 °C lower results and therefore are not suitable for the temperature determination. The biggest uncertainty source of the Lu method comes from the k₀ value. The total uncertainty of this method is ca. 15 °C.

The thermometer labels can be used as reliable alternatives to Lu standards in the extended k₀ NAA for non-1/v nuclides. According to the investigation in this work, the slight discrepancies of temperature determination could create errors of maximum 3% in the analysis of the non-1/v nuclides in the samples. The thermometer labels can be used to determine the local temperature in the samples independently and therefore could provide a possibility to determine the k₀ value of Lu experimentally.