Random Walks in the Hyperbolic Plane and the Minkowski Question Mark Function

Abstract

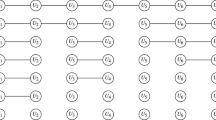
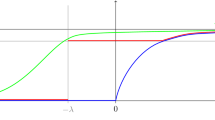
Consider $G=SL_2(\mathbb {Z})/\{\pm I\}$ acting on the complex upper half plane H by $h_M(z)=\frac{az\,+\,b}{cz\,+\,d}$ for $M \in G$. Let $D=\{z \in H: |z|\ge 1, |\mathfrak {R}(z)|\le 1/2\}$. We consider the set ${\mathcal {E}} \subset G$ with the nine elements M, different from the identity, such that $\mathrm{tr\,}(MM^T)\le 3$. We equip the tiling of H defined by $\mathbb {D}=\{h_M(D){:}\, M \in G\}$ with a graph structure where the neighbours are defined by $h_M(D) \cap h_{M'}(D) \ne \emptyset$, equivalently $M^{-1}M' \in {\mathcal {E}}$. The present paper studies several Markov chains related to the above structure. We show that the simple random walk on the above graph converges a.s. to a point X of the real line with the same distribution of $S_2 W^{S_1}$, where $S_1,S_2,W$ are independent with $\Pr (S_i=\pm 1)=1/2$ and where W is valued in (0, 1) with distribution $\Pr (W<w)=\mathbf ? (w)$. Here $\mathbf ?$ is the Minkowski function. If $K_1, K_2, \ldots$ are i.i.d with distribution $\Pr (K_i=n)= 1/2^n$ for $n=1,2,\ldots$, then $W= \frac{1}{K_1+\frac{1}{K_2+\ldots }}$: this known result (Isola in Appl Math 5:1067–1090, 2014) is derived again here.