GAUSSIAN-RBF INTERPOLANT AND THIRD-ORDER COMPACT DISCRETIZATION OF 2D ANOMALOUS DIFFUSION-CONVECTION MODEL ON A MESH-MAPPED NON-UNIFORM GRID NETWORK

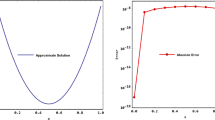
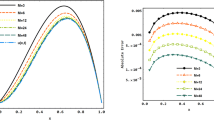
Abstract

We describe a compact finite-difference discretization and Gaussian-radial basis function for the two-dimensional local fractional elliptic PDEs that describe anomalous diffusion-convection of groundwater contamination. Precisely estimating pollutant concentration over a long period helps protect water reservoirs. The local fractional partial differential equations and their discretization described here are the generalization of the integer order elliptic partial differential equations and their high-order scheme. The high-order discretization of fractal gradient and anomalous diffusion on a non-uniformly spaced nine-point single-cell grid network gives the result in small computing time. The new scheme is supported by a detailed convergence analysis describing the monotone property and a strongly connected Jacobian (iteration) matrix graph. The computational illustration of various anomalous diffusion-convection models demonstrates the proposed methodology’s effectiveness.

Appendices

Appendix 1. Expression of weight coefficients in equation (5.2) and (5.3)

 

$a_{l}^{(0)}$	$\left( p_{l}-1\right) \left\{ 2 c^{2} h_{l} / 3+h_{l+1}^{-1}\right\}$	$b_{m}^{(0)}$	$\left( q_{m}-1\right) \left\{ 2 c^{2} k_{m} / 3+k_{m+1}^{-1}\right\}$
$a_{l+1}^{(0)}$	$\left\{ c^{2} h_{l}\left( p_{l}+2\right) / 3+h_{l+1}^{-1}\right\} /\left( p_{l}+1\right)$	$b_{m+1}^{(0)}$	$\left\{ c^{2} k_{m}\left( q_{m}+2\right) / 3+h_{l+1}^{-1}\right\} /\left( 1+q_{m}\right)$
$a_{l-1}^{(0)}$	$-p_{l}\left\{ c^{2} h_{l}\left( 2 p_{l}+1\right) / 3+h_{l}^{-1}\right\} /\left( p_{l}+1\right)$	$b_{m-1}^{(0)}$	$-q_{m}\left\{ c^{2} k_{m}\left( 2 q_{m}+1\right) / 3-k_{m}^{-1}\right\} /\left( q_{m}+1\right)$
$a_{l}^{(1)}$	$\left( p_{l}+1\right) \left\{ c^{2} h_{l}\left( p_{l}+2\right) / 3-h_{l+1}^{-1}\right\}$	$b_{m}^{(1)}$	$\left( q_{m}+1\right) \left\{ c^{2} k_{m}\left( q_{m}+2\right) / 3-k_{m+1}^{-1}\right\}$
$a_{l+1}^{(1)}$	$\left( 2 p_{l}+1\right) \left[ 1 /\left\{ h_{l+1}\left( p_{l}+1\right) \right\} -2 c^{2} h_{l} / 3\right]$	$b_{m+1}^{(1)}$	$\left( 2 q_{m}+1\right) \left[ 1 /\left\{ k_{m+1}\left( 1+q_{m}\right) \right\} -2 c^{2} k_{m} / 3\right]$
$a_{l-1}^{(1)}$	$p_{l}\left[ 1 /\left\{ h_{l}\left( 1+p_{l}\right) \right\} +c^{2} h_{l}\left( 1-p_{l}\right) / 3\right]$	$b_{m-1}^{(1)}$	$q_{m}\left[ 1 /\left\{ k_{m}\left( 1+q_{m}\right) \right\} +c^{2} k_{m}\left( 1-q_{m}\right) / 3\right]$
$a_{l}^{(2)}$	$\left( p_{l}+1\right) \left\{ 1 / h_{l}-c^{2} h_{l}\left( 2 p_{l}+1\right) / 3\right\} / p_{l}$	$b_{m}^{(2)}$	$\left( q_{m}+1\right) \left\{ 1 / k_{m}-c^{2} k_{m}\left( 2 q_{m}+1\right) / 3\right\} / q_{m}$
$a_{l+1}^{(2)}$	$-\left[ 1 /\left\{ h_{l}\left( p_{l}+1\right) \right\} +c^{2} h_{l}\left( p_{l}-1\right) / 3\right] / p_{l}$	$b_{m+1}^{(2)}$	$-\left[ 1 /\left\{ k_{m}\left( q_{m}+1\right) \right\} +c^{2} k_{m}\left( q_{m}-1\right) / 3\right] / q_{m}$
$a_{l-1}^{(2)}$	$\left( p_{l}+2\right) \left[ 2 c^{2} h_{l} / 3-1 /\left\{ h_{l}\left( p_{l}+1\right) \right\} \right]$	$b_{m-1}^{(2)}$	$\left( q_{m}+2\right) \left[ 2 c^{2} k_{m} / 3-1 /\left\{ k_{m}\left( q_{m}+1\right) \right\} \right]$
$a_{l}^{(3)}$	$2\left( 2 p_{l}^{2}-7 p_{l}+2\right) c^{2} /\left( 3 p_{l}\right) -2 /\left( p_{l} h_{l}^{2}\right)$	$b_{m}^{(3)}$	$2\left( 2 q_{m}^{2}-7 q_{m}+2\right) c^{2} /\left( 3 q_{m}\right) -2 /\left( q_{m} k_{m}^{2}\right)$
$a_{l+1}^{(3)}$	$2\left\{ \left( p_{l}^{2}+4 p_{l}-2\right) c^{2} / 3+h_{l}^{-2}\right\} /\left\{ p_{l}\left( p_{l}+1\right) \right\}$	$b_{m+1}^{(3)}$	$2\left\{ \left( q_{m}^{2}+4 q_{m}-2\right) c^{2} / 3+k_{m}^{-2}\right\} /\left\{ q_{m}\left( q_{m}+1\right) \right\}$
$a_{l-1}^{(3)}$	$2\left\{ -\left( 2 p_{l}^{2}-4 p_{l}-1\right) c^{2} / 3+h_{l}^{-2}\right\} /\left( p_{l}+1\right)$	$b_{m-1}^{(3)}$	$2\left\{ -\left( 2 q_{m}^{2}-4 q_{m}-1\right) c^{2} / 3+k_{m}^{-2}\right\} /\left( q_{m}+1\right)$

Appendix 2. Expression of weight coefficients in equation (6.5) and (6.6)

 

$\rho _{0}$	$\left( \rho _{2}-\rho _{1} p_{l}\right) /\left[ \left( p_{l}+1\right) P_{l, m}^{x}\right]$	$\sigma _{0}$	$\left( \sigma _{2}-\sigma _{1} q_{m}\right) /\left[ \left( q_{m}+1\right) Q_{l, m}^{y}\right]$
$\rho _{1}$	$-\frac{\rho _{2} t_{1}-\left( t_{0} \rho _{2}+3 c^{2} p^{+} h_{l} p_{l} q_{m}\right) P_{l, m} Q_{l, m}}{t_{1}-t_{0} P_{l, m} Q_{l, m}}$	$\sigma _{1}$	$-\frac{\sigma _{2} t_{1}-\left( t_{0} \sigma _{2}+3 c^{2} q^{+} k_{l} p_{l} q_{m}\right) P_{l, m} Q_{l, m}}{t_{1}-t_{0} P_{l, m} Q_{l, m}}$
$\rho _{2}$	$\frac{p_{l} q_{m}\left\{ t_{0}\left( 6 c^{2} h_{l} p_{l} P_{l, m}+P_{l, m}^{x}\right) P_{l, m} Q_{l, m}-t_{1} P_{l, m}^{x}\right\} p^{+}}{2 t_{0}\left( t_{1}-t_{0} P_{l, m} Q_{l, m}\right) \left( p_{l}+1\right) P_{l, m}}$	$\sigma _{2}$	$\frac{p_{l} q_{m}\left\{ t_{0}\left( 6 c^{2} k_{m} q_{m} Q_{l, m}+Q_{l, m}^{y}\right) P_{l, m} Q_{l, m}-t_{1} Q_{l, m}^{y}\right\} q^{+}}{2 t_{0}\left( t_{1}-t_{0} P_{l, m} Q_{l, m}\right) \left( q_{m}+1\right) Q_{l, m}}$
$\rho _{3}$	$\rho _{0} h_{l}\left( p_{l}+1\right) Q_{l, m}^{x} /\left[ k_{m}\left( q_{m}+1\right) \right]$	$\sigma _{3}$	$\sigma _{0} k_{m}\left( q_{m}+1\right) P_{l, m}^{y} /\left[ h_{l}\left( p_{l}+1\right) \right]$
$\rho _{4}$	$\frac{t_{2} h_{l} p_{l} q_{m} P_{l, m} Q_{l, m}}{2 t_{0}\left( t_{1}-t_{0} P_{l, m} Q_{l, m}\right) k_{m}\left( p_{l}+1\right) P_{l, m}}$	$\sigma _{4}$	$\frac{t_{2} k_{m} p_{l} q_{m}\left( P_{l, m}\right) ^{2}}{2 t_{0}\left( t_{1}-t_{0} P_{l, m} Q_{l, m}\right) h_{l}\left( q_{m}+1\right) P_{l, m}}$
$t_{0}$	$2 p_{l}^{2} q_{m}^{2}-p_{l}^{2} q_{m}-p_{l} q_{m}^{2}+2 p_{l}^{2}+8 p_{l} q_{m}+2 q_{m}^{2}-p_{l}-q_{m}+2$
$t_{1}$	$h_{l} q_{m}\left( p_{l}-1\right) p^{+} Q_{l, m} P_{l, m}^{x}+k_{m} p_{l}\left( q_{m}-1\right) q^{+} P_{l, m} Q_{l, m}^{y}$
$t_{2}$	$h_{l} q_{m}\left( p_{l}-1\right) p^{+2} Q_{l, m} P_{l, m}^{x}+\left( t_{0} h_{l} p^{+} Q_{l, m}^{x}+k_{m} p_{l}\left( q_{m}-1\right) p^{+} q^{+} Q_{l, m}^{y}-t_{0} p^{+} Q_{l, m}\right.$

Appendix 3. Values of coefficients in equation (6.8)

 

$Z_{10}$	$h_{l}\left\{ a_{l+1}^{(0)}\left( k_{m} b_{m}^{(0)} t_{11}+t_{10}\right) +h_{l} a_{l+1}^{(3)} t_{20}\right\}$	$Z_{21}$	$a_{l-1}^{(0)} b_{m+1}^{(0)}$
$Z_{20}$	$h_{l}\left\{ a_{l-1}^{(0)}\left( k_{m} b_{m}^{(0)} t_{11}+t_{10}\right) +h_{l} a_{l-1}^{(3)} t_{20}\right\}$	$Z_{22}$	$a_{l-1}^{(0)} b_{m-1}^{(0)}$
$Z_{01}$	$k_{m}\left\{ b_{m+1}^{(0)}\left( h_{l} a_{l}^{(0)} t_{11}+t_{01}\right) +k_{m} b_{m+1}^{(3)} t_{02}\right\}$	$Z_{11}$	$a_{l+1}^{(0)} b_{m+1}^{(0)}$
$Z_{02}$	$k_{m}\left\{ b_{m-1}^{(0)}\left( h_{l} a_{l}^{(0)} t_{11}+t_{01}\right) +k_{m} b_{m-1}^{(3)} t_{02}\right\}$	$Z_{12}$	$a_{l+1}^{(0)} b_{m-1}^{(0)}$
$Z_{00}$	$1+h_{l} a_{l}^{(0)} t_{10}+k_{m} b_{m}^{(0)} t_{01}+h_{l} k_{m} a_{l}^{(0)} b_{m}^{(0)} t_{11}+h_{l}^{2} a_{l}^{(3)} t_{20}+k_{m}^{2} b_{m}^{(3)} t_{02}$
$t_{10}$	$\left( p_{l}-1\right) / 3-h_{l} P_{l, m}^{x}\left( p_{l}^{2}+p_{l}+1\right) /\left( 18 P_{l, m}\right)$
$t_{01}$	$\left( q_{m}-1\right) / 3-k_{m} Q_{l, m}^{y}\left( q_{m}^{2}+q_{m}+1\right) /\left( 18 Q_{l, m}\right)$
$t_{11}$	$\left( q_{m}-1\right) \left( p_{l}-1\right) / 9$
$t_{20}$	$\left( p_{l}^{2}-p_{l}+1\right) / 12$
$t_{02}$	$\left( q_{m}^{2}-q_{m}+1\right) / 12$
$\mathcal {C}_{10}$	$\left( p_{l}-1\right) \left\{ 3 P_{l, m}+k_{m}\left( q_{m}-1\right) P_{l, m}^{y}+h_{l}\left( p_{l}-1\right) P_{l, m}^{x}\right\}$
$\mathcal {C}_{01}$	$\left( q_{l}-1\right) \left\{ 3 Q_{l, m}+k_{m}\left( q_{m}-1\right) Q_{l, m}^{y}+h_{l}\left( p_{l}-1\right) Q_{l, m}^{x}\right\}$
$\mathcal {C}_{11}$	$\left( p_{l}-1\right) \left( q_{l}-1\right) \left( P_{l, m}+Q_{l, m}\right)$
$\mathcal {C}_{12}$	$p^{+} h_{l} P_{l, m}^{x} Q_{l, m}-\left[ 2\left( p_{l}-1\right) \left\{ 3 Q_{l, m}-\left( 1-q_{m}\right) k_{m} Q_{l, m}^{y}\right\} +3 p^{-} h_{l} Q_{l, m}^{x}\right] P_{l, m}$
$\mathcal {C}_{21}$	$q^{+} k_{m} P_{l, m} Q_{l, m}^{y}-\left[ 2\left( q_{m}-1\right) \left\{ 3 P_{l, m}-\left( 1-p_{l}\right) h_{l} P_{l, m}^{x}\right\} +3 q^{-} k_{m} P_{l, m}^{y}\right] Q_{l, m}$
$\mathcal {C}_{22}$	$q^{-} h_{l}^{2} P_{l, m}+p^{-} k_{m}^{2} Q_{l, m}$
$\mathcal {C}_{20}$	$12\left( c^{2} h_{l}^{2} p^{+}-3\right) P_{l, m}^{2} Q_{l, m}+2 p^{+} h_{l}^{2}\left( P_{l, m}^{x}\right) ^{2} Q_{l, m}- \Bigg [4 h_{l} k_{m}\left( p_{l}-1\right) \left( q_{l}-1\right) P_{l, m}^{x y} Q_{l, m}+3\Bigg \{4 k_{m}\left( q_{m}- 1\right) P_{l, m}^{y}+4 h_{l}\left( p_{l}-1\right) P_{l, m}^{x}+q^{-} k_{m}^{2} P_{l, m}^{y y}+p^{-} h_{l}^{2} P_{l, m}^{x x}\Bigg \} Q_{l, m}-2 q^{+} k_{m}^{2} P_{l, m}^{y} Q_{l, m}^{y}\Bigg ] P_{l, m}$
$\mathcal {C}_{02}$	$12\left( c^{2} k_{m}^{2} q^{+}-3\right) P_{l, m} Q_{l, m}^{2}+2 q^{+} k_{m}^{2} P_{l, m}\left( Q_{l, m}^{y}\right) ^{2}-\Bigg [4 h_{l} k_{m}\left( p_{l}-1\right) \left( q_{l}-1\right) P_{l, m} Q_{l, m}^{x y}+3\Bigg \{4 k_{m}\left( q_{l}- 1\right) Q_{l, m}^{y}+4 h_{l}\left( p_{l}-1\right) Q_{l, m}^{x}+q^{-} k_{m}^{2} Q_{l, m}^{y y}+p^{-} h_{l}^{2} Q_{l, m}^{x x}\Bigg \} P_{l, m}-2 p^{+} h_{l}^{2} P_{l, m}^{x} Q_{l, m}^{x}\Bigg ] Q_{l, m}$

Fig. 1

Solution profile for the fractal parameter $\alpha = 0.6,\ 0.8,\ 1.0$

Fig. 2

Solution profile for the fractal parameter $\alpha = 0.4,\ 0.7,\ 1.0$

Fig. 3

Solution profile for the fractal parameter $\alpha = 0.4,\ 0.8,\ 1.0$

Fig. 4

Solution profile for the fractal parameter $\alpha = 0.2,\ 0.8,\ 1.0$