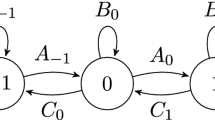
We consider random multi-dimensional lattice walks bounded by a hyperplane, calling them walks over multi-dimensional simplicial lattices. We demonstrate that generating functions of these walks are dynamical correlation functions of a certain type of exactly solvable quantum phase models describing strongly correlated bosons on a chain. Walks over oriented lattices are related to the phase model with a non-Hermitian Hamiltonian, while walks over disoriented ones are related to the model with a Hermitian Hamiltonian. The calculation of the generating functions is based on the algebraic Bethe Ansatz approach to the solution of integrable models. The answers are expressed through symmetric functions. Continuous-time quantum walks bounded by a onedimensional lattice of finite length are also studied. Bibliography: 40 titles.
Similar content being viewed by others
References
R. Stanley, Enumerative Combinatorics, Vols. 1, 2, Cambridge Univ. Press, Cambridge (1996, 1999).
C. Krattenthaler and S. G. Mohanty, Lattice Path Combinatorics – Applications to Probability and Statistics, Wiley, New York (2003).
C. Krattenthaler, The Major Counting of Nonintersecting Lattice Paths and Generating Functions for Tableaux, Memoirs of the Amer. Math. Soc., 115, No. 552, Amer. Math. Soc. (1995).
C. Krattenthaler, “Lattice path enumeration,” arXiv:1503.05930.
M. Fisher, “Walks, walls, wetting and melting,” J. Stat. Phys., 34, 667–729 (1984).
P. Forrester, “Random walks and random permutations,” J. Phys. A, 34, L417–L423 (2001).
S. Bravyi, L. Caha, R. Movassagh, D. Nagaj, and P. W. Shor, “Criticality without frustration for quantum spin-1 chains,” Phys. Rev. Lett., 109, 207202–207205 (2012).
R. Movassagh, “Entanglement and correlation functions of a recent exactly solvable spin chain,” arXiv:1602.07761.
O. Salberger and V. Korepin, “Fredkin spin chain,” arXiv:1605.03842v1.
L. A. Takhtadzhyan and L. D. Faddeev, “The quantum method of the inverse problem and the Heisenberg XY Z model,” Russian Math. Surveys, 34, 11–68 (1979).
V. E. Korepin, N. M. Bogoliubov, and A. G. Izergin, Quantum Inverse Scattering Method and Correlation Functions, Cambridge Univ. Press, Cambridge (1993).
C. Korff and C. Stroppel, “The \( \widehat{sl{(n)}_k} \) -WZNW fusion ring: a combinatorial construction and a realisation as quotient of quantum cohomology,” Adv. Math., 225, 200–268 (2010).
N. V. Tsilevich, “Quantum inverse scattering method for the q-boson model and symmetric functions,” Funct. Anal. Appl., 40, 207–217 (2006).
N. Bogoliubov, “XXO Heisenberg chain and random walks,” J. Math. Sci., 138, 5636–5643 (2006).
N. M. Bogoliubov and C. Malyshev, “Correlation functions of XX0 Heisenberg chain, q-binomial determinants, and random walks,” Nucl. Phys. B, 879, 268–291 (2014).
N. Bogoliubov and C. Malyshev, “Integrable models and combinatorics,” Russian Math. Surveys, 70, 789–856 (2015).
D. M. Bressoud, Proofs and Confirmations. The Story of the Alternating Sign Matrix Conjecture, Cambridge Univ. Press, Cambridge (1999).
I. G. Macdonald, Symmetric Functions and Hall Polynomials, Oxford Univ. Press, Oxford (1995).
Y. Aharonov, L. Davidovich, and N. Zagury, “Quantum random walks,” Phys. Rev. A, 48, 1687–1690 (1993).
E. Farhi and S. Gutmann, “Quantum computation and decision trees,” Phys. Rev. A, 58, 915–928 (1998).
F. Strauch, “Connecting the discrete- and continuous-time quantum walks,” Phys. Rev. A, 74, 030301(R) (2006).
P. Preiss, R. Ma, M. Tai, A. Lukin, M. Rispoli, P. Zupancic, Y. Lahini, R. Islam, and M. Greiner, “Strongly correlated quantum walks in optical lattices,” Science, 347, 1229–1233 (2015).
C. Cedzich, A. Grünbaum, C. Stahl, L. Velázquez, A. Werner, and R. Werner, “Bulk-edge correspondence of one-dimensional quantum walks,” arXiv:1502.0592.
Y. Lahini, G. Steinbrecher, A. Bookatz, and D. Englund, “High-fidelity quantum logic gates with interacting bosons on a 1D lattice,” arXiv:1501.04349.
T. Mackay, S. Bartlett, L. Stephenson, and B. Sanders, “Quantum walks in higher dimensions,” J. Phys. A, 35, 2745–2753 (2002).
K. Watabe, N. Kobayashi, M. Katori, and N. Konno, “Limit distributions of twodimensional quantum walks,” Phys. Rev. A, 77, 062331 (2008).
A. Romanelli, R. Donangelo, R. Portugal, and F. Marquezino, “Thermodynamics of N-dimensional quantum walks,” arXiv:1408.5300.
P. R. G. Mortimer and T. Prelling, “On the number of walks in a triangular domain,” arXiv:1402.4448.
N. Bogoliubov, “Quantum walks and phase operators,” to be published.
P. Carruters and M. Nieto, “Phase and angle variables in quantum mechanics,” Rev. Mod. Phys., 40, 411 (1968).
N. M. Bogoliubov and T. Nassar, “On the spectrum of the non-Hermitian phase-difference model,” Phys. Lett. A, 234, 345–350 (1997).
A. M. Vershik, “Equipped graded graphs, projective limits of simplices, and their boundaries,” J. Math. Sci., 209, 860–873 (2015).
N. Bogoliubov, R. Bullough, and J. Timonen, “Critical behavior for correlated strongly coupled boson systems in 1 + 1 dimensions,” Phys. Rev. Lett., 25, 3933–3936 (1994).
N. Bogoliubov, A. Izergin, and N. Kitanine, “Correlation functions for a strongly correlated boson systems,” Nucl. Phys. B, 516, 501–528 (1998).
N. Bogoliubov, “Calculation of correlation functions in totally asymmetric exactly solvable models on a ring,” Theor. Math. Phys., 175, 755–762 (2013).
N. Bogoliubov, “Boxed plane partitions as an exactly solvable boson model,” J. Phys. A, 38, 9415–9430 (2005).
N. Bogoliubov, “Form factors, plane partitions and random walks,” J. Math. Sci., 158, 771–786 (2009).
N. M. Bogolyubov, A. G. Izergin, N. A. Kitanin, and A. G. Pronko, “On the probabilities of survival and hopping of states in a phase model on a finite lattice,” Proc. Steklov Inst. Math., 226, 29–41 (1999).
N. M. Bogoliubov, A. G. Izergin, N. A. Kitanine, A. G. Pronko, and J. Timonen, “Quantum dynamics of strongly interacting boson systems: atomic beam splitters and coupled Bose–Einstein condensates,” Phys. Rev. Lett., 86, 4439–4442 (2001).
N. Bogoliubov, J. Timonen, and M. Zvonarev, “Coherent quantum oscillations in coupled traps with ultracold atoms,” arXiv:cond-mat/0201335.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Published in Zapiski Nauchnykh Seminarov POMI, Vol. 448, 2016, pp. 48–68.
Rights and permissions
About this article
Cite this article
Bogoliubov, N., Malyshev, C. Multi-Dimensional Random Walks and Integrable Phase Models. J Math Sci 224, 199–213 (2017). https://doi.org/10.1007/s10958-017-3405-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-017-3405-5