Skip to main content
SpringerLink
Log in

Mass Sources and Modeling of Subsurface Heterogeneities in Deformable Solids

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

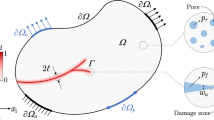
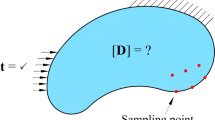
We propose an approach to the description of thermoelastic processes in deformable solids with regard for the structural heterogeneity of the material and the geometric heterogeneity of the surface of the body. In formulating the source relations, we use the methods of thermodynamics of nonequilibrium processes and nonlinear continuum mechanics. We take into account the structure of the material by introducing an irreversible component of the vector of mass flow. The geometric subsurface heterogeneity of the body is taken into account by introducing mass sources modeling its properties and by the dependence of the characteristics of materials, including the moduli of elasticity, on density. We study the equilibrium state of the half space. It is shown that two characteristic sizes correspond to the distributions of stresses and density. One of these sizes is connected with the structural heterogeneity of the material and the other is connected with the geometric heterogeneity of the actual surface of the body. We discuss the limits of applicability of the local gradient approach in the case of linearized approximation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ya. I. Burak, and T. S. Nagirnyi, “Mathematical modeling of local gradient processes in inertial thermomechanical systems,” Prikl. Mekh., 28, No. 12, 3–23 (1992); English translation: Int. Appl. Mech., 28, No. 12, 775–793 (1992).

  2. Ya. Burak, E. Chaplya, T. Nahirnyi, V. Chekurin, V. Kondrat, O. Chernukha, H. Moroz, and K. Chervinka, Physicomathematical Modeling of Complex Systems [in Ukrainian], SPOLOM, Lviv (2004).

  3. P. Glansdorff and I. Prigogine, Thermodynamic Theory of Structure, Stability and Fluctuations, Wiley, London (1971).

    MATH  Google Scholar 

  4. A. N. Guz and J. J. Rushchitsky, “Establishing foundations of the mechanics of nanocomposites (Review),” Prikl. Mekh., 47, No. 1, 4–61 (2011); English translation: Int. Appl. Mech., 47, No. 1, 2–44 (2011).

  5. T. S. Nahirnyi and K. A, Chervinka, Thermodynamic Models and Methods of Thermomechanics with Regard for the Subsurface and Structural Heterogeneities. Fundamentals of Nanomechanics I [in Ukrainian], SPOLOM, Lviv (2012).

  6. T. S. Nahirnyj, K. A. Chervinka, and Z. V. Boiko, “On the choice of boundary conditions in problems of the local gradient approach in thermomechanics,” Mat. Met. Fiz.-Mekh. Polya, 54, No. 3, 199–206 (2011); English translation: J. Math. Sci., 186, No. 1, 130–138 (2012).

  7. W. Nowacki, Teoria Sprężystości, PWN, Warszawa (1970).

    MATH  Google Scholar 

  8. G. G. Adams, “Adhesion at the wavy contact interface between two elastic bodies,” Trans. ASME. J. Appl. Mech., 71, No. 6, 851–856 (2004).

    Article  MATH  Google Scholar 

  9. H. Askes and E. C. Aifantis, “Gradient elasticity in statics and dynamics: An overview of formulations, length scale identification procedures, finite element implementations and new results,” Int. J. Solids Struct., 48, No. 13, 1962–1990 (2011).

    Article  Google Scholar 

  10. H. Askes and I. M. Gitman, “Review and critique of the stress gradient elasticity theories of Eringen and Aifantis,” in: G. A. Maugin and A. V. Metrikine (editors), Mechanics of Generalized Continua: One Hundred Years After the Cosserats, Chapter 21, Ser. Advances in Mechanics and Mathematics, Vol. 21, Springer, New York (2010), pp. 203–210.

  11. E. C. Aifantis, “Exploring the applicability of gradient elasticity to certain micro/nano reliability problems,” Microsyst. Technol., 15, No. 1, 109–115 (2009).

    Article  Google Scholar 

  12. V. A. Buryachenko, “On thermoelastostatics of composites with nonlocal properties of constituents. I. General representations for effective material and field parameters,” Int. J. Solids Struct., 48, No. 13, 1818–1828 (2011).

    Article  Google Scholar 

  13. Z. P. Bažant, Scaling of Structural Strength, Elsevier, London (2005).

    MATH  Google Scholar 

  14. Z. P. Bažant and M. Jirásek, “Nonlocal integral formulations of plasticity and damage: Survey of progress,” J. Eng. Mech.-ASCE, 128, No. 11, 1119–1149 (2002).

    Article  Google Scholar 

  15. M. G. D. Geers, V. G. Kouznetsova, and W. A. M. Brekelmans, “Multi-scale computational homogenization: Trends and challenges,” J. Comput. Appl. Math., 234, No. 7, 2175–2182 (2010).

    Article  MATH  Google Scholar 

  16. N. M. Ghoniem, E. P. Busso, N. Kioussis, and H. Huang, “Multiscale modeling of nanomechanics and micromechanics: An overview,” Phil. Mag., 83, Nos. 31-34, 3475–3528 (2003).

  17. J.-G. Guo and Y.-P. Zhao, “The size-dependent elastic properties of nanofilms with surface effects,” J. Appl. Phys., 98, No. 7, 074306–11 (2005).

    Article  Google Scholar 

  18. T. Nahirnyj and K. Tchervinka, “Interface phenomena and interaction energy at the surface of electroconductive solids,” Comput. Meth. Sci. Technol., 14, No. 2, 105–110 (2008).

    Article  Google Scholar 

  19. G. A. Maugin, “Nonlocal theories or gradient-type theories: A matter of convenience?” Arch. Mech., 31, No. 1, 15–26 (1979).

    MathSciNet  MATH  Google Scholar 

  20. M. D. Paola, G. Failla, and M. Zingales, “The mechanically-based approach to 3D nonlocal linear elasticity theory: Long-range central interactions,” Int. J. Solids Struct., 47, Nos. 18-19, 2347–2358 (2010).

  21. C. Polizzotto, “Unified thermodynamic framework for nonlocal/gradient continuum theories,” Eur. J. Mech. A-Solid, 22, No. 5, 651–668 (2003).

    Article  MathSciNet  MATH  Google Scholar 

  22. C. Polizzotto, P. Fuschi, and A. A. Pisano, “A strain-difference-based nonlocal elasticity model,” Int. J. Solids Struct., 41, Nos. 9-10, 2383–2401 (2004).

  23. C. Sansour and S. Skatulla, “A strain gradient generalized continuum approach for modeling elastic scale effects,” Comput. Meth. Appl. Mech. Eng., 198, Nos. 15-16. 1401–1412 (2009).

  24. S. Schmauder and L Mishnaevsky Jr., Micromechanics and Nanosimulation of Metals and Composites: Advanced Methods and Theoretical Concepts, Springer, Berlin–Heidelberg (2009).

  25. R. M. Shvets, R. M. Martynyak, and A. A. Kryshtafovych, “Discontinuous contact of an anisotropic half plane and a rigid base with disturbed surface,” Int. J. Eng. Sci., 34, No. 2, 183–200 (1996).

    Article  MATH  Google Scholar 

  26. C. P. Ursenbach, “Simulation of elastic moduli for porous materials,” CREWES Res. Rep., 13, 83–98 (2001).

    Google Scholar 

  27. Y. M. Wang and E. Ma, “Mechanical properties of bulk nanostructured metals,” in: M. J. Zehetbauer and Y. T. Zhu (editors), Bulk Nanostructured Materials, Chapter 19, Wiley–VCH, Weinheim (2009), pp. 425–453.

  28. A. Zaoui, “Continuum micromechanics: Survey,” J. Eng. Mech.-ASCE, 128, No. 8, 808–816 (2002).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center of Mechanical Modeling, Pidstryhach Institute for Applied Problems in Mechanics and Mathematics, Ukrainian National Academy of Sciences, Lviv, Ukraine

    T. S. Nahirnyi

  2. University of Zielona Góra, Zielona Góra, Poland

    T. S. Nahirnyi

  3. Franko Lviv National University, Lviv, Ukraine

    K. A. Chervinka

Authors
  1. T. S. Nahirnyi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. A. Chervinka
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 57, No. 4, pp. 84–94, October–December, 2014.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nahirnyi, T.S., Chervinka, K.A. Mass Sources and Modeling of Subsurface Heterogeneities in Deformable Solids. J Math Sci 220, 103–115 (2017). https://doi.org/10.1007/s10958-016-3170-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-016-3170-x

Search

Navigation