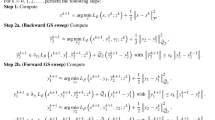Skip to main content
SpringerLink
Log in

Denoising and Inpainting of Images Using Tv-Type Energies: Theoretical and Computational Aspects

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

We discuss variational approaches towards the denoising of images and towards the image inpainting problem combined with simultaneous denoising. Our techniques are based on variants of the TV-model, but in contrast to this case a complete analytical theory is available in our setting. At the same time, numerical experiments illustrate the advantages of our models in comparison with some established techniques. Bibliography: 50 titles. Illustrations: 1 figure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. Acar and C. R., Vogel, “Analysis of bounded variation penalty methods for ill-posed problems,” Inverse Probl. 10, No. 6, 1217–1229 (1994).

  2. G. Aubert and L. Vese, “A variational method in image recovery,” SIAM J. Numer. Anal. 34, No. 5, 1948–1979 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  3. P. Blomgren, T. F. Chan, P. Mulet, L. Vese, and W. L. Wan, “Variational PDE models and methods for image processing,” In: Numerical Analysis 1999, pp. 43–67, Chapman and Hall/CRC, Boca Raton, FL (2000).

  4. V. Caselles, A. Chambolle, and M. Novaga, “Regularity for solutions of the total variation denoising problem,” Rev. Mat. Iberoam. 27, No. 1, 233–252 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  5. A. Chambolle and P.-L. Lions, “Image recovery via total variation minimization and related problems,” Numer. Math. 76, No. 2, 167–188 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  6. T. F. Chan and S. Esedoglu, “Aspects of total variation regularized L1 function approximation,” SIAM J. Appl. Math. 65, No. 5, 1817–1837 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  7. T. Chan, J. Shen, and L. Vese, “Variational PDE models in image processing,” Notices Am. Math. Soc. 50, No. 1, 14–26 (2003).

    MathSciNet  MATH  Google Scholar 

  8. Y. Chen, S. Levine, and M. Rao, “Variable exponent, linear growth functionals in image restoration,” SIAM J. Appl. Math. 66, No. 4, 1383–1406 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  9. B. Kawohl, “Variational versus PDE-based approaches in mathematical image processing,” CRM Proc. Lect. Notes 44, 113–126 (2008).

    MathSciNet  MATH  Google Scholar 

  10. L. Rudin, S. Osher, and E. Fatemi, “Nonlinear total variation based noise removal algorithms,” Physica D 60, 259–268 (1992).

    Article  MathSciNet  MATH  Google Scholar 

  11. L. Vese, “A study in the BV space of a denoising-deblurring variational problem,” Appl. Math. Optimization 44, No. 2, 131–161 (2001).

    Article  MathSciNet  MATH  Google Scholar 

  12. M. Bildhauer and M. Fuchs, “A variational approach to the denoising of images based on different variants of the TV-regularization,” Appl. Math. Optim. 66, No. 3, 331–361 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  13. P. Arias, V. Caselles, G. Facciolo, V. Lazcano, and R. Sadek, “Nonlocal variational models for inpainting and interpolation,” Math. Models Methods Appl. Sci. 22, Suppl.2, 1230003 (2012).

  14. P. Arias, V. Caselles, and G. Sapiro, “A variational framework for non-local image inpainting,” In: Energy Minimization Methods in Computer Vision and Pattern Recognition, pp. 345–358, Springer, Berlin (2009).

  15. P. Arias, G. Facciolo, V. Caselles, and G. Sapiro, “A variational framework for exemplarbased image inpainting,” Int. J. Comput. Vis. 93, No. 3, 319–347 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  16. G. Aubert and P. Kornprobst, Mathematical Problems in Image Processing, Springer, New York (2002).

    MATH  Google Scholar 

  17. M. Bertalmio, G. Sapiro, V. Caselles, and C. Ballester, “Image inpainting,” In: Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, pp. 417–424,

  18. M. Burger, L. He, and C.-B. Schӧnlieb, “Cahn-Hilliard inpainting and a generalization for grayvalue images,” SIAM J. Imaging Sci. 2, No. 4, 1129–1167 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  19. T. F. Chan, S. H. Kang, and J. Shen, “Euler’s elastica and curvature based inpaintings,” SIAM J. Appl. Math. 63, No. 2, 564–592 (2002).

    MathSciNet  MATH  Google Scholar 

  20. T. F. Chan and J. Shen, “Nontexture inpainting by curvature-driven diffusions,” J. Visual Commun. Image Represen. 12, No. 4, 436–449 (2001).

    Article  Google Scholar 

  21. T. F. Chan and J. Shen, “Mathematical models for local nontexture inpaintings,” SIAM J. Appl. Math. 62, No. 3, 1019–1043 (2001).

    MathSciNet  MATH  Google Scholar 

  22. S. Esedoglu and J. Shen, “Digital inpainting based on the Mumford-Shah-Euler image model,” European J. Appl. Math. 13, No. 4, 353–370 (2002).

    Article  MathSciNet  MATH  Google Scholar 

  23. K. Papafitsoros, B. Sengul, and C.-B. Schӧnlieb, Combined First and Second Order Total Variation Impainting Using Split Bregman, IPOL Preprint (2012).

  24. J. Shen, “Inpainting and the fundamental problem of image processing,” SIAM News 36, No. 5, 1–4 (2003).

  25. M. Bildhauer and M. Fuchs, “Image inpainting with energies of linear growth. A collection of proposals,” J. Math. Sci., New York 196, No. 4, 490–497 (2014).

  26. M. Bildhauer and M. Fuchs, “On some perturbations of the total variation image inpainting method. Part I: Regularity theory,” J. Math. Sci., New York 202, No. 2, 154–169 (2014).

  27. M. Bildhauer and M. Fuchs, “On some perturbations of the total variation image inpainting method. Part II: Relaxation and dual variational formulation,” J. Math. Sci., New York 202, No. 2, 121–140 (2015).

  28. M. Bildhauer and M. Fuchs, “On some perturbations of the total variation image inpainting method. Part III: Minimization among sets with finite perimeter,” J. Math. Sci., New York 207, No. 2, 142–146 (2015).

  29. M. Bildhauer, M. Fuchs, and C. Tietz, “C 1,α-interior regularity for minimizers of a class of variational problems with linear growth related to image inpainting,” St. Petersb. Math. J. 27, No. 3, 381–392 (2016).

  30. R. A. Adams, Sobolev Spaces, Academic Press, New York (1975),

    MATH  Google Scholar 

  31. E. Giusti Minimal Surfaces and Functions of Bounded Variation, Birkhӓuser, Basel etc. (1984).

  32. F. Demengel and R. Temam, “Convex functions of a measure and applications,” Ind. Univ. Math. J. 33, 673–709 (1984).

    Article  MathSciNet  MATH  Google Scholar 

  33. O. A. Ladyzhenskaya and N. N. Ural’tseva, Linear and Quasilinear Elliptic Equations [in Russian], Nauka, Moscow (1964); English transl.: Academic Press, New York (1968).

  34. M. Fuchs and C. Tietz, “Existence of generalized minimizers and of dual solutions for a class of variational problems with linear growth related to image recovery,” J. Math. Sci., New York 210, No. 4, 458–475 (2015).

  35. L. Ambrosio, N. Fusco, and D. Pallara, Functions of Bounded Variation and Free Discontinuity Problems, Clarendon Press, Oxford (2000).

    MATH  Google Scholar 

  36. G. Anzellotti and M. Giaquinta, “Convex functionals and partial regularity,” Arch. Rat. Mech. Anal. 102, 243–272 (1988).

    Article  MathSciNet  MATH  Google Scholar 

  37. Yu. G. Reshetnyak, “Weak convergence of completely additive vector functions on a set” [in Russian], Sib. Mat. Zh. 9, No. 6, 1386–1394 (1968); English transl.: Sib. Math. J. 9, No. 6, 1039–1045 (1968).

  38. D. Spector, “Simple proofs of some results of Reshetnyak,” Proc. Am. Math. Soc. 139, No. 5, 1681–1690 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  39. L. Beck and T. Schmidt, “On the Dirichlet problem for variational integrals in BV,” J. Reine Angew. Math. 674, 113–194 (2013).

    MathSciNet  MATH  Google Scholar 

  40. R. J. LeVeque, Finite Difference Methods for Ordinary and Partial Differential Equations, SIAM, Philadelphia, PA (2007).

    Book  MATH  Google Scholar 

  41. K. W. Morton and L. M. Mayers, Numerical Solution of Partial Differential Equations. An Introduction, Cambridge University Press, Cambridge (1994).

  42. S. Fučik, A. Kratochvil, and J. Nečas, “Kačanov–Galerkin method,” Commentat. Math. Univ. Carol. 14, 651–659 (1973).

    MATH  Google Scholar 

  43. J. Weickert, J. Heers, C. Schnӧrr, K. J. Zuiderveld, O. Scherzer, and H. S. Stiehl, “Fast parallel algorithms for a broad class of nonlinear variational diffusion approaches,” Real-Time Imaging 7, No. 1, 31–45 (2001).

  44. D. Geman and C. Yang, “Nonlinear image recovery with half-quadratic regularization,” IEEE Trans. Image Process. 4, 932–945 (1995).

    Article  Google Scholar 

  45. E. Zeidler, Nonlinear Functional Analysis and its Applications II/A: Linear Monotone Operators, Springer, New York etc. (1990).

    Book  MATH  Google Scholar 

  46. S. Gerschgorin, Fehlerabschӓtzung für das Differenzenverfahren zur Lӧsung Partieller Differentialgleichungen. Z. Angew. Math. 10, 373–382 (1930).

    Article  Google Scholar 

  47. E. T. Whittaker, “A new method of graduation,” Proc. Edinburgh Math. Soc. 41, 65–75 (1923).

    Google Scholar 

  48. A. N. Tikhonov, “Solution of incorrectly formulated problems and the regularization method” [in Russian], Dokl. Akad. Nauk SSSR, 151, 501–504 (1963); English transl.: Sov. Math., Dokl. 5, 1035–1038 (1963).

  49. M. Bertero, T. A. Poggio, and V. Torre, “Ill-posed problems in early vision,” Proc. IEEE 76, 869–889 (1988).

    Article  Google Scholar 

  50. A. Beck and M. Teboulle, “Fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM J. Imaging Sci. 2, No. 1, 183–202 (2009).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Universitӓt des Saarlandes, Fachbereich 6.1 Mathematik Postfach 15 11 50, D–66041, Saarbrücken, Germany

    M. Bildhauer & M. Fuchs

  2. Mathematical Image Analysis Group Faculty of Mathematics and Computer Sciences, Saarland University, Campus E1.7, D–66041, Saarbrücken, Germany

    J. Weickert

Authors
  1. M. Bildhauer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Fuchs
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. Weickert
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Bildhauer.

Additional information

Translated from Problemy Matematicheskogo Analiza 87, October 2016, pp. 69-78.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bildhauer, M., Fuchs, M. & Weickert, J. Denoising and Inpainting of Images Using Tv-Type Energies: Theoretical and Computational Aspects. J Math Sci 219, 899–910 (2016). https://doi.org/10.1007/s10958-016-3153-y

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-016-3153-y

Search

Navigation