Skip to main content
SpringerLink
Log in

Discrete Mathematical Model of the Problem of Diffraction for E -Polarized Waves on Slots in the Impedance Plane

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

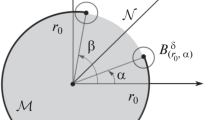
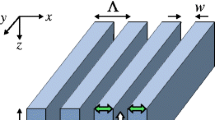
We consider the problem of diffraction for E -polarized plane monochromatic waves on slots in the impedance plane. A discrete mathematical model of the boundary integral equations of this problem is constructed. We also perform a numerical experiment based on the use of the efficient numerical method of discrete singularities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. N. I. Akhiezer, Lectures on Integral Transforms, AMS, Providence, RI (1988).

    MATH  Google Scholar 

  2. G. N. Watson, A Treatise on the Theory of Bessel Functions, Cambridge Univ. Press, Cambridge (1995).

    MATH  Google Scholar 

  3. Yu. V. Gandel’, An Introduction to the Methods of Calculating Singular and Hypersingular Integrals: A Textbook [in Russian], Izd. Kharkov. Nat. Univ., Kharkov (2002).

  4. Yu. V. Gandel’, “Parametric representations of singular integral transformations and boundary-value problems of mathematical physics,” in: Nonlinear Boundary-Value Problems of Mathematical Physics and Their Applications [in Russian], Institute of Mathematics, Ukrainian National Academy of Sciences, Kiev (1995), pp. 65–66.

  5. Yu. V. Gandel’ and V. D. Dushkin, Mathematical Models of Two-Dimensional Diffraction Problems: Singular Integral Equations and Numerical Methods of Discrete Singularities [in Russian], Akad. VV MVD Ukrainy, Kharkov (2012).

  6. A. S. Il’inskii and G. Ya. Slepyan, Oscillations and Waves in Electrodynamic Systems with Losses [in Russian], Moscow University, Moscow (1983).

  7. V. F. Kravchenko, Electrodynamics of Superconducting Structures. Theory, Algorithms, and Methods of Calculations [in Russian], Fizmatlit, Moscow (2006).

  8. D. Colton and R. Kress, Integral Equation Methods in Scattering Theory, Wiley, New York (1983).

    MATH  Google Scholar 

  9. R. Estrada and R. P. Kanwal, Singular Integral Equations, Birkhäuser, Boston (2000).

    Book  MATH  Google Scholar 

  10. I. K. Lifanov, L. N. Poltavskii, and G. M. Vainikko, Hypersingular Integral Equations and Their Application, CRC Press, London (2004).

    Google Scholar 

  11. B. Mandelbrot, The Fractal Geometry of Nature, Freeman, New York (1983).

    Google Scholar 

  12. K. V. Nesvit, “Discrete mathematical model of diffraction on the pre-Cantor set of slits in impedance plane and numerical experiment,” Int. J. Math. Models Methods Appl. Sci., 7, No. 11, 897–906 (2013).

    Google Scholar 

  13. H. Wallén, I. V. Lindell, and A. Sihvola, “Mixed-impedance boundary conditions,” IEEE Trans. Anten. Propag., 59, No. 5, 1580–1586 (2011).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Karazin Kharkiv National University, Kharkiv, Ukraine

    K. V. Nesvit

Authors
  1. K. V. Nesvit
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 57, No. 1, pp. 115–124, January–April, 2014.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nesvit, K.V. Discrete Mathematical Model of the Problem of Diffraction for E -Polarized Waves on Slots in the Impedance Plane. J Math Sci 212, 142–155 (2016). https://doi.org/10.1007/s10958-015-2655-3

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-015-2655-3

Keywords

Search

Navigation