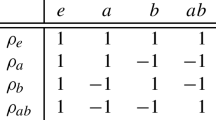
We introduce a group naturally acting on aperiodic necklaces of length n with two colors using a one-to-one correspondence between such necklaces and irreducible polynomials of degree n over the field F2 of two elements. We notice that this group is isomorphic to the quotient group of nondegenerate circulant matrices of size n over that field modulo a natural cyclic subgroup. Our groups turn out to be isomorphic to the sandpile groups for a special sequence of directed graphs. Bibliography: 15 titles.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
T. van Aardenne-Ehrenfest and N. G. de Bruijn, “Circuits and trees in oriented linear graphs,” Simon Stevin, 28, 203–217 (1951).
V. I. Arnold, “From Hilbert’s superposition problem to dynamical dystems,” transcript of a lecture given at the Fields Institute (1997); http://www.pdmi.ras.ru/~arnsem/Arnold/arnlect1.ps.gz.
S. H. Chan, Bachelor’s Thesis, NTU, Singapore (2012).
S. H. Chan, H. D. L. Hollmann, and D. V. Pasechnik, “Critical groups of generalized de Bruijn and Kautz graphs and circulant matrices over finite fields,” in: J. Nešetřil and M. Pellegrini (eds.), Proceedings of EuroComb 2013, The Seventh European Conference on Combinatorics, Graph Theory and Applications, Springer (2013); ISBN 978-88-7642-474-8.
S. Chmutov, S. Duzhin, and J. Mostovoy, Introduction to Vassiliev Knot Invariants, Cambridge Univ. Press, Cambridge (2012); draft version: http://www.pdmi.ras.ru/~duzhin/papers/cdbook.
S. Duzhin, “An explicit expansion of the Drinfeld associator up to degree 12,” web publication http://www.pdmi.ras.ru/~arnsem/dataprog.
S. W. Golomb, “Irreducible polynomials, synchronization codes, primitive necklaces and the cyclotomic algebra,” in: Combinatorial Mathematics and Its Applications (Proc. Conf. Univ. North Carolina), Univ. North Carolina Press, Chapel Hill (1969), pp. 358–370.
M. E. Hoffman, “The algebra of multiple harmonic series,” J. Algebra, 194, 477–495 (1997).
L. Levine, “Sandpile groups and spanning trees of directed line graphs,” J. Combin. Theory, Ser. A, 118, No. 2, 350–364 (2011).
L. Levine and J. Propp, “What is . . . a sandpile?” Notices Amer. Math. Soc., 57, No. 8, 976–979 (2010).
R. Lidl and H. Niederreiter, Finite Fields, Cambridge Univ. Press, Cambridge (2008).
Ch. Reutenauer, Free Lie Algebras, The Clarendon Press, New York (1993).
“Computer algebra system Sage,” http://www.sagemath.org.
N. J. A. Sloane, “Online encyclopaedia of integer sequences,” http://oeis.org/.
E. Witt, “Treue Darstellung Liescher Ringe,” J. reine angew. Math., 177, 152–160 (1937).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Published in Zapiski Nauchnykh Seminarov POMI, Vol. 421, 2014, pp. 81–93.
Rights and permissions
About this article
Cite this article
Duzhin, S.V., Pasechnik, D.V. Groups Acting on Necklaces and Sandpile Groups. J Math Sci 200, 690–697 (2014). https://doi.org/10.1007/s10958-014-1960-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-014-1960-6