On the Asymptotic Distribution of Singular Values of Powers of Random Matrices

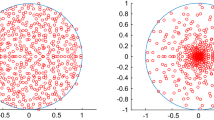
We consider powers of random matrices with independent entries. Let X _ij , i, j ≥ 1, be independent complex random variables with E X _ij = 0 and E|X _ij |² = 1, and let X denote an n × n matrix with |X|_ij − X _ij for 1 ≤ i, j ≤ n. Denote by $s_1^{(m)}\geq \ldots \geq s_n^{(m) }$ the singular values of the random matrix $\mathbf{W}:={n^{{-\frac{m}{2}}}}{{\mathbf{X}}^m}$ and define the empirical distribution of the squared singular values by

$$ \mathcal{F}_n^{(m) }(x)=\frac{1}{n}\sum\limits_{k=1}^n {{I_{{\left\{ {s_k^{{{(m)^2}}}\leq x} \right\}}}}}, $$

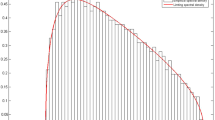
where I _{B} denotes the indicator of an event B. We prove that the expected spectral distribution $F_n^{(m) }(x)=\mathbf{E}\mathcal{F}_n^{(m) }(x)$ converges under the Lindeberg condition to the distribution function G ^(m)(x) defined by its moments

$$ {\alpha_k}(m)\;:=\int\limits_{\mathbb{R}} {{x^k}dG(x)} =\frac{1}{mk+1}\left( {\begin{array}{*{20}{c}} {km+k} \\ k \\ \end{array}} \right). $$