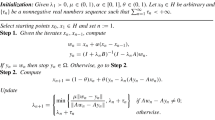Skip to main content
SpringerLink
Log in

Forward–Reflected–Backward Splitting Algorithms with Momentum: Weak, Linear and Strong Convergence Results

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

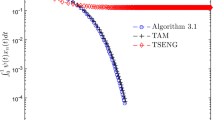
This paper studies the forward–reflected–backward splitting algorithm with momentum terms for monotone inclusion problem of the sum of a maximal monotone and Lipschitz continuous monotone operators in Hilbert spaces. The forward–reflected–backward splitting algorithm is an interesting algorithm for inclusion problems with the sum of maximal monotone and Lipschitz continuous monotone operators due to the inherent feature of one forward evaluation and one backward evaluation per iteration it possesses. The results in this paper further explore the convergence behavior of the forward–reflected–backward splitting algorithm with momentum terms. We obtain weak, linear, and strong convergence results under the same inherent feature of one forward evaluation and one backward evaluation at each iteration. Numerical results show that forward–reflected–backward splitting algorithms with momentum terms are efficient and promising over some related splitting algorithms in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Algorithm 2
Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Availability of supporting data

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Code Availability

The Matlab codes employed to run the numerical experiments are available on request.

References

  1. Aragón-Artacho, F.J., Torregrosa-Belén, D.: A direct proof of convergence of Davis-Yin splitting algorithm allowing larger stepsizes. Set-Valued Var. Anal. 30, 1011–1029 (2022)

    Article  MathSciNet  Google Scholar 

  2. Attouch, H., Peypouquet, J., Redont, P.: Backward–forward algorithms for structured monotone inclusions in Hilbert spaces. J. Math. Anal. Appl. 457, 1095–1117 (2018)

    Article  MathSciNet  Google Scholar 

  3. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. CMS Books in Mathematics, Springer, New York (2011)

    Book  Google Scholar 

  4. Boţ, R.I., Csetnek, E.R.: An inertial forward–backward–forward primal–dual splitting algorithm for solving monotone inclusion problems. Numer. Algorithms 71, 519–540 (2016)

    Article  MathSciNet  Google Scholar 

  5. Boţ, R.I., Sedlmayer, M., Vuong, P.T.: A relaxed inertial forward–backward–forward algorithm for solving monotone inclusion with application to GANS. J. Mach. Learn. Res. 24, 1–37 (2023)

    MathSciNet  Google Scholar 

  6. Brézis, H.: Operateurs maximaux monotones, Chapitre II. N.-Holl. Math. Stud. 5, 19–51 (1973)

    Article  Google Scholar 

  7. Briceño-Arias, L.M., Davis, D.: Forward–backward–half forward algorithm for solving monotone inclusions. SIAM J. Optim. 28, 2839–2871 (2018)

    Article  MathSciNet  Google Scholar 

  8. Cevher, V., Vũ, B.C.: A reflected forward–backward splitting method for monotone inclusions involving Lipschitzian operators. Set-Valued Var. Anal. 29, 163–174 (2021)

    Article  MathSciNet  Google Scholar 

  9. Chen, G.H., Rockafellar, R.T.: Convergence rates in forward–backward splitting. SIAM J. Optim. 7, 421–444 (1997)

    Article  MathSciNet  Google Scholar 

  10. Cholamjiak, P., Van Hieu, D., Cho, Y.J.: Relaxed forward–backward splitting methods for solving variational inclusions and applications. J. Sci. Comput. 88, 85 (2021)

    Article  MathSciNet  Google Scholar 

  11. Combettes, P.L., Pesquet, J.C.: Proximal splitting methods in signal processing. In: Fixed Point Algorithms for Inverse Problems in Science and Engineering pp. 185–212. Springer, New York (2011)

  12. Combettes, P.L., Wajs, V.: Signal recovery by proximal forward–backward splitting. SIAM Multiscale Model. Simul. 4, 1168–1200 (2005)

    Article  MathSciNet  Google Scholar 

  13. Daubechies, I., Defrise, M., De Mol, C.: An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 57, 1413–1457 (2004)

    Article  MathSciNet  Google Scholar 

  14. Davis, D., Yin, W.T.: A three-operator splitting scheme and its optimization applications. Set Valued Var. Anal. 25, 829–858 (2017)

    Article  MathSciNet  Google Scholar 

  15. Dixit, A., Sahu, D.R., Gautam, P., Som, T., Yao, J.C.: An accelerated forward–backward splitting algorithm for solving inclusion problems with applications to regression and link prediction problems. J. Nonlinear Var. Anal. 5, 79–101 (2021)

    Article  Google Scholar 

  16. Duchi, J., Singer, Y.: Efficient online and batch learning using forward–backward splitting. J. Mach. Learn. Res. 10, 2899–2934 (2009)

    MathSciNet  Google Scholar 

  17. Facchinei, F., Pang, J.-S.: Finite-Dimensional Variational Inequalities and Complementarity Problems, vol. II. Springer, New York (2003)

    Google Scholar 

  18. Izuchukwu, C., Reich, S., Shehu, Y., Taiwo, A.: Strong convergence of forward–reflected–backward splitting methods for solving monotone inclusions with applications to image restoration and optimal control. J. Sci. Comput. 94, 73 (2023)

    Article  MathSciNet  Google Scholar 

  19. Latafat, P., Patrinos, P.: Asymmetric forward–backward–adjoint splitting for solving monotone inclusions involving three operators. Comput. Optim. Appl. 68, 57–93 (2017)

    Article  MathSciNet  Google Scholar 

  20. Liang, J., Luo, T., Schönlieb, C.B.: Improving “Fast Iterative Shrinkage-Thresholding Algorithm’’: faster, smarter, and greedier. SIAM J. Sci. Comput. 44, A1069–A1091 (2022)

    Article  MathSciNet  Google Scholar 

  21. Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)

    Article  ADS  MathSciNet  Google Scholar 

  22. Lorenz, D.A., Pock, T.: An inertial forward–backward algorithm for monotone inclusions. J Math Imaging Vis 51, 311–325 (2015)

    Article  MathSciNet  Google Scholar 

  23. Maingé, P.E.: Approximation methods for common fixed points of nonexpansive mappings in Hilbert spaces. J. Math. Anal. Appl. 325(1), 469–479 (2007)

    Article  MathSciNet  Google Scholar 

  24. Malitsky, Y., Tam, M.K.: A forward–backward splitting method for monotone inclusions without cocoercivity. SIAM J. Optim. 30(2), 1451–1472 (2020)

    Article  MathSciNet  Google Scholar 

  25. Malitsky, Y.: Projected reflected gradient methods for monotone variational inequalities. SIAM J. Optim. 25, 502–520 (2015)

    Article  MathSciNet  Google Scholar 

  26. Martinet, B.: Régularisation d’inéquations variationnelles par approximations successives, (French) Rev. Française Informat. Recherche Opérationnelle 4 (1970), Sér. R-3, 154-158

  27. Mewomo, O.T., Okeke, C.C., Ogbuisi, F.U.: Iterative solutions of split fixed point and monotone inclusion problems in Hilbert spaces. J. Appl. Numer. Optim. 5, 271–285 (2023)

    Google Scholar 

  28. Nesterov, Y.: A method of solving a convex programming problem with convergence rate O(\(1/k^2\)). Sov. Math. Dokl. 27, 372–376 (1983)

    Google Scholar 

  29. Ofem, A.E., Mebawondu, A.A., Ugwunnadi, G.C., Cholamjiak, P., Narain, O.K.: Relaxed Tseng splitting method with double inertial steps for solving monotone inclusions and fixed point problems. Numer. Algorithms (2023). https://doi.org/10.1007/s11075-023-01674-y

    Article  Google Scholar 

  30. Opial, Z.: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 73, 591–597 (1967)

    Article  MathSciNet  Google Scholar 

  31. Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Physc. 4(5), 1–17 (1964)

    Article  Google Scholar 

  32. Raguet, H., Fadili, J., Peyre, G.: Generalized forward–backward splitting. SIAM J. Imaging Sci. 6, 1199–1226 (2013)

    Article  MathSciNet  Google Scholar 

  33. Rieger, J., Tam, M.K.: Backward–forward–reflected–backward splitting for three operator monotone inclusions. Appl. Math. Comput. 381, 125248 (2020)

    MathSciNet  Google Scholar 

  34. Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control. Optim. 14, 877–898 (1976)

    Article  MathSciNet  Google Scholar 

  35. Ryu, E.K.: Uniqueness of DRS as the 2 operator resolvent-splitting and impossibility of 3 operator resolvent-splitting. Math. Program. 182, 233–273 (2020)

    Article  MathSciNet  Google Scholar 

  36. Ryu, E.K., Vũ, B.C.: Finding the forward–Douglas–Rachford–Forward method. J. Optim. Theory Appl. 184, 858–876 (2020)

    Article  MathSciNet  Google Scholar 

  37. Saejung, S., Yotkaew, P.: Approximation of zeros of inverse strongly monotone operators in Banach spaces. Nonlinear Anal. 75, 742–750 (2012)

    Article  MathSciNet  Google Scholar 

  38. Tseng, P.: A modified forward–backward splitting method for maximal monotone mappings. SIAM J. Control. Optim. 38, 431–446 (2000)

    Article  MathSciNet  Google Scholar 

  39. Van Hieu, D., Anh, P.K., Muu, L.D.: Modified forward–backward splitting method for variational inclusions, 4OR-Q. J. Oper. Res. 19, 27–151 (2021)

    Google Scholar 

  40. Wang, Z.-B., Lei, Z.-Y., Long, X., Chen, Z.-Y.: A modified tseng splitting method with double inertial steps for solving monotone inclusion problems. J. Sci. Comput. 96, 92 (2023)

    Article  MathSciNet  Google Scholar 

  41. Yu, H., Zong, C., Tang, Y.: An outer reflected forward–backward splitting algorithm for solving monotone inclusions, arXiv:2009.12493v1 (2020)

  42. Zong, C.X., Tang, Y.C., Zhang, G.F.: An inertial semi-forward–reflected–backward splitting and its application. Acta. Math. Sin. English Ser. 38, 443–464 (2022)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Not applicable.

Funding

Not applicable.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Tiangong University, Tianjin, 300387, China

    Yonghong Yao

  2. Center for Advanced Information Technology, Kyung Hee University, Seoul, 02447, South Korea

    Yonghong Yao

  3. Operational Research Center in Healthcare, Near East University, TRNC Mersin 10, 99138, Nicosia, Turkey

    Abubakar Adamu

  4. Charles Chidume Mathematics Institute, African University of Science and Technology, Abuja, 900107, Nigeria

    Abubakar Adamu

  5. School of Mathematical Sciences, Zhejiang Normal University, Jinhua, 321004, People’s Republic of China

    Yekini Shehu

Authors
  1. Yonghong Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abubakar Adamu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yekini Shehu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Y.S. and Y.Y wrote the manuscript and A.A prepared the all the figures and tables.

Corresponding author

Correspondence to Yekini Shehu.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Ethical Approval and Consent to Participate

All the authors gave the ethical approval and consent to participate in this article.

Consent for Publication

All the authors gave consent for the publication of identifiable details to be published in the journal and article.

Additional information

Communicated by Sorin-Mihai Grad.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yao, Y., Adamu, A. & Shehu, Y. Forward–Reflected–Backward Splitting Algorithms with Momentum: Weak, Linear and Strong Convergence Results. J Optim Theory Appl (2024). https://doi.org/10.1007/s10957-024-02410-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10957-024-02410-9

Keywords

Mathematics Subject Classification

Search

Navigation