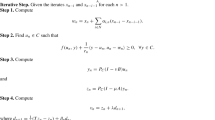Inertial Newton Algorithms Avoiding Strict Saddle Points

Abstract

We study the asymptotic behavior of second-order algorithms mixing Newton’s method and inertial gradient descent in non-convex landscapes. We show that, despite the Newtonian behavior of these methods, they almost always escape strict saddle points. We also evidence the role played by the hyper-parameters of these methods in their qualitative behavior near critical points. The theoretical results are supported by numerical illustrations.

Appendices

A Permutation Matrices

We specify the permutations matrices used to obtain the block diagonalization in (7). Denote by $\textrm{mod}$ the modulo operator. We can choose the permutation matrix $U\in \mathbb {R}^{2P\times 2P}$ as the matrix whose coefficients are all zero except the following, for all $p\in \{1,\ldots ,P\}$,

$$\begin{aligned} \text {{ P} odd:}\ {\left\{ \begin{array}{ll} U_{P-p+1,p} &{}=1-\textrm{mod}(p,2)\\ U_{P+p,2P-p+1}&{}=\textrm{mod}(p,2)\\ U_{p,2P-p}&{} = \textrm{mod}(p,2) \end{array}\right. }, \text { { P} even:}\ {\left\{ \begin{array}{ll} U_{p,p} &{}=\textrm{mod}(p,2)\\ U_{P+p,P+p}&{}=1-\textrm{mod}(p,2)\\ U_{P+p,p} &{}= \textrm{mod}(p,2)\\ U_{p,P+p} &{}= \textrm{mod}(p,2) \end{array}\right. }.\nonumber \\ \end{aligned}$$

(16)

B Proof of Theorem 4.1

We consider functions with possibly uncountably many critical points, this yields additional difficulties, which we overcome using the following result as done in [34].

Lemma B.1

(Lindelõf [27]) For every open cover there is a countable sub-cover.

The proof of Theorem 4.1 follows similar steps as that of Theorem 3.2, so we omit some details and use the notations of Sect. 3.1. First, for any $(\theta ,\psi )\in \mathbb {R}^P\times \mathbb {R}^P$, we redefine G:

$$\begin{aligned} G\begin{pmatrix} \theta \\ \psi \end{pmatrix} = \begin{pmatrix} \theta + \gamma \left[ -(\alpha -\frac{1}{\beta })\theta -\frac{1}{\beta }\psi -\beta \nabla \mathcal {J}(\theta ) \right] \\ \psi + \gamma \left[ -(\alpha -\frac{1}{\beta })\theta -\frac{1}{\beta }\psi \right] \end{pmatrix}, \end{aligned}$$

(17)

so that iterations $k\in \mathbb {N}$ of INNA read $(\theta _{k+1},\psi _{k+1}) = G(\theta _{k},\psi _{k})$. Remark that the set of fixed points of G is $\textsf{S}$, the stationary points of (3), indeed, for any $(\theta ,\psi )\in \mathbb {R}^P\times \mathbb {R}^P$,

$$\begin{aligned} G(\theta ,\psi ) = (\theta ,\psi ) \iff {\left\{ \begin{array}{ll} -(\alpha -\frac{1}{\beta })\theta -\frac{1}{\beta }\psi -\beta \nabla \mathcal {J}(\theta ) = 0\\ -(\alpha -\frac{1}{\beta })\theta -\frac{1}{\beta }\psi = 0 \end{array}\right. } \iff {\left\{ \begin{array}{ll} \nabla \mathcal {J}(\theta ) = 0\\ \psi = (1-\alpha \beta )\theta \end{array}\right. }. \end{aligned}$$

Since G is $C^1$ on $\mathbb {R}^{P}\times \mathbb {R}^P$, the Jacobian matrix of G (displayed by block) reads,

$$\begin{aligned} DG(\theta ,\psi ) = \begin{pmatrix} (1 - \gamma (\alpha -\frac{1}{\beta })) I_P -\gamma \beta \nabla ^2\mathcal {J}(\theta ) &{}&{} -\frac{\gamma }{\beta } I_P\\ -\gamma (\alpha -\frac{1}{\beta }) I_P &{}&{} (1-\frac{\gamma }{\beta })I_P \end{pmatrix}. \end{aligned}$$

We can again block-diagonalize $DG(\theta ,\psi )$ (see (7)), in blocks of the form (up to symmetric permutations): $M_p = \begin{pmatrix} 1 - \gamma (\alpha -\frac{1}{\beta }) -\gamma \beta \lambda _p &{} &{} -\frac{\gamma }{\beta } \\ -\gamma (\alpha -\frac{1}{\beta }) &{} &{} 1-\frac{\gamma }{\beta } \end{pmatrix}$, where $\lambda _p$ is an eigenvalue of $\nabla ^2\mathcal {J}(\theta )$. To use the Theorem 4.2, we need G to be a local diffeomorphism.

Theorem B.1

Under the same assumptions as that of Theorem 4.1, the mapping G defined in (17) is a local diffeomorphism from $\mathbb {R}^P\times \mathbb {R}^P$ to $\mathbb {R}^P\times \mathbb {R}^P$.

This result is proved later in Section B.1. We can now prove Theorem 4.1.

Proof of Theorem 4.1

Let $\alpha$, $\beta$ and $\gamma$ such that the assumptions of the theorem hold and let G defined in (17) with these parameters. By Theorem B.1, G is a local diffeomorphism. Let $(\theta ^\star ,\psi ^\star )\in \textsf{S}_{<0}$, to use Theorem 4.2 we study the magnitude of the eigenvalues of $DG(\theta ^\star ,\psi ^\star )$. Let $\lambda _p<0$ be a negative eigenvalue of $\nabla ^2\mathcal {J}(\theta ^\star )$, using the notations and elements stated in the beginning of this section, the eigenvalues of $M_p$ are the roots of

$$\begin{aligned} \chi _{M_p}(X)= & {} X^2 - \textrm{trace}(M_p)X + \det (M_p) \\= & {} X^2 - (2 - \gamma (\alpha +\beta \lambda _p) )X + 1 - \gamma (\alpha +\beta \lambda _p) + \gamma ^2\lambda _p. \end{aligned}$$

The discriminant of $\chi _{M_p}$ is:

$$\begin{aligned} \Delta _{M_p} = (2 - \gamma (\alpha +\beta \lambda _p) )^2 - 4 (1 - \gamma (\alpha +\beta \lambda _p) + \gamma ^2\lambda _p) = \gamma ^2\left( (\alpha +\beta \lambda _p)^2 - 4\lambda _p\right) . \end{aligned}$$

Remark that Lemma 3.1 gives again the sign of $\Delta _{M_p}$. Thus since $\lambda _p<0$, we necessarily have $\Delta _{M_p}\ge 0$, and can ignore the case $\Delta _{M_p}<0$. So $M_p$ has two real eigenvalues,

$$\begin{aligned} \sigma _{p,+}&= 1 - \frac{1}{2} \gamma (\alpha +\beta \lambda _p) + \frac{1}{2} \gamma \sqrt{(\alpha +\beta \lambda _p)^2 - 4\lambda _p}\\ \sigma _{p,-}&= 1 - \frac{1}{2} \gamma (\alpha +\beta \lambda _p) - \frac{1}{2} \gamma \sqrt{(\alpha +\beta \lambda _p)^2 - 4\lambda _p}. \end{aligned}$$

Since $\lambda _p<0$, then $\vert \alpha +\beta \lambda _p\vert < \sqrt{(\alpha +\beta \lambda _p)^2 - 4\lambda _p}$, so observe that $\sigma _{p,+}>1$ and $\sigma _{p,-}<1$, so $DG(\theta ^\star ,\psi ^\star )$ has at least one eigenvalue with magnitude larger than one.

We can now use the stable manifold theorem and we omit some details since the arguments are the same as for the proof of Theorem 3.1. By Theorem 4.2, around each $(\theta ^\star ,\psi ^\star )\in \textsf{S}_{<0}$, there exists a neighborhood $\mathsf {\Omega }_{(\theta ^\star ,\psi ^\star )}$ on which the stable manifold theorem holds. Denote by $\textsf{A}$ the possibly uncountable union of all these neighborhoods: $\textsf{A} = \bigcup _{(\theta ^\star ,\psi ^\star )\in \textsf{S}_{<0}} \mathsf {\Omega }_{(\theta ^\star ,\psi ^\star )}$. By Lemma B.1, there exists a countable sub-cover of this set, i.e., there exists a sequence $(\theta _i^\star ,\psi _i^\star )_{i\in \mathbb {N}}$ in $\textsf{S}_{<0}$ such that

$$\begin{aligned} \textsf{A} = \bigcup _{i\in \mathbb {N}} \mathsf {\Omega }_{(\theta _i^\star ,\psi _i^\star )}. \end{aligned}$$

(18)

Let $(\theta ^\star ,\psi ^\star )\in \textsf{S}_{<0}$, it need not be an element of $(\theta _i^\star ,\psi _i^\star )_{i\in \mathbb {N}}$, but according to (18), there exists $i\in \mathbb {N}$ such that $(\theta ^\star ,\psi ^\star )\in \mathsf {\Omega }_{(\theta _i^\star ,\psi _i^\star )}$. Let an initialization $(\theta _0,\psi _0)$ such that the associated realization $(\theta _k,\psi _k)_{k\in \mathbb {N}}$ of INNA converges to $(\theta ^\star ,\psi ^\star )$. This means that there exists $k_0\in \mathbb {N}$ such that $\forall k\ge k_0$, $G^k(\theta _0,\psi _0)\in \mathsf {\Omega }_{(\theta _i^\star ,\psi _i^\star )}$ and thus $G^k(\theta _0,\psi _0)\in \textsf{W}^{sc}_{(\theta _i^\star ,\psi _i^\star )}$, where $\textsf{W}^{sc}_{(\theta _i^\star ,\psi _i^\star )}$ is the stable manifold around $(\theta _i^\star ,\psi _i^\star )$ as defined in Theorem 4.2. By Theorem B.1, G is a local diffeomorphism, so we can reverse the iterations and obtain, $(\theta _0,\psi _0) \in \bigcup _{j\in \mathbb {N}}G^{-j}\left( \mathsf {\Omega }_{(\theta _i^\star ,\psi _i^\star )}\cap \textsf{W}^{sc}_{(\theta _i^\star ,\psi _i^\star )}\right)$. Since $(\theta _i^\star ,\psi _i^\star )\in \textsf{S}_{<0}$, we showed that $DG(\theta _i^\star ,\psi _i^\star )$ has at least one eigenvalue with magnitude strictly larger than 1, so by Theorem 4.2, $W^{sc}_{(\theta _i^\star ,\psi _i^\star )}$ has zero measure. Then, by Theorem B.1 for all $j\in \mathbb {N}$, $G^{-j}$ is a local diffeomorphism, so the union above has zero measure. Using (18), the rest of the proof is then similar to the end of that of Theorem 3.1 since $\bigcup _{i\in \mathbb {N}}\left[ \bigcup _{j\in \mathbb {N}}G^{-j}\left( \mathsf {\Omega }_{(\theta _i^\star ,\psi _i^\star )}\cap \textsf{W}^{sc}_{(\theta _i^\star ,\psi _i^\star )}\right) \right]$ is a countable union of zero-measure sets, so it has again measure zero. $\square$

1.1 B.1 Missing Proofs

We begin by proving the lemmas stated in Sect. 3.2.

Proof of Lemma 3.1

Let $\alpha \ge 0$, and $\beta >0$, the function $h(\lambda )=(\alpha +\beta \lambda )^2-4\lambda = \beta ^2\lambda ^2 + 2(\alpha \beta -2)\lambda +\alpha ^2$ is a second-order polynomial in $\lambda$ whose discriminant is $16(1-\alpha \beta )$. If $\alpha \beta >1$ this discriminant is negative so h is always positive. If $\alpha \beta \le 1$, then h has two real roots: $\frac{(2-\alpha \beta )}{\beta ^2} \pm \frac{2\sqrt{1-\alpha \beta }}{\beta ^2}$, which are equal to $l_{\textrm{min}}$ and $l_{\textrm{max}}$ since $X^2\pm 2X+1 = (X\pm 1)^2$. $\square$

Proof of Lemma 3.2

Assume that $\lambda _p>0$, if $\Delta _{M_p}<0$, then $2\Re (\sigma _{p,-}) = 2\Re (\sigma _{p,+}) = -(\alpha +\beta \lambda _p)<0$. If $\Delta _{M_p}\ge 0$ then $\sigma _{p,-}$ and $\sigma _{p,+}$ are real. Remark that $\sigma _{p,-}\sigma _{p,+}=\lambda _p$ so the eigenvalues have the same sign, and $\sigma _{p,-}+\sigma _{p,+}= -(\alpha +\beta \lambda _p)<0,$ so they are negative. $\square$

Proof of Theorem B.1

Let $(\theta ,\psi )\in \mathbb {R}^P\times \mathbb {R}^P$, to prove that G is a local diffeomorphism we prove that $DG(\theta ,\psi )$ is invertible and then use the local inversion theorem. Using again the block transformation of $DG(\theta ,\psi )$, $\det (DG(\theta ,\psi )) = \prod _{p=1}^P \det (M_p)$, where

$$\begin{aligned} \det (M_p)= & {} (1 - \gamma (\alpha -\frac{1}{\beta }) -\gamma \beta \lambda _p)(1-\frac{\gamma }{\beta }) - \frac{\gamma }{\beta }\gamma (\alpha -\frac{1}{\beta })\nonumber \\= & {} 1 - \gamma (\alpha +\beta \lambda _p) + \gamma ^2\lambda _p. \end{aligned}$$

(19)

We want $\gamma$ such that $\det (M_p)\ne 0$ for any $(\theta ,\psi )\in \mathbb {R}^P\times \mathbb {R}^P$, hence for any $\lambda _p\in [-L,L]$ (using Assumption 1). First, if $\lambda _p=0$, from (19), we must take $\gamma \ne 1/\alpha$. Now let $\lambda _p\ne 0$, then (19) is a second-order polynomial in $\gamma$ with discriminant $(\alpha +\beta \lambda _p)^2 - 4\lambda _p= \Delta _{M_p}$ already studied Sect. 3.1 and Lemma 3.1. If $\Delta _{M_p}<0$, then $\det (M_p)$ has no real roots and the choice of $\gamma$ is free. Assume now that $\Delta _{M_p}\ge 0$, there exists two real roots to (19):

$$\begin{aligned} \gamma ^{+}= & {} \frac{(\alpha +\beta \lambda _p)}{2\lambda _p} + \frac{\sqrt{(\alpha + \beta \lambda _p)^2 - 4\lambda _p}}{2 \lambda _p} \ \text {and}\ \gamma ^{-}\nonumber \\= & {} \frac{(\alpha +\beta \lambda _p)}{2\lambda _p} - \frac{\sqrt{(\alpha + \beta \lambda _p)^2 - 4\lambda _p}}{2 \lambda _p}. \end{aligned}$$

(20)

Remark that when $\lambda _p<0$, $\gamma ^+<0$ and when $\lambda _p>0$, $0<\gamma ^-<\gamma ^+$, so in every case we only need to ensure $0<\gamma <\gamma ^-$, for every $\lambda _p\in [-L,L]$. So, for every $\lambda \in \mathbb {R}$ for which it is well defined, consider the function $\gamma ^{-}(\lambda )=\frac{(\alpha +\beta \lambda )}{2\lambda } - \frac{\sqrt{(\alpha + \beta \lambda )^2 - 4\lambda }}{2 \lambda }$. When defined, its derivative is $-\frac{\alpha \sqrt{\left( \alpha +\beta \lambda \right) ^2-4\lambda }+\left( 2-\alpha \beta \right) \lambda -\alpha ^2}{2\lambda ^2\sqrt{\left( \alpha +\beta \lambda \right) ^2-4\lambda }}$. The denominator is always positive so we study the numerator: $h(\lambda )=-\alpha \sqrt{(\alpha +\beta \lambda )^2-4\lambda }-(2-\alpha \beta )\lambda +\alpha ^2$, and we differentiate it:

$$\begin{aligned} h'(\lambda ) = -\frac{\alpha (2\beta (\alpha +\beta \lambda )-4)}{2\sqrt{(\alpha +\beta \lambda )^2-4\lambda }}+\alpha \beta -2, \quad \text {and}\quad h''(\lambda ) = -\frac{4\alpha (\alpha \beta -1)}{((\alpha +\beta \lambda )^2-4\lambda )^{\frac{3}{2}}}. \end{aligned}$$

This allows deducing the minimal value of $\gamma ^-(\lambda )$ in each setting by constructing the tables of variations displayed in Fig. 4. There, it follows from standard computations that $h'(0)=h(0)=0$, $h(l_{\textrm{max}})\le 0$ and $\lim _{\lambda \rightarrow +\infty } h'(\lambda )=-2$ (when $\alpha \beta \le 1$), and via L’Hôpital’s rule we obtained $\lim _{\lambda \rightarrow 0}\gamma ^-(\lambda )=1/\alpha$. We deduce from the tables that G is a local diffeomorphism if $\gamma <\gamma ^-(L)$ when $\alpha \beta >1$ and if $\gamma <\min (\gamma ^-(L),\gamma ^-(-L))$ when $\alpha \beta \le 1$ and $L\notin [l_{\textrm{min}},l_{\textrm{max}}]$. Remark that the condition $\gamma \ne \frac{1}{\alpha }$ is implied in both cases. This proves the theorem. $\square$

Fig. 4

Tables of variations for the proof of Theorem B.1. The sign of $h''$ allows deducing the variations and signs of $h'$ and h which themselves allow deducing the minima of $\gamma ^-$

C Proof of Convergence of INNA

To prove Theorem 4.3, we will use the following lemma.

Lemma C.1

( [4]) If a bounded sequence $(u_k)_{k\in \mathbb {N}}$ in $\mathbb {R}^P$ satisfies, $\lim \limits _{k\rightarrow +\infty } \Vert u_{k+1} - u_k\Vert =0,$ then the set of accumulation points of $(u_k)_{k\in \mathbb {N}}$ is connected. If this set is finite, then it reduces to a singleton and $(u_k)_{k\in \mathbb {N}}$ converges.

Proof of Theorem 4.1

Assume that Assumption 1 holds and $\alpha >0$. Let $(\theta _0,\psi _0)\in \mathbb {R}^P\times \mathbb {R}^P$, and let $\gamma >0$ such that (15) holds. Let $(\theta _k,\psi _k)_{k\in \mathbb {N}}$ be the sequence generated by INNA initialized at $(\theta _0,\psi _0)$. We first show that the sequence $(\mathcal {E}_k)_{k\in \mathbb {N}}$ defined $\forall k\in \mathbb {N}$ by

$$\begin{aligned} \mathcal {E}_k = (1+\alpha \beta -\gamma \alpha )\mathcal {J}(\theta _k) + \frac{1}{2}\Vert \left( \alpha -\frac{1}{\beta }\right) \theta _k +\frac{1}{\beta }\psi _k\Vert ^2 \end{aligned}$$

(21)

converges. The sequence $(\mathcal {E}_k)_{k\in \mathbb {N}}$ represents an “energy” that decreases along the iterations, where the first and second terms in (21) represent “potential” and “kinetic” energies, respectively. This sequence resembles the Lyapunov function of DIN [3, 19] but is more involved to derive, as often for algorithms compared to ODEs. We use the notations $a=\alpha -1/\beta$, $b=1/\beta$, $\Delta \theta _k =\theta _{k+1}-\theta _k$ and $\Delta \psi _k =\psi _{k+1}-\psi _k$, for $k\in \mathbb {N}$, so that INNA is rewritten as:

$$\begin{aligned} \Delta \psi _k= & {} -\gamma a\theta _k -\gamma b\psi _k \nonumber \\ \Delta \theta _k= & {} \Delta \psi _k -\gamma \beta \nabla \mathcal {J}(\theta _k) \end{aligned}$$

(22)

Also denote $\mu = 1+\alpha \beta -\gamma \alpha$, where $\mu >0$ since $\gamma < 1/\alpha + \beta$. Let $k\in \mathbb {N}$, we will prove $\mathcal {E}_{k+1}-\mathcal {E}_{k}\le 0$. From Assumption 1 follows a descent lemma (see [16, Proposition A.24]):

$$\begin{aligned} \mu \mathcal {J}(\theta _{k+1}) - \mu \mathcal {J}(\theta _k) \le \mu \langle \nabla \mathcal {J}(\theta _k), \Delta \theta _k \rangle + \frac{\mu L}{2} \Vert \Delta \theta _k\Vert ^2, \end{aligned}$$

which according to (22), can equivalently be rewritten as,

$$\begin{aligned} \mu \mathcal {J}(\theta _{k+1}) - \mu \mathcal {J}(\theta _k) \le -\mu \langle \frac{\Delta \theta _k-\Delta \psi _k}{\gamma \beta }, \Delta \theta _k \rangle + \frac{\mu L}{2} \Vert \Delta \theta _k\Vert ^2. \end{aligned}$$

(23)

We save this for later and now turn our attention to the other term in $\mathcal {E}_{k+1}-\mathcal {E}_k$,

$$\begin{aligned}{} & {} \frac{1}{2}\Vert a\theta _{k+1} + b\psi _{k+1}\Vert ^2 - \frac{1}{2}\Vert a\theta _{k} + b\psi _{k}\Vert ^2\\{} & {} \quad = \frac{1}{2}\Vert a\theta _{k} + a\Delta \theta _k + b\psi _{k}+b\Delta \psi _k\Vert ^2 - \frac{1}{2}\Vert a\theta _{k} + b\psi _{k}\Vert ^2. \end{aligned}$$

Expanding this and using the fact that $a\theta _{k} + b\psi _{k} = -\Delta \psi _k/\gamma$, we can show that,

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\Vert a\theta _{k} + a\Delta \theta _k + b\psi _{k}+b\Delta \psi _k\Vert ^2 - \frac{1}{2}\Vert a\theta _{k} + b\psi _{k}\Vert ^2 \\=&\frac{a^2}{2}\Vert \Delta \theta _k\Vert ^2 + \frac{b^2}{2} \Vert \Delta \psi _k\Vert ^2 + ab\langle \Delta \theta _k,\Delta \psi _k\rangle -\frac{a}{\gamma }\langle \Delta \theta _k,\Delta \psi _k\rangle -\frac{b}{\gamma }\Vert \Delta \psi _k\Vert ^2. \end{aligned} \end{aligned}$$

(24)

We then use $\Vert \Delta \psi _k\Vert ^2 = \Vert \Delta \theta _k - \Delta \psi _k\Vert ^2 + \Vert \Delta \theta _k\Vert ^2 -2\langle \Delta \theta _k,\Delta \theta _k-\Delta \psi _k\rangle$ and $\langle \Delta \theta _k,\Delta \psi _k\rangle = \Vert \Delta \theta _k\Vert ^2 -\langle \Delta \theta _k,\Delta \theta _k-\Delta \psi _k\rangle$ in (24) to obtain:

$$\begin{aligned}{} & {} \frac{1}{2}\Vert a\theta _{k+1} + b\psi _{k+1}\Vert ^2 - \frac{1}{2}\Vert a\theta _{k} + b\psi _{k}\Vert ^2 = \left( \frac{a^2}{2}+\frac{b^2}{2}+ ab - \frac{a}{\gamma } - \frac{b}{\gamma }\right) \Vert \Delta \theta _k\Vert ^2 \nonumber \\{} & {} \quad +\left( \frac{b^2}{2}-\frac{b}{\gamma }\right) \Vert \Delta \theta _k-\Delta \psi _k\Vert ^2 + \left( -b^2-ab+\frac{a}{\gamma }+\frac{2b}{\gamma }\right) \langle \Delta \theta _k,\Delta \theta _k-\Delta \psi _k\rangle .\nonumber \\ \end{aligned}$$

(25)

We then simplify the factors using the identity $a+b=\alpha$, as well as $\frac{a^2}{2}+\frac{b^2}{2}+ ab = \frac{1}{2}(a+b)^2 = \frac{\alpha ^2}{2}$, and $-b^2-ab = -\alpha /\beta$ to deduce that (25) is equal to

$$\begin{aligned} \left( \frac{\alpha ^2}{2} - \frac{\alpha }{\gamma }\right) \Vert \Delta \theta _k\Vert ^2 +\frac{\gamma -2\beta }{2\gamma \beta ^2}\Vert \Delta \theta _k-\Delta \psi _k\Vert ^2 +\frac{-\gamma \alpha +\alpha \beta +1}{\gamma \beta }\langle \Delta \theta _k,\Delta \theta _k-\Delta \psi _k\rangle .\nonumber \\ \end{aligned}$$

(26)

We can finally combine (23) and (26),

$$\begin{aligned} \begin{aligned} \mathcal {E}_{k+1}-\mathcal {E}_k \le&\left( \frac{\mu L}{2}+\frac{\alpha ^2}{2} - \frac{\alpha }{\gamma }\right) \Vert \Delta \theta _k\Vert ^2 +\frac{\gamma -2\beta }{2\gamma \beta ^2}\Vert \Delta \theta _k-\Delta \psi _k\Vert ^2 \\ {}&+ \left( -\frac{\mu }{\gamma \beta }+\frac{1+\alpha \beta -\gamma \alpha }{\gamma \beta }\right) \langle \Delta \theta _k,\Delta \theta _k-\Delta \psi _k\rangle . \end{aligned} \end{aligned}$$

(27)

Notice that $\mu = 1+\alpha \beta -\gamma \alpha$ is specifically chosen so that the last term in (27) vanishes, so,

$$\begin{aligned} \mathcal {E}_{k+1}-\mathcal {E}_k \le \frac{\gamma \mu L+\gamma \alpha ^2 -2\alpha }{2\gamma }\Vert \Delta \theta _k\Vert ^2 +\frac{\gamma -2\beta }{2\gamma \beta ^2}\Vert \Delta \theta _k-\Delta \psi _k\Vert ^2. \end{aligned}$$

(28)

To prove the decrease of $(\mathcal {E}_k)_{k\in \mathbb {N}}$, it remains to justify that both terms in (28) are negative. First, the condition $\gamma <2\beta$ in (15) makes the second term negative. Then,

$$\begin{aligned} \gamma \mu L+\gamma \alpha ^2 -2\alpha<0 \iff -\alpha L\gamma ^2 + \left( \alpha ^2+ (1+\alpha \beta )L\right) \gamma - 2\alpha <0. \end{aligned}$$

A simpler sufficient condition for this to hold is $\left( \alpha ^2+ (1+\alpha \beta )L\right) \gamma - 2\alpha <0$ or equivalently $\gamma < 2\alpha /\left( \alpha ^2+ (1+\alpha \beta )L\right)$, which holds from (15). So the sequence $(\mathcal {E}_k)_{k\in \mathbb {N}}$ is a decreasing. It is also lower-bounded since $\mathcal {J}$ is lower-bounded, so it converges.

The rest of the proof then relies on exploiting (28). Let $K\in \mathbb {N}$, we sum (28):

$$\begin{aligned} \sum _{k=0}^{K} \mathcal {E}_{k+1} - \mathcal {E}_{k} \le \frac{\gamma \mu L+\gamma \alpha ^2 -2\alpha }{2\gamma } \sum _{k=0}^{K} \Vert \Delta \theta _k\Vert ^2 +\frac{\gamma -2\beta }{2\gamma \beta ^2}\sum _{k=0}^{K} \Vert \Delta \theta _k-\Delta \psi _k\Vert ^2. \end{aligned}$$

The left-hand side is a telescopic series, and it follows from (22) that $\forall k\in \mathbb {N}$, $\Delta \theta _k-\Delta \psi _k = -\gamma \beta \nabla \mathcal {J}(\theta _k)$, so denoting $C_1 = -(\gamma \mu L+\gamma \alpha ^2 -2\alpha )/2\gamma >0$ and $C_2 = -(\gamma ^2-2\gamma \beta )/2>0$,

$$\begin{aligned} \mathcal {E}_{0}-\mathcal {E}_{K+1} \ge C_1 \sum _{k=0}^{K} \Vert \Delta \theta _k\Vert ^2 C_2\sum _{k=0}^{K} \Vert \nabla \mathcal {J}(\theta _k)\Vert ^2. \end{aligned}$$

Then, $\mathcal {E}_{0} - \mathcal {E}_{K+1}$ is upper bounded since $(\mathcal {E}_k)_{k\in \mathbb {N}}$ converges, so $\sum _{k=0}^{K} \Vert \nabla \mathcal {J}(\theta _k)\Vert ^2<+\infty$. This implies that $\lim _{k\rightarrow +\infty }\Vert \nabla \mathcal {J}(\theta _k)\Vert ^2 =0$ and we deduce similarly that $\lim _{k\rightarrow +\infty }\Vert \theta _{k+1}-\theta _{k}\Vert ^2 =0$. Using (14), we also have,

$$\begin{aligned}{} & {} \Vert (\alpha -\frac{1}{\beta })\theta _k +\frac{1}{\beta }\psi _k\Vert ^2\nonumber \\{} & {} \quad = \frac{1}{\gamma ^2}\Vert \psi _{k+1}-\psi _{k}\Vert ^2\le \frac{2}{\gamma ^2}\Vert \theta _{k+1}-\theta _{k}\Vert ^2 +2\beta ^2 \Vert \nabla \mathcal {J}(\theta _k)\Vert ^2 \xrightarrow [k\rightarrow \infty ]{}0. \end{aligned}$$

(29)

The convergence of $(\mathcal {E}_k)_{k\in \mathbb {N}}$ and (29) imply that $(\mathcal {J}(\theta _k))_{k\in \mathbb {N}}$ converges, which proves the first part of the theorem. Assume that the critical points are isolated and that the sequence $(\theta _k)_{k\in \mathbb {N}}$ is uniformly bounded on $\mathbb {R}^P$. According to Lemma C.1, since $(\theta _k)_{k\in \mathbb {N}}$ is bounded and $\lim _{k\rightarrow +\infty }\Vert \theta _{k+1}-\theta _{k}\Vert =0$, the set of accumulation points of $(\theta _k)_{k\in \mathbb {N}}$ is connected. By continuity of $\nabla \mathcal {J}$, accumulation points of $(\theta _k)_{k\in \mathbb {N}}$ are critical points of $\mathcal {J}$, which are assumed to be isolated. So the set of accumulation points is a singleton and $(\theta _k)_{k\in \mathbb {N}}$ converges to it. $\square$