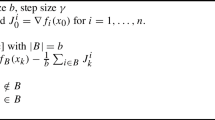Perturbed Iterate SGD for Lipschitz Continuous Loss Functions

Abstract

This paper presents an extension of stochastic gradient descent for the minimization of Lipschitz continuous loss functions. Our motivation is for use in non-smooth non-convex stochastic optimization problems, which are frequently encountered in applications such as machine learning. Using the Clarke $\epsilon$-subdifferential, we prove the non-asymptotic convergence to an approximate stationary point in expectation for the proposed method. From this result, a method with non-asymptotic convergence with high probability, as well as a method with asymptotic convergence to a Clarke stationary point almost surely are developed. Our results hold under the assumption that the stochastic loss function is a Carathéodory function which is almost everywhere Lipschitz continuous in the decision variables. To the best of our knowledge, this is the first non-asymptotic convergence analysis under these minimal assumptions.

Appendix Proofs and Auxiliary Results

1.1 Section 1

Proposition A.1

A bounded function f(w) such that $|f(w)|\le R$ for all $w\in {\mathbb {R}}^d$, with a Lipschitz continuous gradient with parameter $L_1$, is Lipschitz continuous with parameter $L_0=2R+\frac{L_1}{2}d$.

Proof

A function has a Lipschitz continuous gradient if there exists a constant $L_1$ such that for all $x,w\in {\mathbb {R}}^d$, ${\Vert }\nabla f(x)-\nabla f(w){\Vert }_2\le L_1{\Vert }x-w{\Vert }_2$, which is equivalent to (see [22, Lemma 1.2.3])

$$\begin{aligned} |f(x)-f(w)-\langle \nabla f(w),x-w\rangle |&\le \frac{L_1}{2}{\Vert }x-w{\Vert }^2_2. \end{aligned}$$

(30)

By the mean value theorem, if a differentiable function has a bounded gradient such that ${\Vert }\nabla f(w){\Vert }_2\le L_0$ for all $w\in {\mathbb {R}}^n$, then it is Lipschitz continuous with parameter $L_0$. Using (30) with $x=w-y$ for any $y\in {\mathbb {R}}^d$,

$$\begin{aligned} f(w-y)-f(w)+\langle \nabla f(w),y\rangle \le \frac{L_1}{2}{\Vert }y{\Vert }^2_2. \end{aligned}$$

Taking $y_j={{\,\mathrm{sgn}\,}}(\nabla _j f(w))$ for $j=1,\ldots ,d$, and using the boundedness of f(w),

$$\begin{aligned} {\Vert }\nabla f(w){\Vert }_2\le {\Vert }\nabla f(w){\Vert }_1\le 2R+\frac{L_1}{2}d. \end{aligned}$$

$\square$

1.2 Section 3

Proof of Lemma 3.1

Let $D\subseteq \{(w,\xi ):w\in {\mathbb {R}}^d,\text { }\xi \in \varXi \}=:{\overline{\varXi }}$ be the set of points where $F(w,\xi )$ is differentiable in w within the set ${\overline{\varXi }}$ where it is Lipschitz continuous in w. For $F(w,\xi )$ to be differentiable at a point $(w,\xi )$, there exists a unique $g\in {\mathbb {R}}^d$ such that for any $\omega >0$, there exists a $\delta >0$ such that for all $h\in {\mathbb {R}}^d$ where $0<||h||_2<\delta$, it holds that

$$\begin{aligned} \frac{|F(w+h,\xi )-F(w,\xi )-\langle g,h\rangle |}{||h||_2}<\omega . \end{aligned}$$

For simplicity let $H(w,\xi ,h,g):=\frac{|F(w+h,\xi )-F(w,\xi )-\langle g,h\rangle |}{||h||_2}$. The set D can be represented as

$$\begin{aligned} \bigcup _{g\in {\mathbb {R}}^d}\bigcap _{\omega \in {\mathbb {Q}}_{>0}} \bigcup _{\delta \in {\mathbb {Q}}_{>0}}\bigcap _{\begin{array}{c} 0<||h||_2<\delta \\ h\in {\mathbb {Q}}^d \end{array}} \left\{ (w,\xi )\in {\overline{\varXi }}:H(w,\xi ,h,g)<\omega \right\} , \end{aligned}$$

where h can be restricted to be over ${\mathbb {Q}}^d$ as $H(w,\xi ,h,g)$ is continuous in h when $||h||_2>0$ and ${\mathbb {Q}}^d$ is dense in ${\mathbb {R}}^d$. We want to prove that the set ${\hat{D}}$ defined as

$$\begin{aligned} \bigcap _{\omega \in {\mathbb {Q}}_{>0}} \bigcup _{(g,\delta )\in {\mathbb {Q}}^d\times {\mathbb {Q}}_{>0}} \bigcap _{\begin{array}{c} 0<||h||_2<\delta \\ h\in {\mathbb {Q}}^d \end{array}} \left\{ (w,\xi )\in {\overline{\varXi }}:H(w,\xi ,h,g)<\omega \right\} , \end{aligned}$$

is equal to D, proving that D is an element of ${{\mathcal {B}}}_{{\mathbb {R}}^{d+p}}$.

For an element $(w',\xi ')\in D$ with $g'$ being the gradient at $(w',\xi ')$, for any $\omega >0$, take $\delta (\frac{\omega }{2})>0$ such that

$$\begin{aligned} (w',\xi ')\in \bigcap \limits _{\begin{array}{c} 0<||h||_2<\delta (\frac{\omega }{2})\\ h\in {\mathbb {Q}}^d \end{array}} \left\{ (w,\xi )\in {\overline{\varXi }}:H(w,\xi ,h,g')<\frac{\omega }{2}\right\} , \end{aligned}$$

and take $g\in {\mathbb {Q}}^d$ such that $||g'-g||_2<\frac{\omega }{2}$. It follows that

$$\begin{aligned}&H(w',\xi ',h,g')<\frac{\omega }{2}\\&\quad \Longrightarrow \frac{|F(w'+h,\xi ')-F(w',\xi ')-\langle g,h\rangle - \langle g'-g,h\rangle |}{||h||_2}<\frac{\omega }{2}\\&\quad \Longrightarrow H(w',\xi ',h,g)-\frac{|\langle g'-g,h\rangle |}{||h||_2}<\frac{\omega }{2}\\&\quad \Longrightarrow H(w',\xi ',h,g) <\omega \end{aligned}$$

when $0<||h||_2<\delta (\frac{\omega }{2})$, using the reverse triangle inequality for the third inequality, proving that $(w',\xi ')\in {\hat{D}}$.

Considering now an element $(w',\xi ')\in {\hat{D}}$, let $\{\omega _i\}\subset {\mathbb {Q}}_{>0}$ be a non-increasing sequence approaching zero in the limit, with $\{g_i\}\subset {\mathbb {Q}}^d$, and let $\{\delta _i\}\subset {\mathbb {Q}}_{>0}$ be a non-increasing sequence such that for all $i\in {\mathbb {N}}$, $H(w',\xi ',h,g_i)<\omega _i$ when $0<||h||_2<\delta _i$. The sequence $\{g_i\}$ is bounded as

$$\begin{aligned}&H(w',\xi ',h,g_i)<\omega _i\nonumber \\&\quad \Longrightarrow \frac{|F(w'+h,\xi ')-F(w',\xi ')-\langle g_i,h\rangle |}{||h||_2}<\omega _i\nonumber \\&\quad \Longrightarrow \frac{|\langle g_i,h\rangle |}{||h||_2}-\frac{|F(w'+h,\xi ')-F(w',\xi ')|}{||h||_2}<\omega _i \Longrightarrow \frac{|\langle g_i,h\rangle |}{||h||_2} <\omega _i+C(\xi ') \end{aligned}$$

(31)

for all $0<||h||_2<\delta _i$, using again the reverse triangle inequality and the Lipschitz continuity of $F(w,\xi ')$. Taking $h=\delta '_i\frac{g_i}{||g_i||_2}$ for any $\delta '_i<\delta _i$ in (31),

$$\begin{aligned} ||g_i||_2<\omega _i+C(\xi ')\le \omega _1+C(\xi '). \end{aligned}$$

Given that the sequence $\{g_i\}$ is bounded, it contains at least one accumulation point $g'$. There then exists a subsequence $\{i_j\}\subset {\mathbb {N}}$ such that for any $\omega \in {\mathbb {Q}}_{>0}$, there exists a $J\in {\mathbb {N}}$ such that for $j>J$, $\omega _{i_j}<\frac{\omega }{2}$ and $||g_{i_j}-g'||_2<\frac{\omega }{2}$, from which it holds that $H(w',\xi ',h,g')\le H(w',\xi ',h,g_{i_j})+||g'-g_{i_j}||_2<\omega$ when $0<||h||_2<\delta _{i_j}$, proving $g'$ is the gradient of $F(w,\xi )$ at $(w',\xi ')$ and $(w',\xi ')\in D$.

We now want to establish that $F(w,\xi )$ is differentiable almost everywhere in w. Let $\mathbb {1}_{D^c}(w,\xi )$ be the indicator function of the complement of D. The set $D^c$ is the set of points $(w,\xi )$ where $F(w,\xi )$ is not differentiable or not Lipschitz continuous in w. Showing that $D^c$ is a null set is then sufficient. Given that the function $\mathbb {1}_{D^c}(w,\xi )\in L^+({\mathbb {R}}^d\times {\mathbb {R}}^p)$, and $m^d$ and P are $\sigma$-finite, the measure of $D^c$ can be computed by the iterated integral

$$\begin{aligned} {\mathbb {E}}_{\xi }\left[ \int _{w\in {\mathbb {R}}^d}\mathbb {1}_{D^c}(w,\xi )\mathrm{d}w\right] \end{aligned}$$

by Tonelli’s theorem [15, Theorem 2.37 a.]. Let ${\overline{\xi }}\in {\mathbb {R}}^p$ be chosen such that $F(w,{\overline{\xi }})$ is Lipschitz continuous in w. By Rademacher’s theorem, $F(w,{\overline{\xi }})$ is differentiable in w almost everywhere, which implies that $\int _{w\in {\mathbb {R}}^d}\mathbb {1}_{D^c}(w,{\overline{\xi }})\mathrm{d}w=0$. As this holds for almost every $\xi$, ${\mathbb {E}}_{\xi }[\int _{w\in {\mathbb {R}}^d}\mathbb {1}_{D^c}(w,\xi )\mathrm{d}w]=0$ [15, Proposition 2.16].$\square$

Example A.1

Let $e_j$ for $j=1,\ldots ,d$ denote the standard basis of ${\mathbb {R}}^d$. For $i\in {\mathbb {N}}$, let

$$\begin{aligned} h^i_j(w,\xi ) :=i(F(w+i^{-1}e_j,\xi )-F(w,\xi )) \end{aligned}$$

define a sequence $\{h^i_j(w,\xi )\}_{i\in {\mathbb {N}}}$ of real-valued Borel measurable functions. It holds that $h^+_j(w,\xi ):=\limsup \limits _{i\rightarrow \infty } h^i_j(w,\xi )$ and $h^-_j(w,\xi ):=\liminf \limits _{i\rightarrow \infty } h^i_j(w,\xi )$ are extended real-valued Borel measurable functions [2, Lemma 2.9]. For $\zeta \in [0,1]$ and $a\in {\mathbb {R}}$, a family of candidate approximate gradients can be defined as having components

$$\begin{aligned} {\widetilde{\nabla }} F_j(w,\xi )={\left\{ \begin{array}{ll} \zeta h^+_j(w,\xi )+(1-\zeta )h^-_j(w,\xi )&{}\text { if } \{h^+_j(w,\xi ), h^-_j(w,\xi )\}\in {\mathbb {R}}\\ a &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

(32)

The function ${\widetilde{\nabla }} F(w,\xi )$ will equal $\nabla F(w,\xi )$ wherever it exists. The set

$$\begin{aligned} A=\{(w,\xi ): |h^+_j(w,\xi )|<\infty \}\cap \{(w,\xi ):|h^-_j(w,\xi )|<\infty \} \end{aligned}$$

is measurable given that for an extended real-valued measurable function h, the set $\{|h|=\infty \}$ is measurable [2, Page 11]. Let $\mathbb {1}_A(w,\xi )$ and $\mathbb {1}_{A^c}(w,\xi )$ denote the indicator functions of A and its complement. The product of extended real-valued functions is measurable [2, Page 12-13], implying that $\zeta h^+_j(w,\xi )\mathbb {1}_{A}(w,\xi )$, $(1-\zeta )h^-_j(w,\xi )\mathbb {1}_{A}(w,\xi )$, and $a\mathbb {1}_{A^c}(w,\xi )$ are all measurable. Given that all three functions are real-valued,⁵ their sum is measurable, implying the measurability of (32).

Proof of Lemma 3.2

Following the proof of Lemma 3.1, let $D^c\subset \{(w,\xi ):w\in {\mathbb {R}}^d,\text { }\xi \in {\mathbb {R}}^p\}$ be the same Borel measurable set containing the points where $F(w,\xi )$ is not differentiable or not Lipschitz continuous in w. By Tonelli’s theorem, it was established that

$$\begin{aligned} \int _{w\in {\mathbb {R}}^d}{\mathbb {E}}_{\xi }[\mathbb {1}_{D^c}(w,\xi )]\mathrm{d}w=0. \end{aligned}$$

(33)

The function $G(w):={\mathbb {E}}_{\xi }[\mathbb {1}_{D^c}(w,\xi )]$ is measurable in $({\mathbb {R}}^d,{{\mathcal {B}}}_{{\mathbb {R}}^{d}})$, hence the set $D_w:=\{w\in {\mathbb {R}}^d: G(w)=0\}$ is measurable with full measure by (33). As in Example A.1, let $h^i_j(w,\xi ):=i(F(w+i^{-1}e_j,\xi )-F(w,\xi ))$ for $i\in {\mathbb {N}}$. For all $w\in D_w$, $\lim \limits _{i\rightarrow \infty } h^i_j(w,\xi )={\widetilde{\nabla }} F_j(w,\xi )$ for almost all $\xi$, by the assumption that ${\widetilde{\nabla }} F(w,\xi )=\nabla F(w,\xi )$ almost everywhere $F(w,\xi )$ is differentiable. Given the Lipschitz continuity condition of $F(w,\xi )$, for all $i\in {\mathbb {N}}$,

$$\begin{aligned} |h^i_j(w,\xi )| \le iC(\xi )|i^{-1}|=C(\xi ) \end{aligned}$$

for almost all $\xi$. Given that $C(\xi )\in L^1(P_{\xi })$, the dominated convergence theorem can be applied for all $w\in D_w$. It follows that

$$\begin{aligned}&{\mathbb {E}}_{\xi }[{\widetilde{\nabla }} F_j(w,\xi )]{\mathop {=}\limits ^{a.e.}}\lim \limits _{i\rightarrow \infty } {\mathbb {E}}_{\xi }\left[ h_j(w,\xi ,i)\right] \\&\quad =\lim \limits _{i\rightarrow \infty } i(f(w+i^{-1}e_j)-f(w))\\&\quad {\mathop {=}\limits ^{a.e.}}\nabla f_j(w)\\&\quad {\mathop {=}\limits ^{a.e.}}{\widetilde{\nabla }} f_j(w), \end{aligned}$$

where the first equality holds for all $w\in D_w$, the third equality holds for almost all w due to Rademacher’s theorem, and the last equality holds almost everywhere by assumption.$\square$

Proof of Lemma 3.3

The set valued function (6) is outer semicontinuous [17, Proposition 2.7]. The function ${{\,\mathrm{dist}\,}}(0,\partial _{\epsilon }f(w))$ is then lower semicontinuous [25, Proposition 5.11 (a)], hence Borel measurable.$\square$

1.3 Section 4

Proof of Lemma 4.1

Throughout the proof let $\{x,x'\}\in {\mathbb {R}}^d$ be fixed. Consider the function in $v\in [0,1]$,

$$\begin{aligned} {\hat{f}}_z(v)&=f(x'+z+v(x-x')), \end{aligned}$$

for any $z\in {\mathbb {R}}^d$. Where it exists,

$$\begin{aligned} {\hat{f}}_z'(v)&=\lim \limits _{h\rightarrow 0}\frac{f(x'+z+(v+h)(x-x'))-f(x'+z+v(x-x'))}{h}\\&=\lim \limits _{h\rightarrow 0} \frac{f(x'+z+v(x-x')+h(x-x'))-f(x'+z+v(x-x'))}{h} \end{aligned}$$

is equal to the directional derivative of $f({\hat{w}})$ at ${\hat{w}}=x'+z+v(x-x')$ in the direction of $(x-x')$. Let $\mathbb {1}_{D^c}(\cdot )$ be the indicator function of the complement of the set where $f(\cdot )$ is differentiable, which is a Borel measurable function from the continuity of f(w) [14, Page 211]. Its composition with the continuous function ${\hat{w}}$ in $(z,v)\in {\mathbb {R}}^d\times [0,1]$ is then as well. Similar to the proof of Lemma 3.1, using Tonelli’s theorem, the measure of where $f({\hat{w}})$ is not differentiable can be computed as

$$\begin{aligned} \int _0^1\int _{z\in {\mathbb {R}}^d}\mathbb {1}_{D^c}(x'+z+v(x-x'))\mathrm{d}z\mathrm{d}v. \end{aligned}$$

(34)

For any $v\in [0,1]$, $\int _{z\in {\mathbb {R}}^d}\mathbb {1}_{{\overline{D}}}(x'+z+v(x-x'))\mathrm{d}w=0$ by Rademacher’s theorem, implying that (34) equals 0, and $f({\hat{w}})$ is differentiable for almost all (z, v). It follows that for almost all (z, v), the directional derivative exists, the approximate gradient ${\widetilde{\nabla }} f({\hat{w}})$ is equal to the gradient, and

$$\begin{aligned} {\hat{f}}_z'(v)&=\langle {\widetilde{\nabla }} f(x'+z+v(x-x')),x-x'\rangle . \end{aligned}$$

(35)

In addition ${\hat{f}}_z(v)$ is Lipschitz continuous,

$$\begin{aligned} |{\hat{f}}_z(v)-{\hat{f}}_z(v')|&= |f(x'+z+v(x-x'))-f(x'+z+v'(x-x'))|\\&\le L_0{\Vert }x-x'{\Vert }_2|v-v'|. \end{aligned}$$

Choosing $z={\overline{z}}$ such that (35) holds for almost all $v\in [0,1]$, by the fundamental theorem of calculus for Lebesgue integrals,

$$\begin{aligned} f(x+{\overline{z}})&={\hat{f}}_{{\overline{z}}}(1)= {\hat{f}}_{{\overline{z}}}(0)+\int _0^1{\hat{f}}_{{\overline{z}}}'(v)\mathrm{d}v\\&=f(x'+{\overline{z}})+\int _0^1\langle {\widetilde{\nabla }}f(x'+{\overline{z}}+v(x-x')),x-x'\rangle \mathrm{d}v. \end{aligned}$$

Rearranging and subtracting $\langle {\widetilde{\nabla }} f(x'+{\overline{z}}),x-x'\rangle$ from both sides,

$$\begin{aligned}&f(x+{\overline{z}})-f(x'+{\overline{z}})-\langle {\widetilde{\nabla }} f(x'+{\overline{z}}),x-x'\rangle \\&\quad =\int _0^1\langle {\widetilde{\nabla }}f(x'+{\overline{z}}+v(x-x'))-{\widetilde{\nabla }}f(x'+{\overline{z}}),x-x'\rangle \mathrm{d}v. \end{aligned}$$

As for almost all $z\in {\mathbb {R}}^d$, (35) holds for almost all $v\in [0,1]$,

$$\begin{aligned}&f(w)-f(w')-\langle {\widetilde{\nabla }} f(w'),x-x'\rangle =\int _0^1\langle {\widetilde{\nabla }}f(w'+v(x-x'))-{\widetilde{\nabla }} f(w'),x-x'\rangle \mathrm{d}v \end{aligned}$$

holds for almost all $z\in {\mathbb {R}}^n$.$\square$

Proof of Lemma 4.2

As f(w) is differentiable almost everywhere, and ${\widetilde{\nabla }} f(w)$ is equal to the gradient of f(w) almost everywhere it is differentiable, using the directional derivative and Lipschitz continuity of f(w),

$$\begin{aligned} {\Vert }{\widetilde{\nabla }} f(w){\Vert }^2_2&=\lim \limits _{h\rightarrow 0} \frac{f(w+h{\widetilde{\nabla }} f(w))-f(w)}{h}\\&\le L_0{\Vert }{\widetilde{\nabla }} f(w){\Vert }_2 \end{aligned}$$

holds almost everywhere. Similarly, by assumption and Lemma 3.1, $F(w,\xi )$ is Lipschitz continuous and differentiable almost everywhere, with ${\widetilde{\nabla }} F(w,\xi )$ equal to the gradient almost everywhere $F(w,\xi )$ is differentiable. It follows that almost everywhere,

$$\begin{aligned} {\Vert }{\widetilde{\nabla }} F(w,\xi ){\Vert }^2_2&=\lim \limits _{h\rightarrow 0} \frac{F(w+h{\widetilde{\nabla }} F(w,\xi ),\xi )-F(w,\xi )}{h}\\&\le C(\xi ){\Vert }{\widetilde{\nabla }} F(w,\xi ){\Vert }_2. \end{aligned}$$

$\square$

Proof of Lemma 4.3

We first show that

${\mathbb {E}}[{\Vert }{\overline{\nabla }}F{\Vert }^2_2 -{\Vert }{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]= {\mathbb {E}}[{\Vert }{\overline{\nabla }}F-{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]$:

$$\begin{aligned}&{\mathbb {E}}[{\Vert }{\overline{\nabla }}F-{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]\\&\quad ={\mathbb {E}}[{\Vert }{\overline{\nabla }}F{\Vert }^2_2-2\langle {\overline{\nabla }}F,{\mathbb {E}}[{\overline{\nabla }}F|x]\rangle + {\Vert }{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]\\&\quad ={\mathbb {E}}[{\Vert }{\overline{\nabla }}F{\Vert }^2_2] -2{\mathbb {E}}[\langle {\overline{\nabla }}F,{\mathbb {E}}[{\overline{\nabla }}F|x]\rangle ] +{\mathbb {E}}[{\Vert }{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]\\&\quad ={\mathbb {E}}[{\Vert }{\overline{\nabla }}F{\Vert }^2_2] -2{\mathbb {E}}({\mathbb {E}}[\langle {\overline{\nabla }}F,{\mathbb {E}}[{\overline{\nabla }}F|x]\rangle |x]) +{\mathbb {E}}[{\Vert }{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]\\&\quad ={\mathbb {E}}[{\Vert }{\overline{\nabla }}F{\Vert }^2_2] -2{\mathbb {E}}[\langle {\mathbb {E}}[{\overline{\nabla }}F|x],{\mathbb {E}}[{\overline{\nabla }}F|x]\rangle ] +{\mathbb {E}}[{\Vert }{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]\\&\quad ={\mathbb {E}}[{\Vert }{\overline{\nabla }}F{\Vert }^2_2] -2{\mathbb {E}}[{\Vert }{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2] +{\mathbb {E}}[{\Vert }{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]\\&\quad ={\mathbb {E}}[{\Vert }{\overline{\nabla }}F{\Vert }^2_2] -{\mathbb {E}}[{\Vert }{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]. \end{aligned}$$

Let $w_l:=x+z_l$ for $l=1,\ldots ,S$. Analyzing now ${\mathbb {E}}[{\Vert }{\overline{\nabla }}F-{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]$,

$$\begin{aligned}&{\mathbb {E}}[{\Vert }{\overline{\nabla }}F-{\mathbb {E}}[{\overline{\nabla }}F|x]{\Vert }^2_2]\nonumber \\&\quad ={\mathbb {E}}\left[ \sum _{j=1}^d({\overline{\nabla }}_jF-{\mathbb {E}}[{\overline{\nabla }}_jF|x])^2\right] \nonumber \\&\quad ={\mathbb {E}}\left[ \sum _{j=1}^d\left( \frac{1}{S}\sum \limits _{l=1}^S({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])\right) ^2\right] \nonumber \\&\quad =\frac{1}{S^2}\sum _{j=1}^d{\mathbb {E}}\left[ \left( \sum \limits _{l=1}^S({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])\right) ^2\right] \nonumber \\&\quad =\frac{1}{S^2}\sum _{j=1}^d{\mathbb {E}}\bigg ({\mathbb {E}}\bigg [\bigg (\sum \limits _{l=1}^S({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])\bigg )^2\bigg |x\bigg ]\bigg ) \end{aligned}$$

(36)

$$\begin{aligned}&\quad =\frac{1}{S^2}\sum _{j=1}^d{\mathbb {E}}\left( \sum \limits _{l=1}^S{\mathbb {E}}[({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])^2|x]\right) , \end{aligned}$$

(37)

where (37) holds since ${\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x]$ for $l=1,\ldots ,S$ are conditionally independent random variables with conditional expectation of zero with respect to x: Considering the cross terms of ${\mathbb {E}}[(\sum \limits _{l=1}^S({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x]))^2|x]$ in (36) with $l\ne m$,

$$\begin{aligned}&{\mathbb {E}}[({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])({\widetilde{\nabla }}_j F(w_m,\xi _m)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])|x]\\&\quad ={\mathbb {E}}[{\widetilde{\nabla }}_jF(w_l,\xi _l) {\widetilde{\nabla }}_jF(w_m,\xi _m)|x] -{\mathbb {E}}[{\widetilde{\nabla }}_jF(w_l,\xi _l){\mathbb {E}}[{\overline{\nabla }}_jF|x]|x]\\&\qquad -{\mathbb {E}}[{\mathbb {E}}[{\overline{\nabla }}_jF|x]{\widetilde{\nabla }}_jF(w_m,\xi _m)|x] +{\mathbb {E}}[{\mathbb {E}}[{\overline{\nabla }}_jF|x]^2|x]\\&\quad ={\mathbb {E}}[{\widetilde{\nabla }}_jF(w_l,\xi _l)|x]{\mathbb {E}}[{\widetilde{\nabla }}_jF(w_m,\xi _m)|x] -{\mathbb {E}}[{\widetilde{\nabla }}_jF(w_l,\xi _l)|x]{\mathbb {E}}[{\overline{\nabla }}_jF|x]\\&\qquad -{\mathbb {E}}[{\overline{\nabla }}_jF|x]{\mathbb {E}}[{\widetilde{\nabla }}_jF(w_m,\xi _m)|x] +{\mathbb {E}}[{\overline{\nabla }}_jF|x]^2\\&\quad =0. \end{aligned}$$

Continuing from (37),

$$\begin{aligned}&\frac{1}{S^2}\sum _{j=1}^d{\mathbb {E}}\left( \sum \limits _{l=1}^S{\mathbb {E}}[({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])^2|x]\right) \nonumber \\&\quad =\frac{1}{S^2}\sum _{j=1}^d\sum \limits _{l=1}^S{\mathbb {E}}[({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])^2]\nonumber \\&\quad =\frac{1}{S}\sum _{j=1}^d{\mathbb {E}}[({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])^2], \end{aligned}$$

(38)

where the last equality holds for any $l\in \{1,\ldots ,S\}$. Continuing from (38),

$$\begin{aligned}&\frac{1}{S}\sum _{j=1}^d{\mathbb {E}}[({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])^2]\nonumber \\&\quad =\frac{1}{S}\sum _{j=1}^d{\mathbb {E}}({\mathbb {E}}[({\widetilde{\nabla }}_j F(w_l,\xi _l)-{\mathbb {E}}[{\overline{\nabla }}_jF|x])^2|x])\nonumber \\&\quad =\frac{1}{S}\sum _{j=1}^d{\mathbb {E}}({\mathbb {E}}[{\widetilde{\nabla }}_j F(w_l,\xi _l)^2-2{\widetilde{\nabla }}_j F(w_l,\xi _l){\mathbb {E}}[{\overline{\nabla }}_jF|x]+ {\mathbb {E}}[{\overline{\nabla }}_jF|x]^2|x])\nonumber \\&\quad =\frac{1}{S}\sum _{j=1}^d{\mathbb {E}}({\mathbb {E}}[{\widetilde{\nabla }}_j F(w_l,\xi _l)^2|x]-2{\mathbb {E}}[{\widetilde{\nabla }}_j F(w_l,\xi _l)|x]{\mathbb {E}}[{\overline{\nabla }}_jF|x]+ {\mathbb {E}}[{\overline{\nabla }}_jF|x]^2)\nonumber \\&\quad =\frac{1}{S}\sum _{j=1}^d{\mathbb {E}}({\mathbb {E}}[{\widetilde{\nabla }}_j F(w_l,\xi _l)^2|x]-2{\mathbb {E}}[{\overline{\nabla }}_jF|x]^2+ {\mathbb {E}}[{\overline{\nabla }}_jF|x]^2)\nonumber \\&\quad =\frac{1}{S}\sum _{j=1}^d{\mathbb {E}}({\mathbb {E}}[{\widetilde{\nabla }}_j F(w_l,\xi _l)^2|x]-{\mathbb {E}}[{\overline{\nabla }}_jF|x]^2)\nonumber \\&\quad =\frac{1}{S}\sum _{j=1}^d{\mathbb {E}}[{\widetilde{\nabla }}_j F(w_l,\xi _l)^2]-{\mathbb {E}}[{\mathbb {E}}[{\overline{\nabla }}_jF|x]^2]\nonumber \\&\quad \le \frac{1}{S}\sum _{j=1}^d{\mathbb {E}}[{\widetilde{\nabla }}_j F(w_l,\xi _l)^2]\nonumber \\&\quad =\frac{1}{S}{\mathbb {E}}[{\Vert }{\widetilde{\nabla }} F(w_l,\xi _l){\Vert }^2_2]\nonumber \\&\quad \le \frac{Q}{S}, \end{aligned}$$

(39)

where the final inequality uses Lemma 4.2 and the definition $Q:={\mathbb {E}}[C(\xi )^2]$: Similar to showing (14), since $z_l$ and $\xi _l$ are independent of x,

${\mathbb {E}}[{\Vert }{\widetilde{\nabla }} F(x+z_l,\xi _l){\Vert }^2_2|x]=g(x)$, where $g(y):={\mathbb {E}}[{\Vert }{\widetilde{\nabla }} F(y+z_l,\xi _l){\Vert }^2_2]$. By the absolute continuity of $z_l$, for all $y\in {\mathbb {R}}^d$, ${\Vert }{\widetilde{\nabla }} F(y+z_l,\xi _l){\Vert }^2_2\le C(\xi _l)^2$ for almost every $(z_l,\xi _l)$ from Lemma 4.2, hence $g(y)\le {\mathbb {E}}[C(\xi )^2]$ for all $y\in {\mathbb {R}}^d$, and in particular, ${\mathbb {E}}[{\Vert }{\widetilde{\nabla }} F(w_l,\xi _l){\Vert }^2_2]={\mathbb {E}}[g(x)]\le {\mathbb {E}}[C(\xi )^2]$.$\square$

Lemma A.1

For $d\in {\mathbb {N}}$,

$$\begin{aligned} \frac{\lambda (d)d!!}{(d-1)!!}\le \sqrt{d}. \end{aligned}$$

Proof

For $d=1$, $\frac{\lambda (d)d!!}{(d-1)!!}=1$, and for $d=2$, $\frac{\lambda (d)d!!}{(d-1)!!}=\frac{4}{\pi }<\sqrt{2}$. For $d\ge 2$, we will show that the result holds for $d+1$ assuming that it holds for $d-1$, proving the result by induction.

$$\begin{aligned} \frac{\lambda (d+1)(d+1)!!}{d!!}&=\frac{\lambda (d-1)(d+1)(d-1)!!}{d(d-2)!!}\\&=\frac{\lambda (d-1)(d-1)!!}{(d-2)!!}\frac{(d+1)}{d}\\&\le \sqrt{d-1}\frac{(d+1)}{d}\\&=\sqrt{\frac{(d-1)(d+1)^2}{d^2}}\\&=\sqrt{\frac{d^3+d^2-d-1}{d^2}}\\&<\sqrt{d+1}. \end{aligned}$$

$\square$

Proof of Corollary 4.1

From Theorem 4.1, $\sigma =\theta \sqrt{d}K^{-\beta }$, and requiring $\sigma \le \epsilon _1$ implies

$$\begin{aligned} \left( \frac{\theta \sqrt{d}}{\epsilon _1}\right) ^{\frac{1}{\beta }}\le K. \end{aligned}$$

Taking $K_{\epsilon _1}=\left\lceil \left( \frac{\theta \sqrt{d}}{\epsilon _1}\right) ^{\frac{1}{\beta }}\right\rceil <\left( \frac{\theta \sqrt{d}}{\epsilon _1}\right) ^{\frac{1}{\beta }}+1$ and $S_{\epsilon _1}=\lceil K_{\epsilon _1}^{1-\beta }\rceil <K_{\epsilon _1}^{1-\beta }+1$,

$$\begin{aligned} S_{\epsilon _1}<\left( \left( \frac{\theta \sqrt{d}}{\epsilon _1} \right) ^{\frac{1}{\beta }}+1\right) ^{1-\beta }+1<\left( \frac{\theta \sqrt{d}}{\epsilon _1}\right) ^{\frac{1-\beta }{\beta }}+2, \end{aligned}$$

where the second inequality follows from a general result for $a_i>0$ for $i=1,\ldots ,n$ and $\beta \in (0,1)$: $(\sum _{i=1}^na_i)^{1-\beta }=\frac{\sum _{i=1}^na_i}{(\sum _{i=1}^na_i)^{\beta }}<\sum _{i=1}^n\frac{a_i}{a_i^{\beta }}=\sum _{i=1}^na_i^{1-\beta }$. An upper bound on the total number of gradient calls required to satisfy $\epsilon _1$, considering up to $K_{\epsilon _1}-1$ iterations of PISGD is then

$$\begin{aligned} (K_{\epsilon _1}-1)S_{\epsilon _1}<\left( \frac{\theta \sqrt{d}}{\epsilon _1} \right) ^{\frac{1}{\beta }}\left( \left( \frac{\theta \sqrt{d}}{\epsilon _1}\right) ^{\frac{1-\beta }{\beta }}+2\right) =O\left( \epsilon _1^{\frac{\beta -2}{\beta }}\right) . \end{aligned}$$

Choosing K such that

$$\begin{aligned} {\mathbb {E}}[{{\,\mathrm{dist}\,}}(0,\partial _{\sigma }f(x^R))]&< K^{\frac{\beta -1}{2}}\sqrt{2\left( \frac{L_0}{\theta }\varDelta +L_0^2\sqrt{d} K^{-\beta }+Q\right) }\\&\le K^{\frac{\beta -1}{2}}\sqrt{2\left( \frac{L_0}{\theta }\varDelta +L_0^2 \sqrt{d}+Q\right) }\\&\le \epsilon _2 \end{aligned}$$

gives the bound

$$\begin{aligned} \left( \frac{2}{\epsilon ^2_2}\left( \frac{L_0}{\theta }\varDelta +L_0^2\sqrt{d}+Q\right) \right) ^{\frac{1}{1-\beta }}\le K. \end{aligned}$$

Taking $K_{\epsilon _2}=\left\lceil \left( \frac{2}{\epsilon ^2_2}\left( \frac{L_0}{\theta }\varDelta +L_0^2\sqrt{d}+Q\right) \right) ^{\frac{1}{1-\beta }}\right\rceil$ and $S_{\epsilon _2}=\lceil K_{\epsilon _2}^{1-\beta }\rceil$,

$$\begin{aligned} S_{\epsilon _2}&<\left( \left( \frac{2}{\epsilon ^2_2}\left( \frac{L_0}{\theta } \varDelta +L_0^2\sqrt{d}+Q\right) \right) ^{\frac{1}{1-\beta }}+1\right) ^{1-\beta }+1\\&<\frac{2}{\epsilon ^2_2}\left( \frac{L_0}{\theta }\varDelta +L_0^2\sqrt{d}+Q\right) +2, \end{aligned}$$

and the number of gradient calls required to satisfy $\epsilon _2$ is bounded by

$$\begin{aligned} (K_{\epsilon _2}-1)S_{\epsilon _2}&<\left( \frac{2}{\epsilon ^2_2} \left( \frac{L_0}{\theta }\varDelta +L_0^2\sqrt{d}+Q\right) \right) ^{\frac{1}{1-\beta }} \left( \frac{2}{\epsilon ^2_2}\left( \frac{L_0}{\theta }\varDelta +L_0^2\sqrt{d}+Q\right) +2 \right) \\&= O\left( \epsilon _2^{-2\frac{2-\beta }{1-\beta }}\right) . \end{aligned}$$

The number of gradient calls required to satisfy both $\epsilon _1$ and $\epsilon _2$ is then

$$\begin{aligned} \max ((K_{\epsilon _1}-1)S_{\epsilon _1},(K_{\epsilon _2}-1)S_{\epsilon _2}) =O\left( \max \left( \epsilon _1^{\frac{\beta -2}{\beta }}, \epsilon _2^{-2\frac{2-\beta }{1-\beta }}\right) \right) . \end{aligned}$$

$\square$

Proof of Corollary 4.2

Based on Theorem  4.1, an optimal choice for $K\in {\mathbb {Z}}_{>0}$ and $\beta \in (0,1)$ can be written as the following optimization problem for the minimization of the number of gradient calls,

$$\begin{aligned} \min \limits _{K, \beta }\text { }&(K-1)\lceil K^{1-\beta }\rceil \\&\mathrm{s.t.}~\sqrt{d} K^{-\beta }\le \epsilon _1\nonumber \\&K^{\frac{\beta -1}{2}}\sqrt{2\left( L_0\varDelta +L_0^2\sqrt{d} K^{-\beta }+Q\right) }\le \epsilon _2\nonumber \\&K\in {\mathbb {Z}}_{>0},\quad \beta \in (0,1),\nonumber \end{aligned}$$

(40)

requiring $\sigma \le \epsilon _1$ and the right-hand side of (10) to be less than or equal to $\epsilon _2$. Rearranging the inequalities and adding the valid inequality $1\le K^{\beta }$ given the constraints on K and $\beta$, (40) can be rewritten as

$$\begin{aligned} \min \limits _{K, \beta }\text { }&(K-1)\lceil K^{1-\beta }\rceil \\&\mathrm{s.t.}\max \left( 1,\frac{\sqrt{d}}{ \epsilon _1}\right) \le K^{\beta }\nonumber \\&K^{\beta }\le \frac{K\epsilon ^2_2-2L_0^2\sqrt{d}}{2(L_0\varDelta +Q)}\nonumber \\&K\in {\mathbb {Z}}_{>0},\quad \beta \in (0,1).\nonumber \end{aligned}$$

(41)

It is first shown that $K^*$ is a lower bound for a feasible K to problem (41). For the case $\epsilon _1<\sqrt{d}$, minimizing the gap between $\frac{\sqrt{d}}{ \epsilon _1}$ and $\frac{K\epsilon ^2_2-2L_0^2\sqrt{d}}{2(L_0\varDelta +Q)}$ sets K equal to

$$\begin{aligned} K^*_l&=\left\lceil \frac{2\sqrt{d}}{\epsilon ^2_2}\left( \frac{L_0\varDelta +Q}{\epsilon _1}+L_0^2\right) \right\rceil , \end{aligned}$$

i.e., $K^*_l$ is the minimum $K\in {\mathbb {Z}}_{>0}$ such that $\frac{\sqrt{d}}{ \epsilon _1}\le \frac{K\epsilon ^2_2-2L_0^2\sqrt{d}}{2(L_0\varDelta +Q)}$. When $\epsilon _1\ge \sqrt{d}$, minimizing the gap between 1 and $\frac{K\epsilon ^2_2-2L_0^2\sqrt{d}}{2(L_0\varDelta +Q)}$ requires

$$\begin{aligned} K\ge \frac{2}{\epsilon ^2_2}\left( L_0\varDelta +Q+\sqrt{d}L_0^2\right) >2\sqrt{d}, \end{aligned}$$

given that $\epsilon _2<L_0$. A valid lower bound on K equals

$$\begin{aligned} K^*_g&=\left\lfloor \frac{2}{\epsilon ^2_2}\left( L_0\varDelta +Q+\sqrt{d}L_0^2\right) +1\right\rfloor . \end{aligned}$$

The use of $\lfloor \cdot +1 \rfloor$ instead of $\lceil \cdot \rceil$ in this case takes into account of the possibility that $\frac{2}{\epsilon ^2_2}\left( L_0\varDelta +Q+L_0^2\sqrt{d}\right) \in {\mathbb {Z}}_{>0}$. Trying to use $K=\left\lceil \frac{2}{\epsilon ^2_2}\left( L_0\varDelta +Q+L_0^2\sqrt{d}\right) \right\rceil$ would set $\frac{K\epsilon ^2_2-2L_0^2\sqrt{d}}{2(L_0\varDelta +Q)}=1$, which would imply $\beta =0$ as $K>2\sqrt{d}$. Comparing $K^*_l$ and $K^*_g$, for the case when $\epsilon _1<\sqrt{d}$, since $K^*_l>\frac{2}{\epsilon ^2_2}\left( L_0\varDelta +Q+\sqrt{d}L_0^2\right)$, it follows that $K^*_l\ge K^*_g$, and when $\epsilon _1\ge \sqrt{d}$,

$$\begin{aligned} K^*_g\ge \left\lfloor \frac{2\sqrt{d}}{\epsilon ^2_2}\left( \frac{L_0\varDelta +Q}{\epsilon _1}+L_0^2\right) +1\right\rfloor \ge K^*_l, \end{aligned}$$

hence $K^*$ is a valid lower bound for the number of iterations over all values of $\epsilon _1$.

For any fixed K, the objective of (41) is minimized by maximizing $\beta$, so we would want to set $\beta =\beta ^*_K$ such that

$$\begin{aligned} K^{\beta ^*_K}=\frac{K\epsilon ^2_2-2L_0^2\sqrt{d}}{2(L_0\varDelta +Q)}, \end{aligned}$$

which equals

$$\begin{aligned} \beta ^*_K=\frac{\log (K\epsilon ^2_2-2L_0^2\sqrt{d})-\log (2(L_0\varDelta +Q))}{\log (K)}. \end{aligned}$$

We will show the validity of this choice of $\beta$ for all $K\ge K^*_g$, implying the validity for all $K\ge K^*$. For any $K\ge K^*_g>2\sqrt{d}$, the division by $\log (K)$ in $\beta ^*_K$ is defined. We now verify that $\beta ^*_K\in (0,1)$ for $K\ge K^*_g$. To show that $\beta ^*_K<1$, isolating $\epsilon _2^2$, we require

$$\begin{aligned} \epsilon ^2_2< 2(L_0\varDelta +Q)+\frac{2L_0^2\sqrt{d}}{K}, \end{aligned}$$

which holds given that $Q\ge L_0^2$ by Jensen’s inequality and $\epsilon _2<L_0$. The bound $\beta ^*_K>0$ is equivalent to

$$\begin{aligned} 0<K\epsilon ^2_2-2L_0^2\sqrt{d}-2(L_0\varDelta +Q). \end{aligned}$$

For $K\ge K^*_g$,

$$\begin{aligned}&K\epsilon ^2_2-2L_0^2\sqrt{d}-2(L_0\varDelta +Q)\\&\quad > 2\left( L_0\varDelta +Q+L_0^2\sqrt{d}\right) -2L_0^2\sqrt{d}-2(L_0\varDelta +Q)\\&\quad \ge 0, \end{aligned}$$

hence for all $K\ge K^*$, $\beta ^*_K$ is feasible. This also proves that $K^*$ is the minimum feasible value for K, with $\beta ^*=\beta ^*_{K^*}$, proving statement 3.

We now consider the minimization of a relaxation of (41), allowing the number of samples $S\in {\mathbb {R}}$. As statements 1 and 2 concern the computational complexity of $(K^*,\beta ^*)$ we will also now assume $\epsilon _1<1$ for simplicity.

$$\begin{aligned} \min \limits _{K, \beta }\text { }&(K-1)K^{1-\beta }\\&\mathrm{s.t.}~\frac{\sqrt{d}}{ \epsilon _1}\le K^{\beta }\nonumber \\&K^{\beta }\le \frac{K\epsilon ^2_2-2L_0^2\sqrt{d}}{2(L_0\varDelta +Q)}\nonumber \\&\beta \in (0,1),\quad K\in {\mathbb {Z}}_{>0}.\nonumber \end{aligned}$$

(42)

Plugging in $K^{\beta ^*_K}=\frac{K\epsilon ^2_2-2L_0^2\sqrt{d}}{2(L_0\varDelta +Q)}$, the optimization problem becomes

$$\begin{aligned}&\min \limits _{K\in {\mathbb {Z}}_{>0}}&(K-1) \frac{K2(L_0\varDelta +Q)}{K\epsilon ^2_2-2L_0^2\sqrt{d}}\\&\quad \mathrm{s.t.}~~~&K\ge K^*. \end{aligned}$$

For simplicity let

$$\begin{aligned} a:=2(L_0\varDelta +Q)\quad \text {and}\quad b:=2L_0^2\sqrt{d}. \end{aligned}$$

The problem is now

$$\begin{aligned}&\min \limits _{K\in {\mathbb {Z}}_{>0}} \frac{aK(K-1)}{\epsilon ^2_2K-b}\\&\quad \mathrm{s.t.}~\quad \!\!K\ge K^*.\nonumber \end{aligned}$$

(43)

We will prove that $K^*$ is optimal for problem (43) by showing that the derivative of the objective function with respect to K is positive for $K\ge K^*$.

$$\begin{aligned}&\frac{d}{dK}\frac{aK(K-1)}{\epsilon ^2_2K-b}=\frac{a(\epsilon ^2_2K^2-2bK+b)}{(\epsilon ^2_2K-b)^2} \end{aligned}$$

is non-negative for $K\ge \frac{b+\sqrt{b(b-\epsilon ^2_2)}}{\epsilon ^2_2}$ and positive for $K\ge \frac{2b}{\epsilon ^2_2}$ by removing $\epsilon ^2_2$ in the numerator. Written in full form, the objective is increasing in K for

$$\begin{aligned} K\ge&\frac{4L_0^2\sqrt{d}}{\epsilon ^2_2}. \end{aligned}$$

Comparing this inequality with $K^*=K^*_l$ given that $\epsilon _1<1$,

$$\begin{aligned} K^*&>\frac{2\sqrt{d}}{\epsilon ^2_2}\left( L_0\varDelta +Q+L_0^2\right) \ge \frac{2\sqrt{d}}{\epsilon ^2_2}\left( Q+L_0^2\right) \ge \frac{4L_0^2\sqrt{d}}{\epsilon ^2_2} \end{aligned}$$

using $Q\ge L_0^2$, hence over the feasible $K\ge K^*$, the objective (43) is increasing, and $(K^*,\beta ^*)$ is an optimal solution of (42).

Writing $K^*=K^*_l=\left\lceil \frac{1}{\epsilon ^2_2}\left( \frac{a\sqrt{d}}{\epsilon _1}+b\right) \right\rceil$, a bound on the optimal value of the relaxed problem (43) gives

$$\begin{aligned} (K^*-1)\left( \frac{aK^*}{\epsilon ^2_2K^*-b}\right)&<\frac{1}{\epsilon ^2_2}\left( \frac{a\sqrt{d}}{\epsilon _1}+b\right) \left( \frac{aK^*}{\epsilon ^2_2K^*-b}\right) \\&\le \frac{1}{\epsilon ^2_2}\left( \frac{a\sqrt{d}}{\epsilon _1}+b\right) \left( \frac{\frac{a}{\epsilon ^2_2}\left( \frac{a\sqrt{d}}{\epsilon _1}+b\right) }{\left( \frac{a\sqrt{d}}{\epsilon _1}+b\right) -b}\right) \\&=\frac{1}{\epsilon ^4_2}\left( \frac{a\sqrt{d}}{\epsilon _1}+b\right) \left( a+\frac{\epsilon _1b}{\sqrt{d}}\right) \\&=O\left( \frac{1}{\epsilon _1\epsilon ^4_2}\right) , \end{aligned}$$

where for the second inequality $\frac{aK}{\epsilon ^2_2K-b}$ is decreasing in K, $\frac{d}{dK}\frac{aK}{\epsilon ^2_2K-b}=\frac{-ab}{(\epsilon ^2_2K-b)^2}$. This bound cannot be improved as $(K^*-1)\left( \frac{aK^*}{\epsilon ^2_2K^*-b}\right) \ge \left( \frac{1}{\epsilon ^2_2}\left( \frac{a\sqrt{d}}{\epsilon _1}+b\right) -1\right) \left( \frac{a}{\epsilon ^2_2}\right) = O\left( \frac{1}{\epsilon _1\epsilon ^4_2}\right)$. A bound on the gradient call complexity of $(K^*,\beta ^*)$ for finding an expected $(\epsilon _1,\epsilon _2)$-stationary point is then $(K^*-1)\left\lceil \frac{aK^*}{\epsilon ^2_2K^*-b}\right\rceil <(K^*-1)\left( \frac{aK^*}{\epsilon ^2_2K^*-b}+1\right) =O\left( \frac{1}{\epsilon _1\epsilon ^4_2}\right)$, proving statement 1.

Let $({\hat{K}},{\hat{\beta }})$ be an optimal solution to the original problem (41) with $\epsilon _1<1$. The inequalities

$$\begin{aligned} (K^*-1)\frac{aK^*}{\epsilon ^2_2K^*-b}\le ({\hat{K}}-1)\lceil {\hat{K}}^{1-{\hat{\beta }}}\rceil \le (K^*-1)\left\lceil \frac{aK^*}{\epsilon ^2_2K^*-b}\right\rceil \end{aligned}$$

hold since restricting $S\in {\mathbb {Z}}_{>0}$ cannot improve the optimal objective value of (42), and by the optimality of $({\hat{K}},{\hat{\beta }})$ for problem (41), respectively. This proves that using $({\hat{K}},{\hat{\beta }})$ will result in a gradient call complexity of $O\left( \frac{1}{\epsilon _1\epsilon ^4_2}\right)$, proving statement 2.$\square$

Proof of Corollary 4.3

Let ${\overline{\nabla }} f(x):={\mathbb {E}}[{\widetilde{\nabla }} f(x+z)|x]$ for $z\sim U(B(\sigma ))$. Following [16, Eq. 2.28] for the first inequality,⁶

$$\begin{aligned} ||{\overline{\nabla }} f({\bar{x}}^*)||^2_2\le&\,4\min _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} f({\bar{x}}^i)||^2_2+ 4\max _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2\nonumber \\&+\,2||{\overline{\nabla }} F_T({\bar{x}}^*)-{\overline{\nabla }} f({\bar{x}}^*)||^2_2\nonumber \\ \le&\,4\min _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} f({\bar{x}}^i)||^2_2+ 6\max _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2, \end{aligned}$$

(44)

where the second inequality holds since $2||{\overline{\nabla }} F_T({\bar{x}}^*)-{\overline{\nabla }} f({\bar{x}}^*)||^2_2\le 2\max _{i=1,\ldots ,{{\mathcal {R}}}}$ $||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2$. We will compute an upper bound in probability of the left-hand side of (44) using the two terms of the right-hand side. Let B equal the right-hand side of (10),

$$\begin{aligned} B^2=2K^{\beta -1}\left( L_0\varDelta +L_0^2\sqrt{d} K^{-\beta }+Q\right) . \end{aligned}$$

(45)

Since ${\overline{\nabla }} f(x)={\mathbb {E}}[\frac{1}{S'}\sum _{l=1}^{S'}{\widetilde{\nabla }} f(x+z_l)|x]$ for any number of samples $S'\in {\mathbb {Z}}_{>0}$ of z, using inequalities (23) and (24) of the proof of Theorem 4.1, for all $i\in \{1,\ldots ,{{\mathcal {R}}}\}$,

$$\begin{aligned} {\mathbb {E}}[||{\overline{\nabla }} f({\bar{x}}^i)||^2_2]\le B^2. \end{aligned}$$

From Markov’s inequality,

$$\begin{aligned} {\mathbb {P}}(4\min _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} f({\bar{x}}^i)||^2_2\ge 4e B^2)=\varPi _{i=1}^{{{\mathcal {R}}}}{\mathbb {P}}(4||{\overline{\nabla }} f({\bar{x}}^i)||^2_2\ge 4e B^2)\le e^{-{{\mathcal {R}}}}. \end{aligned}$$

Given that also ${\overline{\nabla }} f(x)={\mathbb {E}}[\frac{1}{T'}\sum _{l=1}^{T'}{\widetilde{\nabla }} F(x+z_l,\xi _l)|x]$ for any number of samples $T'\in {\mathbb {Z}}_{>0}$ of z and $\xi$, ${\mathbb {E}}[||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2]\le \frac{Q}{T}$ from Lemma 4.3. For $\psi >0$, it holds that

$$\begin{aligned}&{\mathbb {P}}\bigg (6\max _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2\ge 6\psi \frac{Q}{T}\bigg )\\&\quad ={\mathbb {P}}\bigg (\bigcup _{i=1}^{{\mathcal {R}}}\bigg \{6||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2\ge 6\psi \frac{Q}{T}\bigg \}\bigg )\\&\quad \le \sum _{i=1}^{{{\mathcal {R}}}}{\mathbb {P}}(6||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2\ge 6\psi \frac{Q}{T})\\&\quad \le \sum _{i=1}^{{{\mathcal {R}}}}\frac{1}{\psi }=\frac{{{\mathcal {R}}}}{\psi }, \end{aligned}$$

using Boole’s and Markov’s inequalities for the first and second inequalities, respectively. Using the fact that ${\overline{\nabla }} f({\bar{x}}^*)\in \partial _{\sigma }f({\bar{x}}^*)$ for the first inequality,

$$\begin{aligned}&{\mathbb {P}}\bigg ({{\,\mathrm{dist}\,}}(0,\partial _{\sigma }f({\bar{x}}^*))^2\ge 4e B^2+6\psi \frac{Q}{T}\bigg )\nonumber \\&\quad \le {\mathbb {P}}\bigg (||{\overline{\nabla }} f({\bar{x}}^*)||^2_2\ge 4e B^2+6\psi \frac{Q}{T}\bigg )\nonumber \\&\quad \le {\mathbb {P}}\bigg ( 4\min _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} f({\bar{x}}^i)||^2_2+ 6\max _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2 \ge 4e B^2+6\psi \frac{Q}{T}\bigg )\nonumber \\&\quad \le {\mathbb {P}}\bigg (\bigg \{4\min _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} f({\bar{x}}^i)||^2_2\ge 4e B^2\bigg \}\cup \bigg \{6\max _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2\ge 6\psi \frac{Q}{T}\bigg \}\bigg )\nonumber \\&\quad \le e^{-{{\mathcal {R}}}}+\frac{{{\mathcal {R}}}}{\psi }, \end{aligned}$$

(46)

where the second inequality uses inequality (44), and the third inequality holds given that the event of the left-hand-side is a subset of the right-hand-side: considering the contraposition, if

$$\begin{aligned} \bigg \{4\min _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} f({\bar{x}}^i)||^2_2< 4e B^2\bigg \}\cap \bigg \{6\max _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2<6\psi \frac{Q}{T}\bigg \} \end{aligned}$$

occurs then

$$\begin{aligned} 4\min _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} f({\bar{x}}^i)||^2_2+ 6\max _{i=1,\ldots ,{{\mathcal {R}}}}||{\overline{\nabla }} F_T({\bar{x}}^i)-{\overline{\nabla }} f({\bar{x}}^i)||^2_2< 4e B^2+6\psi \frac{Q}{T}. \end{aligned}$$

The final inequality holds using Boole’s inequality, as the right-hand-side is the sum of the derived upper bounds of the probabilities of the two events of the union.

The total number of gradient calls required for computing ${\overline{X}}$ and then ${\overline{\nabla }} F_{T}(x)$ for all $x\in {\overline{X}}$ to find ${\bar{x}}^*$ is equal to ${{\mathcal {R}}}((K-1)\lceil K^{1-\beta }\rceil +T)$. We can write its minimization requiring that ${\mathbb {P}}({{\,\mathrm{dist}\,}}(0,\partial _{\epsilon _1}f({\bar{x}}^*))> \epsilon _2)\le \gamma$ using (46) with (45) similarly to how (40) was derived, as

$$\begin{aligned}&\min \limits _{\begin{array}{c} K, \beta ,\\ {{\mathcal {R}}},T,\psi \end{array}} \text { }&{{\mathcal {R}}}((K-1)\lceil K^{1-\beta }\rceil +T)\nonumber \\&\mathrm{s.t.}&\sqrt{d}K^{-\beta }\le \epsilon _1\nonumber \\&8e K^{\beta -1}\left( L_0\varDelta +L_0^2\sqrt{d} K^{-\beta }+Q\right) +6\psi \frac{Q}{T}\le \epsilon ^2_2\\&e^{-{{\mathcal {R}}}}+\frac{{{\mathcal {R}}}}{\psi }\le \gamma \nonumber \\&K,{{\mathcal {R}}},T\in {\mathbb {Z}}_{>0},\quad \beta \in (0,1),\quad \psi >0.\nonumber \end{aligned}$$

(47)

Inequality (47) can be rewritten as

$$\begin{aligned} 2 K^{\beta -1}\left( L_0\varDelta +L_0^2\sqrt{d} K^{-\beta }+Q\right) \le \frac{\epsilon ^2_2-6\psi \frac{Q}{T}}{4e}. \end{aligned}$$

We apply the choice of K and $\beta$ from Corollary 4.2 for finding an expected $(\epsilon _1,\epsilon _2')$-stationary point, where $\epsilon _2'=\sqrt{\frac{\epsilon ^2_2-6\psi \frac{Q}{T}}{4e}}$:

$$\begin{aligned} K^*= & {} \max \left( \left\lfloor \frac{2}{(\epsilon '_2)^2}\left( L_0\varDelta +Q+\sqrt{d}L_0^2\right) +1\right\rfloor ,\left\lceil \frac{2\sqrt{d}}{(\epsilon '_2)^2}\left( \frac{L_0\varDelta +Q}{\epsilon _1}+L_0^2\right) \right\rceil \right) \end{aligned}$$

and

$$\begin{aligned} \beta ^*=\frac{\log (K^*(\epsilon '_2)^2-2\sqrt{d}L_0^2)-\log (2(L_0\varDelta +Q))}{\log (K^*)}. \end{aligned}$$

In order to ensure the validity of these choices for K and $\beta$, we require that $0<\epsilon _2'<L_0$. The optimization problem then becomes

$$\begin{aligned}&\min \limits _{{{\mathcal {R}}},T,\psi } \text { } {{\mathcal {R}}}((K^*-1)\lceil (K^*)^{1-\beta ^*}\rceil +T)\nonumber \\&\quad \mathrm{s.t.}\quad e^{-{{\mathcal {R}}}}+\frac{{{\mathcal {R}}}}{\psi }\le \gamma \end{aligned}$$

(48)

$$\begin{aligned}&\quad \qquad \quad \epsilon ^2_2-6\psi \frac{Q}{T}\in (0,4e L^2_0) \\&\quad \qquad \quad {{\mathcal {R}}},T\in {\mathbb {Z}}_{>0},\quad \psi >0,\nonumber \end{aligned}$$

(49)

where (49) ensures that $0<\epsilon _2'<L_0$. Choosing ${{\mathcal {R}}}=\lceil -\ln (c\gamma )\rceil$ and $\psi =\frac{\lceil -\ln (c\gamma )\rceil }{(1-c)\gamma }$ for any $c\in (0,1)$ ensures that (48) holds by satisfying the inequalities

$$\begin{aligned} e^{-{{\mathcal {R}}}}\le c\gamma \quad \text {and}\quad \frac{{{\mathcal {R}}}}{\psi }\le (1-c)\gamma . \end{aligned}$$

Choosing $T=\lceil 6\phi \psi \frac{Q}{\epsilon ^2_2}\rceil$ is feasible for (49):

$$\begin{aligned} 4eL_0^2>\epsilon ^2_2\ge \epsilon ^2_2-6\psi \frac{Q}{T}= \epsilon ^2_2-6\psi \frac{Q}{\lceil 6\phi \psi \frac{Q}{\epsilon ^2_2}\rceil }\ge \epsilon ^2_2-6\psi \frac{Q}{6\phi \psi \frac{Q}{\epsilon ^2_2}}= \epsilon ^2_2-\frac{\epsilon ^2_2}{\phi }>0, \end{aligned}$$

(50)

given the assumptions that $\epsilon _2<L_0$ and $\phi >1$. We have verified that the choices for K, $\beta$, ${{\mathcal {R}}}$, and T ensure that the output ${\bar{x}}^*$ of the proposed method is an $(\epsilon _1,\epsilon _2)$-stationary point with a probability of at least $1-\gamma$. What remains is the computational complexity. The total number of gradient calls equals

$$\begin{aligned} \lceil -\ln (c\gamma )\rceil \bigg ((K^*-1)\lceil (K^*)^{1-\beta ^*}\rceil +\bigg \lceil 6\phi \frac{\lceil -\ln (c\gamma )\rceil }{(1-c)\gamma }\frac{Q}{\epsilon ^2_2}\bigg \rceil \bigg ). \end{aligned}$$

(51)

From Corollary 4.2, $(K^*-1)\lceil (K^*)^{1-\beta ^*}\rceil =O\left( \frac{1}{\epsilon _1(\epsilon _2')^4}\right)$ and from (50) $\epsilon _2'=\sqrt{\frac{\epsilon ^2_2-6\psi \frac{Q}{T}}{4e}}\ge \frac{\epsilon _2}{2}\sqrt{\frac{(1-\phi ^{-1})}{e}}$, hence $(K^*-1)\lceil (K^*)^{1-\beta ^*}\rceil =O\left( \frac{1}{\epsilon _1\epsilon _2^4}\right)$. The total computational complexity from (51) then equals ${\tilde{O}}\left( \frac{1}{\epsilon _1\epsilon ^4_2}+\frac{1}{\gamma \epsilon ^2_2}\right)$.$\square$

1.4 Section 5

Proof of Proposition 5.1

We will ultimately consider the decision variables in a vector form ${\overline{w}}:=[({\overline{w}}^2)^T,({\overline{w}}^3)^T]^T$, where ${\overline{w}}^l:=[W^l_1,b^l_1,W^l_2,b^l_2,\ldots ,W^l_{N_l},b^l_{N_l}]^T$ for $l=2,3$, where $W^l_j$ is the jth row of $W^l$.

The partial derivative of ${{{\mathcal {L}}}}$ with respect to $z^3_j$ is

$$\begin{aligned} \frac{\partial {{{\mathcal {L}}}}}{\partial z^3_j}&=\alpha ^3_j-y^i_j. \end{aligned}$$

Given that $y^i$ is one-hot encoded, and the $\alpha ^3_j$ take the form of probabilities, ${\Vert }\nabla _{z^3} {{{\mathcal {L}}}}{\Vert }_2\le \sqrt{2}$, and ${{{\mathcal {L}}}}$ as a function of $z^3$ is $\sqrt{2}$-Lipschitz continuous. Considering $z^3=H(W^3)\alpha ^{2}+b^3$ as a function of ${\overline{w}}^3$, let

$$\begin{aligned}&{\overline{h}}({\overline{w}}^3):=[H(W^3_1),b^3_1,H(W^3_2),b^3_2,\ldots , H(W^3_{N_3}),b^3_{N_3}]^T\in {\mathbb {R}}^{N_3(N_2+1)}, \end{aligned}$$

${\overline{\alpha }}:=[(\alpha ^2)^T,1]\in {\mathbb {R}}^{N^2+1}$, ${{\textbf {0}}}:=[0,\ldots ,0]\in {\mathbb {R}}^{N^2+1}$, and the matrix

$$\begin{aligned} A:= \begin{bmatrix} {\overline{\alpha }} &{}{{\textbf {0}}}&{} {{\textbf {0}}}&{} \cdots &{} {{\textbf {0}}}\\ {{\textbf {0}}}&{} {\overline{\alpha }} &{} {{\textbf {0}}}&{} \cdots &{} {{\textbf {0}}}\\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ {{\textbf {0}}}&{} {{\textbf {0}}}&{} {{\textbf {0}}}&{} \cdots &{} {\overline{\alpha }}\\ \end{bmatrix} \in {\mathbb {R}}^{N_3\times (N_3(N_2+1))}, \end{aligned}$$

so that $z^3({\overline{w}}^3)=A{\overline{h}}({\overline{w}}^3)$. The Lipschitz constant of $z^3({\overline{w}}^3)$ is found by first bounding the spectral norm of A, which equals the square root of the largest eigenvalue of

$$\begin{aligned} AA^T=\text {diag}({\Vert }{\overline{\alpha }}{\Vert }^2_2,{\Vert }{\overline{\alpha }}{\Vert }^2_2,\ldots ])\in {\mathbb {R}}^{N_3\times N_3}, \end{aligned}$$

hence ${\Vert }A{\Vert }_2={\Vert }[(\alpha ^2)^T,1]{\Vert }_2\le \sqrt{N_2m^2+1}$. The function ${\overline{h}}({\overline{w}}^3)$ is 1-Lipschitz continuous, and the composition of $L_i$-Lipschitz continuous functions is $\prod \limits _i L_i$-Lipschitz continuous [27, Claim 12.7], therefore ${{{\mathcal {L}}}}$ is $\sqrt{2(N_2m^2+1)}$-Lipschitz continuous in ${\overline{w}}^3$.

Considering now $z^3$ as a function of $\alpha ^2$, $z^3(\alpha ^2)$ is ${\Vert }H(W^3){\Vert }_2$-Lipschitz continuous. Given the boundedness of the hard tanh activation function, ${\Vert }H(W^3){\Vert }_2\le {\Vert }H(W^3){\Vert }_F\le \sqrt{N_2N_3}$. The ReLU-m activation functions are 1-Lipschitz continuous. As was done when computing a Lipschitz constant for $z^3({\overline{w}}^3)$, to do so for $z^2({\overline{w}}^2)$, let ${\overline{v}}:=[(v^i)^T,1]$, redefine ${{\textbf {0}}}:=[0,\ldots ,0]\in {\mathbb {R}}^{N^1+1}$, and let

$$\begin{aligned} V:= \begin{bmatrix} {\overline{v}} &{}{{\textbf {0}}}&{} {{\textbf {0}}}&{} \cdots &{} {{\textbf {0}}}\\ {{\textbf {0}}}&{} {\overline{v}} &{} {{\textbf {0}}}&{} \cdots &{} {{\textbf {0}}}\\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ {{\textbf {0}}}&{} {{\textbf {0}}}&{} {{\textbf {0}}}&{} \cdots &{} {\overline{v}}\\ \end{bmatrix}\in {\mathbb {R}}^{N_2\times (N_2(N_1+1))}. \end{aligned}$$

The Lipschitz constant for $z^2({\overline{w}}^2)=V{\overline{w}}^2$ is then ${\Vert }[(v^i)^T,1]{\Vert }_2$. In summary, ${{{\mathcal {L}}}}(z^3)$ is $\sqrt{2}$-Lipschitz, $z^3(\alpha ^2)$ is $\sqrt{N_2N_3}$-Lipschitz, $\alpha ^2(z^2)$ is 1-Lipschitz, and $z^2({\overline{w}}^2)$ is $||(v^i)^T,1||_2$-Lipschitz continuous, hence ${{{\mathcal {L}}}}$ is $\sqrt{2N_2N_3}||(v^i)^T,1||_2$-Lipschitz continuous in ${\overline{w}}^2$.

Computing the Lipschitz constant for all decision variables,

$$\begin{aligned}&{\Vert }{{{\mathcal {L}}}}({\overline{w}})-{{{\mathcal {L}}}}({\overline{w}}'){\Vert }_2\\&\quad ={\Vert }{{{\mathcal {L}}}}({\overline{w}}^2,{\overline{w}}^3)-L({{\overline{w}}^2}',{\overline{w}}^3) +L({{\overline{w}}^2}',{\overline{w}}^3)-{{{\mathcal {L}}}}({{\overline{w}}^2}',{{\overline{w}}^3}'){\Vert }_2\\&\quad \le {\Vert }{{{\mathcal {L}}}}({\overline{w}}^2,{\overline{w}}^3)-{{{\mathcal {L}}}}({{\overline{w}}^2}',{\overline{w}}^3){\Vert }_2 +{\Vert }{{{\mathcal {L}}}}({{\overline{w}}^2}',{\overline{w}}^3)-{{{\mathcal {L}}}}({{\overline{w}}^2}',{{\overline{w}}^3}'){\Vert }_2\\&\quad \le \sqrt{2N_2N_3}{\Vert }(v^i)^T,1{\Vert }_2{\Vert }{\overline{w}}^2-{{\overline{w}}^2}'{\Vert }_2+\sqrt{2(N_2m^2+1)}{\Vert }{\overline{w}}^3-{{\overline{w}}^3}'{\Vert }_2\\&\quad \le \max (\sqrt{2N_2N_3}{\Vert }(v^i)^T,1{\Vert }_2,\sqrt{2(N_2m^2+1)})({\Vert }{\overline{w}}^2-{{\overline{w}}^2}'{\Vert }_2+{\Vert }{\overline{w}}^3-{{\overline{w}}^3}'{\Vert }_2)\\&\quad \le 2\max (\sqrt{N_2N_3}{\Vert }(v^i)^T,1{\Vert }_2,\sqrt{(N_2m^2+1)}){\Vert }({\overline{w}}^2,{\overline{w}}^3)-({{\overline{w}}^2}',{{\overline{w}}^3}'){\Vert }_2, \end{aligned}$$

where the last inequality uses Young’s inequality:

$$\begin{aligned}&2{\Vert }{\overline{w}}^2-{{\overline{w}}^2}'{\Vert }_2{\Vert }{\overline{w}}^3-{{\overline{w}}^3}'{\Vert }_2 \le {\Vert }{\overline{w}}^2-{{\overline{w}}^2}'{\Vert }_2^2+{\Vert }{\overline{w}}^3-{{\overline{w}}^3}'{\Vert }^2_2\\&\quad \Longrightarrow {\Vert }{\overline{w}}^2-{{\overline{w}}^2}'{\Vert }_2^2+2{\Vert }{\overline{w}}^2-{{\overline{w}}^2}'{\Vert }_2{\Vert }{\overline{w}}^3-{{\overline{w}}^3}'{\Vert }_2+{\Vert }{\overline{w}}^3-{{\overline{w}}^3}'{\Vert }^2_2 \\&\quad \le 2({\Vert }{\overline{w}}^2-{{\overline{w}}^2}'{\Vert }_2^2+{\Vert }{\overline{w}}^3-{{\overline{w}}^3}'{\Vert }^2_2)\\&\quad \Longrightarrow ({\Vert }{\overline{w}}^2-{{\overline{w}}^2}'{\Vert }_2+{\Vert }{\overline{w}}^3-{{\overline{w}}^3}'{\Vert }_2)^2 \le 2({\Vert }({\overline{w}}^2,{\overline{w}}^3)-({{\overline{w}}^2}',{{\overline{w}}^3}'){\Vert }_2^2)\\&\quad \Longrightarrow {\Vert }{\overline{w}}^2-{{\overline{w}}^2}'{\Vert }_2+{\Vert }{\overline{w}}^3-{{\overline{w}}^3}'{\Vert }_2 \le \sqrt{2} {\Vert }({\overline{w}}^2,{\overline{w}}^3)-({{\overline{w}}^2}',{{\overline{w}}^3}'){\Vert }_2. \end{aligned}$$

$\square$

Proof of Proposition 5.2

The problematic terms within (29) for which the chain rule does not necessarily apply are

$$\begin{aligned} \frac{\partial H_{jk}}{\partial W_{jk}^3}(t)&=\mathbb {1}_{\{t\ge -1\}}\mathbb {1}_{\{t\le 1\}}\quad \text {and}\quad \frac{\partial \alpha _j^2}{\partial z^2_j}(t)=\mathbb {1}_{\{t\ge 0\}}\mathbb {1}_{\{t\le m\}}. \end{aligned}$$

Using PISGD, $\frac{\partial H_{jk}}{\partial W_{jk}^3}(t)$ is evaluated at $t=W^3_{jk}+z_{W^3_{jk}}$. The probability that $\frac{\partial H_{jk}}{\partial W_{jk}^3}(t)$ is evaluated at a point of non-differentiability, $|W^3_{jk}+z_{W^3_{jk}}|=1$, is zero:

$$\begin{aligned}&{\mathbb {E}}[\mathbb {1}_{\{W^3_{jk}+z_{W^3_{jk}}=1\}}+\mathbb {1}_{\{W^3_{jk}+z_{W^3_{jk}}=-1\}}]\\&\quad ={\mathbb {E}}({\mathbb {E}}[\mathbb {1}_{\{W^3_{jk}+z_{W^3_{jk}}=1\}}+\mathbb {1}_{\{W^3_{jk}+z_{W^3_{jk}}=-1\}}|W^3_{jk}]). \end{aligned}$$

Defining $g(y):={\mathbb {E}}[\mathbb {1}_{\{y+z_{W^3_{jk}}=1\}}+\mathbb {1}_{\{y+z_{W^3_{jk}}=-1\}}]$,

$$\begin{aligned} g(W^3_{jk})={\mathbb {E}}[\mathbb {1}_{\{W^3_{jk}+z_{W^3_{jk}}=1\}}+\mathbb {1}_{\{W^3_{jk}+z_{W^3_{jk}}=-1\}}|W^3_{jk}] \end{aligned}$$

given the independence of $z_{W^3_{jk}}$ with $W^3_{jk}$. Since $z_{W^3_{jk}}$ is an absolutely continuous random variable, for any $y\in {\mathbb {R}}$, $g(y)=0$, hence

${{\mathbb {E}}[\mathbb {1}_{\{W^3_{jk}+z_{W^3_{jk}}=1\}}+\mathbb {1}_{\{W^3_{jk}+z_{W^3_{jk}}=-1\}}|W^3_{jk}]=0}$.

The partial derivative $\frac{\partial \alpha _j^2}{\partial z^2_j}(t)$ is evaluated at $t=(W^2_{j}+z_{W^2_j})v^i+b^2_j+z_{b^2_j}$, which we rearrange as $t=z_{W^2_j}v^i+z_{b^2_j}+W^2_{j}v^i+b^2_j$ for convenience. The points of non-differentiability are when $z_{W^2_j}v^i+z_{b^2_j}+W^2_{j}v^i+b^2_j\in \{0,m\}$. Computing the probability of this event,

$$\begin{aligned}&{\mathbb {E}}[\mathbb {1}_{\{z_{W^2_j}v^i+z_{b^2_j}=-W^2_{j}v^i-b^2_j\}}+\mathbb {1}_{\{z_{W^2_j}v^i+z_{b^2_j}=m-W^2_{j}v^i-b^2_j\}}]\\&\quad ={\mathbb {E}}({\mathbb {E}}[\mathbb {1}_{\{z_{W^2_j}v^i+z_{b^2_j}=-W^2_{j}v^i-b^2_j\}}+\mathbb {1}_{\{z_{W^2_j}v^i+z_{b^2_j}=m-W^2_{j}v^i-b^2_j\}}|W^2_{j},v^i,b^2_j]). \end{aligned}$$

Defining $g(Y^1,y^2,y^3):={\mathbb {E}}[\mathbb {1}_{\{z_{W^2_j}y^2+z_{b^2_j}=-Y^1y^2-y^3\}}+\mathbb {1}_{\{z_{W^2_j}y^2+z_{b^2_j}=m-Y^1y^2-y^3\}}]$,

$$\begin{aligned} g(W^2_{j},v^i,b^2_j)={\mathbb {E}}[\mathbb {1}_{\{z_{W^2_j}v^i+z_{b^2_j}=-W^2_{j}v^i-b^2_j\}}+\mathbb {1}_{\{z_{W^2_j}v^i+z_{b^2_j}=m-W^2_{j}v^i-b^2_j\}}|W^2_{j},v^i,b^2_j], \end{aligned}$$

since $(z_{W^2_j},z_{b^2_j})$ are independent of ($W^2_{j},v^i,b^2_j)$. For any $(Y^1,y^2,y^3)\in {\mathbb {R}}^{2N_1+1}$, $z_{W^2_j}y^2+z_{b^2_j}$ is an absolutely continuous random variable, hence the probability $z_{W^2_j}y^2+z_{b^2_j}\in \{-Y^1y^2-y^3,m-Y^1y^2-y^3\}$ equals zero, and in particular

$$\begin{aligned}&{\mathbb {E}}[\mathbb {1}_{\{z_{W^2_j}v^i+z_{b^2_j}=-W^2_{j}v^i-b^2_j\}}+\mathbb {1}_{\{z_{W^2_j}v^i+z_{b^2_j}=m-W^2_{j}v^i-b^2_j\}}|W^2_{j},v^i,b^2_j]=0. \end{aligned}$$

Given that the formulas (29) evaluated at $x+z$ produce the partial derivatives of ${{{\mathcal {L}}}}_i$ with probability 1, and ${{{\mathcal {L}}}}_i$ is differentiable at $x+z$ with probability 1, the result follows.$\square$