Abstract
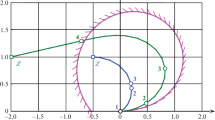
The problem of a planar vehicle moving on a surface, such as aerial drones or small naval vessels, can be treated as a series of trajectory planning problems between way-points. While nominally the movement between each two fourth-dimensional points (positions and velocities) can be treated as a 1D projection of the movement on the vector connecting the two points, in the presence of arbitrary disturbance the full problem on a plane must be considered. The mixed minimum time–energy optimal solution is now dependent on the value and direction of the disturbance, which naturally affects the structure and completion of the movement task. In this work, we address the minimum time–energy problem of a movement on a 2D plane with quadratic drag, under norm state (velocity) and norm control (acceleration) constraints. The structure and properties of the optimal solution are found and analyzed. The Pontryagin’s maximum principle (PMP) with control and state constraints is utilized. Simulations supporting the results are provided and compared with those of the open-source academic optimal control solver Falcon.m.

















Similar content being viewed by others
References
Andreas, W., Biegler, L.T.: On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 106(1), 25–57 (2006). https://doi.org/10.1007/s10107-004-0559-y
Ata, A.a.: Optimal trajectory planning of manipulators: A review. J. Eng. Sci. Technol. 2(1), 32–54 (2007). URL https://jestec.taylors.edu.my/Vol 2 Issue 1 April 07/32-54 Ata.pdf
Ben-Asher, J.Z., Wetzler, M., Rimon, E.D., Diepolder, J.: Optimal trajectories for a mobile robot with bounded accelerations in the presence of a wall or a bounded obstacle. In: Editors for proceedings of the IEEE Mediterranean Conference on Control and Automation (MED), pp. 481–488 (2019). https://doi.org/10.1109/MED.2019.8798561
Berger, A., Ioslovich, I., Gutman, P.O.: Time optimal trajectory planning with feedforward and friction compensation. In: Editors for proceedings of the American Control Conference (ACC), vol. 2015-July, pp. 4143–4148 (2015). https://doi.org/10.1109/ACC.2015.7171979
Bertolazzi, E., Frego, M.: Semianalytical minimum-time solution for the optimal control of a vehicle subject to limited acceleration. Optim. Control Appl. Methods 39(2), 774–791 (2018). https://doi.org/10.1002/oca.2376
Browning, A.W.: A mathematical model to simulate small boat behaviour. Simulation 56(5), 329–336 (1991). https://doi.org/10.1177/003754979105600508
Coles, A., Coles, A., Fox, M., Long, D.: COLIN: Planning with continuous linear numeric change. J. Artif. Intell. Res. 44, 1–96 (2012)
Fernández-González, E., Williams, B., Karpas, E.: Scottyactivity: Mixed discrete-continuous planning with convex optimization. J. Artif. Intell. Res. 62, 579–664 (2018)
Frego, M., Bertolazzi, E., Biral, F., Fontanelli, D., Palopoli, L.: Semi-analytical minimum time solutions with velocity constraints for trajectory following of vehicles. Automatica 86, 18–28 (2017). https://doi.org/10.1016/j.automatica.2017.08.020
Hartl, R.F., Sethi, S.P., Vickson, R.G.: A survey of the maximum principles for optimal control problems with state constraints. SIAM Rev. 37(2), 181–218 (1995). https://doi.org/10.1137/1037043
Ioslovich, I., Gutman, P.O., Berger, A., Moshenberg, S.: On energy-optimal and time-optimal precise displacement of rigid body with friction. J. Optim. Theory Appl. 172(2), 466–480 (2017). https://doi.org/10.1109/10.1007/s10957-016-0913-2
Ioslovich, I., Gutman, P.O.: Time-optimal control of wafer stage positioning using simplified models. Contemp. Math. 619, 99–107 (2014). https://doi.org/10.1090/conm/619/12386
Kirk, D.E.: Optimal Control Theory: An Introduction. Courier Corporation, New York (2012)
Krotov, V.F.: Global Methods in Optimal Control Theory. Marcel Dekker Inc, New York (1995)
Li, H.X., Williams, B.C.: Generative planning for hybrid systems based on Flow Tubes. In: Editors for proceedings of the International Conference on Automated Planning and Scheduling (ICAPS), pp. 206–213 (2008). URL https://www.aaai.org/Papers/ICAPS/2008/ICAPS08-026.pdf
Pontryagin, L.S.: Mathematical Theory of Optimal Processes. CRC Press, New York (1987). https://doi.org/10.1201/9780203749319
Raman-Nair, W., Gash, R., Sullivan, M.: Effect of wind and current on course control of a maneuvering vessel. In: 2014 Oceans - St. John’s, OCEANS 2014 (2014). https://doi.org/10.1109/OCEANS.2014.7003296
Rieck, M., Bittner, M., Gruter, B., Diepolder, J.: Falcon.m (2016). URL http://www.fsd.mw.tum.de/software/falcon-m
Taitler, A., Ioslovich, I., Gutman, P.O., Karpas, E.: Combined time and energy optimal trajectory planning with quadratic drag for mixed discrete-continuous task planning. Optimization 68(1), 125–143 (2019)
Taitler, A., Ioslovich, I., Karpas, E., Gutman, P.O., Ben-Asher, J.Z.: Structural analysis of combined time and energy optimal trajectory planning with quadratic drag. In: Editors for proceedings of the IEEE Mediterranean Conference on Control and Automation (MED), pp. 153–158 (2019). https://doi.org/10.1080/10.1109/MED.2019.8798498. URL https://ieeexplore.ieee.org/document/8798498
Taitler, A., Ioslovich, I., Karpas, E., Gutman, P.O.: Minimum time optimal control of second order system with quadratic drag and state constraints. In: Editors for proceedings of the IEEE Conference on Decision and Control (CDC), vol. 2019-Decem, pp. 523–528. IEEE, Nice (2019). https://doi.org/10.1109/CDC40024.2019.9029668. URL https://ieeexplore.ieee.org/document/9029668
Taitler, A., Ioslovich, I., Karpas, E., Gutman, P.O.: Time optimal control for a non-linear planar vehicle subject to Disturbances. IFAC-PapersOnLine (in print) (2021). 1st IFAC Modeling, Estimation and Control Conference (MECC)
Taitler, A., Ioslovich, I., Karpas, E., Gutman, P.O.: Time-Energy optimal control of a non-linear surface vehicle subject to disturbances. IFAC-PapersOnLine 54(14), 48–53 (2021). https://doi.org/10.1016/j.ifacol.2021.10.327. URL https://www.sciencedirect.com/science/article/pii/S2405896321017328. 3rd IFAC Conference on Modelling, Identification and Control of Nonlinear Systems (MICNON)
Verscheure, D., Demeulenaere, B., Swevers, J., Schutter, J.D., Diehl, M.: Time-energy optimal path tracking for robots: a numerically efficient optimization approach. In: Editors for proceedings of the IEEE International Workshop on Advanced Motion Control (AMC), vol. 1, pp. 727–732. IEEE (2008). https://doi.org/10.1109/AMC.2008.4516157
Yavin, Y., Frangos, C., Miloh, T.: Computation of feasible control trajectories for the navigation of a ship around an obstacle in the presence of a sea current. Math. Comput. Modell. 21(3), 99–117 (1995). https://doi.org/10.1016/0895-7177(94)00218-D
Zhao, Y., Tsiotras, P.: Speed profile optimization for optimal path tracking. In: Editors for proceedings of the American Control Conference (ACC), pp. 1171–1176 (2013). https://doi.org/10.1109/acc.2013.6579994
Acknowledgements
This work was supported by the PMRI—Peter Munk Research Institute—Technion.
Author information
Authors and Affiliations
Additional information
Communicated by Nikolai Osmolovskii.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Rights and permissions
About this article
Cite this article
Taitler, A., Ioslovich, I., Karpas, E. et al. Minimum Mixed Time–Energy Trajectory Planning of a Nonlinear Vehicle Subject to 2D Disturbances. J Optim Theory Appl 192, 725–757 (2022). https://doi.org/10.1007/s10957-021-01990-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-021-01990-0