Abstract
Cyclone separators are widely used in a variety of industrial applications. A low-mass loading gas cyclone is characterized by two performance parameters, namely the Euler and Stokes numbers. These parameters are highly sensitive to the geometrical design parameters defining the cyclone. Optimizing the cyclone geometry therefore is a complex problem. Testing a large number of cyclone geometries is impractical due to time constraints. Experimental data and even computational fluid dynamics simulations are time-consuming to perform, with a single simulation or experiment taking several weeks. Simpler analytical models are therefore often used to expedite the design process. However, this comes at the cost of model accuracy. Existing techniques used for cyclone shape optimization in literature do not take multiple fidelities into account. This work combines cheap-to-evaluate well-known mathematical models of cyclones, available data from computational fluid dynamics simulations and experimental data to build a triple-fidelity recursive co-Kriging model. This model can be used as a surrogate with a multi-objective optimization algorithm to identify a Pareto set of a finite number of solutions. The proposed scheme is applied to optimize the cyclone geometry, parametrized by seven design variables.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Performing physical experiments to test a cyclone geometry is not practical as it is very time-consuming and expensive. Computational fluid dynamics (CFD) simulations offer a faster alternative, but they are still computationally too expensive for integration with optimization algorithms as each simulation takes several weeks. Mathematical models are very cheap to evaluate but less accurate in comparison with CFD simulations.
Due to the prohibitory computational cost of identifying the complete Pareto Front of solutions, the problem setting considered in this work involves finding a Pareto-optimal set (Pareto set) of a finite number of solutions instead of the complete continuous Pareto front. Multi-objective evolutionary algorithms (MOEAs) are a popular choice for solving such problems. However, MOEAs typically require a large number of objective function evaluations to converge and offer viable solutions. Cheap-to-evaluate mathematical models can be used with MOEAs in practice, but solutions cannot be guaranteed to be accurate. Surrogate-based optimization (SBO) algorithms reduce the number of objective function evaluations required during the optimization process and can be used in conjunction with mathematical models and CFD simulations.
Given the expensive nature of high-quality data, it is important to utilize all available fidelities. SBO algorithms typically select data points during the optimization process, which are then evaluated and used to update the surrogate. This acts as a continuous validation mechanism and requires the availability of a simulation code. When only precomputed (old) data are available (e.g., from previous physical experiments or old CFD simulations), time constraints and practicality do not offer the freedom to request additional data at arbitrary locations. Therefore, there is a need for an optimization scheme which can utilize multiple fidelities of available data to optimize the shape of a cyclone separator.
This paper presents an algorithm that trains a surrogate model using multiple fidelities of available data. The surrogate model can then be used as a replacement of mathematical models or CFD simulations by MOEAs to obtain a Pareto set of solutions. Recursive co-Kriging formulation is used to train the model, with the scheme being demonstrated using three fidelities of data (physical experiments, CFD simulations and analytical models in order of decreasing quality). The novelties of this work include triple-fidelity surrogate modeling (not many works can be found in the literature that attempt it), training a sub-Kriging model from a million-point dataset, and handling missing output dimensions.
The paper is organized as follows. Section 2 presents the detailed description of the problem of cyclone shape optimization. Section 3 introduces Kriging models, and the recursive co-Kriging formulation. Section 4 explains the proposed algorithm for training a multi-fidelity recursive co-Kriging model. Sections 5 and 6 list the experimental setup and discuss the results, respectively. Section 7 concludes the paper.
2 Geometry Optimization of a Gas Cyclone Separator
Gas cyclones are separation devices that apply a swirl to separate out the dispersed phase (solid particles) from the continuous phase (gas) [1, 2]. They have been widely used in many industrial applications for many years. The advantages of cyclones over other separation devices include simple construction, low maintenance and no moving parts. The tangential inlet Stairmand high-efficiency cyclone [3] shown in Fig. 1 is widely used to separate particles from a gaseous stream. The gas-solid mixture enters tangentially which produces a swirling motion. The centrifugal forces throw the particles to the wall, and they are eventually collected at the bottom of the cyclone. The gas (with some small particles) changes its direction and exits from the top of the cyclone.
Although the geometry of the gas cyclone is simple, the flow is three-dimensional and unsteady. The swirling flow in the cyclone makes the study of gas cyclones more complicated. A wide range of industrial applications of gas cyclones has stimulated many experimental research studies toward the flow pattern and the performance of gas cyclones [1]. These experiments are generally costly because they involve manufacturing of gas cyclones and using expensive measurement techniques such as laser Doppler anemometry, and particle image velocimetry [4, 5]. With the availability of computing resources, CFD has become an alternative approach to study cyclone separators [2, 6, 7]. CFD is currently used to study the flow pattern [8,9,10,11], as a simulator for CFD based geometry optimization with different surrogate models [7, 12,13,14,15,16] as well as for shape optimization using the adjoint method [17]. Analytical models based on simplified theoretical assumptions are still in use for prediction of cyclone performance [18,19,20,21,22,23]. For further details regarding the most widely used analytical models in gas cyclone performance prediction, the reader is referred to Hoffmann and Stein [23] and Elsayed [24].
The dominant factor influencing the cyclone performance and flow pattern is the cyclone geometry [24]. The cyclone geometry is described by seven basic dimensions, namely the cyclone inlet height a and inlet width b, the vortex finder diameter \(D_{x}\) and length S, barrel height h, total height \(H_{\mathrm{t}}\) and cone-tip diameter \(B_{\mathrm{c}}\) [24] as shown in Fig. 1. All the parameters are given as the respective ratios of cyclone body diameter D.
The two performance indicators widely used in low-mass loading gas cyclones are the pressure drop and the cutoff diameter \(x_{50}\) [12, 24]. The cutoff diameter \(x_{50}\) is defined as the particle diameter which produces a 50% separation efficiency [23]. In some other studies, the overall collection efficiency is used instead of the cutoff diameter. The literature has some empirical formulae that can use \(x_{50}\) to generate the grade efficiency curve (particle diameter versus the collection efficiency) [23].
The problem of geometry optimization for gas cyclones has been well-studied in the literature. Ravi et al. [25] carried out a multi-objective optimization of a system of N identical cyclone separators in parallel. The two objectives were the overall collection efficiency and the pressure drop. Salcedo and Candido [26] conducted two optimization studies to maximize cyclone collection and an efficiency/cost ratio. They applied the Mothes and Loffler [27] analytical models.
Swamee et al. [28] optimized the number of parallel cyclones, the barrel diameter and vortex finder diameter at a certain gas flow rate. The two cost functions (the pressure drop and cutoff diameter) were blended into a single objective problem [17].
Safikhani et al. [29] performed a multi-objective optimization of cyclone separators using an artificial neural network surrogate model. Pishbin and Moghiman [30] applied genetic algorithms with seven geometrical parameters using 2-D axisymmetric CFD simulations.
There are many other optimization studies such as [7, 13,14,15,16] where the source of training data for surrogate models is either experimental data, CFD simulations or analytical models. Elsayed [13] applied co-Kriging in the geometry optimization of gas cyclone using two sources of training data; CFD and an analytical model.
It is preferable to use dimensionless numbers in the design variables and the two performance parameters. The dimensionless pressure drop (Euler number, Eu) is defined as [23],
where \(\varDelta p\) is the pressure difference between the inlet and the exit sections, \(\rho \) is the gas density, and \(V_\mathrm{in}\) is the average inlet velocity [24].
The Euler number can be modeled using different models. Elsayed [24] recommends the Ramachandran et al. [19] model for prediction of the Euler number. It is reported that the Ramachandran model is superior to Shepherd and Lapple [31], and Barth [32] models and results in a better agreement with experimental results. Consequently, this study considers only the Ramachandran model to estimate the Euler number.
The Stokes number [33] \(Stk_{50}\) is a dimensionless representation of cutoff diameter [24],
where \(\rho _p\) is the particle density and \(\mu \) is the gas viscosity.
The Iozia and Leith model [18] exhibits good agreement with experimental data, [23, 24] and will be used in this study to estimate the Stokes number values.
In the calculation of the cyclone performance parameters, the following constants have been used. The barrel diameter equals \(D=31 \times 10^{-3}\) m. This value represents a sampling cyclone (suited to a number of different applications in health-related aerosol sampling [34]). The volume flow rate is 50 L/min. The air and particle densities are 1.225, 860 \(\hbox {kg/m}^3\), respectively. The air viscosity equals \(1.7894\times 10^{-5}\,\hbox {Pa\,s}\).
Finally, the optimization problem is formulated over \(\mathbf{x} = (a,b,D_x,H_\mathrm{t},h,S,B_c)\) as,

3 Surrogate Models
Surrogate-based optimization (SBO) methods have proven themselves to be effective in solving complex optimization problems and are increasingly being used in different fields [35,36,37,38,39]. SBO methods may directly solve the optimization problem (e.g., the EGO [40] or EMO [41] algorithms) or may train a surrogate model to be used in lieu of expensive simulators with traditional optimization algorithms. This work concerns the second scenario: training a surrogate model to replace an expensive simulator.
Evolutionary multi-objective algorithms like NSGA-II [42], SMS-EMOA [43] and SPEA2 [44] are popular but typically consume a large number of function evaluations to converge. This limits their use in computationally expensive multi-objective optimization problems. A possible solution is to use the previously trained cheap-to-evaluate surrogate model instead of the expensive simulator.
Popular surrogate model types include Kriging, radial basis function (RBF), support vector regression (SVR), Splines. This work uses co-Kriging models, which are explained below.
3.1 Kriging
Kriging models are very popular in engineering design optimization [45]. This is partly due to the fact that Kriging models are very flexible and provide the mean and prediction variance which can be exploited by statistical sampling criteria. Their popularity also stems from the fact that many implementations are widely available [46,47,48,49].
Assume a set of n samples \(X=(\mathbf{x}_{1},\ldots ,\mathbf{x}_{n})'\) in d dimensions having the target values \(\mathbf{y}=(y_{1,}\ldots ,y_{n})'\). A Kriging model consists of a regression function h(x) and a centered Gaussian process Z, having variance \(\sigma ^2\) and a correlation matrix \(\varPsi \),
The \(n \times n\) correlation matrix \(\varPsi \) of the Gaussian process is defined as,
with \(\psi (\mathbf{x_i},\mathbf{x_j})\) being the correlation function having hyperparameters \(\theta \). The correlation function greatly affects the accuracy of the Kriging model used for experiments, the smoothness of the model and the differentiability of the surface. This work uses the squared exponential (SE) correlation function,
with \(l=\sqrt{\sum _{i=1}^{d}\theta _{i}(x_{a}^{i}-x_{b}^{i})^{2}}\). The hyperparameters \(\theta \) are obtained using maximum likelihood estimation (MLE).
The prediction mean and prediction variance of Kriging are then derived, respectively, as,
where \(\mathbf {1}\) is a vector of ones, \(\alpha \) is the coefficient of the constant regression function, determined by generalized least squares (GLS), \(r(\mathbf {x})\) is a \(1\times n\) vector of correlations between the point \(\mathbf {x}\) and the samples X, and \(\sigma ^{2}=\frac{1}{n}(\mathbf {y}-\mathbf {1}\alpha )^{\top }\varPsi ^{-1}(\mathbf {y}-\mathbf {1}\alpha )\) is the variance.
3.2 Recursive Co-Kriging
An autoregressive co-Kriging formulation was proposed by Kennedy and O’Hagan [50]. Le Gratiet [51] reformulated the standard autoregressive co-Kriging (introduced by Kennedy and O’Hagan) in a recursive way. This recursive co-Kriging model scales better with the increasing number of fidelities and is used in this work.
Let there be two fidelities of data available—cheap and expensive. The objective is to combine predictions from Kriging models trained using each of the two datasets in order to maximize available training data and increase the accuracy of predictions. The rationale behind recursive co-Kriging is that the two separately trained Kriging models (and indeed the two datasets) are correlated, and there exists a scaling factor \(\gamma \) that can be used to calibrate the predictions from the two Kriging models.
Let \(\hat{y}_c(\mathbf{x})\) and \(\hat{y}_e(\mathbf{x})\) be the function estimates from Kriging models trained using cheap and expensive data (\(X_c, \mathbf{y}_c\)) and (\(X-e, \mathbf{y}_e\)), respectively. Let \(\hat{y}_d(\mathbf{x})\) be the estimate from a Kriging model trained from residuals of the scaled cheap and expensive data (\(X_e, \mathbf{y}_d = \mathbf{y}_e - \gamma \hat{y}_c(X_e))\). Then the co-Kriging estimate \(\hat{y}_{CoK}(\mathbf{x})\) is defined regressively as,
where \(\gamma \) is the scaling hyper-parameter estimated using MLE.
The following section describes the training algorithm used to train a triple-fidelity recursive co-Kriging model using the method described above.
4 The Training Algorithm
Let \(X_\mathrm{A}\), \(X_\mathrm{CFD}\) and \(X_\mathrm{Exp}\) represent the three fidelities of available data, namely data from analytical models, existing data available from CFD simulations and existing experimental data, respectively. The following subsections explain how each fidelity of data is used for training the recursive co-Kriging model.
4.1 Analytical Models
A one-shot Kriging model \(\mathcal {K}_\mathrm{A}\) is trained on the dataset \((X_\mathrm{A}, \mathbf{y}_\mathrm{A})\) using the GPatt framework [52]. The learning process corresponding to the formulation of Kriging described in the previous section involves a complexity of \(\mathcal {O}(n^3)\) for n training instances. The computationally expensive part requires the calculation of the inverse of a correlation matrix \(\varPsi \). This usually involves computing the Cholesky decomposition of \(\varPsi \) requiring \(\mathcal {O}(n^3)\) operations and \(\mathcal {O}(n^2)\) storage. This limits the applicability of the usual formulation of Kriging to relatively smaller datasets.
Assuming data are present on a \({N_\mathrm{s}}^d\) grid, GPatt exploits the grid structure to represent the kernel as a Kronecker product of d matrices. This allows exact inference and hyper-parameter optimization in \(\mathcal {O}(dn^{\frac{d+1}{d}})\) time with \(\mathcal {O}(dn^{\frac{2}{d}})\) storage (for \(d > 1\)).
Let \(\mathcal {X}_1, \mathcal {X}_2,\ldots , \mathcal {X}_d\) be multidimensional inputs along a Cartesian grid with \(\mathbf{x} \in \mathcal {X}_1 \times \mathcal {X}_2 \times \cdots \times \mathcal {X}_d\). Assuming a product correlation function,
the \(n \times n\) correlation matrix \(\varPsi \) can be represented by a Kronecker product \(\varPsi = \varPsi _1 \bigotimes \varPsi _2 \bigotimes \cdots \bigotimes \varPsi _d\). This allows efficient calculation of the eigendecomposition of \(\varPsi = QVQ^\top \) by separately calculating the eigendecomposition of each of \(\varPsi _1,\varPsi _2,\ldots ,\varPsi _d\). Similarly, Kronecker structure can also be exploited to allow fast computation of matrix vector products [53]. For a detailed explanation, the reader is referred to Wilson et al. [52].
Since mathematical or analytical models are cheap to evaluate and allow the freedom of choice of parameter combinations, it makes them an ideal choice to use with the GPatt framework. To this end, a Gaussian process (GP) model is trained on parameter combinations lying on a 7D grid of \(N_\mathrm{s}\) points. This essentially means that \(N_\mathrm{s}\) points span the range of each parameter, and the grid consists of all possible combinations of input parameters, each consisting of \(N_\mathrm{s}\) points. This results in a total of \((N_\mathrm{s})^{7}\) points comprising the grid and form the set of samples \(X_\mathrm{A}\). The analytical model(s) are used to evaluate \(X_\mathrm{A}\) to obtain \(\mathbf{y}_\mathrm{A}\). The model \(\mathcal {K}_\mathrm{A}\) provides estimates as \(\hat{y}_\mathrm{A}(\mathbf{x})\).
4.2 CFD Data
Several validated CFD simulations results conducted by Elsayed and Lacor [14] have been used in the fitting of the multi-fidelity surrogate models in this study. The available CFD data \(X_\mathrm{CFD}\) consist of \(n=33\) points with four of seven dimensions varying (\(X_1\) to \(X_4\), corresponding to the inlet width and height, the vortex finder diameter and the total cyclone height), while the remaining are fixed at \(h=1.5, S=0.5, B_c=0.3750\), respectively. Therefore, only a 4D Kriging model \(\mathcal {K}_\mathrm{CFD}\) was trained on the CFD data using the ooDACE toolbox [48]. The 4D model is extended to 7D by concatenating the hyperparameters of the three fixed dimensions from the model \(\mathcal {K}_\mathrm{A}\) learned above. Model training and description follows the explanation in Sect. 3.1.
Let \(\hat{y}_\mathrm{A}(\mathbf{x})\) be the estimates obtained on a given point \(\mathbf x\) using the model \(\mathcal {K}_\mathrm{A}\). Let \(\hat{y}_{d_{1}}\) be the estimate from the Kriging model trained from residuals of analytical and CFD data scaled using parameter \(\gamma _1\), (\(X_\mathrm{CFD}, \mathbf{y}_{d_{1}} = y_\mathrm{CFD} - \gamma _1 \hat{y}_\mathrm{A} (X_\mathrm{CFD})\)). Then estimates on the point \(\mathbf{x}\) are obtained recursively as,
where \(\gamma _1\) is the scaling parameter described in Sect. 3.2.
4.3 Experimental Data
Experimental data \(X_\mathrm{Exp}\) of \(n=96\) points available in the literature for the Euler number values [16] are used to train the Kriging model \(\mathcal {K}_\mathrm{Exp}\) using the ooDACE toolbox [48]. The model itself is trained as explained in Sect. 3.1.
However, objective function values for only one objective (the Euler number) are available. Consequently, a double-fidelity co-Kriging model is trained in lieu of a triple-fidelity co-Kriging model for the second objective (the Stokes number).
Let \(\gamma _2\) define the scaling between CFD and experimental data. Let \(\hat{y}_{d_2}\) be the estimate from the Kriging model trained from residuals of scaled CFD and experimental data (\(X_\mathrm{Exp}, \mathbf{y}_{d_2} = y_\mathrm{Exp} - \gamma _2 \hat{y}_\mathrm{CFD}(X_\mathrm{Exp})\)). The estimate of the model \(\mathcal {K}_\mathrm{Exp}\) on the point \(\mathbf{x}\) is given by,
The process of estimation of scaling parameters \(\gamma _1\) and \(\gamma _2\) is described below.
4.4 Estimation of the Scaling Parameter
The scaling parameters \(\gamma _1\) and \(\gamma _2\) are estimated using cross-validation using the scheme described by Le Gratiet [51]. Essentially, the cross-validation procedure was performed in two stages. The first stage involved cross-validation the double-fidelity co-Kriging model trained using analytical models and CFD data, with CFD data divided into partitions for training and testing. This yielded the value of \(\gamma _1\) to be used for scaling between the sub-Kriging models trained using CFD and analytical data. Similarly, the second stage involved partitioning the experimental data into folds, while the sub-Kriging models obtained using CFD data and analytical models were not modified. This yielded the value of \(\gamma _2\) for scaling between the sub-Kriging models trained using experimental data, and CFD data.
5 Numerical Settings
For the purpose of obtaining \(X_\mathrm{A}\), the number of points in each dimension of the grid \(N_\mathrm{s} = 7\). This results in \(n = 7^7 = 823{,}543\) training points in \(X_\mathrm{A}\) for \(\mathcal {K}_\mathrm{A}\). The recursive co-Kriging model is used as the objective function to be optimized using the SMS-EMOA algorithm [43]. The size of the initial population is set to 100 individuals allowed to evolve until the total number of objective function evaluations reaches 10,000.
6 Results and Discussion
The SMS-EMOA algorithm evolved the population of size 100 into a Pareto set of 100 solutions, which are shown in Fig. 2 and listed in Table 1. The solutions are well-spread and show an improvement over past approaches. A comparison with previous results obtained using multi-objective surrogate-based optimization with the EMO algorithm [12] can also be seen in Fig. 2. Admittedly, the comparison is not completely fair since the previous approach only utilized data from analytical models, while the proposed approach incorporated experimental and simulated data in addition to data from an analytical model. Nevertheless, the results confirm that a more accurate surrogate model for the optimization problem is obtained when all available data are incorporated.
Since the trained model is used as a surrogate model to be treated as the objective function by SMS-EMOA, its accuracy is crucial. Toward this end, cross-validation of the multi-fidelity recursive co-Kriging model was performed using the scheme described in Sect. 4.4.
Table 2 lists the mean squared error (MSE) and Bayesian estimation error quotient (BEEQ) estimates obtained using cross-validation, as described above. BEEQ [54] quantifies the improvement of error of a Bayesian estimator \(\hat{y}\), over the prior mean \(\bar{y}\), or of the updated estimate \(\hat{y}\) of a recursive estimator over the predicted estimate \(\hat{y}\). It is defined as BEEQ\((\hat{y}) = \Big ( \prod _{i=1}^n \beta _i \Big )^{1/n}\), where:
The closer the value of BEEQ to 0, the better the model. BEEQ brings the advantage of nullifying the effect of very large or small magnitudes of values on error estimates.
The double-fidelity recursive co-Kriging model obtained using CFD data and analytical models is very accurate for the Stokes number with MSE=0.0773 and BEEQ=0.8637. Considering the fact that the absolute range,
for Stokes number is 1.8765, a mean error of \(\sqrt{0.0073} = 0.0854\) is a very good result. Similarly, the absolute range for the Euler number is 3.1139. A mean variation of \(\sqrt{3.1254} = 1.7679\) units and a BEEQ score of 3.1393 is not an excellent result, but considering the model is a 7D model trained using only 33 data points, the results are acceptable. Moreover, using the sub-Kriging model trained from experimental data improves the accuracy of the final triple-fidelity model for the Euler number. The absolute range of the Euler number in the experimental dataset is 4.2124. A mean variation of \(\sqrt{0.6699} = 0.8185\) and a BEEQ score of 0.6776 is a much better result compared to using only the double-fidelity co-Kriging model and serves to capture the general trend of the problem under consideration.
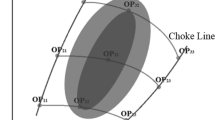
Another advantage of using the co-Kriging model is that it can be used to obtain the variance of prediction of all Pareto-optimal points. Figure 3 shows the variance of prediction for each Pareto-optimal solution as an ellipse. The major axis of a particular ellipse corresponds to the variance of prediction for the Euler number, and the minor axis corresponds to the variance of prediction for the Stokes number. The availability of such information can aid the practitioner in selecting a particular Pareto-optimal solution over another, since it may be impractical to validate all Pareto-optimal solutions using CFD simulations, or experiments. A representative solution is shown in Fig. 4. The solution having the least variance of prediction obtained using the co-Kriging surrogate model was selected to be evaluated as a potential design, and plotted.
7 Conclusions
The problem of cyclone shape optimization involves computationally expensive simulations, and data from time-consuming experiments. Existing approaches do not take multi-fidelity data into account. This work proposes a novel approach to combine existing data from experiments, CFD simulations and mathematical models to train a tripe-fidelity recursive co-Kriging surrogate model. The novelties include handling missing output dimensions and performing co-Kriging with sub-Kriging models trained using million-point datasets. The surrogate model is used as a replacement for the expensive data in a conventional optimization algorithm like SMS-EMOA. Experimental results indicate that the proposed approach leverages the advantages of multiple fidelities of data to result in an accurate surrogate model which leads to a good Pareto set of possible solutions. The accurate surrogate model allows thousands of evaluations to be computed cheaply, enabling optimization algorithms like SMS-EMOA to find high-quality solutions in a very short time. Comparison of the proposed approach to state-of-the-art approaches shows substantial improvement in the obtained solutions.
Abbreviations
- a :
-
Cyclone inlet height (m)
- b :
-
Cyclone inlet width (m)
- \(B_c\) :
-
Cyclone cone-tip diameter (m)
- d :
-
Number of design variables (-)
- D :
-
Cyclone body diameter (m)
- \(D_x\) :
-
Cyclone vortex finder diameter (m)
- h :
-
Cylindrical part height (m)
- \(H_\mathrm{t}\) :
-
Cyclone total height (m)
- \(\mathcal {K}\) :
-
Kriging model
- \(\mathcal {K}_\mathrm{A}\) :
-
Kriging model with training data from analytical models
- \(\mathcal {K}_\mathrm{CFD}\) :
-
Kriging model with training data from CFD simulations
- \(\mathcal {K}_\mathrm{Exp}\) :
-
Kriging model with training data from Experiments
- n :
-
Number of sample points (-)
- \(N_\mathrm{s}\) :
-
Number of sample points in each dimension of gridded data
- \(\mathcal {P}\) :
-
Pareto set
- s :
-
Standard deviation of model prediction
- S :
-
Vortex finder length (m)
- \(V_\mathrm{in}\) :
-
Area-average inlet velocity (m/s)
- \(\mathbf{x}\) :
-
Data instance
- X :
-
Training set of data
- \(X_\mathrm{A}\) :
-
Training set of data from analytical models
- \(X_\mathrm{CFD}\) :
-
Training set of data from CFD simulations
- \(X_\mathrm{Exp}\) :
-
Training set of data from experiments
- \(\hat{y}\) :
-
Mean of model prediction
- \(\mathbf{y}\) :
-
Vector of training set targets
- \(\mathbf{y}_\mathrm{A}\) :
-
Vector of training set targets for data from analytical models
- \(\mathbf{y}_\mathrm{CFD}\) :
-
Vector of training set targets for data from CFD simulations
- \(\mathbf{y}_\mathrm{Exp}\) :
-
Vector of training set targets for data from experiments
- Y :
-
Random variable
- \(\alpha \) :
-
Regression function coefficient
- \(\gamma \) :
-
Scaling parameter for sub-Kriging models
- \(\varDelta P\) :
-
Pressure drop (N/m\(^2\))
- \(\epsilon \) :
-
Distance threshold
- \(\mu \) :
-
Dynamic viscosity (kg/(m s))
- \(\phi (\cdot )\) :
-
Transformation function
- \(\varPhi {\cdot }\) :
-
Normal cumulative distribution function
- \(\psi ^{(i)}\) :
-
Correlations between \(Y(\mathbf {x})\) at the point to be predicted and at the sample data points
- \(\varPsi \) :
-
Correlation matrix of given data samples
- \(\rho \) :
-
Gas density (kg/m\(^3\))
- \(\sigma ^2\) :
-
Variance
- \(\theta \) :
-
Kriging hyper-parameter variables
- \(E_u\) :
-
Euler number
- Re :
-
Reynolds number
- \(Stk_{50}\) :
-
Stokes number corresponding to 50% separation efficiency
- BEEQ:
-
Bayesian estimation error quotient
- CFD:
-
Computational fluid dynamics
- EGO:
-
Efficient global optimization
- EMO:
-
Efficient multi-objective optimization
- MLE:
-
Maximum likelihood estimation
- MOEA:
-
Multi-objective evolutionary algorithm
- MSE:
-
Mean squared error
- NSGA-II:
-
Non-dominated sorting genetic algorithm 2
- RBF:
-
Radial basis function
- SBO:
-
Surrogate-based optimization
- SMS-EMOA:
-
\(\mathcal {S}\)-Metric selection-evolutionary multi-objective optimization algorithm
- SVR:
-
Support vector regression
References
Funk, P., Elsayed, K., Yeater, K., Holt, G., Whitelock, D.: Could cyclone performance improve with reduced inlet velocity? Powder Technol. 280, 211–218 (2015)
Brar, L.S., Sharma, R., Elsayed, K.: The effect of the cyclone length on the performance of Stairmand high-efficiency cyclone. Powder Technol. 286, 668–677 (2015)
Stairmand, C.J.: The design and performance of cyclone separators. Ind. Eng. Chem. 29, 356–383 (1951)
Hu, L.Y., Zhou, L.X., Zhang, J., Shi, M.X.: Studies on strongly swirling flows in the full space of a volute cyclone separator. AIChE J. 51(3), 740–749 (2005)
Zhang, B., Hui, S.: Numerical simulation and PIV study of the turbulent flow in a cyclonic separator. In: International Conference on Power Engineering, Hangzhou, China (2007)
Gimbun, J., Chuah, T., Fakhru’l-Razi, A., Choong, T.S.Y.: The influence of temperature and inlet velocity on cyclone pressure drop: a CFD study. Chem. Eng. Process. 44(1), 7–12 (2005)
Elsayed, K., Lacor, C.: Optimization of the cyclone separator geometry for minimum pressure drop using mathematical models and CFD simulations. Chem. Eng. Sci. 65(22), 6048–6058 (2010)
Elsayed, K., Lacor, C.: Analysis and optimisation of cyclone separators geometry using RANS and LES methodologies. In: Deville, M.O., Estivalezes, J.L., Gleize, V., Le, T.H., Terracol, M., Vincent, S. (eds.) Turbulence and Interactions, Notes on Numerical Fluid Mechanics and Multidisciplinary Design, vol. 125, pp. 65–74. Springer, Berlin (2014)
Elsayed, K., Lacor, C.: The effect of cyclone vortex finder dimensions on the flow pattern and performance using LES. Comput. Fluids 71, 224–239 (2013)
Elsayed, K., Lacor, C.: The effect of the dust outlet geometry on the performance and hydrodynamics of gas cyclones. Comput. Fluids 68, 134–147 (2012)
Elsayed, K., Lacor, C.: The effect of cyclone inlet dimensions on the flow pattern and performance. Appl. Math. Model. 35(4), 1952–1968 (2011)
Singh, P., Couckuyt, I., Elsayed, K., Deschrijver, D., Dhaene, T.: Shape optimization of a cyclone separator using multi-objective surrogate-based optimization. Appl. Math. Modell. 40(5), 4248–4259 (2015)
Elsayed, K.: Optimization of the cyclone separator geometry for minimum pressure drop using co-Kriging. Powder Technol. 269, 409–424 (2015)
Elsayed, K., Lacor, C.: CFD modeling and multi-objective optimization of cyclone geometry using desirability function, artificial neural networks and genetic algorithms. Appl. Math. Model. 37(8), 5680–5704 (2013)
Elsayed, K., Lacor, C.: Modeling and pareto optimization of gas cyclone separator performance using RBF type artificial neural networks and genetic algorithms. Powder Technol. 217, 84–99 (2012)
Elsayed, K., Lacor, C.: Modeling, analysis and optimization of aircyclones using artificial neural network, response surface methodology and CFD simulation approaches. Powder Technol. 212(1), 115–133 (2011)
Elsayed, K.: Design of a novel gas cyclone vortex finder using the adjoint method. Sep. Purif. Technol. 142, 274–286 (2015)
Iozia, D.L., Leith, D.: Effect of cyclone dimensions on gas flow pattern and collection efficiency. Aerosol Sci. Technol. 10(3), 491–500 (1989)
Ramachandran, G., Leith, D., Dirgo, J., Feldman, H.: Cyclone optimization based on a new empirical model for pressure drop. Aerosol Sci. Technol. 15, 135–148 (1991)
Trefz, M.: Die vershiedenen abscheidevorgange im hoher un hoch beladenen gaszyklon unter besonderer berucksichtigung der sekundarstromung. Forschritt–Berichte VDI; VDI-Verlag GmbH: Dusseldorf, Germany 295 (1992)
Trefz, M., Muschelknautz, E.: Extended cyclone theory for gas flows with high solids concentrations. Chem. Ing. Tech. 16, 153–160 (1993)
Cortés, C., Gil, A.: Modeling the gas and particle flow inside cyclone separators. Prog. Energy Combust. Sci. 33(5), 409–452 (2007)
Hoffmann, A.C., Stein, L.E.: Gas Cyclones and Swirl Tubes: Principle, Design and Operation, 2nd edn. Springer, Berlin (2008)
Elsayed, K.: Analysis and Optimization of Cyclone Separators Geometry Using RANS and LES Methodologies. Ph.D. thesis, Vrije Universiteit Brussel (2011)
Ravi, G., Gupta, S.K., Ray, M.B.: Multiobjective optimization of cyclone separators using genetic algorithm. Ind. Eng. Chem. Res. 39, 4272–4286 (2000)
Salcedo, R.L.R., Candido, M.G.: Global optimization of reverse-flow gas cyclones: application to small-scale cyclone design. Sep. Sci. Technol. 36(12), 2707–2731 (2001)
Mothes, H., Loffler, F.: Prediction of particle removal in cyclone separators. Int. Chem. Eng. 28(2), 231–240 (1988)
Swamee, P.K., Aggarwal, N., Bhobhiya, K.: Optimum design of cyclone separator. Am. Inst. Chem. Eng. (AIChE ) 55(9), 2279–2283 (2009)
Safikhani, H., Hajiloo, A., Ranjbar, M., Nariman-Zadeh, N.: Modeling and multi-objective optimization of cyclone separators using CFD and genetic algorithms. Comput. Chem. Eng. 35(6), 1064–1071 (2011)
Pishbin, S.I., Moghiman, M.: Optimization of cyclone separators using genetic algorithm. Int. Rev. Chem. Eng. (I.RE.CH.E.) 2(6), 683–690 (2010)
Shepherd, C.B., Lapple, C.E.: Flow pattern and pressure drop in cyclone dust collectors cyclone without intel vane. Ind. Eng. Chem. 32(9), 1246–1248 (1940)
Barth, W.: Design and layout of the cyclone separator on the basis of new investigations. Brennstow Wäerme Kraft (BWK) 8(4), 1–9 (1956)
Derksen, J.J., Sundaresan, S., van den Akker, H.E.A.: Simulation of mass-loading effects in gas-solid cyclone separators. Powder Technol. 163, 59–68 (2006)
Kenny, L., Gussman, R.: Characterization and modelling of a family of cyclone aerosol preseparators. J. Aerosol Sci. 28(4), 677–688 (1997)
Badhurshah, R., Samad, A.: Multiple surrogate based optimization of a bidirectional impulse turbine for wave energy conversion. Renew. Energy 74, 749–760 (2015)
Chen, X.M., Zhang, L., He, X., Xiong, C., Li, Z.: Surrogate-based optimization of expensive-to-evaluate objective for optimal highway toll charges in transportation network. Comput. Aided Civ. Infrastruct. Eng. 29(5), 359–381 (2014)
Costas, M., Díaz, J., Romera, L., Hernández, S.: A multi-objective surrogate-based optimization of the crashworthiness of a hybrid impact absorber. Int. J. Mech. Sci. 88, 46–54 (2014)
Koziel, S., Ogurtsov, S.: Numerically Efficient Approach to Simulation-Driven Design of Planar Microstrip Antenna Arrays by Means of Surrogate-Based Optimization, pp. 149–170. Springer International Publishing, Cham (2014). doi:10.1007/978-3-319-08985-0_6
Liu, B., He, Y., Reynaert, P., Gielen, G.: Global optimization of integrated transformers for high frequency microwave circuits using a Gaussian process based surrogate model. In: Design, Automation and Test in Europe Conference and Exhibition (DATE), 2011, pp. 1–6. IEEE (2011)
Jones, D.R., Schonlau, M., Welch, W.J.: Efficient global optimization of expensive black-box functions. J. Glob. Optim. 13(4), 455–492 (1998)
Couckuyt, I., Deschrijver, D., Dhaene, T.: Fast calculation of multiobjective probability of improvement and expected improvement criteria for pareto optimization. J. Glob. Optim. 60(3), 575–594 (2014)
Deb, K., Pratap, A., Agarwal, S., Meyarivan, T.: A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6, 182–197 (2002)
Beume, N., Naujoks, B., Emmerich, M.: SMS-EMOA: multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 181(3), 1653–1669 (2007)
Zitzler, E., Laumanns, M., Thiele, L., et al.: Spea 2: improving the strength pareto evolutionary algorithm. Eurogen 3242, 95–100 (2001)
Forrester, A.I.J., Keane, A.J.: Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 45(1–3), 50–79 (2009)
Couckuyt, I., Koziel, S., Dhaene, T.: Surrogate modeling of microwave structures using Kriging, co-Kriging, and space mapping. Int. J. Numer. Model. Electron. Netw. Devices Fields 26(1), 64–73 (2013)
Gorissen, D., Couckuyt, I., Demeester, P., Dhaene, T., Crombecq, K.: A surrogate modeling and adaptive sampling toolbox for computer based design. J. Mach. Learn. Res. 11, 2051–2055 (2010)
Couckuyt, I., Dhaene, T., Demeester, P.: oodace toolbox: a flexible object-oriented Kriging implementation. J. Mach. Learn. Res. 15(1), 3183–3186 (2014)
Lophaven, S.N., Nielsen, H.B., Søndergaard, J.: Aspects of the Matlab Toolbox DACE. Technical Report, Informatics and Mathematical Modelling, Technical University of Denmark, DTU, Richard Petersens Plads, Building 321, DK-2800 Kgs. Lyngby (2002)
Kennedy, M.C., O’Hagan, A.: Bayesian calibration of computer models (with discussion). J. R. Stat. Soc. B 63, 425–464 (2001)
Le Gratiet, L., Garnier, J.: Recursive co-Kriging model for design of computer experiments with multiple levels of fidelity. Int. J. Uncertain. Quantif. 4(5) (2014)
Wilson, A., Gilboa, E., Cunningham, J.P., Nehorai, A.,: Fast multidimensional pattern extrapolation. In: Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q. (eds.) Advances in Neural Information Processing Systems, vol. 27, pp. 3626–3634. Curran Associates, Inc. (2014). http://papers.nips.cc/paper/5372-fast-kernel-learning-for-multidimensional-pattern-extrapolation.pdf
Wilson, A.G., Nickisch, H.: Kernel interpolation for scalable structured gaussian processes (KISS-GP). In: Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6–11 July 2015, pp. 1775–1784 (2015). http://jmlr.org/proceedings/papers/v37/wilson15.html
Li, X.R., Zhao, Z.: Relative error measures for evaluation of estimation algorithms. In: 2005 8th International Conference on Information Fusion, vol. 1, p. 8. IEEE (2005)
Acknowledgements
This work was supported by the Interuniversity Attraction Poles Programme BESTCOM initiated by the Belgian Science Policy Office, and the Research Foundation Flanders (FWO- Vlaanderen). Ivo Couckuyt is a Postdoctoral Researcher of FWO-Vlaanderen.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Zenon Mroz.
Appendix A
Appendix A
1.1 A.1 Ramachandran Model
The Ramachandran et al. [19] model has been constructed through a statistical analysis. The Euler number Eu is given,
1.2 A.2 The Iozia and Leith Model
The Iozia and Leith model [18] is based on the equilibrium-orbit theory (Force balance).
where \(\rho _\mathrm{p}\) is the particle density..
Where \(H_{\mathrm{CS}}\) is the core height and \(V_{\theta _\mathrm{max}}\) is the maximum tangential velocity that occurs at the edge of the control surface CS. In this model, the values of the core diameter \(d_\mathrm{c}\) and the tangential velocity at the core edge \(V_{\theta _\mathrm{max}}\) are calculated via a regression of the experimental data as follows,
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Singh, P., Couckuyt, I., Elsayed, K. et al. Multi-objective Geometry Optimization of a Gas Cyclone Using Triple-Fidelity Co-Kriging Surrogate Models. J Optim Theory Appl 175, 172–193 (2017). https://doi.org/10.1007/s10957-017-1114-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-017-1114-3
Keywords
- Cyclone separator
- Surrogate-based optimization (SBO)
- Multi-fidelity data
- Sparse Kriging
- Recursive co-Kriging