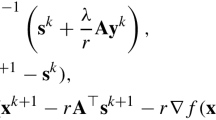1 Introduction

The monotonic regression (MR) is aimed at learning monotonic dependence from a given data set [1, 2]. The enormous amount of publications related to the MR, as well as a growing variety of its application areas, testifies to its exceptional importance. Examples are found in such areas as operations research [3], genetics [4], environmental science [5], meteorology [6], psychology [7], and many others. One can find very large-scale MR problems, e.g., in machine learning [8,9,10] and computer simulations [11].

The MR deals with an ordered data set of observations. In this paper, we restrict our consideration to the case in which the observations are completely (linearly) ordered. Given a data set, the MR consists in finding fitted values which must be as close as possible, in the least square sense, to the corresponding observed values. The fitted values are also required to satisfy monotonicity constraints such that the value of each component of the vector of fitted values must be less than or equal to next one.

Since the constraints of the least-squares formulation of the MR problem are of a very special type, the MR algorithms exploit this feature. The most efficient of these is a so-called pool-adjacent-violators (PAV) algorithm [12,13,14]. It can be viewed as a dual active-set algorithm [15, 16]. The efficiency and popularity of the PAV algorithm is explained mainly by its linear computational complexity.

In applications, it is sometimes required to construct a monotone fitted response function. Such a function, if based on solving the MR problem, is typically composed of segments of constant function values with a sharp increase between the segments. This peculiarity constrains the use of the MR in some areas. For smoothing the fitted response, we introduce a regularization term in the MR problem. The resulting smoothed monotonic regression (SMR) problem is a convex quadratic optimization problem. In the present paper and the accompanying one [17], we propose a smoothed pool-adjacent-violators (SPAV) algorithm for efficiently solving the SMR problem.

In the accompanying paper [17], we present a statistical analysis of the SMR problem. In particular, it is shown how to properly choose the values of the penalty parameters by making use of Bayesian modeling and a cross-validation technique. The numerical results in that paper reveal that the solution to the SMR problem provides a better predictive power in comparison with the commonly used alternative approaches of a similar computational complexity intended for monotonic smoothing and prediction. It is also shown in [17] that the computational complexity of the SPAV algorithm grows quadratically with the problem size, under the assumption that it converges to the optimal solution in number of iterations which does not exceed the problem size. No convergence analysis is conducted in [17].

The present paper is focused on presenting details of this optimization algorithm viewed as a dual active-set algorithm and showing that it converges in a number of iterations that does not exceed the problem size. Its key feature is that the active set is always expanding by making active, typically, more than one constraint per iteration. The version of the SPAV algorithm introduced here is more general than in [17] because it is not restricted to starting from only an empty active set.

The paper is organized as follows. The next section is devoted to formulating and discussing the SMR problem. In Sect. 3, a subproblem determined by the set of active constraints is considered, and the aforementioned version of the SPAV algorithm is introduced. It is also shown that, when the penalty parameter equals zero, the SPAV is reduced to the algorithm of linear complexity developed in [18], where the primal-dual active-set (PDAS) algorithm [19] was tailored to solving the MR problem. Section 4 is devoted to studying some properties of the SPAV algorithm. We show, in particular, that the Lagrange multipliers do not decrease at each iteration, which allows us to prove a finite-step convergence of the algorithm. In Sect. 5, results of numerical experiments are presented. They illustrate how the desired smoothing is performed by the SPAV algorithm. In our experiments, its running time was found to grow almost linearly with the problem size rather than quadratically as suggested by the worst-case analysis. Finally, we close with concluding remarks in Sect. 6 where, in particular, we discuss an extension of the SMR problem from a complete to partially ordered set of observations.

2 Problem Formulation

The applications of monotonic regression are often related to monotonic data fitting, where it is assumed that there exists an unknown monotonic response function \(\chi (t)\) of an explanatory variable t. In this paper, we focus on the univariate case and suppose that \(\chi (t)\) is monotonically increasing, i.e.,

$$\begin{aligned} \chi (t')< \chi (t''), \quad \forall t'< t''. \end{aligned}$$

For a linearly ordered sequence of observed values of the explanatory variable \(t_1<t_2< \cdots <t_n\), the corresponding sequence of observed response values

$$\begin{aligned} a_i = \chi (t_i) + \epsilon _i, \quad i=1, 2, \ldots , n, \end{aligned}$$
(1)

is supposed to be available, where \(\epsilon _i\) is an observation error. Because of the errors, the expected monotonicity \(a_i \le a_{i+1}\) may be violated for some indexes i. The MR problem is aimed at restoring the perturbed monotonicity by finding a least-change correction to the observed values. It can be stated formally as a quadratic optimization problem in the following way:

$$\begin{aligned} \min _{x \in \mathbb {R}^n} \sum _{i=1}^{n} w_i(x_i - a_i)^2, \quad \text {s.t.} \quad x_1 \le x_2\le \cdots \le x_n, \end{aligned}$$
(2)

where \(w \in \mathbb {R}^n_{++}\) is a vector of weights.

Let \(x^*\) be the solution to the MR problem. The active constraints suggest that the components of \(x^*\) are partitioned into blocks of consecutive components of equal values. Let x(t) be a monotonic function which satisfies the interpolation condition:

$$\begin{aligned} x(t_i) = x_i^*, \quad \forall i \in [1,n]. \end{aligned}$$

Here and later, the set of indexes \(\{i, i+1, \ldots , j-1, j\}\) is denoted by [i, j] and referred to as a segment of indexes. Because of the block structure of \(x^*\), the shape of x(t) resembles a step function, suggesting that it may have sharp changes on certain intervals of t, where the response function \(\chi (t)\) does not increase so rapidly. This feature of the MR problem is often criticized, and it motivates the necessity of smoothing the MR solution.

Consider the following regularized monotonic regression problem:

$$\begin{aligned} \min _{x \in \mathbb {R}^n} \sum _{i=1}^{n} w_i(x_i - a_i)^2 + \sum _{i=1}^{n-1} \mu _i (x_i - x_{i+1})^2, \quad \text {s.t.} \quad x_i\le x_{i+1}, \ \forall i\in [1,n-1], \end{aligned}$$
(3)

where \(\mu \in \mathbb {R}^{n-1}_+\) is a vector of penalty parameters. The penalty term in (3) is aimed at smoothing functions which interpolate the solution to this problem. This explains why we refer to (3) as the smoothed monotonic regression (SMR) problem. Note that since (3) is a quadratic optimization problem with a strictly convex objective function, its solution exists and is unique. When \(\mu = 0\), problem (3) is obviously reduced to (2).

To illustrate the smoothing property of the SMR problem, consider

$$\begin{aligned} \mu _i = \frac{\mu }{(t_{i+1} - t_i)^2} \ . \end{aligned}$$
(4)

For this choice of \(\mu _i\), the corresponding penalty term

$$\begin{aligned} \mu \sum _{i=1}^{n-1} \left( \frac{x_{i+1} - x_i}{t_{i+1} - t_i} \right) ^2 \end{aligned}$$

involves a finite-difference approximation of the first derivative.

3 Smoothed Pool-Adjacent-Violators Algorithm

We shall refer to \(x_i \le x_{i+1}\) in the SMR as constraint \(i \in [1,n-1]\). Each iteration of our algorithm is related to choosing an active set \(S\subseteq [1,n-1]\) and solving the corresponding subproblem

$$\begin{aligned} \min _{x \in \mathbb {R}^n} \sum _{i=1}^{n} w_i(x_i - a_i)^2 + \sum _{i=1}^{n-1} \mu _i (x_i - x_{i+1})^2, \quad \text {s.t.} \quad x_i= x_{i+1}, \quad \forall i\in S. \end{aligned}$$
(5)

We denote its unique optimal solution by x(S). For presenting an efficient way of solving this subproblem, we consider the optimality conditions. They will also be used in the next section for studying the convergence properties of the algorithm.

The active set S suggests that there exist sets of consecutive indices of the form \([\ell , r]\subseteq [1,n]\) such that \([\ell , r-1]\subseteq S\), \(\ell -1 \notin S\) and \(r\notin S\). We call these sets blocks. Note that a block may be a singleton when \(\ell =r\). Then the total number of blocks, denoted here by m, is equal to \(n - |S|\). The block partitioning (segmentation) of [1, n] induced by S can be represented as

$$\begin{aligned}{}[1,n] = [\ell _1,r_1], [\ell _2,r_2], \ldots , [\ell _m,r_m], \end{aligned}$$

where \(\ell _1 =1\), \(r_m=n\) and \(r_i + 1 = \ell _{i+1}\) for all \(i\in [1,m-1]\).

Each block i is characterized by its common value

$$\begin{aligned} y_i = x_{\ell _i} = x_{\ell _i+1} = \cdots = x_{r_i}, \end{aligned}$$

its common weight

$$\begin{aligned} w^{\prime }_i = w_{\ell _i} + w_{\ell _i+1} + \cdots + w_{r_i} \end{aligned}$$

and its weighted average observed value

$$\begin{aligned} a^{\prime }_i = \frac{1}{w^{\prime }_i} \sum _{j=\ell _i}^{r_i} w_j a_j . \end{aligned}$$

Denoting \(\mu ^{\prime }_i = \mu _{r_i}\), we can write the subproblem (5) in the notation introduced above as

$$\begin{aligned} \min _{y \in \mathbb {R}^m} c + \sum _{j=1}^{m} w_j^{\prime } (y_j - a_j^{\prime })^2 + \sum _{j=1}^{m-1} \mu _j^{\prime } (y_j - y_{j+1})^2, \end{aligned}$$
(6)

where the scalar c does not depend on y. The optimality conditions for (6) are given by the system of linear equations

$$\begin{aligned} \begin{array}{l} w_1^{\prime }(y_1 - a_1^{\prime }) + \mu _1^{\prime } (y_1 - y_{2}) = 0, \\ \cdots \\ w_j^{\prime }(y_j - a_j^{\prime }) + \mu _{j-1}^{\prime } (y_j - y_{j-1}) + \mu _j^{\prime } (y_j - y_{j+1}) = 0, \\ \cdots \\ w_m^{\prime }(y_m - a_m^{\prime }) + \mu _{m-1}^{\prime } (y_m - y_{m-1}) = 0. \end{array} \end{aligned}$$
(7)

Its solution, denoted by y(S), is unique because the objective function in (6) is strictly convex.

The algorithm starts with any active set such that \(S \subseteq S^*\). The simplest of the valid choices is \(S = \emptyset \). At each iteration, it solves the tridiagonal system of linear equations (7), and then it extends the set S by additionally making active the constraints in (3) for which the strict monotonicity \(y_i(S) < y_{i+1}(S)\) is violated. This, like in the PAV algorithm, assumes merging the corresponding adjacent blocks, which explains why we call our algorithm SPAV (smoothed pool-adjacent-violators). The merging is associated with updating the coefficients that define the linear system (7). The corresponding number of arithmetic operations is proportional to the number of new active constraints. In contrast to the conventional active-set algorithms, SPAV may enlarge the active set with more than one element at once. It operates with the block common values \(y_i\), whereas the values of \(x_i\) are computed only at its terminal stage. The outlined algorithm can be formally expressed as follows.

figure a

It is shown in [17] that the computational complexity of the SPAV algorithm is \(O(n^2)\). This estimate is based on the following two observations. First, the active set S is extended in the while loop by including, at least, one index, which means that the number of the while loop iterations does not exceed \(n-1\). Second, the computational complexity of solving the tridiagonal linear system (7) is O(n). The cost of updating \(a'\), \(w'\), and \(\mu '\) is a small multiple of the number of blocks merged at the same iteration, which means that the total sum of operations, associated with updating these vectors, over all iterations is O(n).

As it will follow from the results of the next section, the active set S produced by the SPAV is such that, at each iteration, the inclusion \(S \subseteq S^*\) is maintained, and after the final iteration it turns out that \(S = S^*\). The algorithm can start from any set \(S \subseteq S^*\), even though some of the Lagrange multipliers in (5) may be negative. This enables the algorithm to be warm-started by providing a good initial point. If there is no guarantee that \(S \subseteq S^*\) holds for the initial S, then the recursive calculation of the Lagrange multipliers, as described in the next section, allows for attaining the desired inclusion \(S \subseteq S^*\) by splitting certain blocks. The negative Lagrange multipliers indicate how to split the blocks, namely, by making inactive the corresponding monotonicity constraints. Given S, if all the Lagrange multipliers are nonnegative, then this guarantees that \(S \subseteq S^*\).

Note that, when \(\mu _i=0\) for all \(i\in [1,n-1]\), the SMR reduces to the MR problem. This permits us to apply the SPAV algorithm to solving the latter problem. In this case, the complexity of the algorithm that we shall refer to as \(\text {SPAV}_0\) reduces to O(n), which is the same as for the PAV algorithm. This follows from the fact that (7) becomes a diagonal linear system whose solution is \(y_j = a_j^{\prime }\) for all \(j \in [1,m]\), and that the merging of blocks changes only those components of y that correspond to the new blocks. The MR version of the SPAV algorithm can be formally expressed for the initial \(S = \emptyset \) as follows.

figure b

It should be mentioned that the iterates generated by \(\text {SPAV}_0\) are not the same as those generated by the PAV algorithm, but they are identical with those generated by the PDAS-type algorithm proposed in [18] when it is also initialized with \(S = \emptyset \).

4 Convergence of Smoothed Pool-Adjacent-Violators Algorithm

Note that the SMR is a strictly convex optimization problem, because the objective function in (3) is strictly convex and the constraints are linear. It has a unique optimal solution determined by the Karush–Kuhn–Tucker (KKT) conditions [20]. For deriving these conditions, we use the Lagrangian function

$$\begin{aligned} L(x, \lambda ) = \sum _{i=1}^{n} w_i(x_i - a_i)^2 + \sum _{i=1}^{n-1} \mu _i (x_i - x_{i+1})^2 + \sum _{i=1}^{n-1} \lambda _i (x_i - x_{i+1}). \end{aligned}$$
(8)

The condition \(\nabla _x L(x, \lambda ) = 0\) is written as

$$\begin{aligned} \begin{array}{l} 2w_1(x_1-a_1) + 2\mu _1(x_1 - x_{2}) + \lambda _1 = 0, \\ 2w_i(x_i-a_i) + 2\mu _{i-1}(x_i - x_{i-1}) + 2\mu _i(x_i - x_{i+1}) + \lambda _i - \lambda _{i-1} = 0, \\ \forall i\in [1,n-1], \\ 2w_n(x_n-a_n) + 2\mu _{n-1}(x_n - x_{n-1}) - \lambda _{n-1} = 0. \end{array} \end{aligned}$$
(9)

The rest of the KKT conditions has the form

$$\begin{aligned} x_i\le x_{i+1}, \quad \forall i\in [1,n-1], \end{aligned}$$
(10)
$$\begin{aligned} \lambda _i \ge 0, \quad \forall i\in [1,n-1], \end{aligned}$$
(11)
$$\begin{aligned} \lambda _i (x_i - x_{i+1}) = 0, \quad \forall i\in [1,n-1]. \end{aligned}$$
(12)

Consider now the subproblem (5). Not only is its solution x(S) unique, but the optimal Lagrange multipliers are also unique because the gradients of the constraints in (5) are linearly independent.

The Lagrangian function for (5),

$$\begin{aligned} L_S(x, \lambda ) = \sum _{i=1}^{n} w_i(x_i - a_i)^2 + \sum _{i=1}^{n-1} \mu _i (x_i - x_{i+1})^2 + \sum _{i\in S} \lambda _i (x_i - x_{i+1}), \end{aligned}$$

is obtained from (8) by setting

$$\begin{aligned} \lambda _i = 0, \quad \forall i\in [1,n-1]{\setminus } S. \end{aligned}$$
(13)

Let \(\lambda (S)\) be the vector in \(\mathbb {R}^{n-1}\) whose components \(\lambda _i(S)\), \(i\in S\), are the optimal Lagrange multipliers for (5), with the remainder being defined by (13). This property of the \(L_S(x, \lambda )\) will later be used to prove the optimality of the solution produced by the SPAV algorithm.

The condition (9) establishes a dependence of the Lagrange multipliers on x, and hence, on the common block values y. We will study now monotonic properties of this dependence. Given an active set S, consider any of the corresponding blocks, say, block i. Let the block be non-singleton, i.e., \(\ell _i < r_i\). If the left neighbor of the block exists, i.e., \(i>1\), then by (13), we have \(\lambda _{\ell _i -1} = 0\). For its right neighbor, if \(i<m\) then we similarly have \(\lambda _{r_i}= 0\). As it will be shown below, the part of the linear equations (9):

$$\begin{aligned} \nabla _{x_k} L(x,\lambda ) = 0, \end{aligned}$$
(14)

where \(k = \ell _i, \ldots , r_i-1\), uniquely determines a dependence of each \(\lambda _j\),

\(j\in [\ell _i, r_i-1]\), on \(y_i\), and if \(i>1\) then also on the value of \(y_{i} - y_{i-1}\). We denote this function by \(\lambda _j (y_i, y_{i} - y_{i-1})\), assuming for \(i=1\) that \(\lambda _j\) does not change with \(y_1 - y_0\), as if \(\mu _0 = 0\). For \(k = \ell _i + 1, \ldots , r_i\), the system of linear equations (14) uniquely determines a dependence of each \(\lambda _j\), \(j\in [\ell _i, r_i-1]\), on \(y_i\), and if \(i<n\) then also on the value of \(y_{i} - y_{i+1}\). Like above, this dependence is conventionally denoted by \(\lambda _j (y_i, y_{i} - y_{i+1})\), assuming that \(\lambda _{j}\) does not change with \(y_{m} - y_{m+1}\). A monotonic dependence of the Lagrange multipliers as a function of the block common values is presented by the following result. It will later be used for showing that, at every iteration of the SPAV algorithm, each component of the vector \(\lambda (S)\) does not decrease.

Lemma 4.1

Let a non-singleton block i be defined by an active set S. Then, for any \(j\in [\ell _i, r_i-1]\), the functions \(\lambda _j (y_i, y_{i} - y_{i-1})\) and \(\lambda _j (y_i, y_{i} - y_{i+1})\) are uniquely determined by the corresponding parts of (9). Furthermore, \(\lambda _j (y_i, y_{i} - y_{i-1})\) decreases with \(y_i\), and it does not increase with \(y_{i} - y_{i-1}\). Finally, \(\lambda _j (y_i, y_{i} - y_{i+1})\) is an increasing and non-decreasing function of \(y_i\) and \(y_{i} - y_{i+1}\), respectively.

Proof

For simplicity, we drop the index i in \(\ell _i\) and \(r_i\). For \(k = \ell , \ldots , r-1\), the linear system (14) recursively defines the Lagrange multipliers as

$$\begin{aligned} \begin{array}{l} \lambda _{\ell } = - 2w_{\ell }(y_i - a_{\ell }) - 2\mu _{\ell -1}(y_{i} - y_{i-1}), \\ \lambda _{j} = \lambda _{j-1} - 2w_{j}(y_i - a_{j}), \quad j = \ell +1, \ell +2, \ldots , r-1, \end{array} \end{aligned}$$

where the term \(-2\mu _{\ell -1}(y_{i} - y_{i-1})\) it to be omitted when \(i=1\). This recursion indicates that each \(\lambda _j (y_i, y_{i} - y_{i-1})\), \(\ell \le j < r\), decreases with \(y_i\), and it does not increase with \(y_{i} - y_{i-1}\), because \(w>0\) and \(\mu \ge 0\). The reverse recursion

$$\begin{aligned} \begin{array}{l} \lambda _{r-1} = 2w_{r}(y_i - a_{r}) + 2\mu _{r}(y_{i} - y_{i+1}), \\ \lambda _{j-1} = \lambda _{j} + 2w_{j}(y_i - a_{j}), \quad j = r-1, r-2, \ldots , \ell + 1, \end{array} \end{aligned}$$

derived from the linear system that corresponds to \(k = \ell + 1, \ldots , r\) in (14), proves the last statement of the lemma. This completes the proof. \(\square \)

For an arbitrary index \(k \in [1,m-1]\), consider the problem obtained from (6) by excluding from the objective function the terms

$$\begin{aligned} w_k^{\prime }(y_k - a_k^{\prime })^2 + w_{k+1}^{\prime }(y_{k+1} - a_{k+1}^{\prime })^2 + \mu _k^{\prime } (y_k - y_{k+1})^2 \end{aligned}$$

and viewing \(y_k\) and \(y_{k+1}\) as parameters. The resulting problem is decoupled into the following two subproblems:

$$\begin{aligned} \min _{y_1, \ldots , y_{k-1}} \sum _{j=1}^{k-1} \left[ w_j^{\prime }(y_j - a_j^{\prime })^2 + \mu _j^{\prime } (y_j - y_{j+1})^2 \right] \end{aligned}$$
(15)

and

$$\begin{aligned} \min _{y_{k+2}, \ldots , y_{m}} \sum _{j=k+2}^{m} \left[ w_j^{\prime }(y_j - a_j^{\prime })^2 + \mu _{j-1}^{\prime } (y_j - y_{j-1})^2 \right] . \end{aligned}$$
(16)

We denote the unique solutions to these subproblems by

$$\begin{aligned} y_1(y_k), \ldots , y_{k-1} (y_k) \quad \text {and} \quad y_{k+2} (y_{k+1}), \ldots , y_{m} (y_{k+1}), \end{aligned}$$
(17)

respectively. In the next result, their monotonic dependence on \(y_k\) and \(y_{k+1}\) is studied.

Lemma 4.2

The components (17) of the optimal solutions to subproblems (15) and (16) are linearly non-decreasing functions of \(y_k\) and \(y_{k+1}\), respectively. Moreover, the differences

$$\begin{aligned} y_{j+1}(y_k) - y_j(y_k), \quad j=1, \ldots ,k-1, \end{aligned}$$

and

$$\begin{aligned} y_{j}(y_{k+1}) - y_{j+1}(y_{k+1}), \quad j=k+1, \ldots ,m-1, \end{aligned}$$

are also non-decreasing functions of \(y_k\) and \(y_{k+1}\), respectively.

Proof

The optimality conditions for (15) are represented by the first \(k-1\) equations in (7). Since the left-hand side of this system of equations is a linear functional of \(y_1, \ldots , y_k\), its solution \(y_1(y_k), \ldots , y_{k-1} (y_k)\) linearly depends on \(y_k\). The linearity of \(y_{k+2} (y_{k+1}), \ldots , y_{m} (y_{k+1})\) is obtained in a similar way.

The first \(k-1\) equations in (7) can be represented as

$$\begin{aligned} M \bar{y}(y_k) = y_k \mu _{k-1}^{\prime } e_{k-1}, \end{aligned}$$
(18)

where \(\bar{y}(y_k) = (y_1(y_k), \ldots , y_{k-1} (y_k))^T\), \(e_{k-1} = (0,\ldots ,0,1)^T\) and

$$\begin{aligned} M= & {} \text {diag} (w_1^{\prime }, \ldots , w_{k-1}^{\prime })\\&+ \left[ \begin{array}{ccccc} \mu _1^{\prime } &{} -\mu _1^{\prime } &{} &{} &{} \\ -\mu _1^{\prime } &{} (\mu _1^{\prime }+\mu _2^{\prime }) &{} -\mu _2^{\prime } &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} -\mu _{k-3}^{\prime } &{} (\mu _{k-3}^{\prime } + \mu _{k-2}^{\prime }) &{} -\mu _{k-2}^{\prime } \\ &{} &{} &{} -\mu _{k-2}^{\prime } &{} (\mu _{k-2}^{\prime } + \mu _{k-1}^{\prime }) \end{array} \right] . \end{aligned}$$

It can be easily seen that the tridiagonal matrix \(M\in \mathbb {R}^{(k-1)\times (k-1)}\) is positive definite. Indeed, for any nonzero vector \(v\in \mathbb {R}^{k-1}\), we have

$$\begin{aligned} v^TMv = \sum _{j=1}^{k-1} w_j^{\prime } v_j^2 + \sum _{j=1}^{k-2} \mu _j^{\prime } (v_j - v_{j+1})^2 + \mu _{k-1}^{\prime } v_{k-1}^2 > 0, \end{aligned}$$

because \(w^{\prime } \in \mathbb {R}^{m}_{++}\) and \(\mu ^{\prime } \in \mathbb {R}^{m-1}_{+}\). Thus, M is a real symmetric positive definite matrix with non-positive off-diagonal entries. Then it is a Stieltjes matrix whose property is that all entries of its inverse are nonnegative [21], which implies that \(M^{-1}e_{k-1} \ge 0\). Hence, each component of the solution \(\bar{y}(y_k)\) to the linear system (18) is a non-decreasing function of \(y_k\).

Note that, if there exists an index \(k'<k\) such that \(\mu _{k'}^{\prime } = 0\), then

\(y_1(y_k), \ldots , y_{k'} (y_k)\) do not change with \(y_k\). Consequently, \(y_{j+1}(y_k) - y_j(y_k)\) are non-decreasing functions of \(y_k\) for all \(j<k'\). The same refers to the function \(y_{k'+1}(y_k) - y_{k'}(y_k)\) because, as it was shown above, \(y_{k'+1}(y_k)\) does not decrease with \(y_k\). If \(\mu _{k-1}^{\prime } > 0\), that is \(k' \ne k-1\), then we need to show that the same refers also to all \(j \in [k'+1, k-1]\), where

$$\begin{aligned} k' = \min _{0\le i < k-1} \{i: \ \mu _{j}^{\prime } > 0, \quad \forall j \in [i+1, k-1]\}. \end{aligned}$$

Here either \(k'=0\), or \(\mu _{k^{\prime }}^{\prime }=0\). In order not to separately consider \(k'=0\) as a special case, we introduce artificial \(\mu _{0}^{\prime }=0\) and constant-valued function \(y_0(y_k)\). This does not change the relations established by (7). The equations of this linear system that correspond to \(j\in [k'+1, k-1]\) can be represented in the form of the following recursive relation

$$\begin{aligned} \mu _j^{\prime } (y_{j+1}(y_k) - y_j(y_k)) = w_j^{\prime }(y_j(y_k) - a_j^{\prime }) + \mu _{j-1}^{\prime } (y_j(y_k) - y_{j-1}(y_k)), \end{aligned}$$

where \(\mu _j^{\prime }>0\). Then, since \(y_{k'+1}(y_k) - y_{k'}(y_k)\) is a non-decreasing function of \(y_k\), it can be easily shown by induction in \(j=k'+1, \ldots , k-1\) that \(y_{j+1}(y_k) - y_j(y_k)\) does not decrease with \(y_k\).

The dependence on \(y_{k+1}\) established by the last \(m-k-1\) equations in (7) is studied in an analogous way. Like above, we represent them as

$$\begin{aligned} M \bar{y}(y_{k+1}) = y_{k+1} \mu _{k}^{\prime } e_{1}, \end{aligned}$$

where \(\bar{y}(y_{k+1}) = (y_1(y_{k+2}), \ldots , y_{m} (y_{k+1}))^T\), \(e_{1} = (1,0,\ldots ,0)^T\), and although here M is not the same as in (18), it is also a Stieltjes matrix of a similar structure. This allows us to prove that each component of \(\bar{y}(y_{k+1})\) is a non-decreasing function of \(y_{k+1}\). Then, to prove that the functions \(y_{j-1}(y_{k+1}) - y_j(y_{k+1})\) decrease with \(y_{k+1}\), we use a reverse induction in decreasing order of j based on the backward recursion:

$$\begin{aligned} \mu _{j-1}^{\prime } (y_{j-1}(y_{k+1}) - y_j(y_{k+1})) = w_j^{\prime }(y_j(y_{k+1}) - a_j^{\prime }) + \mu _j^{\prime } (y_j(y_{k+1}) - y_{j+1}(y_{k+1})). \end{aligned}$$

This concludes the proof. \(\square \)

Let \(y^*\) be the optimal solution to problem (6). Suppose that the monotonicity is violated for some of its components. Let \(k \in [1,m-1]\) be such that the inequality

$$\begin{aligned} y_k^* > y_{k+1}^* \end{aligned}$$
(19)

holds. Consider a strictly convex quadratic optimization problem, which have only one constraint \(y_k \le y_{k+1}\) and the same objective function as in (6). Let \(y^{**}\) stand for the optimal solution to this constrained problem. Clearly, \(y^{**}_k = y_{k+1}^{**}\).

After skipping the constant c in (6), the constrained problem can be written as

$$\begin{aligned} \min _{y_k \le y_{k+1}} w_k^{\prime }(y_k - a_k^{\prime })^2 + w_{k+1}^{\prime }(y_{k+1} - a_{k+1}^{\prime })^2 + \mu _k^{\prime } (y_k - y_{k+1})^2 + \varphi _1(y_k) + \varphi _2(y_{k+1}), \end{aligned}$$
(20)

where

$$\begin{aligned} \varphi _1(y_k) = \sum _{j=1}^{k-1} \left[ w_j^{\prime }(y_j(y_k) - a_j^{\prime })^2 + \mu _j^{\prime } (y_j(y_k) - y_{j+1}(y_k))^2 \right] \end{aligned}$$

and

$$\begin{aligned} \varphi _2(y_{k+1}) = \sum _{j=k+2}^{m} \left[ w_j^{\prime }(y_j(y_{k+1}) - a_j^{\prime })^2 + \mu _{j-1}^{\prime } (y_j(y_{k+1}) - y_{j-1}(y_{k+1}))^2 \right] \end{aligned}$$

are optimal objective function values in problems (15) and (16), respectively. The next result presents a relation between \(y^*\) and \(y^{**}\).

Lemma 4.3

Let inequality (19) hold. Then

$$\begin{aligned} y_k^*> y^{**}_k = y_{k+1}^{**} > y_{k+1}^*. \end{aligned}$$
(21)

Proof

The equality \(y^{**}_k = y_{k+1}^{**}\) is a straightforward implication from the strict convexity of the objective function in problem (20).

By Lemma 4.2, the functions (17) are linear, which means that \(\varphi _1(y_k)\) and \(\varphi _2(y_{k+1})\) are convex quadratic functions. Then problem (20) can be reduced to the two-dimensional problem

$$\begin{aligned} \min _{y_k \le y_{k+1}} w_k^{\prime \prime }(y_k - a_k^{\prime \prime })^2 + w_{k+1}^{\prime \prime }(y_{k+1} - a_{k+1}^{\prime \prime })^2 + \mu _k^{\prime } (y_k - y_{k+1})^2, \end{aligned}$$
(22)

where we skip the terms that do not depend on \(y_k\) or \(y_{k+1}\). Here, as it can be easily verified, the multipliers \(w_k^{\prime \prime }\) and \(w_{k+1}^{\prime \prime }\) are strictly positive. From the optimality conditions for this problem, we obtain

$$\begin{aligned} \begin{array}{l} w_k^{\prime \prime }(y_k - a_k^{\prime \prime }) + \mu _k^{\prime } (y_k - y_{k+1}) + \lambda /2 = 0, \\ w_{k+1}^{\prime \prime }(y_{k+1} - a_{k+1}^{\prime \prime }) - \mu _k^{\prime } (y_k - y_{k+1}) - \lambda /2 = 0, \end{array} \end{aligned}$$
(23)

where \(\lambda \ge 0\) is a Lagrange multiplier. Taking into account that \(y^{**}_k = y_{k+1}^{**}\), we denote this value by \(\bar{y}\). Note that \(y_k^*\) and \(y_{k+1}^*\) solve the unconstrained version of problem (22), and they correspond in (23) to the case of \(\lambda = 0\). Then simple manipulations with (23) yield the relation

$$\begin{aligned} \alpha y_k^* + (1 - \alpha )y_{k+1}^* = \bar{y}, \end{aligned}$$

where

$$\begin{aligned} \alpha = w_k^{\prime \prime } / (w_k^{\prime \prime } + w_{k+1}^{\prime \prime }). \end{aligned}$$

Since \(\alpha \in ]0,1[\), this implies (21) and completes our proof. \(\square \)

In the next result, we study some important properties of merging two adjacent blocks, say blocks k and \(k+1\). If S is a current active set, then the merging assumes making active the constraint \(x_{r_{k}} \le x_{r_{k}+1}\) in addition to the active constraints determined by S.

Lemma 4.4

Let S be an active set such that there exists a block index \(k\le m-1\) for which \(y_k(S) \ge y_{k+1}(S)\). Then

$$\begin{aligned} \lambda (S') \ge \lambda (S), \end{aligned}$$
(24)

where \(S' = S \cup \{r_{k}\}\). Moreover,

$$\begin{aligned} x_i(S) \ge x_{i+1}(S) \ \Rightarrow \ x_i(S') \ge x_{i+1}(S'). \end{aligned}$$
(25)

Proof

The statement of this lemma trivially holds when \(y_k(S) = y_{k+1}(S)\) because the corresponding merging does not change any block common value.

Consider the case when \(y_k(S) > y_{k+1}(S)\). The vector of new block common values \(y(S')\) is obtained from problem (20). Then Lemma 4.3 yields

$$\begin{aligned} y_k(S)> y_k(S') > y_{k+1}(S). \end{aligned}$$

These inequalities together with Lemma 4.2 imply

$$\begin{aligned}&x_i(S') \le x_i(S), \quad \forall i\in [1,r_k], \end{aligned}$$
(26)
$$\begin{aligned}&x_i(S') \ge x_i(S), \quad \forall i\in [r_k+1, n], \end{aligned}$$
(27)
$$\begin{aligned}&x_{j+1}(S') - x_i(S') \le x_{j+1}(S) - x_i(S), \quad \forall i\in [1,n-1], i\ne r_k. \end{aligned}$$
(28)

Statement (25) follows directly from (28). By Lemma 4.1, we conclude from (26)–(28) that

$$\begin{aligned} \lambda _i (S') \ge \lambda _i (S), \quad \forall i\in [1,n-1], i\ne r_k. \end{aligned}$$

Recalling that \(x_{r_k}(S) \ge x_{r_k+1}(S)\), and that \(x(S')\) solves the problem obtained from (5) by adding the constraint \(x_{r_k} = x_{r_k+1}\), we get \(\lambda _{r_k}(S') \ge 0\). Then the inequality

$$\begin{aligned} \lambda _{r_k}(S') \ge \lambda _{r_k}(S) \end{aligned}$$

holds because \(\lambda _{r_k}(S) = 0\), so the proof is complete.

The statement (25) says, in particular, that a monotonicity constraint, if violated, remains violated after making active another violated monotonicity constraint. This property will allow us to justify the potentially massive enlargement of the active set at each iteration of the SPAV algorithm, when more than one violated constraint may be simultaneously turned into active.

We are now in a position to prove a finite-step convergence of the algorithm.

Theorem 4.1

For any initial \(S \subseteq S^*\), the SPAV algorithm converges to the optimal solution of the SMR problem in, at most, \(n - 1 - |S|\) iterations. Moreover, after the final iteration, \(S=S^*\).

Proof

At each iteration of the algorithm, the active set S is extended by adding at least one index of the set \([1,n-1]\), which is not contained in S. The SPAV terminates when y(S) becomes monotone. This happens when either

\(|S| < n-1\) or \(S=[1,n-1]\). In the latter case, \(m=1\) and, therefore, there is no violation of the monotonicity. Hence, the number of iterations is less than \(n - |S|\), where |S| is the number of constraints in the initial active set.

We need now to prove that the algorithm returns the optimal solution to problem (3). To this end, we will, first, show that

$$\begin{aligned} \lambda (S) \ge 0 \ \Rightarrow \ \lambda (S \cup \varDelta S) \ge 0, \end{aligned}$$
(29)

where

$$\begin{aligned} \varDelta S = \{r_i: \ y_i(S) \ge y_{i+1}(S)\}. \end{aligned}$$

Clearly, the result of merging the set of blocks determined by \(\varDelta S\) is equivalent to the result of successively merging the same blocks one by one. By Lemma 4.4, as the result of making active any next monotonicity constraint \(r_k \in \varDelta S\), the Lagrange multipliers do not decrease and the statement (25) remains true for any \(i\in \varDelta S\). Consequently, we obtain the inequality

$$\begin{aligned} \lambda (S \cup \varDelta S) \ge \lambda (S), \end{aligned}$$
(30)

which proves (29).

Consider, first, the case when the initial active set is empty, which means that initially \(\lambda (S)=0\). Consequently, from inequality (30), we get \(\lambda (S) \ge 0\) for the terminal active set S. Moreover, the x(S) returned by the algorithm is feasible in the SMR problem. Since the block common values y(S) satisfy equation (7), the corresponding x(S) and \(\lambda (S)\) satisfy equation (9). Thus, all the KKT conditions (9)–(12) for problem (3) hold, which means for the initial \(S = \emptyset \) that the x(S) returned by the SPAV algorithm solves the SMR problem. Consequently, after the final iteration, we have \(S=S^*\).

Consider now a more general case of the initial active set such that \(S \subseteq S^*\). Note that problem (3) is equivalent to

This problem can be rewritten in terms of \(m=n-|S|\) initial block common values as

$$\begin{aligned} \min _{y \in \mathbb {R}^m} \sum _{i=1}^{m} w_i^{\prime }(y_i - a_i^{\prime })^2 + \sum _{i=1}^{m-1} \mu ^{\prime } _i (y_i - y_{i+1})^2, \quad \text {s.t.} \quad y_i\le y_{i+1}, \ \forall i\in [1,m-1], \end{aligned}$$
(31)

where the vectors \(a^{\prime }\), \(w^{\prime }\) and \(\mu ^{\prime }\) are defined by the initial S. It is clearly an SMR problem. As it was shown above, if the SPAV algorithm starts with empty set of active constraints, it solves this problem, and consequently problem (3). It can be easily seen that the initial vector y, produced in this case by the SPAV, is the same as the y(S) produced by the SPAV for the initial \(S \subseteq S^*\). Hence, the subsequent values of y generated by the SPAV algorithm for problems (31) and (3) are identical. This finally proves that the SPAV algorithm returns the optimal solution to problem (3) for any initial \(S \subseteq S^*\). \(\square \)

It follows from the proof of Theorem 4.1 that if \(\lambda (S) \ge 0\), then \(S \subseteq S^*\). The converse of this statement is not true in general. This is shown by the following counterexample.

Example 4.1

Consider the three-dimensional problem, in which

$$\begin{aligned} a = (0, 30, -45)^T, \quad w = (0.5, 0.5, 0.5)^T,\quad \hbox {and}\quad \mu = (0.5, 0.5)^T. \end{aligned}$$

For the optimal solution, we have

$$\begin{aligned} S^* = \{1, 2\}, \quad x(S^*) = (-5, -5, -5)^T, \quad \hbox {and} \quad \lambda (S^*) = (5, 40)^T. \end{aligned}$$

In the case of \(S = \{1\}\), the system of linear equations (7) gives \(y_1 = 3\) and \(y_2 = -21\). Substituting \(x(S) = (3, 3, -21)^T\) and \(\lambda _2(S) = 0\) into (9), we finally obtain \(\lambda _1(S) = -3\). Thus, in this example, one of the components of \(\lambda (S)\) is negative, whereas \(S \subset S^*\). \(\square \)

As it was shown above, the SPAV algorithm generates at each iteration an active set S such that x(S) and \(\lambda (S)\) satisfy conditions (9), (11), and (12) of all the KKT conditions, but not (10). Since it aims at attaining primal feasibility while maintaining dual feasibility and complementary slackness, the SPAV can be viewed as a dual active-set algorithm, even though the Lagrange multipliers are not calculated. According to (30), the sequence of the generated active sets is such that the corresponding sequence \(\lambda (S)\) is non-decreasing. Note that the same property is inherit in the primal-dual active-set (PDAS) algorithms developed in [19] and also in the version of the PDAS tailored in [18] for solving the MR problem.

5 Numerical Experiments

In our experiments, the data sets were generated by formula (1). The following two response functions were used:

$$\begin{aligned} \chi _1(t) = t, \quad \text {and} \quad \chi _3(t) = t^3. \end{aligned}$$
(32)

Our choice of functions was motivated by the intention to study the case of a linear function, \(\chi _1(t)\), and the case of a nonlinear function, \(\chi _3(t)\), which combines slow and rapid changes. For these two cases, the observed values of explanatory variables \(t_i\) were uniformly distributed on the intervals [0, 1] and \([-2,2]\), respectively. In the both cases, the observation error \(\epsilon _i\) was normally distributed with zero mean and standard deviation 0.3. The penalty parameters \(\mu _i\) in the SMR problem were calculated by formula (4), where the value of \(\mu \) was produced, for each data instance, by the cross-validation-based technique specially designed in [17] for the SMR problem. All components of the vector of weights w were ones.

The algorithms discussed in this section were implemented in R, version 3.2.3. For solving the tridiagonal system of linear equations (7), function Solve.tridiag of package limSolve was used. Function solve.QP of package quadprog was used as an alternative solver for the SMR problems to compare it with our SPAV algorithm. The numerical experiments were performed on a Windows PC with 16 GB RAM and Intel Xeon processor (3.30 GHz).

Figure 1 illustrates the ability of the SMR problem to smooth the solution to the MR problem. The values \(\mu = 0.022\) and \(\mu = 0.024\) were produced by the cross validation [17] for the two data sets, each of the size \(n=100\), that were generated for \(\chi _1(t)\) and \(\chi _3(t)\), respectively. The interpolation of the fitted values was performed by making use of a prediction model proposed in [17]. In what follows, we report results only for the linear response function, because the results for \(\chi _3(t)\) were very similar. The value \(\mu = 0.02\) was used.

Fig. 1
figure 1

MR (dotted red) and SMR (dashed blue) solutions for the data sets of the size \(n=100\) generated for \(\chi _1(t)\) (solid black, left) and \(\chi _3(t)\) (solid black, right)

Full size image

The SMR serves not only for smoothing, but it also breaks blocks of the MR solution. Figure 2 shows how the number of blocks (averaged over all instances generated for each n) grows with \(\mu \) starting from \(\mu = 0\). Recall that the MR problem is a special case of the SMR problem, which corresponds to the zero value of \(\mu \). We observed also that the block breaks caused by increasing \(\mu \) are accompanied by an evident tendency of the number of SPAV iterations to decrease (as in Fig. 2). This indicates a relationship between these two phenomena, although it cannot be viewed as a direct relationship. Indeed, we observed that those values of \(\mu \), for which the number of blocks or the number of iterations was sporadically breaking the aforementioned monotonic tendencies, did not always coincide.

Fig. 2
figure 2

Left number of blocks as a portion of n versus \(\mu \) for \(n=100\) (solid red) and \(n=1000\) (dashed blue). Right the number of SPAV iterations versus \(\mu \) for one typical instance of those generated for \(n=1000\)

Full size image

We compared the running time of the SPAV algorithm and function solve.QP by studying the growth of each individual time with n. To minimize the impact of error in estimating the CPU time, 100 data instances were generated for each n as described above, and then the mean CPU time was calculated for each solver. The sequence of n was \(100, 200, \ldots , 2000\) followed by \(3000, 4000, \ldots , 20{,}000\). The solve.QP failed to solve a fairly large number of the generated problems for numerical reasons related to the too small values of the denominator in (4). For instance, for \(n= 100, 500 \), and 7000, it solved 95, 52, and 18 of 100 problems, respectively. It failed in all runs for \(n \ge 8000\). The average CPU time (in seconds) of solving the generated SMR problems is plotted in Fig. 3, where the average time of the solve.QP is calculated excluding the failures. It shows that the too rapid increase in the running time of the conventional quadratic optimization algorithm does not allow it to solve large-scale SMR problems, whereas the SPAV scales pretty well with the increasing data size.

Fig. 3
figure 3

CPU time of the SPAV algorithm (dashed blue) and solve.QP (solid red) versus n

Full size image

Figure 4 represents for the SPAV the same relation as in Fig. 3, but in the logarithmic scale and for \(n= 100\cdot 2^i\), where \(i=0,1,2,\ldots ,14\). The linear least square estimate of the slope of this graph suggests that the running time of the SPAV grows in our experiments in proportion to \(n^{1.06}\), which is much slower compared to the growth in proportion to \(n^2\) that follows from the worst-case analysis. For the response function \(\chi _3(t)\), the fitted slope was 0.995, which is indicative, to within the experimental error, of an almost linear growth.

Fig. 4
figure 4

CPU time of the SPAV algorithm versus n in the natural logarithmic scale

Full size image

In the worst case, the number of SPAV iterations equals n, while the observed number of iterations was far less than n. Moreover, the size of the linear tridiagonal system (7) to be solved at each iteration decreases in the process of solving SMR problem. It is essential that the most significant drop of its size usually occurs after the first iteration. All this explains why the SPAV algorithm is so fast in practice. To study how the number of iterations changes with n, we generated 10 data instances for each n and then calculated the mean number of iterations. Figure 5 shows that just a few iterations were typically required for the SPAV algorithm to solve the generated SMR problems. Observe that this number remains very small even for very large values of n. The maximal number of iterations over all 500 data instances was five, in which case n was 25,000. One can also see in Fig. 5 that the ratio of the actual number of SPAV iterations to the worst-case number tends to zero as n increases.

Fig. 5
figure 5

Number of SPAV iterations (left) and the same divided by n (right) versus n

Full size image

The same set of numerical experiments, as discussed above, was conducted for a distribution of errors \(\epsilon _i\) other than normal, and also for deterministic test of problems.

The alternative to normal was the double exponential distribution of errors with mean 0 and scale parameter 0.1. Because it has long tails, the observed response may have several outliers. This was the main reason for choosing this alternative.

Our deterministic test problems were related to those kinds of cases often occurring in practice, in which not all of the important predictors are taken into account in studying monotonicity. For simulations, we used the deterministic response function

$$\begin{aligned} f(t,\xi ) = \chi (t) + c\sin (\xi ), \end{aligned}$$
(33)

where the linear and cubic functions (32) were chosen for \(\chi (t)\), and the calibrating parameter c was equal to 0.1 and 1.0, respectively. For any fixed value of the disregarded predictor \(\xi \), the function \(f(t,\xi )\) increases monotonically with t. Monotonicity may be violated when \(\xi \) is not fixed. For generating the response values \(a_i = f(t_i,\xi _i)\), \(i=1,\ldots ,n\), we used the following oblique grid nodes:

$$\begin{aligned} \begin{array}{l} t_i = t_{\min } + (i-1)\frac{t_{\max }-t_{\min }}{n-1} , \\ \xi _i = i \mod (n/10), \end{array} \end{aligned}$$

where the interval \([t_{\min },t_{\max }]\) is specified for \(\chi _1\) and \(\chi _3\) at the beginning of this section. Figure 6 refers to the case of our deterministic function, in which \(\chi (t) = \chi _3(t)\). It provides additional evidence of the ability of the SMR problem to smooth the solution to the MR problem.

Fig. 6
figure 6

Response values (black dots), MR (dotted red), and SMR (dashed blue) solutions for the data set of the size \(n=200\) generated for the deterministic function (33), where \(\chi (t)= \chi _3(t)\) (solid black)

Full size image

The main features of the smoothing property of the SMR problem and the behavior of the SPAV algorithm that were demonstrated for the double exponential distribution and the deterministic function were the same as for the normal distribution. In particular, the running time of the SPAV algorithm grew almost linearly. For example, in the case of \(\chi (t)=\chi _1(t)\), the estimated slopes of the graphs like in Fig. 4 were 0.9678 and 0.9764 for the double exponential distribution and the deterministic function, respectively.

6 Conclusions

The SMR problem was designed for smoothing the solution to the MR problem, and it was statistically motivated in [17]. Here and in [17], we developed a fast dual active-set algorithm for solving the SMR. In the present paper, its finite-step convergence to the optimal solution has been proved. Our computational experiments have verified several important advantages of the SPAV algorithm, in particular its scalability, which allows for regarding it as a practical algorithm for solving large-scale SMR problems. The efficiency of our algorithm originates from its ability to enlarge the active set by adding a large portion of constraints at once. Another advantage is that it admits a warm-starting.

Here and in [17], we focused on the SMR problem associated with a complete (linear) order of observations. Problem (3) admits a natural extension to the case of partial order. Indeed, let a partial order of n observations be defined by a set of pairs \(E \subset [1,n] \times [1,n]\). Then the corresponding SMR problem can be formulated as follows:

$$\begin{aligned} \min _{x \in \mathbb {R}^n} \sum _{i=1}^{n} w_i(x_i - a_i)^2 + \sum _{(i,j) \in E} \mu _{ij} (x_i - x_{j})^2, \quad \text {s.t.} \quad x_i\le x_{j}, \ \forall (i,j) \in E. \end{aligned}$$
(34)

From the computational point of view, this quadratic optimization problem is much more complicated than (3). In evidence of this, it is suffice to compare their simplified versions corresponding to \(\mu = 0\). As it was mentioned earlier, the MR problem (2) can be solved in O(n) arithmetic operations. However, the non-regularized version of (34) is much more computationally demanding, because the best known complexity of algorithms able to solve (34) for \(\mu = 0\) is \(O(n^2|E| + n^3 \log n)\) [3, 22,23,24]. Even its approximate solution requires \(O(n^2)\) operations [25,26,27,28]. Therefore, the development of efficient exact and approximate algorithms for solving problem (34) should be viewed as a challenging task for the future research.

We plan to begin our follow-up research from considering problem (34) for partial orders of two special types, namely star- and tree-structured. The two partial orders are of our interest because, as it was shown in [29], problem (34) can be solved for \(\mu = 0\) in O(n) and \(O(n \log n)\) arithmetic operations, respectively.