Dynamics of Finite Inhomogeneous Particle Systems with Exclusion Interaction

Abstract

We study finite particle systems on the one-dimensional integer lattice, where each particle performs a continuous-time nearest-neighbour random walk, with jump rates intrinsic to each particle, subject to an exclusion interaction which suppresses jumps that would lead to more than one particle occupying any site. We show that the particle jump rates determine explicitly a unique partition of the system into maximal stable sub-systems, and that this partition can be obtained by a linear-time algorithm using only elementary arithmetic. The internal configuration of each stable sub-system possesses an explicit product-geometric limiting distribution, and the location of each stable sub-system obeys a strong law of large numbers with an explicit speed; the characteristic parameters of each stable sub-system are simple functions of the rate parameters for the corresponding particles. For the case where the entire system is stable, we provide a central limit theorem describing the fluctuations around the law of large numbers. Our approach draws on ramifications, in the exclusion context, of classical work of Goodman and Massey on partially-stable Jackson queueing networks.

1 Introduction

The exclusion process is a prototypical model of non-equilibrium statistical mechanics, representing the dynamics of a lattice gas with hard-core interaction between particles, originating in the mathematical literature with [48] and in the applied literature with [37]. In the present paper, we consider systems of $N+1$ particles on the one-dimensional integer lattice ${{\mathbb {Z}}}$, performing continuous-time, nearest-neighbour random walks with exclusion interaction, in which each particle possesses arbitrary finite positive jumps rates. The configuration space of the system is ${{\mathbb {X}}}_{N+1}$, where, for $n \in {{\mathbb {N}}}:= \{1,2,3,\ldots \}$,

$$\begin{aligned} {{\mathbb {X}}}_n:= \{ (x_1, \ldots , x_{n} ) \in {{\mathbb {Z}}}^{n}: x_1< x_2< \cdots < x_{n} \}. \end{aligned}$$

(1.1)

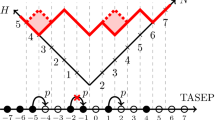
The exclusion constraint means that there can be at most one particle at any site of ${{\mathbb {Z}}}$ at any given time. The dynamics of the interacting particle system are described by a time-homogeneous, continuous-time Markov chain on ${{\mathbb {X}}}_{N+1}$, specified by non-negative rate parameters $a_1,b_1, \ldots , a_{N+1},b_{N+1}$. The ith particle (enumerated left to right) attempts to make a nearest-neighbour jump to the left at rate $a_i$. If, when the corresponding exponential clock rings, the site to the left is unoccupied, the jump is executed and the particle moves, but if the destination is occupied by another particle, the attempted jump is suppressed and the particle does not move (this is the exclusion rule). Similarly, the ith particle attempts to jump to the right at rate $b_i$, subject to the exclusion rule. The exclusion rule ensures that the left-to-right order of the particles is always preserved. See Fig. 1 for a schematic.

Fig. 1

Schematic of the model in the case of $N+1 = 6$ particles, illustrating some of the main notation. Filled circles represent particles, empty circles represent unoccupied lattice sites, and directed arcs represent admissible transitions, with exponential rates indicated

Let $X (t) = (X_1 (t), \ldots , X_{N+1} (t) ) \in {{\mathbb {X}}}_{N+1}$ be the configuration of the Markov chain at time $t \in {{\mathbb {R}}}_+:= [0,\infty )$, started from a fixed initial configuration $X(0) \in {{\mathbb {X}}}_{N+1}$. Denote the number of empty sites (holes) between particles i and $i+1$ at time $t \in {{\mathbb {R}}}_+$ by

$$\begin{aligned} \eta _i (t):= X_{i+1}(t)-X_i(t)-1, \text { for } i \in [N]:= \{1,2,\ldots , N\}, \end{aligned}$$

(1.2)

so $\eta _i (t) \in {{\mathbb {Z}}}_+:= \{ 0,1,2,\ldots \}$. An equivalent description of the system is captured by the continuous-time Markov chain $\xi := ( \xi (t) )_{t \in {{\mathbb {R}}}_+}$, where

$$\begin{aligned} \xi (t):= (X_1 (t), \eta _1(t), \ldots , \eta _N (t) ) \in {{\mathbb {Z}}}\times {{\mathbb {Z}}}_+^N. \end{aligned}$$

(1.3)

An important fact is that $\eta := (\eta (t))_{t \in {{\mathbb {R}}}_+}$, where $\eta (t):= (\eta _1(t), \ldots , \eta _N (t) ) \in {{\mathbb {Z}}}_+^N$, is also a continuous-time Markov chain, which can be represented via a Jackson network of N queues of M/M/1 type (we explain this is Sect. 3). This is the reason that we take $N+1$ particles. The process $\eta$ can also be interpreted as a generalization, with site-dependent rates and emigration and immigration at the boundaries, of the zero-range process on the finite set [N], with $\eta (t)$ being the vector of particle occupancies at time t.

The main contribution of the present paper is to characterize the long-term dynamics of the particle system. In particular, we give a complete and explicit classification with regards to stability (which subsets of particles are typically relatively mutually close) and law of large numbers behaviour (particle speeds), as well as some results on fluctuations in the case where the whole system is stable. Our main results are stated formally in Sect. 2 below; their content is summarized as follows.

Theorem 2.1 shows that there is a unique partition of the system, determined by the parameters $a_i, b_i$, into maximal stable sub-systems, which we call stable clouds. Theorem 2.1 shows that the internal configuration of each stable cloud possesses an explicit product-geometric limiting distribution (this is a precise sense in which the cloud is ‘stable’), while distances between particles in different clouds diverge in probability. Theorem 2.1 also shows that the location of each stable cloud obeys a strong law of large numbers with an explicit speed; speeds of clouds are non-decreasing left to right. The cloud partition is characterized by a finite non-linear system, which is the translation to our setting of the classical Goodman and Massey [23] equations for Jackson networks. Moreover, in Theorem 2.3 we show that the cloud partition can be obtained by a linear-time algorithm of elementary steps, streamlining the Jackson algorithm from [23] by exploiting the additional structure of our model. For the case where the entire system is stable, i.e., there is a single cloud, Theorem 2.12 gives a central limit theorem describing the fluctuations around the law of large numbers; this time, the foundational result for Jackson networks is a general central limit theorem of Anantharam and Konstantopoulos [4]. Section 2 presents these results, and several corollaries and examples, after introducing the necessary notation. First we indicate some relevant previous work.

Many aspects of interacting particle systems and their links to (finite and infinite) queueing networks are well understood, with much attention on systems of infinitely many particles. The exclusion and zero-range processes were introduced in a fundamental paper of Spitzer [48]. The earliest explicit mention of the link between the exclusion process and Jackson’s results for queueing networks that we have seen is by Kipnis [34, p. 399], in the case of homogeneous rates, where the connection to the zero-range process is also given; see also [2, 9, 20]. Versions of these connections have facilitated much subsequent progress. For example, connections between variations on the totally asymmetric exclusion processes (TASEP), in which particles can only move to the right, and tandem queueing networks, in which customers are routed through a sequence of queues in series, are explored in [19, 35, 46]. Other relevant work includes [5, 33, 49]. Aspects of exclusion systems on ${{\mathbb {Z}}}$ with finitely many particles have been studied in the symmetric case [3], and in totally asymmetric systems with different jump rates [42]; exclusion interaction on finite lattice segments has also been studied (see e.g. [14]).

The authors are not aware of previous work on the decomposition into stable sub-systems of finite exclusion systems on ${{\mathbb {Z}}}$, with general nearest-neighbour transition rates. While the connection between the exclusion process and Jackson networks is well known, we have not seen the important work of Goodman and Massey [23] interpreted in the exclusion context before. In the queueing context, the results of [23] characterize systems in which some but not all queues are stable; this phenomenon has subsequently become known in the queueing literature as ‘partial stability’ [1, 7, 10]. Our main result can thus be seen as a classification of partial stability for finite exclusion systems.

Yet another interpretation of $\eta$ is as a random walk on the orthant ${{\mathbb {Z}}}_+^N$ with boundary reflections. For $N \in \{1,2\}$, there are exhaustive criteria for classifying stability of such walks (see e.g. [15, 16]) in terms of readily accessible quantities (first and second moments of increments). For $N \in \{ 3, 4\}$ the generic classification is available, but requires precise knowledge of quantities which are hard to compute, namely stationary distributions for lower-dimensional projections [16, 26]. For $N \ge 5$, additional complexity arising from the structure of high-dimensional dynamical systems means that the generic case is intractable [21]. In the present paper, we demonstrate that the dynamics of the particle system admits a complete, and explicit, stability description for any N, demonstrating the special place of these models in the general theory.

In a continuum setting, there is an interesting comparison between our results and an extensive existing literature on diffusions with rank-based interactions, including the Atlas model of financial mathematics and its relatives [8, 12, 24, 25, 30, 40, 44, 45, 50]. As we explain in Sect. 6, where we describe the continuum setting in more detail, the classification of the asymptotic behaviour of these continuum models has so far been limited to deciding whether the entire system is stable (i.e., a single stable cloud). We believe that the ideas in the present paper indicate a route to obtaining more detailed information (such as the full cloud decomposition) in these continuum models. We aim to address some of these questions in future work. A direct comparison between our model and the continuum model is not obvious, as there is a sense in which the collision mechanism in the continuum model is elastic, whereas the exclusion mechanism is inelastic, but we describe in Sect. 6 an elastic modification of the particle system that bears a closer analogy with the continuum model. In addition, aspects of the comparison go beyond analogy, as it is known that in certain parameter and scaling regimes, the continuum model serves as a scaling limit for certain discrete models; see [30, Sect. 3], and our Sect. 6 below. Many of these models admit versions with infinitely-many particles (e.g. [44, 45]), which in certain cases reside in the famous KPZ universality class [51].

2 Main Results

To state our main results, we define some quantities associated with our system, depending on (subsets of) the parameters $a_i, b_i$. For our main results, we will assume that at least all the $b_i$ are positive.

• (A) Suppose that $0 \le a_i < \infty$ and $0< b_i < \infty$ for all $i \in [N+1]$.

Note that, by reversing the ordering of the particles (i.e., mapping ${{\mathbb {Z}}}$ to $-{{\mathbb {Z}}}$), we can swap the roles of the $a_i$ and $b_i$ in (A) and in the formulas that follow. For $\ell \in {{\mathbb {Z}}}$, $m \in {{\mathbb {N}}}$, call the set

$$\begin{aligned} {[} \ell ; m ]:= \{ \ell , \ell +1, \ldots , \ell +m-1 \} \end{aligned}$$

of m consecutive integers a discrete interval; implicit is that a discrete interval is non-empty. In the case $\ell = 1$, we set $[n]:= [ 1; n]:= \{1,2,\ldots , n \}$ for $n \in {{\mathbb {N}}}$. Given a discrete interval $I = [ \ell ; m] \subseteq [N+1]$, which represents the particles whose labels are in I, define

$$\begin{aligned} \begin{aligned} \alpha (I)&:= \alpha ( \ell ; m ):= \prod _{u=\ell }^{\ell +m-1} \frac{a_{u}}{b_{u}}, \text { and } \\ \beta (I)&:= \beta (\ell ; m):= \frac{1}{b_{\ell +m-1}} \sum _{v=0}^{m-1} \prod _{u=1}^{v} \frac{a_{\ell +m-u}}{b_{\ell +m-u-1}}; \end{aligned} \end{aligned}$$

(2.1)

here and throughout the paper, the convention is that an empty sum is 0 and an empty product is 1. Then define

$$\begin{aligned} {{\hat{v}}}( I ):= {{\hat{v}}}( \ell ; m ):= \frac{1 - \alpha (I)}{\beta (I)}. \end{aligned}$$

(2.2)

The quantities $\alpha$, $\beta$ defined in (2.1) arise as solutions of certain balance equations associated with a dual random walk derived from the dynamics of a tagged empty site of ${{\mathbb {Z}}}$ (a hole). To describe this walk it is more convenient to work in the queueing setting, where the hole corresponds to a customer in the queueing network, and we can impose a priority service policy to make sure the tagged customer is always served; the resulting routing matrix P given by (2.10) below is then the source of the formulas for $\alpha$, $\beta$. The interpretation of ${{\hat{v}}}(I)$ will be as a speed for a putative stable sub-collection of particles. For example, ${{\hat{v}}}(\ell ; 1) = b_\ell - a_\ell$ is the intrinsic speed of a singleton particle in free space; whether its long-term dynamics matches this speed depends on its interaction with the rest of the system. For general $m \in {{\mathbb {N}}}$, definition (2.2) gives the formula

$$\begin{aligned} {{\hat{v}}}(\ell ; m) = \frac{\displaystyle 1 - \frac{a_\ell \cdots a_{\ell +m-1}}{b_\ell \cdots b_{\ell +m-1}}}{\displaystyle \frac{1}{b_{\ell +m-1}} + \frac{a_{\ell +m-1}}{b_{\ell +m-1} b_{\ell +m-2}} + \cdots + \frac{ a_{\ell +m-1} \cdots a_{\ell +1}}{b_{\ell +m-1} \cdots b_\ell }} . \end{aligned}$$

(2.3)

For a discrete interval $I = [ \ell ; m] \subseteq [N+1]$ with $m \ge 2$, define for $j \in [\ell ; m-1]$,

$$\begin{aligned} {{\hat{\rho }}}_I (j):= \alpha ( \ell ; j+1 - \ell ) + \beta ( \ell ; j+1 - \ell ) {{\hat{v}}}( \ell ; m), \end{aligned}$$

(2.4)

where $\alpha , \beta$ are given by (2.1), and ${{\hat{v}}}$ is given by (2.2). The interpretation of ${{\hat{\rho }}}_I (j)$ is as a stability parameter; it corresponds in the language of queueing theory to a workload for the queue associated with gap j in the system I. See Sect. 3 for elaboration of the queueing interpretation.

An ordered n-tuple $\Theta = (\theta _1, \ldots , \theta _n)$ of discrete intervals $\theta _i \subseteq [N+1]$ is called an ordered partition of $[N+1]$ if (i) $\theta _i \cap \theta _j = \emptyset$ for all $i \ne j$; (ii) $\cup _{i=1}^n \theta _i = [N+1]$; and (iii) for every $\ell , r \in [n]$ with $\ell < r$, every $i \in \theta _{\ell }$ and $j \in \theta _{r}$ satisfy $i < j$. Here $n =: \vert \Theta \vert$ is the number of parts in the partition. Write $\theta \in \Theta$ if $\theta$ is one of the parts of $\Theta$. Given an ordered partition $\Theta = (\theta _1, \ldots , \theta _n)$, we write $\Theta ^\star := ( \theta _j: \vert \theta _j \vert \ge 2 )$ for the ordered non-singletons; if $\vert \theta _j \vert = 1$ for all j, we set $\Theta ^\star := \emptyset$.

For $I \subseteq [N+1]$ a discrete interval, define

$$\begin{aligned} R_I (t):= \max _{i \in I} X_i (t) - \min _{i \in I} X_i (t), \text { for } t \in {{\mathbb {R}}}_+, \end{aligned}$$

(2.5)

the total distance between the extreme particles indexed by I. For $I = [\ell ;m]$ a discrete interval with $m \ge 2$ elements, write $I^\circ := [\ell ;m-1]$ for the discrete subinterval that omits the maximal element. If $\vert I\vert \ge 2$, define

$$\begin{aligned} \eta _I (t):= ( \eta _j (t): j \in I^\circ ), \end{aligned}$$

(2.6)

the vector of particle separations restricted to particles in I.

Part of our result will be to identify an ordered partition $\Theta = (\theta _1, \ldots , \theta _n)$ of $[N+1]$ in which each $\theta \in \Theta$ is a stable cloud in the long-term dynamics of the particle system. Stability means that the relative displacements of the particles indexed by $\theta$ are ergodic, in a sense made precise in the statement of Theorem 2.1 below, which includes an explicit limit distribution for $\eta _{\theta } (t)$; moreover, each cloud travels at an asymptotic speed. To describe the limit distribution for the displacements within each cloud, we define, for $I \subseteq [N+1]$ a discrete interval with $\vert I\vert =1+k \ge 2$ elements,

$$\begin{aligned} \varpi _I ( z_1, \ldots , z_{k} ):= \prod _{j \in I^\circ } {{\hat{\rho }}}_I (j)^{z_j} (1-{{\hat{\rho }}}_I(j)), \text { for } (z_1,\ldots , z_{k}) \in {{\mathbb {Z}}}_+^{k}, \end{aligned}$$

(2.7)

where ${{\hat{\rho }}}_I$ is defined at (2.4). For $A \subseteq {{\mathbb {Z}}}_+^k$, set $\varpi _I ( A):= \sum _{z \in A} \varpi _I (z)$. Then, if $0< {{\hat{\rho }}}_I(j) < 1$ for every j, $\varpi _I$ is a non-vanishing probability distribution on ${{\mathbb {Z}}}_+^k$.

The stable cloud decomposition is encoded in a general traffic equation, arising from the connection between our model and a Jackson network of queues in series with nearest-neighbour routing. We describe this connection in detail in Sect. 3; for now we introduce the notation needed to formulate the general traffic equation (2.11). Define

$$\begin{aligned} \mu _i:= b_i + a_{i+1}, \text { for } i \in [N]. \end{aligned}$$

(2.8)

If $N=1$, define $\lambda _1:= a_1 + b_2$; else, for $N \ge 2$, define

$$\begin{aligned} \lambda _1:= a_1, ~ \lambda _{N}:= b_{N+1}, \text { and } \lambda _j:= 0 \text { for } 2 \le j \le N-1. \end{aligned}$$

(2.9)

Also define the matrix $P:= (P_{i,j})_{i,j \in [N]}$ by

$$\begin{aligned} \begin{aligned} P_{i,i-1}&:= \frac{b_i}{\mu _i} = \frac{b_i}{b_i+a_{i+1}}, \text { for } 2 \le i \le N; \\ P_{i,i+1}&:= \frac{a_{i+1}}{\mu _i} = \frac{a_{i+1}}{b_i+a_{i+1}}, \text { for } 1 \le i \le N-1; \end{aligned} \end{aligned}$$

(2.10)

and $P_{i,j}:=0$ for all i, j with $\vert i-j\vert \ne 1$. For vectors $x= (x_i)_{i \in [N]}$ and $y = (y_i)_{i \in [N]}$ in ${{\mathbb {R}}}^N$, write $x \wedge y$ for the vector $(x_i \wedge y_i)_{i \in [N]}$. The general traffic equation is the matrix–vector equation for a vector $\nu \in {{\mathbb {R}}}^N$ given by

$$\begin{aligned} \nu = ( \nu \wedge \mu ) P + \lambda , \end{aligned}$$

(2.11)

where $\mu = (\mu _i)_{i \in [N]}$ and $\lambda = (\lambda _i)_{i \in [N]}$. In (2.11) and elsewhere we view vectors as column vectors when necessary. In the Jackson network context, the quantities $\lambda ,\mu$, and P represent arrival rates of customers, service rates, and routing probabilities, respectively; see Sect. 3 for a precise description. Now we can state our first main result.

Theorem 2.1

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. There exists a unique solution $\nu = (\nu _i)_{i \in [N]}$ to the general traffic equation (2.11). Define $\rho _i:= \nu _i / \mu _i$ for every $i \in [N]$. Then there is a unique ordered partition $\Theta = (\theta _1, \ldots , \theta _n)$ of $[N+1]$, which we call the cloud partition, such that, with ${{\hat{\rho }}}_\theta (j)$ as defined at (2.4),

$$\begin{aligned} \text {for every } \theta \in \Theta ^\star \text { and all } j \in \theta ^\circ , ~ \rho _j = {{\hat{\rho }}}_\theta (j) \in (0,1), \end{aligned}$$

(2.12)

and $\rho _{\max \theta } \ge 1$ for every $\theta \in \Theta$ with $\max \theta \le N$. The following stability statements hold.

• (i) For every $\theta \in \Theta ^\star$, take $A_\theta \subseteq {{\mathbb {Z}}}_+^{k(\theta )}$, where $k(\theta ):= \vert \theta \vert -1 \ge 1$. Then

  $$\begin{aligned} \lim _{t \rightarrow \infty } \frac{1}{t} \int _0^t {\mathbb {1}}\left( \bigcap _{\theta \in \Theta ^\star } \left\{ \eta _{\theta } (s) \in A_\theta \right\} \right) {\mathrm d}s = \lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}\left( \bigcap _{\theta \in \Theta ^\star } \left\{ \eta _{\theta } (t) \in A_\theta \right\} \right) = \prod _{\theta \in \Theta ^\star } \varpi _{\theta } (A_\theta ), \end{aligned}$$

  the first limit holding a.s. and in $L^1$, where $\varpi _\theta$ is defined by (2.7). Moreover,

  $$\begin{aligned} \lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {E}}\,}}R_\theta (t) = \sum _{j \in \theta ^\circ } \frac{1}{1-{{\hat{\rho }}}_\theta (j) }, \text { for every } \theta \in \Theta ^\star . \end{aligned}$$

  (2.13)

• (ii) On the other hand, for $1 \le \ell < r \le n$, we have for every $i \in \theta _\ell$ and $j \in \theta _r$,

  $$\begin{aligned} \lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}\left[ \vert X_j (t) - X_i (t) \vert \le B \right] = 0, \text { for every } B \in {{\mathbb {R}}}_+. \end{aligned}$$

  (2.14)

• (iii) For every $i \in [N+1]$, define $v_i$ by $v_i = {{\hat{v}}}(\theta )$ where $i \in \theta \in \Theta$, and ${{\hat{v}}}(\theta )$ is as defined at (2.2). Then $-\infty< v_1 \le \cdots \le v_n < \infty$, and

  $$\begin{aligned} \lim _{t \rightarrow \infty } \frac{X_i (t)}{t} = v_i, \ \text {a.s.}, \text { for every } i \in [N+1]. \end{aligned}$$

  Moreover, $v_{i+1} - v_i = (\rho _i -1)^+ ( b_i + a_{i+1} )$ for all $i \in [N]$, where $x^+:= x {{\mathbb {1}}\hspace{-0.83328pt}}{\{ x \ge 0\}}$, $x \in {{\mathbb {R}}}$.

Remarks 2.2

• (a) Statement (i) is our ergodicity property for the stable clouds; note it has nothing to say about singletons in the cloud partition $\Theta$. Statement (ii) says that distances between particles in different clouds diverge in probability, or, in other words, the stable clouds given by $\Theta$ are maximal. Statement (iii) says that each stable cloud in $\Theta$ possesses an asymptotic speed at which all particles in that cloud travel.

• (b) If $\theta _\ell , \theta _r$ with $1 \le \ell < r \le \vert \Theta \vert$ are two distinct stable clouds, and if the strict inequality ${{\hat{v}}}(\theta _\ell ) < {{\hat{v}}}(\theta _r)$ holds for the corresponding speeds in part (iii), then $\Delta _{\ell ,r} (t):= \min _{i \in \theta _r} X_i (t) - \max _{i \in \theta _\ell } X_i (t)$ satisfies $\lim _{t \rightarrow \infty } t^{-1} \Delta _{\ell ,r} (t) = {{\hat{v}}}(\theta _r) - {{\hat{v}}}(\theta _\ell ) >0$, a.s., which is much stronger than the statement in (ii). However, if ${{\hat{v}}}(\theta _\ell ) = {{\hat{v}}}(\theta _r)$, it may be the case that $\liminf _{t \rightarrow \infty } \Delta _{\ell ,r} (t) < \infty$, a.s.: see Example 2.8 below.

Theorem 2.1 describes the asymptotic behaviour of the particle system through the cloud partition $\Theta$ and the formulas (2.3) and (2.4) for the ${{\hat{v}}}$ and ${{\hat{\rho }}}$. Partition $\Theta$ is characterized via the solution $\nu$ of the non-linear system (2.11); those i for which $\rho _i \ge 1$ mark boundaries between successive parts of $\Theta$. While it is not, in principle, a difficult task for a computer to solve the system (2.11), we present below an algorithm for obtaining $\Theta$ via a sequence of comparisons involving only applications of the formula (2.3), without directly computing the solution to (2.11).

There is a closely related algorithm due to Goodman and Massey [23], in the general Jackson network context. In our setting we can exploit the linear structure to produce an algorithm that needs only the formula (2.3), involving elementary arithmetic (a similar simplification takes place for the algorithm of [23]). The structure of our algorithm (and Theorem 4.4 below from which it is derived) is of additional interest, as it provides some intuition as to how stable clouds are formed. Roughly, the algorithm goes as follows: start from the ordered partition of all singletons as candidate stable clouds, and successively merge any candidate stable clouds in which the intrinsic speeds, as computed by (2.3), are such that the speed of the candidate cloud to the left exceeds the speed of the candidate cloud to the right. In the Jackson network context, the intuition-bearing quantities in the algorithm of [23] are the net growth rates of the queues, which are differences of our speeds; specifically, $v_{i+1} - v_i= (\nu _i - \mu _i)^+$ is the net growth rate of queue i (see Lemma 3.4 below).

Theorem 2.3

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. Then Algorithm 1 below produces the unique partition $\Theta$ featuring in Theorem 2.1.

Algorithm 1

The algorithm takes as input data $N \in {{\mathbb {N}}}$ and the parameters $a_i, b_i \in (0,\infty )$, $i \in [N+1]$, and outputs an ordered partition $\Theta$ of $[N+1]$.

Remarks 2.4

• (a) If $\vert \Theta ^\kappa \vert =1$ at any point, then Step 3 will terminate the algorithm; thus whenever Step 2 is executed, one has $n = \vert \Theta ^\kappa \vert \ge 2$. Similarly, the set J in Step 4 will always be non-empty.

• (b) The merger executed in Step 4 reduces by one the number of parts in the partition, so Algorithm 1 will terminate in at most N iterations.

• (c) One can in fact perform the merger in Step 4 at every $j \in J$, rather than picking just one; this follows from Theorem 4.4 below. However, for simplicity of presentation we only perform a single pairwise merger per iteration in the description above.

• (d) The algorithm of Goodman and Massey [23, p. 863] is similar, in that it also requires at most N steps, while each step requires inverting a matrix, which, in our case, is tridiagonal and so provides formulas comparable to (2.3); the sequence of cloud mergers in Algorithm 1 is a little more adapted to the linear structure of our setting.

The proofs of Theorems 2.1 and 2.3 are given in Sect. 4 below. Next we state several corollaries to these two results: the proofs of these also appear in Sect. 4. The first two corollaries pertain to the extreme cases of a single stable cloud, and a system in which each particle constitutes its own stable cloud.

Corollary 2.5

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. The partition $\Theta$ consists only of singletons if and only if

$$\begin{aligned} b_1 - a_1 \le b_2 - a_2 \le \cdots \le b_{N+1} - a_{N+1}. \end{aligned}$$

(2.15)

In the case where (2.15) holds, we have that $\lim _{t \rightarrow \infty } t^{-1} X_i (t) = b_i - a_i$, a.s., while, for every $i \ne j$, $\vert X_i (t) - X_j (t) \vert \rightarrow \infty$ in probability as $t \rightarrow \infty$.

Recall that ${{\hat{\rho }}}$ is defined by (2.4). From Theorem 2.1, we have that $\Theta = ([N+1])$ consists of a single stable cloud if and only if $\rho _i = {{\hat{\rho }}}_{[N+1]} (i) < 1$ for all $i \in [N]$, where $\rho _i = \nu _i /\mu _i$ is defined in terms of the solution $\nu$ to the general traffic equation (2.11); see (2.12). Furthermore, if $\rho _i < 1$ for all i, then (2.11) reduces to the linear equation $\nu = \nu P + \lambda$, which can be solved explicitly (see Sect. 3 below), to give the formula (2.16) below. Thus we will sometimes also, with a small abuse of notation, refer to (2.16) as a definition of $\rho _i$ in the stable case.

Corollary 2.6

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. The partition $\Theta$ has a single part if and only if $\rho _i < 1$ for all $i \in [N]$, where, for $i \in [N]$,

$$\begin{aligned} \rho _i = {{\hat{\rho }}}_{[N+1]} (i) = \frac{a_1\cdots a_i}{b_1\cdots b_i} +\left( \frac{1}{b_i}+\frac{a_i}{b_ib_{i-1}}+ \cdots + \frac{a_i\cdots a_2}{b_i\cdots b_1}\right) {{\hat{v}}}_{N+1}, \end{aligned}$$

(2.16)

and where ${{\hat{v}}}_{m}:= {{\hat{v}}}(1; m)$ is given by the $\ell =1$ version of (2.3), i.e.,

$$\begin{aligned} {{\hat{v}}}_m:= \frac{1- \displaystyle \frac{a_1\cdots a_{m}}{b_1\cdots b_{m}}}{\displaystyle \frac{1}{b_{m}} +\frac{a_{m}}{b_{m}b_{m-1}}+ \cdots + \frac{a_{m}\cdots a_2}{b_{m}\cdots b_1}}, \text { for } 1 \le m \le N+1. \end{aligned}$$

(2.17)

Moreover, if $\rho _i < 1$ for all $i \in [N]$, then for all $z_1, \ldots , z_N \in {{\mathbb {Z}}}_+$,

$$\begin{aligned} \lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}\left( \bigcap _{i=1}^N \left\{ \eta _{i} (t) = z_i \right\} \right) = \prod _{i=1}^N \rho _i^{z_i} (1-\rho _i), \end{aligned}$$

(2.18)

and $\lim _{t \rightarrow \infty } t^{-1} X_i (t) = {{\hat{v}}}_{N+1}$, a.s., for every $i \in [N+1]$, where ${{\hat{v}}}_{N+1}$ is given by (2.17).

Remarks 2.7

• (a) A compact, but less explicit, expression of the stability condition in Corollary 2.6 is as $\lambda ( I - P)^{-1} < \mu$, understood componentwise, where $\lambda , \mu , P$ are given by (2.8)–(2.10), and $I-P$ is an invertible tridiagonal matrix; this is the classical Jackson network stability condition translated to our model: see Proposition 3.6 below.

• (b) Here is a more intuitive expression of the stability condition in Corollary 2.6, in the spirit of Algorithm 1. From (2.16), (2.4), and (2.17), we have that ${{\hat{v}}}_i = {{\hat{v}}}(1;i) = (1 - \alpha (1;i))/\beta (1;i)$ and $\rho _i = \rho _{[N+1]} (i) = \alpha (1; i) + \beta (1; i) {{\hat{v}}}_{N+1}$ with the notation at (2.1). Hence

  $$\begin{aligned} \rho _i < 1 \text { if and only if } {{\hat{v}}}_i > {{\hat{v}}}_{N+1}, \end{aligned}$$

  (2.19)

  which expresses the stability condition in terms of the putative intrinsic speed associated with the sub-system of particles $\{1,2,\ldots ,i\}$ compared to the putative intrinsic speed of the whole system. See Sect. 6 for related results in a diffusion context.

In the case of a single stable cloud, Theorem 2.12 below gives a central limit theorem to accompany Corollary 2.6. First we present some illustrative examples.

Example 2.8

(Constant drifts) If $b_i - a_i \equiv u \in {{\mathbb {R}}}$ for all $i \in [N+1]$, then (2.15) clearly holds, and so Corollary 2.5 applies, and each particle is a singleton cloud with $\lim _{t \rightarrow \infty } t^{-1} X_i(t) = u$, a.s. Moreover, for every $i \in [N]$, the gap $X_{i+1} (t) - X_i (t) = 1 + \eta _i (t)$ satisfies $\lim _{h \rightarrow 0} h^{-1} {{\,\mathrm{\mathbb {E}}\,}}[ \eta _i (t + h) - \eta _i (t) \mid {{\mathcal {F}}}_t ] \le 0$ on $\{ \eta _i (t) \ge 1 \}$, where ${{\mathcal {F}}}_t = \sigma ( X(s), s \le t )$. It follows from this, or the corresponding supermartingale condition for the discrete-time embedded Markov chain, that $\liminf _{t \rightarrow \infty } ( X_{i+1} (t) - X_i (t) ) = 1$, a.s. (combine, for example, Thm. 3.5.8 and Lem. 3.6.5 from [38]). Thus although the particles form singleton clouds, nevertheless every pair of consecutive particles meets infinitely often (particles meeting means that they occupy adjacent sites). One can ask whether, say, three or four consecutive particles meet infinitely often or not; we do not address such ‘recurrence or transience’ questions systematically here, but cover some cases in Example 2.18 below.

Example 2.9

(Totally asymmetric case) The assumption (A) permits $a_i= 0$; here is one such example. Suppose that $a_i =0$ for all $i \in [N+1]$, but $b_i >0$ for all $i \in [N+1]$. This is the totally asymmetric case in which particles can jump only to the right, but may do so at different rates: see e.g. [42] and references therein. Corollary 2.6 shows that the system is stable if and only if $b_i > b_{N+1}$ for all $i \in [N]$ and, moreover, if this latter condition is satisfied, $\lim _{t \rightarrow \infty } t^{-1} X_i (t) = {{\hat{v}}}_{N+1} = b_{N+1}$ for all $i \in [N+1]$.

Example 2.10

(Small systems) Suppose that $N=1$ (two particles). Corollary 2.6 implies that the system is stable if and only if $b_1 - a_1 > b_2 - a_2$; if stable, then $\lim _{t \rightarrow \infty } t^{-1} X_1 (t) = \lim _{t \rightarrow \infty } t^{-1} X_2 (t) = {{\hat{v}}}_2$, a.s., where (2.17) gives ${{\hat{v}}}_2 = (b_1 b_2 - a_1 a_2 )/ (a_2 + b_1)$. For a quantitative central limit theorem describing the fluctuations around this strong law, see Theorem 2.14 below. On the other hand, if $b_1 - a_1 \le b_2 - a_2$ then Corollary 2.5 applies, and $\{1\}$ and $\{2\}$ are separate stable clouds.

Suppose that $N=2$ (three particles). Consider the four inequalities

$$\begin{aligned} b_1 - a_1&> b_2 - a_2 ; \end{aligned}$$

(2.20)

$$\begin{aligned} b_2 - a_2&> b_3 - a_3 ; \end{aligned}$$

(2.21)

$$\begin{aligned} b_1 b_2 + b_1 a_3 + a_2 a_3&> a_1 b_2 + a_1 a_3 + b_2 b_3 ; \end{aligned}$$

(2.22)

$$\begin{aligned} b_1 b_2 + b_1 a_3 + a_2 a_3&> a_1 a_2 + b_1 b_3 + a_2 b_3 . \end{aligned}$$

(2.23)

In this case, the complete classification of the system is as follows.

• (i) If (2.22) and (2.23) both hold, then $\{1,2,3\}$ is a stable cloud.

• (ii) If (2.20) holds but (2.23) fails, then the stable clouds are $\{1,2\}$ and $\{3\}$.

• (iii) If (2.21) holds but (2.22) fails, then the stable clouds are $\{1\}$ and $\{2,3\}$.

• (iv) If (2.20) and (2.21) both fail, then the stable clouds are $\{ 1\}$, $\{2\}$, $\{3\}$.

This classification is exhaustive, as can be seen from the following implications:

• (a) If (2.20) and (2.21) both hold, then so do (2.22) and (2.23).

• (b) If (2.20) and (2.23) hold but (2.21) does not, then (2.22) holds.

• (c) If (2.21) and (2.22) hold but (2.20) does not, then (2.23) holds.

To verify (a), note for example that (2.20) and (2.21) imply $(b_1-a_1) (b_2+a_3) > b_2 (b_3-a_3) + a_3 (b_2-a_2) = b_2 b_3 - a_2 a_3$, which is (2.22). For (b), note that (2.20) implies $a_1 a_2 + b_1 b_3 + a_2 b_3 > a_1 ( a_2 + b_3 ) + b_2 b_3 \ge a_1 (a_3 + b_2) + b_2 b_3$ if (2.21) fails, and then (2.23) implies (2.22); (c) is similar.

To see how the classification laid out here follows from the stated results, note that, with $\rho _i$ as defined at (2.16), inequalities (2.22) and (2.23) are equivalent to $\rho _1 < 1$ and $\rho _2 < 1$, respectively. Thus Corollary 2.6 yields (i). On the other hand, Corollary 2.5 gives (iv). For (ii), notice that (2.20) implies that a valid first step for Algorithm 1 is to merge $\{1\}$ and $\{2\}$, but then failure of (2.23) is equivalent to ${{\hat{v}}}( \{1,2\} ) \le {{\hat{v}}}(\{3\})$, where, by (2.3), ${{\hat{v}}}( \{1,2\} ) = (b_1 b_2 - a_1 a_2)/(a_2 + b_1)$ and ${{\hat{v}}}( \{3\} ) = b_3 - a_3$. Similarly for (iii). Finally, note that in the stable case (i), the limiting speed is

$$\begin{aligned} {{\hat{v}}}_3 = \frac{b_1 b_2 b_3 - a_1 a_2 a_3}{b_1 b_2 + b_1 a_3 + a_2 a_3 }, \end{aligned}$$

(2.24)

by (2.17).

Here is one more corollary, which gives a necessary and sufficient condition for all the speeds $v_i$ in Theorem 2.1(iii) to be positive.

Corollary 2.11

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. The following are equivalent.

• (i) $\min _{i \in [N+1]} v_i > 0$.

• (ii) For every $k \in [N+1]$, $\prod _{i=1}^k a_i < \prod _{i=1}^k b_i$.

We next turn to fluctuations. For simplicity, we assume that the system is stable, i.e., the $\rho _i$ given by (2.16) satisfy $\rho _i <1$ for all $i \in [N]$. The following central limit theorem is a consequence of results of Anantharam and Konstantopoulos [4] for counting processes of transitions in continuous-time Markov chains. Let ${{\mathcal {N}}}(\mu ,\sigma ^2)$ denote the normal distribution on ${{\mathbb {R}}}$ with mean $\mu \in {{\mathbb {R}}}$ and variance $\sigma ^2 \in (0,\infty )$.

Theorem 2.12

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. Suppose that the $\rho _i$ given by (2.16) satisfy $\rho _i <1$ for all $i \in [N]$. Let ${{\hat{v}}}_{N+1}$ be given by (2.17). Then there exists $\sigma ^2 \in (0,\infty )$ such that, for all $w \in {{\mathbb {R}}}$ and $z_1, \ldots , z_N \in {{\mathbb {Z}}}_+$,

$$\begin{aligned} \lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}\left[ \frac{X_1(t) - {{\hat{v}}}_{N+1} t}{\sqrt{ \sigma ^2 t}} \le w,\, \eta _1 (t) = z_1, \, \ldots , \, \eta _N (t) = z_N \right] = \Phi (w) \prod _{i =1}^N \rho _i^{z_i} (1-\rho _i ), \end{aligned}$$

where $\Phi$ is the cumulative distribution function of ${{\mathcal {N}}}(0,1)$. In particular, if $Z \sim {{\mathcal {N}}}(0, \sigma ^2)$, then, as $t \rightarrow \infty$,

$$\begin{aligned} \left( \frac{X_i(t) - {{\hat{v}}}_{N+1} t}{\sqrt{t}} \right) _{i \in [N+1]} \overset{\textrm{d}}{\longrightarrow }(Z, \ldots ,Z). \end{aligned}$$

Remarks 2.13

• (a) Theorem 2.12 covers the case of a single stable cloud. In the general (partially stable) case, we anticipate that there is a joint central limit theorem in which the components associated with clouds with different speeds are independent, while those associated with clouds of the same speed are correlated; in the case in which all clouds are singletons, one case of such a result is known in the context of the scaling limit results of [30]: see Sect. 6.3 below.

• (b) In the case $N \ge 2$, Theorem 2.12 is deduced from Thm. 10 of [4], which gives a central limit theorem for counting processes in stable Jackson networks; when $N \ge 2$, Thm. 11 of [4] also gives an expression for the limiting variance $\sigma ^2$, which is in principle computable, but somewhat involved. For $N=1$, Theorem 2.12 does not fall directly under the scope of Thms. 10 and 11 of [4], since one must distinguish between the two different types of arrivals and departures (to the left or to the right); nevertheless, the result can be deduced from the general approach of [4] in the $N=1$ case too (use e.g. their Thm. 5). The main additional ingredient needed to deduce Theorem 2.12 from [4] is the asymptotic independence between the fluctuations of the location of the cloud ($X_1$) and the internal displacements ($\eta$), which is a consequence of a separation of time scales: see Sect. 5 below.

As mentioned in Remarks 2.13(b), the $N=1$ case of Theorem 2.12 is not treated explicitly in [4]. Thus it is of interest to give an explicit computation of $\sigma ^2$ in that case. We will use the properties of the M/M/1 queue to do so: this is the next result.

Theorem 2.14

Suppose that $N =1$, that (A) holds, and $a_1 + b_2 < a_2 + b_1$. Then the central limit theorem in Theorem 2.12 holds, with

$$\begin{aligned} {{\hat{v}}}_2 = \frac{b_1b_2 - a_1 a_2}{a_2 + b_1}, \text { and } \sigma ^2 = \frac{a_1 a_2 + b_1 b_2}{a_2 + b_1}. \end{aligned}$$

(2.25)

That is, if $Z \sim {{\mathcal {N}}}(0, \sigma ^2)$, with $\sigma ^2$ given at (2.25), then, as $t \rightarrow \infty$,

$$\begin{aligned} \left( \frac{X_1 (t) - {{\hat{v}}}_2 t}{\sqrt{t}}, \frac{X_2 (t) - {{\hat{v}}}_2 t}{\sqrt{t}} \right) \overset{\textrm{d}}{\longrightarrow }(Z, Z). \end{aligned}$$

(2.26)

We finish this section with some further examples.

Example 2.15

(1 dog and N sheep; lattice Atlas model) Assume that $a_1=a\in (0,1)$, and $b_1=a_2=b_2=\cdots =b_{N+1}=1$. That is, the leftmost particle (‘the dog’) has an intrinsic drift to the right, while all other particles (‘the sheep’) have no intrinsic drift. In this case $\rho _j$ given by (2.16) satisfies

$$\begin{aligned} \rho _j= a + (1-a) \frac{j}{N+1} \le \frac{N +a}{N+1} < 1, \text { for } j \in [N]. \end{aligned}$$

(2.27)

By Corollary 2.6 the whole system is stable, and, by (2.17), the speed of the cloud is ${{\hat{v}}}_{N+1} =\frac{1-a}{N+1}$. By (2.13) and (2.27), the long-run expected size of the particle cloud satisfies

$$\begin{aligned} \lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {E}}\,}}(X_{N+1}(t) -X_1(t) ) = \frac{N+1}{1-a} \left( 1+\frac{1}{2}+\cdots +\frac{1}{N} \right) \sim (1-a)^{-1}N\log N, \end{aligned}$$

as $N \rightarrow \infty$. In [9, pp. 191–192] the closely related model where $a_1 = 0$, $b_1 = 1$, and $b_i = 1 - a_i = b \ne 1/2$ for all $i \ge 2$ is treated; taking $b \rightarrow 1/2$ in (2.30) in [9] recovers a version of this example. This is a lattice relative of the continuum Atlas model [8, 25], in which the leftmost diffusing particle (Atlas) carries the weight of the rest on its shoulders: see Sect. 6 below for a discussion of such continuum models.

Example 2.16

(Sheep between two dogs, symmetric case) We now set $a_1=b_{N+1}=a\in (0,1)$, and $b_1=a_2=b_2 = \cdots =a_{N+1}=1$; i.e., now the first and the last particles are dogs with drifts directed inside, and the particles between those are sheep. Then, we readily find $\rho _k=a$ for $k=1,\ldots ,N$ and ${{\hat{v}}}_{N+1} =0$ (the last fact is clearly a consequence of symmetry). In particular, the expected size of the cloud is linear in N, unlike in Example 2.15.

Example 2.17

(Sheep between two dogs, asymmetric case) Assume that $a_1=a$ and $b_{N+1}=b$ with $0<a\le b<1$, and $b_1=a_2=b_2= \cdots =a_{N+1}=1$; this is a generalization of Example 2.16, in which the drift of the left dog is permitted to be stronger than the right. Here, (2.16) and (2.17) imply that ${{\hat{v}}}_{N+1} =\frac{b-a}{N+1} \ge 0$ and $\rho _k = a+\frac{(b-a)k}{N+1}$.

Example 2.18

(Recurrence of small systems with constant drifts for $N \le 2$) Consider again the setting of Example 2.8, where $b_i - a_i \equiv u \in {{\mathbb {R}}}$ for all $i \in [N+1]$. If $N=1$ (two particles), then the argument in Example 2.8 shows that the system is recurrent, in the sense that $\liminf _{t \rightarrow \infty } ( X_{2} (t) - X_1 (t) ) = 1$, a.s. In the case $N=2$ (three particles), it can be shown that the system is also recurrent, i.e., $\liminf _{t \rightarrow \infty } ( X_{3} (t) - X_1 (t) ) = 2$, a.s.; it is, however, ‘critically recurrent’ in that excursion durations are heavy-tailed. This follows by considering $(\eta _1(t), \eta _2 (t))_{t \in {{\mathbb {R}}}_+}$ as a random walk with boundary reflection in the quarter-plane ${{\mathbb {Z}}}_+^2$ and applying results of Asymont et al. [6]. To apply these results, it is most convenient to work with the corresponding discrete-time embedded process. Then, in the notation of [6, p. 942], the entries in the interior covariance matrix are

$$\begin{aligned} \lambda _x = \frac{a_1+b_1+a_2+b_2}{r}, ~ \lambda _y = \frac{a_2+b_2+a_3+b_3}{r}, ~ R = -\frac{a_2+b_2}{r}, \end{aligned}$$

where $r:= \sum _{i=1}^3 (a_i + b_i)$, while the reflection vector components are $M'_x = - (u+a_2)/r'$, $M'_y = (a_2+b_3)/r'$, $M''_x = (a_1 +b_2)/r''$, $M''_y = (u - b_2)/r''$, where $r':= a_1 + b_1 + a_2 + b_3$ and $r'':= a_1 + b_2 + a_3 + b_3$. Then [6, Thm. 2.1] shows that one has recurrence if

$$\begin{aligned} - \lambda _x \frac{M''_y}{M''_x} - \lambda _y \frac{M'_x}{M'_y} + 2 R \ge 0, \end{aligned}$$

which in this case amounts, after a little simplification, to

$$\begin{aligned} \frac{(b_2 -u) (b_1 + a_2)}{a_1 +b_2} + \frac{(a_2+u) (b_2+a_3)}{a_2 + b_3} \ge a_2 + b_2, \end{aligned}$$

which is true, with equality, since $b_1 + a_2 = a_1 + b_2$ and $b_2 + a_3 = a_2 + b_3$.

On the other hand, if $N =3$, we believe that $\lim _{t \rightarrow \infty } ( X_{4} (t) - X_1 (t) ) = \infty$, a.s.; when $b_i \equiv a_i \equiv 1$ for all $i \in [4]$, it seems possible to approach this by reducing the problem to a random walk on ${{\mathbb {Z}}}^3$ that is zero drift everywhere, and homogeneous unless one or more coordinates is zero. We conjecture that the same is true for any four (or more) consecutive particles in a constant-drift system with $N \ge 4$, but, since such questions appear rather delicate and are not directly relevant for the main phenomena of the present paper, we do not explore them further here.

It is of interest to extend the questions posed in Example 2.18 to the setting where there are several non-singleton stable clouds with the same speed. For example, if $\Theta = (\theta _1, \theta _2)$ consists of two stable clouds with ${{\hat{v}}}(\theta _1) = {{\hat{v}}}(\theta _2)$, then we believe strongly that the system is recurrent, i.e., $\liminf _{t \rightarrow \infty } ( X_{N+1} (t) - X_1 (t)) < \infty$, a.s. A proof of this might be built on the central limit theorem, Theorem 2.12, as follows. Suppose the contrary, that the system is transient, i.e., the two stable clouds drift apart. Then the clouds evolve essentially independently, so each should satisfy Theorem 2.12 with the same speed and variance on the same scale (with different constants), which suggests they would be in the wrong order with positive probability, providing a contradiction. The following problem deals with the case of more than two clouds, and settling it seems harder.

Conjecture 2.19

Suppose that all clouds have the same speed, i.e., ${{\hat{v}}}(\theta )$ is constant for $\theta \in \Theta$. We expect that, if $\vert \Theta \vert = 3$, then $\liminf _{t \rightarrow \infty } ( X_{N+1} (t) - X_1 (t)) < \infty$, a.s. On the other hand, we expect that, if $\vert \Theta \vert \ge 4$, then $\liminf _{t \rightarrow \infty } ( X_{N+1} (t) - X_1 (t)) = \infty$, a.s.

The mathematical development to prove the results stated above begins in Sect. 3, where we explain the connection between our model and an appropriate Jackson queueing network, and build on the classical work of Goodman and Massey [23] to give some fundamental results on stability and dynamics. Section 4 develops these ideas further to examine the structure underlying Algorithm 1, and here we give the proofs of Theorems 2.1 and 2.3, and their corollaries. Section 5 is devoted to the central limit theorem in the stable case, and presents the proofs of Theorems 2.12 and 2.14. Finally, in Sect. 6 we discuss the relationship between the lattice model that we study here and a family of continuum models that have been studied in the literature, and mention some open problems in that direction.

3 Representation as a Jackson Network

Consider a system of $N \in {{\mathbb {N}}}$ queues, labelled by [N]. The parameters of the system are arrival rates $\lambda = (\lambda _i)_{i \in [N]}$, service rates $\mu = (\mu _i)_{i \in [N]}$ and $P = (P_{ij})_{i,j\in [N]}$, a sub-stochastic routing matrix. Exogenous customers entering the system arrive at queue $i \in [N]$ via an independent Poisson process of rate $\lambda _i \in {{\mathbb {R}}}_+$. Queue $i \in [N]$ serves customers at exponential rate $\mu _i \in {{\mathbb {R}}}_+$. Once a customer at queue i is served, it is routed to a queue j with probability $P_{ij}$, while with probability $Q_i:= 1 - \sum _{j \in [N]} P_{ij}$ the customer departs from the system.

Provided $\sum _{i \in [N]} \lambda _i >0$ and $\sum _{i \in [N]} Q_i >0$, customers both enter and leave the system, and it is called an open Jackson network. We assume that every queue can be filled, meaning that, for every $i \in [N]$, there is a $j \in [N]$ and $k \in {{\mathbb {Z}}}_+$ for which $\lambda _j > 0$ and $(P^k)_{ji}>0$, and that every queue can be drained, meaning that, for every $i \in [N]$, there is a $j \in [N]$ and $k \in {{\mathbb {Z}}}_+$ for which $Q_j > 0$ and $(P^k)_{ij}>0$. The process that tracks the number of customers in each queue at time $t \in {{\mathbb {R}}}_+$ is a continuous-time Markov chain on ${{\mathbb {Z}}}_+^N$ (Fig. 2). Jackson networks are named for early contributions of Jackson [29] and Jackson [27, 28]. For a general overview see e.g. [13, Ch. 2  & 7] or [47, Ch. 1].

Fig. 2

Schematic of a Jackson network on N nodes. The $\lambda _i$ are the exogenous arrival rates, the $\mu _i$ are the service rates, and P is the (substochastic) routing matrix by which customers are redirected following service. From queue i, particles depart the system at rate $Q_i = 1 - \sum _{j} P_{ij}$. The process $\eta$ from (1.2) for the particle system described in Sect. 1 can be interpreted as the queue-length process for a Jackson network with parameters given by (2.8), (2.9) and (2.10)

For $i \in [N]$ recall from (1.2) that $\eta _i (t) = X_{i+1} (t) - X_i (t) -1$, the number of empty sites between consecutive particles at time $t\in {{\mathbb {R}}}_+$. We claim that the process $\eta = (\eta _{i})_{i \in [N]}$ is precisely the queue-length process for a corresponding Jackson network, namely, the Jackson network with parameters $\lambda , \mu$ and P given as functions of $(a_i,b_i)_{i \in [N+1]}$ through formulas (2.8), (2.9) and (2.10).

To see this, observe that ‘customers’ in the queueing network correspond to unoccupied sites between particles in the particle system. Exogenous customers enter the network only when the leftmost particle jumps to the left (rate $a_1$) or the rightmost particle jumps to the right (rate $b_{N+1}$). Customers at queue i are ‘served’ if either the particle at the left end of the interval jumps right (rate $b_i$) or if the particle at the right end of the interval jumps left (rate $a_{i+1}$). If the particle at the left end of the interval jumps right, the customer is routed to queue $i-1$ (if $i \ge 2$, at rate $b_i = \mu _i P_{i,i-1}$) or leaves the system. Similarly in the other case. Customers leave the system only when the leftmost particle jumps to the right (rate $\mu _1 Q_1 = b_1$) or the rightmost particle jumps to the left (rate $\mu _{N} Q_N = a_{N+1}$).

For some of the results in this section, we will relax assumption (A) to the following; but see the remark below (A) about generality.

($\text {A}'$):

Suppose that either $a_i >0$ for all $i \in [N+1]$, or $b_i >0$ for all $i \in [N+1]$.

If ($\text {A}'$) holds, then the parameters $\lambda , \mu$ and P satisfy the conditions to ensure that the system $\eta$ is an open Jackson network in which every queue can be filled and drained: for example, if $b_i >0$ for all i, then customers can enter the network at queue N (since $\lambda _N > 0$), progress in sequence through queues $N-1, N-2, \ldots$, and exit through queue 1 (since $Q_1 = \frac{b_1}{b_1+a_2} >0$). The following statement summarizes the Jackson representation.

Proposition 3.1

Let $N \in {{\mathbb {N}}}$ and suppose that ($\text {A}'$) holds. The evolution of the process $\eta = (\eta _{i})_{i \in [N]}$ can be described by an open Jackson network in which every queue can be filled and drained, with $\eta _i(t)$ being the number of customers at queue $i \in [N]$ at time $t\in {{\mathbb {R}}}_+$. The exogenous arrival rates $\lambda$ are given by (2.9), service rates $\mu$ are given by (2.8), and routing matrix P is given by (2.10).

Remark 3.2

We believe that Proposition 3.1 is known, but we could not find the statement explicitly in the literature, and are not confident of an attribution. For simple exclusion with homogeneous jump rates one can find the result expressed by Kipnis [34, pp. 398–399]. Spitzer [48, pp. 280–281] shows that the gaps of empty sites in exclusion process viewed from a tagged particle have a product-geometric stationary distribution, but queues are not mentioned; the closest we have been able to find in [48] to an identification of exclusion and Jackson dynamics (rather than just stationary distributions) is Spitzer’s report of an observation by Kesten [48, p. 281] that Poisson streams can be identified in exclusion processes.

The Jackson representation given by Proposition 3.1 enables us to obtain the following result, which is, to a substantial degree, a translation to our context of a classical result for Jackson networks due to Goodman and Massey [23], which characterizes the stable subset S of the queues in the network: when $S = [N]$ the network is stable, when $S= \emptyset$ it is unstable, and otherwise it is partially stable (cf. [1]).

Proposition 3.3

Let $N \in {{\mathbb {N}}}$ and suppose that ($\text {A}'$) holds. The general traffic equation (2.11) has a unique solution, which we denote by $\nu = (\nu _i)_{i \in [N]}$. Write $\rho _i:= \nu _i / \mu _i$ for all $i \in [N]$ and $S:= \{ i \in [N]: \rho _i < 1 \}$. For every $z = (z_i)_{i \in S}$ with $z_i \in {{\mathbb {Z}}}_+$, we have

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{1}{t} \int _0^t {\mathbb {1}}\left( \bigcap _{i \in S} \left\{ \eta _i (s) = z_i \right\} \right) {\mathrm d}s&= \lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}\left[ \bigcap _{i \in S} \left\{ \eta _i (t) = z_i \right\} \right] \nonumber \\&= \prod _{i \in S} (1-\rho _i) \rho _i^{z_i} , \end{aligned}$$

(3.1)

where the first equality holds a.s. and in $L^1$. Moreover, for each fixed $\eta (0) \in {{\mathbb {Z}}}_+^N$, there exists $\delta >0$ such that,

$$\begin{aligned} \sup _{t \in {{\mathbb {R}}}_+} {{\,\mathrm{\mathbb {P}}\,}}\left( \eta _i (t) \ge z \right) \le {\textrm{e}}^{-\delta z}, \text { for all } i \in S \text { and all } z \in {{\mathbb {R}}}_+. \end{aligned}$$

(3.2)

On the other hand, for $U:= [N] {\setminus } S = \{ i \in [N]: \rho _i \ge 1\}$ and all $B < \infty$,

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{1}{t} \int _0^t {\mathbb {1}}\left( \bigcup _{i \in U} \left\{ \eta _i (s) \le B\right\} \right) {\mathrm d}s = \lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}\left[ \bigcup _{i \in U} \left\{ \eta _i (t) \le B\right\} \right] = 0, \end{aligned}$$

(3.3)

where the first equality holds a.s. and in $L^1$.

Proof

Existence and uniqueness of the solution to (2.11) under the stated conditions follows from Thm. 1 of Goodman and Massey [23], which also gives the rightmost equalities in (3.1) and (3.3).

The convergence of the time-averages in (3.1) and (3.3) we deduce from the construction of Goodman and Massey. For a stable system, the Markov chain ergodic theorem applies directly; in the general case $U \ne \emptyset$, the idea is to construct modified processes (by adjusting relevant Jackson network parameters) that are stable and satisfy appropriate stochastic comparison inequalities with components of $\eta$, and again appeal to the ergodic theorem. For convenience, we recapitulate the main steps in the construction here, pointing to [23] for some more details; we start with the upper bound.

Following [23, pp. 865–866], we construct a continuous-time Markov chain $\eta ^+$ with components $\eta ^+_i (t)$, $t \in {{\mathbb {R}}}_+$, $i \in [N]$, by re-routing certain customers. Specifically, for every $i \in U$ and $j \in S$ with $P_{ij} > 0$, we (i) declare that customers, instead of flowing from i to j, will depart the system, and (ii) add an exogenous arrival stream into j with rate equal to $\mu _i P_{ij}$, the maximal flow rate from i to j. In other words, the modified system $\eta ^+$ is a Jackson network with parameters $\mu ^+_i = \mu _i$,

$$\begin{aligned} \lambda ^+_j:= \lambda _j + {{\mathbb {1}}\hspace{-0.83328pt}}{\{ j \in S \}} \sum _{i \in U} \mu _i P_{ij}, \text { and } P^+_{ij}:= {{\mathbb {1}}\hspace{-0.83328pt}}{\{ i \notin U \text { or } j \notin S \}} P_{ij}. \end{aligned}$$

Since no customers flow from U to S in $\eta ^+$, the process $\eta ^+_S:= ( \eta ^+_i )_{i \in S}$ observed only on S is itself the queue-length process of a Jackson network, with parameters $\lambda ^+_j = \lambda _j + \sum _{i \in U} \mu _i P_{ij}$, $j \in S$, and $P^+_{ij} = P_{ij}$, $i,j \in S$. The solution to the general traffic equations for $\eta ^+_S$ coincides with the solution $\nu$ to the equations for $\eta$ restricted to S, and hence, by definition of S, $\eta ^+_S$ is stable. Then we apply the ergodic theorem for irreducible, continuous-time Markov chains (see e.g. Thm. 3.8.1 of [39, p. 126]) to obtain

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{1}{t} \int _0^t {\mathbb {1}}\left( \bigcap _{i \in S} \left\{ \eta ^+_i (s) = z_i \right\} \right) {\mathrm d}s = \prod _{i \in S} (1-\rho _i) \rho _i^{z_i}, \ \text {a.s.}\end{aligned}$$

Moreover, we can construct $\eta$ and $\eta ^+$ on the same probability space, so that $\eta _i (t) \le \eta ^+_i (t)$ for all $i \in [N]$ and all $t \in {{\mathbb {R}}}_+$: see [23, pp. 867–868] for details. Hence we conclude that

$$\begin{aligned} \limsup _{t \rightarrow \infty } \frac{1}{t} \int _0^t {\mathbb {1}}\left( \bigcap _{i \in S} \left\{ \eta _i (s) = z_i \right\} \right) {\mathrm d}s \le \prod _{i \in S} (1-\rho _i) \rho _i^{z_i}, \ \text {a.s.}\end{aligned}$$

(3.4)

In the other direction, it is shown in [23, pp. 866–867], that for any $\varepsilon >0$, by increasing the rate of departures from the system for every node in U, one can construct a process $\eta ^\varepsilon$ which is stable, for which $\eta _i (t) \ge \eta ^\varepsilon _i (t)$ for all $i \in [N]$ and all $t \in {{\mathbb {R}}}_+$. In more detail, if $\nu = (\nu _i)_{i \in [N]}$ is the solution to (2.11) for $\eta$, then $\eta ^\varepsilon$ is a Jackson system with parameters $\lambda ^\varepsilon , \mu ^\varepsilon , P^\varepsilon$, where, for $\varepsilon \ge 0$, $\lambda ^\varepsilon _i:= \lambda _i$,

$$\begin{aligned} \mu ^\varepsilon _i:= {\left\{ \begin{array}{ll} \mu _i &{} \text {if } i \in S, \\ \nu _i + \varepsilon &{} \text {if } i \in U, \end{array}\right. } ~\text {and}~ P^\varepsilon _{ij}:= {\left\{ \begin{array}{ll} P_{ij} &{} \text {if } i \in S, \\ \frac{\mu _i}{\nu _i + \varepsilon } P_{ij} &{} \text {if } i \in U. \end{array}\right. } \end{aligned}$$

(3.5)

For $i \in U$, we have $\nu _i \ge \mu _i$, and hence $Q^\varepsilon _i:= 1 - \sum _{j \in [N]} P^\varepsilon _{ij} > 0$ for $\varepsilon >0$, so customers served at states in U may now depart the system. Note that, by (3.5), $\lim _{\varepsilon \rightarrow 0} \mu ^\varepsilon = \mu ^0$ and $\lim _{\varepsilon \rightarrow 0} P^\varepsilon = P^0$. We also note that, for every $\varepsilon \ge 0$, $P^\varepsilon$ is an irreducible substochastic matrix with at least one row sum strictly less than 1, so the matrix power $(P^\varepsilon )^k$ tends to 0 as $k \rightarrow \infty$.

Let $\nu ^\varepsilon$ be the solution of the general traffic equation (2.11) for $\eta ^\varepsilon$. As shown in [23, p. 867], one also has $\lim _{\varepsilon \rightarrow 0} \nu ^\varepsilon = \nu ^0$ where $\nu ^0$ satisfies $\nu ^0 = (\nu ^0 \wedge \mu ^0) P^0 + \lambda$; we will show that $\nu ^\varepsilon \le \nu ^0 = \nu$. By construction, it is the case that $\nu = (\nu \wedge \mu ) P + \lambda = \nu P^0 + \lambda$, and since $P^\varepsilon _{ij} \le P^0_{ij}$ for all i, j, we get $\nu ^\varepsilon \le \nu ^\varepsilon P^0 + \lambda$. Hence ${{\tilde{\nu }}}:= \nu ^\varepsilon - \nu$ satisfies ${{\tilde{\nu }}} \le P^0 \tilde{\nu }$, and since $(P^0)^k$ tends to 0 as $k \rightarrow \infty$, it follows that $\nu ^\varepsilon _i \le \nu _i$ for all $i \in [N]$. Moreover, since $\nu _i < \mu _i^\varepsilon$ for all $i \in [N]$ and every $\varepsilon >0$, by definition of $\mu ^\varepsilon$, this means that $\nu ^\varepsilon _i < \mu _i^\varepsilon$ for all $i \in [N]$. Hence $\eta ^\varepsilon$ is stable for every $\varepsilon >0$. Thus in fact $\nu ^\varepsilon = \nu ^\varepsilon P^\varepsilon + \lambda$, i.e., $\nu ^\varepsilon (I - P^\varepsilon ) = \lambda$, for $\varepsilon >0$. For every $\varepsilon \ge 0$, the matrix $I-P^\varepsilon$ is an M-matrix, and hence invertible (this follows from e.g. Lemma 7.1 of [13] and the fact that $(P^\varepsilon )^k$ tends to 0 as $k \rightarrow \infty$). Therefore $\nu ^\varepsilon = \lambda (I-P^\varepsilon )^{-1}$ for $\varepsilon >0$, and $\nu ^0 = \lim _{\varepsilon \rightarrow 0} \nu ^\varepsilon = \lambda (I - P^0)^{-1} = \nu$. In particular, from (3.5), we have that for $i \in S$, $\lim _{\varepsilon \rightarrow 0} \rho ^\varepsilon _i = \lim _{\varepsilon \rightarrow 0} \nu ^\varepsilon _i / \mu _i = \rho _i <1$, while for $i \in U$, $\lim _{\varepsilon \rightarrow 0} \rho ^\varepsilon _i = \lim _{\varepsilon \rightarrow 0} \nu ^\varepsilon _i / \mu ^\varepsilon _i = 1$. Hence, by another application of the ergodic theorem,

$$\begin{aligned} \liminf _{t \rightarrow \infty } \frac{1}{t} \int _0^t {\mathbb {1}}\left( \bigcap _{i \in S} \left\{ \eta _i (s) = z_i \right\} \right) {\mathrm d}s \ge \prod _{i \in S} (1-\rho ^\varepsilon _i) (\rho _i^\varepsilon )^{z_i}, \ \text {a.s.}\end{aligned}$$

(3.6)

Taking $\varepsilon \rightarrow 0$ in (3.6) and combining with (3.4), we obtain the a.s. convergence in (3.1); the $L^1$ convergence follows from the bounded convergence theorem. On the other hand, if $i \in U$, then, for any $z \in {{\mathbb {N}}}$,

$$\begin{aligned} \limsup _{t \rightarrow \infty } \frac{1}{t} \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _i (s) \le z \}} {\mathrm d}s \le 1 - \liminf _{t \rightarrow \infty } \frac{1}{t} \int _0^t \sum _{k=1}^\infty {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _i (s) = z+k \}} {\mathrm d}s. \end{aligned}$$

Here, by Fatou’s lemma, a.s.,

$$\begin{aligned} \liminf _{t \rightarrow \infty } \frac{1}{t} \int _0^t \sum _{k=1}^\infty {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _i (s) = z+k \}} {\mathrm d}s&\ge \sum _{k=1}^\infty \liminf _{t \rightarrow \infty } \frac{1}{t} \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _i (s) = z+k \}} {\mathrm d}s \\&\ge \sum _{k=1}^\infty ( 1 - \rho _i^\varepsilon ) ( \rho _i^\varepsilon )^{z+k} = ( \rho _i^\varepsilon )^{z+1} , \end{aligned}$$

and then taking $\varepsilon \rightarrow 0$ gives the a.s. convergence (3.3); again, bounded convergence gives the $L^1$ case.

It remains to prove (3.2). Fix $\eta (0) \in {{\mathbb {Z}}}_+^N$. The Goodman and Massey construction furnishes the coupling of $\eta$ and $\eta ^+$ such that $\eta _i(t) \le \eta _i^+(t)$ for all $i \in [N]$ and all $t \in {{\mathbb {R}}}_+$, where $\eta ^+_S$ is an ergodic Jackson network over S, i.e., $\max _{i \in S} \rho ^+_i < 1$. Hence, by (3.1), there exists $\delta >0$ such that $\lim _{t\rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}( \eta _i (t) \ge z ) \le \lim _{t\rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}( \eta ^+_i (t) \ge z ) \le {\textrm{e}}^{-\delta z}$ for all $i \in S$ and all $z \in {{\mathbb {R}}}_+$. Moreover, since a stable Jackson network is exponentially ergodic, as is established in Thm. 2.1 of [18] via a Lyapunov function approach (see also [17]), or in [36] via a spectral gap approach, it follows that there exists $\delta >0$ such that ${{\,\mathrm{\mathbb {P}}\,}}( \eta _i (t) \ge z ) \le {{\,\mathrm{\mathbb {P}}\,}}( \eta ^+_i (t) \ge z ) \le {\textrm{e}}^{-\delta z} + {\textrm{e}}^{-\delta t}$ for all $i \in S$ and all $t, z \in {{\mathbb {R}}}_+$. Thus we can conclude that, for any $\varepsilon >0$ there exists $\delta >0$ such that $\sup _{t \ge \varepsilon z} {{\,\mathrm{\mathbb {P}}\,}}( \eta _i (t) \ge z ) \le {\textrm{e}}^{-\delta z}$ for all $z \in {{\mathbb {R}}}_+$ and all $i \in S$. In addition, if $\zeta _t$ denotes the total number of exogenous arrivals in the Jackson network $\eta$ over time [0, t], then $\max _{i \in [N]} ( \eta _i (t) - \eta _i (0) ) \le \zeta _t$, a.s., and $\zeta _t$ is Poisson with mean Ct for $C:= \sum _{i \in [N]} \lambda _i < \infty$. Hence ${{\,\mathrm{\mathbb {P}}\,}}( \eta _i (t) - \eta _i (0) \ge z ) \le {{\,\mathrm{\mathbb {P}}\,}}( \zeta _t \ge z )$, so, for $\varepsilon >0$ small enough, $\sup _{0 \le t \le \varepsilon z} {{\,\mathrm{\mathbb {P}}\,}}( \eta _i (t) - \eta _i (0) \ge z ) \le {{\,\mathrm{\mathbb {P}}\,}}( \zeta _{\varepsilon z} \ge z )$, and this decays exponentially in z, by standard Poisson tail bounds. Combining these bounds yields (3.2). $\square$

Using Proposition 3.3, we show in Theorem 3.5 that each particle satisfies a law of large numbers with a deterministic asymptotic speed. Before stating that result, we state an algebraic result on the quantities that will play the roles of the speeds.

Lemma 3.4

Let $N \in {{\mathbb {N}}}$ and suppose that ($\text {A}'$) holds. Suppose that $\nu = (\nu _i)_{i \in [N]}$ is the unique solution to the general traffic equation (2.11), whose existence is guaranteed by Proposition 3.3. Write $\rho _i:= \nu _i / \mu _i$, and adopt the convention that $\rho _0 = \rho _{N+1} = 1$. Define

$$\begin{aligned} v_i&:= \left( 1 \wedge \rho _i \right) b_i - \left( 1 \wedge \rho _{i-1} \right) a_i , \text { for all } i \in [N+1]. \end{aligned}$$

(3.7)

Then, writing $x^+:= x {{\mathbb {1}}\hspace{-0.83328pt}}{\{ x \ge 0\}}$ for $x \in {{\mathbb {R}}}$, we have

$$\begin{aligned} v_{i+1} - v_i&= (\rho _i -1)^+ ( b_i + a_{i+1} ) , \text { for all } i \in [N] . \end{aligned}$$

(3.8)

In particular, if $i \in [N]$ is such that $\rho _i \le 1$, then $v_{i+1} = v_{i}$, while if $\rho _i >1$, then $v_{i+1} > v_i$.

Here is our result on existence of speeds that underlies much of our analysis.

Theorem 3.5

Let $N \in {{\mathbb {N}}}$ and suppose that ($\text {A}'$) holds. Then there exist $- \infty< v_1 \le \cdots \le v_{N+1} < \infty$ such that

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{X_i (t)}{t} = v_i, \ \text {a.s.}, \text { for every } i \in [N+1]. \end{aligned}$$

(3.9)

Moreover, if $\nu = (\nu _i)_{i \in [N]}$ is the unique solution to the general traffic equation (2.11), and $\rho _i:= \nu _i / \mu _i$, then the $v_i$ in (3.9) are the quantities defined by (3.7).

We first prove the lemma.

Proof of Lemma 3.4

Suppose that $(\nu _i)_{i \in [N]}$ solves $\nu = ( \nu \wedge \mu ) P + \lambda$. Write $\rho _i:= \nu _i / \mu _i$, and take $\rho _0 = \rho _{N+1} = 1$. Using the expressions (2.8), (2.9), and (2.10), the general traffic equation (2.11) can then be expressed in terms of the $\rho _i$, $a_i$, and $b_i$ as

$$\begin{aligned} (b_i + a_{i+1} ) \rho _i = (1 \wedge \rho _{i-1} ) a_i + (1 \wedge \rho _{i+1} ) b_{i+1}, \text { for all } i \in [N]. \end{aligned}$$

(3.10)

Using (3.7) twice in (3.10), we obtain, for $i \in [N]$,

$$\begin{aligned} (b_i + a_{i+1} ) \rho _i{} & {} = (1 \wedge \rho _{i-1} ) a_i + v_{i+1} + ( 1 \wedge \rho _i ) a_{i+1} \\{} & {} = (1 \wedge \rho _i ) b_i + ( 1 \wedge \rho _i ) a_{i+1} + v_{i+1} - v_i. \end{aligned}$$

This yields (3.8), and hence the final sentence of the lemma. $\square$

Proof of Theorem 3.5

Suppose that $(\nu _i)_{i \in [N]}$ solves $\nu = ( \nu \wedge \mu ) P + \lambda$. Write $\rho _i:= \nu _i / \mu _i$. Fix $i \in [N+1]$. Let $N^-_i (t)$ and $N^+_i (t)$, $t \in {{\mathbb {R}}}_+$, be two independent homogeneous Poisson processes, of rates $a_i$ and $b_i$, respectively. For all $t \in {{\mathbb {R}}}_+$, set $\eta _0 (t):= +\infty$ and $\eta _{N+1} (t):= +\infty$. Then we have the stochastic integral representation

$$\begin{aligned} X_i (t) - X_i (0) = \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i} (s-) \ge 1 \}} {\mathrm d}N^+_i (s) - \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i-1} (s-) \ge 1 \}} {\mathrm d}N^-_i (s), \end{aligned}$$

(3.11)

since the attempted jumps are suppressed if the corresponding ‘queues’ are empty. Here, as usual $\eta _i (s- ):= \lim _{u \uparrow s} \eta _i (u)$ for $s >0$, and $\eta _i (0-):= \eta _i (0)$.

Write $M_i^+ (t):= N_i^+ (t) - b_i t$ and $M_i^-(t):= N_i^- (t) - a_i t$, $t \in {{\mathbb {R}}}_+$. Then $M_i^\pm$ are continuous-time, square-integrable martingales, and we can re-write (3.11) as

$$\begin{aligned} X_i (t) - X_i (0)&= b_i \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i} (s-) \ge 1 \}} {\mathrm d}s - a_i \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i-1} (s-) \ge 1 \}} {\mathrm d}s \nonumber \\&\quad + \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i} (s-) \ge 1 \}} {\mathrm d}M^+_i (s) - \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i-1} (s-) \ge 1 \}} {\mathrm d}M^-_i (s) . \end{aligned}$$

(3.12)

Recall from the statement of Proposition 3.3 that S denotes the set of $i \in [N]$ such that $\rho _i < 1$. Then we have from Proposition 3.3 that, for $i \in [N]$, a.s.,

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i} (s-) \ge 1 \}} {\mathrm d}s&= 1 - \lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i} (s) = 0 \}} {\mathrm d}s \nonumber \\&= 1 - (1- \rho _{i} ) {{\mathbb {1}}\hspace{-0.83328pt}}{\{ i \in S\}} = 1 \wedge \rho _i. \end{aligned}$$

(3.13)

Note that (3.13) also holds, trivially, for $i = 0, N+1$. Let $H^+_i (t):= {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i} (t-) \ge 1 \}} = 1 \wedge \eta _i (t-)$. Then $H_i^+$ is left continuous with right limits, and hence [41, p. 63] $Y_i^+:= H_i^+ \cdot M^+_i$ given by $Y_i^+ (t):= \int _0^t H_i^+ (s) {\mathrm d}M^+_i(s)$ is a right-continuous local martingale. Its quadratic variation process $[ Y_i^+]$ satisfies

$$\begin{aligned} {[} Y_i^+ ]_t = \int _0^t (H^+_i (s))^2 {\mathrm d}[ M^+_i ]_s = \int _0^t H^+_i (s) {\mathrm d}N^+_i (s) \le N^+_i (t), \text { for } t \in {{\mathbb {R}}}_+, \end{aligned}$$

using [41, pp. 75–76], with the fact that $[ M^+_i]_t = [N^+_i]_t = N^+_i (t)$ is the quadratic variation of the (compensated) Poisson process [41, p. 71]. Hence ${{\,\mathrm{\mathbb {E}}\,}}[ (Y^+_i (t))^2 ] = {{\,\mathrm{\mathbb {E}}\,}}( [ Y^+_i]_t ) \le {{\,\mathrm{\mathbb {E}}\,}}N^+_i (t) = b_i t$, so $(Y_i^+)^2$ is a non-negative, right-continuous submartingale. By an appropriate maximal inequality [31, p. 13], for any $p >1$,

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}\left[ \sup _{0 \le s \le t} \vert { Y^+_i (s) } \vert \ge t^{p/2} \right] \le t^{-p} {{\,\mathrm{\mathbb {E}}\,}}[ (Y_i^+ (t))^2 ] \le b_i t^{1-p}, \text { for all } t \in (0, \infty ). \end{aligned}$$

(3.14)

Applying the Borel–Cantelli lemma with (3.14) along subsequence $t = t_n:= 2^n$, it follows that, a.s., for all but finitely many $n \in {{\mathbb {Z}}}_+$, $\sup _{0 \le s \le 2^n} \vert { Y^+_i (s) } \vert \le 2^{np/2}$. Every $t \ge 1$ has $2^n \le t < 2^{n+1}$ for $n = n(t) \in {{\mathbb {Z}}}_+$, and so, a.s., for all $t \in {{\mathbb {R}}}_+$ sufficiently large,

$$\begin{aligned} \sup _{0 \le s \le t} \vert { Y^+_i (s) } \vert \le \sup _{0 \le s \le 2^{n+1}} \vert { Y^+_i (s) } \vert \le 2^{(n+1)p/2} \le 2^{p/2} \cdot t^{p/2}. \end{aligned}$$

It follows that, for any $p'> p >1$, $t^{-p'/2} \vert { Y^+_i (t) } \vert \rightarrow 0$, a.s., as $t \rightarrow \infty$. Together with the analogous argument involving $M_i^-$, we have thus shown that, a.s.,

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{t} \!\int _0^t\! {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i} (s-) \ge 1 \}} {\mathrm d}M^+_i (s) = \lim _{t\rightarrow \infty } \frac{1}{t} \!\int _0^t\! {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta _{i-1} (s-) \ge 1 \}} {\mathrm d}M^-_i (s) = 0. \end{aligned}$$

(3.15)

Combining (3.12) with (3.13) and (3.15), we conclude that $X_i(t) /t \rightarrow v_i$, a.s., where $v_i \in {{\mathbb {R}}}$ is given by (3.7). That $v_1 \le v_2 \le \cdots \le v_{N+1}$ follows from the fact that $X_1(t)< X_2 (t)< \cdots < X_{N+1}(t)$ for all $t \in {{\mathbb {R}}}_+$. This completes the proof of (3.9), with the $v_i$ given by (3.7), establishing the theorem. $\square$

A consequence of Proposition 3.3 is that $S = [N]$ (i.e., the system is stable) if and only if the (unique) solution $\nu$ to (2.11) satisfies $\rho _i:= \nu _i / \mu _i < 1$ for every $i \in [N]$. Any such $\nu$ thus solves also $\nu = \nu P + \lambda$, i.e.,

$$\begin{aligned} \nu ( I - P ) = \lambda , \end{aligned}$$

(3.16)

where I is the N by N identity matrix. We call (3.16) the stable traffic equation; note that unlike the general traffic equation (2.11), the system (3.16) is linear. The system (3.16) in fact classifies whether or not the system is stable, as the following result shows. Since at this point we invoke the formulas (2.16) and (2.17), we now need to assume (A).

Proposition 3.6

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. The stable traffic equation (3.16) has a unique solution $\nu = \lambda (I-P)^{-1}$, which we denote by $\nu = (\nu _i)_{i \in [N]}$. Write $\rho _i:= \nu _i / \mu _i$. Then the following hold.

• (i) The process $\eta$ is stable if and only if $\rho _i < 1$ for all $i \in [N]$. Equivalently, the process is stable if and only if $\lambda (I -P)^{-1} < \mu$, componentwise.

• (ii) The $\rho _i$ are given by the explicit formula (2.16), where ${{\hat{v}}}_{N+1}$ is given by (2.17).

• (iii) If $\rho _i <1$ for all $i \in [N]$, then the quantity ${{\hat{v}}}_{N+1}$ given by (2.17) specifies the speed of the cloud, via $\lim _{t\rightarrow \infty } t^{-1} X_i (t) = {{\hat{v}}}_{N+1}$, a.s., for all $i \in [N+1]$.

Proof

Part (i) is essentially just a specialization of the characterization of stable Jackson networks (which goes back to Jackson [27, 28]; see e.g. [13, Sect. 2.1] or [16, Sect. 3.5]) to our setting; we give a proof using Proposition 3.3. Consider the stable traffic equation (3.16), where $\lambda$ and P are given by (2.9) and (2.10) respectively. The matrix $I-P$ is an M-matrix, and hence invertible (see Lemma 7.1 of [13]) and hence the solution $\nu = \lambda (I-P)^{-1}$ of (3.16) exists and is unique. Proposition 3.3 says that if the system is stable, then there is a solution to (3.16) with $\nu _i < \mu _i$ for all i. Conversely, if there exists a solution to (3.16) for which $\nu _i < \mu _i$ for all $i \in [N]$, this solution is necessarily the (unique) solution to the general traffic equation (2.11), and the system is stable, by Proposition 3.3. This argument proves part (i).

In terms of the loads $\rho _i = \nu _i / \mu _i$, the stable traffic equation (3.16) reads

$$\begin{aligned} (b_i+a_{i+1}) \rho _i = a_i\rho _{i-1}+b_{i+1} \rho _{i+1}, \text { for } i \in [N], \end{aligned}$$

(3.17)

where we impose the boundary condition $\rho _0 = \rho _{N+1} = 1$. Consider first the system (3.17) without any boundary condition; then, the solutions $(\rho _0,\rho _1,\ldots ,\rho _{N+1})$ to (3.17) form a linear subspace of ${{\mathbb {R}}}^{N+2}$, and this subspace is two-dimensional because $\rho _0$ and $\rho _1$ uniquely determine the rest. We identify a basis for this solution space. Define vectors $\alpha =(\alpha _0, \alpha _1, \ldots , \alpha _{N+1})$ and $\beta = (\beta _0,\beta _1, \ldots , \beta _{N+1})$ by $\alpha _0:= 1$, $\beta _0:=0$, and, for $k \in [N+1]$,

$$\begin{aligned} \alpha _k : = \frac{a_1\ldots a_k}{b_1\ldots b_k}, \text { and } \beta _k :=\frac{1}{b_k}+\frac{a_k}{b_kb_{k-1}}+ \cdots + \frac{a_k\ldots a_2}{b_k\ldots b_1}. \end{aligned}$$

Note that in the notation defined at (2.1), $\alpha _k = \alpha (1;k)$ and $\beta _k = \beta (1;k)$. The vectors $\alpha ,\beta \in {{\mathbb {R}}}^{N+2}$ are linearly independent (because one is strictly positive and the other is not). Moreover, it is straightforward to check that both $\alpha$ and $\beta$ solve the system (3.17): this is familiar from the usual solution to the difference equations associated with the general gambler’s ruin problem [32, pp. 106–108]. Then, since $\rho _0=1$, any solution of (3.17) with the given boundary conditions must have the form $\rho _i = \alpha _i + {{\hat{v}}}_{N+1} \beta _i$ for some ${{\hat{v}}}_{N+1}\in {{\mathbb {R}}}$, which is precisely (2.16). Using the condition $\rho _{N+1}=1$, we find that ${{\hat{v}}}_{N+1}$ must be given by (2.17). This proves part (ii).

Suppose that $\rho _i < 1$ for every $i \in [N+1]$. Then, by part (i), the system is stable, and Theorem 3.5 shows that $\lim _{t \rightarrow \infty } t^{-1} X_i (t) = v_i$, a.s., where, by (3.7),

$$\begin{aligned} v_1 = \rho _1 b_1 - a_1; ~~ v_i = \rho _i b_i - \rho _{i-1} a_i, \text { for } 2 \le i \le N; ~~ v_{N+1} = b_{N+1} - \rho _N a_N. \end{aligned}$$

It follows from (3.8) that $v_1 = v_2 = \cdots = v_{N+1}$; that their common value is $v_1 = {{\hat{v}}}_{N+1}$ given by (2.17) follows from the $i=1$ case of (2.16). This proves (iii). $\square$

4 Monotonicity, Restriction, and Mergers

In this section we study the relationship between the stability characterization of the whole system, in terms of appropriate traffic equations, as derived from the Jackson representation and presented in Propositions 3.3 and 3.6 above, with the traffic equations associated with certain sub-systems of the full system. This will allow us to characterize the maximal stable sub-systems, and show that their characteristic parameters can be expressed in terms of their intrinsic parameters only, and hence prove our main stability results, Theorems 2.1 and 2.3, and their corollaries presented in Sect. 2.

Let $I = [ \ell ;m] \subseteq [N+1]$ be a discrete interval with $m \ge 2$; recall that $I^\circ = [\ell ; m-1]$ excludes the rightmost element. Define $\lambda ^I:= (\lambda ^I_{i})_{i \in I^\circ }$ by $\lambda ^I_{\ell }:= a_\ell + b_{\ell +1}$ if $m=2$ ($I^\circ$ is a singleton), and, if $m \ge 3$,

$$\begin{aligned} \lambda ^I_{\ell }:= a_\ell , ~ \lambda ^I_{\ell +m-2}:= b_{\ell +m-1}, \text { and } \lambda ^I_j:= 0 \text { for } \ell +1 \le j \le \ell +m-3. \end{aligned}$$

(4.1)

Also, recalling the definition of $\mu _i$ from (2.8), define the matrix $(P^I_{i,j})_{i,j \in I^\circ }$ by

$$\begin{aligned} \begin{aligned} P^I_{i,i-1}&:= \frac{b_i}{\mu _i} = \frac{b_i}{b_i+a_{i+1}}, \text { for } \ell +1 \le i \le \ell +m-2; \\ P^I_{i,i+1}&:= \frac{a_{i+1}}{\mu _i} = \frac{a_{i+1}}{b_i+a_{i+1}}, \text { for } \ell \le i \le \ell +m-3; \end{aligned} \end{aligned}$$

(4.2)

with $P^I_{ij}:= 0$ otherwise. Set $Q^I_i:= 1 - \sum _{j \in I^\circ } P^I_{ij}$. Define $\mu ^I:= (\mu _i )_{i \in I^\circ }$. Note that in the case $I = [N+1]$, $\lambda ^{[N+1]} = \lambda$ and $P^{[N+1]} = P$ defined by (4.1) and (4.2) coincide with the definitions given previously at (2.9) and (2.10). Given $I \subseteq [N+1]$, we call the system

$$\begin{aligned} \nu ^I = (\nu ^I \wedge \mu ^I ) P^I + \lambda ^I \end{aligned}$$

(4.3)

the reduced traffic equation corresponding to I. For a solution $\nu ^I = (\nu ^I_i )_{i \in I^\circ }$ to (4.3), we write $\rho ^I (i):= \nu ^I_i / \mu _i$ for all $i \in I^\circ$. Then, similarly to (3.10), the reduced traffic equation can be written in terms of $(\rho ^I_i)_{i \in I^\circ }$ as

$$\begin{aligned} ( b_i + a_{i+1} ) \rho _i^I = \bigl ( 1 \wedge \rho ^I_{i-1} \bigr ) a_i + \bigl ( 1 \wedge \rho ^I_{i+1} \bigr ) b_{i+1}, \text { for all } i \in I^\circ , \end{aligned}$$

(4.4)

with the convention that $\rho ^I_{\min I -1} = \rho ^I_{\max I} = 1$. Analogously to (3.7), we then define

$$\begin{aligned} v^I_i:= \bigl ( 1 \wedge \rho ^I_i \bigr ) b_i - \bigl ( 1 \wedge \rho ^I_{i-1} \bigr ) a_i, \text { for all } i \in I,\end{aligned}$$

(4.5)

again with the convention $\rho ^I_{\min I -1} = \rho ^I_{\max I} = 1$. Note that $v^I$ satisfies an appropriate version of the algebraic Lemma 3.4.

The next result concerns solutions of the reduced traffic equation (4.3).

Lemma 4.1

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. Let $I \subseteq [N+1]$ be a discrete interval with $\vert I\vert \ge 2$. There is a unique solution $\nu ^I$ to (4.3); equivalently, there is a unique solution $\rho ^I$ to (4.4). Moreover, if $\rho ^I (j) \le 1$ for all $j \in I^\circ$, then $\rho ^I = {{\hat{\rho }}}_I$ as defined at (2.4) and, for all $i \in I$, $v^I_i = {{\hat{v}}}(I)$ with the definitions at (4.5) and (2.2).

Proof

Existence and uniqueness of the solution to (4.3) follows from the results of [23], exactly as existence and uniqueness of the solution to the general traffic equation (2.11) in Proposition 3.3. If $\rho ^I (j) \le 1$ for all $j \in I^\circ$, then (4.3) coincides with the system $\nu ^I = \nu ^I P^I + \lambda ^I$, a reduced version of the stable traffic equation (3.16), and the argument of Proposition 3.6 implies that $\rho ^I$ and $v^I$ satisfy the appropriate versions of (2.16) and (2.17), which establishes that $\rho ^I = {{\hat{\rho }}}_I$ as defined at (2.4) and $v^I_i = {{\hat{v}}}(I)$ as defined at (2.2). $\square$

Given a discrete interval $I \subseteq [N+1]$, we say I is a candidate stable cloud if the solution to the reduced traffic equation (4.3), or, equivalently, the system (4.4), gives $\rho ^I_i < 1$ for all $i \in I^\circ$. To facilitate the proof of Theorem 2.3, verifying the correctness of Algorithm 1, we need to identify when candidate stable clouds are genuine stable clouds. Here the key property is that a candidate stable cloud is necessarily either a stable cloud, or a subset of a stable cloud; hence we need to test whether a candidate stable cloud is maximal, or whether it can be extended to a larger candidate stable cloud. The next two lemmas present results in this direction.

Lemma 4.2 is a consistency result, which shows, in particular, that the solution $\nu$ to the general traffic equation (2.11), when restricted to a stable cloud $\theta \in \Theta$, coincides with $\nu ^\theta$, the solution to the reduced traffic equation (4.3) for $I = \theta$.

Lemma 4.2

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. Let $I \subseteq [N+1]$ be a discrete interval with $\vert I\vert \ge 2$, and let $I_0 \subseteq I$ be such that (i) either $\min I_0 = \min I$ or $\rho ^I_{\min I_0 -1} \ge 1$, and (ii) either $\max I_0 = \max I$ or $\rho ^I_{\max I_0} \ge 1$. Then $\nu ^I_i = \nu ^{I_0}_i$ for all $i \in I_0^\circ$.

Proof

Consider the solution $\nu ^I$ to the reduced traffic equation (4.3) over I, and let $\rho ^I_i:= \nu _i^I / \mu _i$. Since $\nu ^I$ solves (4.3) for I, we have from (4.4) that the $\rho ^I_i$, $i \in I_0^\circ$, satisfy

$$\begin{aligned} (b_i + a_{i+1} ) \rho ^{I}_i = \bigl ( 1 \wedge \rho ^I_{i-1} \bigr ) a_i + \bigl ( 1 \wedge \rho ^I_{i+1} \bigr ) b_{i+1}, \text { for all } i \in I_0^\circ , \end{aligned}$$

(4.6)

with boundary conditions $\rho ^{I}_{\min I_0-1} = 1$ (because either $\min I_0 = \min I$, in which case $\rho ^{I}_{\min I_0-1} = \rho ^{I}_{\min I-1} = 1$, the left boundary condition for (4.4) over I, or $\min I_0 > \min I$ and $\rho ^I_{\min I_0-1} \ge 1$, so $1 \wedge \rho ^I_{\min I_0 - 1} = 1$) and $\rho ^I_{\max I_0} = 1$ (analogously). In other words, the $\rho ^I_i$ solve exactly the system (4.4) over $I = I_0$, which is also the system solved by the $\rho ^{I_0}_i$. By uniqueness of solutions to the reduced traffic equation (4.3) (see Lemma 4.1), it follows that $\nu ^I_i = \nu ^{I_0}_i$ for all $i \in I_0^\circ$. $\square$

Lemma 4.3 gives conditions when a candidate stable cloud is further stabilized by the external system, and will allow us to extend a candidate stable cloud either to the left or to the right. The proof uses similar restriction ideas to the proof of Lemma 4.2.

Lemma 4.3

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. Let $I \subseteq [N+1]$ be a discrete interval with $\vert I\vert \ge 2$, and let $I_0 \subseteq I$ be such that $\rho ^{I_0}_i \le 1$ for all $i \in I_0^\circ$.

• (i) Suppose that $\min I_0 = \min I$, $\max I_0 < \max I$, and $\rho ^I_{\max I_0} < 1$. Then $v_i^I < v_i^{I_0}$ for all $i \in I^\circ _0$.

• (ii) Suppose that $\min I_0 > \min I$, $\max I_0 = \max I$, and $\rho ^I_{\min I_0 - 1} < 1$. Then $v_i^I > v_i^{I_0}$ for all $i \in I^\circ _0$.

Moreover, if either of the conditions in (i) or (ii) hold, then $\rho _i^I < \rho _i^{I_0}$ for all $i \in I_0^\circ$.

Proof

Suppose that the conditions in (i) hold; for convenience, let $K = \max I_0$. Since $\nu ^{I_0}$ solves (4.3) for $I_0$, and $\rho ^{I_0}_i \le 1$ for all $i \in I_0^\circ$, it follows from Lemma 4.1 that $\rho ^{I_0}_i = {{\hat{\rho }}}_{I_0} (i)$, $i \in I_0^\circ$, for ${{\hat{\rho }}}_{I_0}$ as defined at (2.4). Since $\nu ^I$ solves (4.3) for I, we have from (4.4) that the $\rho ^I_i$, $i \in I_0^\circ$, solve the system (4.6), with $\rho ^I_{\min I-1} = \rho ^I_{\min I_0 -1} = 1$ and $\rho ^I_{K} < 1$. If we set $b_{K}':= \rho ^I_K b_K$, then this system coincides with the reduced traffic equation (4.4) over $I=I_0$, but with $b_K$ replaced by $b_K' < b_K$ (since $\rho ^I_K < 1$). Thus, if we define ${{\hat{\rho }}}'_{I_0}$ by (2.4), but with $b'_K$ in place of $b_K$, then Lemma 4.1 shows that $\rho ^I_i = {{\hat{\rho }}}'_{I_0} (i)$ for all $i \in I_0^\circ$.

Suppose $I_0 = [\ell ; m]$. In the formula (2.4) for ${{\hat{\rho }}}_{I_0} (j)$, $j \in I_0^\circ$, none of $\alpha (\ell ; 1)$, $\beta (\ell ; 1)$, ..., $\alpha (\ell ; m-1)$, $\beta (\ell ; m-1)$ contains $b_K = b_{\ell +m-1}$, which appears only in ${{\hat{v}}}(\ell ; m)$. Moreover, as a function of $b_{\ell +m-1}$, we have ${{\hat{v}}}(\ell ; m) = A b_{\ell +m-1} -B$ for $A >0$, so that ${{\hat{\rho }}}_{I_0} (j)$ is strictly increasing in $b_K$. Since $b'_K < b_K$, it follows that $\rho ^I_j = {{\hat{\rho }}}'_{I_0} (j) < {{\hat{\rho }}}_{I_0} (j) = \rho ^{I_0}_j$ for all $j \in I_0^\circ$, as claimed. In particular, $\rho ^I_j < 1$ for all $j \in I_0^\circ$.

Let $L = \min I = \min I_0$. Then, from (4.5) and the fact that $\rho ^I_L < \rho ^{I_0}_L \le 1$, $v^{I_0}_{L} - v^{I}_{L} = \bigl ( \rho ^{I_0}_{L} - \rho ^{I}_L \bigr ) b_L > 0$, and, by the appropriate version of (3.8), $v^{I_0}_j = v^{I_0}_L > v^{I}_L = v^I_j$ for all $j \in I_0^\circ$. This completes the proof of the lemma in the case where the hypotheses of (i) hold. The argument in the case that the hypotheses in (ii) hold is similar. $\square$

Now we can complete the proof of the main stability result, Theorem 2.1.

Proof of Theorem 2.1

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. Proposition 3.3 shows that there exists a unique solution $\nu = (\nu _i)_{i \in [N]}$ to the general traffic equation (2.11). Define $\rho _i:= \nu _i / \mu _i$ for every $i \in [N]$. Then the $\rho _i$ define uniquely an $n \in [N+1]$ and a partition $\Theta = (\theta _1, \ldots , \theta _n)$ as follows. If $\rho _1 \ge 1$, set $\theta _1 = \{ 1\}$. Otherwise, set $\theta _1 = \{ 1, \ldots , k, k+1\}$ for the maximal $k \le N$ for which $\rho _k <1$. If $k = N$, this completes $\Theta$. Otherwise $k < N$ and $\rho _{k+1} \ge 1$. If $k+2 > N$ or $\rho _{k+2} \ge 1$, set $\theta _2 = \{ k+2\}$, else set $\theta _2 = \{ k+2, \ldots , k+1+m, k+2+m\}$ for the maximal m with $k + 1 + m \le N$ and $\rho _{k+1+m} < 1$. Iterating this definition gives $\Theta = (\theta _1, \ldots , \theta _n)$ where, by construction, $\rho _i \in (0,1)$ for all $i \in \theta ^\circ$, $\theta \in \Theta ^\star$, and $\rho _{\max \theta } \ge 1$ provided $\max \theta \le N$. Lemma 4.2 with $I = [N+1]$ and $I_0 = \theta \in \Theta ^\star$ then shows that $\rho _i = \rho ^{[N+1]}_i = \rho ^\theta _i$ for all $i \in \theta ^\circ$, while Lemma 4.1 says that $\rho ^\theta = {{\hat{\rho }}}_\theta (i)$. Hence $\rho _i = {{\hat{\rho }}}_\theta (i)$ given by (2.4) for $i \in \theta ^\circ$. This proves (2.12).

For statement (i), observe that $S:= \{ i \in [N]: \rho _i < 1\}$ as defined in Proposition 3.3 is given by $S = \cup _{\theta \in \Theta ^\star } \theta ^\circ$, by the property established above that $\rho _i < 1$ if and only if $i \in \theta ^\circ$ for some $\theta \in \Theta ^\star$. Thus the first display in statement (i) follows from Proposition 3.3, using the fact that $\varpi _\theta (i)$ as defined in (2.7) is given by $\varpi _\theta (z_1, \ldots , z_k ) = \prod _{i \in \theta ^\circ } \rho _i^{z_i} (1-\rho _i)$, where $\vert \theta \vert = k+1$ and $\rho _i = {{\hat{\rho }}}_\theta (i)$, by (2.12). We have shown that $\lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}( \eta _j (t) \ge m ) = \rho _j^m$ for $j \in S$, and, by (3.2), $\eta _j (t)$, $t \in {{\mathbb {R}}}_+$, is uniformly integrable, so that $\lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {E}}\,}}\eta _j (t) = \sum _{m \in {{\mathbb {N}}}} \rho _j^m = \rho _j / (1-\rho _j)$. With $R_\theta$ as defined at (2.5), we have that ${{\,\mathrm{\mathbb {E}}\,}}R_\theta (t) = {{\,\mathrm{\mathbb {E}}\,}}\sum _{j \in \theta ^\circ } (1+ \eta _j (t))$, by (1.2), and taking $t \rightarrow \infty$ yields (2.13). This completes the proof of (i).

Consider statement (ii). For $\theta _\ell , \theta _r \in \Theta$ with $\ell < r$, we have from (1.2) that $\min _{i \in \theta _r} X_i (t) - \max _{i \in \theta _\ell } X_i (t) \ge \eta _{\max \theta _\ell } (t)$. Moreover, from the statement after (2.12), we have $\rho _{\max \theta _\ell } \ge 1$. In the notation of Proposition 3.3, this means $\max \theta _\ell \in U$, and hence, by (3.3), $\lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}( \eta _{\max \theta _\ell } (t) \le B ) = 0$ for all $B < \infty$. This proves (2.14).

For statement (iii), existence of the $v_i$ follows from Theorem 3.5. Lemma 3.4 shows that, for each $\theta \in \Theta$, $v_i$ is the same for all $i \in \theta ^\circ$; call the common value ${{\hat{v}}}(\theta )$. The fact that ${{\hat{v}}}(\theta )$ satisfies (2.2) and (2.3) follows from Lemma 4.1. This completes the proof of the theorem. $\square$

The following theorem will be our main tool to prove Theorem 2.3: it takes the results of Lemmas 4.1–4.3 and presents them in terms of pairwise comparisons of adjacent candidate stable clouds, tailored to the structure of Algorithm 1. In particular, Theorem 4.4 shows that if one has two adjacent candidate stable clouds, in which the cloud to the left has a greater intrinsic speed, then the union of the two candidate stable clouds is itself a candidate stable cloud.

Theorem 4.4

Let $N \in {{\mathbb {N}}}$ and suppose that (A) holds. Let $I_1$ and $I_2$ be disjoint discrete interval subsets of $[N+1]$, with $K:= \max I_1 = \min I_2 -1$. Let $\nu ^{I_k}$ be the solution to the reduced traffic equation (4.3) with $I = I_k$, $k \in \{1,2\}$. Define $\rho ^{I_k}_i:= \nu _i^{I_k}/\mu _i$.

Suppose that $\rho ^{I_1}_i \le 1$ for all $i \in I_1^\circ$ and $\rho ^{I_2}_i \le 1$ for all $i \in I_2^\circ$. Recall the definition of ${{\hat{v}}}$ from (2.2). Let $I:= I_1 \cup I_2$, which is also a discrete interval subset of $[N+1]$. Then the following hold.

• (i) If ${{\hat{v}}}({I_1}) > {{\hat{v}}}(I_2)$, then $\rho ^I_i < 1$ for all $i \in I^\circ$, and ${{\hat{v}}}({I_1})> {{\hat{v}}}({I}) > {{\hat{v}}}({I_2})$. Moreover,

  $$\begin{aligned} \rho ^I (i) < {\left\{ \begin{array}{ll} \rho ^{I_1}_i &{} \text {if } i \in I_1^\circ , \\ 1 &{} \text {if } i = K, \\ \rho ^{I_2}_i &{} \text {if } i \in I_2^\circ .\end{array}\right. } \end{aligned}$$

  (4.7)

• (ii) If ${{\hat{v}}}({I_1}) \le {{\hat{v}}}({I_2})$, then

  $$\begin{aligned} \rho ^I_i = {\left\{ \begin{array}{ll} \rho ^{I_1}_i &{} \text {if } i \in I_1^\circ , \\ \rho ^{I_2}_i &{} \text {if } i \in I_2^\circ .\end{array}\right. } \end{aligned}$$

  (4.8)

  Moreover, if ${{\hat{v}}}({I_1}) < {{\hat{v}}}({I_2} )$, then $\rho ^{I}_K > 1$, while if ${{\hat{v}}}({I_1}) = {{\hat{v}}}({I_2})$, then $\rho ^I_K = 1$.

Proof

Let $I_1$ and $I_2$ be disjoint discrete interval subsets of $[N+1]$, with $K:= \max I_1 = \min I_2 -1$. Let $\nu ^{I_k}$ be the solution to the reduced traffic equation (4.3) with $I = I_k$, $k \in \{1,2\}$. Define $\rho ^{I_k}_i:= \nu _i^{I_k}/\mu _i$, and define $v^{I_k}$ by (4.5). Suppose that $\rho ^{I_1} (i) \le 1$ for all $i \in I_1^\circ$ and $\rho ^{I_2}_i \le 1$ for all $i \in I_2^\circ$. Then Lemma 4.1 shows that

$$\begin{aligned} v^{I_1}_i = {{\hat{v}}}(I_1) \text { for all } i \in I_1, \text { and } v^{I_2}_i = {{\hat{v}}}(I_2) \text { for all } i \in I_2. \end{aligned}$$

(4.9)

Consider also the solution $\nu ^I$ to the reduced traffic equation (4.3) over $I:= I_1 \cup I_2$. Suppose first that $\rho ^I ( K ) \ge 1$, i.e., $\nu ^I_{K} \ge \mu _{K}$. Then Lemma 4.2, applied first with $I_0 = I_1$ and second with $I_0=I_2$, implies that (4.8) holds. From (4.5), this means that $v^I_i = v^{I_1}_i$ for all $i \in I_1$ and $v^I_i = v^{I_2}_i$ for all $i \in I_2$. Theorem 3.5 and (3.8) (appropriately adapted) imply that if $\rho ^I ( K ) = 1$, we have $v^I_K = v^I_{K+1}$, while if $\rho ^I_K >1$, we have $v^I_K < v^I_{K+1}$. Thus it follows from (4.9) that

$$\begin{aligned} \rho ^I_K&> 1 \text { implies } {{\hat{v}}}({I_1}) < {{\hat{v}}}({I_2}) ; \end{aligned}$$

(4.10)

$$\begin{aligned} \rho ^I_K&= 1 \text { implies } {{\hat{v}}}({I_1}) = {{\hat{v}}}({I_2}) . \end{aligned}$$

(4.11)

On the other hand, Lemma 4.3 shows that

$$\begin{aligned} \rho ^I_K&< 1 \text { implies } {{\hat{v}}}({I_1})> {{\hat{v}}}(I) > {{\hat{v}}}({I_2}) , \end{aligned}$$

(4.12)

and the final statement in Lemma 4.3 yields (4.7). Combining (4.10)–(4.12), we obtain

$$\begin{aligned} \rho ^I_K&> 1 \text { if and only if } {{\hat{v}}}({I_1}) < {{\hat{v}}}({I_2}) ; \end{aligned}$$

(4.13)

$$\begin{aligned} \rho ^I_K&= 1 \text { if and only if } {{\hat{v}}}({I_1}) = {{\hat{v}}}({I_2}) ; \end{aligned}$$

(4.14)

$$\begin{aligned} \rho ^I_K&< 1 \text { if and only if } {{\hat{v}}}({I_1})> {{\hat{v}}}(I) > {{\hat{v}}}({I_2}) . \end{aligned}$$

(4.15)

The equivalences (4.13)–(4.15) complete the proof of the theorem. $\square$

We now complete the proofs of Theorem 2.3 and the corollaries presented in Sect. 2.

Proof of Theorem 2.3

We claim that Theorem 4.4(i) and an induction shows that, at each step of Algorithm 1, the ordered partition $\Theta ^\kappa$ is such that

$$\begin{aligned} \rho _i^\theta < 1 \text { for all } i \in \theta ^\circ \text { and all } \theta \in \Theta ^\kappa \text { with } \vert \theta \vert \ge 2. \end{aligned}$$

(4.16)

The base case of (4.16), $\kappa = 0$, is trivial since the initial partition consists only of singletons. For the inductive step, the inductive hypothesis deals trivially with any $\theta$ which is unchanged from $\Theta ^\kappa$ to $\Theta ^{\kappa +1}$. Consider adjacent $\theta ^\kappa _{j}, \theta ^\kappa _{j+1} \in \Theta ^\kappa$ with ${{\hat{v}}}( \theta ^\kappa _j ) > {{\hat{v}}}(\theta ^\kappa _{j+1} )$, and define the merger $\theta ^{\kappa +1}_j = \theta ^\kappa _j \cup \theta ^\kappa _{j+1}$. Then Theorem 4.4(i) and the inductive hypothesis completes the proof of (4.16).

From (4.16), the output of Algorithm 1 is an ordered partition $\Theta$ such that $\rho _i^\theta < 1$ for all $i \in \theta ^\circ$ and all $\theta \in \Theta ^\star$. Moreover, if $\Theta = (\theta _1, \ldots , \theta _n)$, the stopping condition for Algorithm 1 implies that ${{\hat{v}}}( \theta _1 ) \le \cdots \le {{\hat{v}}}(\theta _n)$. Thus Theorem 4.4(ii) shows that for every adjacent $\theta _j, \theta _{j+1} \in \Theta$, one has $\rho ^\theta _K \ge 1$ where $K = \max \theta _j$ and $\theta = \theta _j \cup \theta _{j+1}$. Then Lemma 4.2 completes the verification of (2.12), showing that the $\Theta$ produced by Algorithm 1 is the cloud partition characterized in Theorem 2.1. $\square$

Proof of Corollary 2.5

Theorem 2.1 shows that $\Theta$ consists solely of singletons if and only if $\rho _i \ge 1$ for all $i \in [N]$, where $\rho _i =\nu _i/ \mu _i$ and $\nu$ is the unique solution to (2.11). In particular, if $\Theta$ consists only of singletons, then Theorem 2.1(iii) with (2.2) implies that $v_i = {{\hat{v}}}( \{ i \} ) = b_i - a_i$ must satisfy $v_{i+1} \ge v_i$ for all i, which yields (2.15). On the other hand, if (2.15) holds, then Algorithm 1 will terminate immediately, and Theorem 2.3 implies that $\Theta$ consists solely of singletons. The final sentence in Corollary 2.5 follows from Theorem 2.1(ii) and (iii). $\square$

Proof of Corollary 2.6

Theorem 2.1 combined with Proposition 3.6 shows that $\Theta = ([N+1])$ consists of a single part if and only if $\rho _i < 1$ for all $i \in [N]$, where $\rho _i = \nu _i/\mu _i$ and $\nu$ is the unique solution to (3.16), i.e., $\rho _i$ is given by (2.16). If ${{\hat{v}}}_{N+1} = {{\hat{v}}}([N+1])$ as given at (2.2), then (2.17) holds. The limit statement (2.18) follows from Theorem 2.1(i), while Theorem 2.1(iii) gives the $\lim _{t \rightarrow \infty } t^{-1} X_i (t) = {{\hat{v}}}_{N+1}$ for all $i \in [N+1]$. $\square$

Proof of Corollary 2.11

Suppose that $\Theta = (\theta _1, \ldots , \theta _n)$ is the cloud partition described in Theorem 2.1. Then Theorem 2.1(iii) says that $\min _{i \in [N+1]} v_i = v_1 = {{\hat{v}}}(\theta _1)$, where ${{\hat{v}}}$ is defined at (2.2). Suppose that $\theta _1 = [1;m]$ for $m \in [N+1]$. Then ${{\hat{v}}}(\theta _1 ) = {{\hat{v}}}(1;m) > 0$ if and only if $\alpha (1;m) < 1$, where $\alpha$ is defined by (2.1). Thus, ${{\hat{v}}}(\theta _1 ) > 0$ if and only if $\prod _{i=1}^m a_i < \prod _{i=1}^m b_i$. Thus condition (ii) in the corollary implies (i).

Conversely, suppose that ${{\hat{v}}}(\theta _1 ) >0$. If $\theta _1 = [1;m]$ for $m \ge 2$, then ${{\hat{v}}}(\theta _1^\circ )> {{\hat{v}}}(\theta _1) > 0$, by applying Theorem 4.4 with $I_1 = \theta _1^\circ = \{1, \ldots , m-1\}$ and $I_2 = \{m\}$, using (2.12) to characterize the stability of $\theta _1$. Iterating Theorem 4.4, it follows that ${{\hat{v}}}(1;k ) > 0$ for all $k \in [m]$. Suppose that (ii) fails; then there is some $r \ge m$ such that $\prod _{i=1}^k a_i < \prod _{i=1}^k b_i$ for all $k \le r$, but $\prod _{i=1}^{r+1} a_i \ge \prod _{i=1}^{r+1} b_i$. In particular, $a_{r+1} > b_{r+1}$, $a_{r+1} a_r > b_{r+1} b_r$, ..., $a_{r+1} \cdots a_2 > b_{r+1} \cdots b_2$. By (2.2), this means that ${{\hat{v}}}( I ) < 0$ for any I with $\max I = r+1$ and $\min I \ge 2$. Considering Algorithm 1, if $\theta \in \Theta$ is such that $r +1 \in \theta$, it follows that ${{\hat{v}}}(\theta ) < 0$ too. But the speeds of stable clouds increase from left to right, so this is not possible, giving a contradiction. Hence (i) implies (ii). $\square$

5 Central Limit Theorem for the Stable System

In this section we prove Theorems 2.12 and 2.14, the central limit theorems in the case of a stable system.

Proof of Theorem 2.12

Suppose that $\rho _i < 1$ for all $i \in [N]$, where $\rho _i$ is given by (2.16), and define ${{\hat{v}}}_{N+1}$ by (2.17). Consider the processes $\xi$ (on ${{\mathbb {Z}}}\times {{\mathbb {Z}}}_+^N$) and $\eta$ (on ${{\mathbb {Z}}}_+^N$) defined through (1.2) and (1.3); by Corollary 2.6 and (2.7),

$$\begin{aligned} \lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}( \eta (t) = z ) = \prod _{i=1}^N \rho _i^{z_i} (1-\rho _i) = \varpi _{[N+1]} ( z ), \text { for all } z= (z_1, \ldots , z_N ) \in {{\mathbb {Z}}}_+^N. \end{aligned}$$

For ease of notation, write ${{\widetilde{X}}}_1 (t):= X_1 (t) - {{\hat{v}}}_{N+1} t$. As described in Remarks 2.13(b), from the results of [4] one can directly deduce the marginal central limit theorem

$$\begin{aligned} (\sigma ^2 t)^{-1/2} {{\widetilde{X}}}_1 (t) \overset{\textrm{d}}{\longrightarrow }{{\mathcal {N}}}(0, 1 ), \end{aligned}$$

(5.1)

for a constant $\sigma ^2 \in (0,\infty )$.

Take s, t with $0< t-s< t < \infty$, and let $E_{s,t} (w):= \{ (\sigma ^2 t)^{-1/2} {{\widetilde{X}}}_1 (t-s) \le w \}$, for $w \in {{\mathbb {R}}}$. Fix $\varepsilon >0$. Choose a finite set $A \subset {{\mathbb {Z}}}_+^N$ such that $\varpi _{[N+1]} (A) > 1-\varepsilon$. Since $\xi$ and $\eta$ defined by (1.2) and (1.3) are both Markov, we have that ${{\,\mathrm{\mathbb {P}}\,}}( \eta (t) = z \mid \xi (t-s) )$ depends on $\xi (t-s)$ only through $\eta (t-s)$, and not ${{\widetilde{X}}}_1 (t-s)$. Hence

$$\begin{aligned}&{{\,\mathrm{\mathbb {P}}\,}}[ E_{s,t} (w) \cap \{ \eta (t) = z \} ] \\&\quad \le {{\,\mathrm{\mathbb {P}}\,}}[ \eta (t-s) \notin A ] + {{\,\mathrm{\mathbb {E}}\,}}\bigl [ {{\,\mathrm{\mathbb {P}}\,}}[ \eta (t) = z \mid \xi (t-s) ] {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta (t-s) \in A\}} {\mathbb {1}}_{ E_{s,t} (w)} \bigr ] \\&\quad = {{\,\mathrm{\mathbb {P}}\,}}[ \eta (t-s) \notin A ] + {{\,\mathrm{\mathbb {E}}\,}}\bigl [ {{\,\mathrm{\mathbb {P}}\,}}[ \eta (t) = z \mid \eta (t-s) ] {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta (t-s) \in A\}} {\mathbb {1}}_{ E_{s,t} (w)} \bigr ] . \end{aligned}$$

Then we can choose $s_0$ large enough (depending on $\varepsilon$ and z) such that, for all s, t with $s \ge s_0$ and $t-s \ge s_0$, ${{\,\mathrm{\mathbb {P}}\,}}[ \eta (t-s) \in A ] \ge 1 -2 \varepsilon$, and

$$\begin{aligned} \bigl \vert {{\,\mathrm{\mathbb {P}}\,}}[ \eta (t) = z \mid \eta (t-s) ] - \varpi _{[N+1]} (z) \bigr \vert {{\mathbb {1}}\hspace{-0.83328pt}}{\{ \eta (t-s) \in A \}} \le \varepsilon . \end{aligned}$$

The preceding argument, together with a similar argument for a lower bound, shows that for every $\varepsilon >0$, $z \in {{\mathbb {Z}}}_+^N$, and $w \in {{\mathbb {R}}}$, we may choose and fix s (large) such that, for all t with $t-s$ large enough,

$$\begin{aligned} \bigl \vert {{\,\mathrm{\mathbb {P}}\,}}[ E_{s,t} (w) \cap \{ \eta (t) = z \} ] -\varpi _{[N+1]} (z) {{\,\mathrm{\mathbb {P}}\,}}[ E_{s,t} (w) ] \bigr \vert \le \varepsilon .\end{aligned}$$

Now from (5.1) we have that $(\sigma ^2(t-s))^{-1/2} {{\widetilde{X}}}_1 (t-s)$ converges in distribution to ${{\mathcal {N}}}(0, \sigma ^2 )$ as $t \rightarrow \infty$. For fixed s, $\lim _{t \rightarrow \infty } \frac{t}{t-s} = 1$, and so $\lim _{t \rightarrow \infty } {{\,\mathrm{\mathbb {P}}\,}}[ E_{s,t} (w) ] = \Phi (w)$, the standard normal distribution function. Moreover, it is not hard to see that, since $X_1$ has uniformly bounded jump rates with increments $\pm 1$,

$$\begin{aligned} \lim _{t \rightarrow \infty } t^{-1/2} {{\,\mathrm{\mathbb {E}}\,}}\big \vert {{\widetilde{X}}}(t) - {{\widetilde{X}}}(t-s) \bigr \vert = 0, \end{aligned}$$

for fixed s. Hence, for fixed $z \in {{\mathbb {Z}}}_+^N$, for all t large enough it holds that

$$\begin{aligned} \bigl \vert {{\,\mathrm{\mathbb {P}}\,}}[ E_{s,t} (w) \cap \{ \eta (t) = z \} ] - {{\,\mathrm{\mathbb {P}}\,}}[ \{ (\sigma ^2 t)^{-1/2} {{\widetilde{X}}}_1 (t) \le w \} \cap \{ \eta (t) = z \} ] \bigr \vert \le \varepsilon , \end{aligned}$$

using continuity of $\Phi$. Combining these bounds we conclude that, for every $\varepsilon >0$ and all t sufficiently large

$$\begin{aligned} \bigl \vert {{\,\mathrm{\mathbb {P}}\,}}[ \{ (\sigma ^2 t)^{-1/2} {{\widetilde{X}}}_1 (t) \le w \} \cap \{ \eta (t) = z \} ] - \varpi _{[N+1]} (z) \Phi (w) \bigr \vert \le \varepsilon . \end{aligned}$$

This completes the proof. $\square$

Finally, we turn to the proof of Theorem 2.14, the main part of which is to compute the limiting variance $\sigma ^2$ in the $N=1$ case of Theorem 2.12.

Proof of Theorem 2.14

Take $N=1$, so the system consists of $N+1 = 2$ particles, with locations $X_1(t) < X_2(t)$, and a single gap process, given for $t \in {{\mathbb {R}}}_+$ by $\eta (t):= \eta _1 (t) = X_2(t) - X_1(t) - 1 \in {{\mathbb {Z}}}_+$. In this case, $\eta$ is a classical M/M/1 queue, with arrival rate $\lambda := a_1 + b_2$ and service rate $\mu := a_2 + b_1$. Under the conditions of Theorem 2.14, we have $\lambda < \mu$, i.e., the M/M/1 queue is stable. Then $\eta$ has a unique geometric stationary distribution; denote by ${{\,\mathrm{{\widetilde{\mathbb {P}}}}\,}}$ and ${{\,\mathrm{{\widetilde{\mathbb {E}}}}\,}}$ probability and expectation for an initial distribution such that $\eta (0)$ is in stationarity, and, for definiteness $X_1 (0) = 0$.

Theorem 2.12 implies that (2.26) holds, where (2.17) yields ${{\hat{v}}}_{N+1} = {{\hat{v}}}_2$ as in (2.25); it remains to verify that $\sigma ^2$ is given by (2.25). Since Theorem 2.12 applies for any fixed initial state $X(0) \in {{\mathbb {X}}}_{N+1}$, it also holds for any initial distribution; hence also under ${{\,\mathrm{{\widetilde{\mathbb {P}}}}\,}}$, when $\eta (0)$ is stationary. Thus to complete the proof of Theorem 2.14, it suffices to prove

$$\begin{aligned} \lim _{t \rightarrow \infty } t^{-1} {{\,\mathrm{{\widetilde{\mathbb {V}}ar}}\,}}( X_1 (t) ) = \frac{a_1 a_2 + b_1 b_2}{a_2+b_1}. \end{aligned}$$

(5.2)

For $t \in {{\mathbb {R}}}_+$, let

$$\begin{aligned} A(t):= \# \{ s \in [0,t]: \eta (s) = \eta (s-) + 1 \}, \text { and } D(t):= \# \{ s \in [0,t]: \eta (s) = \eta (s-) -1\}, \end{aligned}$$

denote, respectively, the number of arrivals and departures from the queue $\eta$ up to time t. Then $A(t) = A_1 (t) + A_2(t)$, where

$$\begin{aligned} A_1 (t)&:= \#\{ s \in [0,t] : X_1 (s) = X_1(s-) - 1 \},\\ A_2 (t)&:= \#\{ s \in [0,t] : X_2 (s) = X_2(s-) + 1 \} , \end{aligned}$$

count arrivals representing particle 1 jumping left and particle 2 jumping right, respectively. Similarly, $D(t) = D_1 (t) + D_2 (t)$, where

$$\begin{aligned} D_1 (t)&:= \#\{ s \in [0,t] : X_1 (s) = X_1(s-) + 1 \}, \\ D_2 (t)&:= \#\{ s \in [0,t] : X_2 (s) = X_2(s-) - 1 \} . \end{aligned}$$

We have the representations $\eta (t) - \eta (0) = A(t) - D(t)$,

$$\begin{aligned} X_1 (t) - X_1(0) = D_1(t) - A_1(t), \text { and } X_2 (t) - X_2(0) = A_2(t) - D_2 (t), \text { for } t \in {{\mathbb {R}}}_+, \end{aligned}$$

where $X_2(0) = X_1(0) + 1 + \eta (0)$. Conditional on $\eta [0,t]:= (\eta _s)_{s \in [0,t]}$, we have that $A_1(t) \sim \text {Bin} ( A(t), p_1)$, $A_2(t) \sim \text {Bin} (A(t), 1-p_1)$, where $p_1:= a_1/(a_1+b_2)$, and $D_1(t) \sim \text {Bin} ( D(t), p_2)$, $D_2(t) \sim \text {Bin} (D(t), 1-p_2)$, where $p_2:= b_1/(a_2+b_1)$. Moreover, given $\eta [0,t]$, $(A_1(t),A_2(t))$ is independent of $(D_1(t),D_2(t))$. Hence we see that

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}( X_1 (t) - X_1 (0) \mid \eta [0,t] )&= - p_1 A(t) + p_2 D(t), \\ {{\,\mathrm{\mathbb {E}}\,}}( X_2 (t) - X_2 (0) \mid \eta [0,t] )&= (1- p_1) A(t) - (1- p_2) D(t), \\ {{\,\mathrm{\mathbb {V}ar}\,}}( X_i (t) \mid \eta [0,t] )&= p_1 (1-p_1) A(t) + p_2 (1-p_2) D(t) , \text { for } i \in \{1,2\}. \end{aligned}$$

Now, $A(t) \sim \text {Po} (\lambda t)$, and, by Burke’s theorem [11], $D(t) \sim \text {Po} (\lambda t)$ under ${{\,\mathrm{{\widetilde{\mathbb {P}}}}\,}}$. It follows that

$$\begin{aligned} {{\,\mathrm{{\widetilde{\mathbb {E}}}}\,}}\left[ {{\,\mathrm{\mathbb {V}ar}\,}}( X_i (t) \mid \eta [0,t] ) \right]&= \left[ p_1 (1-p_1) + p_2 (1-p_2) \right] \lambda t, \text { and} \\ {{\,\mathrm{{\widetilde{\mathbb {V}}ar}}\,}}\left[ {{\,\mathrm{\mathbb {E}}\,}}( X_1 (t) \mid \eta [0,t] ) \right]&= \left[ p_1^2 + p_2^2 \right] \lambda t - 2p_1 p_2 {{\,\mathrm{{\widetilde{\mathbb {C}}ov}}\,}}( A(t), D(t) ) .\end{aligned}$$

Note that

$$\begin{aligned} A (t) D (t) = \frac{1}{2} \left[ A (t)^2 + D(t)^2 - (A (t) - D (t ))^2 \right] , \end{aligned}$$

so

$$\begin{aligned} {{\,\mathrm{{\widetilde{\mathbb {E}}}}\,}}[ A(t) D(t) ] = \lambda ^2 t^2 + \lambda t - \frac{1}{2} {{\,\mathrm{{\widetilde{\mathbb {E}}}}\,}}[ (\eta (t)-\eta (0))^2 ]. \end{aligned}$$

That is,

$$\begin{aligned} {{\,\mathrm{{\widetilde{\mathbb {C}}ov}}\,}}( A(t), D(t) ) = \lambda t - \frac{1}{2} {{\,\mathrm{{\widetilde{\mathbb {V}}ar}}\,}}( \eta (t) - \eta (0) ). \end{aligned}$$

Under the stationary distribution, $\eta$ has finite variance, so $\sup _{t \in {{\mathbb {R}}}_+} {{\,\mathrm{{\widetilde{\mathbb {V}}ar}}\,}}( \eta (t) - \eta (0) ) < \infty$. Hence, using the total variance formula and collecting the above computations, we get

$$\begin{aligned} {{\,\mathrm{{\widetilde{\mathbb {V}}ar}}\,}}( X_1 (t) )&= {{\,\mathrm{{\widetilde{\mathbb {E}}}}\,}}\left[ {{\,\mathrm{\mathbb {V}ar}\,}}( X_1 (t) \mid \eta [0,t] ) \right] + {{\,\mathrm{{\widetilde{\mathbb {V}}ar}}\,}}\left[ {{\,\mathrm{\mathbb {E}}\,}}( X_1 (t) \mid \eta [0,t] ) \right] \\&= \left[ p_1 (1-p_1) + p_2 (1-p_2) + (p_1 - p_2)^2 \right] \lambda t + O(1) \\&= \left[ p_1 + p_2 - 2 p_1 p_2 \right] \lambda t + O(1) \\&= \frac{a_1 a_2 + b_1 b_2}{a_2+b_1} t + O(1) . \end{aligned}$$

From here, we verify (5.2), to conclude the proof. $\square$

6 Discussion and Connection to Continuum Models

6.1 Diffusions with Rank-Based Interactions

Continuum (diffusion) models, in which $N+1$ particles perform Brownian motions with drifts and diffusion coefficients determined by their ranks, have been extensively studied in recent years, and include the Atlas model and its relatives: see [8, 12, 24, 25, 30, 40, 44, 45, 50] and references therein. An informative recent overview of the literature is given in [45, Sect. 2]. In this section we describe these models using some stochastic differential equations (SDEs) rather informally, so that we can make comparisons; precise formulations, existence and uniqueness results can be found in the references cited.

In the early versions of these models (e.g. [8, 40]), the particles move independently, and are allowed to pass through each other, but exchange drift and diffusion parameters when they do so. For $t\in {{\mathbb {R}}}_+$, denote by $y_i (t)$ the location of particle with label $i \in [N+1]$, and let $x_i (t)$ denote the location of the particle with rank i ($i=1$ being the leftmost particle), so $x_1 (t) \le \cdots \le x_{N+1} (t)$ is an ordering of $y_1 (t), \ldots , y_{N+1} (t)$. Also let $r_i (t)$ denote the rank of particle with label i. Let $u_1, \ldots , u_{N+1} \in {{\mathbb {R}}}$ and $\sigma _1, \ldots , \sigma _{N+1} \in (0,\infty )$ be collections of drift and volatility parameters. Let $W_1, \ldots , W_{N+1}$ be independent, standard ${{\mathbb {R}}}$-valued Brownian motions. Suppose that

$$\begin{aligned} {\mathrm d}y_i (t) = u_{r_i(t)} {\mathrm d}t + \sigma _{r_i(t)} {\mathrm d}W_i (t), \text { for } i \in [N+1], \end{aligned}$$

(6.1)

i.e., particle i performs Brownian motion with drift and volatility parameters determined by its rank; if $u_j \equiv u$ and $\sigma _j \equiv \sigma$ are constant, the particles are independent, otherwise, there is interaction mediated by the ranks. The Atlas model [8, 25] has $u_1 > 0$, $u_2 = \cdots = u_{N+1} = 0$, and $\sigma _1 = \cdots = \sigma _{N+1} =1$; cf. Example 2.15 above.

In terms of the ordered particles, it can be shown (e.g. [25, Lem. 1]) that, for independent standard Brownian motions ${{\widetilde{W}}}_1, \ldots , {{\widetilde{W}}}_{N+1}$,

$$\begin{aligned} {\mathrm d}x_i (t) = u_{i} {\mathrm d}t + \sigma _{i} {\mathrm d}{{\widetilde{W}}}_i (t) + \frac{1}{2} {\mathrm d}L^{i} (t) - \frac{1}{2} {\mathrm d}L^{{i+1}} (t), \text { for } i \in [N+1], \end{aligned}$$

(6.2)

where $L^{i}(t)$ is the local time at 0 of $x_i-x_{i-1}$ up to time t, with the convention $L^1 \equiv L^{N+2} \equiv 0$. The local-time terms in (6.2) maintain the order of the $x_i$, while each particle $x_i$ has its own intrinsic drift and diffusion coefficients, so the continuum process $x = (x_1, \ldots ,x_{N+1})$ shares key features with our particle process $X = (X_1, \ldots , X_{N+1})$ described in Sect. 1. However, it turns out that there are important differences inherent in the reflection mechanisms; before expanding on this, we introduce an extension of (6.2) to more general reflections.

In [30], it is demonstrated that a natural extension to (6.1) is

$$\begin{aligned} {\mathrm d}y_i (t)&= u_{r_i(t)} {\mathrm d}t + \sigma _{r_i(t)} {\mathrm d}W_i (t) \nonumber \\&\quad {} + \left( q^+_{r_i(t)} - \tfrac{1}{2} \right) {\mathrm d}L^{r_i(t)} (t) - \left( q^-_{r_i(t)} - \tfrac{1}{2} \right) {\mathrm d}L^{r_i(t)+1} (t) , \end{aligned}$$

(6.3)

where parameters $q^-_j, q^+_j \in (0,1)$, $j \in [N+1]$, satisfy $q_{j+1}^+ + q_j^- = 1$ for all $j \in [N]$. Equivalently, in terms of the $x_i$, the dynamics (6.3) amounts to

$$\begin{aligned} {\mathrm d}x_i (t) = u_{i} {\mathrm d}t + \sigma _{i} {\mathrm d}{{\widetilde{W}}}_i (t) + q_i^+ {\mathrm d}L^{i} (t) - q_i^- {\mathrm d}L^{{i+1}} (t). \end{aligned}$$

(6.4)

The symmetric case of (6.3)–(6.4) where $q_i^- \equiv q_i^+ \equiv 1/2$ for all i reduces to (6.1)–(6.2); the general case is called asymmetric [45].

As far as we are aware, long-time stability of the continuum system described above has been studied only as far as classifying whether or not the whole system is stable, rather than identifying a full cloud decomposition as we do in Theorem 2.1. In the symmetric case, the criterion for stability was obtained in [40, Thm. 8] (for the case of constant diffusion coefficients) and [8, 25], and in the stable case the asymptotic speed was derived; we summarize these results as follows, referring to e.g. [45, Prop. 2.2] and [25, Prop. 2] for precise formulations.

Theorem 6.1

For the system with symmetric collisions defined by (6.2), write $U_k:= k^{-1} \sum _{j=1}^k u_j$ for $k \in [N+1]$. The system is stable if and only if $U_k > U_{N+1}$ for all $k \in [N]$. Moreover, if stable, there is a strong law of large numbers with limiting speed $U_{N+1}$.

The stability condition here is comparable to (2.19), but different in detail; we elaborate on this in the next section. In the general (asymmetric) setting of (6.4), the criterion for stability is also known: see e.g. [45, Prop. 2.1], and involves the inverse of a tridiagonal matrix, reminiscent of the Jackson criterion (see Remarks 2.7). In the next section, we turn to the relationship between the continuum model and lattice models, which is multifaceted but has been partially elaborated in [30, Sect. 3].

6.2 Particle Models with Elastic Collisions

It turns out that a suitable discrete-space parallel to the continuum model in Sect. 6.1 is obtained by modifying the collision mechanism for the model in Sect. 1 from the exclusion rule to an elastic collision rule. We sketch here only the main idea; a pertinent discussion can also be found in [30, Sect. 3].

In the case $N=1$, two particles have jump rates $a_1, b_1$ and $a_2, b_2$. Under the exclusion rule, if the particles are adjacent, the total activity is reduced (particle 1 jumps left at rate $a_1$, while particle 2 jumps right at rate $b_2$). Suppose instead the total activity is maintained, by particles transferring ‘momentum’ to their neighbours when they attempt to jump, so that particle 1 jumps left at rate $a_1+a_2$, while particle 2 jumps right at rate $b_1 + b_2$. We call this the elastic collision rule; see Fig. 3 for an illustration for a 6-particle configuration. A slight variation on this is to modify the process so that ‘collisions’ mean that two particles occupy the same site, rather than adjacent sites. The elastic interaction is then equivalent to the two particles being permitted to pass each other, exchanging jump parameters as they do so (similarly to the diffusion model described in Sect. 6.1).

Fig. 3

Schematic of a lattice model with $N+1 = 6$ particles and an elastic collision rule. Filled circles represent particles, empty circles represent unoccupied lattice sites. Within each block of adjacent particles, only the particles at the extreme left or right can jump, but their jump rates are the sum of the intrinsic rates for all particles in the block. An essentially equivalent model is obtained by permitting particles to pass through each other, exchanging parameters as they do so

The elastic model is more homogeneous than the exclusion model, in the following sense: regardless of the present configuration, the rate at which a single coordinate changes by $+1$ is constant (namely $B_{N+1}:=\sum _{i=1}^{N+1} b_i$), as is the rate at which a single coordinate changes by $-1$ ($A_{N+1}:=\sum _{i=1}^{N+1} a_i$). Another way of saying this is that the centre of mass of the particle system performs a continuous-time simple random walk on $(N+1)^{-1} {{\mathbb {Z}}}$ with left jump rate $A_{N+1}$ and right jump rate $B_{N+1}$; thus it has speed $U_{N+1}:=(B_{N+1} - A_{N+1})/(N+1)$. Furthermore, considering just the leftmost $k \in [N+1]$ particles, their centre of mass has jump rates $A_k$, $B_k$, and speed $U_k = (B_k-A_k)/k$. By a similar reasoning to Algorithm 1, it becomes very plausible that the condition for stability of the system should be $U_k > U_{N+1}$ for all $k \in [N]$, exactly as in Theorem 6.1. It is natural to conjecture:

Conjecture 6.2

In the lattice model with elastic collisions, the system consists of a single stable cloud if and only if $U_k > U_{N+1}$ for all $k \in [N]$. Moreover, if the system is stable, there is a strong law of large numbers with limiting speed $U_{N+1}$.

As this model is not the focus of the present paper, we do not attempt to establish Conjecture 6.2 here. Additionally, we anticipate that a similar algorithm to Algorithm 1, based on the (somewhat simpler) algebra of cloud speeds in the elastic case, can be developed to obtain the full cloud decomposition for the elastic model.

This stability criterion in Conjecture 6.2 coincides with ours in Corollary 2.6 when $N=1$ (but not for $N \ge 2$), and even for $N=1$, the limiting speed is different. As an example, take $N=1$ and $a_1 = a$, $b_1 = b$, $a_2 = b_2 = 1$. Then the stable case of the exclusion model $(b>a)$ has asymptotic speed ${{\hat{v}}}_2 = (b-a)/(1+b)$, while the stable case of the elastic model has asymptotic speed $U_2 = (b-a)/2$.

6.3 Scaling Limits and Heavy Traffic

We indicate briefly, by an example, how the diffusion models of Sect. 6.1 arise as scaling limits of certain near-critical particle system models, and that the limits are elastic even when the particle system is not: see [30, Sect. 3] for more detail. As an elementary starting point, suppose that $X^{(s)}_t$, $t\in {{\mathbb {R}}}_+$ is a continuous-time, simple random walk on ${{\mathbb {Z}}}$ with jump rate 1 to the left and $1 + s^{-1/2} u$ to the right, where $u \in {{\mathbb {R}}}$ and $s \in (0,\infty )$ is a scale parameter. Then ${{\,\mathrm{\mathbb {E}}\,}}( X^{(s)}_{s(t+\delta )} - X^{(s)}_{st} ) = u \delta \sqrt{s}$, $\lim _{s \rightarrow \infty } {{\,\mathrm{\mathbb {E}}\,}}( ( X^{(s)}_{s(t+\delta )} - X^{(s)}_{st} )^2 / s) = 2\delta$, and standard functional central limit theorem arguments show that $( s^{-1/2} X_{st} )_{t \in [0,1]}$ converges weakly, as $s \rightarrow \infty$, to $(x_t)_{t \in [0,1]}$, a diffusion with drift u and volatility 2, i.e., satisfying the SDE ${\mathrm d}x_t = u {\mathrm d}t + 2 {\mathrm d}W_t$.

More generally, consider the particle model with exclusion interaction from Sect. 1, with $N+1$ particles with jump rates $a_1 = \cdots = a_{N+1} = 1$ and $b_i = 1 + s^{-1/2} u_i$ for $i \in [N+1]$, for parameters $u_i \in {{\mathbb {R}}}$. Then, ignoring the interactions, as $s \rightarrow \infty$ the particle motions converge to diffusions with drifts $u_i$ and volatility 2. In the presence of exclusion interactions, it can be shown that the particle system in this case converges weakly, as $s \rightarrow \infty$, to the system (6.2) with $\sigma _i^2 \equiv 2$; this is a special case of the results of [30, Sect. 3]. Equivalently, in the Jackson network context, this is a heavy traffic limit, as each queue is asymptotically critically loaded [43]; see e.g. [22] for some of the vast literature on heavy-traffic limits for queueing networks and their connections to reflecting diffusions.

The apparent discrepancy between the stability criterion for the inelastic (exclusion) system in Corollary 2.6 with that for the elastic (diffusion) system in Theorem 6.1 can now be resolved. For simplicity, take $N=2$, as in Example 2.10. Then the stability condition is that (2.22) and (2.23) both hold; for $a_i=1$ and $b_i = 1 + s^{-1/2} u_i$, inequality (2.22) takes the form $2 u_1 + u_2 > 2 u_2 + u_3 + o(1)$, as $s \rightarrow \infty$, which, in the limit, gives $U_1 > U_3$ in the notation of Theorem 6.1. Similarly (2.23) translates in the limit to the condition $U_2 > U_3$. Thus the stability condition in Theorem 6.1 emerges via a particular limiting regime of our Corollary 2.6. Moreover, the stable limiting speed (2.24) converges to the simple linear average $U_3$ in the $s \rightarrow \infty$ limit.