The Blume–Emery–Griffiths Model on the FAD Point and on the AD Line

Abstract

We analyse the Blume–Emery–Griffiths (BEG) model on the lattice ${\mathbb {Z}}^d$ on the ferromagnetic-antiquadrupolar-disordered (FAD) point and on the antiquadrupolar-disordered (AD) line. In our analysis on the FAD point, we introduce a Gibbs sampler of the ground states at zero temperature, and we exploit it in two different ways: first, we perform via perfect sampling an empirical evaluation of the spontaneous magnetization at zero temperature, finding a non-zero value in $d=3$ and a vanishing value in $d=2$. Second, using a careful coupling with the Bernoulli site percolation model in $d=2$, we prove rigorously that under imposing $+$ boundary conditions, the magnetization in the center of a square box tends to zero in the thermodynamical limit and the two-point correlations decay exponentially. Also, using again a coupling argument, we show that there exists a unique zero-temperature infinite-volume Gibbs measure for the BEG. In our analysis of the AD line we restrict ourselves to $d=2$ and, by comparing the BEG model with a Bernoulli site percolation in a matching graph of ${\mathbb {Z}}^2$, we get a condition for the vanishing of the infinite-volume limit magnetization improving, for low temperatures, earlier results obtained via expansion techniques.

1 Introduction

The Blume–Emery–Griffiths (BEG) model was introduced in 1971 in order to explain the superfluidity and phase transition of $He^3$–$He^4$ mixtures [1] and has been extended and generalized to many other applications, among them, ternary fluids [9, 25], phase transitions in $UO_2$ [11] and $DyVO_4$ [35], phase changes in microemulsions [32], solid–liquid-gas systems [17] and semiconductor alloys [6]. This model is defined in the d-dimensional cubic lattice ${\mathbb {Z}}^d$ by supposing that in each site $x\in {\mathbb {Z}}^d$ there is a random variable $\sigma _x$ (the spin at x) taking values in the set $\{0,\pm 1\}$. For $\Lambda \subset {\mathbb {Z}}^d$ (typically a cubic box centered at the origin of ${\mathbb {Z}}^d$) a spin configuration $\sigma$ in $\Lambda$ is a function $\sigma : \Lambda \rightarrow \{0,\pm 1\}: x\mapsto \sigma _x$ and $\Sigma _\Lambda$ will denote the set of all spin configurations in $\Lambda$. Given a finite $\Lambda \subset {\mathbb {Z}}^d$, the Hamiltonian of the system in $\Lambda$ (with zero magnetic field) is a function from $\Sigma _\Lambda$ to ${\mathbb {R}}$ which has the following expression:

$$\begin{aligned} { H}_\Lambda (\sigma )=-\sum _{\begin{array}{c} \{x,y\}\subset \Lambda \\ |x-y|=1 \end{array}} (\sigma _x\sigma _y+\textrm{Y}\sigma _x^2\sigma _y^2+\textrm{X}(\sigma _x^2+\sigma _y^2)+\mathcal{B}_\Lambda (\sigma )) \end{aligned}$$

(1)

where $|\cdot |$ is the usual $L_1$ norm in ${\mathbb {Z}}^d$, $\textrm{X},\textrm{Y}\in {\mathbb {R}}$, and ${{{\mathcal {B}}}}_\Lambda (\sigma )$ is a boundary term representing the interaction of the spins inside the box $\Lambda$ with the world outside. Along the paper we will sometimes also use the shorter notation $x\sim y$ to mean that $\{x,y\}$ is an unordered pair of nearest neighbors in ${\mathbb {Z}}^d$.

The probability $P_\Lambda (\sigma )$ (i.e. the finite volume Gibbs measure) of a configuration $\sigma \in \Sigma _\Lambda$ is defined as

$$\begin{aligned} P_{\Lambda ,\beta }(\sigma _\Lambda ) =\frac{ e^{-\beta {H}_\Lambda (\sigma _\Lambda )}}{Z_{\Lambda ,\beta }} \end{aligned}$$

where $\beta$ is the inverse of the temperature in units of the Boltzmann constant and the normalization constant $Z_{\Lambda ,\beta }$ is the partition function of the model. To understand the low-temperature properties of the model the starting point is to establish its ground state configurations. The ground states of the system are defined via the formal Hamiltonian on the whole ${{\mathbb {Z}}}^d$, which, given $\sigma \in \Sigma _{{{\mathbb {Z}}}^d}$ is

$$\begin{aligned} H (\sigma )=-\sum _{\begin{array}{c} \{x,y\}\subset {{\mathbb {Z}}}^d\\ x\sim y \end{array}} (\sigma _x\sigma _y+\textrm{Y}\sigma _x^2\sigma _y^2+\textrm{X}(\sigma _x^2+\sigma _y^2)) \doteq \sum _{\begin{array}{c} \{x,y\}\subset {{\mathbb {Z}}}^d\\ x\sim y \end{array}}h(\sigma _x,\sigma _y). \end{aligned}$$

(2)

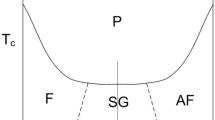
According to the standard definition (see e.g. [34]), a configuration $\sigma \in \Sigma _{{{\mathbb {Z}}}^d}$ is a ground state if, for any configuration $\sigma '\in \Sigma _{{{\mathbb {Z}}}^d}$ which differs from $\sigma$ only in a finite number of sites, we have that $\sum _{\{x,y\}\subset {{\mathbb {Z}}}^d,\,x\sim y}(h(\sigma '_x,\sigma '_y)-h(\sigma _x,\sigma _y))\ge 0$. The classification of the ground states of the BEG model is done, for instance, in [2], where the $\textrm{XY}$-plane is decomposed into three regions (according to the lowest spin pair energies), namely

$$\begin{aligned} F= & {} \{(\textrm{X}, \textrm{Y}): 1 + 2\textrm{X}+ \textrm{Y}> 0 \text{ and } 1 + \textrm{X}+ \textrm{Y}> 0\}\\ D= & {} \{(\textrm{X}, \textrm{Y}): 1 + 2\textrm{X}+ \textrm{Y}< 0 \text{ and } \textrm{X}< 0\}\\ A= & {} \{(\textrm{X}, \textrm{Y}): 1 + \textrm{X}+ \textrm{Y}< 0 \text{ and } \textrm{X}> 0\}, \end{aligned}$$

called in the physics literature ferromagnetic, disordered and antiquadrupolar, respectively. In these regions the spin nearest neighbor pairs with lowest energies are $\{++,--\}$, $\{00\}$ and $\{0+,0-\}$, respectively. In particular, for $(\textrm{X}, \textrm{Y})\in D$ the constant configuration $\sigma _x=0$, for all x, is the only ground state. For $(\textrm{X}, \textrm{Y})\in F$ there are two ground states, namely the constant configurations $\sigma _x=+1$, for all x, and $\sigma _x=-1$, for all x, respectively. For $(\textrm{X}, \textrm{Y}) \in A$ the model has infinitely many ground states separated into two disjoint classes. The first class is formed by those configurations $\sigma$ such that $\sigma _x=0$ for all x in the even sublattice of ${\mathbb {Z}}^d$ and $\sigma _x=\pm 1$ for all x in the odd sublattice, and the second class is the set of those configurations $\sigma$ such that $\sigma _x=0$ for all x in the odd sublattice of ${\mathbb {Z}}^d$ and $\sigma _x=\pm 1$ for all x in the even sublattice.

The boundaries of the above regions (see Fig. 1) are the lines $DF=\{(\textrm{X},\textrm{Y}):\, 1+2\textrm{X}+\textrm{Y}=0 \text{ and } \textrm{X}<0\}$, $AF =\{(\textrm{X},\textrm{Y})\,: \, \textrm{X}+\textrm{Y}+1=0 \text{ and } \textrm{X}>0\}$ and $AD =\{(0,\textrm{Y})\,:\, \textrm{Y}<-1\}$, and the point $\{(0,-1)\}$ which we call the FAD point. For the values of parameters $(\textrm{X},\textrm{Y})$ at the AF, AD lines and at FAD point, the BEG model has nonzero residual entropies. The references [2, 3, 22] provide lower and upper bounds for their values in two dimensions, by means of the transfer matrix method.

Fig. 1

The Phase diagram of the BEG model at zero temperature

In the high-temperature regime (i.e $\beta$ small) the behavior of the model for any values of the parameters $\textrm{X}$ and $\textrm{Y}$ can be described via standard polymer-expansion techniques. In [21], by using the Dobrushin uniqueness criterion, the existence of a subset of D is shown for which there is a unique Gibbs state for all temperatures, while in [23], via cluster expansion techniques, another subset of D is exhibited where the pressure of the system is analytic at all temperatures. It is a matter of controversy whether or not in the whole disordered region D we have a unique Gibbs measure at all temperatures, see for instance [16] and [4, 26].

In [20] some correlation functions of the BEG model are analysed for $(\textrm{X}, \textrm{Y})$ in the region D and on the AD line and, among other results, it is shown that for $|\textrm{Y}|$ sufficiently large, depending on d, the magnetization is zero for all temperatures.

For those parameters $(\textrm{X},\textrm{Y})$ for which there are only a finite number of ground states, namely, in the regions F and D and at the line DF, the low-temperature description of the model is given by the usual Pirogov-Sinai theory [8, 34]. When $(\textrm{X},\textrm{Y})$ is in the region A, where the model has an infinite number of ground states separated into two disjoint classes, an extension of the Pirogov-Sinai theory given in [13] allows to prove that at low temperature there are only two translation-periodic Gibbs states (see [2]). The situation at the AF, AD lines and at the FAD point is quite different: besides the fact that the degeneracies of their ground states are higher than the ones of the region A, the ground states at the AF, AD lines and at the FAD point do not split into a finite number of equivalence classes and the usual Pirogov-Sinai theory and its known extensions fail to work. Consequently, at the AF, AD lines and at the FAD point the behavior of the model at low temperature, even at zero-temperature, is less clear.

It is worth mentioning that for any temperature, by spin flipping of the spins in one of the sublattices of ${\mathbb {Z}}^d$, the BEG model with parameters $\textrm{X}=2$ and $\textrm{Y}=-3$ (a point on the AF line) is mapped into the three-state antiferromagnetic Potts model. Moreover, by this operation, the zero-temperature BEG model at the whole AF line is mapped into the three-state antiferromagnetic Potts model, namely the proper three-colorings problem. Generally, concerning the q-state antiferromagnetic Potts model (with $q\ge 3$) on a given lattice ${{{\mathcal {L}}}}$, it is expected that there is a value $q_c({{{\mathcal {L}}}})$ such that if $q<q_c({{{\mathcal {L}}}})$ the model orders at low temperature, if $q=q_c({{{\mathcal {L}}}})$ the model has a critical point at zero temperature, and if $q>q_c({{{\mathcal {L}}}})$ it is disordered at all temperatures (see e.g. [28] for an upper bound on $q_c({{{\mathcal {L}}}})$ when ${{{\mathcal {L}}}}$ is a quasi-transitive infinite graph). For the case ${{{\mathcal {L}}}}={\mathbb {Z}}^d$ and $q=3$ it is expected that the ordered phase is such that one of the two sublattices (i.e. either the even sublattice or the odd sublattice) is mostly occupied by a single state, while the spin values on the other sublattice are split equally between the remaining two states (the so called broken-sublattice-symmetry (BSS) phases). For the case ${{{\mathcal {L}}}}={\mathbb {Z}}^2$ and $q=3$ strong theoretical arguments, which however fall short of a rigorous proof, predict that this model has a critical point at zero temperature [31]. There are some rigorous results in this direction that support this prediction, see e.g., [5, 10]

Rigorous proofs of the existence of BSS-like Gibbs states on the AD line and (possibly) on the FAD point are available only for d sufficiently large, see [27] and references therein. Finally, we also mention that the zero-temperature BEG model on the whole AD line is equivalent to the self-repulsive hard-core gas (see [33] for a review on this model) with activity 2 which, in the two-dimensional case, has been showed to be in the uniqueness phase [30].

The present paper consists of two parts. The first part (Sect. 2) is devoted to the analysis of the zero-temperature BEG model on the lattice ${\mathbb {Z}}^d$ at the FAD point while in the second part (Sect. 3) we consider the low-temperature BEG model on the lattice ${\mathbb {Z}}^2$ at the AD line.

In our analysis of the FAD point we introduce in Sect. 2.1 a Gibbs sampler of the ground states at zero temperature, and we exploit it in two different ways. First, we perform via perfect sampling an empirical evaluation of the spontaneous magnetization at zero-temperature, finding a non-zero value in $d=3$ and a vanishing value in $d=2$. Next, in Sect. 2.2, using a careful coupling with the Bernoulli site percolation model in $d=2$, we prove rigorously (Theorem 1) that under imposing $+$ boundary conditions, the magnetization in the center of a square box tends to zero in the thermodynamical limit. We further show in Sect. 2.3, using again a coupling argument, that the infinite-volume Gibbs measure of the zero-temperature BEG is unique (Theorems 2 and 3). Finally in Sect. 2.4 we prove the exponential decay of the two-point correlations of the two-dimensional BEG model on the FAD point at zero-temperature (Theorem 4). The arguments used in the whole Sect. 2 are all dynamical ones.

Concerning the low-temperature BEG model on ${\mathbb {Z}}^2$ at the AD line, by a comparison with a Bernoulli site percolation in a matching graph of the square lattice, we get a $(\beta ,|Y|)$-dependent condition for the vanishing of the infinite-volume limit magnetization, improving, for low temperatures, earlier results obtained in [20] via expansion techniques (Theorem 5).

An anonymous referee of a previous version of this paper has pointed out to us that the zero-temperature BEG model at the FAD point coincides with the discrete Widom-Rowlinson model [18] with activity value equal to 1 and in the context of the Widom-Rowlinson model the uniqueness of the Gibbs measure has been established in an old (and quite overlooked) paper by Higuchi [15] for a region of activities which includes the value 1.

2 The Zero-Temperature BEG Model on the FAD Point

In what follows, given any finite set S, we let |S| be its cardinality. Moreover we will consider ${\mathbb {Z}}^d$ as the vertex set of the graph ${\mathbb {L}}^d$ whose edge set is formed by the nearest neighbors pairs so that given any two points x and y of ${\mathbb {Z}}^d$ the $L_1$ norm $|x-y|$ coincides with the usual graph distance in ${\mathbb {L}}^d$. The symbol $\Lambda$ will always denote from now on a finite cubic subset $\Lambda \subset {\mathbb {Z}}^d$ with sidelength L containing in its midpoint the origin o of ${\mathbb {Z}}^d$ and $\partial _e\Lambda$ and $\partial _i\Lambda$ will denote the external and internal boundaries respectively, given by

$$\begin{aligned} \partial _e\Lambda =\{x\in {\mathbb {Z}}^d\setminus \Lambda : |x-y|=1\;\mathrm{for\,\, some}\,\, y\in \Lambda \} \end{aligned}$$

and

$$\begin{aligned} \partial _i\Lambda =\{x\in \Lambda : |x-y|=1\;\mathrm{for\,\, some}\,\, y\in {\mathbb {Z}}^d\setminus \Lambda \}. \end{aligned}$$

The notation $\lim _{\Lambda \uparrow \infty }$ (i.e. the thermodynamic limit) means here $\lim _{L\rightarrow \infty }$. We stress however that by standard arguments it is possible to prove that the rigorous results obtained in this paper continue to hold when the limit $\lim _{\Lambda \uparrow \infty }$ is taken along more general sequences of sets invading ${{\mathbb {Z}}}^d$.

According to formula (1) in the Introduction, the Hamiltonian of the BEG model in $\Lambda \subset {{\mathbb {Z}}}^d$ on the FAD point (i.e. $\textrm{X}=0$, $\textrm{Y}=-1$) is given by

$$\begin{aligned} H_\Lambda ^\xi (\sigma )=-\sum _{\begin{array}{c} \{x,y\}\subset \Lambda \\ |x-y|=1 \end{array}}\sigma _x\sigma _y(1-\sigma _x\sigma _y)-\sum _{x\in \partial _{i}\Lambda }\,\,\sum _{\begin{array}{c} y\in \partial _e\Lambda \\ |x-y|=1 \end{array}}(\xi _y \sigma _x - \xi _y^2\sigma _x^2). \end{aligned}$$

(3)

The boundary term ${{{\mathcal {B}}}}_\Lambda (\sigma )=-\sum _{x\in \partial _{i}\Lambda }\,\,\sum _{y\in \partial _e\Lambda , |x-y|=1}(\xi _y \sigma _x - \xi _y^2\sigma _x^2)$ in (3) is determined by a fixed configuration $\xi \in \Sigma _{{\mathbb {Z}}^d}$ (called boundary condition) having in mind that in the thermodynamic limit, as $\Lambda$ invades ${{\mathbb {Z}}}^d$, the sites of $\xi$ entering in $\Lambda$ are disregarded and those in ${\mathbb {Z}}^d\setminus \Lambda$ are kept. Three special boundary conditions will play an important role in what follows. Namely the boundary condition “$\xi =+$" is the configuration such that $\xi _x=+1$ for all $x\in {\mathbb {Z}}^d$, the boundary condition “$\xi =-$" is the configuration such that $\xi _x=-1$ for all $x\in {\mathbb {Z}}^d$, and the boundary condition “$\xi =0$" is the configuration such that $\xi _x=0$ for all $x\in {\mathbb {Z}}^d$. Let us denote by $F^\xi _\Lambda$ the set of all ground states in $\Lambda$ with fixed boundary conditions, namely

$$\begin{aligned} F_\Lambda ^\xi =\{\sigma \in \Sigma _\Lambda : \sigma _x\sigma _y\ne -1 ~\mathrm{for ~all}~ \{x,y\}\subset \Lambda \cup \partial _e\Lambda ~\mathrm{such~that}~|x-y|=1\}. \end{aligned}$$

Then the energy $H_\Lambda ^\xi (\sigma )$ of a configuration $\sigma \in \Sigma _\Lambda$ is zero whenever $\sigma \in F^\xi _\Lambda$ and it is positive, being simply twice the number of nearest neighbor edges $\{x,y\}$ such that $\sigma _x\sigma _y=-1$ when $\sigma \in \Sigma _\Lambda \setminus F^\xi _\Lambda$. The probability ${{\mathbb {P}}}_{\Lambda ,\beta }^\xi (\sigma )$ of a given configuration $\sigma \in \Sigma _\Lambda$ at finite inverse temperature $\beta$ is defined via the Gibbs measure, i.e.

$$\begin{aligned} {{\mathbb {P}}}_{\Lambda ,\beta }^\xi (\sigma ) = {e^{-\beta H_\Lambda ^\xi (\sigma )}\over Z_{\Lambda ,\beta }^\xi } \end{aligned}$$

(4)

where

$$\begin{aligned} Z_{\Lambda ,\beta }^\xi = \sum _{\sigma \in \Sigma _\Lambda } e^{-\beta H_\Lambda ^\xi (\sigma )}. \end{aligned}$$

When $\beta =\infty$ (i.e. zero temperature) any configuration $\sigma \in \Sigma _\Lambda \setminus F^\xi _\Lambda$ has zero probability, and hence the finite-volume, zero-temperature Gibbs measure given in (4) becomes the uniform measure on $F^\xi _\Lambda$, namely

$$\begin{aligned} {{\mathbb {P}}}_{\Lambda ,\beta =\infty }^\xi (\sigma ) = {\left\{ \begin{array}{ll}{1\over N_\Lambda ^\xi } &{} {\text { if}}\; \sigma \in F^\xi _\Lambda \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(5)

where $N_{\Lambda }^\xi = |F^\xi _\Lambda | = Z_{\Lambda ,\beta =+\infty }^\xi$ is the number of ground states in $\Lambda$ with boundary condition $\xi$ outside $\Lambda$. In the rest of this section we will omit the index $\beta =\infty$ for the zero temperature Gibbs measure with $\xi$ boundary conditions and denote it with the shorten symbol ${{\mathbb {P}}}_{\Lambda }^\xi (\sigma )$. Given a function $f:\Sigma _\Lambda \rightarrow {\mathbb {R}}$ we will denote by $\langle (\sigma )\rangle _{\Lambda }^\xi$ the expected value of $f(\sigma )$ with respect to the uniform measure ${{\mathbb {P}}}_{\Lambda }^\xi (\sigma )$ under $\xi$ boundary conditions.

2.1 Sampler for the BEG Model on the FAD Point, Zero Temperature

In the present section we will perform a numerical analysis of the expected value of the spin at the origin o of ${{\mathbb {Z}}}^d$ under $+$ boundary conditions, i.e. the following quantity.

$$\begin{aligned} \langle \sigma _o\rangle _\Lambda ^+={1\over N^+_\Lambda }\sum _{\sigma \in F^+_\Lambda }\sigma _o ={1\over N^+_\Lambda }\left[ \sum _{\begin{array}{c} \sigma \in {F^+_{\Lambda }}\\ \sigma _o=+1 \end{array}}1-\sum _{\begin{array}{c} \sigma \in F^+_\Lambda \\ \sigma _o=-1 \end{array}}1\right] . \end{aligned}$$

(6)

We will further study numerically the two-point correlation function under free boundary conditions, namely

$$\begin{aligned} \langle \sigma _{x}\sigma _y\rangle _\Lambda ^0= {1\over N^0_\Lambda }\left[ \sum _{\begin{array}{c} \sigma \in {F^0_{\Lambda }}\\ \sigma _x\sigma _y=+1 \end{array}}1-\sum _{\begin{array}{c} \sigma \in F^0_\Lambda \\ \sigma _x\sigma _y=-1 \end{array}}1\right] . \end{aligned}$$

(7)

In order to do that we will define a symmetric and ergodic Markov Chain whose stationary measure coincides with the zero-temperature Gibbs measure of the BEG model at FAD. We also will introduce a coupling between two Markov chains as above on systems with different boundary conditions which preserves the natural partial order on the configuration set $\{-1,+1,0\}^\Lambda$. This coupling allows us to perform a perfect sampling simulation of our system producing numerical results on the behavior of $\langle \sigma _o\rangle _\Lambda ^+$ in two and three dimensions as the size of the box $\Lambda$ increases, and on the decay of the two-point correlations $\langle \sigma _{x}\sigma _y\rangle _\Lambda ^0$ in $d=2$ for different values of the distance $|x-y|$.

The Markov Chain. Given a box $\Lambda$ and a boundary condition $\xi$ (hence spins at sites of $\partial _e\Lambda$ are fixed), we recall that the Gibbs distribution at zero temperature is uniform on $F^\xi _\Lambda$. We call feasible a configuration $\sigma \in F^\xi _\Lambda$ and we define a Markov chain (a standard Glauber dynamics) that is symmetric ($P_{\sigma \tau }=P_{\tau \sigma }$) for all pairs of feasible configurations $\sigma ,\tau$, while $P_{\sigma \tau }=0$ when at least one between $\sigma$ and $\tau$ is not feasible. More explicitly, the Markov chain is defined as follows: assume $\sigma$ feasible, and call $N_x(\sigma )$ the set of values of the spin that are present in the neighborhood of the site x. The transition probabilities of our sampler are defined to be $P_{\sigma \tau }=0$ if $\sigma$ and $\tau$ differ in more than one site while, for couple of configurations differing at most in one site, they are defined by the following procedure.

• 1. Choose a site $x\in \Lambda$ uniformly at random (u.a.r.).

• 2. Set $\tau _y=\sigma _y$ for all $y\ne x$.

• 3. Set the value $\tau _x$ of the spin in the site x with uniform distribution among the feasible values.

Step 3 means that

• if $N_x(\sigma )=\{0\}$ then $\tau _x=1,0,-1$ with probability 1/3;

• if $N_x(\sigma )=\{0, +1\}$ or $N_x(\sigma )=\{ +1\}$ then $\tau _x=0,+1$ with probability 1/2;

• if $N_x(\sigma )=\{0, -1\}$ or $N_x(\sigma )=\{ -1\}$ then $\tau _x=0,-1$ with probability 1/2;

• if $N_x(\sigma )$ contains both $-1$ and $+1$ then $\tau _x=0$ with probability 1.

This procedure defines a Markov chain C(t) ($t=0,1,2,\dots$) with the following features. First of all, the chain is ergodic. To prove this it is sufficient to observe that in a finite number of steps it is possible to reach with nonzero probability any state starting from any state: simply, pass through the state $\sigma _x=0$ for all $x\in \Lambda$. The chain is obviously aperiodic, since $P_{\sigma \sigma }\ne 0$ for all $\sigma$. Second, starting from a feasible configuration, the evolution of the system remains on feasible configurations, since according to the rules above it is impossible to create an edge $x\sim y$ such that $\sigma _x\sigma _y=-1$. Third, the probability transition matrix $P_{\sigma \tau }$ is evidently symmetric, $P_{\sigma \tau }=P_{\tau \sigma }$. Hence the (unique) stationary measure of our chain is uniform on all the feasible configurations, and therefore it coincides with ${{\mathbb {P}}}^\xi _\Lambda$ (i.e. the uniform Gibbs measure of the zero-temperature BEG model at FAD).

Observe now that the spin configurations $\sigma \in F^\xi _\Lambda$ are partially ordered: the partial order relation $\sigma \prec \tau$ is defined trivially by $\sigma \prec \tau \Leftrightarrow \sigma _x\le \tau _x$, $\forall x\in \Lambda$. This circumstance permits to define an order preserving coupling in the implementation of our Markov chain. Namely, we let evolve together two chains C and $C'$ (starting in general from two different initial spin configurations $\sigma (0)$ and $\sigma '(0)$) in such a way that the marginal of the evolution of each chain represents exactly the probabilities $P_{\sigma \tau }$ defined above, but the two evolutions are coupled in such a way that if the initial configurations $\sigma (0)$ and $\sigma '(0)$ are such that $\sigma (0)\prec \sigma '(0)$, then their evolutions $\sigma (t)$ and $\sigma '(t)$ are such that $\sigma (t)\prec \sigma '(t)$ at any $t\ge 1$. This is easily realized by defining judiciously the updating rules of the two chains according to the values of the sets $N_x(\sigma (t))$ and $N_x(\sigma '(t))$. Assuming thus that at step 0 we have $\sigma (0)\prec \sigma '(0)$, our coupling will be defined as follows. At each step t of the implementation of the Markov chain we update in the two configurations $\sigma (t)$ and $\sigma '(t)$ by chosing u.a.r. a site $x\in \Lambda$, extracting then a single random variable U uniformly distributed in [0, 1] and letting $\sigma (t+1)$ and $\sigma '(t+1)$ such that $\sigma _y(t+1)=\sigma _y(t)$ and $\sigma '_y(t+1)=\sigma '_y(t)$ for all $y\in \Lambda {\setminus }\{x\}$ and setting $\sigma _x(t+1)$ and $\sigma '_x(t+1)$ according to the same value of U as follows. We define a set of thresholds in the segment [0, 1] according to the sets $N_x(\sigma (t))$ and $N_x(\sigma '(t))$ exploiting the fact that the probability of U is uniform and hence U enters a segment of length $\ell$ contained in [0, 1] with probability $\ell$. The thresholds however are fixed in such a way that we will always have $\sigma _x(t+1)\le \sigma '_x(t+1)$. We list in the Table 1 all possible pairs $N_x(\sigma (t))$ and $N_x(\sigma '(t))$ together with the drawings of the segments [0, 1] with relative thresholds for $\sigma _x(t+1)$ and $\sigma '_x(t+1)$.

Aiming to perform computer simulations using this Markov chain, an important feature of the order preserving coupling described above is that it is possible to perform with it a perfect sampling on the stationary measure. We choose the boundary condition $\xi =+$ and let $\sigma ^{\textrm{min}}\in F^+_\Lambda$ be the configuration such that $\sigma ^{\textrm{min}}_x=-1$ for all $x\in \Lambda {\setminus }\partial _i\Lambda$ and $\sigma ^{\textrm{min}}_x=0$ for $x\in \partial _i\Lambda$. Moreover we let $\sigma ^{\textrm{max}}\in F^+_\Lambda$ be the configuration such that $\sigma ^{\textrm{max}}_x=+1$ for all $x\in \Lambda$. Clearly $\sigma ^{\textrm{min}}$ and $\sigma ^{\textrm{max}}$ are the infimum and the supremum respectively over all configurations in $F^+_\Lambda$, i.e. for all the configurations $\sigma \in F^+_\Lambda$ we have $\sigma ^{\textrm{min}}\prec \sigma \prec \sigma ^{\textrm{max}}$.

We can now run the coupled chains, starting respectively from $\sigma (0)=\sigma ^{\textrm{min}}$ and $\sigma '(0)=\sigma ^{\textrm{max}}$ according to the standard procedure of perfect sampling (coupling from the past). It is not difficult to prove (see for instance [14] for an introductory reference) that the obtained configurations are distributed uniformly, i.e. according to the stationary measure. We computed empirically, according to this procedure, the magnetization in the origin for various values of $|\Lambda |$ in 2 and 3 dimensions.

Fig. 2

Magnetization at the origin for the zero-temperature BEG model on the FAD point in $d=2$ (left) and $d=3$ (right). Results of $10^6$ samples obtained running the BEG model sampler according to the perfect sampling procedure

The results we obtained show quite clearly that in 2 dimensions the magnetization in the origin tends to vanish, while in 3 dimensions it tends to a strictly positive value. Figure 2 clarifies the previous statements.

Furthermore, we applied the BEG sampler to compute empirically the two-point correlations in 2-dimensions at various distances $|x-y| \in \{ 1,2,\dots ,8\}$ around the origin o. Figure 3 shows the results on logarithmic scale where the exponential nature of the decay of the two-point correlations clearly shows up. The rest of the section is devoted to a rigorous study of the two-dimensional, zero-temperature BEG model on the FAD point. In this study the Markov chain and the coupling introduced defined above will play a fundamental role.

Fig. 3

Two-point correlation for the zero-temperature BEG model on the FAD point in $d=2$. Results of $2\cdot 10^6$ samples obtained running the BEG model sampler according to the perfect sampling procedure in a box $\Lambda$ of side 17. Correlations are thus computed at different spin distances $|x-y|$

2.2 Magnetization at Zero-Temperature in the $d=2$ BEG Model on the FAD Point

Here our goal is to analyze rigorously the behaviour of the expected value $\langle \sigma _o\rangle _{\Lambda }^+$ of the spin at the origin o defined in (6) as $\Lambda \uparrow \infty$ and when $d=2$. The thermodynamic limit of $\langle \sigma _o\rangle _{\Lambda }^+$, if it exists, will be denoted hereafter by $\langle \sigma _o\rangle ^+$, i.e.

$$\begin{aligned} \langle \sigma _o\rangle ^+=\lim _{\Lambda \uparrow \infty }\langle \sigma _o\rangle _{\Lambda }^+. \end{aligned}$$

(8)

The main result of this section is the following theorem.

Theorem 1

For the BEG model at zero-temperature and on the FAD point in $d=2$ we have that

$$\begin{aligned} \langle \sigma _0\rangle ^+=\langle \sigma _0\rangle ^-=0. \end{aligned}$$

In order to prove Theorem 1 we start by proving the following lemma.

Lemma 1

The expected value of the spin at the origin for the two-dimensional and zero-temperature BEG model on the FAD point confined in the box $\Lambda$ with $+$ boundary conditions defined in (6) admits the relation

$$\begin{aligned} \langle \sigma _0\rangle ^+_{\Lambda } = {{\mathbb {P}}}_\Lambda ^+(o\rightsquigarrow \partial \Lambda ) \end{aligned}$$

(9)

where ${{\mathbb {P}}}_\Lambda ^+$ is the zero-temperature Gibbs measure with $+$ boundary conditions defined in (5) and the symbol $o\rightsquigarrow \partial \Lambda$ denotes the event that the origin o is connected to a point $z\in \partial _e\Lambda$ through a path p such that $\sigma _x\ne 0$ for all $x\in p$.

Proof

First of all note that we can rewrite the quantity $\langle \sigma _0\rangle ^+_\Lambda$ defined in (6) as

$$\begin{aligned} \langle \sigma _o\rangle ^+_\Lambda ={1\over N^+_\Lambda }\left[ N^+_\Lambda |_{\sigma _o=+1} - N^+_\Lambda |_{\sigma _o=-1}\right] \end{aligned}$$

(10)

where $N^+_\Lambda |_{\sigma _o=\pm 1}$ is the number of ground states in $\Lambda$ with $+$ boundary conditions at $\partial _e\Lambda$ and with the spin at the origin fixed at the value $\sigma _o=\pm 1$. We further denote by the complementary event of $o\rightsquigarrow \partial _e\Lambda$ and by $N^+_\Lambda |_{\sigma _o=\pm 1, o\rightsquigarrow \partial \Lambda }$ (resp. ) the number of ground states in $\Lambda$ with the spin at the origin fixed at the value $\sigma _o=\pm 1$ and such that $o\rightsquigarrow \partial \Lambda$ (resp. ) and we observe that

(11)

while

(12)

since clearly $N^+_\Lambda |_{\sigma _o=-1, o\rightsquigarrow \partial \Lambda }=0$. Inserting (11) and (12) into (10) we get

Let us introduce some further notation. A set of vertices $\gamma \subset \Lambda$ is said to be a barrier (surrounding the origin) if any path starting at the origin and ending at some vertex of $\partial _e\Lambda$ contains a vertex of $\gamma$. A contour (surrounding the origin) in $\Lambda$ is a barrier $\gamma \subset \Lambda$ such that, for any $x\in \gamma$, $\gamma \setminus \{x\}$ is not a barrier. We denote by ${\mathcal {C}}^o_\Lambda$ the set of all contours surrounding the origin in $\Lambda$. Given $\gamma \in {\mathcal {C}}^o_\Lambda$, the interior of $\gamma$, denoted by $I_\gamma$, is the set formed by those vertices $y\in \Lambda$ for which there exists a path p starting at the origin o and ending at y such that $p\cap \gamma =\emptyset$. We also denote $E^\Lambda _\gamma =\Lambda {\setminus } (\gamma \cup I_\gamma )$. Finally given a contour $\gamma$ and a configuration $\sigma \in \Sigma _\Lambda$, we set $I_\gamma ^0(\sigma )= \{x\in I_{\gamma }: \sigma _x=0\}$. Now note that if $\sigma$ is a configuration in $\Lambda$ belonging to the event , then necessarily there is a unique minimal contour $\gamma _\sigma$ such that $\sigma _x=0$ for all $x\in \gamma _\sigma$ and such that the unique contour contained in the subset $I^0_{\gamma _\sigma }(\sigma )\cup \gamma _\sigma$ is $\gamma _\sigma$. Given $\gamma \in {\mathcal {C}}^0_\Lambda$, let us denote by $N^+_\Lambda |_{\sigma _0=\pm 1, \gamma }$ the number of ground states $\sigma \in F^+_\Lambda$ such that $\sigma _o=\pm 1$, and $\gamma _\sigma =\gamma$. Then we have that

$$\begin{aligned} N^+_\Lambda |_{\sigma _0=\pm 1, \gamma }=N^{+}(E^\Lambda _\gamma )N^*_{\sigma _o=\pm 1}(I_\gamma ) \end{aligned}$$

where $N^{+}(E^\Lambda _\gamma )$ is the number of ground states in $E^\Lambda _\gamma$ with boundary conditions $+$ at $\partial _e\Lambda$ and zero at $\gamma$ and $N^*_{\sigma _o=\pm 1}(I_\gamma )$ is the number of ground states $\sigma$ in $\gamma \cup I_\gamma$ (with zero boundary condition at $\gamma$) under the constraint that $\sigma _0=\pm 1$ and that the unique contour contained in $\gamma \cup I^0_\gamma (\sigma )$ is $\gamma$. With these notations we can write

Therefore we have that

$$\begin{aligned} \langle \sigma _0\rangle ^+_\Lambda (\beta =+\infty )={1\over N^+(\Lambda )}\left[ N^+_{\Lambda }|_{\sigma _o=+1,\,0^{+}_\rightsquigarrow \partial \Lambda }+ \sum _{\gamma \in {\mathcal {C}}^0_\Lambda } N^+(E^\Lambda _\gamma )\Big [N^*_{\sigma _0=+1}(I_\gamma )-N^*_{\sigma _0=-1}(I_\gamma )\Big ]\right] \nonumber \\ \end{aligned}$$

(13)

But now, by the spin flip symmetry we have that, for any $\gamma \in {\mathcal {C}}^o_\Lambda$

$$\begin{aligned} N^*_{\sigma _0=+1}(I_\gamma )=N^*_{\sigma _0=-1}(I_\gamma ) \end{aligned}$$

(14)

and so, inserting (14) into (13) we get

$$\begin{aligned} \langle \sigma _0\rangle ^+_\Lambda ={N^+_\Lambda |_{\sigma _o=+1, o\rightsquigarrow \partial \Lambda }\over N^+_\Lambda }= {{\mathbb {P}}}_\Lambda ^+(o\rightsquigarrow \partial \Lambda ). \end{aligned}$$

(15)

which concludes the proof of Lemma 1. $\square$

Let us now consider the Bernoulli site percolation in ${{\mathbb {Z}}}^2$ with parameter $p={1\over 2}$. Namely, suppose that in each site $x\in {{\mathbb {Z}}}^2$ an independent variable $\omega _x$ is defined. Such $\omega _x$ takes the value $\omega _x=+1$ with probability ${1\over 2}$ indicating that the site is open. When $\omega _x$ takes the value $\omega _x=0$ with probability ${1\over 2}$ it indicates that the site is closed. Given a square $\Lambda \subset {{\mathbb {Z}}}^2$ centered at the origin, let $\Omega _\Lambda =\{0,1\}^\Lambda$ be the set of all possible site configurations in $\Lambda$. We will denote by ${{\mathbb {P}}}^{\textrm{perc}}_\Lambda$ the probability product measure of the site percolation on $\Omega _\Lambda =\{0,1\}^\Lambda$ for $p={1\over 2}$.

Let us introduce a Markov chain D(t) on $\Omega _\Lambda$ whose transition probabilities $P_{\omega \omega '}$ for $\omega , \omega '\in \Omega _\Lambda$ are defined by the following sampler.

• 1. Choose a site $x\in \Lambda$ uniformly at random.

• 2. Set $\omega '_y=\omega _y$ for all $y\in \Lambda {\setminus }\{x\}$.

• 3. Extract U uniformly distributed in [0, 1], and set $\omega '_x=+1$ if $U<1/2$, and set $\omega '_x=0$, otherwise.

It is immediate to see that this is a sampler of the Bernoulli site percolation with $p=1/2$, and that D(t) is distributed exactly according the probability measure ${{\mathbb {P}}}^{\textrm{perc}}_\Lambda$ provided at time t each site x has been visited at least once.

Percolation-BEG Coupling Given a box $\Lambda \subset {{\mathbb {Z}}}^2$, let D(t) be the Markov chain described above with stationary measure ${{\mathbb {P}}}^{\textrm{perc}}_\Lambda$ and let C(t) be the Markov chain introduced in Sect. 2.1 with stationary measure ${{\mathbb {P}}}^+_\Lambda$ (i.e. the uniform Gibbs measure of the zero-temperature BEG model on the FAD point with $+$ boundary conditions). We define a coupling between D(t) and C(t) as follows. Assume the initial site configuration Y(0) is the configuration where all sites are closed (i.e. $\omega _x(0)=0$ for all $x\in \Lambda$) and the initial spin configuration X(0) is the configuration where all spins are zero (i.e. $\sigma _x(0)=0$ for all $x\in \Lambda$). We then let evolve together the two chains Y and X in such a way that at each step t of the implementation of the two coupled Markov Chains we update the two configurations $\omega (t)$ and $\sigma (t)$ by choosing u.a.r. a site $x\in \Lambda$, extracting then a single random variable U uniformly distributed in [0, 1] and letting $\omega (t+1)$ and $\sigma (t+1)$ be such that $\omega _y(t+1)=\omega _y(t)$ and $\sigma _y(t+1)=\sigma _y(t)$ for all $y\in \Lambda {\setminus }\{x\}$ and setting $\sigma _x(t+1)$ and $\omega _x(t+1)$ according to the same value of U as illustrated in the Table 2.

Lemma 2

Let D(t) and C(t) be the two Markov chains introduced above coupled according to the procedure of Table 2. Consider the connected cluster $\gamma _{\textrm{BEG}}$ of spins $+1$ containing the origin, if any, in the configuration C(t), and the connected cluster $\gamma _{\textrm{Perc}}$ of spins $+1$ containing the origin, if any, in the configuration D(t). Then

$$\begin{aligned} \gamma _{\textrm{BEG}}\subseteq \gamma _{\textrm{Perc}}. \end{aligned}$$

Proof

The proof trivially follows from the fact that in the sampler of BEG model the probability to choose $\sigma _x=+1$ is, according Table 2, never bigger that 1/2. In fact, it is even true that $C(t) \prec D (t)$ $\square$

Proof of Theorem 1

We may compute empirically by the strong law of large numbers, via the Markov chains D(t) and C(t) coupled as above, the probabilities ${{\mathbb {P}}}_\Lambda ^{\textrm{Perc}}(o \rightsquigarrow \partial \Lambda )$ and ${{\mathbb {P}}}_\Lambda ^+(o \rightsquigarrow \partial _e\Lambda )$ where ${{\mathbb {P}}}_\Lambda ^{\textrm{Perc}}(o \rightsquigarrow \partial \Lambda )$ is the probability that the origin is connected to the boundary of $\Lambda$ by a connected set of open sites in the two dimensional site percolation in $\Lambda$ with parameter $p=1/2$ and ${{\mathbb {P}}}_\Lambda ^+(o \rightsquigarrow \partial _e\Lambda )$ is the probability that that the origin is connected to $\partial _e\Lambda$ by a connected set of $+$ in the zero-temperature two dimensional BEG model on the FAD point in $\Lambda$ with $+$ boundary conditions. Lemma 2 then immediately implies that ${{\mathbb {P}}}_\Lambda ^+(o\rightsquigarrow \partial _e\Lambda )\le {{\mathbb {P}}}^{\textrm{perc}}_\Lambda (o\rightsquigarrow \partial \Lambda )$.

Now, it is well known (see e.g. Grimmett [12]) that for two dimensional Bernoulli site percolation the value $p=1/2$ is subcritical hence

$$\begin{aligned} \lim _{\Lambda \uparrow \infty } {{\mathbb {P}}}_\Lambda ^{\textrm{Perc}}(o \rightsquigarrow \partial \Lambda )=0 \end{aligned}$$

and thus

$$\begin{aligned} \langle \sigma _o\rangle ^+=\lim _{\Lambda \uparrow \infty } {{\mathbb {P}}}_\Lambda ^+(o \rightsquigarrow \partial _e\Lambda )\le \lim _{\Lambda \uparrow \infty }{{\mathbb {P}}}_\Lambda ^\textrm{Perc}(o \rightsquigarrow \partial \Lambda )=0. \end{aligned}$$

Finally observe that for any $\Lambda$ we have by symmetry $\langle \sigma _o\rangle _\Lambda ^-=-\langle \sigma _o\rangle _\Lambda ^+$ and thus Theorem 1 follows. $\square$

2.3 Uniqueness of the Gibbs State of the Zero-Temperature BEG Model at FAD Point

In this section we prove the existence and the independence on boundary conditions of the thermodynamic limit for the n-point correlation functions, proving in this way the uniqueness of the Gibbs state. Usually this kind of results are obtained by FKG inequalities (see e.g. [8]), and it is possible to prove that FKG inequalities hold for the BEG model on the FAD point even at zero temperature [7, 19]. We think however it is worth to provide here a proof of the uniqueness of the Gibbs state based solely on dynamical methods. Notice also that e.g. at the AD line (i.e. $\textrm{X}=0$ and $\textrm{Y}<-1$) the FKG inequalities are no longer satisfied so in principle the methods used here could be useful in situations where FKG inequalities cannot be used.

We will denote by $o_\Lambda (1)$ any positive vanishing quantity in the thermodynamic limit, i.e., in the limit $L\rightarrow \infty$. We will denote by $[n]=\{1,2,\ldots ,n\}$.

Given U and Wsubsets of $\Lambda \cup \partial _e\Lambda$, we will denote by $U\rightsquigarrow W$ the event (in the probability space $(F^\xi _\Lambda , {{\mathbb {P}}}_\Lambda ^\xi )$) in which at least one vertex in U is connected by a path of vertices of non-zero spins having the same sign to at least one vertex in W. The complementary event will be denoted by . Moreover, given $U\subset \Lambda$ and given a fixed spin configuration $\sigma _U$ in U we denote by the symbol ${{\mathfrak {e}}}_{\sigma _U}$ the event that in U the spins are fixed at the configuration $\sigma _U$.

Then Theorem 1 implies the following corollary on conditional probabilities in the BEG model.

Corollary 1

Let $U,W\subset \Lambda$ be fixed subsets. Let $\xi$ be any boundary condition on $\partial _e\Lambda$ and let $\sigma _U$ be any fixed configurations of spins in the sites of U. Then

$$\begin{aligned} {{\mathbb {P}}}_\Lambda ^\xi (W\rightsquigarrow \partial _e\Lambda |{{\mathfrak {e}}}_{\sigma _U})=o_\Lambda (1). \end{aligned}$$

(16)

Proof

We can proceed as in the proof of Theorem 1 using the coupling between site percolation and the BEG model described in Sect. 2.2. The only difference is that now the two coupled samplers choose a site $x\in \Lambda$ uniformly at random in the set $\Lambda \setminus U$ and concerning the BEG model sampler one must take into account that in the set $\Lambda \setminus U$ the boundary conditions $\xi$ are imposed on $\partial _e\Lambda$ and the boundary condition $\sigma _U$ are imposed at sites in U. $\square$

We will now state a result on n-point correlations, and then we will prove the uniqueness of the Gibbs measure. In order to do that, let us introduce some notations. In general, given a collection ${{\mathfrak {e}}}_1, {{\mathfrak {e}}}_2, \dots , {{\mathfrak {e}}}_n$ of subsets of $F^\xi _\Lambda$ (i.e. events) we denote by $N^\xi _\Lambda |_{{{\mathfrak {e}}}_1,\dots ,{{\mathfrak {e}}}_n}$ the number of ground states in $F^\xi _\Lambda$ such that the events ${{\mathfrak {e}}}_1, {{\mathfrak {e}}}_2, \dots , {{\mathfrak {e}}}_n$ occur.

Theorem 2

Given $x_1,x_2, \dots ,x_n\in {{\mathbb {Z}}}^2$ not necessarily distinct, for any pair $\xi , \xi '$ of boundary conditions we have

$$\begin{aligned} \lim _{\Lambda \uparrow \infty } [\langle \sigma _{x_1}\ldots \sigma _{x_n}\rangle ^{\xi }_\Lambda - \langle \sigma _{x_1}\ldots \sigma _{x_n}\rangle ^{\xi '}_\Lambda ]=0. \end{aligned}$$

Proof

Given $I^-\subset [n]$, let $I_+=[n]\backslash I_-$. We denote shortly by ${{\mathfrak {e}}}_{I_+}$ the event $(\sigma _{x_i}=+1\ \forall i\in {I_+})$ and by ${{\mathfrak {e}}}_{I_-}$ the event $(\sigma _{x_i}=-1\ \forall i\in {I_-})$. Note that the event ${{\mathfrak {e}}}_{I_+}$ is increasing while ${{\mathfrak {e}}}_{I_-}$ is decreasing. With these notations we can write

$$\begin{aligned} \langle \sigma _{x_1}\ldots \sigma _{x_n}\rangle ^{\xi }_\Lambda = \frac{1}{N_\Lambda ^\xi }\sum _{I_-\subset [n]}(-1)^{|I_-|}N^\xi _\Lambda |_{{{\mathfrak {e}}}_{I_+},{{\mathfrak {e}}}_{I_-}} = \sum _{I_-\subset [n]}(-1)^{|I_-|} {{\mathbb {P}}}_\Lambda ^\xi ({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-}). \end{aligned}$$

(17)

Therefore the theorem follows if we prove that for all choices of $I_-$ and for all pairs of boundary conditions $\xi ,\xi '$ we have

$$\begin{aligned} \lim _{\Lambda \uparrow \infty }\left[ {{\mathbb {P}}}_\Lambda ^\xi ({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})-{{\mathbb {P}}}_\Lambda ^{\xi '}({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})\right] =0. \end{aligned}$$

(18)

Observe that

$$\begin{aligned} {{\mathbb {P}}}_\Lambda ^\xi ({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})={{\mathbb {P}}}_\Lambda ^\xi ({{\mathfrak {e}}}_{I_+}|{{\mathfrak {e}}}_{I_-}){{\mathbb {P}}}_\Lambda ^\xi ({{\mathfrak {e}}}_{I_-}). \end{aligned}$$

So (18) follows if we show that

$$\begin{aligned} \lim _{\Lambda \uparrow \infty } \left[ {{\mathbb {P}}}_\Lambda ^\xi ({{\mathfrak {e}}}_{I_+}|{{\mathfrak {e}}}_{I_-}) - {{\mathbb {P}}}_\Lambda ^{\xi '}({{\mathfrak {e}}}_{I_+}|{{\mathfrak {e}}}_{I_-})\right] =0\qquad \text { and } \quad \lim _{\Lambda \uparrow \infty } \left[ {{\mathbb {P}}}_\Lambda ^\xi ({{\mathfrak {e}}}_{I_-}) - {{\mathbb {P}}}_\Lambda ^{\xi '}({{\mathfrak {e}}}_{I_-})\right] =0. \end{aligned}$$

Let us prove the first limit. The proof that $\lim _{\Lambda \uparrow \infty } \left[ {{\mathbb {P}}}_\Lambda ^\xi ({{\mathfrak {e}}}_{I_-}) - {{\mathbb {P}}}_\Lambda ^{\xi '}({{\mathfrak {e}}}_{I_-})\right] =0$ is similar (and easier).

Since the event ${{\mathfrak {e}}}_{I_+}$ is increasing, for any boundary condition $\xi$ we have

$$\begin{aligned} {{\mathbb {P}}}^{-}_\Lambda ({{\mathfrak {e}}}_{I_+}|{{\mathfrak {e}}}_{I_-})\le {{\mathbb {P}}}^{\xi }_\Lambda ({{\mathfrak {e}}}_{I_+}|{{\mathfrak {e}}}_{I_-})\le {{\mathbb {P}}}^{+}_\Lambda ({{\mathfrak {e}}}_{I_+}|{{\mathfrak {e}}}_{I_-}). \end{aligned}$$

Indeed, setting $U_{I_\pm }=\{x_i|i\in I_\pm \}$ and evaluating empirically the three probabilities as described in the proof of Corollary 1 (i.e. the coupled samplers are defined in $\Lambda \setminus U_{I_-}$ with spins fixed at the value $-1$ in sites $U_{I_-}$). Call now $S^\xi$ the set of $+$ obtained in the sampling with boundary condition $\xi$. We have by order preserving coupling that $S^-\subset S^\xi \subset S^+$.

Now we can write

By Corollary 1 we get

$$\begin{aligned} {{\mathbb {P}}}^{+}_\Lambda ({{\mathfrak {e}}}_{I_+}\cap (U_{I_+}\rightsquigarrow \partial _e\Lambda )|{{\mathfrak {e}}}_{I_-}) \le {{\mathbb {P}}}^{+}_\Lambda (U_{I_+}\rightsquigarrow \partial _e\Lambda |{{\mathfrak {e}}}_{I_-})=o_\Lambda (1). \end{aligned}$$

Moreover

Hence we can write

The required independence of $\ P^{\xi }_\Lambda ({{\mathfrak {e}}}_{I_+}|{{\mathfrak {e}}}_{I_-})$ from $\xi$ now follows from the following observation that

(19)

Indeed, by definition

and

By spin flip symmetry we have so that

(20)

Moreover, again by spin flip symmetry we have that so that

where in the last equality we have used that ${{\mathbb {N}}^-_\Lambda |_{{{\mathfrak {e}}}_{I_-},U_{I_-}\rightsquigarrow \partial _e\Lambda }\over N^-_\Lambda |_{{{\mathfrak {e}}}_{I_-}}}={{\mathbb {P}}}^{-}_\Lambda (U_{I_-}\rightsquigarrow \partial _e\Lambda |{{\mathfrak {e}}}_{I_-})=o_\Lambda (1)$ again by Corollary 1. Therefore we get

$$\begin{aligned} {N^+_\Lambda |_{{{\mathfrak {e}}}_{I_-}}\over N^-_\Lambda |_{{{\mathfrak {e}}}_{I_-}}}=1-o_\Lambda (1). \end{aligned}$$

(21)

Inserting (21) into (20) we get (19). $\square$

We can now prove the following result.

Theorem 3

For any choice of $x_1,\ldots ,x_n\in \Lambda$ not necessarily distinct and for any boundary condition $\xi$ the limit

$$\begin{aligned} \lim _{\Lambda \uparrow \infty } \langle \sigma _{x_1}\ldots \sigma _{x_n}\rangle ^{\xi }_\Lambda \end{aligned}$$

(22)

exists and it is independent of $\xi$. In other words, there is a unique infinite-volume Gibbs measure for the two-dimensional, zero-temperature BEG model at the FAD point.

Proof

To prove that the limit (22) is independent of $\xi$ it is enough to prove, by (18), that for all choices of $I_-$ and e.g. for boundary conditions 0 the limit

$$\begin{aligned} \lim _{\Lambda \uparrow \infty } {{\mathbb {P}}}^{0}_\Lambda ({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-}) \end{aligned}$$

(23)

exists. Note that using 0 (which is equivalent to the free) boundary conditions the event $U_{I_{\pm }}\rightsquigarrow \partial _e\Lambda$ is empty.

Consider two sets $\Lambda$ and $\Lambda '$ such that $\Lambda '\subset \Lambda$ and $U_{I_{\pm }}\subset \Lambda '$. Given a configuration $\sigma \in F^0_\Lambda$, let $\sigma _{\partial _e\Lambda '}$ be its restriction to $\partial _e\Lambda '$ and let $S=\{\sigma _{\partial _e\Lambda '}\}_{\sigma \in F^+_\Lambda }$ the set of all feasible configurations $\xi$ on $\partial _e\Lambda '$. Let moreover denote by $N^{0,\xi }_{\Lambda \backslash {\bar{\Lambda }}'}$ the number of ground states in the ring $\Lambda \setminus (\Lambda '\cup \partial _e\Lambda ')$ compatible with boundary conditions 0 on $\partial _e\Lambda$ and $\xi$ on $\partial _e\Lambda '$. Then we can write

$$\begin{aligned} {{\mathbb {P}}}^{0}_\Lambda ({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})= {N^{0}_{\Lambda }|_{{{\mathfrak {e}}}_{I_+},{{\mathfrak {e}}}_{I_-}}\over N^{0,\xi }_{\Lambda }}= \frac{\sum _{\xi \in S} N^{0,\xi }_{\Lambda \setminus {\bar{\Lambda }}'} N^{\xi }_{\Lambda '}|_{{{\mathfrak {e}}}_{I_+},{{\mathfrak {e}}}_{I_-}}}{\sum _{\xi \in S} N^{0,\xi }_{\Lambda \backslash {\bar{\Lambda }}'}N^{\xi }_{\Lambda '}} = \frac{\sum _{\xi \in S} N^{0,\xi }_{\Lambda \backslash {\bar{\Lambda }}' }N^{\xi }_{\Lambda '} {{\mathbb {P}}}^\xi _{\Lambda '}({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})}{\sum _{\xi \in S} N^{0,\xi }_{\Lambda \backslash {\bar{\Lambda }}'}N^{\xi }_{\Lambda '}}. \end{aligned}$$

By (18) we have that

$$\begin{aligned} P^{\xi }_{\Lambda '}({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})= P^{0}_{\Lambda '}({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})+o_{\Lambda '}(1) \end{aligned}$$

and hence we have obtained

$$\begin{aligned} {{\mathbb {P}}}^{0}_\Lambda ({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})= \frac{\sum _{\xi \in U} N^{+,\xi }_{\Lambda \backslash {\bar{\Lambda }}' }N^{\xi }_{\Lambda '} [{{\mathbb {P}}}^{0}_{\Lambda '}({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})+o_{\Lambda '}(1)]}{\sum _{\xi \in U} N^{+,\xi }_{\Lambda \backslash {\bar{\Lambda }}'}N^{\xi }_{\Lambda '}}= {{\mathbb {P}}}^{0}_{\Lambda '}({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})+o_{\Lambda '}(1). \end{aligned}$$

Therefore as $\Lambda \uparrow \infty$ along a chosen sequence of square boxes $\{\Lambda _n\}_{n\in {\mathbb {N}}}$, the sequence ${{\mathbb {P}}}^{0}_{\Lambda _n}({{\mathfrak {e}}}_{I_+}\cap {{\mathfrak {e}}}_{I_-})$ is Cauchy and therefore the limit (23) exists. Moreover this limit is the same for all boundary conditions $\xi$ because of (18). $\square$

2.4 Exponential Decay of the Two Point Correlation for the Zero-Temperature BEG Model at FAD Point

We have shown in the previous section that $\langle \sigma _x\sigma _y\rangle =\lim _{\Lambda \uparrow \infty }\langle \sigma _x\sigma _y\rangle _\Lambda ^\xi$ exists and its is independent on the boundary condition $\xi$. The main result of this section is stated in the following theorem.

Theorem 4

There exist positive constants C and k such that

$$\begin{aligned} \langle \sigma _x\sigma _y\rangle \le C e^{-k|x-y|}. \end{aligned}$$

Proof

We can write

$$\begin{aligned} \langle \sigma _{x}\sigma _y\rangle _\Lambda ^0= {1\over N^0_\Lambda }\left[ N^0_\Lambda |_{\sigma _x\sigma _y=1}-N^0_\Lambda |_{\sigma _x\sigma _y=-1}\right] . \end{aligned}$$

Recalling that the event $\{x,y\}\rightsquigarrow \partial _e\Lambda$ is empty under 0 boundary conditions, let $x^{_{\;+}}_{^\leftrightsquigarrow }y$ (resp. $x^{_{\;-}}_{^\leftrightsquigarrow }y$) be the event that x and y are in the same connected cluster of + spins (resp. - spins) and let be the event that x and y are in different connected clusters, each of them with spins of the same sign. With this definitions we have that

and

Now observe that by spin flip symmetry

Therefore we get

and hence

$$\begin{aligned} \langle \sigma _{x}\sigma _y\rangle _\Lambda ^0=2{{\mathbb {P}}}^0_\Lambda (x^{_{\;+}}_{^\leftrightsquigarrow }y) \end{aligned}$$

(24)

Taking thus the limit $\Lambda \uparrow \infty$ in (24)(which, according to Theorem 3, exists and does not depend on boundary conditions) we get

$$\begin{aligned} \langle \sigma _{x}\sigma _y\rangle = \lim _{\Lambda \uparrow \infty } 2{{\mathbb {P}}}^0_\Lambda (x^{_{\;+}}_{^\leftrightsquigarrow }y). \end{aligned}$$

Now, using the coupling BEG-Percolation introduced in Lemma 2 we get that

$$\begin{aligned} {{\mathbb {P}}}^+_\Lambda (x^{_{\;+}}_{^\leftrightsquigarrow }y)\le {{\mathbb {P}}}^{\textrm{Perc}}_\Lambda (x\leftrightsquigarrow y) \end{aligned}$$

where ${{\mathbb {P}}}^{\textrm{Perc}}_\Lambda (x\leftrightsquigarrow y)$ is the probability that x and y are in the same connected open cluster in the two-dimensional Bernoulli site percolation with parameter $p={1 \over 2}$. It is well known (see e.g. [12] and references therein) that, for some $k>0$ and $C'>0$, ${{\mathbb {P}}}^\textrm{Perc}_\Lambda (x\leftrightsquigarrow y)\le C'e^{-k|x-y|}$. Hence we finally get

$$\begin{aligned} \langle \sigma _{x}\sigma _y\rangle \le Ce^{-k|x-y|} \end{aligned}$$

with $C=2C'$. $\square$

3 Magnetization in the Low Temperature Two-Dimensional BEG Model on the AD Line

In this section we will focus our attention on the AD line of the BEG model in two dimensions confined in a box $\Lambda \subset {{\mathbb {Z}}}^2$ centered at the origin o of ${{\mathbb {Z}}}^2$ with $+$ boundary conditions at finite inverse temperature $\beta$. The Hamiltonian in this case is as follows.

$$\begin{aligned} H_{\Lambda ,\textrm{Y}}^+(\sigma )=-\sum _{\begin{array}{c} x\sim y\\ \{x,y\}\cap \Lambda \ne \emptyset \end{array}}\sigma _x\sigma _y(1+\textrm{Y}\sigma _x\sigma _y) \end{aligned}$$

(25)

where $\textrm{Y}<-1$ and we agree that $\sigma _x=+1$ when $x\in \partial _e\Lambda$. The Gibbs mesure ${{\mathbb {P}}}_{\Lambda ,\beta }^+(\sigma )$ of a given configuration $\sigma \in \Sigma _\Lambda$ is now given by

$$\begin{aligned} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ) = {e^{-\beta H_{\Lambda ,\textrm{Y}}^+(\sigma )}\over Z^+_\Lambda (\beta ,\textrm{Y})}, \end{aligned}$$

(26)

where

$$\begin{aligned} { Z^+_\Lambda (\beta ,{\textrm{Y}})} = {\sum _{\sigma \in \Sigma _\Lambda } }e^{-\beta H_{\Lambda ,\textrm{Y}}^+(\sigma )}. \end{aligned}$$

As before, our goal is to evaluate the expected value $\langle \sigma _o\rangle _{\Lambda ,\beta ,\textrm{Y}}^+$ of the magnetization in the origin o with respect to the Gibbs measure (26), which is now given by

$$\begin{aligned} \langle \sigma _o\rangle _{\Lambda ,\beta ,\textrm{Y}}^+=\sum _{\sigma \in \Sigma _\Lambda } \sigma _o\,{{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ), \end{aligned}$$

(27)

in the thermodynamic limit $\Lambda \uparrow \infty$. The main result of this section is the following theorem.

Theorem 5

For the BEG model on the AD line in $d=2$ and inverse temperature $\beta$, we have that

$$\begin{aligned} \lim _{\Lambda \uparrow \infty }\langle \sigma _o\rangle _{\Lambda ,\beta ,\textrm{Y}}^+=\lim _{\Lambda \uparrow \infty }\langle \sigma _o\rangle _{\Lambda ,\beta ,\textrm{Y}}^-= 0, \end{aligned}$$

for any $\beta$ such that

$$\begin{aligned} e^{-\beta |\textrm{Y}|}\cosh (\beta ) < \frac{1-p_c}{2p_c}, \end{aligned}$$

(28)

where $p_c$ is the critical site percolation threshold in the square lattice.

In order to prove the theorem above we need to prove a preliminary lemma analogous to Lemma 1 of Sect. 2.2.

Let thus $[o \rightarrow \partial \Lambda ]$ be the event formed by those configurations $\sigma \in \Sigma _\Lambda$ for which there is a path $\ell$ of vertices connecting the origin o to the boundary $\partial _e\Lambda$ in the original lattice $\Lambda$ such that $|\sigma _x|=1$ for all $x\in \ell$. The complementary event will be denoted by $[o\not \rightarrow \partial \Lambda ]$.

Lemma 3

The mean value of the spin in the origin in the BEG model on the AD line confined in a box $\Lambda$ with $+$ boundary conditions is given by

$$\begin{aligned} \langle \sigma _o\rangle _{\Lambda ,\beta ,\textrm{Y}}^+ \le {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ]), \end{aligned}$$

(29)

where ${{\mathbb {P}}}_\Lambda ^+$ is Gibbs measure defined in (26).

Proof

Recalling the definition of contours surrounding the origin given in Sect. 2.2, similarly to what was remarked in the proof of Lemma 1, if $\sigma$ is a configuration in $\Lambda$ belonging to the event $[o\not \rightarrow \partial \Lambda ]$, then necessarily there is a unique contour $\gamma _\sigma$ surrounding the origin such that $\sigma _x=0$ for all $x\in \gamma _\sigma$ and such that the unique contour contained in the subset $I_{\gamma _\sigma }^0(\sigma )\cup \gamma _\sigma$ is $\gamma _\sigma$. Let us denote by $\Sigma ^{\pm }_{I_\gamma }$ the set of all configurations $\sigma$ in $I_\gamma$ such that the unique contour in $I^0_{\gamma }(\sigma )$ is $\gamma$ and such that $\sigma _o=\pm 1$. Let ${{\mathfrak {e}}}_o^\pm$ denotes the event that $\sigma _o=\pm 1$ and let us consider the quantity

$$\begin{aligned}{} & {} \sum _{\sigma \in [o\not \rightarrow \partial \Lambda ]} \sigma _o\,{{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma )=\sum _{\begin{array}{c} \sigma \in [o\not \rightarrow \partial \Lambda ]\\ \sigma _o=+1 \end{array}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma )\nonumber \\{} & {} \quad -\sum _{\begin{array}{c} \sigma \in [o\not \rightarrow \partial \Lambda ]\\ \sigma _o=-1 \end{array}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ). \end{aligned}$$

(30)

Then, according to the notations above, we have that

$$\begin{aligned} \sum _{\begin{array}{c} \sigma \in [o\not \rightarrow \partial \Lambda ]\\ \sigma _o=\pm 1 \end{array}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma )= {1\over Z^+_\Lambda (\beta ,\textrm{Y})} \sum _{\begin{array}{c} \sigma \in [o\not \rightarrow \partial \Lambda ]\\ \sigma _o=\pm 1 \end{array}}e^{-\beta H_{\Lambda ,\textrm{Y}}^+(\sigma )} = {1\over Z^+_\Lambda (\beta ,\textrm{Y})} \sum _{\gamma \in {\mathcal {C}}^o_\Lambda }\sum _{\begin{array}{c} \sigma \in \Sigma _\Lambda \\ \sigma _o=\pm 1, \gamma _\sigma =\gamma \end{array}}e^{-\beta H_{\Lambda ,\textrm{Y}}^+(\sigma )}.\nonumber \\ \end{aligned}$$

(31)

Now observe that, for each minimal contour $\gamma \in {\mathcal {C}}^o_\Lambda$, we have

$$\begin{aligned} \sum _{\begin{array}{c} \sigma \in \Sigma _\Lambda \\ \sigma _o=\pm 1, \gamma _\sigma =\gamma \end{array}}e^{-\beta H_{\Lambda ,\textrm{Y}}^+(\sigma )}= \sum _{\sigma \in \Sigma _{E^\Lambda _\gamma }}e^{-\beta H_{E^\Lambda _\gamma ,\textrm{Y}}^+(\sigma )}\sum _{\sigma \in \Sigma ^{\pm }_{I_\gamma }}e^{-\beta H_{I_\gamma ,\textrm{Y}}^0(\sigma )}, \end{aligned}$$

where given $\sigma \in \Sigma _{E^\Lambda _\gamma }$, $H_{E^\Lambda _\gamma ,\textrm{Y}}^+(\sigma )$ is the energy of $\sigma$ with boundary conditions $\sigma _x=+1$ when $x\in \partial _e\Lambda$ and $\sigma _x=0$ when $x\in \gamma$, and, given $\sigma \in \Sigma ^{\pm }_{I_\gamma }$, $H_{I_\gamma ,\textrm{Y}}^0(\sigma )$ is the energy of the configurations $\sigma$ with boundary conditions $\sigma _x=0$ when $x\in \gamma$. By the spin flip symmetry we have that $H_{I_\gamma ,\textrm{Y}}^0(\sigma )= H_{I_\gamma ,\textrm{Y}}^0(-\sigma )$ and that $|\Sigma ^{+}_{I_\gamma }|=|\Sigma ^{-}_{I_\gamma }|$, which imples that

$$\begin{aligned} \sum _{\sigma \in \Sigma ^{+}_{I_\gamma }}e^{-\beta H_{\Lambda ,\textrm{Y}}^0(\sigma )}= \sum _{\sigma \in \Sigma ^{-}_{I_\gamma }}e^{-\beta H_{\Lambda ,\textrm{Y}}^0(\sigma )} \end{aligned}$$

(32)

and thus

$$\begin{aligned} \sum _{\begin{array}{c} \sigma \in [o\not \rightarrow \partial \Lambda ]\\ \sigma _o=-1 \end{array}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma )=\sum _{\begin{array}{c} \sigma \in [o\not \rightarrow \partial \Lambda ]\\ \sigma _o=+1 \end{array}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ). \end{aligned}$$

So we get that

$$\begin{aligned} \sum _{\sigma \in [o\not \rightarrow \partial \Lambda ]} \sigma _o\,{{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma )=0, \end{aligned}$$

(33)

In conclusion we can bound from above the magnetization as follows:

$$\begin{aligned} \begin{aligned} \langle \sigma _o\rangle _\Lambda ^+&= \sum \limits _{\sigma \in [o \rightarrow \partial \Lambda ]} \sigma _o {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma )+ \sum \limits _{\sigma \in [o \not \rightarrow \partial \Lambda ]} \sigma _o {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma )\\&= \sum \limits _{\sigma \in [o \rightarrow \partial \Lambda ]} \sigma _o {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ) \\&= \sum \limits _{\begin{array}{c} \sigma \in [o \rightarrow \partial \Lambda ] \\ \sigma _o = +1 \end{array}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ) - \sum \limits _{\begin{array}{c} \sigma \in [o \mapsto \partial \Lambda ] \\ \sigma _o = -1 \end{array}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma )\\&\le \sum \limits _{\sigma \in [o \rightarrow \partial \Lambda ]} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ) = {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ])\\ \end{aligned} \end{aligned}$$

(34)

and this concludes the proof of the lemma. $\square$

Proof of Theorem 5

By Lemma 3, Theorem 5 is proved once we show that

$$\begin{aligned} \lim _{\Lambda \uparrow \infty }{{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ])=0. \end{aligned}$$

(35)

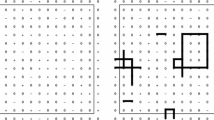
To prove (35), we look for an upper bound of ${{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ])$. In order to do that we need to introduce some notations and definitions. Let ${\mathbb {Z}}^2_{\textrm{odd}}$ (resp. ${\mathbb {Z}}^2_{\textrm{even}}$) be the odd (resp. even) sublattices of ${\mathbb {Z}}^2$, i.e. ${\mathbb {Z}}^2_{\textrm{odd}}$ (resp. ${\mathbb {Z}}^2_{\textrm{even}}$) is formed by those $(n_1,n_2)\in {\mathbb {Z}}^2$ such that $n_1+n_2$ is odd (resp. even). Let $\Lambda ^{\textrm{e}}=\Lambda \cap {\mathbb {Z}}^2_{\textrm{even}}$ and $\Lambda ^{\textrm{o}}=\Lambda \cap {\mathbb {Z}}^2_{\textrm{odd}}$. Note that the origin o belongs to the sublattice $\Lambda ^{\textrm{e}}$ and that $\Lambda = \Lambda ^{\textrm{e}}\cup \Lambda ^{\textrm{o}}$ and $\Lambda ^{\textrm{e}}\cap \Lambda ^{\textrm{o}}=\emptyset$. We denote by $\sigma ^{\textrm{e}}$ ($\sigma ^{\textrm{o}}$) a generic spin configuration on the even sublattice $\Lambda ^{\textrm{e}}$ (on the odd sublattice $\Lambda ^{\textrm{o}}$), so that (by a somehow abuse of notations) $\sigma ^{\textrm{e}}\cup \sigma ^{\textrm{o}}$ will denote a spin configuration on the original lattice $\Lambda$ where $\sigma |_{\Lambda ^{\textrm{e}}}=\sigma ^{\textrm{e}}$ and $\sigma |_{\Lambda ^{\textrm{o}}}=\sigma ^{\textrm{e}}$. Given a configuration $\sigma ^{\textrm{e}}$ in $\Lambda ^{\textrm{e}}$ we recall that ${{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}$ denotes the event formed by all configurations $\sigma \in \Sigma _\Lambda$ such that $\sigma _z=\sigma ^{\textrm{e}}_z$ for all $z\in \Lambda ^{\textrm{e}}$. We let $\Sigma _{\Lambda ^{\textrm{e}}}$ ($\Sigma _{\Lambda ^{\textrm{o}}}$) be the set of all spin configurations in the even lattice $\Lambda ^{\textrm{e}}$ (in the odd lattice $\Lambda ^{\textrm{o}}$). Observe that if $\{x,y\}\subset \Lambda ^{\textrm{o}}$ (or $\{x,y\}\subset \Lambda ^{\textrm{e}}$) then necessarily $|x-y|\ge 2$. Let us denote by ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$ (resp. ${\mathbb {G}}_{\Lambda ^{\textrm{e}}}$) the graph with vertex set $\Lambda ^{\textrm{o}}$ (resp. $\Lambda ^{\textrm{e}}$) and edge set formed by the pairs $\{x,y\}\subset \Lambda ^{\textrm{o}}$ (resp. $\{x,y\}\subset \Lambda ^{\textrm{e}}$) such that $|x-y|=2$. E.g., looking at Fig. 4, the edges of the graph ${\mathbb {G}}_\Lambda ^{\textrm{o}}$ are either horizontal and vertical lines connecting two black (odd) sites passing through a white (even) site or dashed diagonal lines indicated in Fig. 4. Therefore ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$ (and similarly ${\mathbb {G}}_{\Lambda ^{\textrm{e}}}$) has as vertex set a subset of a square lattice ${\mathbb {Z}}^2$ in which each site is connected by an edge to 8 neighbors, namely 4 nearest neighbor (at Euclidean distance $\sqrt{2}$) and 4 next nearest neighbors (at Euclidean distance 2). Finally, given a spin configuration $\sigma ^{\textrm{e}}$ on the even lattice $\Lambda ^{\textrm{e}}$ we denote by ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ the subgraph of ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$ with vertex set $\Lambda ^{\textrm{o}}$ and edge set formed by those pairs $\{x,y\}\in \Lambda ^{\textrm{o}}$ which are end points of a three-vertex path $\{x,z,y\}$ in $\Lambda$ such that $|\sigma _z|=1$.

Fig. 4

AD lattice

Given a configuration $\sigma =\sigma ^{\textrm{e}}\cup \sigma ^{\textrm{o}}\in \Sigma _\Lambda$ and denoting for any site $x\in \Lambda ^{\textrm{o}}$ by $\Gamma _x$ the set if its neighbors (i.e. $\Gamma _x=\{y\in \Lambda ^{\textrm{e}}: |x-y|=1\}$), we set

$$\begin{aligned} H_x(\sigma ^{\textrm{o}}_x|\sigma ^{\textrm{e}})= -\sum _{y\in \Gamma _x}[\sigma ^{\textrm{o}}_x\sigma ^{\textrm{e}}_y-|\textrm{Y}|(\sigma ^{\textrm{o}}_x)^2(\sigma ^{\textrm{e}}_y)^2]. \end{aligned}$$

Notice that, by definition of conditional probability and due to the structure of the Hamiltonian (25), we have

$$\begin{aligned}{} & {} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ^{\textrm{o}}|{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}})=\frac{e^{-\beta H(\sigma ^{\textrm{e}}\cup \sigma ^{\textrm{o}})}}{\sum _{\xi ^{\textrm{o}}}e^{-\beta H(\sigma ^{\textrm{e}}\cup \xi ^{(\textrm{o})})}}= \prod _{x\in \Lambda ^{\textrm{o}}} \left( {e^{-\beta H_x(\sigma ^{\textrm{o}}_x|\sigma ^{\textrm{e}})}\over 1+\sum _{\xi ^{o}_x=\pm 1}e^{-\beta H_x(\xi ^{\textrm{o}}_x|\sigma ^{\textrm{e}})}}\right) \\{} & {} \quad :=\prod _{x\in \Lambda ^{\textrm{o}}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ^{\textrm{o}}_x|{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}). \end{aligned}$$

We are now ready to bound ${{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ])$ from above. According to the notations previously introduced, we can write ${{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ])$ as follows.

$$\begin{aligned} \begin{aligned} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ])&= \sum _{\sigma ^{\textrm{e}}\in \Sigma _{\Lambda ^{\textrm{e}}}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ] \cap {{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) \\&= \sum _{\sigma ^{\textrm{e}}\in \Sigma _{\Lambda ^{\textrm{e}}}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ] |{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+({{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}). \end{aligned} \end{aligned}$$

(36)

Let $[o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{e}}}}\partial \Lambda }]$ (resp. $[o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}}\partial \Lambda }]$) be the event formed by those configurations $\sigma ^{\textrm{e}}$ in $\Sigma _{\Lambda ^{\textrm{e}}}$ (resp. $\sigma ^{\textrm{o}}$ in $\Sigma _{\Lambda ^{\textrm{o}}}$) for which the origin o (resp. some neighbor of the origin o) is connected in ${\mathbb {G}}_{\Lambda ^{\textrm{e}}}$ (in ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$) to the boundary $\partial _e\Lambda$ via a path $\ell ^{\textrm{e}}$ ($\ell ^{(\mathrm o}$) such that $|\sigma ^{\textrm{e}}_x|=1$ for all $x\in \ell ^{\textrm{e}}$ ($|\sigma ^{\textrm{o}}_x|=1$ for all $x\in \ell ^{\textrm{o}}$). Note that if $\sigma ^{\textrm{e}}\cup \sigma ^{\textrm{o}}\in [o\rightarrow \partial \Lambda ]$ then necessarily $\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{e}}}}\partial \Lambda }]$ and $\sigma ^{\textrm{o}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}}\partial \Lambda }]$.

Let us also define $[o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]$ the event formed by all configurations $\sigma ^{\textrm{o}}$ in $\Sigma _{\Lambda ^{\textrm{o}}}$ for which some neighbor of the origin o is connected in the graph ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ to the boundary $\partial \Lambda$ via a path $\ell ^{\textrm{o}}$ such that $|\sigma ^{\textrm{o}}_x|=1$ for all $x\in \ell ^{\textrm{o}}$. Note that, given $\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_\Lambda ^{\textrm{e}}}\partial \Lambda }]$, the graph ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ is in general not connected (as a subgraph of ${\mathbb {G}}_{\Lambda ^{\textrm{o}}})$. On the other hand, for all $\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_\Lambda ^{\textrm{e}}}\partial \Lambda }]$, the graph ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ has necessarily a connected subgraph ${\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ with vertex set $V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ and edge set $E_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ such that $V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ contains a neighbor of the origin and a vertex of $\partial _i\Lambda \cap \Lambda ^{\textrm{o}}$. Moreover, for any $\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{e}}}}\partial \Lambda }]$, each vertex $x\in V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ is such that $\sum _{y\sim x}|\sigma ^{\textrm{e}}_y|\ge 1$. By this observations, we have

$$\begin{aligned} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ])\le & {} \sum _{\sigma ^{\textrm{e}}\in \Sigma _{\Lambda ^{\textrm{e}}}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ] |{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+({{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) \\= & {} \sum _{\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{e}}}}\partial \Lambda }]} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \rightarrow \partial \Lambda ] |{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+({{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) \\= & {} \sum _{\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{e}}}}\partial \Lambda }]} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]|{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+({{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) \\\le & {} \sup _{\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{e}}}}\partial \Lambda }]} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ] |{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) \\= & {} \sup _{\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{e}}}}\partial \Lambda }]} \sum _{\sigma ^{\textrm{o}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]}{{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma ^{\textrm{o}}|{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}) \\= & {} \sup _{\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{e}}}}\partial \Lambda }]} \sum _{\sigma ^{\textrm{o}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]} \prod _{x\in \Lambda ^{\textrm{o}}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma _x^{\textrm{o}}|{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}}). \end{aligned}$$

Given now $\sigma ^{\textrm{o}}\in \Sigma _{\Lambda ^{\textrm{o}}}$, for any $x\in \Lambda ^{\textrm{o}}$ let us set $\omega _x=|\sigma ^{\textrm{o}}_x|$. Let $\omega$ be a generic configuration in $\{0,1\}^{\Lambda ^{\textrm{o}}}\equiv \Omega _{\Lambda ^{\textrm{o}}}$, as in Sect. 2.2, we say that the site x is open if $\omega _x=1$ and closed if $\omega _x=0$. Let $[o{\xrightarrow [\Omega _{\Lambda ^{\textrm{o}}}]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]$ be the set of all configurations $\omega \in \Omega _{\Lambda ^{\textrm{o}}}$ such that there exists a path in ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ of open sites connecting (a neighbor of) the origin to the boundary $\partial \Lambda$. Then we can rewrite

$$\begin{aligned} \sum _{\sigma ^{\textrm{o}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]} \prod _{x\in \Lambda ^{\textrm{o}}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma _x^{\textrm{o}}|{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}})= \sum _{\omega \in \left[ o{\xrightarrow [\Omega ^\textrm{o}_\Lambda ]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda \right] }\prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\\ \omega _x=1 \end{array}}p_x(\sigma ^{\textrm{e}}) \prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\\ \omega _x=0 \end{array}}(1-p_x(\sigma ^{\textrm{e}})), \end{aligned}$$

where

$$\begin{aligned} p_x(\sigma ^{\textrm{e}})= {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(|\sigma _x^{\textrm{o}}|=1 | \sigma ^{\textrm{e}}). \end{aligned}$$

Hence

$$\begin{aligned} \begin{aligned} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \mapsto \partial \Lambda ])&\le \sup _{\sigma ^\textrm{e}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{e}}}}\partial \Lambda }]} \sum _{\sigma ^{\textrm{o}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]} \prod _{x\in \Lambda ^{\textrm{o}}} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+(\sigma _x^{\textrm{o}}|{{\mathfrak {e}}}_{\sigma ^{\textrm{e}}})\\&= \sup _{\sigma ^{(\mathrm e)}\in [o{\xrightarrow {{\mathbb {G}}_\Lambda ^{\textrm{e}}}\partial \Lambda }]} \sum _{\omega \in [o{\xrightarrow [\Omega ^\textrm{o}_\Lambda ]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]}\prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\\ \omega _x=1 \end{array}}p_x(\sigma ^{\textrm{e}}) \prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\\ \omega _x=0 \end{array}}(1-p_x(\sigma ^{\textrm{e}}))\\&= \sup _{\sigma ^{(\mathrm e)}\in [o{\xrightarrow {{\mathbb {G}}_\Lambda ^{\textrm{e}}}\partial \Lambda }]} {\mathbb {P}}^{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{\{p_x(\sigma ^{\textrm{e}})\}_{x\in \Lambda ^{\textrm{o}}}}\left( \left[ o{\xrightarrow [\Omega ^\textrm{o}_\Lambda ]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda \right] \right) , \end{aligned} \end{aligned}$$

(37)

where ${\mathbb {P}}^{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{\{p_x(\sigma ^{\textrm{e}})\}_{x\in \Lambda ^{\textrm{o}}}}$ is the Bernoulli site percolation measure in the graph ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$, where each site $x\in \Lambda ^{\textrm{o}}$ is open with probability $p_x(\sigma ^{\textrm{e}})$ and closed with probability $1-p_x(\sigma ^{\textrm{e}})$.

Recall now that, as said above, the subgraph ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ of ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$ has a unique connected (in ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$) component ${\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ with vertex set $V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ containing the origin o and a site of the boundary $\partial \Lambda$. This means that the event $[o{\xrightarrow [\Omega ^{\textrm{o}}_\Lambda ]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]$ may only depend of the values of the $\omega _x$ with $x\in V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ and it is independent of $\omega _x$ for $x\in \Lambda ^{\textrm{o}}{\setminus } V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$. Therefore for any $\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]$, we have

$$\begin{aligned} \begin{aligned} {\mathbb {P}}^{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{\{p_x(\sigma ^{\textrm{e}})\}_{x\in \Lambda ^{\textrm{o}}}}\left( [o{\xrightarrow [\Omega ^\textrm{o}_\Lambda ]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]\right)&= \sum _{\omega \in [o{\xrightarrow [\Omega ^\textrm{o}_\Lambda ]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]}\prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\\ \omega _x=1 \end{array}}p_x(\sigma ^{\textrm{e}}) \prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\\ \omega _x=0 \end{array}}(1-p_x(\sigma ^{\textrm{e}}))\\&= \sum _{\omega \in \{0,1\}^{V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}: \;[o{\xrightarrow [\Omega _{\Lambda ^{\textrm{o}}}]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]} \sum _{\omega \in \{0,1\}^{\Lambda ^{\textrm{o}}\setminus V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}} \prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\\ \omega _x=1 \end{array}}p_x(\sigma ^{\textrm{e}}) \prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\\ \omega _x=0 \end{array}}(1-p_x(\sigma ^{\textrm{e}})) \\&= \sum _{\omega \in \{0,1\}^{V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}: \;[o{\xrightarrow [\Omega _{\Lambda ^{\textrm{o}}}]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]} \prod _{\begin{array}{c} x\in V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}\\ \omega _x=1 \end{array}}p_x(\sigma ^{\textrm{e}}) \prod _{\begin{array}{c} x\in V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}\\ \omega _x=0 \end{array}}(1-p_x(\sigma ^{\textrm{e}})) \times \\&~~~~\times \sum _{\omega \in \{0,1\}^{\Lambda ^{\textrm{o}}\setminus V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}} \prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\setminus V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}\\ \omega _x=1 \end{array}}p_x(\sigma ^{\textrm{e}}) \prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\setminus V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}\\ \omega _x=0 \end{array}}(1-p_x(\sigma ^{\textrm{e}}))\\&= \sum _{\omega \in \{0,1\}^{V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}: \;[o{\xrightarrow [\Omega _{\Lambda ^{\textrm{o}}}]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]} \prod _{\begin{array}{c} x\in V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}\\ \omega _x=1 \end{array}}p_x(\sigma ^{\textrm{e}}) \prod _{\begin{array}{c} x\in V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}\\ \omega _x=0 \end{array}}(1-p_x(\sigma ^{\textrm{e}})), \end{aligned} \end{aligned}$$

since

$$\begin{aligned} \sum _{\omega \in \{0,1\}^{\Lambda ^{\textrm{o}}\setminus V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}} \prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\setminus V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}\\ \omega _x=1 \end{array}}p_x(\sigma ^{\textrm{e}}) \prod _{\begin{array}{c} x\in \Lambda ^{\textrm{o}}\setminus V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}\\ \omega _x=0 \end{array}}(1-p_x(\sigma ^{\textrm{e}}))=1. \end{aligned}$$

Therefore, we have that

$$\begin{aligned} {\mathbb {P}}^{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{\{p_x(\sigma ^{\textrm{e}})\}_{x\in \Lambda ^{\textrm{o}}}}\left( [o{\xrightarrow [\Omega _{\Lambda ^{\textrm{o}}}]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]\right) = {\mathbb {P}}^{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{\{p_x(\sigma ^{\textrm{e}})\}_{x\in V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\left( [o{\xrightarrow [V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}]{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]\right) \end{aligned}$$

Moreover, recalling that for any $\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_\Lambda ^{\textrm{e}}}\partial \Lambda }]$ each vertex $x\in V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ is such that $\sum _{y\sim x}|\sigma ^{\textrm{e}}_y|\ge 1$, and setting

$$\begin{aligned} p \doteq \sup _{\sum _{y\sim x}|\sigma ^{\textrm{e}}_y|\ge 1}p_x(\sigma ^{\textrm{e}}), \end{aligned}$$

(38)

we can bound

$$\begin{aligned} {\mathbb {P}}^{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{\{p_x(\sigma ^{\textrm{e}})\}_{x\in V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\left( [o{\xrightarrow [V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}]{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]\right) \le {\mathbb {P}}^{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{p}\left( [o{\xrightarrow [V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}]{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]\right) , \end{aligned}$$

where now ${\mathbb {P}}^{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{p}$ is the homogeneous Bernoulli site percolation probability measure in the graph ${\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ with parameter p given by (38).

So we get that

$$\begin{aligned} \begin{aligned} {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \mapsto \partial \Lambda ])&\le \sup _{\sigma ^{(\mathrm e)}\in [o{\xrightarrow {{\mathbb {G}}_\Lambda ^{\textrm{e}}}\partial \Lambda }]} {\mathbb {P}}^{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{p}\left( [o{\xrightarrow [V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}]{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ]\right) \\&\le {\mathbb {P}}^{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}}_{p}([o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}}}\partial \Lambda ]) \end{aligned} \end{aligned}$$

(39)

where ${\mathbb {P}}^{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}}_{p}$ is the Bernoulli site percolation probability in the graph ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$. The last inequality in (39) follows from the fact that for any $\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_\Lambda ^{\textrm{e}}}\partial \Lambda }]$ the connected component ${\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}$ is a subgrah ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$ and the probability that the origin is connected to the boundary in any subgraph C of ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$ is always less than (or at most equal to) the probability that the origin is connected to the boundary in the whole graph ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$. Therefore in (39) ${\mathbb {P}}^{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}_{p}([o{\xrightarrow [V_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}]{{\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}}}\partial \Lambda ])$ attains the supremum over the configurations ${\sigma ^{\textrm{e}}\in [o{\xrightarrow {{\mathbb {G}}_\Lambda ^{\textrm{e}}}\partial \Lambda }]}$ such that $|\sigma ^{\textrm{e}}_x|=1$ for all $x\in \Lambda ^{\textrm{e}}$, i.e. those $\sigma ^{\textrm{e}}$ for which ${\mathbb {C}}_{\Lambda ^{\textrm{o}}}^{\sigma ^{\textrm{e}}}= {\mathbb {G}}_{\Lambda ^{\textrm{o}}}$.

Let now ${\mathbb {G}}_1$ be the graph whose vertices set is ${\mathbb {Z}}^2$ and whose edges set are $\{x,y\}\in {\mathbb {Z}}^2$ such that $||x-y||_\infty =1$. It is well known (see e.g. [12] and references therein) that the site percolation threshold $p^*_c$ of the 8-neighbor square lattice ${\mathbb {G}}_1$ defined above is $p^*_c=1-p_c$ where $p_c$ is the site percolation threshold in the usual square lattice ${\mathbb {Z}}^2$ (with 4 neighbors). It is also well known via numerical simulations that $p_c=0.592\ldots$ so that $1-p_c=0.407\ldots$ (see again [12] and also [24]). Let moreover ${\mathbb {G}}^{\textrm{o}}$ be the graph whose vertices set is ${\mathbb {Z}}^2_{\textrm{odd}}$ and set of edges those $\{x,y\}\in {\mathbb {Z}}^2_{\textrm{odd}}$ such that $||x-y||_\infty =2$. Then ${ {\mathbb {G}}}_1$ and ${\mathbb {G}}^{\textrm{o}}$ are isomorphic so that ${\mathbb {P}}^{{ {\mathbb {G}}}^{\textrm{o}}}_{p}([o \xrightarrow {} \infty ])={\mathbb {P}}^{{ {\mathbb {G}}}_1}_{p}([o \xrightarrow {} \infty ])$. Also, the graph ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}$ previously introduced is the restriction of ${\mathbb {G}}^{\textrm{o}}$ to $\Lambda ^{\textrm{o}}$ and therefore ${\mathbb {G}}_{\Lambda ^{\textrm{o}}}\rightarrow {\mathbb {G}}^{\textrm{o}}$ as $\Lambda \rightarrow \infty$.

Therefore, by (39) and Lemma 3, we get

$$\begin{aligned}{} & {} \lim _{\Lambda \rightarrow \infty } \langle \sigma _o\rangle ^+_\Lambda =\lim _{\Lambda \rightarrow \infty } {{\mathbb {P}}}_{\Lambda ,\beta ,\textrm{Y}}^+([o \mapsto \partial \Lambda ])\le \lim _{\Lambda \rightarrow \infty }{\mathbb {P}}^{{\mathbb {G}}_{\Lambda ^{\textrm{o}}}}_{p}([o{\xrightarrow {{\mathbb {G}}_{\Lambda ^{\textrm{o}}}}}\partial \Lambda ])={\mathbb {P}}^{{\mathbb {G}}^\textrm{o}}_{p}([o \xrightarrow {} \infty ])\\{} & {} \quad ={\mathbb {P}}^{{ {\mathbb {G}}}_1}_{p}([o \xrightarrow {} \infty ]). \end{aligned}$$

By means of a simple calculation, we will show below that p defined in (38) is given by

$$\begin{aligned} p= \frac{2e^{-\beta |\textrm{Y}|}\cosh (\beta )}{1+2e^{- \beta |\textrm{Y}|}\cosh (\beta )}. \end{aligned}$$

(40)

In conclusion, recalling that $p<(1-p_c)$ is subcritical for the site percolation in ${\mathbb {G}}_1$ and recalling (40), we get that $\lim _{\Lambda \rightarrow \infty } \langle \sigma _o\rangle ^+_\Lambda =0,$ whenever

$$\begin{aligned} \frac{2e^{-\beta |\textrm{Y}|}\cosh (\beta )}{1+2e^{- \beta |\textrm{Y}|}\cosh (\beta )}<1-p_c, \end{aligned}$$

which is equivalent go (28) and, by spin flipping symmetry, $\langle \sigma _o\rangle ^-=-\langle \sigma _o\rangle ^+=0$, and this concludes the proof of Theorem 5. $\square$

Next we will prove (40). Let $x \in \Lambda ^{\textrm{o}}$ and suppose $k\ge 1$ is the number of nonzero spins in $\Gamma _x$. Let their sum be denoted by $N_k$, then $N_1\in \{-1,1\}$, $N_2\in \{-2,0,2\}$, $N_3\in \{-3,-1, 1, 3\}$ and $N_4\in \{-4,-2,2,4\}$. Notice that

$$\begin{aligned} P(|\sigma _x|=1|\sigma ^{\textrm{e}})=P(\sigma _x=1|\sigma ^{\textrm{e}})+P(\sigma _x=-1|\sigma ^{\textrm{e}})=\frac{2e^{-k \beta |\textrm{Y}|}\cosh (\beta N_k)}{1+2e^{-k \beta |\textrm{Y}|}\cosh (\beta N_k)}, \end{aligned}$$

which is even in $N_k$, so we may restrict ourselves to non-negative values of $N_k$. For each fixed k, $P(|\sigma _x|=1|\sigma ^{\textrm{e}})$ is non-decreasing in $N_k$, besides, $N_k\le k$, then

$$\begin{aligned} P(|\sigma _x|=1|\sigma ^{\textrm{e}})\le \frac{2e^{-k\beta |\textrm{Y}|}\cosh (\beta k)}{1+2e^{-k \beta |\textrm{Y}|}\cosh (\beta k)}. \end{aligned}$$

Since $|Y|>1$, then $\frac{2e^{-k\beta |\textrm{Y}|}\cosh (\beta k)}{1+2e^{-k \beta |\textrm{Y}|}\cosh (\beta k)}$ is non-incresing in k and since $k\ge 1$, we are done.

To conclude this section, let us compare our condition (28), which can be rewritten as

$$\begin{aligned} \frac{2p_c}{1-p_c}\, e^{-\beta |\textrm{Y}|}\cosh (\beta ) <1, \end{aligned}$$

(41)

with the condition for vanishing of the magnetization for the two dimensional BEG model at the AD line obtained in [20] via expansion methods, namely,

$$\begin{aligned} 64e^{-\beta |\textrm{Y}|}\sinh (\beta )<1. \end{aligned}$$

(42)

A simple computation shows that, as long as,

$$\begin{aligned} \beta \ge 1/2 \ln \left( \frac{32(1-p_c)+1}{32(1-p_c)-1}\right) \approx 0.0783, \end{aligned}$$

then

$$\begin{aligned} \frac{2p_c}{1-p_c} e^{-\beta |\textrm{Y}|} \cosh \beta \le 64 e^{ -\beta |\textrm{Y}|}\sinh (\beta ), \end{aligned}$$

for all $|\textrm{Y}|>1$, in particular, for such values of $\beta$, the condition (41) is better than (42).

4 Conclusions and Open Problems

In this paper we focus our attention on the zero-temperature BEG model at the FAD point and we analyze the low temperature behavior of the model on the AD line. We first perform some simulations on the two-dimensional and three-dimensional cases via a perfect sampling of an ergodic and symmetric Markov Chain whose stationary measure coincides with the zero-temperature Gibbs measure (uniform on the ground states). Our numerical data indicates that the magnetization of the model is zero in the two-dimensional case and it is different from zero in the three-dimensional case. These data also indicate that the two-point correlation decays exponentially at large distance in the two-dimensional case. Next, we obtain several rigorous results about the zero-temperature BEG model on the FAD point in two dimensions. Namely, we prove rigorously, using dynamical arguments, that the mean value of the spin at the origin is zero in the two-dimensional case and we use this result, together with some additional dynamical arguments, to conclude the existence and uniqueness of the zero-temperature Gibbs measure for the two-dimensional BEG model on the FAD point and to prove rigorously that the two-point correlation decays exponentially fast at large distances. Finally we prove, via comparison with Bernoulli site percolation, the absence of magnetization of the BEG model in the whole AD line at low temperatures, such a condition improves earlier results obtained in [20], via expansions.

Several interesting open problems can be addressed in the next future. Concerning the two dimensional BEG model on the FAD point, one could try to prove rigorously (maybe using cluster expansion methods) that for $\beta$ large but finite the magnetization is still zero as indicated by the Monte Carlo simulations presented in [29]. We also point out that the uniqueness in $d=2$ of the BEG Gibbs measure on the FAD point also for large but finite $\beta$ would show that the two-dimensional behaviour is very different from the phase diagram shown in Fig. 1 (f) of reference [16] obtained via mean field methods. Indeed, according to this diagram, as soon as the temperature is turned on, the BEG model on the FAD point should be in the ferromagnetic phase. We want to stress that the mean field approach used in ref. [16], which has been used frequently in many other works to tackle the BEG model, might not give a precise picture about the expected behavior of model at low temperatures when d is not large because we already know that $d=2$ and the $d=3$ cases are completely different: even at zero temperature magnetization is zero in $d=2$ and numerical results strongly indicate non-zero magnetization in $d=3$.

A possible shift of the phase diagram of Fig. 1 at low temperature seems reasonable (e.g. see [16] where authors claim that for $d\ge 3$ their mean field results predict such shift of the zero temperature diagram, see in [16] figures (f), (g), (h). (i)). This should imply that the AD coexistence line at $T=0$ becomes a coexistence curve which needs not be a straight line at positive T, but for the moment our approach does not seem to be robust enough to tackle this problem and probably new ideas will be needed.

Again about the two-dimensional zero-temperature BEG model on the FAD point, it would be interesting to obtain tighter rigorous bounds on the exponential decay of the two-point correlation function.

Concerning the d-dimensional zero-temperature BEG model on the FAD point when $d\ge 3$, the non-uniqueness of the Gibbs measure has been established rigourously only when d is sufficiently high (see in Sect. 3.1.3 of [27] the quantitative results about the Widom-Rowlisnson model with activity $\lambda =1$). It remains completely open, even in the three-dimensional case, to prove rigorously (possibly using dynamical arguments?) that the Gibbs measure is not unique at zero-temperature.