Synchronization for Networks of Globally Coupled Maps in the Thermodynamic Limit

Abstract

We study a network of finitely many interacting clusters where each cluster is a collection of globally coupled circle maps in the thermodynamic (or mean field) limit. The state of each cluster is described by a probability measure, and its evolution is given by a self-consistent transfer operator. A cluster is synchronized if its state is a Dirac measure. We provide sufficient conditions for all clusters to synchronize and we describe setups where the conditions are met thanks to the uncoupled dynamics and/or the (diffusive) nature of the coupling. We also give sufficient conditions for partially synchronized states to arise—i.e. states where only a subset of the clusters is synchronized—due to the forcing of a group of cluster on the rest of the network. Lastly, we use this framework to show emergence and stability of chimera states for these systems.

1 Introduction

Coupled map systems are simple models of spatially ordered interacting units, also referred to as sites to emphasize their location in space. The evolution of each unit is prescribed by the same dynamical system, the uncoupled or local dynamic, plus a perturbation given by the interaction with neighbouring sites—the role of the spatial structure is to define the neighbours of each site. Coupled map lattices, where the sites are placed at the nodes of a regular lattice, were studied extensively, see for example [9, 15, 20, 21] and the references therein. Our current work will focus on the case where the maps are globally coupled, meaning that the neighbours of one unit are all the other units and each site interacts in the same way with every other site so that the system has full permutation symmetry. This model is amenable to taking a particular infinite-sites limit called the themodynamic limit, well known from classical mechanics in the continuous time setting [24]. In our situation, the limit results into a system whose state is given by a probability measure and whose time evolution is given by a self-consistent operator¹ (see below for a definition).

In this paper we study networks where each node of the network (which we will refer to as a cluster) is a system of globally coupled maps in the thermodynamic limit. Our goal is to investigate the mechanisms that can lead to synchronization of the states within clusters, meaning that the state of a cluster converges to a Dirac measure by the effect of the dynamics. Below we will make these ideas more precise.

1.1 Thermodynamic Limit for a System of N Coupled Clusters

Consider a collection of $n\in \mathbb N$ interacting units divided into $N\in \mathbb N$ clusters. Given numbers $0< m_1, \,m_2,\,...,\,m_N<1$ with $\sum _i m_i=1$, we assume that for $i<N$, cluster i is made of $M_i(n):=\lfloor m_in\rfloor \in \mathbb N$ units, and cluster N is made of the $M_N(n)$ remaining units. Units in the same cluster evolve according to the same deterministic law, which is perturbed by the same type of interactions from units in any other given cluster. This system is described by n coordinates $\varvec{\xi }=(\xi _{11},...,\xi _{1M_1};\,\xi _{21},...,\xi _{2M_2};...)\in \mathbb T^n$ whose evolution is given by

$$\begin{aligned} \xi _{ij}(t+1)=f_i\circ \Phi _i(\xi _{ij}(t);\,\varvec{\xi }(t)) \end{aligned}$$

(1)

where $f_i:\mathbb T\rightarrow \mathbb T$ is the uncoupled evolution for units in cluster i and

$$\begin{aligned} \Phi _i(\xi _{ij};\,\varvec{\xi })=\xi _{ij}+\frac{1}{n}\sum _{\ell =1}^N\sum _{k=1}^{M_\ell }\frac{1}{m_\ell }h_{i \ell }(\xi _{ij},\xi _{\ell k}) \end{aligned}$$

gives the pairwise coupling between units where the coupling function $h_{i,\ell }$ can vary between different clusters of nodes. Take the thermodynamic limit for $n\rightarrow \infty$ assuming that at a given time $t\in \mathbb N$, for all i, there is a probability measure $\mu _i$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{M_i}\sum _{j=1}^{M_i}\delta _{\xi _{i j}(t)}= \mu _i \end{aligned}$$

where the limit is with respect to the weak topology on the space of probability measures of $\mathbb T$. Then, if all the $f_i$ and the $h_{i\ell }$ are continuous, the time evolution can be written as

$$\begin{aligned} \xi _{i j}(t+1)=f_i\circ \Phi _{\varvec{\mu },i}(\xi _{ij}(t))\quad \text{ where }\quad \Phi _{\varvec{\mu },i}(x)=x+\sum _{\ell =1}^N\int h_{ i\ell }(x, y)d\mu _\ell (y) \end{aligned}$$

and where we denoted $\varvec{\mu }=(\mu _1,...,\mu _N)$.

Let $\mathcal M_1(\mathbb T)$ be the set of Borel probability measures on $\mathbb T$. The transfer operator of a measurable map $T: \mathbb T\rightarrow \mathbb T$ is defined as $T_*: \mathcal M_1(\mathbb T) \rightarrow \mathcal M_1(\mathbb T)$

$$\begin{aligned} T_*\mu =\mu \circ T^{-1}. \end{aligned}$$

By this notation, $f_{i*}$ and $\Phi _{\varvec{\mu },i*}$ are the transfer operators of the maps $f_i$ and $\Phi _{\varvec{\mu },i}$ and one has that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{M_i}\sum _{j=1}^{M_i}\delta _{\xi _{ij}(t+1)}= f_{i*}\Phi _{\varvec{\mu },i*}\mu _i \end{aligned}$$

The evolution of the probability measures describing the states of the clusters is therefore given by application of a transfer operator which depends on the measures themselves.² So in the thermodynamic limit, we have a particular sequential (also called non-autonomous) dynamical system on the circle $\mathbb T$. Defining

$$\begin{aligned}(\mathcal F \varvec{\mu })_i=f_{i*}\Phi _{\varvec{\mu },i*}\mu _i, \quad i=1,\dots ,N,\end{aligned}$$

we obtain a nonlinear operator describing the evolution of the system state, which we will call the self consistent transfer operator.

Existence of fixed points for self-consistent operators, their stability, and their behavior under perturbations have been first investigated by [6, 19] and more recently by [14, 29, 30]. Most of the results cited above have been stated having in mind self-consistent operators arising from small nonlinear perturbations of transfer operators having a spectral gap on some space of absolutely continuous probability measures with densities in a Banach space of regular functions (e.g. transfer operators for uniformly expanding maps).

In contrast, the measures we are most interested in are singular with respect to Lebesgue, and the mechanisms that lead to synchronization need/allow for large nonlinear perturbations. First steps in this direction are contained in [3, 29] where convergence to a Dirac measure is shown when the strength of interaction is sufficiently strong.

We note that in the continuous time case, synchronization for self-consistent systems has been investigated extensively in the special setting of coupled oscillator models. For the more classical results on the Kuramato model and synchronization in this scenario see [11] and the references therein, and [5] for a multi-population extension more closely related to our model.

1.2 Synchronization

Two units $\xi _{ij_1}$ and $\xi _{ij_2}$ in a given cluster are synchronized if they are in the same state and follow the same evolution. Roughly speaking, one says that two units synchronize if the distance between their state variables converges asymptotically to zero. Synchronization is an important concept in applications being often associated to function or malfunction of real-world systems (e.g. [16, 28]).

Synchronization for systems of finitely many coupled maps has been extensively investigated. See for example [2, 22, 27]. The main objects of study are synchronization manifolds, which are the subsets in phase space where part of the units have their state variables equal to each other: in a system with n coupled units having coordinates $\{\xi _1,...,\xi _n\}$, fixed $1\le i_1<i_2<...<i_k\le n$, one can define the associated synchronization manifold as

$$\begin{aligned} M_{(i_1,...,i_k)}:=\{\xi _{i_1}=\xi _{i_2}=....=\xi _{i_k}\}. \end{aligned}$$

When the set $M_{(i_1,...,i_k)}$ is invariant under the coupled dynamics, one usually studies conditions for the stability of this manifold.

In the thermodynamic limit of the cluster model, we study synchronization within each cluster. We say that a cluster is synchronized if the probability measure describing its state is a Dirac measure. If at the thermodynamic limit a cluster is in the state $\delta _x$, this can be understood as almost every unit in that cluster (in a suitable probabilistic sense) is in the state x. We say that the system is in a completely synchronized state if this holds for all clusters. By our definition, not all clusters need to be in the state of the same Dirac measure, $\delta _{x_i}$ is free to depend on cluster i, and our general goal is not to discuss synchronization between clusters. However, we will do so in special cases when also synchronization between clusters is expected. We speak of a partially synchronized state when only a subset of the clusters are synchronized. Effectively, by synchronization we mean the dynamical stability of synchronized states. We say that a set of states $\mathcal S$ is dynamically stable, when given a small perturbation of one of these states (from a prescribed set of perturbations), the system converges to an element of $\mathcal S$ under the effect of the dynamics.

1.3 Organization of the Paper

In this paper we give a definition of stability of synchronized states, and discuss criteria implying stability under the evolution of the self-consistent operator. In Sect. 2 we present the setup, give a rigorous definition of synchronized states, and define their stability. In Sect. 3 we give sufficient conditions for stability of completely synchronized states and we describe two mechanisms that can produce stable completely synchronized states: in one the synchronized state is a consequence of the uncoupled dynamics, and in the other it is due to the diffusive nature of the coupling. Most importantly, checking the sufficient conditions that we give only requires the analysis of a finite dimensional dynamical system constructed from the infinite-dimensional self-consistent operator. In Sect. 4 we study the stability of partially synchronized states, where the synchronization is due to the influence of the unsynchronized clusters on the clusters that synchronize. Finally, we discuss applications on chimera states and illustrate our result with some numerical simulations.

2 Setup

2.1 The Self-consistent Transfer Operator

We now describe our model considering a network made of $N\in \mathbb N$ clusters in the thermodynamic limit. Denote by $\mathcal M_1$ the set of Borel probability measures on $\mathbb T$. A state of the network is described by an element $\varvec{\mu }=(\mu _1,...,\mu _N)$ in $\mathcal M_1^N$, where $\mu _i$ is the state of the $i-$th cluster.

The dynamics is prescribed by maps $\{f_i\}_{i=1}^N$, $f_i:\mathbb T\rightarrow \mathbb T$ and interaction functions $\{h_{ij}\}_{i,j=1}^N$, $h_{ij}:\mathbb T\times \mathbb T\rightarrow \mathbb R$. We are going to assume throughout the paper that $\{f_i\}_{i=1}^N$ and $\{h_{ij}\}_{i,j=1}^N$ are smooth maps, in particular twice continuously differentiable in all variables.

Given $\varvec{\mu }\in \mathcal M_1^N$, for $i=1,...,N$ define the maps $\{F_{\varvec{\mu },i}\}_{i=1}^N$ on $\mathbb T$

$$\begin{aligned} F_{\varvec{\mu },i}(x):= f_i\circ \Phi _{\varvec{\mu },i}(x) \end{aligned}$$

(2)

where

$$\begin{aligned} \Phi _{\varvec{\mu },i}(x) := x+\sum _{j=1}^N\int _\mathbb Th_{ij}(x,y)d\mu _j(y) \end{aligned}$$

(3)

is a mean-field coupling map. The evolution of a state $\varvec{\mu }\in \mathcal M_1^N$ is given by $\mathcal F:\mathcal M_1^N\rightarrow \mathcal M_1^N$ defined as

$$\begin{aligned} \mathcal F\varvec{\mu }=(F_{\varvec{\mu },1*}\mu _1,...,F_{\varvec{\mu },N*}\mu _N) \end{aligned}$$

where $F_{\varvec{\mu },i*}$ denotes the transfer operator of the map $F_{\varvec{\mu },i}$. Later on we are going to denote by $F_{\varvec{\mu }}:\mathbb T^N\rightarrow \mathbb T^N$ the product map $F_{\varvec{\mu }}(\varvec{x})=(F_{\varvec{\mu },1}(x_1),...,F_{\varvec{\mu },N}(x_N))$ where $\varvec{x}=(x_1,...,x_N)$.

In some cases we are going to write $\alpha _{ij}h_{ij}$ instead of $h_{ij}$, to highlight the dependence on a parameter $\alpha _{ij} \in \mathbb R$ that allows us to “tune" the coupling strength of the interactions from nodes in cluster j to nodes in cluster i.

2.2 Synchronized States

As we have already mentioned in the introduction, a cluster is synchronized if its state is a $\delta$-measure concentrated at some point.

Our main focus will be on particular synchronized states where the support of the Dirac masses is contained in some specific subset of $\mathbb T^N$.

Definition 2.1

Let $X \subset \mathbb T^N$ and

$$\begin{aligned} \mathcal S_X:=\{\varvec{\mu }\in \mathcal M_1^N:\,\,\,\exists \varvec{x}\in X \text{ s.t. } \mu _{i}=\delta _{x_i}, \forall i=1,\dots ,N\} \end{aligned}$$

denote the set of completely synchronized states in X.

Definition 2.2

Let $k< N$, $X \subset \mathbb T^k$, and

$$\begin{aligned} \mathcal{PS}\mathcal{}^{(i_1,\dots ,i_k)}_{X}:=\{\varvec{\mu }\in \mathcal M_1^N:\,\,\,\exists \varvec{x}\in X \text{ s.t. } \mu _{i_j}=\delta _{x_{j}} \forall j=1,\dots ,k\} \end{aligned}$$

denote the set of partially synchronized states in X where the clusters $i_1,\dots ,i_k$ are synchronized.

A particularly interesting choice for X is the diagonal $\Delta = \{(x_1,\dots ,x_N) \in \mathbb T^N: x_1 = \dots = x_N\}$. If $\mu \in S_X$, all the clusters are (1) completely synchronized on their own, as their individual state is described by a Dirac measure (2) the clusters are synchronized with respect to each other, as their states are described by the same Dirac measure.

From now on we will assume without loss of generality that in a partially synchronized state, the last k clusters are synchronized, while the first $N-k$ might not be, and we will denote the set of partially synchronized states by

$$\begin{aligned} \mathcal{PS}\mathcal{}_{X}=\mathcal M_1^{N-k}\times \mathcal S_X. \end{aligned}$$

Remark 2.1

From the definition of the self-consistent transfer operator it follows immediately that $\mathcal F \mathcal S_{\mathbb T^N}\subset \mathcal S_{\mathbb T^N}$, and therefore also $\mathcal F \left( \mathcal{PS}\mathcal{}_{ \mathbb T^k}\right) \subset \mathcal{PS}\mathcal{}_{ \mathbb T^k}$, implying that synchronized states are invariant under the self-consistent operator. We will see that in many particular cases of interest, $\mathbb T^N$ (and $\mathbb T^k$) can be restricted to particular subsets X, and $\mathcal M_1^{N-k}$ can be narrowed down to a much smaller set of measures.

One then wonders if a given synchronized state is stable under $\mathcal F$, i.e. if perturbing a synchronized state $\varvec{\mu }$ slightly, in a sense that will be made precise below, $\mathcal F^n\varvec{\mu }$ converges to a synchronized state.

2.3 Stability of Synchronized States

In the following we denote by $\mathcal M$ the set of finite signed Borel measures on $\mathbb T$, and $d_W$ the Wasserstein distance between measures in $\mathcal M_1$ (Wasserstein distance associated to the Euclidean metric on $\mathbb T$³). Given $N\in \mathbb N$, for $\varvec{\mu }=(\mu _1,...,\mu _N),\varvec{\nu }=(\nu _1,...,\nu _N)\in \mathcal M_1^N$ we extend the definition of $d_W$ as follows

$$\begin{aligned} d_W(\varvec{\mu }, \varvec{\nu }):=\max _id_W(\mu _i, \nu _i). \end{aligned}$$

For a measure $\mu \in \mathcal M_1$, we denote by ${{\,\mathrm{supp}\,}}\mu$ its topological support; for a state $\varvec{\mu }=(\mu _1,...,\mu _N)\in \mathcal M_1^N$ we denote

$$\begin{aligned} {{\,\mathrm{supp}\,}}\varvec{\nu }:= {{\,\mathrm{supp}\,}}\mu _1\times \cdots \times {{\,\mathrm{supp}\,}}\mu _N\subset \mathbb T^N, \end{aligned}$$

and we define

$$\begin{aligned} |{{\,\mathrm{supp}\,}}\varvec{\nu }|_{\infty }:=\max _{i}|{{\,\mathrm{supp}\,}}\mu _i| \end{aligned}$$

with $|{{\,\mathrm{supp}\,}}\mu _i|:=\inf \{|I|:\, I \text{ arc } \text{ s.t. } {{\,\mathrm{supp}\,}}\mu _i\subset I\}$ where |I| is the length of the arc I. Let further

$$\begin{aligned} B_R(X):=\left\{ \varvec{y}:\, \inf _{\varvec{x}\in X}d(\varvec{y},\varvec{x})<R\right\} \end{aligned}$$

for some $X \subset \mathbb T^N$.

In the following section we are going to discuss the stability of synchronized states under perturbation. We mean stability in the following sense:

Definition 2.3

Consider $\mathcal {S}_{X}$ for some $X \subset \mathbb T^N$. We say that $\mathcal {S}_{X}$ is a set of stable synchronized states if there is $\varepsilon >0$, $R > 0$ such that for every $\varvec{\mu }\in \mathcal M_1^{N}$ with $|{{\,\mathrm{supp}\,}}\varvec{\mu }|_\infty <\varepsilon$ and ${{\,\mathrm{supp}\,}}\varvec{\mu }\subset B_R(X)$

$$\begin{aligned} \lim _{n\rightarrow \infty }d_{W}\left( \mathcal F^n\varvec{\mu },\, \mathcal {S}_{ X}\right) =0. \end{aligned}$$

In the partially synchronized case, we mean the following:

Definition 2.4

Consider $\mathcal{PS}\mathcal{}_{X}$ for some $X \subset \mathbb T^{N-N_1}$. We say that $\mathcal{PS}\mathcal{}_{X}$ is a set of stable partially synchronized states if there are $\mathcal N \subset \mathcal M_1^{N_1}$ and $\varepsilon >0$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }d_{W}\left( \mathcal F^n(\varvec{\mu },\varvec{\nu }),\, \mathcal{PS}\mathcal{}_X\right) =0. \end{aligned}$$

for every $\varvec{\mu }\in \mathcal N$ and $\varvec{\nu }\in \mathcal M_1^{N-N_1}$ with $|{{\,\mathrm{supp}\,}}\varvec{\nu }|_\infty <\varepsilon$ and and ${{\,\mathrm{supp}\,}}\varvec{\nu }\subset B_R(X)$.

3 Stability of Completely Synchronized States

We first give a criterion for the stability of completely synchronized states, and then we apply it to obtain a perturbative result on stability of synchronized state in the small coupling regime, and stability of synchronized states in the case of diffusive coupling.

3.1 Criterion for Stability of Completely Synchronized States

Consider the map $G:\mathbb T^N\rightarrow \mathbb T^N$ that describes the action of $\mathcal F$ on the completely synchronized states $\varvec{\mu }\in \mathcal S_{\mathbb T^N}$ defined in the following way: for every $\varvec{x}=(x_1,\dots ,x_N)\in \mathbb T^N$

$$\begin{aligned} G(\varvec{x}):=\varvec{x}'\,\, \text{ where } \,\,\mathcal F(\delta _{x_1},\dots ,\delta _{x_N})=(\delta _{x_1'},\dots ,\delta _{x_N'}). \end{aligned}$$

(4)

For every $i=1,...,N$, define functions $g_{i}:\mathbb T^N\rightarrow \mathbb R$ as

$$\begin{aligned} g_i(\varvec{x}):=(F_{(\delta _{x_1},...,\delta _{x_N}),i})'(x_i)=\partial _x\left[ f_i\left( x+\sum _{j}h_{ij}(x,x_{ j})\right) \right] |_{x=x_i}. \end{aligned}$$

(5)

These functions control the derivative of $F_{\varvec{\mu },i}$ for states $\varvec{\mu }$ close to completely synchronized states.

The following result gives a criterion for stability of synchronization in terms of the finite dimensional dynamics of G and the finite set of functions $\{g_i\}_{i=1}^N$.

Theorem 3.1

Assume that there are $\lambda \in (0,1)$ and $n_0\in \mathbb N$ such that

• (1) G has an invariant set $X\subset \mathbb T^N$ which is uniformly attracting, i.e. $\exists U\supset X$ open such that $G(U)\subset U$ such that

  $$\begin{aligned} d(G^{n_0}(\varvec{x}),X)\le \lambda d(\varvec{x},X)\quad \quad \forall \varvec{x}\in U; \end{aligned}$$

• (2) $|\prod _{j=0}^{n_0-1}g_i(G^{j}\varvec{x})|\le \lambda <1$ for every $\varvec{x}\in X$.

Then there are $R>0$, $\varepsilon >0$, and $\Lambda \in (0,1)$ such that if $\varvec{\mu }=(\mu _1,...,\mu _N)$ satisfies

$$\begin{aligned} |{{\,\mathrm{supp}\,}}\varvec{\mu }|_\infty <\varepsilon \quad \text{ and } \quad {{\,\mathrm{supp}\,}}\varvec{\mu }\subset B_R(X), \end{aligned}$$

one has

$$\begin{aligned} d_W(\mathcal F^n\varvec{\mu },\,\mathcal S_X)\le \mathcal O(\Lambda ^n). \end{aligned}$$

Proof

We first treat the case $n_0=1$ and then show how to modify the proof for $n_0>1$. We are going to use the notation $\varvec{\mu }^{(n)}=\mathcal F^n\varvec{\mu }$ for some fixed initial $\varvec{\mu }$.

Step 1 Here we compare G with the product map $F_{\varvec{\mu }}:\mathbb T^N\rightarrow \mathbb T^N$

$$\begin{aligned} F_{\varvec{\mu }}(\varvec{x}):=(F_{\varvec{\mu },1}(x_1),...,F_{\varvec{\mu },N}(x_N)), \end{aligned}$$

and $g_i$ with $(F_{\varvec{\mu },i})'$ when $\varvec{\mu }$ is close to a synchronized state.

For every $\delta >0$ there is $\varepsilon '>0$ such that if

$$\begin{aligned} {{\,\mathrm{supp}\,}}\varvec{\mu }\subset B^{\infty }_{\varepsilon '}(\varvec{x}):=\{\varvec{x}' \in \mathbb T^N: \max _{i}|x_i-x'_i| < \varepsilon '\}, \end{aligned}$$

then $\forall \varvec{y}\in B^{\infty }_{\varepsilon '}(\varvec{x})$

$$\begin{aligned} |G(\varvec{y})-F_{\varvec{\mu }}(\varvec{y})|<\delta . \end{aligned}$$

This can be inferred by the equations

$$\begin{aligned} |(G(\varvec{y}))_i-(F_{\varvec{\mu }}(\varvec{y}))_i|&=|(G(\varvec{y}))_i- F_{\varvec{\mu },i}(y_i)|\\&=f_i\left( y_i+\sum _j\alpha _{ij} h_{ij}(y_i,y_j)\right) \\&\quad -f_i\left( y_i+\sum _j\alpha _{ij}\int h_{ij}(y_i,y)d\mu _j(y)\right) , \end{aligned}$$

and by the regularity assumptions on h and $f_i$, that imply that the above quantity can be made as small as wanted by picking $\max _i d_W(\mu _i,\delta _{y_i})$ as small as needed. In particular, $\max _i d_W(\mu _i,\delta _{y_i})$ can be made small by requiring that for all i, ${{\,\mathrm{supp}\,}}\mu _i\subset (x_i-\varepsilon ',x_i+\varepsilon ')$ and $y_i\in (x_i-\varepsilon ',x_i+\varepsilon ')$, with $\varepsilon '>0$ small.

By a similar reasoning, we can deduce that for every $\delta '>0$ there is $\eta >0$ such that if ${{\,\mathrm{supp}\,}}\varvec{\mu }\subset B^{\infty }_\eta (\varvec{y})$, then

$$\begin{aligned} |g_i(\varvec{y})-F_{\varvec{\mu },i}'(z)|<\delta '\quad \quad \forall z\in {{\,\mathrm{supp}\,}}(\mu _i). \end{aligned}$$

Step 2 By assumption 2) and continuity of $g_i$, for every $\Lambda '\in (\lambda ,1)$ there is $R>0$ such that

$$\begin{aligned}|g_i(\varvec{y})|\le \Lambda '<1,\quad \quad \forall \varvec{y}\in B_R(X)\subset U.\end{aligned}$$

This and the conclusion of Step 1 imply that for every $\Lambda \in (\Lambda ',1)$ there is $\eta '>0$ sufficiently small such that if ${{\,\mathrm{supp}\,}}\varvec{\mu }^{(k)}\subset B^\infty _{\eta '}(\varvec{y}^{(k)})$ with $\varvec{y}^{(k)}\in B_{R}(X)$, then

$$\begin{aligned} |(F_{\varvec{\mu }^{(k)},i})'(z_i^{(k)})|\le \Lambda ,\quad \quad \forall \varvec{z}^{(k)}\in {{\,\mathrm{supp}\,}}(\varvec{\mu }_i^{(k)}). \end{aligned}$$

(6)

Step 3 Fix $\Lambda \in (\Lambda ',1)$ and let $\eta '>0$ be as in Step 2. Pick $\delta >0$ sufficiently small so that

$$\begin{aligned} \Lambda R+\delta <R \end{aligned}$$

(7)

and such that for any $H:\mathbb T^N\rightarrow \mathbb T^N$ with $|G-H|<\delta$

$$\begin{aligned} H(B_R(X))\subset B_{R}(X). \end{aligned}$$

(8)

Then pick $\varepsilon <\eta '$ that satisfies the conclusion of Step 1 for $\delta >0$ as above.

With this choice of $\varepsilon$, if ${{\,\mathrm{supp}\,}}\varvec{\mu }^{(n)}\subset B_R(X)$ and $|{{\,\mathrm{supp}\,}}\varvec{\mu }^{(n)}|_\infty <\varepsilon$, then by (6) we have that

$$\begin{aligned} |{{\,\mathrm{supp}\,}}\varvec{\mu }^{(n+1)}|_\infty<\Lambda |{{\,\mathrm{supp}\,}}\varvec{\mu }^{(n)}|_\infty <{ \Lambda }^{}\varepsilon , \end{aligned}$$

and since $|G-F_{\varvec{\mu }^{(n)}}|<\delta$, by (8) and (7)

$$\begin{aligned}{{\,\mathrm{supp}\,}}\varvec{\mu }^{(n+1)}=F_{\varvec{\mu }^{(n)}}({{\,\mathrm{supp}\,}}\varvec{\mu }^{(n)})\subset B_{\lambda R+\delta }(X)\subset B_{R}(X). \end{aligned}$$

Step 4 Choosing $\varvec{\mu }$ with ${{\,\mathrm{supp}\,}}\varvec{\mu }\subset B_R(X)\cap B^\infty _\varepsilon (X)$ where R and $\varepsilon >0$ are as in the steps above, by induction one can show that

$$\begin{aligned} |{{\,\mathrm{supp}\,}}\varvec{\mu }^{(n)}|_\infty <\Lambda ^n|{{\,\mathrm{supp}\,}}\varvec{\mu }|_\infty . \end{aligned}$$

which implies that $\varvec{\mu }^{(n)}$ converges exponentially fast, w.r.t. $d_W$, to $\mathcal S_{X}$ as $n\rightarrow +\infty$.

When $n_0>1$, consider $\widetilde{\mathcal F}:=\mathcal F^{n_0}$, and notice that

$$\begin{aligned} \widetilde{\mathcal F}(\delta _{x_1},...,\delta _{x_N})=(\delta _{G^{n_0}(x_1)},...,\delta _{G^{n_0}(x_N)}). \end{aligned}$$

So we define ${{\widetilde{G}}}:= G^{n_0}$. Furthermore, defining

$$\begin{aligned} {{\widetilde{F}}}_{\varvec{\mu }^{(0)},i}(x):=F_{\varvec{\mu }^{(n_0-1)},i}\circ ...\circ F_{\varvec{\mu }^{(1)},i}\circ F_{\varvec{\mu }^{(0)},i}(x) \end{aligned}$$

(9)

one has that for $\varvec{\mu }=(\mu _1,...,\mu _N)$, $(\widetilde{ \mathcal F}\varvec{\mu })_i={{\widetilde{F}}}_{\varvec{\mu },i*}\mu _i$. We can then consider for all $\varvec{x}=(x_1,..,x_N)\in X$

$$\begin{aligned} {{\widetilde{g}}}_i(\varvec{x}):= (\widetilde{F}_{(\delta _{x_1},...,\delta _{x_N}),i})'(x_i)=\prod _{j=0}^{n_0-1}g_i(G^j\varvec{x}). \end{aligned}$$

Now it’s easy to see that: ${{\widetilde{G}}}(X)=X$, ${{\widetilde{G}}}(U)\subset U$,

$$\begin{aligned} d({{\widetilde{G}}}(\varvec{x}),X)\le \lambda d(\varvec{x},X)\quad \quad \forall \varvec{x}\in U, \end{aligned}$$

and $|{{\widetilde{g}}}_i(\varvec{x})|\le \lambda <1$ for every $\varvec{x}\in X$. One can check that mutatis mutandis, steps from 1 to 4 above hold for $\widetilde{\mathcal F}$ in place of $\mathcal F$⁴ proving that there are $R>0$, $\varepsilon >0$, and $\Lambda \in (0,1)$ such that if $\varvec{\mu }=(\mu _1,...,\mu _N)$ satisfies

$$\begin{aligned} |{{\,\mathrm{supp}\,}}\varvec{\mu }|_\infty <\varepsilon \quad \text{ and } \quad {{\,\mathrm{supp}\,}}\varvec{\mu }\subset B_R(X), \end{aligned}$$

one has

$$\begin{aligned} d_W(\widetilde{\mathcal F}^n\varvec{\mu },\,\mathcal S_X)\le \mathcal O(\Lambda ^n) \end{aligned}$$

which in turn implies the conclusion of the theorem. $\square$

Remark 3.1

In general, it is not clear whether the orbit of $\mathcal F^n\varvec{\mu }$ in $\mathcal M_1^N$ will converge to an orbit in X. In the particular case where X is an attracting periodic orbit of G, this can be checked to be true. We are going to show an instance of this in the next section.

In the following subsections we are going to discuss some applications of the theorem above.

3.2 Weak Coupling

In this section we will consider interaction functions of the form $\alpha _{ij}h_{ij}$ for some $\alpha _{ij} \in \mathbb R$. We talk of weak coupling when $\alpha _{ij}$ are close to zero. Whenever the uncoupled maps $f_i$ have attracting periodic orbits, these give rise to synchronized states that are stable, and stay such when switching on a sufficiently weak coupling.

Definition 3.1

We say that $x \in Y$ is an attracting k-periodic point of the map $T \in C^1(Y;Y)$ if $T^k(x)=x$ and there exists $\lambda \in (0,1)$ such that $\Vert DT^{ k}(x)\Vert \le \lambda$.

Notice that this implies that $\Vert DT^{ k}(T^{\ell }(x))\Vert \le \lambda$ for all $\ell \in \{0,\dots ,k-1\}$ as $DT^{ k}(x)=\prod _{i=0}^{k-1}D(T^{i}(x))=DT^{ k}(T^{\ell }(x))$ for all $\ell \in \{0,\dots ,k-1\}$.

In the next theorem we are going to denote $G=G_{\alpha }$ and $g_i=g_{i,\alpha }$, $i=1,\dots ,N$ to highlight the dependence on the coupling strength $\alpha =(\alpha _{ij})_{i,j}$.

Proposition 3.1

Let $\varvec{x} \in \mathbb T^N$ be an attracting k-periodic point for $\varvec{f}=f_1 \times \dots \times f_N:\mathbb T^N\rightarrow \mathbb T^N$. There is $\varepsilon >0$ such that if $|\alpha _{ij}|<\varepsilon$ holds for all $i,j \in \{1,\dots ,N\}$ we have the following:

• 1. there exists $\varvec{x}_{\alpha } \in \mathbb T^N$ such that $G_{\alpha }^k(\varvec{x}_{\alpha })=\varvec{x}_{\alpha }$,

• 2. denoting $X_{\alpha }=\{G_{\alpha }^{\ell }(\varvec{x}_{\alpha }):\,\ell =0,...,k-1\}$, there are $R>0$, $\delta >0$ and $\Lambda '\in (0,1)$ such that if $\varvec{\mu }=(\mu _1,...,\mu _N)$ satisfies

  $$\begin{aligned} |{{\,\mathrm{supp}\,}}\varvec{\mu }|_\infty <\delta \quad \text{ and } \quad {{\,\mathrm{supp}\,}}\varvec{\mu }\subset B_R\left( X_{\alpha }\right) , \end{aligned}$$

  one has

  $$\begin{aligned} d_W(\mathcal F^n\varvec{\mu },\, \mathcal S_{X_{\alpha }})\le \mathcal O((\Lambda ')^n) \end{aligned}$$

Example 3.1

Consider f such that it has an attracting fixed point at z and define the 1-cluster system by the dynamics

$$\begin{aligned} F_{\mu }(x) = f\left( x + \alpha \int _{\mathbb T} h(x,y)d\mu (y) \right) \end{aligned}$$

Assuming $h(x,x)=0$ for all $x \in \mathbb T$, $F_{\delta _{z}}(z)=f(z)=z$ (that is, $G_{\alpha }(z)=z$), and it is easy to see that this fixed point is attracting for small enough $|\alpha |$ (so $|g_{\alpha }(z)| < 1$). Thus $X_{\alpha }=\{z\}$ is satisfies the conditions of Theorem 3.1. If we don’t assume $h(x,x)=0$, for small enough $|\alpha |$ we can argue the existence of $z_{\alpha }$ such that $G_{\alpha }(z_{\alpha })=z_{\alpha }$ by the implicit function theorem.

Proof

We prove the statement by checking the assumptions of Theorem 3.1.

Since $\varvec{x}$ is an attracting periodic point of the smooth map $\varvec{f}=G_0$, there exists a $\rho > 0$ and $\lambda _0 < 1$ such that $\Vert DG_0^{k}(\varvec{y})\Vert \le \lambda _0$ for all $\varvec{y} \in B_{\rho }(X_0)$ ( recall that $X_{0}=\{\varvec{f}^{\ell }(\varvec{x}):\,\ell =0,...,k-1\}$).

The map $G_{\alpha }$ writes

$$\begin{aligned} (G_{\alpha }(\varvec{z}))_i=f_i\left( z_i+\sum _{j=1}^N \alpha _{ij}h_{ij}(z_i,z_j) \right) , \quad i=1,\dots ,N \end{aligned}$$

implying that $\alpha \mapsto G_{\alpha } \in C^2$. By the implicit function theorem we get that for all sufficiently small $\varepsilon _1 > 0$, choosing $|\alpha _{ij}| < \varepsilon _1$, $\forall i,j$ there exists $\varvec{x}_{\alpha }$ such that $G_{\alpha }^k(\varvec{x}_{\alpha })=\varvec{x}_{\alpha }$. Furthermore, the distance of $\varvec{x}$ and $\varvec{x}_{\alpha }$ can be made arbitrarily small by decreasing $\alpha _{ij}$. Let us choose $\varepsilon _1$ such that $\Vert \varvec{x} - \varvec{x}_{\alpha } \Vert _{\infty } < \rho /2$ for all $|\alpha _{ij}| < \varepsilon _1$, $\forall i,j$.

We are going to show the following:

• 1. $DG_{\alpha }^k(\mathbf {\varvec{y}})$ is uniformly contracting for all $\varvec{y}$ sufficiently close to $X_{\alpha }$.

• 2. $g^k_{i,\alpha }(\varvec{z})$ is uniformly contracting for all $\varvec{z} \in X_{\alpha }$.

By the regularity assumptions on f the mapping $\alpha \mapsto DG^k_{\alpha }$ is continuous. This implies that there exists $\varepsilon _2 > 0$ such that for $|\alpha _{ij}| < \varepsilon _2$, $\forall i,j$ there exists a $\lambda _1 < 1$ such that $\Vert DG_{\alpha }^{k}(\varvec{y})\Vert \le \lambda _1$ for all $\varvec{y} \in B_{\rho }(X_0)$. This implies that $\Vert DG_{\alpha }^{k}(\varvec{y})\Vert \le \lambda _1$ for all $\varvec{y} \in B_{\rho /2}(X_{\alpha })$ and (1) is proved.

As for (2), $\alpha \mapsto g^k_{i,\alpha }$ is continuous, so there exists a $\varepsilon _3 > 0$ such that for $|\alpha _{ij}| < \varepsilon _3$, $\forall i,j$ we obtain $|g_{i,\alpha }^k(\varvec{z})| \le \lambda _1$.

Thus Theorem 3.1 proves our statement with the choice of $\lambda =\lambda _1$, $X=X_{\alpha }$ and $U=B_{\rho /2}(X_{\alpha })$. $\square$

3.3 Diffusive Coupling

In contrast with the previous section where the system exhibited synchronization due to the uncoupled dynamics, in this section we use Theorem 3.1 to prove persistence of stable synchronized states due to strong coupling. In particular, we consider a kind of coupling well known in applications called diffusive coupling, that takes its name from the fact that the resulting dynamics can be viewed as a discrete-time analogue of a generalized reaction-diffusion process. For an overview on diffusive coupling see [10] and the references therein. We talk of diffusive coupling when the interaction function has the form

$$\begin{aligned} h(x,y)=\varphi (y-x) \end{aligned}$$

where $\varphi :\mathbb T\rightarrow \mathbb T$ is usually taken to be a function with

$$\begin{aligned} \varphi (0)=0\quad \text{ and }\quad \varphi '(0)>0. \end{aligned}$$

(10)

This will be a standing assumption throughout this section.

The following results give synchronization criterion in the presence of multiple clusters having equal uncoupled dynamics ($f_i=:f$ for all i) with diffusive coupling. In this situation equation (2) reads

$$\begin{aligned} F_{\varvec{\mu },i}(x)=f\left( x+\sum _j\int \varphi _{ij}(y-x)d\mu _j(y)\right) \end{aligned}$$

(11)

and the $i-$th coordinate of G – defined in (4) – has expression

$$\begin{aligned} (G(\varvec{x}))_i=f\left( x+\sum _j \varphi _{ij}(x_j-x_i)\right) \end{aligned}$$

where the functions $\varphi _{ij}:\mathbb T\rightarrow \mathbb T$ satisfy (10). - As can be easily verified, the diagonal set

$$\begin{aligned} \Delta :=\{(x,...,x):\,x\in \mathbb T\}\subset \mathbb T^{N} \end{aligned}$$

(12)

is invariant under the map G. Below, we can establish conditions for the the existence of stable synchronized states for the self-consistent operator when $\Delta$ is an attracting set for G, i.e. when $\Delta$ plays the role of X in Theorem 3.1. Conditions under which $\Delta$ is attracting for G have been extensively studied in the literature of finite (and countable) site coupled maps⁵ (see e.g. [13, 17]).

Proposition 3.2

Assume that the set $\Delta :=\{(x,...,x):\,x\in \mathbb T\}\subset \mathbb T^N$ is an attracting invariant set for G—as per assumption 1) of Theorem 3.1—and that

$$\begin{aligned} \max _x |f'(x)| \left| 1-\sum _j \varphi _{ij}'(0)\right| <1\quad \quad \forall i. \end{aligned}$$

(13)

Then the set of synchronized states $\mathcal S_{\Delta }$ is stable.

Proof

We should check condition 2 of Theorem 3.1 when $X=\Delta$. From the expression of $g_i$ in (5), plugging in the expression for $F_{\varvec{\mu },i}$ in (11), we get for $\varvec{x}=(x_1,...,x_N)$

$$\begin{aligned} g_i(\varvec{x}):=\left( 1-\sum _j\varphi '_{ij}(x_j-x_i)\right) \cdot f'\left( x_i+\sum _j\varphi _{ij}(x_j-x_i)\right) \end{aligned}$$

and for $\varvec{x}\in \Delta$

$$\begin{aligned} g_i(\varvec{x}):= f'\left( x_i\right) \left( 1-\sum _j\varphi '_{ij}(0)\right) . \end{aligned}$$

The condition in (13) implies that there is $\lambda \in (0,1)$ such that $|g_i(\varvec{x})|\le \lambda$ for every $\varvec{x}\in \Delta$ and every i. $\square$

Remark 3.2

Notice that in the case with one cluster, the dynamics of the self-consistent operator is completely determined by

$$\begin{aligned} F_\mu =f\left( x+\int \varphi (y-x)d\mu (y)\right) . \end{aligned}$$

In this case condition (13) reads $(\max _x|f'(x)|)(1-\varphi '(0))<1.$

Example 3.2

Assume that $f_i=f \in C^1$ for all $i=1,\dots ,N$ and the restriction of $\varphi _{ij}$ to an arc $(-\eta ,\eta )\subset \mathbb T$ satisfies $\varphi _{ij}|_{(-\eta ,\eta )}(u)=\frac{\alpha }{N} u$, where $\alpha \in \mathbb R$ is a uniform coupling strength. We are going to show that one can find some conditions on $\alpha$ such that the assumptions of Proposition 3.2 are satisfied.

Consider the set

$$\begin{aligned} \Delta _{\omega }=\{\varvec{x} \in \mathbb T^N: |x_i-x_j| < \omega , \text { for all } i,j=1,\dots ,N\}. \end{aligned}$$

We now show that for $\alpha$ in a certain range, $G(\Delta _{\eta }) \subset \Delta _{\lambda \eta }$ for some $\lambda < 1$. Indeed, assume that $\varvec{x}\in \Delta _\eta$. Then $\varphi _{m\ell }(x_m-x_{\ell })=\frac{\alpha }{N}(x_m-x_{\ell })$ and $\varphi _{m\ell }'(x_m-x_{\ell })=\frac{\alpha }{N}$ for all $m,\ell$. So, calling $x'_j:=(G(\varvec{x}))_j$

$$\begin{aligned} |x'_m-x_\ell '|&=\left| f\left( x_{\ell }+\sum _{j=1}^N \varphi _{\ell j}(x_j-x_\ell ) \right) -f\left( x_{m}+\sum _{j=1}^N \varphi _{mj}(x_j-x_{m}) \right) \right| \\&\le \max |f'|\left| x_\ell -x_{m}+\frac{\alpha }{N}\sum _{j=1}^N(x_j-x_\ell -x_j+x_{m}) \right| \\&=\max |f'||1-\alpha ||x_\ell -x_{m}| \end{aligned}$$

which is less than $\eta$ if $\lambda :=\max |f'||1-\alpha |<1$. This can always be achieved by choosing $\alpha$ sufficiently close to 1: notice that in this case is the strong coupling that induces synchronization, not the uncoupled dynamics f.

It is also easy to see that (13) holds: since $\varphi _{ij}'(0)=\frac{\alpha }{N}$

$$\begin{aligned} (\max _x |f'(x)|) \left| 1-\sum _j \varphi _{ij}'(0)\right|&=(\max _x |f'(x)|) \left| 1-\sum _j\frac{\alpha }{N}\right| \\&=(\max _x |f'(x)|) \left| 1-\alpha \right| \\&=\lambda . \end{aligned}$$

4 Partially Synchronized States

We present and motivate the content of this section starting from a simple example illustrating a mechanism by which an unsynchronized cluster can drive another cluster to synchrony, giving rise to a stable partially synchronized state.

Example 4.1

Consider a network with two clusters, 1 and 2, whose self-consistent dynamics at state $(\mu ,\nu )\in \mathcal M_1^2$ is prescribed by the set of equations

$$\begin{aligned} \begin{array}{ll} F_{(\mu ,\nu ),1}(x)&{}= f(x)\\ F_{(\mu ,\nu ),2}(x)&{}= f\left( x+ \alpha \varphi (x) \int \psi (y) d\mu (y)\right) \end{array} \end{aligned}$$

(14)

with $f:\mathbb T\rightarrow \mathbb T$ a $C^2$ uniformly expanding map, i.e. $|f'|\ge \sigma >1$, and where we picked $h_{11}=h_{12}=h_{22}=0$ and

$$\begin{aligned}h_{21}(x,y)=\alpha \varphi (x)\psi (y)\end{aligned}$$

for some $\varphi ,\psi :\mathbb T\rightarrow \mathbb R$. Notice that the dynamic of cluster 1 does not depend on the state of the system $(\mu ,\nu )$, and in particular does not depend on $\nu$, while the evolution of cluster 2 depends on the state of cluster 1. Recall that f has a unique absolutely continuous invariant probability measure ${{\overline{\mu }}}$ [23], and every sufficiently regular density evolves to ${{\overline{\mu }}}$ under iterations of the transfer operator of f (see e.g. [7]).

Notice also that if $\mu$ is such that $\int \psi (y)d\mu (y)=0$, we have that

$$\begin{aligned} F_{(\mu ,\nu ),2}(x)=f(x), \end{aligned}$$

so cluster 2 feels the influence of cluster 1 only in the case where the above integral is nonzero.

Now assume that $f(0)=0$ and $\varphi (0)=0$. Then, $F_{(\mu ,\nu ),2}(0)=0$ and, in particular, $({{\overline{\mu }}}, \delta _0)$ is a fixed state for the self-consistent transfer operator. Below we study the stability of this fixed state.

First of all we find conditions for which 0 is an attracting fixed point of $F_{(\mu ,\nu ),2}$ when $\mu ={{\overline{\mu }}}$. We are going to denote ${{\overline{\mu }}}(\psi ):=\int \psi d{{\overline{\mu }}}$ to shorten the notation. Then

$$\begin{aligned} (F_{(\mu ,\nu ),2})'(x) = f'\left( x+\alpha \varphi (x)\overline{\mu }(\psi )\right) \,(1+\alpha {{\overline{\mu }}}(\psi ) \varphi '(x)) \end{aligned}$$

and evaluating it at zero

$$\begin{aligned} (F_{(\mu ,\nu ),2})'(0) = f'\left( 0\right) (1+\alpha {{\overline{\mu }}}(\psi ) \varphi '(0)). \end{aligned}$$

Imposing that 0 is attracting we obtain

$$\begin{aligned} -1-f'(0)<\alpha {{\overline{\mu }}}(\psi ) \varphi '(0)f'\left( 0\right)<1-f'(0)<0; \end{aligned}$$

if ${{\overline{\mu }}}(\psi ) \varphi '(0)f'\left( 0\right) >0$ then

$$\begin{aligned} \alpha \in \left( \frac{-1-f'(0)}{{{\overline{\mu }}}(\psi ) \varphi '(0)f'\left( 0\right) }, \frac{1-f'(0)}{{{\overline{\mu }}}(\psi ) \varphi '(0)f'\left( 0\right) }\right) \end{aligned}$$

(15)

if ${{\overline{\mu }}}(\psi ) \varphi '(0)f'\left( 0\right) <0$ then

$$\begin{aligned} \alpha \in \left( \frac{1-f'(0)}{{{\overline{\mu }}}(\psi ) \varphi '(0)f'\left( 0\right) }, \frac{-1-f'(0)}{{{\overline{\mu }}}(\psi ) \varphi '(0)f'\left( 0\right) }\right) . \end{aligned}$$

(16)

It is rather straightforward to show that if $\alpha$ satisfies one of the conditions above, then any state obtained from a sufficiently small perturbation⁶ of $({{\overline{\mu }}},\delta _0)$ converges to $({{\overline{\mu }}},\delta _0)$ under evolution of the self-consistent transfer operator, and therefore $({{\overline{\mu }}},\delta _0)$ is a stable attracting state (this will be made more precise in Sect. 4.2). We can interpret this as cluster 2 evolving to a synchronized state (in a stable way) as an effect of the interaction it receives from cluster 1 when the state of cluster 1 is in the vicinity of ${{\overline{\mu }}}$.

In the remark below we list some conclusions about this example that will be proved in the following sections.

Remark 4.1

In the example above:

• (i) Assuming that ${{\overline{\mu }}}(\psi ) \varphi '(0)\ne 0$, there is an interval for $\alpha$ – given explicitly in (15) and (16) – for which the fixed state $({{\overline{\mu }}},\delta _0)$ is stable: for any $(\mu ,\nu )$ with $\mu$ close to ${{\overline{\mu }}}$ having regular density (e.g. Lipschitz) and $\nu$ being supported on $(-\eta ,\eta )$ for a sufficiently small $\eta >0$, $\mathcal F^n(\mu ,\nu )\rightarrow ({{\overline{\mu }}},\delta _0)$ weakly;

• (ii) if $\alpha =0$ – i.e. no interaction – or ${{\overline{\mu }}}(\psi )=0$ – i.e. no net effect of the interaction – $F_{(\mu ,\nu ),2}=f$ and the partially synchronized state $({{\overline{\mu }}},\,\delta _0)$ has no hope of being stable, which means that a nonzero interaction is necessary for the partially synchronized state to be stable;

• (iii) adding small interaction terms to cluster 1, i.e.

  $$\begin{aligned}\begin{array}{ll} F_{(\mu ,\nu ),1}(x)&{}= f\left( x+ \varepsilon \int h_{11}(x,y)d\mu (y)+ \varepsilon \int h_{12}(x,y)d\nu (y)\right) \\ F_{(\mu ,\nu ),2}(x)&{}= f\left( x+\alpha \int \varphi (x)\psi (y)d\mu (y)\right) \end{array} \end{aligned}$$

  (where $h_{11}(0,y)=h_{12}(0,y)=0$) preserves the stability of a partially synchronized state. The main difficulty here is that perturbing the synchronized state $\delta _0$ can potentially change the evolution of cluster 1 in such a way that its state gets away from ${{\overline{\mu }}}$ under evolution, and in turn this can destroy the stability of $\delta _0$. We are going to show that this cannot happen whenever $\varepsilon$ is sufficiently small.

Below we provide a framework to make all of this precise and prove points i) and iii) of the remark above (see Sect. 4.2).

4.1 A Criterion for Stability of Partially Synchronized States

In this section, unless specified otherwise, we consider a network of N clusters where the clusters are divided into two groups, Group 1 and Group 2, one made of $N_1$ and the other of $N_2=N-N_1$ clusters. Without loss of generality we can assume that the clusters in Group 1 have been labeled $\{1,...,N_1\}$ and those in Group 2 have labels $\{N_1+1,...,N\}$.

Define $\Pi _i:\mathcal M_1^N\rightarrow \mathcal M_1^{N_i}$ the projections on the first $N_1$ coordinates and last $N_2$ coordinates respectively. After fixing $\varvec{\nu }\in \mathcal M_1^{N_2}$, one can define $\mathcal F_{1,\varvec{\nu }}:\mathcal M_1^{N_1}\rightarrow \mathcal M_1^{N_1}$ as $\mathcal F_{1,\varvec{\nu }}\mu := \Pi _1\mathcal F(\varvec{\mu },\varvec{\nu })$. $\mathcal F_{2,\varvec{\mu }}:\mathcal M_1^{N_2}\rightarrow \mathcal M_1^{N_2}$ is defined analogously.

To fix ideas, we think of the second group of clusters as those that synchronize, while those in the first group might be unsynchronized. Under this perspective, for every fixed $\varvec{\mu }\in \mathcal M_1^{N_1}$, define $G_{\varvec{\mu }}:\mathbb T^{N_2}\rightarrow \mathbb T^{N_2}$ and $g_{\varvec{\mu },i}:\mathbb T^{N_2}\rightarrow \mathbb R$ as in (4) and (5) for the self-consistent operator $\mathcal F_{2,\varvec{\mu }}$.

Theorem 4.1

Consider a network with two groups of clusters as above, and suppose that there are $\mathcal N'\subset \mathcal M_1^{N_1}$, $U\subset \mathbb T^{N_2}$, $\varepsilon _0>0$, $\delta >0$, and $\lambda \in [0,1)$ such that

• A1) for every $\varvec{\mu }\in \mathcal N'$, $G_{\varvec{\mu }}(U) \subset U$, $d(G_{\varvec{\mu }}({{\overline{U}}}),\partial U)>\delta$ and $|g'_{\varvec{\mu },i}(x)|\le \lambda$ for all $x\in U$;

• A2) letting $\mathcal S_{\varepsilon ,U}:= \{ \varvec{\nu }\in \mathcal M_1^{N_2}: \,|{{\,\mathrm{supp}\,}}\varvec{\nu }|_\infty <\varepsilon , \,\, {{\,\mathrm{supp}\,}}\varvec{\nu }\subset U\}$, there is $\mathcal N\subset \mathcal N'$ s.t.

  $$\begin{aligned} \Pi _1\mathcal F^n (\mathcal N\times \mathcal S_{\varepsilon ,U} )\subset \mathcal N',\quad \quad \forall n\in \mathbb N, \quad \forall \varepsilon \in (0,\varepsilon _0]. \end{aligned}$$

Then there is $\varepsilon \in (0,\varepsilon _0]$ such that if $(\varvec{\mu },\varvec{\nu })\in \mathcal N\times \mathcal S_{\varepsilon ,U}$, then

$$\begin{aligned} \lim _{n\rightarrow \infty }d_W\left( \mathcal F^n(\varvec{\mu },\varvec{\nu }), \, \mathcal{PS}\mathcal{}_U\right) =0, \end{aligned}$$

(17)

Assumption A1) ensures that the clusters in Group 2 synchronize as long as the state of Group 1 is controlled and belongs to a given set $\mathcal N$. Assumption A2) requires that when the clusters of Group 2 are close to synchrony, the clusters in Group 1 evolve in a controlled way and their state remains inside $\mathcal N$. A typical situation we have in mind is when, for $\nu$ close to a synchronized state, the maps $F_{(\varvec{\mu },\varvec{\nu }),i}$ for $i=1,...,N_1$ are close to maps ${{\overline{F}}}_i$ with a spectral gap whose invariant measure is stable under perturbations. It is known that in many such situations, an arbitrary composition of maps which are all close to given statistically stable maps ${{\overline{F}}}_i$, keep the measures close to the invariant measures of ${{\overline{F}}}_i$ (see e.g. [31].)

Proof of Theorem 4.1

For $\varepsilon >0$ take $\varvec{\nu }\in \mathcal M_1^{N_2}$ with $|{{\,\mathrm{supp}\,}}\varvec{\nu }|_{\infty }<\varepsilon$ and ${{\,\mathrm{supp}\,}}\varvec{\nu }\subset U$. It immediately follows from A1) that $|{{\,\mathrm{supp}\,}}\mathcal F_{\varvec{\mu },2}\varvec{\nu }|_{\infty }<\lambda \varepsilon$. Arguing as in Step 1 of the proof of Theorem 3.1, one can pick $\varepsilon >0$ sufficiently small, so that

$$\begin{aligned} d(G_{\varvec{\mu }}(\varvec{x}), F_{\varvec{\mu },2}(\varvec{x}))<\frac{\delta }{2},\quad \quad \forall \varvec{x}\in \mathbb T^{N_2} \end{aligned}$$

where $F_{\varvec{\mu },2}=(F_{\varvec{\mu },N_1+1},...,F_{\varvec{\mu },N})$. Therefore, if $|{{\,\mathrm{supp}\,}}\varvec{\nu }|_{\infty }<\varepsilon$

$$\begin{aligned} d({{\,\mathrm{supp}\,}}\mathcal F_{\varvec{\mu },2}\varvec{\nu }, \partial U)= d(F_{\varvec{\mu },2}({{\,\mathrm{supp}\,}}\varvec{\nu }),\partial U) \ge d(G_{\varvec{\mu }}({{\,\mathrm{supp}\,}}\varvec{\nu }),\partial U)-\frac{\delta }{2}=\frac{\delta }{2}, \end{aligned}$$

and ${{\,\mathrm{supp}\,}}\mathcal F_{\varvec{\mu },2}\varvec{\nu }\subset U$.

It follows from A2) that if $(\varvec{\mu },\varvec{\nu })$ are such that $\varvec{\mu }\in \mathcal N$ and $|{{\,\mathrm{supp}\,}}\varvec{\nu }|_{\infty }<\varepsilon$ and ${{\,\mathrm{supp}\,}}\varvec{\nu }\subset U$, then by A1) $\Pi _1\mathcal F_{(\varvec{\mu },\varvec{\nu })}^n(\varvec{\mu },\varvec{\nu })\in \mathcal N'$ and $|{{\,\mathrm{supp}\,}}\Pi _2\mathcal F^n_{(\varvec{\nu },\varvec{\mu })}(\varvec{\mu },\varvec{\nu })|_{\infty }<\lambda ^n\varepsilon$, ${{\,\mathrm{supp}\,}}\Pi _2\mathcal F^n_{(\varvec{\nu },\varvec{\mu })}(\varvec{\mu },\varvec{\nu })\subset U$ for every $n\in \mathbb N$ which implies (17).

This theorem has mostly a descriptive purpose as the conclusion immediately follows from the assumptions. In the next section we show how to verify assumptions A1) and A2) to prove points i) and iii) of Remark 4.1, and in Sect. 4.3 we present an application to chimera states.

4.2 Example 4.1 Continued

In this section we apply Theorem 4.1 to prove points i) and iii) of Remark 4.1.

Proof of Remark 4.1 point i)

We are going to exploit the spectral properties of f. Consider the Banach space $\mathcal C^1$ of absolutely continuous finite signed measures with densities in $C^1(\mathbb T,\mathbb R)$ . We endow this space with the following norm: for a measure $d\mu =\rho dm$ we define $\Vert \mu \Vert =\int |\rho '|+\int |\rho |$. We further consider $L^1$ as a weak norm $|\cdot |_{L^1} \le \Vert \cdot \Vert$ on this space as $|\mu |_{L^1}=\int |\rho |$. It is known that the transfer operator $f_*$ has a spectral gap on this Banach space, i.e. there is ${{\overline{\mu }}}\in \mathcal C^1$ such that $f_*{{\overline{\mu }}}={{\overline{\mu }}}$, and there are $C>0$ and $\lambda \in (0,1)$ satisfying

$$\begin{aligned} \Vert f_*^n\mu \Vert \le C\lambda ^n\Vert \mu \Vert ,\quad \quad \forall \mu \in \mathcal C^1_0 \end{aligned}$$

(18)

where $\mathcal C^1_0=\{\mu \in \mathcal C^1:\,\mu (\mathbb T)=0\}$. Fix any $\lambda '\in (\lambda ,1)$ and define the norm $\Vert \cdot \Vert '$ on $\mathcal C^1_0$ by

$$\begin{aligned} \Vert \mu \Vert '= \sum _{k=0}^\infty \frac{\Vert f_*^n\mu \Vert }{(\lambda ')^n} \end{aligned}$$

which is well defined in virtue of (18). Notice that

$$\begin{aligned} \Vert \mu \Vert \le \Vert \mu \Vert '\le \frac{C}{1-\frac{\lambda }{\lambda '}} \Vert \mu \Vert \end{aligned}$$

(19)

and so $\Vert \cdot \Vert '$ and $\Vert \cdot \Vert$ are equivalent. Let us call ${{\widetilde{C}}}:= \frac{C}{1-\frac{\lambda }{\lambda '}}$. The advantage of working with $\Vert \cdot \Vert '$ is that $f_*$ contracts in one step with respect to this norm:

$$\begin{aligned} \Vert f_*\mu \Vert '= \sum _{k=0}^\infty \frac{\Vert f_*^{n+1}\mu \Vert }{(\lambda ')^n}= \lambda '\Vert \mu \Vert '. \end{aligned}$$

(20)

Now we proceed to verify the assumptions of Theorem 4.1. Notice that $F_{(\mu ,\nu ),2}=F_{\mu ,2}$ since $F_{ (\mu ,\nu ),2}$ does not depend on $\nu$. Recall that $F_{\mu ,2}(0)=0$ for every $\mu$ and that, with the assumptions on $\varphi$ and $\psi$, and the choice of $\alpha$, $|(F_{{{\overline{\mu }}},2})'(0)|<1$. Now,

$$\begin{aligned} | F_{\mu ,2}'(0)-F_{{{\overline{\mu }}},2}'(0)|&= \left| f'\left( 0\right) (1+\alpha \mu (\psi ) \varphi '(0))-f'\left( 0\right) \left( 1+\alpha {{\overline{\mu }}}(\psi ) \varphi '(0)\right) \right| \\&=|\alpha f'\left( 0\right) \varphi '(0)||\mu (\psi )-{{\overline{\mu }}}(\psi )|. \end{aligned}$$

By Hölder inequality we get that

$$\begin{aligned} |\mu (\psi )-{{\overline{\mu }}}(\psi )|\le \sup _x|\psi (x)|\, |\mu -{{\overline{\mu }}}|_{L^1}. \end{aligned}$$

Therefore, one can find $\delta _1>0$ such that if $|\mu -{{\overline{\mu }}}|_{L^1}<\delta _1$

$$\begin{aligned} | F_{\mu ,2}'(0)|<1. \end{aligned}$$

With an analogous reasoning involving the second derivative, we conclude that, possibly decreasing $\delta _1>0$, there is all neighbourhood $I=[-\Delta ,\Delta ]\subset \mathbb T$ of 0 such that

$$\begin{aligned} \left| F_{\mu ,2}'|_{I}\right| <1 \end{aligned}$$

(21)

for every $\mu$ such that $|\mu -{{\overline{\mu }}}|_{L^1}<\delta _1$.

Pick $\mathcal N':=\{\mu \in \mathcal B\cap \mathcal M_1:\,\Vert \mu -{{\overline{\mu }}}\Vert '<\delta _1 \}$ and $U=I$. It follows from the first inequality in (19) together with (21) that for every $\mu \in \mathcal N'$

$$\begin{aligned} G_{\mu }(U)=F_{\mu ,2}(I)\subset I=U \end{aligned}$$

and that $d(G_{\mu }(U),\partial U)>\delta$ for some $\delta >0$⁷. Which proves that this choice of $\mathcal N'$ and U satisfies assumption A1). By (20), $\Vert f_*\mu -{{\overline{\mu }}}\Vert '=\Vert f_*\mu -f_*{{\overline{\mu }}}\Vert '<\lambda '\delta _1$, therefore

$$\begin{aligned} \mathcal F_{1,\nu }(\mathcal N')=f_*(\mathcal N')\subset \{\mu \in \mathcal B\cap \mathcal M_1:\, \Vert \mu -{{\overline{\mu }}}\Vert '<\lambda '\delta _1\}\subset \mathcal N'. \end{aligned}$$

Moreover, $|\mu -{{\overline{\mu }}}|_{L^1}\le \Vert \mu -{{\overline{\mu }}}\Vert '$ and therefore (21) is satisfied for every $\mu \in \mathcal N$. Picking $\mathcal N=\mathcal N'$, assumption A2) is proved.

Proof of Remark 4.1 point iii)

Define the distance $d_{\mathcal B}$ between linear operators $\mathcal P_1,\mathcal P_2:\mathcal B\rightarrow \mathcal B$

$$\begin{aligned} d_{\mathcal B}(\mathcal P_1,\mathcal P_2):=\sup _{\eta \in \mathcal B:\Vert \eta \Vert \le 1}|\mathcal P_1\eta -\mathcal P_2\eta |_{L^1}. \end{aligned}$$

Recall that now $F_{(\mu ,\nu ),1}=f\left( x+ \varepsilon \int h_{11}(x,y)d\mu (y)+ \varepsilon \int h_{12}(x,y)d\nu (y)\right)$ according to point iii) of Remark 4.1.

The following lemma shows that the transfer operator of $F_{(\mu ,\nu ),1}$ and f are close, more precisely at a distance of order $\varepsilon$.

Lemma 4.1

There is $C_1>0$ such that

$$\begin{aligned} d_{\mathcal B}((F_{(\mu ,\nu ),1})_*,f_*)<C_1\varepsilon . \end{aligned}$$

Proof

By [18, Lemma 13], we have $d_{\mathcal B}((F_{(\mu ,\nu ),1})_*,f_*) \le 12d(F_{(\mu ,\nu ),1},f)$, where

$$\begin{aligned} d(T_1,T_2)=\inf \{&\kappa> 0 : \exists A \subset \mathbb T\text { and } \sigma : \mathbb T\rightarrow \mathbb T\text { such that } Leb(A) > 1-\kappa \\&\sigma \text { is a diffeomorphism, } T_2|_A=T_1 \circ \sigma |_A \text { and for all } x\in \mathbb T: \\&|\sigma (x)-x|< \kappa , |1/\sigma '(x)-1| < \kappa \}. \end{aligned}$$

Now since $F_{(\mu ,\nu ),1} = f \circ \Phi _{(\mu ,\nu ),1}$ where

$$\begin{aligned} \Phi _{(\mu ,\nu ),1}(x)=x+ \varepsilon \int h_{11}(x,y)d\mu (y)+ \varepsilon \int h_{12}(x,y)d\mu _2(y) \end{aligned}$$

is a diffeomorphism of $\mathbb T$ (for $\varepsilon$ sufficiently small) and we have the bounds

$$\begin{aligned} |\Phi _{(\mu ,\nu ),1}(x)-x|&\le \varepsilon (\sup |h_{11}|+\sup |h_{12}|) \\ |1/\Phi '_{(\mu ,\nu ),1}(x)-1|&\le \varepsilon \cdot \frac{\sup |\partial _xh_{11}|+\sup |\partial _xh_{12}|}{1-\varepsilon (\sup |\partial _xh_{11}|+\sup |\partial _xh_{12}|)} \\ \end{aligned}$$

we can conclude that $d(F_{(\mu ,\nu ),1},f) \le C_1\varepsilon$ and by consequence $d_{\mathcal B}((F_{(\mu ,\nu ),1})_*,f_*) \le C_1\varepsilon$, which proves the lemma. $\square$

We now use the above result to prove that when $\varepsilon >0$ is sufficiently small, the maps $F_{(\mu ,\nu ),1}$ satisfy Lasota-Yorke inequalities with uniform constants.

Lemma 4.2

There exist $\alpha \in (0,1)$, $K > 0$, and $\varepsilon _1 > 0$ such that when $|\varepsilon | < \varepsilon _1$

$$\begin{aligned} \Vert (F_{(\mu ,\nu ), 1})_*\eta \Vert&\le \alpha \Vert \eta \Vert +K|\eta |_{L^1}. \end{aligned}$$

for all $\eta \in \mathcal C^1$ and $(\mu ,\nu ) \in \mathcal M_1^2$.

Proof

Denote the density of $\eta$ by $\rho$, the inverse branches of $F_{(\mu ,\nu ), 1}$ by $(F_{(\mu ,\nu ), 1})_i^{-1}$, and the action of $(F_{(\mu ,\nu ), 1})_*$ on $C^1$ densities by $\mathcal L_{F_{(\mu ,\nu ), 1}}: C^1(\mathbb T,\mathbb R)\rightarrow C^1(\mathbb T,\mathbb R)$. Then

$$\begin{aligned} {\mathcal {L}}_{F_{(\mu ,\nu ), 1}}\rho =\sum _i \frac{\rho }{|(F_{(\mu ,\nu ), 1})'|} \circ (F_{(\mu ,\nu ), 1})_i^{-1} \end{aligned}$$

and

$$\begin{aligned} \int |({\mathcal {L}}_{F_{(\mu ,\nu ), 1}}\rho )'|&=\int \left| \left( \sum _i \frac{\rho }{|(F_{(\mu ,\nu ), 1})'|} \circ (F_{(\mu ,\nu ), 1})_i^{-1}\right) ' \right| \\&\le \int \left| \sum _i \frac{\rho '}{| (F_{(\mu ,\nu ), 1})'|^2} \circ (F_{(\mu ,\nu ), 1})_i^{-1} \right| \\&\quad +\int \left| \sum _i \frac{\rho \cdot ( F_{(\mu ,\nu ), 1})''}{| (F_{(\mu ,\nu ), 1})'|^3} \circ (F_{(\mu ,\nu ), 1})_i^{-1} \right| \\&\le \int \left| \frac{\rho '}{ (F_{(\mu ,\nu ), 1})'} \right| +\int \left| \frac{\rho \cdot (F_{(\mu ,\nu ), 1})''}{( (F_{(\mu ,\nu ), 1})')^2} \right| \end{aligned}$$

We can compute that for $\varepsilon$ sufficiently small we have

$$\begin{aligned} |(F_{(\mu ,\nu ), 1})'| \ge \,&\omega (1-\varepsilon (\sup |\partial _xh_{11}|+\sup |\partial _xh_{12}|)) \ge \frac{1}{\alpha } > 1 \\ |(F_{(\mu ,\nu ), 1})''| \le \,&\sup |f''|(1+\varepsilon (\sup |\partial _xh_{11}|+\sup |\partial _xh_{12}|))^2 \\&+\varepsilon \cdot \sup |f'|(\sup |\partial _x^2h_{11}|+\sup |\partial _x^2h_{12}|) \le D \end{aligned}$$

for some $\alpha \in (0,1)$ and $D>0$. This gives

$$\begin{aligned} \int |({\mathcal {L}}_{F_{(\mu ,\nu ), 1}}\rho )'| \le \alpha \int |\rho '|+ D \alpha ^2\int |\rho |_{} \end{aligned}$$

and finally

$$\begin{aligned} \Vert (F_{(\mu ,\nu ), 1})_*\eta \Vert \le \alpha \Vert \eta \Vert +K|\eta |_{L^1} \end{aligned}$$

with $K=1+D\alpha ^2$. $\square$

Given $(\mu ^{(0)},\nu ^{(0)})\in \mathcal M_1^2$, let $(\mu ^{(n)},\nu ^{(n)}):=\mathcal F^n(\mu ^{(0)},\nu ^{(0)})$ its orbit under the self-consistent transfer operator.

Lemma 4.3

Assume that $|\varepsilon |<\varepsilon _1$, with $\varepsilon _1$ as in Lemma 4.2. There is $K>0$ such that if $\Vert \mu ^{(0)}\Vert \le K$, then $\Vert \mu ^{(k)}\Vert \le K$ for every $k\in \mathbb N$. In particular, $\Vert {{\overline{\mu }}}\Vert \le K$.

Proof

Immediately follows from the fact that

$$\begin{aligned} \mu ^{(k)}=(F_{ (\mu ^{(k-1)},\nu ^{(k-1)}),1})_*...(F_{ (\mu ^{(0)},\nu ^{(0)}),1})_*\mu ^{(0)}\end{aligned}$$

and that by Lemma 4.2$(F_{ (\mu ^{(i)},\nu ^{(i)}),1})_*$ all satisfy Lasota-Yorke inequalities with uniform constants. $\square$

For every $k\in \mathbb N\cup \{0\}$

$$\begin{aligned} \left| \mu ^{(k)}-{{\overline{\mu }}} \right| _{L^1}&=\left| (F_{ (\mu ^{(k-1)},\nu ^{(k-1)}),1})_*...(F_{ (\mu ^{(0)},\nu ^{(0)}),1})_*\mu ^{(0)}-f_*^k{{\overline{\mu }}} \right| _{L^1}\le |f_*^k(\mu ^{(0)}-{{\overline{\mu }}})|_{L^1} \nonumber \\&\quad +\sum _{j=0}^{k-1}\left| (F_{ (\mu ^{(k-1)},\nu ^{(k-1)}),1})_*...\left[ (F_{ (\mu ^{(j)},\nu ^{(j)}),1})_*-f_*\right] f^{j-1}_*{{\overline{\mu }}}\right| _{L^1} \end{aligned}$$

(22)

$$\begin{aligned}&\le C\lambda ^k\Vert \mu ^{(0)}-{{\overline{\mu }}}\Vert +k\delta _0\Vert {{\overline{\mu }}}\Vert \end{aligned}$$

(23)

where going from (22) to (23) we used

$$\begin{aligned} |f_*^k(\mu ^{(0)}-{{\overline{\mu }}})|_{L^1}\le \Vert f_*^k(\mu ^{(0)}-{{\overline{\mu }}})\Vert \le C\lambda ^k\Vert \mu ^{(0)}-{{\overline{\mu }}}\Vert \end{aligned}$$

and

$$\begin{aligned} \left| (F_{ (\mu ^{(k-1)},\nu ^{(k-1)}),1})_*...\left[ (F_{ (\mu ^{(j)},\nu ^{(j)}),1})_*-f_*\right] f^{j-1}_*{{\overline{\mu }}}\right| _{L^1}&\le \left| [ (F_{ (\mu ^{(j)},\nu ^{(j)}),1})_*-f_*]{{\overline{\mu }}}\right| _{L^1}\\&\le \delta _0\Vert {{\overline{\mu }}}\Vert . \end{aligned}$$

Fix $n\in \mathbb N$ such that $2C\lambda ^n K<\frac{\delta _1}{4}$, where K is as in Lemma 4.3 and $\delta _1$ such that (21) is satisfied when $|\mu -{{\overline{\mu }}}|_{L^1}<\delta _1$. Then pick $\delta _0$ so that $n\delta _0\Vert {{\overline{\mu }}}\Vert <\frac{\delta _1}{4}$. With these choices

$$\begin{aligned} \left| \mu ^{(n)}-{{\overline{\mu }}} \right| _{L^1}<\frac{\delta _1}{2}, \end{aligned}$$

and arguing by induction (redefining $(\mu ,\nu )^{(0)}:=(\mu ,\nu )^{((m-1)n)}$)

$$\begin{aligned} \left| \mu ^{(mn)}-{{\overline{\mu }}} \right| _{L^1}<\frac{\delta _1}{2} \end{aligned}$$

for every $m\in \mathbb N$. Now, picking $|\mu ^{(0)}-\overline{\mu }|_{L^1}<\frac{\delta _1}{2}$, for every $m\in \mathbb N$ and $q\in \{1...,n-1\}$, using (22),

$$\begin{aligned} \left| \mu ^{(mn+q)}-{{\overline{\mu }}} \right| _{L^1}&\le |f_*^q(\mu ^{(mn)}-{{\overline{\mu }}})|_{L^1}+q\delta _0\Vert {{\overline{\mu }}}\Vert \\&\le |\mu ^{(mn)}-{{\overline{\mu }}}|_{L^1}+n\delta _0\Vert {{\overline{\mu }}}\Vert \\&<\frac{\delta _1}{2}+\frac{\delta _1}{4}\\&<\delta _1. \end{aligned}$$

Assumptions A1) and A2) from Theorem 4.1 are satisfied picking $\mathcal N:=\{\mu \in \mathcal C^1\cap \mathcal M^1:\,\,\Vert \mu \Vert \le K,\, |\mu -{{\overline{\mu }}}|_{L^1}<\delta _1/2\}$ and $\mathcal N':=\{\mu \in \mathcal C^1\cap \mathcal M^1:\,\,\Vert \mu \Vert \le K,\, |\mu -{{\overline{\mu }}}|_{L^1}<\delta _1\}$. $\square$

4.3 Chimera States

There is no consensus on a mathematical rigorous definition of a chimera state. Loosely speaking one can describe a chimera in the following way. Consider a system of finitely many interacting units. If the structure of the interaction has some symmetry, a chimera state is a persistent state of the network that breaks this symmetry. For example, consider a system of n globally coupled units described by the variables $(\xi _1,...,\xi _n)\in \mathbb T^n$ with time evolution given by

$$\begin{aligned} \xi _i(t+1)= f\left( \xi _i(t)+\frac{1}{n}\sum _{j=1}^n h(\xi _i(t),\xi _j(t))\right) . \end{aligned}$$

(24)

In this case, every unit is indistinguishable from all the other units: the system has full permutation symmetry. Then, for example, a state for this system where part of the coordinates are synchronized and part are unsynchronized, and such that this distinction persists under the time evolution can be called a chimera state.

Chimeras have been studied in systems of coupled maps ([1, 4] among many others), and observed in real world systems [25].

Below we give an heuristic explanation of how chimera states can arise assuming that the thermodynamic limit and the self-consistent transfer operator approximate (at least for finite time) the evolution of the finite dimensional system. Roughly speaking, by dividing the units in (24) into different clusters and initializing them according to different measures one can produce a breaking of symmetry in the self-consistent transfer operator and produce asymmetric stable state for the self-consistent transfer operator that correspond to persistent asymmetric chimera states for the finite dimensional system. In our examples, we bring numerical evidence that the stable state of the self-consistent transfer operator approximates the evolution of the finite dimensional systems. It is not known if these chimera states are close to equilibrium states for the finite-dimensional system or they are just long transient.

More precisely, consider a system as in (24). Fix $\ell \in [0,1]$, for every $n\in \mathbb N$, divide the units into two groups of $\lfloor \ell n\rfloor$ and $n-\lfloor \ell n\rfloor$ units respectively. Assume that the units $\{\xi _i\}_{i=1}^{\lfloor n\ell \rfloor }$ are distributed according to $\mu _1$ while $\{\xi _{i}\}_{i=\lfloor n\ell \rfloor +1}^{k}$ are distributed according to the measure $\mu _2$, meaning that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{j=1}^{\lfloor n\ell \rfloor } \delta _{\xi _j}=\ell \mu _1,\quad \text{ and }\quad \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{j=\lfloor n\ell \rfloor +1}^{n} \delta _{\xi _j}=(1-\ell )\mu _2 \end{aligned}$$

where convergence is with respect to the weak topology. Then in the thermodynamic limit, if h is continuous, for every $\xi$

$$\begin{aligned} \lim _{n\rightarrow \infty }f\left( \xi +\frac{1}{n}\sum _{j=1}^nh(\xi ,\xi _j)\right)&=\lim _{n\rightarrow \infty }f\left( \xi + \left[ \frac{1}{n}\sum _{j=1}^{\lfloor n\ell \rfloor }h(\xi ,\xi _j)+\frac{1}{n}\sum _{j=\lfloor n\ell \rfloor +1}^{n}h(\xi ,\xi _j)\right] \right) \\&= f\left( \xi +\ell \int h(\xi ,y)d\mu _1(y)+(1-\ell )\int h(\xi ,y)d\mu _2(y)\right) . \end{aligned}$$

The above defines the self-consistent transfer operator on two clusters associated to

$$\begin{aligned} F_{(\mu _1,\mu _2),i}(x)=f\left( x+\ell \int h(x,y)d\mu _1(y)+(1-\ell )\int h(x,y)d\mu _2(y)\right) \end{aligned}$$

(25)

independent of i. $(\mu _1,\mu _2)$ is a chimera state for this system if $\mu _1\ne \mu _2$ and $\mu _1$ and $\mu _2$ are measures fixed by $F_{(\mu _1,\mu _2),i}=F_{(\mu _1,\mu _2)}$.

We now give two examples. The understanding of stability in both examples goes beyond the statement of the main theorem on partially synchronized states, as the stabilty of the unsynchronized state is also discussed.

In the first example, part of the network converges to a fixed state given by a single point, while the other part has a fixed state supported on two points. This phenomenon is also known as dynamical clustering).

Example 4.2

Let $f(x)=2x \mod 1$ and $h(x,y)=-\frac{1}{10\pi }\sin (6\pi x)\cos (6\pi y)$. Let $\mu _{1}:=\frac{1}{2}(\delta _{1/3}+\delta _{2/3})$ and $\mu _2:=\delta _0$. Notice that $h(0,y)=h(1/3,y)=h(2/3,y)=0$ and this implies that $F_{(\mu _1,\mu _2)}(0)=f(0)=0$, $F_{(\mu _1,\mu _2)}(1/3)=f(1/3)=2/3$ and $F_{(\mu _1,\mu _2)}(2/3)=f(2/3)=1/3.$ Then $(F_{(\mu _1,\mu _2)})_*\left( \frac{1}{2}(\delta _{1/3}+\delta _{2/3}) \right) =\frac{1}{2}(\delta _{1/3}+\delta _{2/3})$ and $(F_{(\mu _1,\mu _2)})_*\delta _0=\delta _0$, so $(\mu _1,\mu _2)$ is a chimera state.

To investigate stability of this state, notice that

$$\begin{aligned}&F_{(\nu _1,\nu _2)}'(x)\\&=2\left( 1+\ell \int \partial _xh(x,y)d\nu _1(y)+(1-\ell )\int \partial _xh(x,y)d\nu _2(y)\right) \\&=2\left( 1-\frac{6\ell }{10} \int \cos (6\pi x)\cos (6\pi y)d\nu _1(y)-\frac{6(1-\ell )}{10}\int \cos (6\pi x)\cos (6\pi y)d\nu _2(y)\right) . \end{aligned}$$

Assume that $(\nu _1,\nu _2)$ is such that ${{\,\mathrm{supp}\,}}\nu _1 \subset B_{r}(1/3)\cup B_{r}(2/3)$ and ${{\,\mathrm{supp}\,}}\nu _1 \subset B_{r}(0)$. Notice that $\cos (6\pi x)\cos (6\pi y)=1$ if $x^*,y^* \in \{0,1/3,2/3\}$. So fixing r sufficiently small we can achieve that $F_{(\nu _1,\nu _2)}'|_{B_{r}(0)}<9/10$, $F_{(\nu _1,\nu _2)}'|_{B_{r}(1/3)}<9/10$ and $F_{(\nu _1,\nu _2)}'|_{B_{r}(2/3)}<9/10$. Now we easily see that the conditions of Theorem 4.1 hold with $U=B_{r}(0)$ and $\mathcal N'=\mathcal N=\{\mu \in \mathcal M_1: {{\,\mathrm{supp}\,}}\mu \subset B_{r}(1/3)\cup B_{r}(2/3)\}$. This gives us that $d_W(\mathcal F^n (\nu _1,\nu _2),\mathcal{PS}\mathcal{}_{U}) \rightarrow 0$.

But in fact more is true. By using the notation $\nu _1^{(1)}:=(F_{(\nu _1,\nu _2)})_*\nu _1$ and $\nu _2^{(1)}:=(F_{(\nu _1,\nu _2)})_*\nu _2$ it will hold that ${{\,\mathrm{supp}\,}}\nu _1^{(1)} \subset B_{9/10 \cdot r} (1/3)\cup B_{9/10 \cdot r} (2/3)$ and ${{\,\mathrm{supp}\,}}\nu _2^{(1)} \subset B_{9/10 \cdot r} (0)$. Iterating this gives that

$$\begin{aligned} d_W((\nu _1^{(n)},\nu ^{(n)}_2),(\mu _1,\mu _2)) \rightarrow 0 \end{aligned}$$

as $n \rightarrow \infty$.

Fig. 1

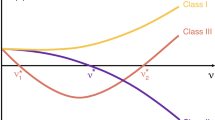
The graph of f in Example 4.3

In the second example we sketch how to obtain a chimera state for a self-consistent operator with a chaotic phase, i.e. a cluster having an a.c. invariant measure, and a cluster with an attracting fixed point.

Example 4.3

Divide the interval [0, 1] (thought of having the extrema identified, $0\sim 1$) into two intervals: $I_1=[0,1/2]$ and $I_2=[1/2,1]$. Consider $f:[0,1]\rightarrow [0,1]$ defined as

$$\begin{aligned} f|_{I_1}(x)= 4x(1-2x), \end{aligned}$$

i.e. f is a rescaled version of the logistic map $4x(x-1)$ on $I_1$; $f|_{I_2}$ joins smoothly with $f|_{I_1}$, has a single repelling fixed point $x^*$ (aside from $1\sim 0$) and is defined such that full Lebesgue measure of trajectories leave $I_2$ eventually (see Fig. 1). Notice that by construction $f(I_1)\subset I_1$, and furthermore there is a unique a.c.p. measure invariant under f is $\eta$ with density

$$\begin{aligned} \psi (x)=\left\{ \begin{array}{ll}\frac{2}{\pi \sqrt{2x(1-2x)}} &{} x\in I_1\\ 0 &{} x\in I_2 \end{array} \right. \end{aligned}$$

Consider $h(x,y)= \alpha v(x)u(y)$ with $u,v:[0,1]\rightarrow \mathbb R$ periodic and smooth such that $v(x)=0$ on $I_1$ and at $x^*$, while $v'(x^*)=-1$. u is a positive function on $I_1$ and zero on $I_2$, and finally $\alpha$ is a real parameter. With these prescriptions equation (25) becomes

$$\begin{aligned} F_{(\nu _1,\nu _2)}(x)=f\left( x+\alpha v(x)\ell \int ud\nu _1\right) . \end{aligned}$$

First of all, notice that $( \nu _1,\nu _2)=(\eta ,\delta _{x^*})$ is a fixed state under the self-consistent operator (since v is zero on $I_1$ and at $x^*$, so $F_{(\nu _1,\nu _2)}$ equals f on $I_1$ and at $x^*$.) Since u is positive on $I_1$, there is $K>0$ such that

$$\begin{aligned} K:=\int ud \nu _1>0. \end{aligned}$$

Now we tune $\alpha \ell$ in such a way that $|1-\alpha \ell K|<1/|f'(x^*)|$. With this choice, for every $\nu _2$, $|F_{(\nu _1 ,\nu _2)}'(x^*)|=|f'(x^*)(1-\alpha \ell K)|<1$, and therefore $|F_{( \nu _1,\nu _2)}'(x)|\le \lambda <1$ for every x in some neighborhood U of $x^*$. We can apply Theorem 4.1 with this set U and $\mathcal N'=\mathcal N=\{\eta \}$ and obtain that $d_W(\mathcal F^n (\eta ,\nu _2),\mathcal{PS}\mathcal{}_{U}) \rightarrow 0$.

In fact more is true. If we take $\nu _2$ supported on U, then under application of the self-consistent operator the state of cluster 2 converges to $\delta _{x^*}$. Using the properties of the logistic map, one can show that starting with $\nu _1$ a suitable (small) perturbation of $\eta$ (supported on $I_1$), $\mathcal F^n(\nu _1,\nu _2)$ converges to $(\eta ,\delta _{x^*})$.

4.4 Numerical Evidence of Chimeras in Finite Networks

Below we present some simulations showing how the chimera states, $(\mu _1,\mu _2)$, found in the examples above for the self-consistent transfer operator can be numerically detected also in the corresponding systems of finite size. We would like to stress that the simulations presented in this section have mostly illustrative purposes.

We start from a system of N coupled units evolving as in Eq. (24). Assuming N is even, we divide the units into two clusters of size N/2 each. We draw an initial condition $\varvec{\xi }_0=(\xi _{0,1},...,\xi _{0,N})$ in the following way: for $1\le i\le N/2$ we draw $\xi _{0,i}$ at random according to a probability measure close to $\mu _1$, while for $N/2+1\le i\le N$, we draw $\xi _{0,i}$ according to a probability measure close to $\mu _2$.

We then let the initial condition evolve according to the set of N discrete equations in Eq. (24) and thus get a piece of orbit $\{\varvec{\xi }_t\}_{t=1}^T$ for some $T>0$. For a few values of time t, we plot the histograms for the points $\{\xi _{t,i}\}_{i=1}^{N/2}$ in cluster 1, and $\{\xi _{t,i}\}_{i=N/2+1}^N$ in cluster 2 to get a visual of the distribution of these points. Then, for every $t=1,..,T$, we compare the empirical distribution obtained from $\{\xi _{t,i}\}_{i=1}^{N/2}$ with that of $\mu _1$, and the empirical distribution of $\{\xi _{t,i}\}_{i=N/2+1}^N$ with that of $\mu _2$ by numerically computing

$$\begin{aligned} \mathcal D_1(t)=d_W\left( \frac{1}{N/2}\sum _{i=1}^{N/2}\delta _{\xi _{t,i}},\mu _1\right) \quad \text{ and }\quad \mathcal D_2(t)=d_W\left( \frac{1}{N/2}\sum _{i=N/2+1}^{N}\delta _{\xi _{t,i}},\mu _2\right) . \end{aligned}$$

where $d_W$ denotes the Wasserstein distance.⁸ We observe that $\mathcal D_1$ and $\mathcal D_2$ tend to remain small across the time span analyzed ($T=1500$). Then we study how $\mathcal D_1$ and $\mathcal D_2$ vary varying N. We expect these values to decrease as N increases since for large N, the finite system should be better approximated by the self-consistent operator. To do so, we average $\mathcal D_i(t)$ for the values obtained when $1000\le t\le 1500$, and plot this average values as a function of N with error bars denoting max and min of $\mathcal D_i(t)$ on the interval of t considered.

The results of this analysis for Example 4.2 and Example 4.3 are reported in Figs. 2 and 3.

We performed simulations for larger time spans that are in accord with what is observed for time spans showed in the figures below.

The simulations we present in this section have mainly illustrative purpose, and a more careful numerical analysis would be needed to draw any quantitative conclusion.

Fig. 2

Result of the numerical analysis of the dynamic in (24) with $f(x)=2x$ mod 1 and $h(x,y)=-\frac{1}{10\pi }\sin (6\pi x)\cos (6\pi y)$ as in Example 4.2. The first column in Panel a reports the histograms for initial conditions in cluster 1, first row, and cluster 2, second row, when $N=5\times 10^4$. Second and third column report the histograms at two later instants of time after 500 and 1000 time steps respectively. Notice that we represented $\mathbb T$ as the interval $[-1/2,1/2]$ with extrema identified. We observe that the points tend to pile up around 0 in cluster 1 and to evenly distribute around $-1/3$ and 1/3 in cluster 2 (the fixed point at 2/3 in the representation of $\mathbb T$ as [0, 1], corresponds to $-1/3$ in the representation of $\mathbb T$ as $[-1/2,1/2]$). The first column of panel b) shows $\mathcal D_1$ and $\mathcal D_2$ as a function of time when $N=5\times 10^4$. The last column on panel b shows averages of $\mathcal D_i(t)$ varying $N=10^2,\,5\times 10^2,\,10^3,\,5\times 10^3,\,10^4,\,5\times 10^4$. When the average of $\mathcal D_i(t)$ is below $10^{-5}$ we draw a point at zero

Fig. 3

Result of the numerical analysis of the dynamic in (24) with f(x) mod 1 and h(x, y) as in Example 4.3. The first column in Panel a) reports the histograms for initial conditions in cluster 1, first row, and cluster 2, second row, respectively when $N=5\times 10^4$. Second and third column report the histograms at two later instants of time after 500 and 1000 time steps respectively. Here we represented $\mathbb T$ as the interval [0, 1] with extrema identified. We observe that the points tend to pile up around $x^*=0.5625$ in cluster 2 and to distribute according to the density $\psi$ in cluster 1. The first column of panel b) shows $\mathcal D_1$ and $\mathcal D_2$ as a function of time when $N=5\times 10^4$. The last column shows averages of $\mathcal D_i(t)$ varying $N=10^2,\,5\times 10^2,\,10^3,\,5\times 10^3,\,10^4,\,5\times 10^4$. When the average of $\mathcal D_i(t)$ is below $10^{-5}$ we draw a point at zero. The last column on panel b) we distinctively observe that the values obtained for $\mathcal D_1$ decrease increasing N