Moderate Deviation and Exit Time Estimates for Stationary Last Passage Percolation

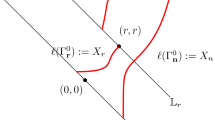
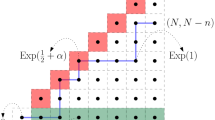
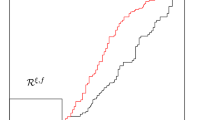
Abstract

We consider planar stationary exponential last passage percolation in the positive quadrant with boundary weights. For $\rho \in (0,1)$ and points $v_N=( (1-\rho )^2 N, \rho ^2 N)$ going to infinity along the characteristic direction, we establish right tail estimates with the optimal exponent for the exit time of the geodesic, along with optimal exponent estimates for the upper tail moderate deviations for the passage time. For the case $\rho =\frac{1}{2}$ in the stationary model, we establish the lower bound estimate with the optimal exponent for the lower tail of the passage time. Our arguments are based on moderate deviation estimates for point-to-point and point-to-line exponential last passage percolation which are obtained via random matrix estimates.

Appendix

We first give the proof of Lemmas 4.5 and 4.6.

Proof of Lemma 4.5

Using the explicit form of the moment generating function for the exponential distribution, we have that

$$\begin{aligned} \mathbb {E}^{\rho }\left[ \exp \left( \frac{\lambda (G^1_{\text {stat}}(\overline{\mathbf{x }})-\frac{\overline{x}}{1-\rho })}{\frac{\sqrt{r+1}N^{1/3}}{1-\rho }}\right) \right] =\left( \frac{1}{1-\frac{\lambda }{\sqrt{\overline{x}}}}e^{-\frac{\lambda }{\sqrt{\overline{x}}}} \right) ^{\overline{x}}. \end{aligned}$$

Now, just note that there is a constant $\delta _0\in (0,1)$ such that the function $\left( \frac{1}{1-\frac{y}{n}}e^{-\frac{y}{n}} \right) ^{n^2}$ is at most $e^{C^*y^2}$ if $\frac{y}{n}<\delta _0$. This can be seen right away by taking a logarithm and doing a Taylor expansion. $\square$

Proof of Lemma 4.6

We will directly use Lemma 4.5. Note that $\frac{\lambda }{\sqrt{\overline{x}}}=\frac{C_1}{C^*}\frac{r^{3/2}}{\sqrt{r+1}N^{1/3}}\le \frac{C_1}{C^*}\frac{r}{N^{1/3}}$, where $C_1$ depends only on $\rho$. Hence, by Lemma 4.5, we just require that $\frac{C_1}{C^*}\gamma _1\le \delta _0$ which can be arranged by choosing $C^*$ large enough because $\delta _0\rightarrow 1$ as $C^*\rightarrow \infty$. $\square$

We now give the details of the proof of Proposition  3.4.

Proof of Proposition 3.4

Notice that we only need to prove the result for y larger than any fixed $y_0>0$ and the case for small y can be handled by adjusting the constants. We use $A_m$ to denote the event $\left\{ \max _{x\in \mathbb {L}_m(N)}\left\{ G(\mathbf{x} ^{\uparrow },v_N)-\mathbb {E}[G(\mathbf{x} ^{\uparrow },v_N)]\right\} >y N^{1/3}\right\}$; note that $A_m$ is measurable with respect to the vertex weights in $\mathbb {Z}^2_{>0}$. We now condition on the occurence of $A_m$. By definition, there now exists a random point $u\in \mathbb {L}_m(N)$ attaining the maximum in the definition of $A_m$ and thus satisfying $G(\mathbf{u} ^{\uparrow },v_N)-\mathbb {E}G(\mathbf{u} ^{\uparrow },v_N)>yN^{1/3}$. Now consider the event

$$\begin{aligned} B_{u}=\left\{ G(2N^{2/3}{} \mathbf{m} -v_N,\mathbf{u} )-f(\mathbf{u} -(2N^{2/3}{} \mathbf{m} -v_N))>-\frac{y}{2}N^{1/3} \right\} . \end{aligned}$$

Since we have conditioned on the occurence of $A_m$, the occurence of $B_u$ would immediately imply that

$$\begin{aligned} G(2N^{2/3}{} \mathbf{m} -v_N,v_N)\ge f(\mathbf{u} -(2N^{2/3}{} \mathbf{m} -v_N))+\mathbb {E}G(\mathbf{u} ^{\uparrow },v_N)+\frac{y}{2}N^{1/3}. \end{aligned}$$

Firstly, we can use the same reasoning as in (4.6) to get that for some constant $C'$ depending only on $\psi$, we have that $|\mathbb {E}G(\mathbf{u} ^\uparrow ,v_N)-f(v_N-\mathbf{u} ^\uparrow )|\le CN^{1/3}$. Since $|u-mN^{2/3}|\le N^{2/3}$, we can now use a Taylor expansion calculation very similar to Lemma 3.1 to obtain that $f(v_N-(2N^{2/3}{} \mathbf{m} -v_N))-f(\mathbf{u} -(2N^{2/3}{} \mathbf{m} -v_N))-f(v_N-\mathbf{u} ^\uparrow )\sim C'' \frac{(u-mN^{2/3})^2}{N}$, where $C''$ depends on $\frac{m}{N^{1/3}}$ and can only take values in a bounded interval for a fixed value of $\psi$. In our case, we have that $|u-mN^{2/3}|\le N^{2/3}$ and the above calculation would yield that there exists a constant C dependent only on $\psi$ such that

$$\begin{aligned} |f(v_N-(2N^{2/3}{} \mathbf{m} -v_N))-f(\mathbf{u} -(2N^{2/3}{} \mathbf{m} -v_N))-f(v_N-\mathbf{u} ^\uparrow )|\le CN^{1/3}. \end{aligned}$$

(6.7)

By taking $y_0$ large to absorb the constants C and $C'$, it follows now that the occurence of $B_u$ would imply that

$$\begin{aligned} G(2N^{2/3}{} \mathbf{m} -v_N,v_N)\ge f(v_N-(2N^{2/3}{} \mathbf{m} -v_N))+\frac{y}{4}N^{1/3}. \end{aligned}$$

Since the events $B_u$ are independent of the vertices in $\mathbb {Z}^2_{>0}$, we immediately obtain that

$$\begin{aligned} C_1e^{-c_1y^{3/2}}&\ge \mathbb {P}\left( G(2N^{2/3}{} \mathbf{m} -v_N,v_N)\ge f(v_N-(2N^{2/3}{} \mathbf{m} -v_N))+\frac{y}{4}N^{1/3} \right) \nonumber \\&\ge \mathbb {P}(A_m)\min _{u\in \mathbb {L}_m(N)}\mathbb {P}(B_u), \end{aligned}$$

(6.8)

where we have used the first part of Proposition  3.2 to obtain the first inequality. On using the second part of Proposition 3.2, we immediately have that

$$\begin{aligned} \min _{u\in \mathbb {L}_m(N)}\mathbb {P}(B_u)\ge 1-C_2e^{-c_2y^3}\ge \frac{1}{2} \end{aligned}$$

if $y_0$ is large enough. Combining this with (6.8), we obtain the needed result, that is

$$\begin{aligned} \mathbb {P}(A_m)\le 2C_1 e^{-c_1y^{3/2}}. \end{aligned}$$

$\square$

Recall the notation $\vec {n}$ for (n, n). We now describe the coupling which implies Proposition 6.1 and Proposition 6.2.

Proposition 6.7

For each fixed $n>0$, there exists a coupling between the two stationary representations such that for each $v\in \mathbb {Z}^2_{\ge 0}$ with $v\le \vec {n}$, we have $G^1_{\text {stat}}(v)=G^2_{\text {stat}}(v)$.

Proof

The coupling proceeds by a version of the Burke property for the boundary representation of stationary LPP (Lemma 4.2 in [4]). To be precise, construct a boundary stationary model with its origin shifted to the point $(-n,-n)$; call the associated environment on $-\vec {n}+\mathbb {Z}^2_{\ge 0}$ as $\nu$, and let $G^1_{\text {stat}}( -\vec {n},\cdot )$ denote the associated stationary passage times. From $\nu$, derive the environment $\nu '$ on $\mathbb {Z}^2_{\ge 0}$ as follows:

$$\begin{aligned} \nu '_v= {\left\{ \begin{array}{ll} \nu _v, &{} \text { for } v\in \mathbb {Z}^2_{>0}\\ G^1_{\text {stat}}\left( -\vec {n},i\text {e}_1 \right) -G^1_{\text {stat}}\left( -\vec {n},(i-1)\text {e}_1 \right) , &{} \text { for } v=i\text {e}_1\\ G^1_{\text {stat}}\left( -\vec {n},j\text {e}_2 \right) -G^1_{\text {stat}}\left( -\vec {n},(j-1)\text {e}_2 \right) , &{} \text { for } v=j\text {e}_2\\ 0 \text { for } v=\mathbf{0} . \end{array}\right. } \end{aligned}$$

Use $\nu '$ to define a boundary stationary model on $\mathbb {Z}^2_{\ge 0}$, and use $G^1_{\text {stat}}(\cdot )$ for the associated stationary passage times. We now derive a point-to-line stationary model from $\nu$. Recall that we only want to define $G^2_{\text {stat}}(v)$ for $v\le \vec {n}$ and we need to define the environment accordingly. Define the environment $\nu ''$ to be the same as $\nu$ in region $\{x+y> 0\} \cap \{(x,y)\le \vec {n}\}$. Define the weight function T on $\{x+y=0\}\cap \{(x,y)\le \vec {n}\}$ as follows:

$$\begin{aligned} T(\mathfrak {t})= G^1_{\text {stat}}(-\vec {n},\mathfrak {t})-G^1_{\text {stat}}(-\vec {n},\mathbf{0} ). \end{aligned}$$

Use T and $\nu ''$ to construct the point-to-line representation as in (2.2) and thus define $G^2_{\text {stat}}(v)$ for all $0\le v\le n$. By an application of Lemma 4.2 in [4], the quantities $G^1_{\text {stat}}(\cdot )$ and $G^2_{\text {stat}}(\cdot )$ have the correct marginal distributions. It is easy to see that because of the coupling, we have (cf. Lemmas 3.3 and 3.4 from [26])

$$\begin{aligned} G^1_{\text {stat}}(v)=G^2_{\text {stat}}(v)= G^1_{\text {stat}}\left( -\vec {n},v \right) -G^1_{\text {stat}}\left( -\vec {n},\mathbf{0} \right) . \end{aligned}$$

(6.9)

for all $0\le v \le \vec {n}$. To summarise, we first considered a stationary model having an environment $\nu$. We then applied deterministic operations to $\nu$ to obtain the environments $\nu '$ and $\nu ''$ and their respective stationary models. This gave us a coupling of $\nu '$ and $\nu ''$ via $\nu$ which we were able to use to get the needed result. $\square$

Proof of Proposition 6.1

Immediate from Proposition 6.7. $\square$

Proof of Propositon 6.2

By the almost sure uniqueness of geodesics, for either representation, the stationary geodesic to $v_N$ (restricted to $\mathbb {Z}^2_{>0}$) can be reconstructed just by knowing the stationary passage times for all v with $\mathbf{0} \le v\le v_N$. For example, working with the point-to-line representation, if we have $G^2_{\text {stat}}(v_N-\text {e}_1)>G^2_{\text {stat}}(v_N-\text {e}_2)$, then the stationary geodesic to $v_N$ is just the stationary geodesic till $v_N-\text {e}_1$ concatenated with the singleton $\{v_N\}$, and one can proceed recursively to obtain the portion of the stationary geodesic in $\mathbb {Z}^2_{>0}$. By Proposition  6.7, there is a coupling for which $G^1_{\text {stat}}(v)=G^2_{\text {stat}}(v)$ for all $\mathbf{0} \le v\le v_N$. By the above discussion, this implies that the stationary geodesics till $v_N$ agree in the region $\mathbb {Z}^2_{>0}$ for both the representations and Proposition  6.2 follows immediately. $\square$