Abstract
A review on the fluctuation relation, fluctuation theorem and related topics.








Similar content being viewed by others
Notes
For example, “Whether or not speculations concerning such hypothetical Anosov systems are an aid or a hindrance to understanding seems to be an aesthetic question” [8, p. 221].
If M is a smooth (i.e. \(\infty \)-differentiable) bounded manifold and S is an invertible smooth (i.e. \(\infty \)-differentiable together with the inverse \(S^{-1}\)) map on M, the system (M, S) is an Anosov map if
-
(a)
at every point \(x\in M\) there are two complementary tangent planes \(T_s(x)\) and \(T_u(x)\), transverse in x, which depend continuosly on x, are covariant in the sense that the Jacobian \({\partial }S(x)^{\pm 1}\) acts on the plane tangent to the attracting set so that \({\partial }S(x)^{\pm 1} T_\gamma (x)=T_\gamma (S(x)^{\pm 1}), \gamma =u,s\),
-
(b)
furthermore there are \(C>0,\lambda <1\) such that \(|{\partial }S^n(x) v|< C \lambda ^n |v|, n>0\) if \(v\in T_s(x)\) and \(|{\partial }S^{-n}(x) v|< C \lambda ^n |v|, n>0\) if \(v\in T_u(x)\),
-
(c)
there is a point whose orbit is dense in M.
The definition of Anosov flow is similar: the covariant mutually transversal planes are now three: \(T_u(x),T_s(x)\) on which expansion and contraction take place under action of the flow \(S_t\) as in the map case and a third 1-dimensional tangent plane parallel to f(x), if \(\dot{x}=f(x)\) is the differential equation defining the flow \(S_t\); this is a tangent vector supposed not zero, \(|f(x)|>0\), and which, of course, neither expands nor contracts under the \({\partial }S_t(x)\).
The stable and unstable planes of Anosov systems (maps or flows) can be integrated (i.e. there is a smooth surface everywhere tangent to them) to define stable and unstable manifolds \(W_u(x),W_s(x)\) which are dense on M.
-
(a)
This means that for all times \(t_0\) the closure of the trajectory of \(\{S^tx\}_{t>t_0}\) is \({\mathcal {A}}\).
Evolutions defined by maps arise typically when studying evolutions in continuous time through observations triggered by “timing events”, i.e. observations that are made every time a specified event takes place: for instance every time that the evolving trajectory crosses a given surface in phase space. These are referred as observations performed on a Poincaré’s section.
Which contrasts the picture of \({\mathcal {A}}\) as a fractal set. In systems of \(\sim 10^{20}\) molecules with a fractal attractor of dimension \(6\cdot 10^{19}+3.141\) this means that it ’behaves’ as a smooth surface of dimension \(6\cdot 10^{19}\); or in a Navier–Stokes fluid (an \(\infty \)-dimensional system) at large Reynolds number R an attracting set of dimension \(R^{\frac{9}{3}}+.33\) ’behaves’ as a smooth surface of dimension integral part of \(R^{\frac{9}{3}}\).
Often, if the dynamical system depends on a parameter \(\varepsilon \), the chaotic motion might occupy, asymptotically, an attracting set \({\mathcal {A}}_\varepsilon \) with a dimension dependent on \(\varepsilon \) and equal to that of the full phase space only for a small (if any) interval of variability of \(\varepsilon \).
For example, a change in variables \(y=w(x)\) leads to \(u(x)=-\log |\det {\partial }_{x_j}{w_i}|\).
For example, changing x into \(y=w(x)\) leads to \(U(x)= -\log |{\partial }_{x_j}w_j|\).
Since the CH-evolutions that we consider proceed towards a bounded attracting set it is \(\sigma _+\ge 0\) [29].
The above thermostatting forces choice can be seen to coincide with the ones obtained via Gauss’ least effort principle for ideal anholonomic constraints applied to the constraints \(K_a=const\), see [2, Chap. 2]: this is a criterion that has been adopted in several simulations [32, Sect. 5.2, p. 103]. Independently of Gauss’ principle it is immediate to check that if \(\alpha _a\) is defined by Eq. (4.3) then the kinetic energies \(K_a\) are, strictly, constants of motion.
With density on the phase space \({\mathcal {C}}_0\times R^{3N_0}\).
The physical picture is that the energy generated by work performed by the active forces on the particles in \({\mathcal {C}}_0\) and by the interactions between the particles in \({\mathcal {C}}_0\) and those in the thermostats is ceded to the thermostats creating in them heat currents \(J_a\) which decrease as the inverse of the square distance to \({\mathcal {C}}_0\): so the thermostats remain asymptotically, as the distance from \({\mathcal {C}}_0\) tends to \(\infty \), in equilibrium.
But the choice of \(T_0\) has no particular physical meaning and the distribution in \({\mathcal {C}}_0\) could be replaced by “any” distribution, with some density on the \(X_0,\dot{X}_0\) variables.
A positive \(\sigma (x)\) means that the volume contracts near x: hence in stationary states the average \(\sigma _+\) of \(\sigma \) must be \(\ge 0\) [29].
The rate \(\zeta (p)\) is defined so that the probability of finding \(\frac{1}{\tau }\int _0^\tau \frac{\sigma (S_tx)}{\sigma _+}dt dt\in [p,p+\delta p]\) is \(\exp \tau \max _{[p,p+\delta p]}\zeta (p)\) for \(p\in (-p^*,p^*)\) where \(p^*\ge 1\); it exists and is analytic if \(\sigma (x)\) is the phase space contraction of an Anosov evolution.
The problem is considered, by some colleagues, a “disaster” for FR, making it physically irrelevant.
Doubts have been raised in [44]: which might be related to the use of a rather large value of \(\nu \) in a strongly truncated NS equation in 2D: it is hoped that the latter results will be tested again at smaller \(\nu \) (in spite of computational difficulties).
The proof of the pairing symmetry in the above mentioned cases is that the Jacobian matrix \({\partial }_i (S_t x)_j|_{t=0}\) is seen to be the sum of the Jacobian for the Hamiltonian flow of \(H(\mathbf{p},\mathbf{q})-\frac{\nu }{2}(\mathbf{p}^2+\mathbf{q}^2)\) plus the identity times \(-\frac{\nu }{2}\) [47]. In the case of \(\alpha \) a similar property holds replacing \(\nu \) with \(\alpha \), as is seen via a calculation. If \(J(t)={\partial }_i (S_t x)_j\) then \(J(t)PJ(t)^T=P e^{-n\nu t}\) (or \(P e^{-n\int _0^t\alpha (x(t))dt}\)) where \(P=\begin{pmatrix}0&{}\mathbf{1}\\ \mathbf{-1}&{}0\\ \end{pmatrix}\) (\(\mathbf{1}\) being the \(n\times n\) identity) because \(J(t){\mathop {=}\limits ^{def}}J_0e^{-\frac{1}{2} \nu t}\) with \(J_0\) a symplectic matrix so that \( J_0PJ_0^T=P\) (Proposition 24, Sect. 3.12 in [50]). Therefore let v be an eigenvector \(J_0^TJ_0 v=\lambda v\) then the following chain of identities, using \(P^2=-1\) shows that \(\lambda ^{-1}\) is an eigenvalue, with eigenvector Pv:
$$\begin{aligned} \begin{aligned}&J_0^TJ_0 v=\lambda v \ \rightarrow \ P J_0^TJ_0 v=\lambda P v\ \rightarrow \ -J_0^{-1}P J_0 P P v=\lambda P v \\&\rightarrow \ J_0^{-1}J_0^{-1T} Pv=\lambda Pv\ \rightarrow \ (J_0^T J)^{-1} Pv=\lambda Pv \end{aligned} \end{aligned}$$impliyng pairing to \(-\frac{\nu }{2}\) (respectively to \(-t^{-1}\int _0^t\frac{1}{2} \alpha (x(t))dt\)) for the matrix \((J(t)^TJ(t))^{\frac{1}{2}}\). [47, 48].
Failure to realize the difference between Anosov motions on the attracting surface versus Anosov motions on the entire phase space in chaotic systems satisfying the CH together with time reversal symmetry is responsible for statements [8, p. 220], like: “If there were such systems then it could be proved that they would generate relatively simple attractors, with equal numbers of positive and negative Lyapunov exponents. Because the simple geometric argument of Section 7.8 shows that nonequilibrium attractors are actually generated by any stable time reversible, steady dynamics, the applicability of the Anosov proofs is evidently rare to vanishing” [1, 20, 51].
It would seem that smoothness of \(\widetilde{I}\) should also be required because the axiom C implies only Hölder continuity for \(\widetilde{I}\), see [53]. However a careful examination of the FT proof shows that it is sufficient that the restrictions to \({\mathcal {A}}\) of the stable and unstable manifolds of the points \(a\in {\mathcal {A}}\) are smooth manifolds and this is implied by the assumed smoothness of \({\mathcal {A}}\) itself (by CH) and by the smoothness of the global manifolds.
To fix ideas think of a Hamiltonian system constrained to keep the total kinetic energy constant, for instance via a Gaussian constraint, as considered in many applications [32]: in absence of external forcing, and assuming CH, the SRB distribution is quite generally explicitly known and equivalent to the canonical distribution [32].
In other words at \(\mathbf{E}=\mathbf{0}\) the evolution is a Anosov system.
The symmetry could also depend on \(\mathbf{E}\), becoming \(I_{\mathbf{E}}\), however further assumptions would be needed, like differentiability [54].
Remark that this is an important case whose occurrence has been considered “rare to evanescent” in [8, p. 220].
i.e. as long as structural stability maintains the system an Anosov system.
“À la vérité, les choses ne peuvent pas se passer rigoureusement comme nons l’avons supposé ... [59, p. 13–14].
Strictly speaking equilibrium will be reached after infinite time; however it can be considered reached for practical purposes after \(\tau '\), which has the meaning of a time scale.
The two terms in Eq. (13.1) have in general different dependence on particles number N: as of O(N) in the case of volume variations or \(O(N^{\frac{2}{3}})\) if P(t) only involves boundary temperature variations (hence the heat exchange is a boundary effect).
Supposed to be the same for all t, for simplicity.
Remark that the variation of \({\overline{\sigma }}_{(k+1)\delta ,+}-{\overline{\sigma }}_{k\delta ,+}\) is, in general, of order \(\kappa \delta \) as a consequence of the differentiability [60], of the SRB states with respect to the parameters.
This means that the initial potential energy is \(m g N h_0\), where \(h_0\) is the height of the center of mass, and varies at time 0 to \(m g' N h_0\).
Disconnected intersections may happen if the maximum diameter of the \(P_i\) can be dilated by the action of S or \(S^{-1}\) to become larger than the diameter of M.
i.e. the intersection with the stable manifolds in \({\partial }P_i\).
The code that associates with \(x\in M\) the history \({\varvec{\sigma }}\) of x is closely related to the “structural stability” of Anosov maps. Structural stability of Anosov maps means that if an Anosov map S is smoothly perturbed to become a map \(S_\varepsilon \), as a function of a parameter \(\varepsilon \), with \(S_0=S\) then, if \(\varepsilon \) is small enough, also \(S_\varepsilon \) is an Anosov map and \(S_\varepsilon \) is conjugated to S in the sense that there is a Hölder continuous homeomorphism \(\Theta \) of M such that \(S_\varepsilon =\Theta \,S_0\,\Theta ^{-1}\). An essential step to prove this property is to show that a Markovian partition \({\mathcal {P}}\) for S can be deformed “by continuity” into a Markovian partition \({\mathcal {P}}_\varepsilon \) for \(S_\varepsilon \)with the same transition matrix: so that the conjugation is the map \(x\leftrightarrow x'\) associating pairs with the same histories: under \(S_0\) on \({\mathcal {P}}\) and under \(S_\varepsilon \) on \({\mathcal {P}}_\varepsilon \).
Here a spin is a variable that can assume a finite number of values, e.g. \(\sigma =\pm 1\) or \(\sigma =1,2,..,m\).
If \(B=[a,b]\) and \(B+t=[a+t,b+t]\) then \({\varvec{\Phi }}^\pm _{B+t}({\varvec{\sigma }}_{B})\equiv {\varvec{\Phi }}^\pm _{B}({\varvec{\sigma }}_{B})\) for all t.
Very large fluctuations can hint at “violations” of the second principle [35], hence cannot be observed in large systems.
The average \(\langle \sigma \rangle \) cannot be \(<0\), i.e. phase space cannot keep expanding forever if a stationary state can be reached [29].
The CH implies that there is no vanishing exponent for the map.
More generally the forcing can be supposed to have \(f_{\mathbf{k}}\ne 0\) only for \(|{\mathbf{k}}|<F\), with F being a fixed cut-off. The cases \({\mathbf{k}}=(0,\pm 1)\) and \({\mathbf{k}}=(\pm 1,0)\) are somewhat trivial, see [75].
Viscosity plays the role of a model of thermostat: the fluid keeps a constant temperature in spite of the viscosity: therefore viscosity is a model for the undisclosed mechanism keeping the temperature constant.
In dimension \(d=3\): \(\alpha =\alpha ({\mathbf{u}})\) has to be modified by adding to the numerator of Eq. (17.3) be quantity \( \sum _{{\mathbf{k}}_1,{\mathbf{k}}_2} ({\mathbf{k}}_1+{\mathbf{k}}_2)^2\)
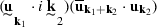 .
.For instance if \(f_{\mathbf{k}}\) is real and \({\mathbf{k}}\cdot \mathbf{a}=0\) if \(f_{\mathbf{k}}\ne 0\), there is a solution with \(u_{\mathbf{k}}\) real: and we have infinitely many invariant sets in which \(u_{\mathbf{k}}\) has the form \(v_{\mathbf{k}}e^{\theta _0\,{\mathbf{k}}\cdot \mathbf{a}}\), parameterized by \(\theta _0\).
They are defined in terms of the diagonal elements of the QR decomposition of the matrix \({\partial }_u (S_\tau u)\), linearizing the flow, with \(\tau \) fixed: in the picture \(\tau =h 2^{10}\) was chosen, which is a small fraction of the time unit fixed by the integration step (which is in the pictures \(h=2^{-17}\)). Approximating the matrix \({\partial }_u (S_\tau u)\) as \(V=(1+h J(u))^{\tau h^{-1}}\), where \(J(u)={\partial }_u\dot{u}\) is the Jacobian matrix of the flow, the QR decomposition of V gives a triangular matrix \(R>0\) and the logarithms of its eigenvalues divided by \(\tau \), denoted \(\Lambda _k(u)\), \(k=1,2,\ldots \), are sampled as u(t) evolves in time every \(4 h^{-1}\) steps and their averages are the definition adopted here of the local Lyapunov exponents \(\lambda _k\). A much more accurate definition would be replacing V with the time ordered product \(\prod _{k=0}^{\tau h^{-1}} (1+h J(S_k u))\): but this greatly increases the computation time (by a factor \(2^7\) here). Alternatively one could consider the eigenvalues of the symmetric part of J(u) [82]: but this also requires a large computation time.
Simple examples of the meaning of Eq. (19.1) compared to FR can be constructed: which exhibit systems, as chaotic as wished, evolving towards a stationary state with average phase space contraction \(\sigma _+>0\) and which for every finite time satisfy Eq. (19.1) but at infinite time do not satisfy the FR. An example of such a map follows: let \(S_0\) be a map on the unit circle \({\mathcal {T}}\) defined by the evolution at time \(t=1\) (say) of \({\dot{\varphi }}=-\sin \varphi \): it has \(\varphi =\pi \) as an unstable fixed point and \(\varphi =0\) as a stable fixed point (with Lyapunov exponents \(\lambda _0=\pm 1\), respectively). Let I be the reflection of the point \(\varphi \) at the circle center. Then the evolution is I-reversible and the distribution \(\mu _0(d\varphi )=\frac{d\varphi }{2\pi }\) is I-symmetric. Hence Eq. (19.1) holds for all finite \(\tau \): at \(\tau =\infty \) the distribution of \(p=\frac{1}{\tau }\sum _{k=0}^\tau \cos (S_0^k\varphi )=\frac{1}{\tau }A\) evolves to \(\delta (p)\) which does not satisfy the FR for any \(p>0\) although \(\sigma _+=1\). The example can be easily adapted to deal with a chaotic evolution: it is enough to consider the dynamical system acting on pairs \((\varphi ,x)\) which evolve in \((S_0\varphi ,S_\Xi x)\), where \(\Xi \) is any Anosov map reversible under a map J. This is reversible under the time reversal \((\varphi ,x)\rightarrow (I\varphi ,J x)\). Then Eq. (19.1) holds but leads to a relation with slope \(\sigma _+=\sigma (\Xi )+1\), where \(\sigma (\Xi )\) is the phase space contraction of the map \(\Xi \)), while FR predicts the correct slope \(\sigma (\Xi )\), because the example is a simple example of a system with a smooth hyperbolic attracting set (i.e. the pairs (0, x)), hence it satisfies the Chaotic Hypothesis: a case in which the FR is a theorem. Likewise a flow example can be easily constructed. The example is due to F.Bonetto.
Sometimes claiming to have checked it and sometimes claiming the opposite, while very often dealing with unrelated transient phenomena.
This time the reason is not “for simplicity”, but because in the case of coupled flows, even if the coupling has short range and is weak, there seems to be no detailed and constructive general theory of the SRB distributions, because no simple conditions are known that, via perturbation techniques, yield hyperbolicity of the flow and allow studying its properties. (For a glimpse on the kind of complications which arise when studying flows consult [91, 92].) Instead, at least in the case of coupled maps, the theory is quite well understood [11, 36, 93, 94], as in the example in Eq. (B.1) below, at small coupling \(\varepsilon \).
The SRB distribution for the evolution \({\overline{S}}_\varepsilon \) with \(L=\infty \) could also be defined via the SRB distribution \(\mu _{srb,\varepsilon }^L\) for the system \({\overline{S}}_\varepsilon \) consisting of the sites labeled from \(-L \) and L and then taking the limit \(\mu _{srb}=\lim _{L\rightarrow \infty }\mu _{srb,L}\) [93]. This is possible because of the uniformity in \(\varepsilon <\varepsilon _0\): below, however, \(L<\infty \) will be fixed, keeping in mind that the results will hold for all L if \(|\varepsilon |<\varepsilon _0\).
Likewise the space-time limit \(\eta _{\varepsilon ,+}\) exists because of the space-time ergodicity of the short range Gibbs processes describing the volume as well as the SRB distributions.
Relatively vanishing as \(L^{-1}\) uniformly in x.
Notation: diff(T) denotes the set of the general torus diffeomorphisms and Sdiff(T) is the subset of diffeomorphisms with Jacobian \(J({\varvec{\delta }})({\varvec{\xi }})\equiv \det (\frac{{\varvec{\partial }}{\varvec{\delta }}({\varvec{\xi }})}{\delta {\varvec{\partial }}{\varvec{\xi }}})=1\)e.g. , if \(d=3\), \(J({\varvec{\delta }})({\varvec{\xi }})={\varvec{\partial }}\delta _1({\varvec{\xi }})\wedge {\varvec{\partial }}\delta _2({\varvec{\xi }})\cdot {\varvec{\partial }}\delta _3({\varvec{\xi }})\equiv 1\).
References
Gallavotti, G., Cohen, D.: Dynamical ensembles in nonequilibrium statistical mechanics. Phys. Rev. Lett. 74, 2694–2697 (1995)
Gallavotti, G.: Nonequilibrium and irreversibility. Theoretical and Mathematical Physics. Springer-Verlag and http://ipparco.roma1.infn.it & arXiv:1311.6448, Heidelberg (2014)
Jakŝ ić, V., Pillet, C.-A.: Ergodic properties of classical dissipative systems I. Acta Math. 181, 245–282 (1998)
Kurchan, J.: Fluctuation theorem for stochastic dynamics. J.Phys. A 31, 3719–3729 (1998)
Eckmann, J.P., Pillet, C.A., Rey-Bellet, L.: Non-equilibrium statistical mechanics of anharmonic chains coupled to two heat baths at different temperatures. Commun. Math. Phys. 201, 657–697 (1999)
Lebowitz, J., Spohn, H.: A Gallavotti-Cohen type symmetry in large deviation functional for stochastic dynamics. J. Stat. Phys. 95, 333–365 (1999)
Maes, C.: The fluctuation theorem as a Gibbs property. J. Stat. Phys. 95, 367–392 (1999)
Hoover, W.: Time Reversibility Computer Simulation, and Chaos. World Scientific, Singapore (1999)
Arnold, V.I., Avez, A.: Ergodic Probems of Classical Mechanics. Mathematical Physics Monographs. Benjamin Publishing, Amsterdam (1968)
Smale, S.: Differentiable dynamical systems. Bull. Am. Math. Soc. 73, 747–818 (1967)
Gallavotti, G., Bonetto, F., Gentile, G.: Aspects of the ergodic, qualitative and statistical theory of motion. Springer Verlag, Berlin (2004)
Sinai, YaG: Lectures in Ergodic Theory. Lecture notes in Mathematics. Princeton University Press, Princeton (1977)
Sinai, Y.G.: Topics in Ergodic Theory. Princeton Mathematical Series, vol. 44. Princeton University Press, Princeton (1994)
Sinai, Y.G.: Markov partitions and \(C\)-diffeomorphisms. Funct. Anal. Appl. 2(1), 64–89 (1968)
Sinai, Y.G.: Construction of Markov partitions. Funct. Anal. Appl. 2(3), 70–80 (1968)
Bowen, R., Ruelle, D.: The ergodic theory of axiom A flows. Invent. Math. 29, 181–205 (1975)
Ruelle, D., Takens, F.: On the nature of turbulence. Commun. Math. Phys. 20, 167–192 (1971)
Ruelle, D.: Turbulence, strange attractors and chaos. World Scientific, New-York (1995)
Ruelle, D.: Chaotic Motions and Strange Attractors. Accademia Nazionale dei Lincei, Cambridge University Press, Cambridge (1989)
Bonetto, F., Gallavotti, G.: Reversibility, coarse graining and the chaoticity principle. Commun. Math. Phys. 189, 263–276 (1997)
Bonetto, F., Gallavotti, G., Garrido, P.: Chaotic principle: an experimental test. Physica D 105, 226–252 (1997)
Ruelle, D.: Measures describing a turbulent flow. Ann. N. Y. Acad. Sci. 357, 1–9 (1980)
Gallavotti, G., Cohen, D.: Dynamical ensembles in stationary states. J. Stat. Phys. 80, 931–970 (1995)
Boltzmann, L.: Über die mechanische Bedeutung des zweiten Hauptsatzes der Wärmetheorie. Wiener Berichte, 53, (W.A.,#2):195–220, (9–33) (1866)
Clausius, R.: Ueber die Zurückführung des zweites Hauptsatzes der mechanischen Wärmetheorie und allgemeine mechanische Prinzipien. Ann. Phys. 142, 433–461 (1871)
Boltzmann, L.: Studien über das gleichgewicht der lebendigen kraft zwischen bewegten materiellen punkten. Wiener Berichte, 58, (W.A.,#5):517–560, (49–96), (1868)
Maxwell, J.C.: On Boltzmann’s theorem on the average distribution of energy in a system of material points. Trans. Camb. Philos. Soc. 12, 547–575 (1879)
Gallavotti, G.: Ergodicity: a historical perspective: equilibrium and nonequilibrium. Eur. Phys. Journal H 41, 181–259 (2016)
Ruelle, D.: Positivity of entropy production in nonequilibrium statistical mechanics. J. Stat. Phys. 85, 1–25 (1996)
de Groot, S., Mazur, P.: Non equilibrium thermodynamics. Dover, Mineola, NY (1984)
Feynman, R.P., Vernon, F.L.: The theory of a general quantum system interacting with a linear dissipative system. Ann. Phys. 24, 118–173 (1963)
Evans, D.J., Morriss, G.P.: Statistical Mechanics of Nonequilibrium Fluids. Academic Press, New-York (1990)
Gallavotti, G., Presutti, E.: Thermodynamic limit for isokinetic thermostats. J. Math. Phys. 51, 0353303 (+9) (2010)
Gallavotti, G.: Reversible Anosov diffeomorphisms and large deviations. Math. Phys. Electron. J. 1, 1–12 (1995)
Evans, D.J., Cohen, E.G.D., Morriss, G.P.: Probability of second law violations in shearing steady flows. Phys. Rev. Lett. 71, 2401–2404 (1993)
Bricmont, J., Kupiainen, A.: Coupled analytic maps. Nonlinearity 8, 379–396 (1995)
Shang, X.D., Tong, P., Xia, K.Q.: Test of steady-state fluctuation theorem in turbulent Rayleigh–Bnard convection. Phys. Rev. E 015301(R), 1–4 (2005)
Ruelle, D.: Statistical Mechanics. Benjamin, New York (1974)
Lanford, O., Ruelle, D.: Observables at infinity and states with short range correlations in statistical mechanics. Commun. Math. Phys. 13, 194–215 (1969)
Gallavotti, G.: Statistical Mechanics: A Short Treatise. Springer Verlag, Berlin (2000)
Maxwell, J.C.: On the dynamical theory of gases. In: Niven, W.D. (ed.) The Scientific Papers of J. C. Maxwell, vol. 2, pp. 26–78. Cambridge University Press, Cambridge (1866)
She, Z.S., Jackson, E.: Constrained Euler system for Navier–Stokes turbulence. Phys. Rev. Lett. 70, 1255–1258 (1993)
Gallavotti, G., Rondoni, L., Segre, E.: Lyapunov spectra and nonequilibrium ensembles equivalence in 2d fluid. Physica D 187, 358–369 (2004)
Rondoni, L., Mejia-Monasterio, C.: Fluctuations in nonequilibrium statistical mechanics: models, mathematical theory, physical mechanisms. Nonlinearity 20, R1–R37 (2007)
Gallavotti, G., Lucarini, V.: Equivalence of non-equilibrium ensembles and representation of friction in turbulent flows: the Lorenz 96 model. J. Stat. Phys. 156, 1027–10653 (2014)
Biferale, L., Cencini, M., DePietro, M., Gallavotti, G., Lucarini, V.: Equivalence of non-equilibrium ensembles in turbulence models. Phys. Rev. E 98, 012201 (2018)
Dressler, U.: Symmetry property of the Lyapunov exponents of a class of dissipative dynamical systems with viscous damping. Phys. Rev. A 38, 2103–2109 (1988)
Dettman, C., Morriss, G.: Proof of conjugate pairing for an isokinetic thermostat. Phys. Rev. E 53, 5545–5549 (1996)
Chernov, N.I., Eyink, G.L., Lebowitz, J.L., Sinai, Ya G.: Steady state electric conductivity in the periodic Lorentz gas. Commun. Math. Phys. 154, 569–601 (1993)
Gallavotti, G.: The Elements of Mechanics, 1st edn. Springer Verlag, New York (1983)
Gallavotti, G.: Breakdown and regeneration of time reversal symmetry in nonequilibrium statistical mechanics. Physica D 112, 250–257 (1998)
Gallavotti, G.: Dynamical ensembles equivalence in fluid mechanics. Physica D 105, 163–184 (1997)
Pollicot, M.: Maximal Lyapunov exponents for random matrix products. Invent. Math. 181, 209–226 (2010)
Porta, M.: Fluctuation theorem, non linear response and the regularity of time reversal symmetry. Chaos 20, 023111 (2010)
Gallavotti, G.: Extension of Onsager’s reciprocity to large fields and the chaotic hypothesis. Phys. Rev. Lett. 77, 4334–4337 (1996)
Gentile, G.: A large deviation theorem for Anosov flows. Forum Math. 10, 89–118 (1998)
Gallavotti, G.: Chaotic hypothesis: onsager reciprocity and fluctuation–dissipation theorem. J. Stat. Phys. 84, 899–926 (1996)
Gallavotti, G., Ruelle, D.: SRB states and nonequilibrium statistical mechanics close to equilibrium. Commun. Math. Phys. 190, 279–285 (1997)
Carnot, S.: Réflections sur la puissance motrice du feu et sur les machines propres à développer cette puissance. https://gallica.bnf.fr; original Bachelier, 1824; reprinted Gabay, 1990., Paris (1824)
Ruelle, D.: Differentiation of srb states. Commun. Math. Phys. 187, 227–241 (1997)
Bowen, R.: Markov partitions for axiom A diffeomorphisms. Am. J. Math. 92, 725–747 (1970)
Bowen, R.: Equilibrium States and the Ergodic Theory of Anosov Diffeormorphisms. Lecture Notes in Mathematics, vol. 470. Springer-Verlag, Berlin (1975)
Franceschini, V., Russo, L.: Stable and unstable manifolds of the Hénon mapping. J. Stat. Phys. 25, 757–769 (1981)
Bowen, R.: Markov partitions are not smooth. Proc. Am. Math. Soc. 71, 130–132 (1978)
Sinai, Ya G.: Gibbs measures in ergodic theory. Russ. Math. Surv. 27, 21–69 (1972)
Viavattene, G., Consolini, G., Berrilli, F., Calchetti, D., Del Moro, D., Gianattanasio, F., Giacomelli, L., Penza, V.: Testing tha steady state fluctuation theorem in the solar photospheric convection. Uniroma 2, 1–4 (2019)
Garrido, P.L., Goldstein, S., Lebowitz, J.L.: Boltzmann entropy for dense fluids not in local equilibrium. Phys. Rev. Lett. 92, 050602 (+4) (2004)
Presutti, E.: Scaling Limits in Statistical Mechanics and Microstructures in Continuum Mechanics. Springer, Berlin (2009)
Ruelle, D.: Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press, New-York (1989)
Gallavotti, G.: Equivalence of dynamical ensembles and Navier Stokes equations. Phys. Lett. A 223, 91–95 (1996)
Gallavotti, G.: Non equilibrium in statistical and fluid mechanics, ensembles and their equivalence, entropy driven intermittency. J. Math. Phys. 41, 4061–4081 (2000)
Gallavotti, G.: Fluctuations and entropy driven space-time intermittency in Navier–Stokes fluids. In: Fokas, E., Grigoryan, A., Kibble, T., Zegarlinski, B. (eds.) Mathematical Physics 2000. World Scientific, London (2000)
Gallavotti, G.: Entropy driven intermittency. Markov Process. Relat. Fields 7, 135–144 (2001)
Gallavotti, G.: Microscopic chaos and macroscopic entropy in fluids. J. Stat. Mech. 2006, P10011 (+9) (2006)
Marchioro, C.: An example of absence of turbulence for any Reynolds number. Commun. Math. Phys. 105, 99–106 (1986)
Baive, D., Franceschini, V.: Symmetry breaking on a model of five-mode truncated Navier–Stokes equations. J. Stat. Phys. 26, 471–484 (1980)
Franceschini, V., Tebaldi, C.: Sequences of infinite bifurcations and turbulence in a five-mode truncation of the Navier–Stokes equations. J. Stat. Phys. 21, 707–726 (1979)
Franceschini, V., Tebaldi, C., Zironi, F.: Fixed point limit behavior of N-mode truncated Navier–Stokes equations as N increases. J. Stat. Phys. 35, 387–397 (1984)
Franceschini, V., Tebaldi, C.: Truncations to 12, 14 and 18 modes of the Navier–Stokes equations on a two-dimensional torus. Meccanica 20, 207–230 (1985)
Franceschini, V., Giberti, C., Nicolini, M.: Common periodic behavior in larger and larger yruncations of the Navier–Stokes. J. Stat. Phys. 50, 879–896 (1988)
Franceschini, V., Giberti, C.: Qualitative and quantitative stabilized behavior of truncated two-dimensional Navier–Stokes equations. Theor. Comput. Fluid Dyn. 2, 185–192 (1991)
Ruelle, D.: Large volume limit of the distribution of characteristic exponents in turbulence. Commun. Math. Phys. 87, 287–302 (1982)
Lieb, E.: On characteristic exponents in turbulence. Commun. Math. Phys. 92, 473–480 (1984)
Gallavotti, G.: Navier–stokes equation: irreversibility turbulence and ensembles equivalence. arXiv:1902.09610, 1902:09160 (2019)
Evans, D.J., Searles, D.: Equilibrium microstates which generate second law violating steady state. Phys. Rev. E 50, 1645–1648 (1994)
Jarzynski, C.: Nonequilibrium equality for free energy difference. Phys. Rev. Lett. 78, 2690–2693 (1997)
Hoover, W., Griswold, C.: Time Reversibility Computer simulation, and Chaos, vol. 13, 2d edn. World Scientific, Singapore (1999)
Ruelle, D.: Smooth dynamics and new theoretical ideas in non-equilibrium statistical mechanics. J. Stat. Phys. 95, 393–468 (1999)
Gallavotti, G.: Chaotic dynamics, fluctuations, non-equilibrium ensembles. Chaos 8, 384–392 (1998)
Gallavotti, G.: Chaotic hypothesis and universal large deviations properties. Documenta Mathematica, extra volume ICM98, vol. I:205–233 (1998)
Ruelle, D., Wilkinson, A.: Absolutely singular dynamical foliations. Commun. Math. Phys. 219, 481–487 (2001)
Gallavotti, G., Gentile, G., Giuliani, A.: Fractional Lindstedt series. J. Math. Phys. 47, 012702 (+33) (2006)
Pesin, Y.B., Sinai, Y.G.: Space-time chaos in chains of weakly inteacting hyperbolic mappimgs. Adv. Soviet Math. 3, 165–198 (1991)
Bricmont, J., Kupiainen, A.: Infinite dimensional srb measures. Physica D 103, 18–33 (1997)
Gallavotti, G.: A local fluctuation theorem. Physica A 263, 39–50 (1999)
Sato, K., Sekimoto, K., Hondou, T., Takagi, F.: Irreversibility resulting from contact with a heat bath caused by the finiteness of the system. Phys. Rev. E 66, 016119+6 (2002)
Arnold, V.: Sur la géométrie différentielle des groupes de Lie de dimension infinie et ses applications à l’hydrodynamique des fluides parfaits. Ann. Inst. Fourier 16, 319–361 (1966)
Tao, T.: The Euler–Arnold Equation. Expository Sections, https://terrytao.wordpress.com/2010/06/07/the-euler-arnold-equation:1--15 (2010)
Acknowledgements
I profited from discussions with L.Biferale, M.Cencini, M.De Pietro, V.Lucarini in Sect. 18 , and L.S.Young in Sect. Appendix B , whom I thank warmly.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Sheldon Goldstein.
This review is dedicated to Joel Lebowitz to witness my gratitude for his constant guidance and teaching which influenced indelibly my work.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
About Certain Comments on CH
In the above sections quotes from [8] have been reproduced without really commenting them. The reason is that the quotes were written when the Chaotic Hypothesis had been just developed and many had not yet had the time to really study the subject.
But the same comments have appeared in a second edition of the just quoted book [87], which I have seen only very recently (after completion of the present text). Since the comments have had some resonance the next few lines try to clarify some of the issues.
The Author of [87] criticizes the use of the Anosov systems as paradigm of chaotic motions. The full section from pages 344 to 347 discusses the merits and demerits of Anosov systems. On p. 344 begins
... has discussed the possibility that the useful properties exhibited by certain oversimplified and quite rare dynamical systems, termed “Anosov systems”, have counterparts in the more usual thermostatted systems studied with nonequilibrium simulation methods. Anosov systems are oversimplifications, like square clouds or spherical chickens...
This seems to refer to the proposal that the “Axiom A” systems should be the right paradigm for generic chaotic systems [19, 88]: a proposal which however is not centered on Anosov systems. The Axiom A systems are systems which have an the attracting set \({\mathcal {A}}\) on which motion has strong chaotic properties (is essentially hyperbolic).
And the CH just proposes, in its final formulation, (1996), that for many purposes the axiom A paradigm can be strengthened and simplified by requiring in addition that \({\mathcal {A}}\) is an attracting surface, possibly of dimension lower than that of phase space, on which the motion is an Anosov system. Even in time reversible cases \({\mathcal {A}}\)can be different from its time reversal image. This is explicitly stated with related problems and examples in [20, 21] and in several successive publications.
The underlying idea being that it is not possible to distinguish, in a system of physical interest, a fractal of Hausdorff dimension \(=10^6+3.1415...\) from a surface of exactly \(10^6\) dimensions.
In summary the Chaotic Hypothesis only assumes that the dynamics under consideration behaves (in some respects) like Anosov dynamics. This is after all not too astonishing if the most relevant degrees of freedom are chaotic like those of Anosov systems.
Most of the subsequent criticism in [87] is anchored on keeping the identification between the CH and the proposal that the whole dynamical system is an Anosov system.
On p. 346 the fluctuation theorem is called a “retrospective result” and identified with the true Fluctuation Theorem, Sect. 6 above, claiming: “These same “results” were actually given earlier by Denis Evans and several of his coworkers, for more general circumstances and through more elementary arguments.”
but no reference is made here to the applicability of the “earlier retrospective result” to stationary nonequilibria to which the Fluctuation Theorem applies, see\(^{46}\).
Then on p. 347 the view is found that:
“Theoretical constructs such as “measures”, should be viewed with a healthy suspicion until algorithms for evaluating them are supplied. The chaos inherent in interesting differential equations guarantees that our only access to the “strange sets” which constitute attractors and repellers will be representative time series from dynamical simulations. In no way can we construct, or even conceive of constructing, a Sinai-Ruelle-Bowen measure for an interesting system.”
However for most purposes by the CH Hamiltonian systems should be considered Anosov systems (literally, except of course the integrable ones). Hence the assumption that the attracting set is the full phase space is not always unreasonable.
Furthermore it is useful to stress that there are easy examples of systems satisfying the CH, with equal or disjoint attracting and repelling surfaces, time reversible, with as many degrees of freedom and negative Lyapunov exponents as wished (unrelated to the number of positive ones) and whose SRB measure is explicitly and completely constructed [11, Sect. 10.2].
Local Fluctuations: An Example
The phase space contraction in the evolution of a macroscopic system is typically a macroscopic quantity: whether it is the amount of heat ceded to the thermostats or the amount of work performed by the systems.
Therefore the average phase space contraction \(\sigma _+\) which controls the large fluctuations, Sect. 6 and the occurrence of “anomalous” patterns, Sect. 12, cannot be really observed in measurements on macroscopic systems.
Avoiding comments on the many experimental fluctuations observations which claim to check the FR,Footnote 47 the question asked here is whether a kind of fluctuation relation could be defined, and constrain quantities depending on events that can be observed in very small parts of the system.
In other words is it possible to give a meaning to a local fluctuation relation? [2, Chap. 4.9].
The following relies on Sect. 15: it is inserted as it provides a quite interesting example on how to make use of the symbolic dynamics representation of the Anosov systems.
A simple example, in a system with time reversal symmetry, will be discussed in which a local entropy production rate can be defined and checked to satisfy a local version of FR. A general view on the matter can be found in [89, 90].
The analysis deals again with maps rather than flows.Footnote 48
Consider a system with a translation invariant spatial structure, e.g. a periodic chain, or a d-dimensional square lattice \([-L,L]^d\) with periodic boundary, of \((2L)^d\) weakly interacting Anosov maps.
The phase space of the system is \(M=\{\mathbf{x}=(\ldots x_1,x_0,x_1,x_2,\ldots )\}={\mathcal {M}}_0^{(2L)^d}\), where \(x_i\in {\mathcal {M}}_0\) are points in a manifold \({\mathcal {M}}_0\): to fix ideas we take\({\mathcal {M}}_0\)to be a torus, on which an Anosov map \({\overline{S}}_0\) acts; then define the “coupled map”:
where g is a smooth perturbation, i.e. a smooth periodic function on \({\mathcal {M}}_0^3\).
If \(\varepsilon \) is small and the perturbation has short range it is proved in [36, 93, 94] that, defining the map \({\overline{S}}_\varepsilon \) as in Eq. (B.1) with periodic boundary condition (i.e. identifying the site \(-L \) with L), the map \({\overline{S}}_\varepsilon \) remains, if \(\varepsilon \) is small enough, still Anosov. It is conjugated to \({\overline{S}}_0\), via a Hölder continuous correspondence \({\varvec{\Theta }}_\varepsilon \), see\(^{34}\), by associating points x and \(x'\) with the same history under \({\overline{S}}_0\) and \({\overline{S}}_\varepsilon \). Furthermore there is \(\varepsilon _0>0\) such that the above holds for \(|\varepsilon |<\varepsilon _0\)uniformly in the system size L.Footnote 49
Here the purpose is to study whether a local version of the FR can hold at least in an example derived from \({\overline{S}}_\varepsilon \): but the \({\overline{S}}_\varepsilon \) is, in general, not reversible. A related reversible map \(S^{rev}_\varepsilon \) can be easily constructed on the “doubled” phase space \({\mathcal {M}}={\mathcal {M}}_0\times {\mathcal {M}}_0\) by setting:
which is reversible for the time reversal map \(I:(\mathbf{x},\mathbf{y})=(\mathbf{y},\mathbf{x})\). In the rest of this section this system will be considered in more detail.
A Markovian partition \({\mathcal {P}}^L_0\) for \({\overline{S}}^L_0\times ({\overline{S}}^L_0)^{-1}\) will be chosen to be the product of partitions \({\mathcal {P}}_{-\frac{L}{2}},\ldots ,{\mathcal {P}}_{\frac{L}{2}-1}\) for the single site maps \({\overline{S}}_0\) and \({\overline{S}}_0^{-1}\); and \({\mathcal {P}}^L_\varepsilon \) will be the partition \({\varvec{\Theta }}_\varepsilon {\mathcal {P}}^L_0\) existing and defined by the structural stability map \({\varvec{\Theta }}_\varepsilon \), conjugating \({\overline{S}}_0^{rev}\) to \({\overline{S}}_\varepsilon ^{rev}\) [11, Sec.10.2].
Hence the history of a point x will be a sequence of labels \(\sigma _{i;j}\) with \(i\in M\) and \(j\in (-\infty ,\infty )\): naturally i can be called a “space label” while j a “time label”. The superscript rev will be omitted in what follows, to simplify notations.
The analysis in Sect. 15 applied to the Anosov map \(S_\varepsilon \), will give a representation of the volume distribution \(\mu _0\) and of the SRB distribution \(\mu _{srb,\varepsilon }\) for \(S_\varepsilon \) via, respectively, suitable potentials \({\varvec{\Phi }}_\varepsilon ,{\varvec{\Phi }}_{\varepsilon }^\pm \).
Let \([0,\tau ]\) be a time interval and \(\Lambda =[-\frac{1}{2}L,\frac{1}{2}L]^d=M\), \(|\Lambda ]=L^d\). Via the Jacobian matrix \(J_\Lambda (x)={\partial }_x (S_\varepsilon x)\) define the phase space contraction and the time averaged contraction per site as, respectively:
The limit of \(\eta _{L,\varepsilon ,+}\) in Eq. (B.3) as \(\tau \rightarrow \infty \) exists with probability 1 with respect to the volume \(\mu _{vol}\), as well to the SRB distribution \(\mu _{srb,\varepsilon }\), and is x-independent aside x’s in a set of 0 volume: because the statistical properties of the volume distribution are those of the Gibbs distribution with potential \({\varvec{\Phi }}^+_\varepsilon \), hence enjoy strong ergodicity properties, as any SRB distribution, with respect to time translations.Footnote 50
The phase space contraction \(\sum _{t=0}^\tau \eta _{L,\varepsilon }(S_\varepsilon ^t x)\) can be expressed, see Sect. 15, via the potentials \({\varvec{\Phi }}^+_{\varepsilon },{\varvec{\Phi }}^-_{\varepsilon },{\varvec{\Phi }}_{\varepsilon }^\varphi \), where \({\varvec{\Phi }}^\varphi _{\varepsilon }\) is a potential that describes the interpolation between \({\varvec{\Phi }}_{\varepsilon }^-\) to \({\varvec{\Phi }}_{\varepsilon }^+\) and which is therefore “localized” [see comment to Eq. (15.1)] in the sense that \({\varvec{\Phi }}^\varphi _{\varepsilon }({\varvec{\sigma }}_I)\ne 0\) only if I contains the sites 0 or L and \(|{\varvec{\Phi }}_{\varepsilon ,I}^\varphi ({\varvec{\sigma }}_{I})|\le C e^{-\kappa |I|}\) for some \(C,\kappa >0\)). Given the symbolic history \({\varvec{\sigma }}\) of x, the Eq. (15.6) can be expressed as:
where \(K=I\times [a,b]\) is a parallelepiped in \(\Lambda \times [0,\tau ]\), and \({\varvec{\Phi }}^z_{\varepsilon ,K}{\mathop {=}\limits ^{def}}\sum _{t\in [a,b]}{\varvec{\Phi }}^z_{I+t}\) for \(z=\pm ,\varphi \), and the \(\ldots \) indicate a correction \(\sum _K {\varvec{\Phi }}^\varphi _{\varepsilon ,K}({\varvec{\sigma }}_K)\),Footnote 51. t A natural mathematical definition of the “local average phase space contraction” could be the \(-\frac{1}{\tau \Lambda _0}\sum _{t=0}^\tau \log J_{\Lambda _0}(S^x)\) where \(J_{\Lambda _0}(x)=|\det ({\partial }_i (S_\varepsilon x)_{i'})|\). But this is a quantity difficult to express in a useful way.
However it is also possible to propose a different definition of local average phase space contraction based on the representation Eq. (B.4) of the average of the logarithms of the full Jacobian. The latter can be expressed as Eq. (B.4) up to a quantity uniformly bounded in L: and the contribution to Eq. (B.4) from the parallelepipeds K’s entirely contained in \(\Lambda _0\times [0,\tau ]\) is:
see Eqs. (15.1), (15.4); the \( \eta _{\Lambda _0,\varepsilon ,\tau }^{loc}\) can be, heuristically, called the “local contraction rate”. It can be uniformly bounded (in \(\tau ,L\)).
Given \(\Lambda _0\) let \(\eta ^{loc}_{\Lambda _0,\varepsilon ,+}\) be the time average \(\eta _{\Lambda _0,\varepsilon ,\tau }^{loc}\) define:
and remark that \(\eta _{\Lambda _0,\varepsilon ,+}^{loc}=\eta _{\Lambda ,\varepsilon ,+}+o(L_0^{-1})\) (because of the SRB distribution representation of a Gibbs process).
It can also be shown that to leading order as \(L_0,L,\tau \rightarrow \infty \) the large deviation rates for \(p',p\) in Eq. (B.6) have the form \(\tau L^d\zeta _\infty (p'),\ \tau L_0^d\zeta ^0_\infty (p)\), with \(\zeta _\infty =\zeta ^0_\infty \) because \(\zeta _\infty \) is obtained as a thermodynamic limit of a kind of partition function: for a proof see [95, (5.14)].
Therefore by the FT applied to \(S_\varepsilon \) it is \(L^d\zeta _\infty (p')-L^d\zeta _\infty (-p')= L^d p' \eta _{\Lambda ,\varepsilon ,+}\) and, since \(\eta _{\Lambda _0,\varepsilon ,+}^{loc}= \eta _{\Lambda ,\varepsilon ,+}+o(L_0^d)\), the large deviations rate for p in Eq. (B.6) satisfies a FR of the form
with \(r=\frac{L_0^d}{L^d}\) and \(|p|\le p^*, p^*\ge 1\), up to corrections of \(O(L_0^{d-1})\): which means that the global and local large fluctuations rates are proportional and trivially related by a rescaling which equals \(r=(\frac{L_0}{L})^d\) up to a correction bounded \(\kappa ^{-1} L_0^{d-1}\) with \(\kappa \) bounding the range of the SRB potential, as in Eq. (15.1).
The universal slope 1 in the global FR is modified into \(r=(\frac{L_0}{L})^d\) in the local FR. The Eq. (B.7) can be proved for the system in Eq. (B.2).
However p in Eq. (B.6) is not related to a measurable quantity, as it cannot be hoped to be able to measure directly the local phase space contraction .defined as in Eq. (B.5).
Still the phase space contraction is often related to the amount of heat ceded or the work done on the surroundings by a system in a stationary state, as exemplified in the case of Eq. (4.4): hence it is tempting to test, in cases in which the latter quantities are accessible to local measurements, whether Eq. (B.7) holds. This is attempted in some simulations [45].
The interest of the above special example lies in the statements independence on the total size of the systems: they also mean that the fluctuation theorems may lead to observable consequences if one looks at the far more probable microscopic fluctuations of the local entropy production rate,[36, 93, 94]. For more details see [34].
Reversible Heating
Imagine a rarefied gas enclosed in a cubic container of side L described by a canonical distribution at inverse temperature \(\beta ^{-1}\). The potential energy is \(\sum _{i=1}^N mg z_i +\sum _{i,j} v(x_i-x_j){\mathop {=}\limits ^{def}}M\,g\,H +V\), with M=total mass and H the height of the center of mass. The initial free energy if \(F(\beta ,g)=-\beta ^{-1} \log \int e^{-\beta (V+gP)} d^{3N}pd^{3N}q\). The entropy can be computed via Gibbs’ formula \(S_0=-\int \rho (p,q)\log \rho (p,q)d^{3N}pd^{3N}q\).
The gas is set out of equilibrium by changing the gravity g to a new value \(g'\) for instance suddenly at time \(t=0\) or following a given prescription \(t\rightarrow g(t), t\in [0,\tau ]\) with \(g(\tau )=g', \tau <\infty \). Then it is let to evolve.
Since the evolution is Hamiltonian (although not autonomous) \(\rho (p,q)\) evolves in \(\rho (p,q;t)\) and the latter tends, as \(t\rightarrow \infty \), to a new equilibrium state in the gravity potential \(m g'z\); but \(-\int \rho (p,q;t)\log \rho (p,q;t)d^{3N}pd^{3N}q\) remains equal to \(S_0\). Therefore at the end of the evolution the new distribution \(\rho (p,q,\infty )\) will be an equilibrium state of the system in the modified gravity field.
It will not be, however, any more a canonical Gibbs state at temperature \(\beta ^{-1}\) in a gravity field with acceleration \(g'\); if the system is ergodic on the energy surface then the final distribution reached at infinite time after suddenly increasing the gravity g to a new value \(g'\) will be (integration over \(p',q'\) only)”
where \(\mu ^{mc}_{E}(dpdq)\) is the microcanonical distribution with energy E and \(E'(p',q')= K(p')+V(q')+Mg'H(q')\) is the sum of the kinetic energy, internal potential energy and energy of the center of mass in a gravity acceleration \(g'\).
The distribution Eq. (C.1) will be equivalent to a canonical Gibbs distribution (with temperature different from \(\beta ^{-1}\)) only in the thermodynamic limit: in the finite system that we are considering it will be different by corrections vanishing in the thermodynamic limit. Yet the new state will be a stationary state close to a canonical (or any other equivalent) equilibrium state,
To estimate, actually to define, the temperature \(\beta ^{'-1}\) of the new state imagine to identify the above \(\mu ^\infty \) with a canonical distribution \(\mu _{\beta '}\), i.e. neglect the finite volume corrections. Computing the Gibbs entropy \(S_\infty \) of the new equilibrium (reached after infinite time) and make use of the identity between the Gibbs entropies of the initial and final states:
with \(T=\beta ^{-1}\), \(P=MgH\) and \({\partial }_g S|_\beta \ne 0\) at \(g=0\): thus the new equilibrium cannot have the same entropy as the initial state if the temperature remained the same unless \(\beta '\ne \beta \) (because in general \({\partial }_g S|_\beta \ne 0\), e.g. if \(V\simeq 0\) it is \(\langle P^2 \rangle > \langle P \rangle ^2\)). If the final state has to become a canonical distribution at some temperature (e.g. the above estimated \(\beta ^{'-1}\)) then the system will have to be attached to a thermostat and some heat exchange will take place and the entire transformation will be irreversible: in any event, if the system container was really adiabatic and at any finite (or infinite) time the gravity acceleration was dropped back to the initial value, then the system should in the same time return to the initial canonical state. See also [96] for the analysis of equally interesting cases.
Arnold–Euler Geodesics
The analysis of [47] applies to the geodesic flows: which are Hamiltonian flows with Hamiltonian \(H(\mathbf{p},\mathbf{q})= \frac{1}{2} g(\mathbf{q})^{-1}{\mathbf{p}}{\mathbf{p}}\). Hence the Lyapunov exponents of \(\dot{\mathbf{q}}=g(\mathbf{q}) \mathbf{p}, \dot{\mathbf{p}}=-\frac{1}{2}({\varvec{\partial }}_{\mathbf{q}}g(\mathbf{q})^{-1}){\mathbf{p}}\,{\mathbf{p}}-\nu \mathbf{p}+{\mathbf{f}}\) with \(\mathbf{f}\) independent of \(\mathbf{p},\mathbf{q}\) are paired to \(-\frac{1}{2}\nu \), see footnote\(^{18}\), with a general \(H(\mathbf{p},\mathbf{q})\).
The Euler flow is a geodesic flow [97, 98], and the canonical coordinates are \(\mathbf{u},{\varvec{\delta }}\) where \({\varvec{\delta }}\) is the diffeomorphism bringing the reference state O of the fluid into the actual state A: if a force \(\mathbf{f}\) is added which does not change the Hamiltonian nature of the motion (e.g. if, as in [47], \(\mathbf{f}(\mathbf{q})\) is locally conservative) and if, furthermore, a viscosity force of the form \(-\nu \mathbf{u}\) is also added, then the above shows that pairing takes place (formally) to \(-\frac{\nu }{2}\).
A formal proof that the Euler equations for a fluid can be written as Arnold’s geodesic flow is summarized as follows (correcting also typos in the somewhat obscure argument in the appendix theof [52]). Let \({\varvec{\xi }}\rightarrow {\mathbf{x}}={\varvec{\delta }}({\varvec{\xi }})\) be the diffeomorphism in \(Sdiff(T)\subset diff(T)\)Footnote 52 mapping the reference fluid configuration O into the actual one A. Here and below the differential operators are denoted \({\partial },\ldots \) but are intended to be \({\partial }_{{\varvec{\delta }}({\varvec{\xi }})},\ldots \) when operating on functions of \({\varvec{\delta }}({\varvec{\xi }})\).
A map from O to a configuration \(A'\in diff(T)\)infinitesimally close to one in Sdiff(T) can be parameterized by \({\varvec{\delta }},{\varvec{\zeta }}\) with \({\varvec{\delta }}\in Sdiff(T)\) and \({\varvec{\zeta }}\) an infinitesimal variation of the form \({\varvec{\partial }}z({\varvec{\delta }}({\varvec{\xi }}))\) for some scalar z.
The coordinates \({\varvec{\delta }},{\varvec{\zeta }}\) can be checked to form a system of coordinates “orthogonal and well adapted”, in the sense of definition 12 in [50], to the surface \(J({\varvec{\delta }}({\varvec{\xi }}))=1\) in the space diff(T) of torus diffeomorphisms in the metric \(g({\varvec{\delta }},{\varvec{\zeta }})\) attributing to an infinitesimal variation \((\mathbf{w}+\mathbf{z})\) of \(({\varvec{\delta }},{\varvec{\zeta }})\) the square length:
for the infinitesimal variations \((\mathbf{w},{\varvec{\partial }}z)\) of \(({\varvec{\delta }},{\varvec{\zeta }})\) with \(\mathbf{w}\) a divergence free field and \({\varvec{\partial }}z\) a gradient field. Furthermore if \({\varvec{\xi }}\rightarrow {\varvec{\delta }}({\varvec{\xi }})\) is an incompressible configuration in Sdiff(T) and \({\varvec{\delta }}'({\varvec{\xi }})={\varvec{\delta }}({\varvec{\xi }})+\mathbf{u}({\varvec{\delta }}({\varvec{\xi }}))+{\varvec{\partial }}z({\varvec{\delta }}({\varvec{\xi }}))\) an infinitesimally close one in diff(T) then
depending only on the “violation of the constraint” \(J-1\) in the above orthogonal and well adapted coordinates.
Therefore a general theorem on constrained motions, (for the constraint \(J({\varvec{\delta }}({\varvec{\xi }}))=1\)) can be applied: because the perfection criteria for the constraint are met as a consequence of Eqs. (D.1), (D.2), see Definition 13, Sects. 3.7, and Proposition 13, Sect. 3.8 in [50]. Hence the motions obey Euler-Lagrange equations for the Lagrangian \({\mathcal {L}}({\dot{{\varvec{\delta }}}},{\varvec{\delta }})=\int \frac{1}{2}\dot{{\varvec{\delta }}}({\varvec{\xi }})^2 d{\varvec{\xi }}\) with the ideal holonomic constraint\(J({\varvec{\delta }}({\varvec{\xi }}))\equiv 1\).
In other words the motions driven by the Lagrangian \({\mathcal {L}}_\Lambda ({\dot{{\varvec{\delta }}}},{\varvec{\delta }})=\int d{\varvec{\xi }}\Big (\frac{1}{2}\dot{{\varvec{\delta }}}({\varvec{\xi }})^2 + \Lambda (J({\varvec{\delta }}(\xi ))-1)^2\Big )\), in the space \(diff(T)\supset Sdiff(T)\), are motions which depend on the auxiliary parameter \(\Lambda \) and, if the initial data are an incompressible configuration \({\varvec{\delta }}\in Sdiff(T)\), in the limit as \(\Lambda \rightarrow +\infty \) converge, at any prefixed time, to motions driven by the constrained Lagrangian \({\mathcal {L}}\).
Explicitly, let \({\mathbf{u}}({\mathbf{x}})={\dot{{\varvec{\delta }}}}({\varvec{\xi }})\): since at time \(\varepsilon >0\)\({\varvec{\delta }},{\mathbf{u}}\) become \({\varvec{\delta }}_\varepsilon ({\varvec{\xi }})\) and \({\mathbf{u}}_\varepsilon ({\mathbf{x}})={\varvec{\delta }}_\varepsilon ({\mathbf{x}}+\varepsilon {\mathbf{u}}({\mathbf{x}}))\), it follows that  and the Euler-Lagrange equations for the constrained \({\mathcal {L}}\) become the Euler equations for a perfect incompressible fluid, obtained as a geodesic flow for the Hamiltonian \(H({\mathbf{u}},{\varvec{\delta }})\) defined as
and the Euler-Lagrange equations for the constrained \({\mathcal {L}}\) become the Euler equations for a perfect incompressible fluid, obtained as a geodesic flow for the Hamiltonian \(H({\mathbf{u}},{\varvec{\delta }})\) defined as

with  interpreted as “pressure”.
interpreted as “pressure”.
If a force \(\mathbf{f}({\mathbf{x}})=(-{\partial }_2\Phi ({\mathbf{x}}),{\partial }_1\Phi ({\mathbf{x}}))\), with \(\Phi \) a given scalar independent of the fluid configuration, acts on the fluid then to Eq. (D.3) a term \({\varvec{\delta }}({\varvec{\xi }})\cdot (-{\partial }_2\Phi ({\varvec{\delta }}({\varvec{\xi }})),{\partial }_1\Phi ({\varvec{\delta }}({\varvec{\xi }})))\) has to be added.
Recalling that \({\mathbf{x}}={\varvec{\delta }}({\varvec{\xi }})\), the equations of motion are the pair:

and by the just mentioned result in [47], display a set of Lyapunov exponents, local and global, paired to \(-\nu /2\).
In the Euler–Arnold case the exponents are naturally divided in two classes: the exponents relative to the \(\mathbf{u}\) coordinates, ’fluid exponents’, which do not depend (explicitly) from the evolution of the \({\varvec{\delta }}\) coordinates and the others.
It would be natural to think that the other exponents are simply a copy of the first: if so the fluid exponents, alone, would be paired. However if true this cannot be a general property of geodesic flows to which friction and forcing are added (as it fails in the flow with Hamiltonian \(H=\frac{1}{2} p^2\), i.e. for the equations \(\dot{q}=p, \dot{p}=-\nu p+f\)). I neither succeded in proving the just mentioned double degeneracy of the Lyapunov spectrum for the Arnold–Euler equations nor in convincing myself that it is a reasonable hypothesis.
The results just discussed do not apply to the NS flow because the viscosity is \(\nu \Delta \mathbf{u}\): however a pairing to a line which is not constant but which depends on the scale in which the motion is studied, compatible with the above simulations, was proposed in [52].
Rights and permissions
About this article
Cite this article
Gallavotti, G. Nonequilibrium and Fluctuation Relation. J Stat Phys 180, 172–226 (2020). https://doi.org/10.1007/s10955-019-02376-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-019-02376-3




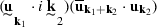 .
.