Entropy of Negative Temperature States for a Point Vortex Gas

Abstract

We study the dynamics and statistical mechanical equilibria of a neutral two-dimensional point vortex gas with Coulomb-like interactions confined in a squared and a rectangular domain. Using a punctuated Hamiltonian model in which we model the process of vortex–antivortex annihilation in superfluids by removing vortex dipoles, we show that this leads to evaporative heating of the system. Consequently, the vortex gas enters the negative temperature regime and subsequently relaxes to a maximum entropy configuration. We demonstrate that the large scale flows that emerge in this regime can be explained by using an equilibrium statistical mechanical mean field theory of point vortices based on a Poisson–Boltzmann equation. In particular, we observe that the emergent large scale flows in our point vortex simulations in the squared domain give rise to a spontaneous acquisition of angular momentum whereas the flows in the rectangular domain prefers a state with zero angular momentum. In addition to the observed qualitative agreement between the dynamical simulations and the theory that we demonstrate for the two geometries, we also present an approach that allows us to accurately compute a coarse-grained vorticity field, and henceforth recover the entropy from our dynamical runs. This allows us to perform a quantitative comparison between the dynamical point vortex simulations and the statistical mechanical predictions of the mean field theory thereby allowing us to clearly assert the validity of the assumptions of the statistical approaches as applied to this system with long-range interactions.

1 Introduction

The point vortex model is an archetypal model for studying many aspects of two-dimensional vortex dynamics in both classical fluids and superfluids. Historically, the study of point vortices to model the motion of a fluid dates back to Helmholtz [1] and Kirchhoff [2]. Subsequent interest in this model was revived by the work of Onsager [3] who attempted to use it as a means to understand certain aspects of two-dimensional hydrodynamic turbulence. Both Kirchoff and Onsager recognised that if point vortices are confined to move within a finite-sized domain, the phase space is also bounded. Onsager went on to show that, if the phase space is bounded, this provides a sufficient condition for the existence of negative temperature states for a system consisting of $N \gg 1$ point vortices in statistical equilibrium. Thereafter, Taylor [4] and Edwards and Taylor [5] were able to find the critical energy of the vortex gas such that above this critical energy the system exhibits negative temperature states. A particularly interesting attribute of the negative temperature regime is that energy considerations imply that it must correspond to the presence of vortex clusters within the system. Such vortex clusters can replicate the motion of large scale coherent vortex structures in classical fluids. In particular, this can be used to explain how an ordered large scale flow can emerge from a coarse-grained description of the flow produced by a large ensemble of vortices.

Joyce and Montgomery [6, 7] subsequently extended the work of Onsager by developing a mean-field theory that can predict the large scale flow patterns which correspond to entropy maxima at fixed energy. Further important developments along this direction were later carried out by Pointin and Lundgren [8,9,10]. The validity of the theory was subsequently tested against direct numerical simulations of classical fluids [11,12,13,14]. However, the use of point vortices to model a continuum vorticity field of a classical fluid was a contentious issue. In fact, Dürr and Pulvirenti, and Marchioro and Pulvirenti [15, 16] showed that any smooth 2D Euler solution of the classical fluid equations could be approximated to any desirable accuracy by the motion of point vortices for a finite time. However, for statistical equilibrium of $N \gg 1$ point vortices, this result is not sufficient. Subsequently, Robert et al. [17,18,19] pointed out that an ideal classical fluid has additional constants of motion, the so-called Casimirs, that correspond to integrals of moments of the vorticity field. These works, therefore, proceeded to derive alternative mean-field theories that are argued to be more relevant for classical fluids. The differences between these approaches has been further discussed and elaborated on in the work of Kiessling and Wang [20], and Chavanis [21]. A comprehensive review of the key developments that have been made in the statistical mechanical description of point vortices can also be found in [22].

Despite these potential shortcomings in using point vortices in modelling classical fluids, in this work we are predominantly interested in using the point vortex description as a simplified model for studying the motion of quantised vortices in superfluids. Indeed, given the rapid experimental advances that have taken place within the field of ultracold atomic condensates in recent years, there has been increasing interest in understanding the role of quantised vortices on the nonequilibrium relaxation and the properties of quantum turbulence in these systems [23,24,25,26,27]. Unlike classical fluids, in these systems, singular distributions of vorticity coinciding with point vortices are not merely mathematical idealisations of the flow, but rather accurately represent the vorticity field of a superfluid. Moreover, the point vortex model turns out to be an excellent description for the motion of superfluid vortices in the case when they are well separated (relative to their healing length) [28, 29].

In view of the above considerations, we will resort to the original theory of Joyce and Montgomery [6, 7], and Pointin and Lundgren [8,9,10], as a suitable mean-field theory for describing a large ensemble of well-separated quantised vortices. A peculiar feature of the Coulomb-like interactions of a point vortex model is that the interaction potential is long-range. This leads to a number of subtle properties when attempting to define the thermodynamic limit of a point vortex gas. A standard thermodynamic limit would correspond to taking the area of the domain $\varDelta \rightarrow \infty$, and the number of vortices and energy $N \rightarrow \infty$, $E \rightarrow \infty$ such that $N/\varDelta$ and $E/\varDelta$ tend to a finite limit [30] while keeping the circulation of each vortex fixed (we note that the circulation is quantized in a superfluid and can not be be allowed to vary in any limiting procedure). This limit was studied in [31, 32]. However, it turns out to result in only the positive temperature states. To recover the negative temperature regime, the limit on energy must be modified so that $E/(N\varDelta )$ must be taken to be finite. Under such conditions the mean-field theory of Joyce and Montgomery can be recovered. This limit was carefully analysed in [33,34,35,36,37] in both the canonical and micro-canonical ensembles. We will refer to this extension of the thermodynamic limit to the negative temperature regime as the hydrodynamic limit. We note that in the negative temperature regime, the point vortex gas can admit negative specific heats. Under such conditions, ensemble equivalence can no longer be assumed. It follows that the micro-canonical ensemble should be used to analyse the statistical equilibrium properties of the point vortex gas with fixed number of vortices N and energy E. Moreover, because of the long-range interactions of the point vortices, the hydrodynamic limit has the peculiar property that the effects of the boundaries do not vanish as in standard thermodynamic limits. This property manifests itself by having solutions of the mean-field theory that turn out to be sensitive to the shape of the confining domain as revealed in [19, 38,39,40,41].

The long-range nature of the Coulomb interactions of point vortices has also raised questions concerning the ergodicity of the point vortex gas, an assumption that has often been argued to be central to the application of any statistical mechanical approach to a given problem [42, 43]. However, the validity of this basic underlying assumption for the point vortex gas was revisited in the recent work of [44]. Their results indicate that, in practice, the system can appear ergodic, a fact that is further reinforced in [40, 45, 46] by the remarkable qualitative agreement observed between the mean-field theory and the distribution of point vortices seen in direct numerical simulations based on a point vortex model and a microscopic model of a superfluid in the form of the Gross–Pitaesvkii equation. It is interesting to note that the flow patterns observed in some of these works also closely resemble similar flow structures observed in classical fluids [47, 48]. Indeed, in recent years, increasing evidence has accumulated which suggests that a large ensemble of point vortices/quantised vortices can replicate certain features of classical 2D turbulence including the direct enstrophy cascade [49] and the inverse energy cascade [50, 51]. Moreover, the signature of vortex clustering in the energy spectrum and its relation to the Kolmogorov spectrum in classical fluids was considered in [52, 53].

These developments motivate a more in-depth analysis of how well direct numerical simulations agree with mean-field predictions that are derived from a statistical mechanical framework. Despite the extensive amount of analytical and computational work that has been performed on the PB equation of point vortices, relatively few attempts have been made in order to directly compare the statistical mechanical predictions with direct numerical simulations. Of the few attempts that have been carried out to date, the majority of these simply integrate the Hamiltonian system of equations for the vortices from a given initial condition. However, we recall that since the system is Hamiltonian, the energy of the point vortex model will also be conserved. Consequently, if the initial conditions correspond to energies below the threshold for negative temperatures to arise, no vortex clustering will emerge. In contrast, in superfluids, quantised vortices can annihilate with antivortices upon close encounters. It was shown in [29], that this mechanism plays an essential role in facilitating the migration of the gas of vortex excitations from the positive to negative temperature regime. To our knowledge, these works are the first examples where the realization of negative temperature states emerges spontaneously through this evaporative heating process induced by vortex–antivortex annihilation. Therefore, the use of a Hamiltonian model of point vortices punctuated by vortex pair removal turns out to be essential to a complete understanding of the evolution of vortices in superfluids. Using this punctuated model, in our previous work [45] we proceeded to present a qualitative comparison with the predictions of the mean field theory. However, a more thorough quantitative analysis demonstrating a more direct link between the two predictions was not possible due to the difficulties in evaluating the entropy from numerical simulations containing of the order of only 100 vortices. Such numbers are at the threshold of what is currently achievable in experiments.

In this paper, we will present a systematic comparison between the two models for two specific domains; a squared domain and a rectangular domain with an aspect ratio of 1.5. In such domains, angular momentum is not conserved as is the case for a circular domain. Therefore, the system is able to explore a broader part of the phase space and can thus display a diversity of solutions of the PB equation. These provide more stringent tests for purposes of comparing the two models. The remainder of the paper is organised as follows. In Sect. 2 we introduce the point vortex model and describe the negative temperature states for a vortex gas. In Sect. 3, working with a micro-canonical ensemble, we apply a maximum entropy principle to re-derive the PB equation. In Sect. 4, we investigate the dynamics of point vortices in the squared and the rectangular domains with aspect ratio $\varLambda =1.5$. This analysis allows us to qualitatively validate the predictions given by the solutions of the PB equation by showing that the late time flows that emerge will have either zero or non-zero angular momentum depending on the geometry of the domain. In Sect. 5 we present several results including, a reconstruction of the smoothed vorticity fields associated with the distribution of vortices in point vortex simulations and how they compare with the mean-field theory; a quantitative analysis of the entropies of the emergent flow configurations observed during the dynamics; and a quantitative analysis on the associated angular momenta of the computed flows. We end with a discussion of the implications of vortex annihilations occurring at the boundaries, a scenario which can occur in a real superfluid.

2 Hamiltonian of Point Vortices and Negative Temperature States

The equations of motion of N point vortices located within some domain at $\mathbf{x}_k=(x_k,y_k)$, $k=1,\dots ,N$ each with circulation $\gamma _k$, are given by

$$\begin{aligned} {\dot{x}}_k=\frac{1}{\gamma _k}\frac{\partial {\mathcal {H}}}{\partial y_k}, \qquad {\dot{y}}_k=-\frac{1}{\gamma _k}\frac{\partial {\mathcal {H}}}{\partial x_k} \, ,\qquad \end{aligned}$$

(1)

where ${\mathcal {H}}$ is the Hamiltonian. This can also be interpreted as a regularised kinetic energy of the fluid which corresponds to neglecting the self-interaction energies of the vortices (i.e. this leads to the condition $j \ne k$ appearing in the double sum of Eq. (9)). In this model, the total energy ${\mathcal {H}}$ and the number of vortices N are conserved during the dynamics.

If ${\mathcal {H}}$ is also invariant with respect to rotations and translations in x and y, there are other constants of motion that are given by

$$\begin{aligned} A= -\sum _{k=1}^N\gamma _k||\mathbf {x}_k||^2, \qquad I_x= \sum _{k=1}^N\gamma _k y_k,\qquad I_y= - \sum _{k=1}^N\gamma _k x_k \, . \end{aligned}$$

(2)

These express the conservation of the angular impulse, A, and the linear impulse, $\mathbf {I}=(I_x,I_y)$, respectively. The conditions under which these additional invariants arise are dependent upon the shape of the domain. For example, the linear momentum is conserved for an unbounded or periodic domain whereas one component of the momentum will be conserved for a channel. On the other hand, the angular momentum will be conserved for an unbounded region and for a circular domain. The above expressions for linear and angular impulse can be derived from the total linear momentum and total angular momentum of a continuum incompressible fluid of constant density such that $\nabla \cdot \mathbf {u}=0$. This reveals that the essential difference between the impulse and momenta is related to boundary terms. Setting $\rho =1$, we have

$$\begin{aligned} L&= \iint _{\mathcal {A}} (x v - y u) \mathrm{d}x\mathrm{d}y = -\iint _{\mathcal {A}} \omega |\mathbf {x}|^2 \mathrm{d}x\mathrm{d}y + \oint |\mathbf {x}|^2 (n_x v-n_y u) \mathrm{d} s \, , \end{aligned}$$

(3)

$$\begin{aligned} \mathbf {P}&= \iint _{\mathcal {A}} \mathbf {u} \mathrm{d}x\mathrm{d}y = \iint _{\mathcal {A}} (y,-x)\omega \mathrm{d}x\mathrm{d}y - \oint _{\partial \mathcal {A}} (y,-x)(n_x v-n_y u) \mathrm{d} s\, . \end{aligned}$$

(4)

Here, $\mathbf {u}=(u,v)$ is the velocity field, $\omega$ is the vorticity field, and $(n_x,n_y)$ is the outward pointing normal to the boundary $\partial {\mathcal {A}}$ of the region of integration ${\mathcal {A}}$. Given that the fluid is assumed to be incompressible, we can introduce the streamfunction of the flow, $\psi$, such that $\mathbf {u}=(\partial _y\psi ,-\partial _x\psi )$. The magnitude of the angular momentum can then also be written as $L=2\int \psi \mathrm{d}x \mathrm{d}y$.

An interesting property of the Hamiltonian system described by Eq. (1) is that the set of coordinates ${x_k,y_k}$ are canonically conjugate variables and hence define the phase space of the system. This continues to be the case for vortices in a bounded domain. It follows that for a domain with area $\varDelta$, the phase space has a finite volume given by $\varDelta ^N$. Working within a micro-canonical ensemble, and following Onsager [3], and Pointin and Lundgren [9], the volume of the phase space $\varPhi$ that corresponds to states with energies less than E is defined as

$$\begin{aligned} \varPhi (E)=\int _{-\infty }^{E}{\mathcal {W}}(E')dE' \, . \end{aligned}$$

(5)

Here, ${\mathcal {W}}(E)=\mathrm{d}\varPhi /\mathrm{d}E$ denotes the density of states with energy E. To define this quantity we identify the microstate of the system by the instantaneous configuration $(\mathbf {x}_1,\mathbf {x}_2,\ldots ,\mathbf {x}_N)$ of the N vortices. To make the connection with a statistical mechanical description of the problem, we let $P_N(\mathbf {x}_1,\mathbf {x}_2,\ldots ,\mathbf {x}_N)$ denote the probability density for the system of vortices such that $P_N \mathrm{d}\mathbf {x}_1 \mathrm{d}\mathbf {x}_2 \cdots \mathrm{d}\mathbf {x}_N$ is the probability that $\mathbf {x}_1$ is in $\mathrm{d}\mathbf {x}_1$, $\mathbf {x}_2$ is in $\mathrm{d}\mathbf {x}_2$ and so forth. Then if we assume that the only conserved quantities associated with the Hamiltonian point vortex dynamics are the point vortex energy and the number of vortices, the probability distribution associated with the N vortex system of the micro-canonical ensemble is given by

$$\begin{aligned} P_N = \frac{\delta (\mathcal {H}(\mathbf {x}_1,\mathbf {x}_2,\ldots ,\mathbf {x}_N) - E)}{\varPhi (E)} \, . \end{aligned}$$

(6)

Therefore, $\varPhi (E)$ plays the role of the normalizing factor. This equation implies that microstates corresponding to the same energy are equally likely. Moreover, since $\int P_N \mathrm{d}\mathbf {x}_1 \mathrm{d}\mathbf {x}_2 \cdots \mathrm{d}\mathbf {x}_N = 1$, we find that

$$\begin{aligned} \varPhi (E) = \int \delta ({\mathcal {H}} - E) \mathrm{d}\mathbf {x}_1 \mathrm{d}\mathbf {x}_2 \cdots \mathrm{d}\mathbf {x}_N \, . \end{aligned}$$

(7)

It follows that $\varPhi (E)$ is positive for all the energies with $\varPhi (-\infty )=0$ and $\varPhi (+\infty )=\varDelta ^N$. Therefore, ${\mathcal {W}}(E)$ must have a maximum at some critical energy $E={\bar{E}}$. On the other hand, the equilibrium temperature T of a system with thermodynamic entropy S and energy E, is given by

$$\begin{aligned} \frac{1}{k_BT}=\left( \frac{\partial S}{\partial E}\right) _{\varDelta }, \qquad S=k_B\log {\mathcal {W}}(E) \, , \end{aligned}$$

(8)

where $k_B$ is Boltzmann’s constant and the subscript denotes that the partial derivative is evaluated at constant volume. From these considerations, it follows that a system which has a value ${\bar{E}}$ such that ${\mathcal {W}}'({\bar{E}})=0$, admits negative temperatures for energies $E>{\bar{E}}$.

Now, for a system of point vortices in an unbounded domain, the Hamiltonian is given by

$$\begin{aligned} {\mathcal {H}}=-\frac{1}{4\pi }\sum _{j=1}^N\sum \limits _{\begin{array}{c} k=1\\ j\ne k \end{array}}^{N} \gamma _j\gamma _k\ln |\mathbf {x}_j-\mathbf {x}_k| \, . \end{aligned}$$

(9)

Then, if we consider a collection of point vortices consisting of two species corresponding to vortices with positive and negative circulation, negative temperatures correspond to clustering of like signed vortices. Due to the long-range nature of the interactions between point vortices, the thermodynamic limit of the vortex gas at negative temperatures retains dependence on the boundaries [19, 38, 40, 41, 54]. The large scale vortex structures that are predicted to form at these negative temperatures will, therefore, be sensitive to the shape of the domain [9, 38, 41]. Similar observations have previously been made for classical fluids [12,13,14, 55] and in the context of magneto-hydrodynamics [56].

In 1976, Joyce and Montgomery derived a mean-field model in the form of a PB equation in order to predict the resulting flow patterns that are expected to emerge at negative temperatures in the context of the guided centre plasma problem. This model was derived under the hypothesis of statistical equilibrium of the point vortex gas. A thorough exposition of the resulting PB equation and its classification within the framework of the microcanonical ensemble is presented in the work of Chavanis [38]. In the next section, we will present the key arguments leading to the derivation of this mean field theory of the point vortex gas.

3 Mean-Field Theory of a Vortex Gas

We will now assume a bounded region, ${\mathcal {A}}$, with area $\varDelta$ containing a total of N point vortices divided into different species denoted by the subscript, a, each containing $N_a$ vortices with circulation $\gamma _a$. Working within a microcanonical ensemble, we will assume that the energy of this system E and the total number of each vortex specie, $N_a$, are fixed. This last constraint is equivalent to fixing the total circulation $N_a\gamma _a$ of each specie. The statistical equilibrium for the vortex gas then can be determined by dividing the area of the domain, $\varDelta$, into a large number of cells with size $h^2\ll \varDelta$ which can contain an arbitrary large number of point vortices. The macrostate is defined once the number of point vortices of each specie, a, with circulation $\gamma _a$ in all the cells, denoted by the set $\left\{ N_{i,a}\right\}$, have been prescribed. Here, the index, i, denotes the cell number. The statistical weight corresponding to the macrostate $\left\{ N_{i,a}\right\}$ is then given by [57]

$$\begin{aligned} {\mathcal {W}}(\left\{ N_{i,a} \right\} )=\prod _a \left\{ \prod _i \frac{N_a!}{N_{i,a}!}\left( \frac{h^2}{\varDelta }\right) ^{N_{i,a}}\right\} ,\qquad N_a=\sum _iN_{i,a} \, . \end{aligned}$$

(10)

We can then introduce the coarse-grained vorticity of each specie $\omega _a(x,y)$ and the total vorticity $\omega$ such that

$$\begin{aligned} \omega _a(x,y)=\gamma _a n_a(x,y) \, ,\qquad n_a(x,y)=\frac{N_{i,a}}{h^2} \, , \qquad \omega =\sum _a\omega _a \, . \end{aligned}$$

(11)

By inserting Eqs. (10) and (11) into Eq. (8) and using Stirling’s approximation, it follows that in the continuum limit $h\rightarrow 0$, the differential entropy S becomes a functional of $\omega _a$ and is given by [21]

$$\begin{aligned} S\left[ \omega _a\right] =- k_B\sum _a \int _{{\mathcal {A}}} \frac{\omega _a}{\gamma _a}\log \left( \frac{\omega _a \varDelta }{\gamma _a N_a}\right) \mathrm{d}x\mathrm{d}y \, . \end{aligned}$$

(12)

For a general domain, ${\mathcal {A}}$, that does not contain any continuous symmetries, we assume that the only conserved quantities are given by the total energy E and the circulation $\varGamma _a$ of each specie of vortices

$$\begin{aligned} E=\frac{1}{2}\int _{{\mathcal {A}}}\psi \omega \mathrm{d}x \mathrm{d}y \, ,\qquad \varGamma _a=\int _{{\mathcal {A}}}\omega _a \mathrm{d}x \mathrm{d}y \, . \end{aligned}$$

(13)

We note that the coarse-grained vorticity and the coarse-grained streamfunction are related by $\nabla ^2\psi _a=-\omega _a$ so that $\psi =\sum _a\psi _a$. Introducing the inverse temperature $\beta$ and the chemical potentials $\mu _a$ of each specie of vortices, the vorticity distribution which maximises the entropy has to satisfy

$$\begin{aligned} \delta S - \beta \delta E-\sum _a\mu _a\delta \varGamma _a =0 \, , \end{aligned}$$

(14)

where the variations are calculated with respect to $\omega _a$. This leads to the Boltzmann distribution for the vorticity fields of each specie which are given by

$$\begin{aligned} \omega _a = \frac{N_a}{\varDelta }\gamma _a A_ae^{-\rho \beta \gamma _a\psi } \, , \end{aligned}$$

(15)

The terms $A_a=\varDelta \left( \int _{{\mathcal {A}}} e^{-\rho \beta \gamma _a\psi }\mathrm{d}x\mathrm{d}y\right) ^{-1}$ provide the necessary normalisation conditions that allow the second of Eq. (13) to be satisfied. Applying Eq. (15), to a neutral vortex gas composed of two species of vortices with circulation $\gamma _\pm =\pm \gamma$, the equation $\nabla ^2\psi =-\omega$ reduces to the Poisson–Boltzmann (PB) [8] equation

$$\begin{aligned} \nabla ^2\varPsi +\frac{\lambda ^2}{2}\left[ \frac{e^{\varPsi }}{\alpha _+} - \frac{e^{-\varPsi }}{\alpha _-}\right] =0,\qquad \varPsi =0\quad on \quad \partial {\mathcal {A}} \, , \end{aligned}$$

(16)

where $\partial {\mathcal {A}}$ is the boundary of the domain, $\varPsi =\rho \beta \gamma \psi$ is the non-dimensional streamfunction, $\lambda ^2=-N\gamma ^2\rho \beta /\varDelta$, and $\alpha _{\pm }=\varDelta ^{-1} (\int e^{\pm \varPsi } \mathrm{d}x \mathrm{d}y)$. If $\alpha _+=\alpha _-$ the PB equation reduces to the Sinh–Poisson equation with the trivial boundary condition $\varPsi =0$. This equation was considered in some previous works (e.g. [6]). However, the condition $\alpha _+=\alpha _-$ will not be true in general. We note that the PB and Sinh–Poisson equations can have non-trivial solutions only when the system is in the negative temperature regime so that $\lambda ^2$ is positive.

Using Eq. (15), we can also express the entropy, S, and the energy, E, as

$$\begin{aligned} {\hat{S}}=-\frac{1}{2}\log \left( A_+A_-\right) + 8\lambda ^2{\hat{E}} \varDelta \, , \qquad {\hat{E}}=-\frac{1}{8\lambda ^4\varDelta ^2}\int _{{\mathcal {A}}} \varPsi \nabla ^2\varPsi \mathrm{d}x \mathrm{d}y \, . \end{aligned}$$

(17)

Here, we introduced the non-dimensional entropy per vortex, ${\hat{S}}=S/Nk_B$, in units of the Boltzmann constant, and the non-dimensional energy ${\hat{E}}=E/4N^2\gamma ^2\rho$ [38, 39] which will be used to classify the solutions $\varPsi$ of the PB equation.

Linearising Eq. (16) about the trivial solution $\varPsi = 0$ [38, 39] reveals the importance of two particular solutions of the full PB equation: the first corresponds to a monopole flow field whilst the second corresponds to a dipolar flow field. Moreover, such an analysis reveals that there is a qualitative change in the maximum entropy solution of the PB equation as the aspect ratio approaches $\varLambda \approx 1.122$ resulting in a geometry induced transition between the two flows [8, 38, 39]. We will, therefore, be interested in solutions of the PB equation for two particular geometries: a square with sides $L_x=L_y=2$ and a rectangle with aspect ratio $\varLambda =L_x/L_y=1.5$ with sides $L_x=2\sqrt{\varLambda }$ and $L_y=2/\sqrt{\varLambda }$.

Fig. 1

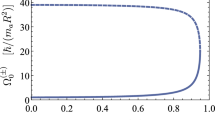
Normalised entropy as a function of energy of mean flows predicted by the Poisson–Boltzmann equation for a square domain (dipole, diagonal dipole and monopole solutions) and for the rectangular domain (dipole and monopole solutions). The values of the parameter ${\tilde{\lambda }}^2$ used are indicated at the beginning and at the end of each branch and each marker corresponds to an increment of ${\tilde{\lambda }}^2=0.5$. The inset shows the streamfunction contours of mean flows (positive and negative contours correspond to red and blue lines, respectively) (Color figure online)

This choice ensures that the areas $\varDelta$, and therefore the phase spaces of the two domains are equal. We have solved the PB equation numerically by adapting the algorithm described in [58] for the Sinh–Poisson equation. In order to enhance the numerical stability of the iterative algorithm, the above form of the PB equation was rewritten in the form

$$\begin{aligned} \nabla ^2\varPsi +{\tilde{\lambda }}^2\left[ \sqrt{\frac{\alpha _{-}}{\alpha _+}} \frac{e^{\varPsi }}{2} - \sqrt{\frac{\alpha _{+}}{\alpha _{-}}} \frac{e^{-\varPsi }}{2}\right] =0,\qquad {\tilde{\lambda }}^2=\frac{\lambda ^2}{\sqrt{\alpha _+ \alpha _{-}}} \, . \end{aligned}$$

(18)

We note that the algorithm presented in [58] which was later used in [8], and further extended in [59], converges to non-trivial solutions of the PB equation which, by definition, are local extrema of the entropy.

This form of the PB equation was solved for different values of the parameter ${\tilde{\lambda }}^2$ by using solutions of the linearised form of the equations as initial guesses. The solutions for $\varPsi$ have been classified in terms of their energy ${\hat{E}}$ and the entropy per unit energy ${\hat{S}}/{\hat{E}}$ (see Eqs. (17)). The results are presented in Fig. 1 which shows the energy-entropy analysis for the dipole (solid blue line), diagonal dipole (solid red line) and monopole (solid green line) in the squared domain; and for the monopole (dashed green line) and dipole (dashed blue line) in the rectangular domain.

The inset figures show the corresponding streamline patterns of the flows obtained in the two geometries. Although all the solutions presented are local extrema of the entropy, the state with the maximum entropy for the square appears to be the monopole whereas in the rectangle the maximum appears to correspond to the dipolar flow. These predictions turn out to be in full agreement with the findings in [9, 38] for the linearised PB equation. We note that the branch representing the diagonal dipole solution is missing for the rectangular domain. In fact, by symmetry, the dipoles in the square can be arranged either horizontally or vertically. Within a linear approximation of the PB equation, a superposition of these two equally probable configurations gives rise to a diagonal dipole configuration. However, for a rectangle, this argument no longer holds. In fact, we could not find any diagonal dipole solutions for the particular values of the aspect ratio $\varLambda =1.5$ we have considered although they can be found for smaller values of the aspect ratio.

Any solution $\varPsi$ corresponds to a flow with an angular momentum with magnitude $L=2\int \varPsi \mathrm{d}x \mathrm{d}y$ [39] which, in the case of the dipole or diagonal dipole, is identically zero by symmetry. However, L turns out to be finite for the monopole. We, therefore, conclude that the statistical equilibrium of a neutral system composed of point vortices in a square, is associated with a flow with non-zero angular momentum. In contrast, when the vortices are contained in a rectangular domain with aspect ratio $\varLambda >\varLambda _C= 1.122$ [9, 38] the configuration associated with the highest entropy turns out to correspond to a flow with zero angular momentum.

4 Point Vortex Model in the Square and the Rectangle

In order to derive the Hamiltonian ${\mathcal {H}}$, following Campbell et al. [32], we assume that the N vortices are contained in a rectangular box with sides $L_x$ and $L_y$ which is a 1 / 4 of a periodic cell. The remaining 3 / 4 of the cell contains 3N images which allows us to satisfy the condition of no flow normal to the solid boundary $\partial {\mathcal {A}}$. The Hamiltonian of the system is then given by

$$\begin{aligned} {\mathcal {H}}=\frac{\rho }{4\pi } \sum _{i=1}^N\gamma _i^2 b(\mathbf {x}_i;\varLambda ) + \frac{\rho }{4\pi } \sum _{i=1}^{N-1}\sum _{j=i+1}^{N}\gamma _i\gamma _j h(\mathbf {x}_i,\mathbf {x}_j;\varLambda ) \, . \end{aligned}$$

(19)

$h(\mathbf {x}_i,\mathbf {x}_j;\varLambda )$ represents the interaction between two vortices as well as the interaction between a vortex and the images of another vortex so that

$$\begin{aligned} h (\mathbf{x}_i,\mathbf{x}_j;\varLambda )&=f(|x_i-x_j|,|y_i-y_j|;\varLambda ) +f(L_x-x_i-x_j,L_y-y_i-y_j;\varLambda )\nonumber \\&\quad -\, f(L_x-x_i-x_j,|y_i-y_j|;\varLambda ) -f(|x_i-x_j|,L_y-y_i-y_j;\varLambda ) \, , \end{aligned}$$

(20)

while $b(\mathbf {x}_i;\varLambda )$ represents the interaction between a single vortex and its own images

$$\begin{aligned} b (\mathbf{x}_i;\varLambda )&= \frac{1}{2}f(2L_x-2x_i,2L_y-2y_i;\varLambda )\nonumber \\&\quad -\frac{1}{2}f(2L_x-2x_i,0;\varLambda ) - \frac{1}{2}f(0,2L_y-2y_i;\varLambda ) \, . \end{aligned}$$

(21)

In the expression given above, the function $f(x,y;\varLambda )$ is described by [60]

$$\begin{aligned} f(x,y;\varLambda )=\left\{ \frac{2\pi }{\varLambda }\left[ \frac{y}{L_y}\left( \frac{y}{L_y} -1\right) + \frac{1}{6}\right] - \log \prod _{k =-\infty }^{+\infty }\zeta \left( \frac{x}{L_x},\frac{y}{L_y};k,\varLambda \right) \right\} \, , \end{aligned}$$

(22)

and

$$\begin{aligned} \zeta (x,y;k,\varLambda )=1-2\cos \left( 2\pi x\right) e^{-\frac{2\pi |y+k|}{\varLambda }} + e^{-\frac{4\pi |y+k|}{\varLambda }} \, . \end{aligned}$$

(23)

For a system of point vortices, the vorticity field is given by $\omega (\mathbf {x})=\sum _i\gamma _i\delta (\mathbf {x}-\mathbf {x}_i)$, where $\mathbf {x}=(x,y)$. By referring to Eq. (13), the corresponding streamfunction $\psi (\mathbf {x})$ of the flow can then be recovered from the Hamiltonian ${\mathcal {H}}$ to obtain

$$\begin{aligned} \psi (\mathbf {x})=\frac{\rho }{2\pi } \sum _{i=1}^{N}\gamma _i h(\mathbf {x},\mathbf {x}_i;\varLambda ) \, . \end{aligned}$$

(24)

The dynamics of N point vortices described by Eqs. (1), (19)–(23) is constrained to a hypersurface $\left\{ E={\mathcal {H}}\right\}$ in phase space where the energy E is a given constant. Since the thermodynamic definition of temperature is in terms of the change of entropy with respect to energy as given by Eq. (8), the temperature of the equilibrium vortex gas is dependent on the initial energy of the system. Therefore, unless the vortex gas is initialised at sufficiently high energy (i.e. where clustering is specified in the initial condition), no negative temperature and emergence of large scale flows is realised. However, vortex–antivortex annihilation in a superfluid is an important physical mechanism that changes the energy of the vortex gas as well as the number of vortices. Building on the work of Campbell [32], Simula et al. [29] and subsequently Salman and Maestrini [45] demonstrated that this process can drive a vortex gas with initial energies coinciding with the positive temperature regime into negative temperatures. The reason is that, although the energy of the system can decrease as vortices annihilate, the energy per vortex remaining in the system increases which can result in the spontaneous emergence of large scale coherent flows. Given these observations, we have modelled the process of vortex–antivortex annihilation by removing a vortex–antivortex dipole whenever their separation fell below a critical threshold set by the annihilation parameter $\delta$. For superfluids, the length scale set by this parameter is related to the healing length associated with the vortex cores. Therefore, our numerical solution procedure involved forward integrating the equations of motion of our model given by Eqs. (1), (19)–(23) using the built-in ODE45 MATLAB function [61] based on an adaptive 4th-5th order Runge-Kutta scheme with a maximum time step of $\varDelta \tau =0.005$. At each time step, any pair of vortices with opposite circulation whose mutual distance fell below the annihilation parameter $\delta =0.01$ was removed from the subsequent dynamics.

To establish the most probable vortex equilibrium configuration as a function of energy, we also numerically computed the statistical weight ${\mathcal {W}}({\mathcal {H}})$ by evaluating the energy of a large number of random neutral configurations of N vortices and constructing the related histograms. The interaction energy per vortex ${\mathcal {H}}/N$ of the system is evaluated by using Eq. (19). The probability distributions are then evaluated from the histograms $\{W_i\}$ by using a normalised Gaussian kernel [62] such that

$$\begin{aligned} {\mathcal {W}}(x)=\frac{1}{M}\sum _{i=1}^{N_b}\frac{W_i}{\sqrt{2\pi }\sigma }\exp (-(x-{\mathcal {H}}_i)^2/2\sigma ^2) \, , \end{aligned}$$

(25)

where $\sigma$ is the kernel width, $N_b=50$ is the total number of bins that we used, and $W_i$ is the number of realizations with energy lying within the interval $[{E},{E}+\varDelta {E}]$. The value of $\sigma =0.01$ was chosen to provide a kernel width that is sufficiently large with respect to the spacing of the histogram but sufficiently small in relation to the characteristic length scale of the distribution. Within such intermediate scales, we found that the results obtained are essentially independent of the specific value of $\sigma$ used while allowing us to recover a continuous and differentiable representation of the discrete distribution that was initially represented by the histogram $\{W_i\}$. For each value of N, a total of $M=100,000$ samples was used to construct the histograms. In order to accurately replicate the finite size effects of real superfluid vortices, a constraint was imposed when generating the samples to avoid vortices from lying too close to one another or to the boundaries. A minimum intervortex separation of $\delta _V=0.08$ and a minimum vortex-boundary separation of $\delta _B=0.12$ was therefore used.

Fig. 2

Statistical weight for vortices in a squared and b rectangular domains as a function of energy per vortex computed with different numbers of vortices as indicated in the legend. The minimum intervortex separation $\delta _V=0.08$ and the minimum vortex-boundary separation $\delta _B=0.12$ were imposed on the vortex distributions. The vertical dashed lines correspond to the energy of the initial vortex configurations used for the numerical simulations that contained $N^+=N^-=60$ vortices as shown in the insets on the top right of each plot

Fig. 3

Instantaneous vortex configurations of vortices (red circles) and antivortices (blue circles) taken at different times in the square and in the rectangle that depict the characteristic clustering observed in the simulations. The time $\tau$ is in units of $t_v=\varDelta /|\gamma |$ (Color figure online)

The results are shown in Fig. 2 for systems composed of different numbers of vortices $N=10, 20, 40, 80$ and 160. Since the energy and the entropy are related through Eq. (8), this allows us to identify the range of energies for which negative temperature states will arise for our squared and rectangular domains. Figure 2a, b show the statistical weights in the square and the rectangle respectively. In comparison to the unconstrained case where the graphs converge as N is continually increased [32], here the graphs begin to deviate for very large values of N since the constraints $\delta _V$ and $\delta _B$ introduce a packing factor. However, the qualitative features of the distributions persist. In particular, the probability distributions presented in Fig. 2 contain a maximum turning point with a positive slope at lower interaction energies and a negative slope at higher interaction energies which correspond to positive and negative temperatures, respectively.

5 Results

5.1 Emergent Flow Structures in Numerical Simulations

The vertical dotted lines in the graphs presented in Fig. 2 represent the energy of the initial configurations we used for the dynamical runs in the square and the rectangle. These consisted of $N^+=60$ and $N^-=60$ vortices with circulation $\gamma _{\pm }=\pm 1$ which are shown in the insets of the figures. The two initial conditions we chose both lie within the positive temperature range. Figure 3 presents the instantaneous vortex configuration in the squared and the rectangular domains at different stages in the dynamics. In the square, we have found that, throughout the dynamics, the system explores the diagonal dipole (Fig. 3a), the dipole (Fig. 3b) and the monopole (Fig. 3c) configurations. On the other hand, for the rectangle, the system has been found in the monopole (Fig. 3d) and the dipole (Fig. 3e) configurations. We note that these states in the square and in the rectangle emerge at later times in the numerical simulations once the process of vortex annihilation has had time to act to drive the system deep into the negative temperature regime. Considering the relatively small number of vortices that remain in our simulations at late times, the patterns we observe are in good agreement with the type of flows predicted by the PB equation. Moreover, we find that the very long-time dynamics give rise to configurations which are global entropy maxima predicted by the theory. A striking feature of our results is that the statistical mechanical predictions lead to accurate predictions even though the number of vortices in our simulations is relatively small.

An improved understanding of the dynamics of point vortices in both geometries is given by analysing the time variation of the angular momentum L since this measure clearly distinguishes a symmetric configuration such as a dipole from a monopole. Figure 4a, b show the variation of the angular momentum in the square and in the rectangle as a function of time. In Fig. 4a, we observe extended intervals where L deviates from zero which is a clear signature of the spontaneous emergence of the monopole configuration in the square. An interesting observation is the sudden flipping of the sign of L which can be attributed to a sudden flipping to the monopole configuration from one where vortices are located in the central cluster to one where antivortices occupy the central region of the domain. In contrast, in Fig. 4b, we observe a tendency for L to persistently oscillate about zero throughout the duration of the dynamical run. This is a clear signature that the system spends much more time in a symmetric configuration which coincides with a dipole. We note that the flipping of the angular momentum we observed in our numerical simulations for the square is also consistent with the analysis of the mean-field predictions previously discussed in [38, 63].

Fig. 4

Time variation of the normalised angular momenta (see Eq. (35)) in the square (a) and in the rectangular geometry (b). The time $\tau$ is in units of $t_v$. The red lines in a are the values of the maximum angular momentum $L_{\text {max}} = {\mathcal {I}} \varOmega$ accessible to the system which correspond to solid body rotation and provide bounds on the values that are expected for the monopole configuration (Color figure online)

5.2 Smoothing the Vorticity Field with a Heat Kernel

From our simulations of the dynamics of point vortices, we have identified time intervals throughout which the point vortices can be found in configurations that are consistent with the predictions of the mean-field theory. Yet this provides only a qualitative comparison between the theory and numerical simulations. In this section, we will seek to provide a more quantitative comparison. This is essential since thus far we have implicitly assumed that our simulations give rise to flow structures that coincide with the same energy interval used to find solutions of the PB equation. Only if this is indeed true can we make the claim that the maximum entropy solutions predicted by the theory are consistent with our numerical observations.

To proceed we will invoke the assumption of ergodicity in order to use a time sequence of vortex positions within the respective time intervals in order to construct a large ensemble of vortex positions. This could then be used to reconstruct a coarse-grained vorticity field though an appropriate smoothing procedure that thereafter will allow us to perform a direct comparison between the simulations and the theory. For each of the respective time intervals, we have generated an ensemble made up of a superposition of all vortex positions corresponding to the diagonal dipole (Fig. 5a), the dipole (Fig. 5b) and the monopole (Fig. 5c) in the square, and for the monopole (Fig. 6a) and the dipole (Fig. 6b) in the rectangle. Each ensemble contains about $N\sim 8000$ point vortices. To smooth out the vorticity field associated with this superposition of vortices, we will use a heat kernel for our respective square and rectangular domains subject to the boundary condition that the vorticity vanishes at the boundaries. Separating positive and negative vortices, we therefore seek solutions of the problem defined by

$$\begin{aligned}&\frac{\partial \omega ^{\pm }}{\partial \tau }=\nu \nabla ^2\omega ^{\pm } \, , \end{aligned}$$

(26)

$$\begin{aligned}&\omega ^{\pm }(\mathbf {x};\tau =0)=\sum _{i=1}^{N^{\pm }}\gamma _i\delta (\mathbf {x}-\mathbf {x}_i) \, , \end{aligned}$$

(27)

$$\begin{aligned}&\omega ^{\pm }=0 \quad \text {on } \partial {\mathcal {A}} \, , \end{aligned}$$

(28)

where $\nu$ sets the extent of the heat kernel. The positive and negative vorticity fields which satisfy Eq. (26) and the boundary condition given by Eq. (28) are given by

$$\begin{aligned} \omega ^{\pm }(x,y;\tau )=\sum _{n,m=1}^{+\infty }C^{\pm }_{n,m}e^{-\nu \tau (n^2\pi ^2 /L_x^2+m^2\pi ^2 /L_y^2)}\sin \left( \frac{n\pi x}{L_x}\right) \sin \left( \frac{m\pi y}{L_y}\right) \, . \end{aligned}$$

(29)

It is important to notice that in Eq. (16), the terms $\alpha _+$ and $\alpha _-$ are equal in the case of the dipole and the diagonal dipole solutions, but they are not equal in the case of the monopole. As a consequence, along the boundaries where the streamfunction is zero, the value of the vorticity is zero for the dipole and diagonal dipole but it is given by $(\lambda ^2/2)(1/\alpha _+ - 1/\alpha _-)$ in the case of the monopole. Therefore, in the case of the monopole, the expression given by Eq. (29) will approximate everywhere the vorticity distribution over the domain, ${\mathcal {A}}$, but not along the boundaries. There, the solutions given by Eq. (29) converge to the correct vorticity fields but in a weak sense.

We can see that the smoothed vorticity fields $\omega ^{\pm }$ will depend on the combination, $\nu \tau$. We will, therefore, introduce the single parameter $\sigma =\sqrt{2\nu \tau }$ that needs to be specified to smooth the vorticity field associated with each ensemble. The corresponding streamfunctions can then be determined from $\nabla ^2\psi ^{\pm }=-\omega ^{\pm }$, and hence, they are given by

$$\begin{aligned} \psi ^{\pm }(x,y;t)=\sum _{n,m=1}^{+\infty } a^{\pm }_{n,m}\sin \left( \frac{n\pi x}{L_x}\right) \sin \left( \frac{m\pi y}{L_y}\right) \, , \end{aligned}$$

(30)

with the coefficients

$$\begin{aligned} a^{\pm }_{n,m}=\frac{C^{\pm }_{n,m}e^{-\nu \tau (n^2\pi ^2 /L_x^2+m^2\pi ^2 /L_y^2)}}{\left( \frac{n^2\pi ^2}{L_x^2} + \frac{m^2\pi ^2}{L_y^2} \right) } \, . \end{aligned}$$

(31)

Fig. 5

Ensembles for the dipole (a), diagonal dipole (b) and monopole (c) in the square: the number of vortices in each ensemble is $N=8580$, $N=8360$ and $N=8502$ respectively. The red and the blue points represent vortices and antivortices, respectively (Color figure online)

Fig. 6

Ensembles for the monopole (a) and the dipole (b) in the rectangle: the number of vortices in each ensemble are $N=8022$ and $N=8086$ respectively. The red and the blue points represent vortices and antivortices, respectively (Color figure online)

The coefficients $C^{\pm }_{n,m}$ in Eqs. (29) and (31) are determined from the initial condition given by Eq. (27) which requires knowledge of a representation of Dirac’s delta function in a rectangular domain. The vortex distribution at $\tau =0$ in a bounded rectangular domain can be imposed by using a periodic representation of Dirac’s delta function, the so called Dirac comb [64] given by

$$\begin{aligned} \sum _{m_1=-\infty }^{+\infty }\delta (x- x_0 -2m_1L_x) = \frac{1}{2L_x}+\frac{1}{L_x}\sum _{n=1}^{+\infty }\cos \left( \frac{n\pi (x-x_0)}{L_x}\right) \, , \end{aligned}$$

(32)

where $2L_x$ is the period along the x-direction. It is straightforward to extend this representation to two dimensions. Extension to the case of vortices in a domain with no flow through the boundaries can then be achieved by considering this to be a 1 / 4 of a cell of a periodic region with sides $2L_x$ and $2L_y$ in direct analogy with the procedure introduced in Sect. 4 to represent the Hamiltonian of the point vortex model. For simplicity, we will initially consider the case of a single vortex contained in a rectangular box with sides $L_x$ and $L_y$ and then, by using the principle of superposition, the result will be extended to an arbitrary number of point vortices in the domain. Let $\gamma _0$ be the circulation of the vortex located at $(x_0,y_0)$. The initial vorticity distribution in the extended domain $[0,2L_x]\times [0,2L_y]$, denoted by ${\tilde{\omega }}$, is therefore given by

$$\begin{aligned} {\tilde{\omega }}(x,y;t=0)&= \gamma _0 \sum _{\begin{array}{c} m_1=-\infty \\ m_2=-\infty \end{array}}^{+\infty }\delta (x-x_0+2m_1 L_x)\delta (y-y_0+2m_2 L_y) \nonumber \\&\quad + \gamma _0 \sum _{\begin{array}{c} m_1=-\infty \\ m_2=-\infty \end{array}}^{+\infty } \delta (x-(2L_x-x_0)+2m_1 L_x)\delta (y - (2L_y-y_0)+2m_2 L_y) \nonumber \\&\quad - \gamma _0 \sum _{\begin{array}{c} m_1=-\infty \\ m_2=-\infty \end{array}}^{+\infty } \delta (x-(2L_x-x_0)+2m_1 L_x)\delta (y-y_0+2m_2 L_y) \nonumber \\&\quad - \gamma _0 \sum _{\begin{array}{c} m_1=-\infty \\ m_2=-\infty \end{array}}^{+\infty } \delta (x-x_0+2m_1 L_x)\delta (y- (2L_y-y_0)+2m_2 L_y) \, , \end{aligned}$$

(33)

where the first term refers to the vortex in the quarter cell, and the other three terms refer to its three images in the containing periodic cell. It is evident that the above formula is equivalent to Eq. (20) when the Hamiltonian of a distribution of point vortices in the rectangle was considered. The coefficients $C^{\pm }_{n,m}$ can now be determined by projecting Eq. (29) onto Eq. (33) and using Eq. (32) to express the respective delta functions. Details of the derivation can be found in the Appendix and lead to the expression

$$\begin{aligned} C^{\pm }_{n,m}=\frac{4}{L_xL_y}\sum _{i=1}^{N^{\pm }}\gamma _i\sin \left( \frac{n\pi x_i}{L_x}\right) \sin \left( \frac{m\pi y_i}{L_y}\right) . \end{aligned}$$

(34)

For very large values of $\sigma$, the smoothed out positive and negative vorticity fields generated by Eq. (29) for the configurations presented in Figs. 5 and 6 will overlap and cancel resulting in an essentially zero vorticity field within the domain. On the other hand, for very small values of $\sigma$, the vorticity fields will resemble more closely the distribution of point vortices. Since the entropy of the system is strongly sensitive to how well the vorticity fields of the two species are mixed together, we will seek to identify a suitable range of values of the parameter $\sigma$ such that the entropy evaluated by using Eq. (12) is independent of the values of $\sigma$. This will occur if we have a sufficiently large number of vortices leading to a clear separation between length scales associated with the large scale flows and the typical intervortex separation within the ensembles we constructed for Fig. 5 and 6. In order to find a suitable value for the parameter $\sigma$, ensembles with different number of vortices have been generated and their entropy per vortex S / N has been evaluated by using Eq. (12).

The results for the dipole in the square are presented in Fig. 7a, b. This shows that, as the number of vortices in each ensemble increases, the curves tend to converge to a constant value within an intermediate range of scales. The optimal range of values for $\sigma$ has been evaluated by seeking the smallest slope of |S / N| within this intermediate range of values for $\sigma$.

Fig. 7

a The value of the entropy per number of vortices |S / N| as a function of the parameter $\sigma$ for the dipole configuration in the square generated from different ensembles (each with different amount of vortices indicated in the legend) presented on a $\log$-$\log$ scale; b a magnification of a in the range of the values of the parameter $0.035\le \sigma \le 0.07$ for which the entropy remains almost constant. c and d show the same analysis but for the monopole in the square

In the case of the dipole in the squared domain, the minimum value of the slope of |S / N| for $N=8580$ corresponds to the values of $\sigma$ in the interval $0.035\le \sigma \le 0.07$. The same analysis has been performed for the diagonal dipole and the monopole in the square and for these two configurations the intervals of the parameter $\sigma$ are given by $0.035\le \sigma \le 0.07$ and $0.045\le \sigma \le 0.095$, respectively. These intervals have been found by considering the ensembles with $N=8360$ for the diagonal dipole and $N=8502$ for the monopole. For the rectangle, the number of vortices contained in the ensemble and the range of $\sigma$ for the monopole and the dipole are given by $N=8022$ and $0.035\le \sigma \le 0.105$, and $N=8086$ and $0.04\le \sigma \le 0.085$, respectively. With these range of values of the parameter $\sigma$, we are able to generate the desired smoothed vorticity fields and the streamfunction of all the flow configurations presented in Figs. 5 and 6. We note that since all the ensembles contain a different number of vortices, we have ensured that the total circulation of each vortex type is held fixed by renormalising the vorticity fields of each ensemble to the initial number of vortices and antivortices considered for the dynamical runs, corresponding to $\int \omega ^{\pm } \mathrm{d}x \mathrm{d}y=\pm 60$.

5.3 Smoothed Vorticity Fields

To establish to what extent our procedure for constructing smoothed vorticity fields from the point vortex distribution agrees with the predictions of the PB equation, in this section we will compare the two sets of vorticity fields. We begin by analysing scatter plots of $\omega (\psi )$ as in [11] which are constructed from our smoothed fields and we compare these against the mean-field predictions. These are presented in Fig. 8 for both the monopole flow in the square and the dipolar flow in the rectangle. The fluctuations observed in the field are indicative of the unsteady features in the flow that lead to deviations from the exact Poisson–Boltzmann results that are presented as red lines in the figure. We observe that the largest fluctuations occur for positive values of the streamfunction in the square. These can be attributed to the difficulty in resolving the small eddies in the corners of the square with relatively few vortices. Nevertheless, overall the fluctuations in both cases are reasonably small relative to the characteristic variation of $\omega$ over the range of values of $\psi$ considered. These results illustrate that, even for the relatively small number of vortices used in the simulations, the results approach the predictions of the mean-field vortex theory.

Fig. 8

Scatter plots of $\omega (\psi )$ against $\psi$ that are computed from the smoothed vorticity and streamfunction fields of the point vortex numerical simulations (PV) and the solution of the Poisson–Boltzmann equation (PB) for a monopole flow in square domain; b for dipole flow in rectangular domain. The solutions presented for the Poisson–Boltzmann equation correspond to a${\tilde{\lambda }}^2=9$ for the square; b${\tilde{\lambda }}^2=8$ for the rectangle

Given the similar features that are observed for flows in the squared and rectangular domains, we will now focus attention on a more detailed comparison for the flow in the square. The vorticity profiles evaluated by using Eq. (29) are presented in Figs. 9 and 10 for the dipolar and monopole flows in the square, respectively. These can be compared with the theoretical vorticity fields obtained from the term proportional to $\lambda ^2$ of Eq. (16). For the comparisons, the fields obtained from the PV dynamics have been normalised to coincide with the normalization of the fields recovered from the solutions of the PB equation. We have also plotted the vorticity profiles along $\omega (X,Y=0.5)$, $\omega (X,Y=1)$, $\omega (X=0.5,Y)$, and $\omega (X=1,Y)$. The profiles presented reproduce the main trends seen in solutions of the PB equation. However, significant deviations are evident which is consistent with the large fluctuations we expect to find from our PV dynamics since our initial condition contained only 120 vortices which subsequently decreases throughout the simulations. It is also clear from Fig. 9 that for the dipole, both the smoothed vorticity fields of the PV simulations and the fields obtained from the PB equation, vanish at the boundaries as expected. On the other hand, since we have used a sine basis expansion in Eq. (29), we observe in Fig. 10 that the smoothed field for the monopole is also zero even though it is finite for the field recovered from the solution of the PB equation. As pointed out earlier, the sine basis can in principle still be used to represent a field that is non-vanishing at the boundary, but the convergence is weak and is, therefore, to be interpreted in terms of a distribution. Despite this anomalous behaviour observed at the boundaries, the key features within the bulk are in good agreement.

Fig. 9

Comparison of the smoothed vorticity field recovered from the point vortex dynamics and mean field prediction of the Poisson-Boltzmann (PB) equation for the dipole in the squared domain. The solutions presented for the PB equation correspond to ${\tilde{\lambda }}^2=10.5$. Contour plots of the vorticity fields are shown in a and d. The dashed lines represent the directions along which the vorticity profiles are evaluated; b, c, e and f present the theoretical vorticity profiles (red lines) obtained from the solution of the PB equation and the profiles obtained from the simulations (blue lines) (Color figure online)

Fig. 10

Comparison of the smoothed vorticity field recovered from the point vortex dynamics (PV) and mean field prediction of the Poisson-Boltzmann (PB) equation for the monopole in the squared domain. The solutions presented for the PB equation correspond to ${\tilde{\lambda }}^2=9$. Contour plots of the vorticity fields are shown in a and d. The dashed lines represent the directions along which the vorticity profiles are evaluated; b, c, e and f present the theoretical vorticity profiles (red lines) and the profiles obtained from the simulations (blue lines) (Color figure online)

5.4 Quantitative Analysis of Entropy

Having verified the agreement between the vorticity fields obtained from the PV simulations and the PB equation, we will now attempt to determine the entropy and energy of the states corresponding to the point vortex distributions presented in Figs. 5 and 6. This will allow us to assert whether the vortex distributions seen in the simulations coincide with an energy interval that corresponds to the solutions of the PB equation as presented in Fig. 1. This would then allow us to establish whether a direct comparison can be performed between the solutions of our numerical simulations and the predictions of the PB equation.

The evaluation of the non-dimensional entropy ${\hat{S}}$ requires knowledge of the inverse temperature $\beta$. To computationally evaluate the value of $\beta$ for a given ensemble, we start by evaluating the energy of the ensemble ${\hat{E}}_\sigma =(8N^2)^{-1}\int \psi _{\sigma }\omega _{\sigma } \mathrm{d}x \mathrm{d}y$ for all the values of the parameter $\sigma$ previously found. We then identify the energy of the ensemble with the expectation of the energy, $\langle {\hat{E}}\rangle$, that is evaluated with respect to $\sigma$. By assuming statistical equilibrium, the corresponding value of the inverse temperature $\beta$ can then be recovered from the parameter ${\tilde{\lambda }}^2$ using Fig. 1. Using this procedure, we obtained the values ${\tilde{\lambda }}^2=10.5$ for the dipolar flow, and ${\tilde{\lambda }}^2= (9+8.5)/2$ for both the diagonal dipole and the monopole in the squared domain. On the other hand, for the rectangle, we found ${\tilde{\lambda }}^2=11$ for the monopole and ${\tilde{\lambda }}^2= 8$ for the dipole. Consequently, this allowed us to recover the non-dimensional streamfunction $\varPsi _{\sigma }$, and hence the non-dimensional entropy ${\hat{S}}_{\sigma }$ for all values of the parameter $\sigma$. The entropy of an ensemble is then evaluated as the expectation, $\langle {\hat{S}}_{\sigma }\rangle$, that is computed with respect to the range of $\sigma$ determined previously.

Fig. 11

a Energy-entropy comparison obtained from the solution of the PB equation and analysis of the PV simulations in the squared domain. Included are three magnified plots for; b monopole, c diagonal dipole, d dipole. Each marker represents the energy ${\hat{E}}_{\sigma }$ and the entropy ${\hat{S}}_{\sigma }$ for different values of the parameter $\sigma$. The vertical dashed lines represent the mean energy $\langle {\hat{E}}_{\sigma }\rangle$ of the configuration

Fig. 12

a Energy-entropy comparison obtained from the solution of the PB equation and analysis of the PV simulations in the rectangular domain. Included on the right are three magnified plots for; b dipole, c monopole. Each marker represents the energy ${\hat{E}}_{\sigma }$ and the entropy ${\hat{S}}_{\sigma }$ for different values of the parameter $\sigma$. The vertical dashed lines represent the mean energy $\langle {\hat{E}}_{\sigma }\rangle$ of the configuration

The results of this analysis for the ensembles in the squared domain have been plotted together with the solutions of the PB equation and are presented in Fig. 11. These indicate that although the energies, $\langle {\hat{E}}_{\sigma }\rangle$, of the dipole and the diagonal dipole are different, their entropies are similar. In contrast, there is a considerable difference between the values of the entropy for the diagonal dipole and the monopole. These observations suggest that the ensemble for the dipole and the diagonal dipole do not coincide with true equilibrium states that are established at later times in the simulation but are quasi-equilibrium states. The numerical values of the entropy for the dipole, the diagonal dipole and the monopole are given by $\langle {\hat{S}}_{\sigma }\rangle _{\text {dipo}}=-203.4$, $\langle {\hat{S}}_{\sigma }\rangle _{\text {diago}}=-203.7$ and $\langle {\hat{S}}_{\sigma }\rangle _{\text {mono}}=-190.8$, respectively. The corresponding values obtained from the solutions of the PB equation are ${\hat{S}}_{\text {dipo}}=-201.9$, ${\hat{S}}_{\text {diago}}=-200.9$ and ${\hat{S}}_{\text {mono}}=-188.1$.

Presented in Fig. 12 are analogous results for the rectangular geometry. In this geometry, the numerical values for the entropy obtained for the monopole and the dipole are given by $\langle {\hat{S}}_{\sigma }\rangle _{\text {mono}}=-196.1$ and $\langle {\hat{S}}_{\sigma }\rangle _{\text {dipo}}=-170.8$. The corresponding values obtained from the solutions of the PB equation for the monopole and the dipole are given by ${\hat{S}}_{\text {mono}}=-191.3$ and ${\hat{S}}_{\text {dipo}}=-170.3$, respectively. This again confirms the good agreement between the PV simulations and the predictions of the PB equation.

5.5 Comparison of Angular Momentum

Next, we will compare the values of the angular momenta between the simulations and the theory. The relation between the streamfunction $\varPsi$ and the angular momentum of the flow L shows that any asymmetric distribution of vortices which corresponds to an asymmetric streamfunction has a non-zero value of angular momentum L. We define the normalised angular momentum ${\hat{L}}$ as the value of L divided by the maximum value of the angular momentum accessible to the system; this corresponds to the angular momentum that the system will have if it would rotate as a solid body [39]. The normalised angular momentum is therefore given by

$$\begin{aligned} {\hat{L}}=\frac{2\varDelta {\overline{\varPsi }}}{\sqrt{{\hat{E}}_{\text {lin}}{\mathcal {I}}}}=4\sqrt{\frac{3}{\lambda ^2 \varDelta }}\left[ \left( \frac{L_xL_y}{L_x^2+L_y^2}\right) \left( \frac{({\overline{\varPsi }})^2}{\overline{(\varPsi ^2)} - ({\overline{\varPsi }})^2}\right) \right] ^{1/2} \, , \end{aligned}$$

(35)

where $\overline{(\cdot )}$ denotes spatially integrated quantities. In the above equation, ${\hat{E}}_{\text {lin}}=(\lambda ^2\varDelta /2)\left[ (\overline{\varPsi ^2}) - ({\overline{\varPsi }})^2\right]$ [38] is the non-dimensional linearised energy obtained by linearising the PB equation about $\varPsi =0$, and ${\mathcal {I}}$ is the moment of inertia of a rectangular body with density $\rho =1$. For a given ensemble in either geometry, the non-dimensional streamfunction is given by $\varPsi _{\sigma }=\rho \beta \gamma \psi _{\sigma }$ where $\psi _{\sigma }$ need to be evaluated using Eq. (30). The values of ${\hat{L}}_\sigma$ for each configuration can then be evaluated and the value of the angular momentum of a given ensemble is then associated with the expectation $\langle {\hat{L}}_\sigma \rangle$. With these definitions, we found that the expectation of the angular momenta obtained from the ensembles in the square and corresponding to the dipole, diagonal dipole, and the monopole are given by

$$\begin{aligned} \langle {\hat{L}}_\sigma \rangle _{\text {dipo}}=0.0596,\qquad \langle {\hat{L}}_\sigma \rangle _{\text {diago}}=0.0629,\qquad \langle {\hat{L}}_\sigma \rangle _{\text {mono}}=0.4324 \, . \end{aligned}$$

(36)

Here, we have used the same values of $\sigma$ as those identified above. The corresponding non-dimensional theoretical values for the dipole, and the monopole in the rectangle are given by

$$\begin{aligned} {\hat{L}}_{\text {dipo}}={\hat{L}}_{\text {diago}}=0,\qquad {\hat{L}}_{\text {mono}}=0.4509 \, , \end{aligned}$$

(37)

where ${\hat{L}}_{\text {mono}}$ was evaluated as the mean of L for ${\tilde{\lambda }}^2=8.5$ and ${\tilde{\lambda }}^2=9$. The percentage error between the value predicted from the PB equation and the values of ${\hat{L}}$ for the monopole recovered from the numerical simulations in the squared domain is given by $PE_{\text {mono}}=4.3\%$. The maximum absolute error for the dipole and the diagonal dipole is $6\%$.

A similar analysis for the rectangle gives

$$\begin{aligned} \langle {\hat{L}}_\sigma \rangle _{\text {mono}}=0.3696,\qquad \langle {\hat{L}}_\sigma \rangle _{\text {dipo}}=0.0298 \, , \end{aligned}$$

(38)

whilst values obtained from the solutions of the PB equation are given by

$$\begin{aligned} {\hat{L}}_{\text {mono}}=0.3844, \qquad {\hat{L}}_{\text {dipo}}=0 \, . \end{aligned}$$

(39)

The percentage error in the case of the monopole is equal to $PE_{\text {mono}}=3.8\%$ whilst the absolute error for the dipole is approximately $3\%$. We can, therefore, conclude that the values of the angular momentum evaluated from the point vortex dynamics is comparable with the theoretical values.

5.6 Vortex Annihilation with Wall Boundaries

We end our study by explaining the effects of vortex annihilation at the boundaries on the emergent flow states at late times. We have argued that the annihilation of vortex–antivortex pairs throughout the vortex dynamics results in the increase of the energy per vortex which subsequently allows the system to migrate into the negative temperature regime while retaining the neutral value of the circulation. However, in a real physical system such as a BEC, point vortices can also annihilate at the boundaries as was confirmed by the numerical simulations presented in [45] and the experiments of Kwon et al. [26]. This additional effect can lead to an asymmetry in the number of vortices resulting in the system becoming polarised (flow with non-zero circulation). In order to study how annihilations at the boundaries change the dynamics of a vortex gas, we have simulated the dynamics in the squared and rectangular domains by introducing an additional annihilation parameter $\delta /2=0.005$ such that any vortex, regardless of its charge, is now removed from the system if its distance from the boundary becomes less than $\delta /2$. To permit direct comparison with the results presented previously, we have used the same initial conditions as shown in Fig. 2.

It turns out that this additional mechanism of vortex annihilation at the boundaries dramatically modifies the late-time dynamics of the system. In particular, we have observed that, in both geometries, the late-time dynamics leads to the emergence of a monopole configuration.

Fig. 13

a Shows the number of vortices (blue curve) and antivortices (green curve) in the square, normalised with respect to the initial value. The red curve represents the polarisation $P(N^+,N^-)$ whereas the black dashed line corresponds to the reference case with zero polarisation. The inset figures show an example of the vortex positions and the corresponding streamfunction $\psi$ at a late time. Above the configuration, the number of vortices and antivortices are indicated; b shows the trend of the angular momentum in the square (blue curve) and in the rectangle (green curve) when the annihilation at the boundaries is included (Color figure online)

An example of the long time dynamics is presented in the inset of Fig. 13a where the configuration of point vortices and the corresponding streamfunction $\psi$ for the square are presented. The annihilation at the boundaries generates an asymmetry in the number of positive and negative vortices. This asymmetry can be quantified by evaluating the polarization $P(N^+,N^-)=(N^+-N^-)/(N^++N^-)$ which is included in Fig. 13a. In Fig. 13b, the time variation of the angular momentum L for both geometries is presented. These results clearly indicate that vortex annihilation at the boundaries can promote the emergence of a polarised monopole state at late times. This asymmetry allows the system to acquire a well defined value of the angular momentum L. We remark that these results are consistent with the analysis presented in [38] where it was also demonstrated that, for non-neutral flows, a monopole can become the most probable state even in a rectangular domain.

6 Conclusions

We have studied the relaxation of a two-dimensional gas of point vortices in a squared and a rectangular domain as a model of quantised vortices for superfluids when the intervortex separation is large in relation to the core size (healing length) of the vortex. An important feature of the model we studied is the pairwise removal of vortex–antivortex pairs to model the process of vortex annihilation, a process that results in the evaporative heating of the vortex gas. This mechanism allows the gas to evolve from a positive temperature regime to a negative temperature regime that results in the spontaneous emergence of large scale flows at late times.

Our numerical simulations have revealed that the emergent large scale flows are in agreement with the mean-field predictions of the Poisson–Boltzmann (PB) equation that is derived from equilibrium statistical mechanical arguments. This reveals that throughout the relaxation, local maximum entropy states of the PB equation are realized but ultimately give way to the maximum entropy configuration at late times. In particular, the simulations show that the flow emerging at late times in the squared domain corresponds to a monopole whereas a dipolar flow field emerges for the rectangular domain with aspect ratio equal to 1.5. This provides clear evidence that the relaxation of the vortex gas proceeds in a quasi-equilibrium manner.

To reinforce our assertions, we have developed a method that allowed us to recover the coarse-grained vorticity fields from our point vortex simulations thereby allowing us to evaluate the entropy and energy of the observed flow structures. The approach we developed rests on the assumption of ergodicity such that ensemble averages can be replaced by time averages. The question of ergodicity of the point vortex model has been widely studied and discussed. However, there is increasing evidence following recent works [44, 45] that the statistical mechanical formulation remains applicable for the point-vortex model. Our work provides further evidence that supports this view. Indeed by replacing ensemble averages with time averages, we have been able to carry out a direct comparison between the predictions of the statistical mechanical approach and our direct numerical simulations of point vortices. Our analysis has revealed good agreement between the two predictions for a neutral vortex gas even for a system containing only $\sim 40$ vortices at late times.

A key feature of the monopole flow that emerges at late times in the squared domain is that it corresponds to a flow with non-zero angular momentum spontaneously forming at late times. An interesting feature of this emergent macroscopic quantity is that the system can undergo sudden transitions in which the sense of the monopole switches as vortices reorganise during rapid events with a consequent flipping in the measured angular momentum. This behaviour is reminiscent of similar observations recently made in classical fluids and of spectrally truncated numerical simulations of the Navier–Stokes equations [65,66,67]. This phenomenology is an interesting feature to study in its own right as it represents an example of extreme rare events arising throughout the late time dynamics in the square. Nevertheless, we have found that regardless of the sense of rotation, the magnitude of the angular momentum of these states as determined from our numerical simulations is in excellent agreement with the theoretical mean field predictions.

We end by remarking that in practice, for a real superfluid, such as a Bose-Einstein condensate in a box trap, the neutrality of the vortex gas may not be preserved as vortices or antivortices can annihilate at the boundaries of the domain. Our simulations have revealed that such a scenario would result in a polarized vortex gas and can thus favour the emergence of the monopole configuration at very late times.

Appendix

The coefficients $C^{\pm }_{n,m}$ in Eq. (29) can be determined by multiplying the right hand side of Eq. (33) by $\sin \left( n'\pi x/L_x\right)$ and $\sin \left( m'\pi y/L_y\right)$ where $n', m'$ are non-zero integers, and integrating the resulting expression over the domain with sides $L_x$ and $L_y$. In order to do so, it is useful to consider the following integral

$$\begin{aligned} I=\gamma _0\sum _{m_1=-\infty }^{+\infty }\int _0^{L_x}\delta (x-(2L_x-x_0)+2m_1L_x)\sin \left( \frac{n'\pi x}{L_x}\right) \mathrm{d}x,\quad n'\ne 0 \, . \end{aligned}$$

(40)

Since Dirac’s delta function is an even function, by performing the change of variable $x \rightarrow 2L_x-x$, the integral becomes

$$\begin{aligned} I=-\gamma _0\sum _{m_1=-\infty }^{+\infty }\int _{L_x}^{2L_x}\delta (x-x_0+2m_1L_x)\sin \left( \frac{n'\pi x}{L_x}\right) \mathrm{d}x \, . \end{aligned}$$

(41)

This shows that the integral over the domain $[0,L_x]\times [0,L_y]$ of the third term of Eq. (33) multiplied by $\sin \left( n'\pi x/L_x\right)$ and $\sin \left( m'\pi y/L_y\right)$ is equivalent to integrating the first term of Eq. (33) multiplied by $\sin \left( n'\pi x/L_x\right)$ and $\sin \left( m'\pi y/L_y\right)$ over the interval $[L_x,2L_x]\times [0,L_y]$. By applying the same property to the other terms, the integral of the vorticity given by Eq. (33) at the initial time, denoted by $I_{{\tilde{\omega }}}$, can be expressed as

$$\begin{aligned} I_{{\tilde{\omega }}}=\int _0^{2L_x}\int _0^{2L_y}{\tilde{\omega }}_1(x,y)\sin \left( \frac{n'\pi x}{L_x}\right) \sin \left( \frac{m'\pi y}{L_y}\right) \mathrm{d}x \mathrm{d}y,\quad n',m'\ne 0 \, . \end{aligned}$$

(42)

where ${\tilde{\omega }}_1(x,y)$ is the first term in Eq. (33). Inserting the representation of the Dirac’s comb (32) along both x and y directions, into the above expression, and using the identity

$$\begin{aligned} \frac{1}{L_x}\int _0^{2L_x}\sum _{n=1}^{+\infty }\cos \left( \frac{n\pi (x-x_0)}{L_x}\right) \sin \left( \frac{n'\pi x}{L_x}\right) \mathrm{d}x =\sin \left( \frac{n\pi x_0}{L_x}\right) \, , \end{aligned}$$

(43)

we obtain

$$\begin{aligned} I_{{\tilde{\omega }}}=\gamma _0\sin \left( \frac{n'\pi x_0}{L_x}\right) \sin \left( \frac{m'\pi y_0}{L_y}\right) \, . \end{aligned}$$

(44)

Combining this with the projection of Eq. (29) onto the modes $\sin \left( n'\pi x/L_x\right)$ and $\sin \left( m'\pi y/L_y\right)$ at the initial time, $t=0$, allows us to recover the coefficients $C^{\pm }_{n,m}$. For $N^{\pm }$ vortices with circulation $\gamma _i$ located at $(x_i,y_i)$, $i=1,\dots ,N$, the coefficients $C^{\pm }_{n,m}$ are given by

$$\begin{aligned} C^{\pm }_{n,m}=\frac{4}{L_xL_y}\sum _{i=1}^{N^{\pm }}\gamma _i\sin \left( \frac{n\pi x_i}{L_x}\right) \sin \left( \frac{m\pi y_i}{L_y}\right) \, . \end{aligned}$$

(45)