Random Forests and Networks Analysis

Abstract

Wilson (Proceedings of the twenty-eight annual acm symposium on the theory of computing, pp. 296–303, 1996) in the 1990s described a simple and efficient algorithm based on loop-erased random walks to sample uniform spanning trees and more generally weighted trees or forests spanning a given graph. This algorithm provides a powerful tool in analyzing structures on networks and along this line of thinking, in recent works (Avena and Gaudillière in A proof of the transfer-current theorem in absence of reversibility, in Stat. Probab. Lett. 142, 17–22 (2018); Avena and Gaudillière in J Theor Probab, 2017. https://doi.org/10.1007/s10959-017-0771-3; Avena et al. in Approximate and exact solutions of intertwining equations though random spanning forests, 2017. arXiv:1702.05992v1; Avena et al. in Intertwining wavelets or multiresolution analysis on graphs through random forests, 2017. arXiv:1707.04616, to appear in ACHA (2018)) we focused on applications of spanning rooted forests on finite graphs. The resulting main conclusions are reviewed in this paper by collecting related theorems, algorithms, heuristics and numerical experiments. A first foundational part on determinantal structures and efficient sampling procedures is followed by four main applications: (1) a random-walk-based notion of well-distributed points in a graph, (2) a framework to describe metastable-like dynamics in finite settings by means of Markov intertwining dualities, (3) coarse graining schemes for networks and associated processes, (4) wavelets-like pyramidal algorithms for graph signals.

1 Introduction: Networks, Trees and Forests

The aim of this paper is to survey some recent results [2,3,4,5] on a certain measure on spanning forests of a given graph and its applications within the context of networks analysis. We call a network on $n\in \mathbb {N}$ vertices a directed and weighted graph

$$\begin{aligned} {\mathcal G}=({\mathcal V},{\mathcal E}, w), \end{aligned}$$

where ${\mathcal V}$ denotes a finite vertex set of size $|{\mathcal V}|=n$, ${\mathcal E}$ stands for a directed edge set seen as a prescribed collection of ordered pairs of vertices $\{ (x,y) \in {\mathcal V}\times {\mathcal V}\}$, and $w: {\mathcal V}\times {\mathcal V}\mapsto \mathbb {R}^+$ is a weight function, which associates to each ordered pair $(x,y)\in {\mathcal E}$ a strictly positive weight w(x, y). We will consider irreducible networks where for every two distinct vertices $x,y\in {\mathcal V}$, there is always a directed path connecting them, that is, a sequence $\{e_i=(x_i,y_i)\}_{i=1}^{l}\subset {\mathcal E}$ for some $l\in \mathbb {N}$ such that $x_1=x, y_l=y$ and $y_i=x_{i+1}$ for every $i\le l-1$. Let us introduce the measure at the core of this work. A rooted spanning forest $\phi$ is a subgraph of ${\mathcal G}$ without cycle, with ${\mathcal V}$ as set of vertices and such that, for each $x \in {\mathcal V}$, there is at most one $y \in {\mathcal V}$ such that (x, y) is an edge of $\phi$. The root set ${\mathcal R}(\phi )$ of the forest $\phi$ is the set of points $x \in {\mathcal V}$ for which there is no edge (x, y) in $\phi$; the connected components of $\phi$ are trees, each of them having edges that are oriented towards its own root. We call ${\mathcal F}$ the set of all rooted spanning forests and we see each element $\phi$ in ${\mathcal F}$ as a subset of ${\mathcal E}$. See Fig. 1. For fixed positive $q\in \mathbb {R}^+$, we are interested in the random forest $\Phi _q$ defined as the random variable with values in ${\mathcal F}$ with law:

$$\begin{aligned} \mathbb {P}(\Phi _q=\phi )=\frac{w(\phi ) q^{|{\mathcal R}(\phi )|}}{Z(q)}, \quad \quad \phi \in {\mathcal F}, \end{aligned}$$

(1)

where $w(\phi ) = \prod _{e \in \phi } w(e)$ is the weight associated to the forest $\phi \in {\mathcal F}$, $|{\mathcal R}(\phi )|$ is the number of roots, which is also the number of trees, and $Z(q) = \sum _{\phi \in {\mathcal F}} w(\phi ) q^{|{\mathcal R}(\phi )|}$ is the normalizing partition function. In particular $\emptyset \in {\mathcal F}$ is the spanning forest made of n degenerate trees reduced to simple roots and $w(\emptyset ) = 1$. We can include the case $q = +\infty$ in our definition by setting $\Phi _\infty = \emptyset \in {\mathcal F}$ in a deterministic way. In the sequel we denote by $\mathbb {E}$ expectation w.r.t. the random forest law $\mathbb {P}$.

Fig. 1

An example of an element of ${\mathcal F}$ with 5 roots on a two-dimensional $5 \times 4$ box of $\mathbb {Z}^2$

Fig. 2

A sample of ${\mathcal P}(\Phi _q)$ and ${\mathcal R}(\Phi _q)$ on a two-dimensional box of $\mathbb {Z}^2$ with constant unitary nearest-neigbour weights and periodic boundary conditions. We used different shades of blue for blocks in the partition identified by different trees. Cyan lines separate neighbouring trees and roots are at the centers of red diamonds (Color figure online)

Let us notice that the random forest $\Phi _q$ induces a partition of the graph into trees, and hence the measure in (1) can be seen on the one hand as a clustering measure similar in spirit to the well-known FK-percolation [19]. On the other hand, the forest $\Phi _q$ is rooted and the set of roots ${\mathcal R}(\Phi _q)$ forms an interesting random subset of vertices whose distribution can be explicitly characterized. Figures 2 and 3 show how the associated partition denoted by ${\mathcal P}(\Phi _q)$ and set of roots ${\mathcal R}(\Phi _q)$ look like in two different geometrical settings. As we will show, the presence of the tuning parameter q, controlling size and number of trees, and related efficient sampling algorithms make this measure particularly flexible and suitable for applications.

1.1 Content of the Paper

This survey is organized in two parts. The first three sections constitute a first foundational part, followed by a second part on applications presented in the remaining sections. We will start by presenting basic properties of the measure in (1), Sect. 2, and some sampling algorithmic counterparts, Sect. 3. We then move to three main applications:

(I):

In Sect. 4, we will show how the set of roots ${\mathcal R}(\Phi _q)$ can be used to define a probabilistic notion of subset of well distributed points in a graph and to practically sample it.

(II):

As a second application, a network coarsening scheme is presented in Sect. 5, based on the forest $\Phi _q$ and the notion of Markov chain intertwining. Motivations stem from questions in metastability and in signal processing and we provide two different algorithms and related theorems to control the quality of the resulting coarse grained network.

(III):

We conclude with a last application, which actually constitutes our most developed novelty (at the current stage) as far as the real-world-analysis of data sets on networks is concerned. Supported by theorems and related experiments, in Sect. 6 we propose a new wavelet basis construction and an associated multiscale algorithm for signal processing on arbitrary weighted graphs.

To conclude this introductory part, we describe briefly the origin of this measure and related literature, Sect. 1.2, and introduce some basic crucial objects and notation needed along the paper, Sect. 1.3. Apart from Wilson’s algorithm, Theorem 1, Propositions 8 and 13, and parts of Theorems 2 and 11, all other statements, algorithms and experiments are original and they were recently derived by the authors.

1.2 Uniform Spanning Tree and a Zoo of Random Combinatorial Models

The uniform spanning tree (UST) constitutes a by now classical topic in probability theory and it consists of a random spanning tree sampled uniformly among all possible spanning trees of a given graph. The analysis of this object can be traced back at least to the work of Kirchhoff [23] where the number of spanning trees of a graph was characterized in terms of minors of the corresponding discrete Laplacian matrix (matrix-tree theorem). In the last decades, UST has been playing a central role in probability and statistical mechanics due to its deep relation with Markov chain theory and its surprising connections with challenging random combinatorial objects of current interest: e.g. loop erased random walks, percolation, dimers, sandpile models, Gaussian fields. We refer to [6, 10, 17, 19,20,21,22, 24,25,26] for an overview on the vast literature on the subject. What makes this object particularly interesting is in part its determinantal nature, namely, related local statistics have a closed-form expression in terms of determinants of certain kernels, together with the fact that there is an efficient random-walk-based-algorithm due to Wilson [40] for sampling, which will be presented in Sect. 3.1. The forest measure in (1) is actually a simple variant of the UST measure and it appeared already as a remark in [40] where the author mentions how to sample it. As for the UST measure, there are many interesting questions related to scaling and infinite volume limits of observables of the forest measure in (1). Nonetheless, our focus here is on applications within the context of networks analysis and for this reason we will not insist on this very interesting fundamental line of investigation and we will restrict only to networks with finite number of vertices.

1.3 Basic Objects and Notation: Random Walks, Graph Laplacian, Green’s Function

Given the finite, irreducible, directed and weighted graph ${\mathcal G}=({\mathcal V},{\mathcal E}, w)$ on n vertices, let $X = \{X(t) : t \ge 0\}$ be the irreducible continuous-time Markov process with state space ${{\mathcal V}}$ and generator L given by

$$\begin{aligned} (L f)(x) = \sum _{y \in {\mathcal V}} w(x, y)\bigl [f(y) - f(x)\bigr ], \qquad f:{\mathcal V}\rightarrow \mathbb {C}, \qquad x \in {\mathcal V}. \end{aligned}$$

(2)

In view of the finiteness and irreducibility assumptions, there exists a unique invariant measure for the Markov process X which will be denoted by $\mu$. Averages of functions w.r.t. $\mu$ will be denoted by $\mu (f)$. We recall that the invariance of $\mu$ is equivalent to $\mu (L f)=0$ for arbitrary functions f. We will denote by $P_x$ and $E_x$, respectively, law and expectation w.r.t. the random walk X starting from $x\in {\mathcal V}$. Note that L acts on functions as the matrix, still denoted by L:

$$\begin{aligned} L(x,y)=w(x,y) \text{ for } x \ne y \, ; \, \, L(x,x)= -\sum _{y\ne x} w(x,y)\,. \end{aligned}$$

(3)

We refer to the operator L as the weighted graph Laplacian and we set

$$\begin{aligned} w_{\max }=\max _{x\in {\mathcal V}} -L(x,x). \end{aligned}$$

(4)

We will denote by $\hat{X}$ the discrete-time skeleton chain associated to L defined as the Markov chain with state space ${\mathcal V}$ and transition matrix

$$\begin{aligned} P= \frac{L}{w_{\max }}+\text{ Id }_{{\mathcal V}}, \end{aligned}$$

(5)

with $\text{ Id }_{{\mathcal V}}$ being the identity matrix of size $|{\mathcal V}|$.

In the sequel we deal with restrictions of various matrices: for any ${\mathcal A}, {\mathcal B}\subset {\mathcal V}$ and any matrix $M = \bigl (M(x, y) : x, y \in {\mathcal V}\bigr )$, we write $[M]_{{\mathcal A}, {\mathcal B}}$ for the restricted matrix

$$\begin{aligned}{}[M]_{{\mathcal A}, {\mathcal B}} =\, \bigr (M(x, y) : x \in {\mathcal A}, y \in {\mathcal B}\bigl ) \, . \end{aligned}$$

In case ${\mathcal A}={\mathcal B}$, we will simply write $[M]_{{\mathcal A}}$.

For a subset ${\mathcal A}\subset {\mathcal V}$

$$\begin{aligned} T_{{\mathcal A}}=\inf \{t \ge 0: X(t)\in {\mathcal A}\} \text { is }\mathbf{the } \, \mathbf{hitting }\,\mathbf{time }\text { of the set } {\mathcal A}, \end{aligned}$$

(6)

with the convention $T_{\emptyset }=\infty$.

Finally, for a given (possibly random) time T and arbitrary $x,y\in {\mathcal V}$, we write :

$$\begin{aligned} G_T(x,y)= E_x\Biggl [\int _0^{T}{\mathbb 1}_{\{X(t) = y\}}\,dt\Biggr ] \text { for }\mathbf{the }\, \mathbf{Green's }\, \mathbf{function }\, \mathbf{up }\, \mathbf{to }\, \mathbf{time }\, T, \end{aligned}$$

(7)

i.e. the mean time X spends in y up to time T when starting from x. In case T is a random variable independent of the random walk, we will slightly abuse notation and still use $E_x$ for expectation w.r.t. the random walk and the extra randomness.

Let us conclude with basic notation for normed spaces. We will denote by

$$\begin{aligned} \ell _{p}({\mathcal V}, \mu )= \{ f: {\mathcal V}\rightarrow \mathbb {R}\mid \left\| {f}\right\| _{p,{\mathcal V}} <\infty \}, \quad p\ge 1, \end{aligned}$$

(8)

the $\ell _p$ -space of functions on ${\mathcal V}$ w.r.t. the norm

$$\begin{aligned} \left\| {f}\right\| _{p,{\mathcal V}} = \left( {\sum _{x \in {\mathcal V}} \left| {f(x)}\right| ^p {\mu (x)}}\right) ^{1/p}\, . \end{aligned}$$

(9)

For $\bar{\mathcal V} \subset {\mathcal V}$ and $\bar{f}: \bar{\mathcal V} \rightarrow \mathbb {R}$, we will also use

$$\begin{aligned} \left\| {\bar{f}}\right\| _{p,\bar{\mathcal V}} = \left( {\sum _{\bar{x} \in \bar{\mathcal V}} \left| {\bar{f}(\bar{x})}\right| ^p \frac{\mu (\bar{x})}{\mu (\bar{\mathcal V})}}\right) ^{1/p}\, . \end{aligned}$$

(10)

Further, for arbitrary probability measures $\nu _1$ and $\nu _2$ on ${\mathcal V}$, their total variation distance is given by

$$\begin{aligned} d_{TV}(\nu _1, \nu _2) = \frac{1}{2} \sum _{x \in {\mathcal V}} \left|{\nu _1(x)-\nu _2(x)}\right| \, . \end{aligned}$$

(11)

2 Random Spanning Forests

2.1 Laplacian Spectrum and Determinantality

We start here an account of the basic fundamental results characterizing the distribution of the main objects related to the random forest $\Phi _q$. It will be convenient for the sequel to consider the following generalized version of the random forest. For any ${\mathcal B}\subset {\mathcal V}$ we denote by $\Phi _{q, {\mathcal B}}$ a random variable in ${\mathcal F}$ with the law of $\Phi _q$ conditioned on the event $\bigl \{{\mathcal B}\subset {\mathcal R}(\Phi _q)\bigl \}$. We then have, for any $\phi$ in ${\mathcal F}$,

$$\begin{aligned} {\mathbb P}\bigl (\Phi _{q, {\mathcal B}} = \phi \bigr ) = {w(\phi ) q^{|{\mathcal R}(\phi )| - |{\mathcal B}|} \over Z_{\mathcal B}(q)} {\mathbb 1}_{\{{\mathcal B}\subset {\mathcal R}(\phi )\}} \end{aligned}$$

(12)

with

$$\begin{aligned} Z_{\mathcal B}(q) = \sum _{\phi : {\mathcal R}(\phi ) \supset {\mathcal B}} w(\phi ) q^{|{\mathcal R}(\phi )| - |{\mathcal B}|}. \end{aligned}$$

(13)

The original definition in Eq. (1) is recovered by simply setting ${\mathcal B}=\emptyset$, so that $\Phi _q=\Phi _{q, \emptyset }$ and $Z(q)=Z_\emptyset (q)$. This extended law is non-degenerate even for $q = 0$, provided that ${\mathcal B}$ is non-empty. And if ${\mathcal B}$ is a singleton $\{r\}$, then $\Phi _{0, \{r\}}$ is the classical random spanning tree with a given root r, namely, a spanning tree $\tau$ rooted at r sampled with probability proportional to $\prod _{e \in \tau } w(e)$. Let us emphasize that actually, for $q > 0$, $\Phi _q = \Phi _{q, \emptyset }$ itself is also a special case of the usual random spanning tree on the extended weighted graph ${\mathcal G}' = ({\mathcal V}',{\mathcal E}', w')$ obtained by addition of an extra point r to ${\mathcal V}$—to form ${\mathcal V}' = {\mathcal V}\cup \{r\}$—and by adding extra edges to r with weights $w'(x, r) = q$ and $w'(r, x) = 0$ for all x in ${\mathcal V}$. Indeed, to get $\Phi _q$ from the random spanning tree on ${\mathcal V}'$ rooted in r, one only needs to remove all the edges going from ${{\mathcal V}}$ to r.

As a first result we characterize the partition function in terms of the Laplacian spectrum. To this end we denote by $\lambda _{0, {\mathcal B}} \le \lambda _{1, {\mathcal B}} \le \cdots \le \lambda _{l - 1, {\mathcal B}}$, with $l = |{\mathcal V}\setminus {\mathcal B}|$ and some ${\mathcal B}\subset {\mathcal V}$, the eigenvalues of $[-L]_{{\mathcal V}\setminus {\mathcal B}}$ in increasing order.

Theorem 1

(Partition function and Laplacian spectrum) For any ${\mathcal B}\subset {\mathcal V}$, $Z_{\mathcal B}$ is the characteristic polynomial of $[L]_{{\mathcal V}\setminus {\mathcal B}}$, i.e.,

$$\begin{aligned} Z_{\mathcal B}(q) = \det \left[ q \text{ Id }_{{\mathcal V}\setminus {\mathcal B}} - [L]_{{\mathcal V}\setminus {\mathcal B}}\right] = \prod _{j < l}(q + \lambda _{j, {\mathcal B}}), \quad q \in {\mathbb R}. \end{aligned}$$

The above result can be seen as a version of the well-known matrix-tree-theorem (see for instance [1]). The proof can be derived in several ways. We refer to [3, Prop. 2.1] for an elementary proof by a classical argument based on loop-erased random walks and using the notation herein.

As mentioned above, one of the nice features of the forest measure (as well as for the random spanning tree measure) is its determinantal structure which allows for explicit computations. We start by recalling the determinantality of the edge set for which we need some more notation.

For an oriented edge $e=(x,y)$ we denote the starting and ending vertex, respectively, as $e_-=x$ and $e_+=y$. We will also write $-e$ for (y, x). For any given ${\mathcal B}\subset {\mathcal V}$ and $q>0$, we write $G_{q,{\mathcal B}}$ for the Green’s function in Eq. (7) with $T=T_q \wedge T_{{\mathcal B}}$ , the minimum between the hitting time of ${\mathcal B}$ (see Eq. (6)) and time $T_q$ denoting an independent exponential time of parameter q. $G_{q,{\mathcal B}}$ can then be identified with the operator $[q \text{ Id }- L]_{{\mathcal V}\setminus {{\mathcal B}}}^{-1}$ so that,

$$\begin{aligned} G_{q,{\mathcal B}}(x,y)=E_x\left[ \int _0^{T_q \wedge T_{{\mathcal B}}}{\mathbb 1}_{\{X(t)=y\}} dt\right] = \left\{ \begin{array}{ll} [q \text{ Id }- L]_{{\mathcal V}\setminus {{\mathcal B}}}^{-1}(x,y) &{}\quad \text{ for }\,x,y\in {\mathcal V}\setminus {{\mathcal B}} \, \\ 0 &{}\quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

For $x\in {\mathcal V}$ and e in ${\mathcal E}$, we call

$$\begin{aligned} J_{q,{\mathcal B}}^+(x, e) = {E_x\left[ { \left| \left\{ {s \le T_q \wedge T_{{\mathcal B}}: X(s_-) =e_- ; X(s)=e_+}\right\} \right| }\right] } = G_{q,{\mathcal B}}(x, e_-) w(e) \end{aligned}$$

the expected number of crossings of the (oriented) edge e up to time $T_q \wedge T_{{\mathcal B}}$, and

$$\begin{aligned} J_{q,{\mathcal B}}(x, e) = J_{q,{\mathcal B}}^+(x, e) - J_{q,{\mathcal B}}^+(x, -e) \,, \end{aligned}$$

the net flow through e starting from x.

Theorem 2

(Determinantal edges: transfer-current) Fix ${\mathcal B}\subset {\mathcal V}$ and $q>0$. Then, for any ${\mathcal A}_k=\{e_1, \dots , e_k\} \subset {\mathcal E}:$

$$\begin{aligned} {\mathbb P}\left( {\mathcal A}_k \subset \Phi _{q,{\mathcal B}} \right) = {\mathbb P}\left( e_1, e_2, \dots , e_k \in \Phi _{q,{\mathcal B}} \right) = \mathrm{det} \left[ I_{q,{\mathcal B}}^+\right] _{{\mathcal A}_k} \end{aligned}$$

with

$$\begin{aligned} I_{q,{\mathcal B}}^+(e, e') = J_{q,{\mathcal B}}^+(e_-, e') - J_{q,{\mathcal B}}^+(e_+, e') \,, \quad e, e' \in {\mathcal E}\,. \end{aligned}$$

(14)

In addition, denoting by $\{\pm e_1, \dots , \pm e_k \in \Phi _{q,{\mathcal B}}\}$ the event that for all $i \le k$ either $e_i$ or $-e_i$ belong to $\Phi _{q,{\mathcal B}}$, it holds

$$\begin{aligned} {\mathbb P}\left( \pm e_1, \dots , \pm e_k \in \Phi _{q,{\mathcal B}} \right) =\mathrm{det}\left[ I_{q,{\mathcal B}}\right] _{{\mathcal A}_k} \end{aligned}$$

(15)

with

$$\begin{aligned} I_{q,{\mathcal B}}(e, e') = J_{q,{\mathcal B}}(e_-, e') - J_{q,{\mathcal B}}(e_+, e') \,, \quad e, e' \in {\mathcal E}\,. \end{aligned}$$

(16)

The above theorem is a version of the celebrated transfer-current theorem due to Burton and Pemantle [10]. In its original form, this theorem was proven in an undirected graph, extensions to the directed setup have appeared for e.g. in the recent Chang [12] and the statement in Theorem 2 is nothing but a probabilistic reformulation of Thm. 5.2.3 and Coro. 5.2.4 in [12]. For a simple proof using our notation, we refer the reader to [2, Thm. 7.1].

Theorem 2 says that $\Phi _{q,{\mathcal B}}$ is a determinantal process with kernel $I_{q,{\mathcal B}}^+$ interpretable in terms of random-walk-flow. If from a computational point of view, this allows to get explicit formulas, from a phenomenological perspective, when the kernel is symmetric, being determinantal means that the corresponding objects tend to repel each other, more precisely, they are negatively correlated:

$$\begin{aligned} \mathbb {P}(e_1, e_2 \in \Phi _{q,{\mathcal B}})\le \mathbb {P}(e_1\in \Phi _{q,{\mathcal B}})\mathbb {P}(e_2 \in \Phi _{q,{\mathcal B}})\quad \text {for any } e_1,e_2\in {\mathcal E}. \end{aligned}$$

Inherited by the determinantal nature of $\Phi _{q,{\mathcal B}}$, also the set of roots ${\mathcal R}(\Phi _{q,{\mathcal B}})$ is determinantal with a remarkable stochastic kernel given by the random walk X killed at time $T_q \wedge T_{{\mathcal B}}$:

Theorem 3

(Determinantal roots with killed random walk kernel) Fix ${\mathcal B}\subset {\mathcal V}$ and $q>0$. Then, for any ${\mathcal A}\subset {\mathcal V}:$

$$\begin{aligned} {\mathbb P}\left( {\mathcal A}\subset {\mathcal R}(\Phi _{q,{\mathcal B}})\right) = \mathrm{det} \left[ K_{q,{\mathcal B}}\right] _{{\mathcal A}}, \end{aligned}$$

with

$$\begin{aligned} K_{q,{\mathcal B}}(x,y):=qG_{q,{\mathcal B}}(x,y)=P_x\bigl (X(T_q \wedge T_{{\mathcal B}}) = y\bigr ), \quad x, y \in {\mathcal V}\,. \end{aligned}$$

In case ${\mathcal B}=\emptyset$, $\Phi _{q,\emptyset }=\Phi _q$ and we simply write

$$\begin{aligned} K_{q}(x,y):=P_x\bigl (X(T_q) = y\bigr ), \quad x, y \in {\mathcal V}. \end{aligned}$$

(17)

This theorem has been derived in [3, Prop. 2.2]. We next move to the characterization of $|{\mathcal R}(\Phi _{q,{\mathcal B}})|$, that is, the number of roots/connected components/trees. The next statement corresponds to [3, Prop. 2.1]. Recall that $\mathrm{Re}(\lambda _{j, {\mathcal B}}) \ge 0$ for any ${\mathcal B} \subset {\mathcal V}$ and $j \ge 0$ as a consequence of Gershgorin circle theorem.

Theorem 4

(Number of roots) Fix ${\mathcal B}\subset {\mathcal V}$ and $q\ge 0$ and let $l = |{\mathcal V}\setminus {\mathcal B}|$. Set

$$\begin{aligned} p_j(q) = {q \over q + \lambda _{j, {\mathcal B}}}\,,\quad 0\le j \le l-1, \end{aligned}$$

(18)

Decompose

$$\begin{aligned} J_0= & {} \bigl \{j \le l-1 : \lambda _{j, {\mathcal B}} \in {\mathbb R}\bigr \},\\ J_+= & {} \bigl \{j \le l-1 : \mathrm{Im}(\lambda _{j, {\mathcal B}}) > 0\big \},\\ J_-= & {} \bigl \{j : \mathrm{Im}(\lambda _{j, {\mathcal B}}) < 0\big \}, \end{aligned}$$

and define independent random variables $B_j$’s and $C_j$’s, respectively, with laws:

$$\begin{aligned} \mathbb {P}(B_j = 1) = p_j(q), \quad \mathbb {P}(B_j = 0) = 1 - p_j(q), \quad j \in J_0, \end{aligned}$$

and for $j \in J_+$,

$$\begin{aligned} {\mathbb P}(C_j = 2)= & {} |p_j(q)|^2,\\ {\mathbb P}(C_j = 1)= & {} 2 \mathrm{Re}\left( p_j(q)\right) - 2|p_j(q)|^2, \\ {\mathbb P}(C_j = 0)= & {} 1 - 2\mathrm{Re}\left( p_j(q)\right) + |p_j(q)|^2 \, . \end{aligned}$$

Then, whenever $q>0$ or ${\mathcal B}\ne \emptyset$, the random variable $|{\mathcal R}(\Phi _{q,{\mathcal B}})|$ is distributed as

$$\begin{aligned} S_{q, {\mathcal B}} = |{\mathcal B}| + \sum _{j \in J_0} B_j + \sum _{j \in J_+} C_j. \end{aligned}$$

Notice that in case the spectrum of the graph Laplacian is real and ${\mathcal B}$ is empty, $|{\mathcal R}(\Phi _{q})|$ is simply given by the sum of independent Bernoulli’s $B_j$’s ($J_+$ being empty). In particular, since $\lambda _0=0$, $B_0 = 1$ and we recover the fact that $\left|{{\mathcal R}(\Phi _q)}\right| \ge 1$ a.s.

Further, we emphasize that in general momenta of the $|{\mathcal R}(\Phi _{q})|$ have simple expressions and can be easily obtained by differentiating w.r.t. q the normalizing partition function Z(q). For example, mean and variance are given by

$$\begin{aligned} \mathbb {E}\bigl [ |{\mathcal R}(\Phi _{q}) | \bigr ] = \sum _{j< n} {q \over q + \lambda _j}\quad \text { and }\quad \mathrm{Var}\bigl [ |{\mathcal R}(\Phi _{q}) | \bigr ] = \sum _{j < n} {q \over q + \lambda _j}- \Bigl ({q \over q + \lambda _j}\Bigr )^2. \end{aligned}$$

(19)

2.2 Dynamics: Forests, Roots and Partitions

Before moving to sampling algorithms, it is worth mentioning that it is possible to construct a stochastic process with values in ${\mathcal F}$ which allows to couple at once all $\Phi _q$’s as q varies in $\mathbb {R}^+$. A few comments on this coupling are postponed to Sect. 3.3 and Fig. 5. We state here the main theoretical results and collect some related remarks. The following statement corresponds to [3, Thm. 2].

Theorem 5

(Forest dynamics: coupling all q’s) There exists a (non-homogeneous) continuous-time Markov process $F=\{F(s): s\ge 0\}$ with state space ${\mathcal F}$ that couples together all forests $\Phi _q$ for $q > 0$ as follows: for all $s \ge 0$ and $\phi \in {\mathcal F}$ it holds

$$\begin{aligned} \mathbb {P}(F(s) = \phi ) = \mathbb {P}(\Phi _{1 / t} = \phi ) = \mathbb {P}(\Phi _q = \phi ) \end{aligned}$$

with $t = 1/q$, $s = \ln (1 + w_{\max } t)$ and $w_{\max }$ as in (4).

The coupling $t \mapsto \Phi _{1/t} = F(\ln (1 + w_{\max } t))$ is associated with a fragmentation and coalescence process, for which coalescence is strongly predominant, and at each jump time one component of the partition is fragmented into pieces that possibly coalesce with the other components. In particular, the process F starts from $F(0)=\Phi _\infty =\emptyset \in {\mathcal F}$, that is, the degenerate spanning forest made of n trees reduced to simple roots, and eventually reaches in finite time a unique spanning rooted tree.

As a corollary of the above coupling theorem, we get a determinantal characterization of the finite-dimensional distributions of the process $t \mapsto {\mathcal R}(\Phi _{1 / t})$, which can be seen as a dynamical extension of Theorem 3.

Corollary 6

(Dynamic roots distribution) For any choice $0< t_1< \cdots< t_k < t_{k + 1} = 1 / q_{k + 1}$ and any sequence ${\mathcal A}_1$, ..., ${\mathcal A}_k$, ${\mathcal A}_{k + 1}$ of subsets of ${\mathcal V}$, it holds

$$\begin{aligned} \begin{aligned} {\mathbb P}&\bigl ({\mathcal A}_{k + 1} \subset {\mathcal R}(\Phi _{1 / t_{k + 1}}) \bigm | {\mathcal A}_{k} \subset {\mathcal R}(\Phi _{1 / t_{k}}), \dots , {\mathcal A}_{1} \subset {\mathcal R}(\Phi _{1 / t_{1}})\bigr )\\&= \sum _{{\mathcal B}_k \subset {\mathcal A}'_k} \sum _{{\mathcal B}_{k - 1} \subset {\mathcal A}'_{k - 1}} \cdots \sum _{{\mathcal B}_{1} \subset {\mathcal A}'_{1}} \prod _{i = 1}^k \biggl ({t_i \over t_{k + 1}}\biggr )^{|{\mathcal B}_i|} \biggl (1 - {t_i \over t_{k + 1}}\biggr )^{|{\mathcal A}'_i \setminus {\mathcal B}_i|} \det \bigl [K_{q_{k + 1}, {\mathcal B}}\bigr ]_{{\mathcal A}_{k + 1}} \\ \hbox {with} \quad {\mathcal A}'_k&= {\mathcal A}_k, \quad {\mathcal A}'_{k - 1} = {\mathcal A}_{k - 1} \setminus {\mathcal A}_k, \quad \dots \quad {\mathcal A}'_1 = {\mathcal A}_{1} \setminus ({\mathcal A}_k \cup {\mathcal A}_{k - 1} \cup \cdots \cup {\mathcal A}_2)\\ \hbox {and}\quad \quad {\mathcal B}&= \bigcup _{i = 1}^k {\mathcal B}_i. \end{aligned} \end{aligned}$$

(20)

This statement corresponds to [3, Prop. 2.4]. We do not have a similar characterization for the partition process $t \mapsto {\mathcal P}(\Phi _{1 / t})$. More generally, as we saw, while a precise understanding and characterization of $\Phi _q$ and ${\mathcal R}(\Phi _q)$ is possible, we know very little about the induced partition ${\mathcal P}(\Phi _{q}).$

We conclude this part on the relevant theoretical results by mentioning a last property of the root set, namely, by conditioning on the induced partition ${\mathcal P}(\Phi _{q})$ the roots are distributed according to the equilibrium measure $\mu$ of the random walk X restricted to each component of the partition:

Theorem 7

(Roots at restricted equilibria) Let $[{\mathcal A}_1, \dots , {\mathcal A}_m]$ be denoting an arbitrary partition of ${\mathcal V}$ in $m \le n$ subsets and fix $r_i\in {\mathcal A}_i, i=1,\ldots ,m$. Then

$$\begin{aligned} \mathbb {P}\Bigl ({\mathcal R}(\Phi _q) = \{r_1, \dots , r_m\} \Bigm | {\mathcal P}(\Phi _q) = [{\mathcal A}_1, \dots , {\mathcal A}_m]\Bigr ) = \prod _{i = 1}^m \mu _{{\mathcal A}_i}(r_i) \end{aligned}$$

provided that the conditioning event has non-zero probability and with $\mu _{{\mathcal A}_i}$ denoting the invariant measure of the restricted dynamics with generator $L_i$ defined by

$$\begin{aligned} (L_i f)(x) = \sum _{y \in {\mathcal A}_i} w(x, y)\bigl [f(y) - f(x)\bigr ], \quad x \in {\mathcal A}_i, \quad f: {\mathcal A}_i \rightarrow {\mathbb C}. \end{aligned}$$

This statement is a consequence of the well-known Markov chain tree theorem (cf. e.g. [1]), see [3, Prop. 2.3].

3 Sampling Algorithms

The flourishing literature around the random spanning tree theme is mainly due to Wilson’s algorithm (cf. [32, 40]), which is not only a practical procedure to sample $\Phi _{q,{\mathcal B}}$, but actually also a powerful tool to analyze its law. The reader not acquainted with this topic is invited to look into the proofs of the results presented in Sect. 2 which heavily exploit the power of this algorithm in action. We will start by recalling it, Sect. 3.1. We then explain how to get an approximate sample of a forest with a prescribed number of roots, Sect. 3.2, and we conclude this sampling algorithmic part with some comments about sampling the forest dynamics in Theorem 5, Sect. 3.3.

3.1 Wilson’s Algorithm: Sampling a Forest for Fixed q

The following algorithm due to Wilson [40] samples $\Phi _{q, {\mathcal B}}$ for $q > 0$ or ${\mathcal B}\ne \emptyset$:

• a. start from ${\mathcal B}_0 = {\mathcal B}$ and $\phi _0 = \emptyset$, choose x in ${\mathcal V}\setminus {\mathcal B}_0$ and set $i = 0$;

• b. run the Markov process starting at x up to time $T_q \wedge T_{{\mathcal B}_i}$ with $T_q$ an independent exponential random variable with parameter q (so that $T_q = +\infty$ if $q = 0$) and $T_{{\mathcal B}_i}$ the hitting time of ${\mathcal B}_i$;

• c. with

  $$\begin{aligned} \Gamma ^x_{q, {\mathcal B}_i} = (x_0,x_1, \dots , x_k) \in \{x\} \times \bigl ({\mathcal V}\setminus ({\mathcal B}_i \cup \{x\})\bigr )^{k - 1} \times \bigl ({\mathcal V}\setminus \{x\}\bigr ) \end{aligned}$$

  the loop-erased trajectory obtained from $X : [0, T_q \wedge T_{{\mathcal B}_i}] \rightarrow {\mathcal V}$, set

  $$\begin{aligned} {\mathcal B}_{i + 1} = {\mathcal B}_i \cup \{x_0, x_1, \dots , x_k\} \end{aligned}$$

  and $\phi _{i + 1} = \phi _i \cup \{(x_0, x_1), (x_1, x_2), \dots , (x_{k - 1}, x_k)\}$ (so that $\phi _{i + 1} = \phi _i$ if $k = 0$);

• d. if ${\mathcal B}_{i + 1} \ne {\mathcal V}$, choose x in ${\mathcal V}\setminus {\mathcal B}_{i + 1}$ and repeat b–c with $i + 1$ in place of i, and, if ${\mathcal B}_{i + 1} = {\mathcal V}$, set $\Phi _{q, {\mathcal B}} = \phi _{i + 1}$.

It is worth stressing that in steps a. and d. the choice of the starting points x is arbitrary, a remarkable fact which represents the main strength of this algorithm.

There are at least two ways to prove that this algorithm indeed samples $\Phi _{q, {\mathcal B}}$ with the desired law. One option is to follow Wilson’s original proof in [40], which makes use of the so-called Diaconis–Fulton stack representation of Markov chains, cf. [15]. An alternative option is to follow Marchal who first computes in [28] the law of the loop erased trajectory $\Gamma ^x_{q, {\mathcal B}}$ obtained from the random trajectory $X : [0, T_q \wedge T_{\mathcal B}] \rightarrow {\mathcal V}$ started at $x \in {\mathcal V}\setminus {\mathcal B}$ and stopped in ${\mathcal B}$ or at an exponential time $T_q$ if $T_q$ is smaller than the hitting time $T_{\mathcal B}$. One has indeed:

Proposition 8

(Distribution of loop-erased walks) If $(x_0, x_1, \dots , x_k) \in {\mathcal V}^{k + 1}$ is a self-avoiding path such that $x_0 = x, x_1, \ldots , x_{k-1}$ in ${\mathcal V}\setminus {\mathcal B}$, then

$$\begin{aligned} {\mathbb P}\bigl (\Gamma ^x_{q, {\mathcal B}} = (x_0, x_1, \dots , x_k)\bigr ) = {\left\{ \begin{array}{ll} \displaystyle \prod _{j< k} w(x_j, x_{j + 1}) {\det [q \text{ Id }- L]_{{\mathcal V}\setminus ({\mathcal B}\cup \{x_0, \dots , x_{k - 1}\})} \over \det [q \text{ Id }- L]_{{\mathcal V}\setminus {\mathcal B}}} &{} \hbox {if }x_k \in {\mathcal B}\hbox {,}\\ \displaystyle q \prod _{j < k} w(x_j, x_{j + 1}) {\det [q \text{ Id }- L]_{{\mathcal V}\setminus ({\mathcal B}\cup \{x_0, \dots , x_k\})} \over \det [q \text{ Id }- L]_{{\mathcal V}\setminus {\mathcal B}}} &{} \hbox {if }x_k \not \in {\mathcal B}\hbox {.} \end{array}\right. } \end{aligned}$$

From this result one can easily compute the law of $\Phi _{q, {\mathcal B}}$ following the steps of the algorithm above to get the law in Eq. (12). Further, from this statement we see how determinants of the Laplacian emerge. Concerning the average running time of Wilson’s algorithm, it is smaller than n / q—so that the numerical complexity is of order $n w_{\max } / q$—and typically much smaller than the random walk cover time. In particular, it can be explicitly characterized in spectral terms as the sum of the inverse of the $n-|{\mathcal B}|$ eigenvalues of $[q -L]_{{\mathcal V}\setminus {\mathcal B}}$, see e.g. [28, Prop. 1].

3.2 Forests with a Prescribed Number of Roots: Approximate Sampling

We have seen that Wilson’s algorithm provides a practical way to sample $\Phi _q$. In applications, one might be interested in sampling $\Phi _q$ conditioned on having a prescribed number of roots, that is, conditioned on $\bigl \{|{\mathcal R}(\Phi _q)| = m\bigr \}$ for fixed $m<n$. Unfortunately, we do not know any efficient algorithm providing such an outcome. Nevertheless we can exploit Theorem 4 to get a procedure to sample $\Phi _q$ with approximately m roots, with an error of order $\sqrt{m}$ at most. In fact, it is not difficult to check that $\mathrm{Var}\bigl (|{\mathcal R}(\Phi _q)|\bigr ) \le 2 \mathbb {E}\bigl [|{\mathcal R}(\Phi _q)|\bigr ]$ and, in view of (19), it suffices to find the solution $q^*$ of the equation

$$\begin{aligned} \sum _{j < n} {q \over q + \lambda _j} = m. \end{aligned}$$

(21)

However, solving Eq. (21) requires to compute the eigenvalues $\lambda _j$’s of $-L$ which is in general computationally costly especially if we are dealing with a big size network. One way to find an approximate value of the solution $q^*$ is to use, on the one hand, the fact that $q^*$ is the only one stable attractor of the recursive sequence defined by $q_{k + 1} = f(q_k)$ with

$$\begin{aligned} f : q \mapsto q \times {m \over \sum _{j< n} {q \over q + \lambda _j}} = {m \over \sum _{j < n} {1 \over q + \lambda _j}}\,, \end{aligned}$$

and on the other hand, the fact that $|{\mathcal R}(\Phi _q)|$ and $\mathbb {E}\bigl [|{\mathcal R}(\Phi _q)|\bigr ]$ are typically of the same order, at least when $\mathbb {E}\bigl [|{\mathcal R}(\Phi _q)|\bigr ]$, i.e. q, is large enough, since $\mathrm{Var}\bigl (|{\mathcal R}(\Phi _q)|\bigr ) / \mathbb {E}^2\bigl [|{\mathcal R}(\Phi _q)|\bigr ] \le 2 / \mathbb {E}\bigl [|{\mathcal R}(\Phi _q)|\bigr ]$. We then propose the following algorithm to sample $\Phi _q$ with $m \pm 2\sqrt{m}$ roots.

• a. Start from any $q_0 > 0$, for example $q_0 =w_{\max }=\max _{x\in {\mathcal V}} -L(x,x)$, and set $i = 0$.

• b. Sample $\Phi _{q_i}$ with Wilson’s algorithm.

• c. If $|{\mathcal R}(\Phi _{q_i})| \not \in \bigl [m - 2 \sqrt{m}, m + 2 \sqrt{m}\bigr ]$, set $q_{i + 1} = m q_i / |{\mathcal R}(\Phi _{q_i})|$ and repeat b with $i + 1$ instead of i. If $|{\mathcal R}(\Phi _{q_i})| \in \bigl [m - 2 \sqrt{m}, m + 2 \sqrt{m}\bigr ]$, then return $\Phi _{q_i}$.

We refer the reader to [3, Section 2.2] to argue that indeed this algorithm rapidly stops.

3.3 Coalescence-Fragmentation Process: Sampling for Different q’s at Once

The Markov process F in Theorem 5 is based on the construction of a coalescence-fragmentation process with values in ${\mathcal F}$ making use of Diaconis–Fulton’s stack representation of random walks. For a detailed account on this algorithm and a number of related open questions, we refer the reader to [3, Section 2.3].

We mention that this algorithm allows to couple forests for different values of q’s. The corresponding coupling is not monotone, in the sense that if $q'<q$, it is not true that $|{\mathcal R}(\Phi _{q'})|\le |{\mathcal R}(\Phi _{q})|$ a.s. under the coupling measure, despite the fact that $\mathbb {E}\bigl [|{\mathcal R}(\Phi _{q'})|\bigr ] < \mathbb {E}\bigl [|{\mathcal R}(\Phi _{q})|\bigr ]$, see e.g. Eq. (19). Yet this coupling is a very valuable tool in applications. In fact, it allows to practically sample $\Phi _{q'}$ starting from a sampled $\Phi _{q}$ for any $q'<q$, and more generally, by running this algorithm once in a chosen interval $[0,t^*]$, we get samples of the whole forest trajectory $(\Phi _{1 / t} : t \le t^*)$.

4 Applications: Well Distributed Points in a Network

Given a map of a city modeled as a network ${\mathcal G}$ where road crossings are identified with vertices, assume that we are interested in locating a number of monumental statues at some crossings in an optimal way so that random walkers through the city will take on average the same amount of time to reach the statues independently of where they started. We can rephrase this problem by finding a subset ${\mathcal B}\subset {\mathcal V}$ for the locations of the statues such that for any $x\in {\mathcal V}$:

$$\begin{aligned} E_x[T_{{\mathcal B}}] \text { is independent of } x. \end{aligned}$$

(22)

In other words, ${\mathcal B}\subset {\mathcal V}$ would constitute a set of well distributed points in the network. We immediately realize that unless we have as many statues as the number of crossings, ${\mathcal B}={\mathcal V}$, there is no deterministic proper subset R satisfying the property in (22). Hence this notion of well distributed points is in principle meaningless but, by thinking in terms of disorder, we can turn it into a well-posed definition by finding a random set satisfying (22) in an averaged sense. That is, a random set ${\mathcal B}(\omega )\subset {\mathcal V}$ is chosen according to some law with expectation $\mathbb {E}$ so that

$$\begin{aligned} \mathbb {E}\Bigl [E_x\bigl [T_{{\mathcal B}(\omega )}\bigr ]\Bigr ] \text { is independent of } x. \end{aligned}$$

(23)

It then raises the question: does it exist such a random subset?

Our set of roots ${\mathcal R}(\Phi _q)$ might be a good candidate since as previously noticed, the determinantality of the roots set stated in Theorem 3 implies (in the undirected setup) negative correlations suggesting that the roots in $\Phi _q$ tend to spread far apart from each other irrespective of the given network structure. It turns out that indeed ${\mathcal R}(\Phi _q)$ gives a positive answer to this question for any q (even in the general directed setup). Further, as the next statement shows, the same is true when conditioning on having exactly m statues, that is, with random subsets of prescribed size:

Theorem 9

(Roots are well distributed) For all $x \in {\mathcal V}$ and all positive integer $m \le n$ it holds

$$\begin{aligned} \mathbb {E}\Bigl [E_x\bigl [T_{{\mathcal R}(\Phi _q)}\bigr ]\Bigr ] = {1 \over q} \left( 1 - \prod _{j > 0} {\lambda _j \over q + \lambda _j} \right) \end{aligned}$$

and

$$\begin{aligned} \mathbb {E}\Bigl [E_x\bigl [T_{{\mathcal R}(\Phi _q)}\bigr ] \Bigm | |{\mathcal R}(\Phi _q)| = m\Bigr ] = {a_{m + 1} \over a_m}\,, \end{aligned}$$

(24)

where $a_{n + 1} = 0$, and $a_k$ denotes the coefficient of order k of the characteristic polynomial of L.

This statement corresponds to [3, Thm. 1]. When conditioning in Eq. (24) with either $m=1$ or $m=n-1$, it turns out that the property in (23) actually characterizes the law of ${\mathcal B}(\omega )$. In particular, for $m=1$, the Markov tree-theorem, see e.g. [1], ensures that conditionnally on $\left\{ {|{\mathcal R}(\Phi _q)| = 1}\right\}$, ${\mathcal R}(\Phi _q)$ coincides with a point sampled according to the equilibrium measure $\mu$ of X. In this case, Eq. (24) was already known in the literature and often referred to as the random target lemma, cf. e.g. [25, Lemma 10.8]. Our theorem is therefore a natural extension of this random target to subsets of arbitrary sizes. To get some insights in the corresponding proof, it is worth mentioning that the expected hitting time of a given deterministic set ${\mathcal B}$ in Eq. (22) admits the following characterization due to Freidlin and Wentzell in terms of forests, cf. [3, Lemma 3.1] and [18, Lemma 3.3]:

$$\begin{aligned} E_x\bigl [T_{\mathcal B}\bigr ] = \sum _{z \not \in {\mathcal B}} G_{\mathcal B}(x, z) = {1 \over Z_{\mathcal B}(0)} \sum _{z \not \in {\mathcal B}} \sum _{\begin{array}{c} \phi : {\mathcal R}(\phi ) = {\mathcal B}\cup \{z\} \\ \scriptstyle {\mathcal R}(\tau _x(\phi )) = z \end{array}} w(\phi ), \end{aligned}$$

with $G_{\mathcal B}$ denoting the Green’s function in Eq. (7) stopped at the hitting time $T=T_{\mathcal B}$, and $\tau _x(\phi )$ standing for the tree in $\phi \in {\mathcal F}$ containing $x\in {\mathcal V}$ (Fig. 3).

Fig. 3

Illustration of the roots in a non-trivial geometrical setup. The network is given by a triangulation of a brain cortex model due to J. Lefèvre (LSIS, Marseille, France) with 1868 roots denoted by white squares sampled from $(\Phi _q)$ out of 19,576 vertices (Color figure online)

Concrete applications of this result will be given in the next sections to build up suitable subsampling procedures in the context of networks reduction and signal processing.

5 Applications: Network Coarse Graining Via Intertwining

The goal of this section is to propose a random network coarse graining procedure which exploits the rich and flexible structure of the random spanning forest. The problem can be formulated as follows:

(P1) :

Given a network ${\mathcal G}$ on n nodes, find a smaller network $\bar{{\mathcal G}}$ on $m<n$ nodes “mimicking” the original network ${\mathcal G}$.

For the sake of simplicity, we will restrict ourselves to networks in a reversible setup, that is, when $\mu (x)w(x,y)=\mu (y)w(y,x)$ for any $x,y\in {\mathcal V}$, with $\mu$ being the invariant measure of the Markov process X. Now, it is a priori not clear what “mimicking” means and any meaningful answer would strongly depend on the implemented method and on the specific applications one has in mind.

Our approach will be process-driven. Namely, we saw that the structure of the starting network ${\mathcal G}$ is encoded in the weighted graph Laplacian in Eq. (2) which characterizes the Markov process X with state space ${\mathcal V}$. In view of the one-to-one correspondence between ${\mathcal G}$ and the process X, we can look for a $\bar{{\mathcal G}}$ in correspondence to another process $\bar{X}$ on a state space $\bar{\mathcal V}$ with $m=|\bar{\mathcal V}|<|{\mathcal V}|=n$ points being some sort of coarse grained version of the process X. In this way, we are shifting perspective from graphs to Markov processes and, within this context, there is an interesting duality notion called Markov chain intertwining which will be our lighthouse while addressing (P1). Before discussing this duality, we anticipate that for the applications, our main motivation stems from two different problems:

• metastability studies outside any asymptotic regimes (like low temperature or large volume limits),

• signal processing on arbitrary networks.

We will hence propose in Sects. 5.2 and 5.3 two network reduction procedures (similar in spirit) well-suited for these two problems. If for the applications in metastability, the framework described in Sect. 5.2 deserves still a deeper investigation to fully understand its potential, the framework presented in Sect. 5.3 forms the basis for the new wavelets-transform on graphs described in Sect. 6 (and derived in [5]) which can be considered a novel general method to process data sets on networks. It is worth mentioning that the latter was developed as a consequence of our understanding (even though still partial) on the metastability problem and framework discussed in Sect. 5.2. Further, the presented reduction schemes might also be useful for other applications, hence we will start by discussing where the difficulties lie when looking at network reduction problems through intertwining equations. We start by introducing and discussing the intertwining duality.

5.1 Intertwining and Squeezing

Given two Markov chains with transition matrices P and $\bar{P}$, and state spaces ${\mathcal V}$ and $\bar{{\mathcal V}}$, and given a rectangular stochastic matrix ${\Lambda }: \bar{{\mathcal V}} \times {\mathcal V}\rightarrow [0, 1]$, we say that the two chains are intertwined w.r.t. $\Lambda$ if :

$$\begin{aligned} \Lambda P= \bar{P} \Lambda . \end{aligned}$$

(25)

Denoting by $\{\nu _{\bar{x}} = \Lambda (\bar{x}, \cdot ) : \bar{x}\in \bar{{\mathcal V}} \}$ the family of probability measures on ${\mathcal V}$ identified by $\Lambda$, we see that this algebraic relation among matrices can be rewritten as

$$\begin{aligned} \nu _{\bar{x}}P = \Lambda P(\bar{x}, \cdot ) = \bar{P} \Lambda (\bar{x}, \cdot ) = \sum _{\bar{y} \in \bar{{\mathcal V}} } \bar{P}(\bar{x}, \bar{y}) \nu _{\bar{y}} , \quad \text {for all } \bar{x} \in \bar{\mathcal V}, \end{aligned}$$

(26)

which says that:

the one-step-evolution of the $\nu _{\bar{x}}$ ’s according to P remains in their convex hull.

This duality notion can be equivalently formulated for continuous-time Markov processes by saying that two Markov processes X and $\bar{X}$ with generators L and $\bar{L}$ and state spaces ${\mathcal V}$ and $\bar{\mathcal V}$ are intertwined w.r.t. $\Lambda$ if

$$\begin{aligned} \Lambda L= \bar{L} \Lambda . \end{aligned}$$

(27)

By associating to the Markov process X with generator L in (2) the discrete-time skeleton chain $\hat{X}$ as in (5), we see that (27) is equivalent to (25) if $\bar{P}= \frac{\bar{L}}{w_{\max }}+\text{ Id }_{\bar{{\mathcal V}}}$, and Eq. (26) reads as :

$$\begin{aligned} \nu _{\bar{x}}L = \sum _{\bar{y}\in \bar{{\mathcal V}} \setminus \{\bar{x} \}} \bar{L}(\bar{x}, \bar{y}) [\nu _{\bar{y}}-\nu _{\bar{x}}], \end{aligned}$$

(28)

which says again that, for each $\bar{x}\in \bar{\mathcal V}$, by evolving the distribution $\nu _{\bar{x}}$ according to L, the process under consideration, with rate $\bar{L}(\bar{x}, \bar{y})$ is distributed according to $\nu _{\bar{y}}$.

5.1.1 Intertwining in the Literature

Intertwining relations appeared in the context of diffusion processes in a paper by Rogers and Pitman [33] as a tool to state identities in laws when the measures $\nu _{\bar{x}}$’s have disjoint supports. This method was later successfully applied to many other examples (see for instance [11, 29]). In the context of Markov chains, intertwining was used by Diaconis and Fill [14] without the disjoint support restriction to build strong stationary times and to control convergence rates to equilibrium. At the time being, applications of intertwining include random matrices [16], particle systems [39], random partitioning [8], etc.

5.1.2 Solutions to Intertwining Equations, Overlap and Heisenberg Principle

In the above references, intertwining relations have often been considered with $|\bar{\mathcal V}|$ being (much) larger than or equal to $| {\mathcal V}|$. To address (P1), we will instead be naturally interested in the complementary case $|\bar{\mathcal V}| < |{\mathcal V}|$ and with the coarse grained process (or network identified by) $\bar{P}$ being irreducible. In this setup it is not difficult to show the existence of solutions $(\Lambda , \bar{P})$ to Eq. (25), how they are related to the spectrum of P , and how to construct some of them. We refer the interested reader to [4, Section 2.2]. On the other hand, there is still the problem of building explicit solutions that are “good” for our applications. Let us remark here two important consequences of the statements in [4, section 2.2]:

• the intertwining equations generally have many solutions, including the trivial ones when, for any $\bar{P}$, all the $\nu _{\bar{x}}$ are equal to the invariant measure $\mu$ of P,

• the stability of the convex hull of the $\nu _{\bar{x}}$ implies the stability of the vector space they span and the fact that the $\nu _{\bar{x}}$ have to be linear combinations of at most $|\bar{\mathcal V}|$ left eigenvectors of P.

Looking at the eigenvectors of the generator L as the analogue of the usual Fourier basis, which diagonalizes the Laplacian operator, we will say that the solutions $\nu _{\bar{x}}$’s of the intertwining equations have to be frequency localized. But for our applications in metastability and signal processing, we will naturally look for solutions for which the corresponding $\nu _{\bar{x}}$’s should also be “space localized” or with “small joint overlap”. We next make precise what is meant here. Let us simply stress for now that having both frequency and space localization would contradict a (unfortunately not well established for arbitrary graphs) Heisenberg principle, see [5, Section 1.3] for more details. To overcome this difficulty we will look at approximate solutions of intertwining equations and we will focus on their squeezing, which is a measure of their joint overlap or space localization, that we can now introduce.

5.1.3 The Squeezing Functional

On the space of probability measures on ${\mathcal V}$ with $|{\mathcal V}|=n$, let us denote by $\langle \cdot , \cdot \rangle _{\mu }$ the scalar product defined as

$$\begin{aligned} {\langle \nu _{1}, \nu _{2}\rangle _\mu } =\sum _{x\in {\mathcal V}}{\nu _1(x) \over \mu (x)} {\nu _2(x) \over \mu (x)} \mu (x) =\sum _{x\in {\mathcal V}}{\nu _1(x)\nu _2(x) \over \mu (x)}\,, \end{aligned}$$

(29)

for arbitrary probability measures $\nu _1,\nu _2$ on ${\mathcal V}$, with respect to a reference measure $\mu$ on ${\mathcal V}$ (which will be chosen to be the invariant measure of the Markov process in consideration), and let $\left\| {\cdot }\right\| _{\mu }$ be the corresponding norm.

Given a family $\{\nu _{\bar{x}} = \Lambda (\bar{x}, \cdot ) : \bar{x}\in \bar{{\mathcal V}} \}$, since these measures form acute angles between them ($\langle \nu _{\bar{x}}, \nu _{\bar{y}}\rangle _{\mu } \ge 0$ for all $\bar{x}$ and $\bar{y}$ in $\bar{{\mathcal V}}$) and have disjoint supports if and only if they are orthogonal, one could use the volume of the parallelepiped they form to measure their “joint overlap”. The square of this volume is given by the determinant of the Gram matrix $\Gamma _{\mu }$:

$$\begin{aligned} \mathrm{Vol}(\Lambda ) = \sqrt{\det \Gamma _{\mu }}, \end{aligned}$$

with $\Gamma _{\mu }$ the square matrix on $\bar{\mathcal V}$ with entries $\Gamma _{\mu }(\bar{x}, \bar{y}) = \langle \nu _{\bar{x}},\nu _{\bar{y}}\rangle _{\mu }$, that is

$$\begin{aligned} {\Gamma _{\mu }}= {\Lambda } D(1/\mu ) {\Lambda }^t \, , \end{aligned}$$

(30)

where $D(1/\mu )$ is the diagonal matrix with entries given by $(1/\mu (x), x \in {\mathcal V})$, and ${\Lambda }^t$ is the transpose of ${\Lambda }$. Loosely speaking, the less overlap, the largest the volume.

We will instead use the squeezing of $\Lambda$ (w.r.t. $\mu$), that we defined by

$$\begin{aligned} {{\mathcal S}_{\mu }({\Lambda })}:=\left\{ \begin{array}{ll} +\infty &{}\quad \text{ if } \det (\Gamma _{\mu })=0,\\ \sqrt{\text{ Trace }\big (\Gamma _{\mu }^{-1}\big )} \in \,]0,+\infty [&{}\quad \text{ otherwise, } \end{array}\right. \end{aligned}$$

(31)

to measure this “joint overlap”. We call it “squeezing” not only because the $\nu _{\bar{x}}$ and the parallelepiped they form is squeezed when ${{\mathcal S}_{\mu }({\Lambda })}$ is large, but also because ${{\mathcal S}_{\mu }({\Lambda })}$ is half the diameter of the rectangular parallelepiped that circumscribes the ellipsoid defined by the Gram matrix ${\Gamma _{\mu }}$ : this ellipsoid is squeezed too when ${{\mathcal S}_{\mu }({\Lambda })}$ is large. We note finally that our squeezing controls the volume of $\Lambda$. Indeed, by the comparison between harmonic and geometric mean applied to the eigenvalue of the Gram matrix, small squeezing implies large volume: $\mathrm{Vol}(\Lambda )^{1 / n}{{\mathcal S}_{\mu }({\Lambda })} \ge \sqrt{n}$.

The next statement, corresponding to [4, Prop. 1], gives bounds on this squeezing functional suitable for our approach.

Theorem 10

(Bounds on the squeezing functional) Let $\{\nu _{\bar{x}} : \bar{x}\in \bar{{\mathcal V}} \}$ be a collection of $m=|\bar{{\mathcal V}}|$ probability measures on ${\mathcal V}$. Consider a probability measure $\mu$ on ${\mathcal V}$. Then:

• $$\begin{aligned} {{\mathcal S}_{\mu }({\Lambda }) \ge \sqrt{ \sum _{\bar{x}\in \bar{{\mathcal V}}} \frac{1}{\left\| {\nu _{\bar{x}}}\right\| _\mu ^{2}}}} \, . \end{aligned}$$

  (32)

  Equality holds if and only if the $\nu _{\bar{x}}$’s are pairwise orthogonal.

• Assume further that $\mu$ is a convex combination of the $\{\nu _{\bar{x}} : \bar{x}\in \bar{{\mathcal V}} \}$. Then,

  $$\begin{aligned} {{\mathcal S}_{\mu }({\Lambda })}\ge 1 \, . \end{aligned}$$

  Equality holds if and only if the $\nu _{\bar{x}}$’s are pairwise orthogonal.

We notice in particular that ${{\mathcal S}_{\mu }({\Lambda })}$ is maximal when the measures $\{\nu _{\bar{x}} : \bar{x}\in \bar{{\mathcal V}} \}$ are linearly dependent, and minimal when they are orthogonal. Moreover, we know the minimal value of ${{\mathcal S}_{\mu }({\Lambda })}$, when $\mu$ is a convex combination of the $\nu _{\bar{x}}$’s. Note that this is necessarily the case if the convex hull of the $\nu _{\bar{x}}$ is stable under P, i.e. when (25) holds for some stochastic $\bar{P}$. Indeed it is then stable under $e^{t{ L}}$ for any $t > 0$ and the rows of $\Lambda e^{t{ L}}$ converge to $\mu$ when t goes to infinity. We are now in shape to move to the applications.

Fig. 4

Snapshots of a kinetic Ising model at times 471, 7482 and 13,403 for the first line, 14,674, 15,194, 15,432, 15,892 and 16,558 for the second line, 17,328, 23,645 and 40,048 for the last line (Color figure online)

5.2 Intertwining and Metastability Without Asymptotics

A classical problem in metastability studies can be described as follows. Associated with Markovian models one is interested in making a coarse grained picture of a dynamics which evolves on a large, possibly very large, configuration space, according to some generator L. A metastable state can be thought as a stationary distribution on this large configuration space up to some random exponential time that triggers a transition to a different metastable state, possibly a more stable one. By different metastable states we mean distributions “concentrated on different parts of the large configuration space.” In the literature, this is usually addressed in some asymptotic regime such as low temperature or large volume limits, see e.g. [9] for a recent account. As Theorem 11 below shows, a natural and mathematically rigorous way to perform such a coarse graining avoiding limiting procedures, would be to provide solutions $(\Lambda , \bar{L})$ to (27) with linking measures $\{\nu _{\bar{x}}=\Lambda (\bar{x} , \cdot ) : {\bar{x}} \in {\bar{\mathcal V}} \}$ having minimal squeezing ${\mathcal S}_\mu ({\Lambda })$. In such an intertwining $\bar{L}$ would be the generator of the coarse grained Markovian dynamics, and the measures $\nu _{\bar{x}}$’s (i.e. the rows of $\Lambda$) would describe the different metastable states. To better explain our proposal, let us recall a canonical example of challenging metastable dynamics: the kinetic Ising model. In the following pictures (cf. Fig. 4) we consider a Metropolis–Glauber kinetic Ising model for a spin system started from aligned minus spins (yellow pixels on the pictures, red pixels standing for plus spins) and evolving under a small magnetic field $h = 0.14$, at subcritical temperature $T = 1.5$, in a $n \times n$ rectangular box ${\mathcal B}_n$ with periodic boundary conditions and $n=256$ (thus here ${\mathcal V}=\{+,-\}^{{\mathcal B}_{256}}$). The first three pictures can be thought as samples of a metastable state, which is concentrated on “a minus phase” of the system, that is stationary up to the appearance (nucleation) of a supercritical droplet. We do not mean here the usual minus phase of the Ising model which is associated with 0 magnetic field and—boundary condition. We simply mean some distribution for which—spins dominate and that is stationary conditionally on the fact that the system did not escape the set ${\mathcal R}$ of subcritical configurations introduced in [34] for the infinite volume dynamics. We refer to [7] for a description of metastable systems with such conditionally stationary or quasi-stationary distributions. The appearance of this droplet triggers the relaxation to a stable state, which is concentrated on “a plus phase”, where $+$ spins dominate, and samples of which are given by the last three pictures. In this case, if we do not want to take infinite volume or low temperature limits, we may consider two probability measures on ${\mathcal V}=\{+,-\}^{{\mathcal B}_{n}}$ that describe these − and $+$ phases and hope to find $\bar{L}$, a $2 \times 2$ matrix, solving (27). Actually, in this case since the nucleation time is “long” (in the simulation, the time needed for the supercritical droplet to invade the whole box is short with respect to the time needed for its appearance), solving (27) with little overlapping $\nu _{\bar{x}}$’s (if possible), would lead to $\bar{L}$ with very small entries. It is therefore natural to look, with the same kind of link $\Lambda$, for an intertwining relation between Markovian kernels (rather than generators) of the form:

$$\begin{aligned} \Lambda K_{q'} = \bar{P} \Lambda , \end{aligned}$$

(33)

with $K_{q'}(x, \cdot )$ as in (17). The measure $K_{q'}(x, \cdot )$ is indeed the distribution of the original process, with generator L, started at a configuration $x\in {\mathcal V}$ and looked at an exponential time $T_{q'}$ with parameter $q'$. This parameter should be of the same order as the nucleation rate in the kinetic Ising model example. The next theorem explains in which sense such a program, if feasible, gives a coarse grained description of the evolution of the original process in terms of a smaller chain that describes its evolution among different “metastable states” or local equilibria. We state it in discrete-time since (33) is as in (25) with $P=K_{q'}$.

Theorem 11

(Local equilibria and intertwining) Let $\hat{X}$ be an irreducible Markov chain with finite state space ${\mathcal V}$ and transition kernel P. Assume Eq. (25) holds for some $(\Lambda , \bar{P})$. Then for each $\bar{x}$ in $\bar{{\mathcal V}}$, there exists a stopping time $\bar{T}_{\bar{x}}$ for $\hat{X}$ and a random variable $\bar{Y}_{\bar{x}}$ with values in $\bar{{\mathcal V}} \setminus \{\bar{x}\}$ and law $\mathbb {P}$ such that:

• $\bar{T}_{\bar{x}}$ is distributed as a geometric variable with parameter $1 - \bar{P}(\bar{x}, \bar{x})$;

• $\nu _{\bar{x}}$ is stationary up to time $\bar{T}_{\bar{x}}$, i.e., for all $t \ge 0$,

  $$\begin{aligned} P_{\nu _{\bar{x}}}\left( \hat{X}(t) = \cdot \bigm | t < \bar{T}_{\bar{x}}\right) = \nu _{\bar{x}} \,; \end{aligned}$$

  (34)

• $\mathbb {P}\left( \bar{Y}_{\bar{x}} = \bar{y}\right) = \frac{\bar{P}(\bar{x}, \bar{y})}{1 - \bar{P}(\bar{x}, \bar{x})}$ for all $\bar{y}$ in $\bar{{\mathcal V}}\setminus \{\bar{x}\}$;

• $P_{\nu _{\bar{x}}}\left( \hat{X}(\bar{T}_{\bar{x}}) = \cdot \bigm | \bar{Y}_{\bar{x}} = \bar{y}\right) = \nu _{\bar{y}}(\cdot )$;

• $\left( \bar{Y}_{\bar{x}}, \hat{X}(\bar{T}_{\bar{x}})\right)$ and $\bar{T}_{\bar{x}}$ are independent.

This statement (cf. [4, Prop. 6] ) is a partial rewriting of [14, Section 2.4] in the spirit of [30]. The first two points explain why we can refer to $\nu _{\bar{x}}$’s solution of (33), as local equilibria that last for a time of order $(q'(1-\bar{P}(\bar{x}, \bar{x}))^{-1}$. The last three points make then precise in which sense the process X can be described through the Markov chain $\bar{X}$ with kernel $\bar{P}$. We emphasize that this program is clearly of no use if, for example, we take the “most overlapping” $\Lambda$, that is, with all its rows $\nu _{\bar{x}}$’s identically equal to the equilibrium measure $\mu$ of the considered process X (as previously mentioned, for any $m\le n$, any $\bar{P}$ can be intertwined to any P with respect to such a trivial $\Lambda$). This is why we introduced the squeezing ${\mathcal S}_{\mu }({\Lambda })$ as a measure of overlap between the rows $\nu _{\bar{x}}$’s of $\Lambda$ and for a given P we think of a “good solution” for a pair $(\Lambda , \bar{P})$ satisfying (25) with ${\mathcal S}_{\mu }({\Lambda })$ small. The good news is that as it turns out, for all positive $m \le n$, there always exists non-degenerate solutions $(\Lambda , \bar{P})$, i.e. with $\Lambda$ of rank m, see [4, Section 2.2], but except for peculiar models, we can not expect for such solutions that the corresponding $\nu _{\bar{x}}$’s have disjoint supports (as clearly desirable). Further, for interesting truly metastable models with huge configuration spaces, as for the Glauber example in Fig. 4, we do not know how to write explicitly down solutions of such intertwining equations with $\Lambda$ having small squeezing (even with non-empty intersections for the supports of the corresponding $\nu _{\bar{x}}$’s). Nonetheless, while the main results in metastability studies are usually written in some asymptotic regime, e.g. $h \ll 1$ for the Glauber dynamics in [34], in view of Theorem 11, looking at metastable dynamics through intertwining equations makes possible to deal with such dynamics outside of any asymptotic regime. It remains the problem of constructing explicit “good solutions” to Eq. (33) for interesting relevant models. At the present stage, we do not know how to give a satisfactory answer to this problem which certainly deserves further investigation. However, in the next section we will present a practical algorithmic scheme which can lead (depending on the model and the number of nodes) to build “good approximate solutions”. Our Glauber dynamics of Fig. 4, with its state space of size $2^{256^2}$, will be out of reach, but we will give examples of applications for smaller networks.

5.2.1 A Coarse-Graining Algorithm for Metastability: From Processes to Measures

To make use in practice of the result in Theorem 11, as motivated so far, starting from P one wish to find explicit good solutions $(\Lambda , \bar{P})$ to (33), i.e. with corresponding $\nu _{\bar{x}}$’s having small joint overlap (small squeezing ${\mathcal S}_{\mu }({\Lambda })$ ). Unfortunately for relevant non-trivial examples such a quest could be too difficult if not unfeasible. We introduce here a deterministic algorithm depending on some tuning parameters to circumvent this problem. For a given Markov process X with a big state space (or equivalently the given associated network ${\mathcal G}$), the goal is to build a measure-valued process on a small state space “mimicking” dynamical aspects of the original process in the sense of Theorem 11. We will accomplish our task if the generator of the resulting measure-valued process is close to be intertwined with the original one, and if the associated $\Lambda$ has small squeezing. To guarantee these properties, we will then randomize the procedure through the random forests and give appropriate estimates for the tuning of the involved parameters.

Deterministic Algorithm Based on Partitioning

Given an irreducible and reversible network ${\mathcal G}$ on n vertices (as usual, denote by X the associated Markov process and by $\mu$ its invariant measure):

• a. Pick $m\le n$ and consider a partition of the vertices of the graph ${\mathcal P}({\mathcal G})=[{\mathcal A}_1,\ldots , {\mathcal A}_m]$ into m blocks.

• b. Set $\bar{\mathcal V}:=\{1,\ldots ,m\}$ for the new vertex set;

• c. Set the duality linking matrix $\Lambda$ to be the matrix with rows given by the restricted equilibria associated to each block, i.e. : for any $\bar{x}\in \bar{\mathcal V}$,

  $$\begin{aligned} \Lambda (\bar{x}, \cdot )=\nu _{\bar{x}}(\cdot ) := \mu _{{\mathcal A}_{\bar{x}}}(\cdot ), \end{aligned}$$

  (35)

  with $\mu _{\mathcal A}$ being the probability measure $\mu$ conditioned to ${\mathcal A}\subset {\mathcal V}$, i.e. $\mu _{\mathcal A}= \mu (\cdot | {\mathcal A})$;

• d. The new process is given by

  $$\begin{aligned} \bar{P}_{q'}(\bar{x},\bar{y}):= P_{\nu _{\bar{x}}}\left[ {X(T_{q'}) \in {{\mathcal A}_{\bar{y}}}}\right] , \end{aligned}$$

  (36)

  for any $\bar{x},\bar{y}\in \bar{{\mathcal V}}$ and with $T_{q'}$ being an independent exponential random variable of parameter $q'>0$. In other words, $\bar{P}_{q'}(\bar{x},\bar{y})$ is the probability that on time scale $T_{q'}$, X reaches the set ${\mathcal A}_{\bar{y}}$ when starting from its restricted equilibrium associated to the set ${\mathcal A}_{\bar{x}}$.

A few remarks are in place:

• The linking measures in (35) have minimal squeezing ${\mathcal S}_\mu (\Lambda )$ equal to one: they have disjoint supports.

• Provided that the pair $(\Lambda ,{\bar{P}}_{q'})$ given by (35) and (36) is close to be a solution to the intertwining Eq. (33), Theorem 11 says that the network $\bar{\mathcal G}=\bar{\mathcal G}(q')$ identified by ${\bar{P}}_{q'}$ can be seen, up to an error, as a reduced measure-valued description of the original network ${\mathcal G}$ on time-scale $T_{q'}$, hence a possible answer to our original problem (P1). In particular, by construction, inherited from X, ${\bar{P}}_{q'}$ is again irreducible and reversible w.r.t. $\mu$.

• For any choice of the parameter $q'>0$, in view of step d. and the irreducibility assumption, the resulting network $\bar{\mathcal G}$ will be given by a complete graph with non-homogenous weights identified by (36).

It remains to clarify how to choose the initial partition ${\mathcal P}({\mathcal G})$ in step a. above and how to guarantee that $(\Lambda ,{\bar{P}}_{q'})$ is an approximate solution to the intertwining Eq. (33). To this end, we can exploit the nice properties of the random forests in (1) and randomize this deterministic algorithm as follows.

Randomization through forests:

Set

$$\begin{aligned} m=m(q):=|{\mathcal R}(\Phi _{q})|\le n \quad \text { and } \quad {\mathcal P}({\mathcal G}):={\mathcal P}(\Phi _{q})=[{\mathcal A}_1,\ldots , {\mathcal A}_{m(q)}] \end{aligned}$$

(37)

in step a. of the previous algorithm, for some $q>0$. The choice of the random partition ${\mathcal P}(\Phi _{q})$ is motivated by Theorems 7 and 9 and the fact that by Wilson’s algorithm, two nodes $x,y\in {\mathcal V}$ tend to be in the same block of ${\mathcal P}(\Phi _{q})$ if on scale $T_{q}$, the process X is likely to walk from x to y or vice-versa.

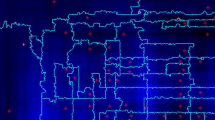
Figure 5 illustrates the coupled partitions (cf. Sect. 3.3) associated with different values of q for a random walk in random potential. We consider a Metropolis nearest-neighbour random walk associated with Brownian sheet potential V and inverse temperature $\beta$ on the square box $[0, 511]^2 \cap \mathbb {Z}^2$. This means that the rates w(x, y) are given by $w(x, y) = \exp \bigl \{-\beta [V(y) - V(x)]_+\bigr \}$ if x and y are nearest neighbours, and 0 if not. In this picture, the vertical and horizontal axes are oriented southward and eastward respectively, so that V is 0 on the left and top boundaries. Since the value of V at the bottom-right corner is of order 500 (it is the sum of $510^2$ independent normal random variables), we already have a metastable situation for the case $\beta = 0.16$, illustrated in Fig. 5: on the time scales 1 / q corresponding to the different partitions ${\mathcal P}(\Phi _q)$, the random walk tends to be trapped in each piece of the partition.

Fig. 5

Coupled partitions ${\mathcal P}(\Phi _q)$ for a Metropolis random walk in Brownian sheet potential at inverse temperature $\beta = 0.16$ and in a $512 \times 512$ square grid. Cyan lines separate neighbouring trees, the roots are at the center of red diamonds and the other vertices are colored according to their potential: the darker the blue, the deeper the potential. The values of q are $1.22 \times 10^{-4}$, $3.05 \times 10^{-5}$, $7.63 \times 10^{-6}$, $1.91 \times 10^{-6}$, $4.77 \times 10^{-7}$, $1.19 \times 10^{-7}$, $2.98 \times 10^{-8}$ and $7.45 \times 10^{-9}$ (Color figure online)

The following theorem quantifies in which sense the pair $(\Lambda , {\bar{P}}_{q'})$ identified by (35) and (36) and randomized as in (37) is an approximate solution to (33) and can serve as a guideline to tune the involved parameters $(q,q')$. Since for each $\bar{x}\in \bar{{\mathcal V}}$, $\Lambda K_{q'} (\bar{x},\cdot )$ and ${\bar{P}}_{q'} \Lambda (\bar{x},\cdot )$ are probability measures on ${\mathcal V}$, we will use the total variation distance defined in (11).

Theorem 12

(Control on intertwining error for metastability) Let $p \ge 1$, and $p^*$ its conjugate exponent, i.e., $\frac{1}{p} + \frac{1}{p^*} = 1$. Fix positive parameters $(q,q')$, and let $(\Lambda , {\bar{P}}_{q'})$ be the pair given by (35) and (36) randomized through $\Phi _q$ as in (37). Then,

$$\begin{aligned} \mathbb {E}\left[ {\sum _{\bar{x}=1}^{|{\mathcal R}(\Phi _{q})|} d_{TV}\big (\Lambda K_{q'}(\bar{x}, \cdot ), \bar{P}_{q'} \Lambda (\bar{x}, \cdot )\big )}\right] \le \left( {\mathbb {E}\left[ {\left|{{\mathcal R}(\Phi _{q})}\right|}\right] }\right) ^{1/p} \left( {\frac{q'}{q} \sum _{x \in {\mathcal V}} \mathbb {E}\left[ {|\Gamma ^x _{q'}|}\right] }\right) ^{1/p^*}, \end{aligned}$$

(38)

where $|\Gamma ^x _{q'}|$ in the r.h.s. denotes the length (i.e. the number of crossed edges) of the trajectory of a loop-erased random walk on the original graph started from $x\in {\mathcal V}$ and stopped at an exponential time $T_{q'}$ (recall Proposition 8), and $K_{q'}$ as in (17).

The proof of the above statement, together with some insights on how to tune $(q,q')$ to guarantee the bound in the r.h.s. to be small, can be found in [4, Thm. 4] and related discussion therein. The r.h.s. in Eq. (38) gives an explicit upper bound on the error in such an intertwining. Our choice of $\bar{P}_{q'}$ in (36) was partially motivated by the “nice” form of this bound, in fact, we notice that if the loop-erased walk starts from a point sampled from a “metastable state” (which can be thought as a valley of a potential energy or a local minima of an hamiltonian for spin-like systems as the Glauber dynamics previously mentioned) then its typical length will be short. If one is intended to simulate the Markov chain on a long time scale $1/q'$, the iterative procedure described in Sect. 5.3.3 will be more useful than Theorem 12. But this result already shows that the random forest captures some structure of the metastable states.

Let us summarize a few advantages and disadvantages of the framework and algorithmic scheme proposed in this section, as well as the main points that according to us deserve further investigation.

5.2.2 Advantages and Limitations of the Proposed Scheme

• As discussed, Theorem 11 gives a clear notion of coarse-grained description of the evolution of the distribution of a given dynamics in a finite setup. Further, such a notion can be related to the renormalization scheme derived in [35] for low-temperature regimes.

• For truly interesting metastable dynamics on huge state spaces, finding an exact good solution to the intertwining relation in Theorem 11 seems in general out of reach and that is why we looked for approximate solutions. Still, for some systems with nice geometrical structures we may hope to find analytically good exact solutions. As a simple example, one may consider a random walk on two copies of a complete graph linked by one bottleneck edge (possibly weighted).

• It is worth mentioning that in the proposed deterministic algorithm, it is always possible to modify the measures in (35) to get an exact intertwined relation though for small enough $q'$ which we are currently not capable of quantifying. The interested reader is referred to [4, Thm. 5] and corresponding proof for the latter statement.

• At the current stage, we do not know how the conclusions in Theorem 11 get affected by a small intertwining error.

• For many systems inherited from statistical mechanics it is practically impossible to run such algorithms: the configurations space is too large. For the Glauber dynamic illustrated in Fig. 4, we would need to deal with a network made of $|{\mathcal V}|=2^{65536}$ nodes. Still, it could be that a different but similar coarse-graining procedure applied on the graph on which the spin are defined (the $256 \times 256$ two-dimensional torus in our example), rather than on the configuration graph (with its $2^{65536}$ nodes), can be used to derive a coarse description of the original dynamics. We believe that such an approach would deserve some deeper analysis.

• Another difficulty is that working with metastable dynamics one can have to go to very small values of q, then very long running times, to get partitions into a few blocks. The last three pictures of Fig. 5 show that the partition hardly changed when q decreased by a factor of order 10. To overcome such a difficulty we can use a renormalization procedure in the spirit of [35]: we will work with smaller and smaller coarse grained graphs rather than coupled partitions of a constant and large state space. But contrarily to [35] we will not need any “low temperature limit”, we will use a different coarse-graining procedure, inspired by signal processing issues and still based on approximated solutions of intertwining equations. After describing it in the next section we will illustrate this approach with another “metastable Brownian sheet” in Sect. 5.3.3.

5.3 Network Coarse-Graining for Signal Processing

We present here a different network reduction scheme. Our original motivation will be fully explained in the next Sect. 6 where we construct a pyramidal algorithm to process signals (i.e. real valued functions) defined on the vertex set of a network. In first approximation, the idea of these pyramidal algorithms is to build from a given network and associated signal, a multiscale invertible reduction scheme where at each scale, after so-called downsampling and filtering procedures, one can define a network of smaller size (typically having a fraction of the original nodes) with associated a coarse grained approximation of the signal. We again have to address problem (P1) from the beginning of this section, but the purpose is different. We will follow a similar strategy as for metastability, but looking at solutions $(\Lambda , \bar{L})$ to Eq. (27) under a different perspective. In this case, as intertwining rectangular matrix of size $|\bar{{\mathcal V}}| \times |{\mathcal V}|$, we use

$$\begin{aligned} \Lambda =\Lambda _{q'}:=[K_{q'}]_{\bar{{\mathcal V}}, {\mathcal V}}, \quad \text { with parameter } q'>0, \end{aligned}$$

(39)

that is, the matrix obtained by restricting the kernel in (17) to indexes in $\bar{{\mathcal V}}\times {\mathcal V}$. This is a convenient choice for our application explained in more details in Sect. 6. Based on the specific problem under investigation, other suitable kernels could also be used. As for metastability, the measures identified by the rows of $\Lambda$ should concentrate on different regions of the underlying state space. As we will see in Sect. 6, they will play the role of low frequency filters in the wavelets construction to build coarse-grained versions of the original signal through local averages. In particular, for the wavelets construction to come, the intertwining relation guarantees frequency localization properties. Anyhow, in this section, we focus only on the network reduction step, that is, on the $\bar{L}$ we want to consider, and how we can guarantee that it is almost intertwined with the given L.

5.3.1 Graph Reduction Via Roots Subsampling and the Trace Process

The reduction algorithm presented here makes use of the notion of Schur complement of a matrix which we first recall. Let M be a matrix of size $n=p+r$ and let

$$\begin{aligned} M= \begin{pmatrix} A &{} B \\ C &{} D \end{pmatrix} \end{aligned}$$

be its block decomposition, A being a square matrix of size p and D a square matrix of size r. If D is invertible, the Schur complement of D in M is the square matrix of size p defined by

$$\begin{aligned} S_M(D) := A - B D^{-1} C \, . \end{aligned}$$

Deterministic Algorithm Based on Representative Vertices

Given an irreducible and reversible network ${\mathcal G}$ on n vertices:

• a. Let $\bar{\mathcal V}\subset {\mathcal V}$ be a subset of $m=|\bar{{\mathcal V}}| \le n$ selected vertices in ${\mathcal G}$.

• b. For the reduced process, set

  $$\begin{aligned} \bar{L} \text { to be the Schur complement of } [L]_{\breve{{\mathcal V}}} \text { in } L \end{aligned}$$

  (40)

  with $\breve{{\mathcal V}}={\mathcal V}\setminus \bar{{\mathcal V}}$.

• c. The coarse-grained network $\bar{\mathcal G}$ is the graph with vertex set $\bar{\mathcal V}$, weights $\bar{w}(\bar{x},\bar{y}):= \bar{L}(\bar{x},\bar{y})$ and edge set identified by positive weights among vertices, that is, $\bar{\mathcal E}=\{(\bar{x},\bar{y})\in \bar{\mathcal V}\times \bar{\mathcal V}: \bar{w}(\bar{x},\bar{y})>0\}$ .

This graph reduction is known as Kron’s reduction. Before discussing this algorithm, in the following proposition, we recall relevant properties of the Schur complement and its probabilistic interpretation. Its proof can be found in [5, Lemma 8].

Proposition 13

(Schur complement and trace process) Let $\bar{\mathcal V}$ be any subset of ${\mathcal V}$ and L as in (2) reversible w.r.t. $\mu$. Set $\breve{{\mathcal V}}={\mathcal V}\setminus \bar{{\mathcal V}}$. Then the restricted matrix $[L]_{\breve{{\mathcal V}}}$ is invertible, and the Schur complement $\bar{L}$ of $[L]_{\breve{{\mathcal V}}}$ in L is an irreducible Markov generator on $\bar{{\mathcal V}}$ reversible w.r.t. $\mu$. This Markov process with generator $\bar{L}$ is often referred to as trace process on the set $\bar{\mathcal V}$. Further, the discrete-time kernel given by $\bar{P}= \text{ Id }+ \bar{L}/w_{\max }$ admits the following interpretation:

$$\begin{aligned} \bar{P}(\bar{x},\bar{y})=P_{\bar{x}}\left[ {\hat{X}(T_{\bar{{\mathcal V}}}^+)=\bar{y}}\right] , \quad \text { for all }\bar{x},\bar{y}\in \bar{{\mathcal V}}, \end{aligned}$$

(41)

with $T_{\bar{{\mathcal V}}}^+$ being the first return time of X in $\bar{{\mathcal V}}$.

Fig. 6

Two successive reductions of the Minnesota’s graph using the algorithm in Sect. 5.3. The wider the edge (in grey), the larger its weight. The roots downsampled on each graph to obtain the successive one are in blue (Color figure online)

Let us stress the main features of the presented algorithm.

• In view of Proposition 13 we may sum up the proposed algorithm as follows: subsample a desired number of nodes in ${\mathcal V}$ to build the set $\bar{{\mathcal V}}$, link any such nodes $\bar{x}, \bar{y}\in \bar{{\mathcal V}}$ with a weight (possibly zero) proportional to (41), that is, the probability that the original walk X starting from $\bar{x}$ lands in $\bar{y}$ when hitting again the subset $\bar{{\mathcal V}}\subset {\mathcal V}$.

• As for the algorithm in Sect. 5.2.1, the resulting process with generator $\bar{L}$ is still irreducible and reversible (due to Proposition 13), thus allowing for successive iterations of this coarse graining procedure (see example in Fig. 6).

• The resulting network $\bar{\mathcal G}$ tends to be (depending on local bottlenecks and the locations of the selected vertices in the original graph) a complete graph with non-homogenous weights, cf. Eq. (41). Depending on the specific problem, one may wish to obtain a sparser graph (e.g. when iterating the scheme, dealing with sparse matrices can reduce the algorithmic complexity). To this aim, a possibility is to disconnect edges with weights below a certain threshold and redistribute part of the masses in (41). An example of such a “sparsification” procedure will be briefly mentioned in Sect. 5.3.2 below.

• Unlike the algorithm presented in Sect. 5.2.1, for any $q'>0$, the measures identified by $\Lambda _{q'}$ do not have disjoint supports. Thus quantitative bounds on their squeezing are desirable (cf. Eq. (45) below).

• As in the case of metastability, the pair $(\Lambda _{q'}, {\bar{L}})$ identified by  (39) and (40) is not a solution to (27), but can be turned into an approximate solution as explained below (see Eq. (43)).

In view of the well distributed property of the roots in Theorem 7, a natural way to select the reduced vertex set in step a. of the above algorithm is to consider

$$\begin{aligned} \bar{{\mathcal V}}=\bar{{\mathcal V}}(q):= {\mathcal R}(\Phi _q), \quad \text { for some } q>0, \end{aligned}$$

(42)

which, as for metastability, makes the pair $(\Lambda _{q'}, {\bar{L}})$ randomized w.r.t. $\Phi _q$. We next move to control squeezing and intertwining error for this pair $(\Lambda _{q'}, {\bar{L}})$ for which we use the $\ell _{p}$-norms in (9)and in (10) rather than the total variation distance as in Theorem 12.

Theorem 14

(Squeezing vs. intertwining) Fix $q'>0$. Consider $\bar{{\mathcal V}}\subset {\mathcal V}$, and set $\breve{{\mathcal V}}= {\mathcal V}\setminus \bar{{\mathcal V}}$. Then the deterministic pair $(\Lambda _{q'}, {\bar{L}})$ given by (39) and (40) satisfies:

$$\begin{aligned} \left\| {\left( {\bar{L} \Lambda _{q'} - \Lambda _{q'} L}\right) f}\right\| _{p,\bar{{\mathcal V}}} \le 2 q' \left( {\frac{w_{\max } }{\beta }}\right) ^{1/p^*} \frac{1}{\mu (\bar{{\mathcal V}})^{1/p}} \left\| {f}\right\| _{p,{\mathcal V}} \, \end{aligned}$$

(43)

for any $p \ge 1$, $p^*$ being its conjugate exponent, and any f in $\ell _p({\mathcal V},\mu )$, where

$$\begin{aligned} \frac{1}{\beta } = \max _{\bar{x}\in \bar{{\mathcal V}}} \sum _{z \in {\mathcal V}} P(\bar{x}, z) E_{z}\left[ {T_{\bar{{\mathcal V}}}}\right] \text { and } P \text { as in }(5). \end{aligned}$$

(44)

Further, by randomizing $(\Lambda _{q'}, {\bar{L}})$ as in Eq. (42) for some $q>0$, we get the squeezing control:

$$\begin{aligned}&\mathbb {E}\left[ { {\mathcal S}\left( \Lambda _{q'}\right) \bigm | |{\mathcal R}(\Phi _q)|=m}\right] \\\nonumber&\qquad \le \frac{ \min \left\{ \sqrt{1 + \sqrt{\frac{T_n}{S_n}}} \; \exp \left( {\sqrt{S_n T_n}- V_n}\right) ; \sqrt{1 + T_n} \exp \left( {\frac{\left( 1 + S_n T_n)\right) }{2} - V_n}\right) \right\} }{\mathbb {P}\left[ {|{\mathcal R}(\Phi _q)| = m}\right] } \end{aligned}$$

(45)

for any $m \le n$ , with

$$\begin{aligned} {S_n=S_n(q, q') = \sum _{j=1}^{n-1} p_j(q')^2 \left( 1-p_j(q)\right) ^2 \,, \qquad T_n=T_n(q, q')= \sum _{j=1}^{n-1} \frac{p_j(q)^2}{p_j(q')^2 } }, \end{aligned}$$

$V_n =V_n(q)= \sum _{j=1}^{n-1} p_j(q) \left( 1-p_j(q)\right)$ and $p_j(\cdot )$ as in (18) with ${\mathcal B}=\emptyset$.

This result corresponds to part of [4, Thm. 3] and [5, Proposition 16]. Note that the upper bound on the squeezing depends on L through its spectrum only. For general remarks and insights on how to tune $(q,q')$ based on this result, we refer the reader to [5, Section 6]. In particular, [5, Section 6.2] gives estimates on $\beta$ defined in (44). We conclude this part on coarse-graining algorithms by giving two concrete examples.

5.3.2 An Experiment: Reduction of Minnesota Road Network

As previously mentioned in the comments after Prop. 13, an original sparse graph can rapidly be reduced into a dense one after a few Kron’s reductions. To get a sparser network at each iteration-step, we may build a sparsification procedure on the basis of the intertwining error in (43) as follows. After computing the Schur complement $\bar{L}$ and hence the weights $\bar{w}(\bar{x}, \bar{y})$ of the reduced network, we set down to 0 all weights below a certain threshold (and in particular we remove the corresponding edges) to obtain a sparser reduced Laplacian, say, $\bar{L}_s$. This threshold is chosen in such a way that for each $\bar{x}$ the new error $\Vert \nu _{\bar{x}} L - \bar{L}_s\Lambda (\bar{x}, \cdot )\Vert _\infty$ does not exceed the original one $\Vert \nu _{\bar{x}} L - \bar{L}\Lambda (\bar{x}, \cdot )\Vert _\infty$ by more than a fraction of it. We refer to [5, Section 7.2] for more details.

Figures 6 and 7 illustrate a few iterations of our recursive coarse-graining algorithm in Sect. 5.3.1 with and without sparsification procedure on the Minnesota road network with unitary weights [31]. Some insights on the choice of the involved parameters is given in Sect. 6.4.

Fig. 7

Two successive reductions of the Minnesota’s graph using the algorithm in Sect. 5.3 with sparsification. Colors are as in Fig. 6 (Color figure online)

Figure 6 illustrates the graph densification issue. Figure 7 shows the much sparser graphs we obtain after sparsification. These graph sequences are associated with approximate intertwining equations with errors of the same order. Our graph reduction has been used in Sect. 6.5 to analyse and compress signals defined on non-regular graphs. Figure 18 shows that as far as compression is concerned, our procedure is good, and that when we add a sparsification step, not only the computation time is shortened, but also the numerical results are improved.

5.3.3 A Metastable Example: Reduction of a Random Walk in Random Potential

As mentioned in the last remark of Sect. 5.2.2, the very nature of metastable dynamics makes impossible in practice to run Wilson’s algorithm with very small q (the running time would be huge) to get a partition ${\mathcal P}(\Phi _q)$ with a few pieces only, even for relatively small networks. However, the recursive procedure described in Sect. 5.3.1, with at each step a downsampling parameter q of the same order as the current maximal jumping rate $w_{\max }$, is indeed feasible and hence gives a possible coarse-grained description of the long time dynamics through the computation of the trace process on a very small set of points. Figure 8 shows some of these reduced graphs for the random walk in Brownian potential as in Fig. 5 on a grid of size $64 \times 64$ (thus smaller than the one in Fig. 5 but with larger inverse temperature $\beta = 2.56$, so that the same kind of difficulty holds). In particular, this reduction allows to describe this dynamics up to convergence to equilibrium, which occurs on a time scale of order $10^{33}$. Indeed, by Theorem 9 and Markov inequality, $X=X_0$ visits $\rho (\Phi _{q_0})$ with large probability within time $1/q'_0 \gg 1/q_0$, regardless of the starting point. In the spirit of [35], the trace process $X_1$ of $X_0$ on $\rho (\Phi _{q_0})$ is then a coarse-grained version of $X_0$ on time scale $1/q'_0$. In the same way, each $X_{k+1}$ is a coarse-grained version of $X_k$ on time scale $1/q'_k \gg 1/q_k$. Since $1/q_k \ge 1/q_0$, $X_{k+1}$ is also a coarse-grained version of $X_0$ on time scale $1/q'_k$. The last nine networks of Fig. 8 are the graph representations of these $X_k$ when $\rho (\Phi _{q_k})$ is reduced to 36, 26, 19, 16, 10, 8, 6, 3 and 2 roots, which are coarse-grained representations of X on time scales that are large with respect to $10^5$, $10^6$, $10^7$, $10^8$, $10^9$, $10^{13}$, $10^{15}$, $10^{15}$ and $10^{28}$. Since this last coarse-grained version, which is a two-state Markov chain, has a relaxation time of order $10^{33}$, so has X.

Fig. 8

Successive reduced networks for a random walk in Brownian sheet potential described at the end of Sect. 5.2.2. The starting grid has size $64\,\times \,64$. The vertex number as well as the largest jump rate are reported on each picture

6 Applications: Intertwining Wavelets, Multiresolution for Graph Signals

Weighted graphs provide a flexible representation of geometric structures of irregular domains, and they are now a commonly used tool to encode and analyze data sets in numerous disciplines including neurosciences, social sciences, biology, transport, communications... Edges between vertices represent interactions between them, and weights on edges quantify the strength of the interaction. In data modeling, it is often the case that a graph signal comes along with the network structure ${\mathcal G}$, this is simply a real-valued function on the vertex set of the network:

$$\begin{aligned} f:{\mathcal V}\rightarrow \mathbb {R}. \end{aligned}$$

Functional magnetic resonance images measuring brain activity in distinct functional regions are classical examples of such a graph signal. Signal processing is the discipline devoted to develop tools and theory to process and analyze signals. Depending on concrete instances, processing means e.g. classifying, removing noise, compressing or visualizing. In case of signals on regular domains very robust tools and algorithms have been developed over more than half a century mainly based on Fourier analysis. For signals on arbitrary networks studies are less advanced and only in recent years significant efforts from different communities have been dedicated to develop suitable efficient methods. We refer to [36] for a recent review on this growing investigation line. We present here a new and rather general multiresolution scheme we introduced in [5]. Multiresolution scheme is a generic name for several multiscale algorithms allowing to decompose and process signals. We will start with a quick recap of classical multiresolution schemes on regular domains. In Sect. 6.2 we then present our new forest-algorithmic-scheme and in Sect. 6.3 we collect the main theorems providing a solid theoretical framework to our method and guidelines for the practice. Illustrative numerical experiments of various nature are given in the concluding Sect. 6.5.

6.1 Classical Multiresolution: Wavelets and Pyramidal Algorithms on Regular Grids

Let us consider a discrete periodic function $f:\mathbb {Z}_n=\mathbb {Z}/n\mathbb {Z}\rightarrow \mathbb {R}$, viewed as a vector in $\mathbb {R}^n$. The multiresolution analysis of f is based on wavelet analysis which roughly amounts to compute an “approximation” $\bar{f}\in \mathbb {R}^{n/2}$ and a “detail” component $\breve{f}\in \mathbb {R}^{n/2}$ through classical operations in signal processing such as “filtering” and “downsampling”. The idea is that the approximation gives the main trends present in f whereas the detail contains more refined information. This is done by splitting the frequency content of f into two components: the approximation $\bar{f}$ focuses on the low frequency part of f whereas the high frequencies in f are contained in $\breve{f}$.

• Filtering is the operation allowing to perform such frequency splittings and it consists of computing a convolution $f\star k$ for some well chosen kernel k: $K_{l}(f)=f \star k_{l}$ yields $K_{l}(f)$ as a low frequency component of f and $K_{h}(f)=f \star k_{h}$ yields $K_{h}(f)$ as a high frequency version of f.

• Downsampling: The vectors $\bar{f}$ and $\breve{f}$ are “downsampled” versions of $K_l(f)$ and $K_h(f)$ by a factor of 2, which means that one keeps one coordinate of $K_l(f)$ and $K_h(f)$ out of two, to build $\bar{f}$ and $\breve{f}$ respectively. Thus the total length of the concatenation of the two vectors $[\bar{f},\breve{f}]$ is exactly n, hence the length of f.

To sum up we have

$$\begin{aligned} \bar{f}(\overline{x})= & {} K_l(f)(\overline{x})=\langle \varphi _{\overline{x}},f\rangle = \text {Approximation}\\= & {} \text {downsampled low-frequency components of} f, \end{aligned}$$

and

$$\begin{aligned} \breve{f}(\overline{x})= & {} K_h(f)(\overline{x})=\langle \psi _{\overline{x}},f\rangle = \text {Detail}\\= & {} \text { downsampled high-frequency components of } f, \end{aligned}$$

where

• $\overline{x}$ belongs to the set of downsamples $\overline{\mathbb {Z}_n}$ isomorphic to $\mathbb {Z}/\frac{n}{2}\mathbb {Z}$.

• $\{\varphi _{\overline{x}},\overline{x}\in \overline{\mathbb {Z}_n}\}$ is the set of functions such that the equality between linear forms $<\varphi _{\overline{x}},.>=K_l(\cdot )(\overline{x})$ holds for all $\overline{x}\in \overline{\mathbb {Z}_n}$.

• In the same way, $\{\psi _{\overline{x}},\overline{x}\in \overline{\mathbb {Z}_n}\}$ is such that $<\psi _{\overline{x}},.>=K_h(\cdot )(\overline{x})$ holds for all $\overline{x}\in \overline{\mathbb {Z}_n}$.

The choice of $k_l$ and $k_h$ is clearly crucial and done in a way that perfect reconstruction of f from $\bar{f}$ and $\breve{f}$ is possible with no loss of information in the representation $[\bar{f},\breve{f}]$. By denoting $f_0=f$, $f_1=\bar{f}$ and $g_1=\breve{f}$, we see that this splitting scheme can be successively iterated starting from $f_1$ to obtained a sequence $f_{N}\in \mathbb {R}^{n/2^{N}}, g_{N}\in \mathbb {R}^{n/2^{N}},\ldots ,g_{1}\in \mathbb {R}^{n/2}$, for any integer N where the total length of the concatenated vectors $[f_{N},g_{N},\ldots ,g_{1}]$ is exactly n. This leads to

The Multiresolution scheme:

$$\begin{aligned} \begin{matrix} f_0 = f &{} \rightarrow &{} f_1=\bar{f}&{} \rightarrow &{} f_2 &{} \cdots &{} \rightarrow &{} f_N \\ &{} \searrow &{} &{} \searrow &{} &{} &{} \searrow &{} \\ &{} &{} g_1=\breve{f}&{} &{}g_2 &{} &{} &{} g_N \end{matrix} \end{aligned}$$

(46)

with $f_i, g_i \in \mathbb {R}^{n/2^{i}}, i=0 \ldots , N.$

We remark that the perfect reconstruction condition amounts to have $\{\varphi _{\overline{x}},\psi _{\overline{x}},\overline{x}\in \overline{\mathbb {Z}_n}\}$ a basis for the signals f on $\mathbb {Z}_n$. A famous construction by Ingrid Daubechies [13] derives several families of orthonormal compactly supported such basis. It is worth mentioning that these families combine localization in space around the point $\overline{x}$ and localization properties in frequency due to the filtering step they have been built from. Using this space-frequency localization one can derive key properties of the wavelet analysis of a signal which rely on the deep links between the local regularity properties of f and the behavior and decay properties of detail coefficients. We refer the interested reader to one of the numerous books on wavelet methods and their applications such as [13] or [27]. In all these methods the word wavelets denotes the family $\{\psi _{\overline{x}},\overline{x}\in \overline{\mathbb {Z}_n}\}$ spanning for the high-frequencies components.

6.2 Forest-Multiresolution-Scheme on Arbitrary Networks

When considering signals f on irregular networks ${\mathcal G}$, it is not clear how to reproduce the classical multiresolution scheme described above. In other words, in a non-regular network, there are no canonical neither obvious answers to the following questions:

(Q1) :

What kind of downsampling should one use? What is the meaning of “every other point”?

(Q2) :

On which weighted graph should the approximation $f_1$ be defined to iterate the procedure?

(Q3) :

Which kind of filters should one use? What is a good notion of low frequency components of a signal?

In light of the properties and applications of the random spanning forests described in the previous sections, we do have natural answers to the first two questions. In fact, Theorem 9 suggests that the set of roots is a random downsample tailored to any network providing a possible answer to (Q1).¹ And the network coarse-graining algorithm presented in Sect. 5.3 is a good candidate to address (Q2). It remains to make sense of filtering in (Q3), that is, how to capture the low frequencies components or the main trend of a graph signal f. But if we use the algorithm in Sect. 5.3, then it is natural to define the approximation component $\bar{f}(\bar{x})$ as a local average around the downsampled $\bar{x}\in \bar{{\mathcal V}}$ w.r.t. the measures identified by the intertwining matrix $\Lambda =\Lambda _{q}$ in (39). That is, for each downsampled $\bar{x}\in \bar{{\mathcal V}}$:

$$\begin{aligned} \bar{f}(\bar{x}) := \nu _{\bar{x}}(f) = \sum _{x \in {\mathcal V}} \Lambda (\bar{x},x) f(x) \,. \end{aligned}$$

Before proceeding with our construction, let us give some remarks on one of the main problems in defining good filters in signal processing.

6.2.1 Filtering: Fighting Against Heisenberg

To be of any practical use in signal processing, the filters $\{\nu _{\bar{x}}, \bar{x}\in \bar{{\mathcal V}}\}$ have to be well localized both in space and frequency. This is violating Heisenberg uncertainty principle, a delicate problem which needs a proper compromise. In the graph context, frequency localization means that the filters belong to an eigenspace of the graph laplacian L. Hence, we are interested in solutions to Eq. (27) such that the measures $\{\nu _{\bar{x}}, \bar{x}\in \bar{{\mathcal V}}\}$ (our proposed filters) are linearly independent measures tending to be non-overlapping (space localization), and contained in eigenspaces of L. We already observed that saying that $(\Lambda , \bar{L})$ is an exact solution to (27) implies that the linear space spanned by the measures $\{\nu _{\bar{x}}, \bar{x}\in \bar{{\mathcal V}}\}$ is stable by L, and is therefore a direct sum of eigenspaces of L, so that these measures provide filters which are frequency localized. Hence the error in the intertwining relation is a measure of frequency localization: the smaller the intertwining error, the better the frequency localization. And through Theorem 14 we can control such frequency localization.

Concerning space localization, we then want small squeezing on $\Lambda$. Notice further that our $\Lambda$ in (39) is just the restriction of the Green’s kernel $K_{q'}$ which is very sensitive to localization by tuning the parameter $q'$. In fact:

• when $q'$ goes to 0, for any $\bar{x}\in \bar{{\mathcal V}}$, $K_{q'}(\bar{x},y)$ goes to $\mu (y)$ so that (27) is trivially satisfied. Since $\mu$ is the left-eigenvector of L corresponding to the eigenvalue 0, the $K_{q'}(\bar{x},y)$ are well localized in frequency. However, the vectors $\{K_{q'}(\bar{x}, \cdot ) \mid \bar{x}\in \bar{{\mathcal V}}\}$ become linearly dependent and very badly localized in space.

• On the other extreme, when $q'$ goes to $\infty$, $K_{q'}(\bar{x}, \cdot )$ goes to $\delta _{\bar{x}}$. Hence, the space localization is perfect. However, the frequency localization is lost, and the error in (27) tends to grow.

A compromise has to be made for the choice of $q'$. Since in our method there is also the parameter q controlling the fraction of downsampled points, we will need a suitable joint tuning of the pair $(q,q')$ to optimize localization properties. As explained in Sect. 6.4, our tuning choice is indeed guided by Theorem 14 but also on stability results of the proposed method which we state in Sect. 6.3 below. For a detail discussion on the actual choice of the parameters, we refer to [5, Section 6].

6.2.2 Approximation, Detail and the Full Forest-Multiresolution

Let us summarize our proposed forest-multiresolution-scheme and present the corresponding basis construction. For arbitrary real-functions f, g on ${\mathcal V}$, we will denote by

$$\begin{aligned} \left\langle f,g \right\rangle _{\mu }= \sum _{x \in {\mathcal V}} f(x) g(x) \mu (x) \end{aligned}$$

(47)

the scalar product w.r.t. $\mu$.²

Intertwining Wavelets

Given an irreducible and reversible network ${\mathcal G}=({\mathcal V}, w)$ on n vertices and a signal $f: {\mathcal V}\rightarrow \mathbb {R}$.

• a. Forest-downsampling: Choose a fix $q>0$, let $\bar{{\mathcal G}}=\bar{{\mathcal G}}(q)=(\bar{{\mathcal V}},\bar{w})$ be the randomized coarse-grained (irreducible and reversible) network given by the algorithm in Sect. 5.3.1 with $\bar{{\mathcal V}}=\bar{{\mathcal V}}(q)$ as in (42), and set $\breve{{\mathcal V}}={\mathcal V}\setminus \bar{{\mathcal V}}$.

• b. Forest-filtering: Fix $q'>0$ and let $\Lambda =\Lambda _{q'}$ be as in (39). Define the approximation component of f as the function $\bar{f}$ defined on $\bar{{\mathcal V}}$ by

  $$\begin{aligned} \bar{f}(\bar{x}) := \Lambda f(\bar{x})= K_{q'}f(\bar{x}) \, , \quad \forall \bar{x}\in \bar{{\mathcal V}}\, , \end{aligned}$$

  (48)

  and the detail component of f as the function $\breve{f}$ defined on $\breve{{\mathcal V}}$ by

  $$\begin{aligned} \breve{f}(\breve{x}) := (K_{q'}-\text{ Id }_{\breve{{\mathcal V}}})f(\breve{x}) \, , \quad \forall \breve{x}\in \breve{{\mathcal V}}\, . \end{aligned}$$

  (49)

Theorem 15

(Basis and wavelets) Fix a parameter $q'>0$. For each $\bar{x}\in \bar{{\mathcal V}}\subset {\mathcal V}$ and $\breve{x}\in \breve{{\mathcal V}},$ respectively, define on ${\mathcal V}$ the densities functions of the measures $\Lambda (\bar{x},\cdot )$ w.r.t. $\mu$:

$$\begin{aligned} \phi _{\bar{x}}(\cdot ) := \frac{\Lambda (\bar{x},\cdot )}{\mu (\cdot )}=\frac{ K_{q'}(\bar{x},\cdot )}{\mu (\cdot )} \, \, , \end{aligned}$$

(50)

and the functions

$$\begin{aligned} \psi _{\breve{x}}(\cdot ) := \frac{ (K_{q'}-\text{ Id }_{\breve{{\mathcal V}}})(\breve{x}, \cdot )}{ \mu (\cdot )} \, , \end{aligned}$$

(51)

and abbreviate $\{\xi _x\}_{x \in {\mathcal V}}= \{ (\phi _{\bar{x}},\psi _{\breve{x}}) \mid \, \bar{x}\in \bar{{\mathcal V}}, \breve{x}\in \breve{{\mathcal V}}\}.$ Then the family $\{\xi _x\}_{x \in {\mathcal V}}$ is a basis of $\ell _2({\mathcal V},\mu )$. In particular, for any $\breve{x}\in \breve{{\mathcal V}}$, $\left\langle {\psi _{\breve{x}},\hbox { 1I}}\right\rangle _{\mu } = 0$.

The statement above corresponds to [5, Lemma 9]. As in classical multiresolution analysis, the functions $\{\psi _{\breve{x}}, \breve{x}\in \breve{{\mathcal V}}\}$ represent our wavelets. The basis functions given by $\{\xi _x\}_{x \in {\mathcal V}}$ are not pairwise orthogonal w.r.t. $\left\langle {\cdot ,\cdot }\right\rangle _{\mu }$ but, by considering the corresponding dual basis in $\ell _2({\mathcal V},\mu )$, that is, the family $\{\tilde{\xi }_x\}_{x \in {\mathcal V}}$ defined through

$$\begin{aligned} \left\langle {\tilde{\xi }_x,\xi _y}\right\rangle _{\mu } = \delta _{xy}, \quad x,y \in {\mathcal V}, \end{aligned}$$

for any $f\in \ell _2({\mathcal V},\mu )$, we get the following representation

$$\begin{aligned} f = \sum _{x \in {\mathcal V}} \left\langle {\xi _x,f}\right\rangle _{\mu } \tilde{\xi }_x=\sum _{\bar{x}\in \bar{{\mathcal V}}} \left\langle {\phi _{\bar{x}},f}\right\rangle _{\mu } \tilde{\xi }_{\bar{x}} + \sum _{\breve{x}\in \breve{{\mathcal V}}} \left\langle {\psi _{\breve{x}},f}\right\rangle _{\mu } \tilde{\xi }_{\breve{x}}\, \end{aligned}$$

(52)

identifying our “split into low and high frequency” components. We notice that the last remark in the above theorem, which is a direct consequence of (51), is saying that constant functions have no details or zero high frequencies components. We call analysis operator $U=U_{q'}$ the operator

$$\begin{aligned} U: \begin{array}[t]{lcl} \ell _2({\mathcal V},\mu ) &{} \rightarrow &{} \mathbb {R}^{{\mathcal V}}= \mathbb {R}^{\bar{{\mathcal V}}} \times \mathbb {R}^{\breve{{\mathcal V}}}\\ f &{} \mapsto &{} \{\left\langle {\xi _x,f}\right\rangle _{\mu }\}_{x\in {\mathcal V}}=\{\left\langle {\phi _{\bar{x}},f}\right\rangle _{\mu }, \left\langle {\psi _{\breve{x}},f}\right\rangle _{\mu }\}_{\bar{x}\in \bar{{\mathcal V}}, \breve{x}\in \breve{{\mathcal V}}}=[\bar{f},\breve{f}] \end{array} \, \end{aligned}$$

(53)

assigning to $f\in \ell _2({\mathcal V},\mu )$ its coefficients in the expansion in (52). As explained in the following theorem, the reconstruction of f from the knowledge of its coefficients U(f) can be made operative:

Theorem 16

(Reconstruction formula) Fix $q'>0$. For any $f \in \ell _2({\mathcal V},\mu )$, consider $\bar{f}\in \ell _2(\bar{{\mathcal V}},\mu )$ and $\breve{f}\in \ell _2(\breve{{\mathcal V}},\mu )$ respectively given by

$$\begin{aligned} \bar{f}(\bar{x})= & {} K_{q'}f(\bar{x})=U(f)(\bar{x}) \, , \quad \bar{x}\in \bar{{\mathcal V}}\, ,\\ \breve{f}(\breve{x})= & {} ( K_{q'}-\text{ Id }_{\breve{{\mathcal V}}})f(\breve{x})=U(f)(\breve{x}) \, , \quad \breve{x}\in \breve{{\mathcal V}}. \end{aligned}$$

Then,

$$\begin{aligned} f = \bar{R}_{q'} \bar{f}+ \breve{R}_{q'} \breve{f}\, , \end{aligned}$$

where

$$\begin{aligned} \bar{R}_{q'} = \begin{pmatrix} \text{ Id }_{\bar{{\mathcal V}}} - \frac{1}{q'} \bar{L}\\ [-L]_{\breve{{\mathcal V}}}^{-1} [L]_{\breve{{\mathcal V}}} \end{pmatrix} = \mathbf{approximation }\,\mathbf{operator }\, \mathbf{, } \end{aligned}$$

(54)

and

$$\begin{aligned} \breve{R}_{q'} =\begin{pmatrix} [L]_{\bar{{\mathcal V}}} [-L]_{\breve{{\mathcal V}}}^{-1} \\ - \text{ Id }_{\breve{{\mathcal V}}} - q' [-L]_{\breve{{\mathcal V}}}^{-1} \end{pmatrix} = \mathbf{detail }\, \mathbf{operator } \, . \end{aligned}$$

(55)

This last statement correspond to [5, Prop. 10] and fully describes our multiresolution scheme. In fact, in view of the properties of $\bar{{\mathcal G}}$, we can simply iterate the procedure with $(\bar{{\mathcal V}},\bar{L},\mu _{\bar{{\mathcal V}}})$ in place of $({\mathcal V}, L,\mu )$ resulting into a pyramidal algorithm as described in Eq. (46).

Still, we have not enough motivated the choice of the filter bank given in (48) and (49) for our “high and low frequencies” components in relation to regularity properties of signals. To clarify this point, let us first emphasize that in any reasonable wavelets construction, as mentioned in Sect. 6.2.1, good space and frequency localization properties are necessary ingredients. And in our approach, this issue is partially addressed via Theorem 14. Notice in particular that space localization is achieved using the determinantality of $\bar{{\mathcal V}}$, and the fact that $\bar{{\mathcal V}}$ is well spread on ${\mathcal V}$. Since $\breve{{\mathcal V}}= {\mathcal V}\setminus \bar{{\mathcal V}}$ is also a determinantal process, with kernel $\text{ Id }-K_q$, this suggested the detail definition (49) (the sign convention for the $\psi _{\breve{x}}$ is chosen to have a self-adjoint analysis operator $U: f \mapsto [\bar{f}, \breve{f}]$ in $\ell _2({\mathcal V},\mu )$). On the other hand, another fundamental ingredient is that if the signal f is “regular enough”, then the corresponding detail component $\breve{f}$ should be small. For instance, if the original function is constant it should not contain any high frequency component, that is, the corresponding $\breve{f}$ being identically zero. As the last remark in Theorem 15 states, this is in fact the case in our intertwining wavelets. However, more generally, a way to capture and guarantee that the size of the details is small for non-constant but regular functions is desirable. In the next section we give bounds on the involved operators as a function of $q'$ and we make sense of this latter regularity issue through the norm of Lf in Theorems 19 and 21.

6.3 Quality and Stability of Intertwining Wavelets

We collect here our results to guarantee numerical stability when using the forest-multiresolution-scheme and to guide in the choice of the parameters. We stress that the scheme presented in the previous section can be implemented when the downsample $\bar{{\mathcal V}}\subset {\mathcal V}$ is chosen according to any (even deterministic) rule. For this reason, the following statements controlling norms and sizes of the main involved objects are stated for arbitrary $\bar{{\mathcal V}}\subset {\mathcal V}$ and will not depend on q. We start by the control on the approximation and detail operators in (54) and (55), respectively, corresponding to [5, Prop. 14] and [5, Prop. 11].

Theorem 17

(Bound on the norm of the approximation operator) Fix $q'>0$. Let $\bar{{\mathcal V}}$ be any subset of ${\mathcal V}$, $\breve{{\mathcal V}}= {\mathcal V}\setminus \bar{{\mathcal V}}$, and let $\bar{R}_{q'}$ be the operator defined in (54). For any $p \ge 1$, for any $f \in \ell _{p}(\bar{{\mathcal V}}, \mu _{\bar{{\mathcal V}}})$,

$$\begin{aligned} \left\| {\bar{R}_{q'} f}\right\| _{p,{\mathcal V}} \le \left[ {\left( {1+ 2 \frac{\bar{w}_{\max }}{q'}}\right) ^p + \frac{w_{\max }}{\beta }}\right] ^{1/p} \, \mu (\bar{{\mathcal V}})^{1/p} \left\| { f}\right\| _{p,\bar{{\mathcal V}}} \, , \end{aligned}$$

(56)

with $w_{\max }$ as in (4), $\bar{w}_{\max }$ defined analogously w.r.t. the generator $\bar{L}$, and $\beta$ as in (44).

Theorem 18

(Bound on the norm of the detail operator) Fix $q'>0$. Let $\bar{{\mathcal V}}$ be any subset of ${\mathcal V}$, $\breve{{\mathcal V}}= {\mathcal V}\setminus \bar{{\mathcal V}}$, and let $\breve{R}_{q'}$ be the operator defined in (55). For all $p \ge 1$, for all $f \in \ell _{p}(\breve{{\mathcal V}}, \mu _{\breve{{\mathcal V}}})$,

$$\begin{aligned} \left\| {\breve{R}_{q'} f}\right\| _{p,{\mathcal V}} \le \left[ {\left( {\frac{w_{\max }}{\beta }}\right) ^{p/p^*} + \left( {1+ \frac{q'}{\gamma }}\right) ^p}\right] ^{1/p} \, \mu (\breve{{\mathcal V}})^{1/p} \left\| { f}\right\| _{p,\breve{{\mathcal V}}} \,, \end{aligned}$$

(57)

where $p^*$ is the conjugate exponent of p, $\beta$ as in (44), and

$$\begin{aligned} \frac{1}{\gamma } = \max _{\breve{x}\in \breve{{\mathcal V}}} E_{\breve{x}}\left[ {T_{\bar{{\mathcal V}}}}\right] . \end{aligned}$$

(58)

We refer to [5, Sections 6.1, 6.2 and 6.3] for estimates on $\gamma$ (defined in in (58), $\beta$ and $\bar{w}_{\max }$. We now move to the regularity issue mentioned above, that is, for “regular” signal we wish small details. By measuring the modulus of continuity of the original function through $\left\| {L f}\right\| _{p, {\mathcal V}}$, we get the following statement corresponding to [5, Prop. 15]:

Theorem 19

(Control on the size of details) For any $p \ge 1$ and any $f \in \ell _{p}({\mathcal V},\mu )$,

$$\begin{aligned} \left\| {\breve{f}}\right\| _{p,\breve{{\mathcal V}}} = \left\| {(K_{q'}-\text{ Id }) f}\right\| _{p,\breve{{\mathcal V}}} \le \frac{\max _{x\in {\mathcal V}} K_{q'}(x,\breve{{\mathcal V}})^{1/p}}{q' \mu (\breve{{\mathcal V}})^{1/p}} \left\| {L f}\right\| _{p, {\mathcal V}} \, . \end{aligned}$$

The next result gives a control on the size of the coefficients at arbitrary scale $i\le N$ when $\bar{{\mathcal V}}={\mathcal R}(\Phi _q)$, implementing the multiresolution scheme with $N\ge 1$ successive reductions. To this end, let us introduce suitable abbreviations for the objects at the different scales $i=1,\ldots ,N$. We have a given sequence of N (non-empty) nested vertex sets

$$\begin{aligned} {\mathcal V}_0 \supsetneq {\mathcal V}_1 \supsetneq \cdots \supsetneq {\mathcal V}_N , \quad \text { starting from } {\mathcal V}_0= {\mathcal V}, \end{aligned}$$

with associated parameters $\{q'_i \mid i = 0, \cdots N-1\}$.

For each $i=0,\ldots , N-1$ set:

• $\breve{{\mathcal V}}_i = {\mathcal V}_i \setminus {\mathcal V}_{i+1}$,

• $L_0 = L$, and $L_{i+1}$ the Schur complement of $[L_i]_{\breve{{\mathcal V}}_i}$ in $L_i$,

• the kernels $K_i=q'_i(q'_i \text{ Id }_{{\mathcal V}_i} -L_i)^{-1}$,

• $w_{i}, \beta _i$ and $\gamma _i$ as in (4), (44) and (58), respectively, w.r.t. $L_i$.

• $f_0=f$, and the successive approximation and detail components $f_{i+1}=K_i f_i$ and $g_{i+1}=(K_{i} - \text{ Id }_{\breve{{\mathcal V}}_i}) f_i$ as in (48) and (49), respectively, so that

  $$\begin{aligned} f_i = \bar{R}_{i} f_{i+1} + \breve{R}_{i} g_{i+1} \, , \end{aligned}$$

  with

  $$\begin{aligned} \bar{R}_i = \begin{pmatrix} \text{ Id }_{{\mathcal V}_{i+1}} - \frac{1}{q'_i} L_{i+1} \\ [- L_i]_{\breve{{\mathcal V}}_i}^{-1} [L_i]_{\breve{{\mathcal V}}_i {\mathcal V}_{i+1}} \end{pmatrix} \, \,\, \text{ and } \quad \breve{R}_i =\begin{pmatrix} [L_i]_{{\mathcal V}_{i+1} \breve{{\mathcal V}}_i} [- L_i]_{\breve{{\mathcal V}}_i}^{-1} \\ q' _i [L_i]_{\breve{{\mathcal V}}_i}^{-1} - \text{ Id }_{\breve{{\mathcal V}}_i} \end{pmatrix} \, . \end{aligned}$$

We can now extend the analysis operator in (53) to arbitrary scale $N\ge 1$ by setting

$$\begin{aligned} U_N : \begin{array}[t]{lcl} \ell _p({\mathcal V}) &{} \rightarrow &{} \ell _p({\mathcal V}_N,\mu _{{\mathcal V}_N}) \times \ell _p(\breve{{\mathcal V}}_{N-1}, \mu _{\breve{{\mathcal V}}_{N-1}}) \times \cdots \times \ell _p(\breve{{\mathcal V}}_{0}, \mu _{\breve{{\mathcal V}}_{0}}) \\ f &{} \mapsto &{} [f_N,g_N,g_{N-1},\ldots , g_1] \end{array} \end{aligned}$$

where the space $\ell _p({\mathcal V}_N,\mu _{{\mathcal V}_N}) \times \ell _p(\breve{{\mathcal V}}_{N-1}, \mu _{\breve{{\mathcal V}}_{N-1}}) \times \cdots \times \ell _p(\breve{{\mathcal V}}_{0}, \mu _{\breve{{\mathcal V}}_{0}})$ is endowed with the norm

$$\begin{aligned} \left\| {[f_N,g_N,g_{N-1},\ldots , g_1]}\right\| _p = \left( { \mu ({\mathcal V}_N) \left\| {f_N}\right\| _{p,{\mathcal V}_N}^p + \sum _{i=1}^N \mu (\breve{{\mathcal V}}_{i-1}) \left\| {g_i}\right\| _{p,\breve{{\mathcal V}}_{i-1}}^p}\right) ^{1/p} \, . \end{aligned}$$

Here is the control on the vectors identified by $U_N$ we derived in [5, Prop. 17].

Theorem 20

(Bound on the norm of the analysis operator) Let $p\ge 1$ and $p^*$ be its conjugate exponent. For any $N\ge 1$ and $f \in \ell _p({\mathcal V},\mu )$,

$$\begin{aligned} \left\| {U_N(f)}\right\| _p \le 2^{1/p^*} (1+N)^{1/p} \left\| {f}\right\| _p \, . \end{aligned}$$

(59)

Our last result is a form of so-called Jackson’s inequality. This result is in general crucial for numerical stability in approximation theory and multiresolution analysis (and in particular it plays an important role in our approach to tune the involved parameters, see [5, Section 6]). It guarantees small error for “smooth” functions, when reconstructing an approximating function of the original one after setting the details $g_i$’s to zero at all scales. This is clearly relevant if e.g. the aim of the multiresolution is to compress a signal. To formulate it, notice that by performing N reduction steps in our multiresolution, from the coefficients $[f_N,g_N,g_{N-1},\ldots , g_1]$ we can reconstruct $f=f_0$ as follows:

$$\begin{aligned} f=f_0&= \bar{R}_0 f_1 + \breve{R}_0 g_1\\&= \bar{R}_0 \bar{R}_1 f_2 + \bar{R}_0 \breve{R}_1 g_2 + \breve{R}_0 g_1\\&= \bar{R}_0 \bar{R}_1 \cdots \bar{R}_{N-1} f_N + \sum _{j=0}^{N-1} (\bar{R}_0 \cdots \bar{R}_{j-1}) \breve{R}_j g_{j+1} . \end{aligned}$$

Fig. 9

Two steps of the multiresolution for the intertwining wavelets (upper plot) and Daubechies-12 wavelets (lower plot). The three parts of each plot give respectively $g_1,g_2$ and $f_2$. Notice e.g. that the size of $g_2$ is half the size of $g_1$ only for Daubechies-12 wavelets, reason being that the subsampled nodes are random (given by the roots) in our method

Fig. 10

Original signal for analysis on the one dimensional torus

The compression of f associated to scale N is thus the function on ${\mathcal V}$:

$$\begin{aligned} \tilde{f}(N)=\bar{R}_0 \bar{R}_1 \cdots \bar{R}_{N-1} f_N, \end{aligned}$$

(60)

and we have the following Jackson’s inequality measuring its quality.

Theorem 21

(Jackson’s inequality: quality of the compression of a signal) For any $p \ge 1$ and any $f \in \ell _p({\mathcal V},\mu )$, let $\tilde{f}(N)$ be the compression associated to scale $N\ge 1$ in (60). Then

$$\begin{aligned}&\left\| {f-\tilde{f}(N)}\right\| _{p,{\mathcal V}} \nonumber \\&\quad \le \left\{ {\sum _{j=0}^{N-1} \prod _{i=0}^{j-1} \left[ {\left( {1 + 2 \frac{w_{i+1}}{q'_i}}\right) ^p + \frac{w_{i}}{\beta _i}}\right] ^{1/p} \left[ {\left( {\frac{w_{j}}{\beta _j}}\right) ^{p/p^*} + \left( {1 + \frac{q'_j}{\gamma _j}}\right) ^p}\right] ^{1/p} \frac{1}{q'_j} }\right\} \left\| {L f}\right\| _{p,{\mathcal V}} \nonumber \\&\qquad + \left\{ {\sum _{j=0}^{N-1} \prod _{i=0}^{j-1} \left[ {\left( {1 + 2 \frac{w_{i+1}}{q'_i}}\right) ^p + \frac{w_{i}}{\beta _i}}\right] ^{1/p} \left[ {\left( {\frac{w_{j}}{\beta _j}}\right) ^{p/p^*} + \left( {1 + \frac{q'_j}{\gamma _j}}\right) ^p}\right] ^{1/p} \frac{1}{q'_j} \sum _{k=0}^{j-1} 2 q'_{k} \left( {\frac{w_{k}}{\beta _k}}\right) ^{1/p^*}}\right\} \left\| {f}\right\| _{p,{\mathcal V}} \end{aligned}$$

(61)

For the proof of this statement see [5, Prop. 18]. It is worth stressing that the second summand involving $\left\| {f}\right\| _{p,{\mathcal V}}$ is due to the propagation of the error in the intertwining relation, it would vanish if the generators at all scales were perfectly intertwined.

6.4 Choosing the Downsampling and Concentration Parameters

Intertwining error and localization property have to be our guidelines to choose our downsampling parameter q and our concentration parameter $q'$. Beyond squeezing measurement, another way to look at localization properties is to focus on the reconstruction operator norm: spread out wavelets $\phi _{\breve{x}}$ and scaling functions $\psi _{\bar{x}}$ will lead to bad reconstruction properties, i.e., to a large operator norm. These norms are controlled by Eqs. (56) and (57). Since the $\bar{R}$ operators only are composed together in the reconstruction scheme, Eq. (56) is the crucial inequality and we look at it for $p = + \infty$. As far as the intertwining error is concerned we look at Eq. (43), for $p = +\infty$ too. These inequalities say that we want $q'/\beta$ and $\bar{w}_{\max }/q'$ as small as possible. This implies that we want $\bar{w}_{\max } / \beta$ as small as possible. Note that this is a random function of q. It does not depend on $q'$, but it is very costly to estimate it by direct Monte-Carlo methods.

Fig. 11

Relative compression error of signal in Fig. 10 in terms of the percentage of kept normalized detail coefficients. In red, the error using intertwining wavelets. In blue, error using Daubechies-12 wavelets (Color figure online)

Fig. 12

Original signal (blue line) and compression (red line) with intertwining wavelets keeping $10\%$ of normalized detail coefficients (Color figure online)

Fig. 13

A compressed white rectangle with Haar wavelets on the first line, for which the percentage of kept detail coefficients is reported in each picture. The same rectangle is compressed with intertwining wavelets on the second line, with the same number of kept coefficients

Fig. 14

Compression with Haar wavelets on the left, with intertwining wavelets on the right. In both case the last picture is the original signal

Fig. 15

Approximation components for Haar and intertwining wavelets, with 256 and 205 coefficients, respectively

Fig. 16

Approximation components for Haar and intertwining wavelets, with 256 and 246 coefficient, respectively

Fig. 17

Two steps of the intertwining wavelets multiresolution upsampled to the original graph: a $f_0$; b $\bar{R}_0 \bar{R}_1 f_2$; c $\breve{R}_0 g_1$; d $\bar{R}_0 \breve{R}_1 g_2$. a Original signal. b Approximation. Size of $f_2$: 206. c Detail at scale 1. Size of $g_1$: 188. d Detail at scale 2. Size of $g_2$: 106 (Color figure online)

Fig. 18

Relative compression errors of signal in Fig. 17a, in terms of the number of kept coefficients. In red, the error using intertwining wavelets. In blue, error using the spectral graph wavelets pyramidal algorithm. Experiments without (left plot) and with (right plot) sparsification (Color figure online)

Now the same kind of algebra we used to prove that the mean hitting time of the root set does not depend on the starting point, offers a workaround. We can estimate $\bar{w}_{\max }$ with

$$\begin{aligned} \tilde{w} = \mathbb {E}\left[ {1 \over |{\mathcal R}(\Phi _q)|} \sum _{\bar{x} \in {\mathcal R}(\Phi _q)} -\bar{L}(\bar{x}, \bar{x}) \right] \end{aligned}$$

and $1 / \beta$ with

$$\begin{aligned} {1 \over \tilde{\beta }} = \mathbb {E}\left[ {1 \over |{\mathcal R}(\Phi _q)|} \sum _{\bar{x} \in {\mathcal R}(\Phi _q)} \sum _{z \in {\mathcal V}} P(\bar{x}, z) E_z[T_{\mathcal R}(\Phi _q)] \right] . \end{aligned}$$

It turns out that these expected values are respectively equal to

$$\begin{aligned} \tilde{w} = q \mathbb {E}\left[ {|{\mathcal V} \setminus {\mathcal R}(\Phi _q)| \over 1 + |{\mathcal R}(\Phi _q)|} \right] \end{aligned}$$

and

$$\begin{aligned} {1 \over \tilde{\beta }} = {1 \over w_{\max }} \mathbb {E}\left[ {|{\mathcal V} \setminus {\mathcal R}(\Phi _q)| \over |{\mathcal R}(\Phi _q)|} \right] . \end{aligned}$$

These expected values are easy to estimate by Monte-Carlo simulations for q between two bounds of order $w_{\max }$—such a restriction is natural if we expect $|\bar{\mathcal V}|$ to be a fraction of $|{\mathcal V}|$—since we have a practical algorithm to sample all the $\Phi _q$ together. We can then choose q by optimization between the two bounds. We refer to [5, Section 6] for more details.

It remains to choose $q'$ once we have chosen q and sampled $\Phi _q$. It turns out that the previous estimations on $\bar{w}_{\max }$ and $1 / \beta$ suggest that the norm of the composed $\bar{R}$ could be bounded by $|{\mathcal V}|$ by choosing $\bar{w}_{\max } / q'$ and $q' / \beta$ of the same order. This is actually ensured by setting

$$\begin{aligned} q' = 2 w_{\max }{|{\mathcal R}(\Phi _q)| \over |{\mathcal V} \setminus {\mathcal R}(\Phi _q)|}\,. \end{aligned}$$

While ensuring numerical stability of the algorithm, this, in turn, essentially amounts to make intertwining error and localization property of the same importance. We refer once again to [5, Section 6] for details and we conclude this survey with giving some numerical experiments based on these results.

6.5 Experiments, Intertwining Wavelets in Action

We collect here some numerical experiments on well-known benchmarks in signal processing illustrating the performances of our method. Intertwining wavelets have been thought and are naturally suited to signals on irregular graphs, yet, our experiments show that they perform well also on classical euclidian spaces. To see that, we present a few examples of different nature and a comparison of the error with some of the most common methods used in the corresponding setup. We start from classical one-dimensional and two-dimensional signals in Sect. 6.5.1 and then move to a non-regular network setup in Sect. 6.5.2. Unless specified, in all experiments we always include the sparsification procedure mentioned in Sect. 5.3.2.

6.5.1 Comparison with Classical Wavelet Algorithms on the Torus

In Fig. 9, we show two steps of the multiresolution analysis for intertwining wavelets and Daubechies-12 wavelets [13] applied to the commonly used benchmark signal shown in Fig. 10. Figure 11 shows the compared relative compression errors in terms of the percentage of kept detail coefficients while compressing the above benchmark on the 1d-torus, we see in particular than even on regular networks intertwining wavelets are a valuable tool. We refer to [5] for a detailed account on the compression algorithm associated with our multiresolution scheme. In Fig. 12, we compare the original signal with the compressed one we obtained with our wavelets by keeping $10\%$ of the detail coefficients.

We next move on signals on a 2d-torus. In Figs. 13 and 14, we show the compressions (obtained by setting to zero a fraction of the smallest detail coefficients) of two different images (a rectangle and a cameramen) obtained with Interwining and Haar [13] wavelets. Figures 15 and 16 show the related approximation components.

6.5.2 A Signal on a Non-regular Graph

We took from [37] and the GSP toolbox [31] the sensor graph and the signal represented in Fig. 17 together with two steps of the multiscale analysis. In Fig. 18 we compare the results of the intertwining compression algorithm with those of the spectral graph wavelet pyramidal algorithm [37]. In this last figure we added the result of the algorithm also without sparsification. It is worth noting that, in this example at least, sparsification helps significantly, not only for algorithmic complexity.