Spectral Analysis for a Discrete Metastable System Driven by Lévy Flights

Abstract

In this paper we consider a finite state time discrete Markov chain that mimic the behaviour of solutions of the stochastic differential equation

$$\begin{aligned} X_{t}^{\varepsilon }(x)=x-\int _0^t U^{\prime }(X_{s}^{\varepsilon })\, \mathrm {d}s+\varepsilon L_{t}, \end{aligned}$$

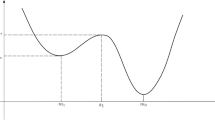
where U is a multi-well potential with $n\ge 2$ local minima and $L=(L_t)_{t\ge 0}$ is a symmetric $\alpha$-stable Lévy process (Lévy flights process). We investigate the spectrum of the generator of this Markov chain in the limit $\varepsilon \rightarrow 0$ and localize the top n eigenvalues $\lambda ^\varepsilon _1,\ldots ,\lambda ^\varepsilon _n$. These eigenvalues turn out to be of the same algebraic order $\mathcal O(\varepsilon ^\alpha )$ and are well separated from the rest of the spectrum by a spectral gap. We also determine the limits $\lim _{\varepsilon \rightarrow 0}\varepsilon ^{-\alpha } \lambda ^\varepsilon _i$, $1\le i\le n$, and show that the corresponding eigenvectors are approximately constant over the domains which correspond to the potential wells of U.