Resonance frequency of an orthotropic layer to non-principal vertically incident SH body and surface waves

Abstract

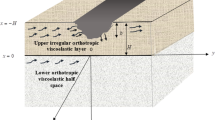
In this study, non-principal waves propagating in an isotropic elastic half-space covered by an orthotropic layer are examined. The main objective is to establish a formula for the SH transfer function induced by an vertically incident SH wave and a formula for the H/V ratio of surface waves. The peak frequencies of both the SH transfer function and the H/V ratio curve are examined for models with low to high impedance contrasts to verify the applicability of the quarter wave-length rule for both SH body waves and surface waves. It is numerically shown that the quarter wave-length rule applies well for non-principal SH body wave. Non principal surface waves are shown to be a composition of Love and Rayleigh waves, and their peaks follow the quarter wave-length rule only in the case of high impedance contrast. For medium or low impedance contrasts, the peak frequencies of surface waves could differ from the peak frequencies of SH body wave with relative differences up to $50\%$.

Appendix

1.1 Appendix A. The elements of matrix Q

The element of matrix $\textbf{Q}$ in (6) are:

$$\begin{aligned} Q_{11}= & {} c_{11} \cos ^4 \theta +\dfrac{1}{2} (c_{13} + 2 c_{55}) \sin ^2 (2 \theta ) \nonumber \\{} & {} + c_{33} \sin ^4 \theta , \nonumber \\ Q_{22}= & {} c_{22}, \nonumber \\ Q_{33}= & {} c_{33} \cos ^4 \theta +\dfrac{1}{2} (c_{13} + 2 c_{55}) \sin ^2 (2 \theta ) \nonumber \\{} & {} + c_{11} \sin ^4 \theta , \nonumber \\ Q_{44}= & {} c_{44} \cos ^2\theta + c_{66} \sin ^2\theta , \nonumber \\ Q_{55}= & {} \dfrac{1}{8} [c_{11}-2 c_{13}+c_{33}+4c_{55}\nonumber \\{} & {} -\left( c_{11}-2 c_{13}+c_{33}-4c_{55}\right) \cos (4 \theta ) ] ,\nonumber \\ Q_{66}= & {} c_{66} \cos ^2\theta + c_{44} \sin ^2\theta , \nonumber \\ Q_{12}= & {} c_{12} \cos ^2 \theta + c_{23} \sin ^2 \theta , \nonumber \\ Q_{13}= & {} \dfrac{1}{8} [c_{11}+6 c_{13}+c_{33}-4c_{55}\nonumber \\{} & {} -\left( c_{11}-2 c_{13}+c_{33}-4c_{55}\right) \cos (4 \theta ) ], \nonumber \\ Q_{15}= & {} -\dfrac{1}{4}[c_{11} - c_{33} \nonumber \\{} & {} + (c_{11} - 2 c_{13} + c_{33} - 4 c_{55}) \cos (2 \theta )]\sin (2 \theta ), \nonumber \\ Q_{23}= & {} c_{23} \cos ^2 \theta + c_{12} \sin ^2 \theta ,\nonumber \\ Q_{25}= & {} (-c_{12} + c_{23}) \cos \theta \sin \theta , \nonumber \\ Q_{35}= & {} \dfrac{1}{4}[-c_{11} + c_{33}\nonumber \\{} & {} + (c_{11} - 2 c_{13} + c_{33} - 4 c_{55}) \cos (2 \theta )]\sin (2 \theta ), \nonumber \\ Q_{46}= & {} (c_{44} - c_{66} ) \cos \theta \sin \theta . \end{aligned}$$

(A.1)

1.2 Appendix B. The elements of matrix S

The block matrices in equation (52) are

$$\begin{aligned} \textbf{S}_1= & {} \dfrac{1}{\alpha _1-\alpha _2}\nonumber \\{} & {} \times \left[ {\begin{array}{*{20}{c}} \alpha _1\cos (\varepsilon _1)-\alpha _2\cos (\varepsilon _2)&{}\alpha _1\alpha _2[-\cos (\varepsilon _1)+\cos (\varepsilon _2)]\\ \cos (\varepsilon _1)-\cos (\varepsilon _2)&{}-\alpha _2\cos (\varepsilon _1)+\alpha _1\cos (\varepsilon _2) \end{array}} \right] \nonumber \\ \end{aligned}$$

(B.1)

$$\begin{aligned} \textbf{S}_2= & {} \dfrac{i}{(\alpha _1\gamma _2-\alpha _2\gamma _1)I_L^{\pi /2}I_L^0}\nonumber \\{} & {} \times \left[ {\begin{array}{*{20}{c}} -\alpha _1\gamma _2I_L^0\sin (\varepsilon _1)+\alpha _2\gamma _1I_L^{\pi /2}\sin (\varepsilon _2)&{}\alpha _1\alpha _2[I_L^0\sin (\varepsilon _1)-I_L^{\pi /2}\sin (\varepsilon _2)]\\ -\gamma _2I_L^0\sin (\varepsilon _1)+\gamma _1I_L^{\pi /2}\sin (\varepsilon _2)&{}\alpha _2I_L^0\sin (\varepsilon _1)-\alpha _1I_L^{\pi /2}\sin (\varepsilon _2) \end{array}} \right] \nonumber \\ \end{aligned}$$

(B.2)

$$\begin{aligned} \textbf{S}_3= & {} \dfrac{i}{\alpha _1-\alpha _2}\nonumber \\{} & {} \times \left[ {\begin{array}{*{20}{c}} -\alpha _1I_L^{\pi /2}\sin (\varepsilon _1)+\alpha _2I_L^0\sin (\varepsilon _2)&{}\alpha _1\alpha _2[I_L^{\pi /2}\sin (\varepsilon _1)-I_L^0\sin (\varepsilon _2)]\\ -\gamma _1I_L^{\pi /2}\sin (\varepsilon _1)+\gamma _2I_L^0\sin (\varepsilon _2)&{}\alpha _2\gamma _1I_L^{\pi /2}\sin (\varepsilon _1)-\alpha _1\gamma _2I_L^0\sin (\varepsilon _2) \end{array}} \right] \nonumber \\ \end{aligned}$$

(B.3)

$$\begin{aligned} \textbf{S}_4= & {} \dfrac{1}{\alpha _1\gamma _2-\alpha _2\gamma _1}\nonumber \\{} & {} \times \left[ {\begin{array}{*{20}{c}} \alpha _1\gamma _2\cos (\varepsilon _1)-\alpha _2\gamma _1\cos (\varepsilon _2)&{}\alpha _1\alpha _2[\cos (\varepsilon _1)-\cos (\varepsilon _2)]\\ \gamma _1\gamma _2[\cos (\varepsilon _1)-\cos (\varepsilon _2)]&{}-\alpha _2\gamma _1\cos (\varepsilon _1)+\alpha _1\gamma _2\cos (\varepsilon _2) \end{array}} \right] \nonumber \\ \end{aligned}$$

(B.4)

where $\varepsilon _1=k_1h$ and $\varepsilon _2=k_2h$.