1 Introduction

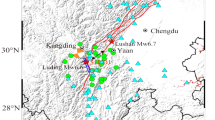
At 22:55:37 (Beijing time) on June 17, 2019 (14:56 UTC), an earthquake with Mw 5.8 occurred in Changning County in the southeast of Sichuan Province, China. According to the report from the China Earthquake Networks Center (CENC) (http://www.cenc.ac.cn/), the epicenter was located in Changning County (28.34° N, 104.90° E) approximately 260 km from the city of Chengdu (CEA 2019). The most serious structural damage occurred in Changning County, especially in the village of Fuxing (http://www.iem.net.cn/). Since December 2018, the occurrence probability of earthquake for Ms > 5 has gradually increased in southeast Sichuan. On December 16, 2018, an earthquake with Mw 5.5 (Ms 5.7) occurred in Wenxing County, and on January 16, 2019, an earthquake with Mw 5.1 (Ms 5.3) struck Gongxian County; epicenters of these two earthquakes are very close to that of the Changning earthquake (see Fig. 1) (http://news.ceic.ac.cn/). The Mw 5.8 (Ms 6.0) Changning earthquake occurred at a focal depth of 16 km coming from CENC, while Yi et al. (2019)’s seismic inversion results indicate that the focal depths of this series of earthquakes range from 0 to 10 km. Seismic inversion of Yi’s result is adopted in this paper. The main shock was followed by 44 aftershocks that persisted until June 24; among them, there were three Mw 5.0–5.9 aftershocks and four Mw 4.0–4.9 aftershocks as shown in Fig. 1 (http://www.cea.gov.cn/). On the basis of the regional tectonic background, the Changning earthquake was caused by a secondary fault distinct from the seismogenic faults of the Lushan earthquake and Wenchuan earthquake, which occurred within the Longmenshan thrust fault zone (Yin and Guo 2019).

Fig. 1
figure 1

Map of the Changning main shock and its aftershocks in Sichuan Province on June 17, 2019, the focal mechanism parameters of aftershocks are adopted from Hu et al. (2019)

Full size image

The fault zone of the Changning earthquake ranged from Shuanghe County to Gongxian County and was oriented roughly northwest-southeast (see Fig. 2). Public buildings, including the schools, hospitals, and government buildings, within the fault zone are mainly reinforced concrete structures, whereas the civil buildings are mainly masonry and masonry-timber structures and a small number of timber structures. Based on field survey, representative structures in the fault zone that were seriously damaged are shown in Fig. 2. Severe ground shaking caused heavy damage to many reinforced concrete buildings, masonry structures, and timber houses. Especially, the failure of filled walls of frame structures is commonly seen (Dai and Yang 2019).

Fig. 2
figure 2

Representative damaged structures in the fault zone. Inner graphs labeled “A” represent schools and “B” is a hospital; they were designed based on the seismic design code. Graph “C” represents residential buildings which had not been designed for earthquake resistance. Graph “D” represents high-rise building which is designed based on the seismic design code. The rectangle is the prediction of the fault plane on the surface given by Shan et al. (2009)

Full size image

The focal mechanism parameters are given in Table 1 (https://earthquake.usgs.gov/).

Table 1 Earthquake parameters of the Changning main shock and the fault geometry
Full size table

As shown in Fig. 2, the nonstructural components, such as the filled walls and dropped ceilings of frame structures, were severely damaged during the earthquake, especially for a large number of rural masonry and timber buildings without seismic design. The main damage failure mode to timber structures in the Changning earthquake was collapse of roofs, cracking, and dislocation of walls (Dai and Yang 2019).

Compared with the Yibin earthquake, Xingwen earthquake, Xiahe earthquake, and Hualian earthquake, the number of deaths and injuries is relatively high in the Changning earthquake, as shown in Table 2 (https://www.cea.gov.cn/cea/dzpd/dzzt/index.html). Thirteen people died, and 226 people were injured during the Changning earthquake, which is similar to the casualties of the Hualien earthquake, but the magnitude of the Hualien earthquake was 6.5, while that of the Changning earthquake was 6.0. The casualties from the Changning earthquake were far more numerous than those from other earthquakes with similar magnitude. Strong motions of the Changning main shock were recorded by the China Strong Motion Network Center (CSMNC). Fifty-eight groups of three-component accelerograms were recorded during the main shock (see the electronic Supplemental Table). The triggered strong-motion stations are mainly located in Sichuan Province at Joyner-Boore distances of 0–394 km. Among these stations, the Joyner-Boore distances of seven strong-motion stations are within 100 km. The largest peak ground acceleration (PGA) of 599 cm/s2 during the main shock was recorded in station 51GXT, which is located at a soil site. Of all the 58 strong-motion stations, 49 stations are installed at soil sites, while 9 stations are installed at rock sites. In this paper, to understand the heavy damage caused by the Changning earthquake in terms of the ground motion characteristics, we studied a dataset of strong-motion observations and presented an overview of these data from this event. The characteristics of the strong-motion records are analyzed in terms of the amplitudes, durations, and spectra of the ground motions. The total residual, within-event residual, and between-event residual are calculated based on the BSSA14 model, CB12 model, and AS16 model (Boore et al. 2013; Campbell and Bozorgnia 2012; Afshari and Stewart 2016). Ultimately, from the perspective of ground motion characteristics, the cause of high amplitude of ground motion during the Changning earthquake from the source, path, and site effects was studied.

Table 2 Comparison of casualties from similar magnitude earthquakes
Full size table

2 Strong-motion dataset

The strong-motion data were obtained from the CSMNC (http://www.smsd-iem.com). We select 58 sets of three-component records from free-field stations in Sichuan Province recorded by digital instrument. To achieve more reliable PGAs, PGVs, and PGDs, all 58 sets of three-component records were processed with a bandwidth of 0.1–30.0 Hz by using a Butterworth filter and baseline adjustment. To obtain more useful information, the values recorded in the Changning earthquake were compared with the estimated values from ground motion models (GMMs) of the NGA-West2 project. The Joyner-Boore distances (Rjb) were calculated and used in the GMM of the NGA-West 2 project. The locations of the strong-motion stations used in this study are shown in the Supplemental Material Figure.

Figure 3a shows the strong-motion stations at Joyner-Boore distances of less than 100 km and the fault projection by Shan et al. 2019). The largest PGA was observed at station 51GXT on the hanging-wall side (see Fig. 2) in Gongxian County, the recorded PGA of EW, NS, and UD component is 599.4 cm/s2, 499.0 cm/s2, and 414.7 cm/s2, respectively, while the PGAs at other stations are less than 50 cm/s2. The largest PGV of EW, NS, and UD components is 26.4, 28.1, and 9.4 cm/s, respectively, while the PGVs at other stations are less than 4 cm/s. The largest PGD of EW, NS, and UD components is 1.8, 2.6, and 1.4 cm, respectively, while the PGDs at other stations are less than 1 cm. Figure 3b–d shows the acceleration, velocity, and displacement of UD component, respectively. The horizontal time histories of EW and NS components are given in the Supplemental Material Figure.

Fig. 3
figure 3

a Locations of strong-motion stations (Rjb < 100 km) and time histories for b acceleration, c velocity, and d displacement of the vertical (UD) component. The rectangle shown in a is the prediction of the fault plane on the surface given by Shan et al. 2019). Regular triangles denote strong-motion stations. The fault projection is indicated by solid lines. The spatial division of the hanging wall (HW) and foot wall (FW) is illustrated by the dashed lines (Abrahamson and Somerville 1996). Joyner-Boore distance and name of the station are marked in the low-right corner of each panel

Full size image

To analyze the near-source characteristics of the ground motion on 51GXT, the horizontal components of the ground motion are rotated to the fault normal and fault parallel. The results are shown in Fig. 4; for PGA, the ground motion in fault normal is different from the ground motion in fault parallel. For PGV and PGD, there is almost no difference between the ground motion in fault normal and in fault parallel components.

Fig. 4
figure 4

a Acceleration, b velocity, and c displacement of ground motion rotated to fault normal and fault parallel direction in station 51GXT

Full size image

To study the difference between the observed values and predicted values by the GMMs, a GMM from the NGA-West2 project (Boore et al. 2013) for shallow crustal earthquakes is used in this paper. In this model, the average shear-wave velocity over the upper 30 m (VS30) is used to represent the site condition. The VS30 values for most stations in this study are not measured from the velocity profile with depth zp > 30 m; they are adopted from the database by Seyhan et al. (2014) and Yu and Li (2015). The values of VS30 are provided in the Supplemental Table.

3 Instrumental seismic intensity

The instrumental seismic intensity is a ground-motion-based parameter which can be used to estimate the extent of structural damage. The instrumental seismic intensity is derived from the related ground-motion parameters (PGA and PGV) through empirical relationships (Trifunac and Brady 1975); it was used in the U.S. Geological survey’s ShakeMap (Wald et al. 1999, Wald et al. 2006). In order to understand the distribution of the seismic intensity of Changning earthquake, the instrumental intensity was calculated based on the calculation code of China (CEA 2015). The corresponding equations are as follows:

$$ {\displaystyle \begin{array}{c}{I}_{\mathrm{PGA}}=3.17\lg \left(\mathrm{PGA}\right)+6.59\ \\ {}{I}_{\mathrm{PGA}}=3.17\lg \left(\mathrm{PGA}\right)+9.77\ \end{array}} $$
(1)

where

$$ \mathrm{PGA}=\max \left(a\left({t}_i\right)\right) $$
(2)
$$ \left(a\left({t}_i\right)\right)=\sqrt{a{\left({t}_i\right)}_{\mathrm{EW}}^2+a{\left({t}_i\right)}_{\mathrm{NS}}^2+a{\left({t}_i\right)}_{\mathrm{UD}}^2} $$
(3)

and

$$ \mathrm{PGV}=\max \left(v\left({t}_i\right)\right) $$
(4)
$$ v\left({t}_i\right)=\sqrt{v{\left({t}_i\right)}_{\mathrm{EW}}^2}+v{\left({t}_i\right)}_{\mathrm{NS}}^2+v{\left({t}_i\right)}_{\mathrm{UD}}^2 $$
(5)

Based on the calculation code of China (CEA 2015), instrumental seismic intensity is divided into 12 levels. When the level of instrumental seismic intensity is below VI, people can feel strong ground shaking. When the level of instrumental seismic intensity is between level VI and VII, brittle failure occurs to the structures of the building. When the level of instrumental seismic intensity is larger than level VII, plastic failure occurs to the structures of the building. The higher the instrumental seismic intensity, the more severe the damage. The distribution of the instrumental seismic intensity is shown in Fig. 5. The largest intensity reaches IX at station 51GXT. The mean value of the intensity is approximately V at Joyner-Boore distances from 100 to 200 km.

Fig. 5
figure 5

Spatial distribution of the instrumental seismic intensity. The regular triangles denote soil stations, while inverted triangles represent rock stations. The rectangle denotes the fault plane of the Changning main shock. Values of the instrumental seismic intensity are shown by the color scale

Full size image

4 Ground motion amplitude characteristics

4.1 PGA and PGV

The PGA and PGV are the most concerned amplitude parameters of ground motion. Figure 6 presents an overview of the spatial variation of the observed horizontal PGA and PGV. The largest PGA and PGV are noted on the hanging wall. The maximum horizontal geometric mean value of the PGA is 536.1 cm/s2, and the maximum horizontal geometric mean value of the PGV is 29.6 cm/s. Both of these maximum values are recorded on station 51GXT.

Fig. 6
figure 6

Spatial distributions of observed horizontal ground motion. The a PGA and b PGV values are shown on the color scale

Full size image

4.2 Ground motion attenuation

The ground motions models are used to describe the attenuation relation of ground motion with distances. A few models have been developed for Western China, of which three attenuation models are often used, the first widely accepted attenuation model for Southwest China given by Huo (1989), the Yu et al. 2006 model for Western China (Yu and Wang 2006), and the Yu et al. 2013 model applied in the latest seismic hazard map of China (Yu et al. 2013). However, these models were basically transferred from the seismic intensity attenuation relation based on field survey, other than directly from strong ground motions, and the site conditions are defined by the Chinese seismic design code (China Ministry of Construction 2010). There is no suitable local GMM that can be used for studying the residuals and evaluating the between-event and within-event components. GMMs in NGA-West2 for shallow crustal earthquakes provided basis for the analysis of residuals in this study (Ancheta et al. 2014). Ren et al. (2018) applied the ASK14 (Abrahamson et al. 2013) and BSSA14 (Boore et al. 2013) models in analyzing the ground motion of Mw 6.6 Lushan earthquake and Mw 6.5 Jiuzhaigou earthquake. In this paper, the BSSA14 model is adopted to study the residuals and evaluate the between-event and within-event components. The functional form of BSSA14 model is given as follows:

$$ {\displaystyle \begin{array}{l}\ln Y={F}_E\left(M, mech\right)+{F}_p\left({R}_{\mathrm{jb}},M, region\right)\\ {}+{F}_s\left({V}_{\mathrm{S}30},{R}_{\mathrm{jb}},M, region,{z}_1\right)+\sigma \end{array}} $$
(6)

where lnY is the natural logarithm of the observed values, such as PGV, PGA, and Sa. FE, Fp, and Fs are functions of the source, path, and site effects, respectively. σ is the standard deviation of the BSSA14 model; and the M, VS30, mech, region, Rjb, and ZTOR are the variables. The application of the model and the ranges of the variables are shown in Table 3 (Boore et al. 2013).

Table 3 The application of the model and the range of the variables
Full size table

The observed horizontal PGV, PGA, and Sa values at periods of 0.2 and 2.0 s are compared with the predicted values from BSSA14 model. To calculate the median predicted values of the Changning earthquake, Mw = 5.8, VS30 = 370 m/s, ZTOR = 0 km, and reversed strike-slip fault type are used by Boore et al. (2014). As shown in Fig. 7a, the observed values of PGV are larger than the predicted values of BSSA14 model. For PGA and Sa at typical periods of 0.2 and 2.0 s, the difference between the observed and predicted values becomes less pronounced with the increase of period. The total residuals show a clear amplification at distance around 150 km. As we all know, the records of shallow crustal earthquake are characterized in most part by large-amplitude Lg waves for epicentral distances beyond 150 km. These waves travel with a wide ranging between 3.2 and 2.5 km/s. It is recognized that the observed large amplitudes are most likely to be the P and S wave reflections from the Moho discontinuity with the long epicentral distance (Campillo 1990). Usually these effects are noted at high frequencies (PGA, PGV, and Sa at T = 0.2 s). As is shown in Fig. 7, the measured values of PGV are larger than the predicted values of PGV with the same magnitude of global shallow crustal earthquakes. The correlation between PGV parameters and structural damage is very good (Li et al. 2007; Zhai et al. 2013). Therefore, the large PGV may also be one of the reasons causing relatively serious damage.

Fig. 7
figure 7

a Comparison of observed horizontal PGV, PGA, and Sa with the predicted values of BSSA14. The solid line represents the predicted values of BSSA14. The dotted lines are the standard deviation of BSSA14 model. The green solid points represent the observed ground motion values of Changning earthquake. b Residuals versus Rjb. Residuals are calculated based on the real values of Mw = 5.8, VS30 for each site, ZTOR = 0 km and reversed strike-slip fault type. The point with Rjb = 0 is plotted on the vertical axis

Full size image

To quantitatively analyze the difference of ground motion between the Changning earthquake and the BSSA14 model with the same magnitude, the residuals are calculated.

$$ {\delta}_{es}=\ln {Y}_{observed}-\ln {Y}_{predicted} $$
(7)

where δes is the residual, and lnYobserved and lnYpredicted are the observed values and predicted values for each site. As shown in Fig. 7b, the residuals of PGV, PGA, and Sa of Changning earthquake are basically greater than zero, especially for PGV.

4.3 Residual analysis

Residual analysis of ground motion is an effective way to analyze the effect of the source, path, and site on the ground motions (Al Atik and Abrahamson 2010). The total residuals of earthquake can be divided into between-event residuals and within-event residuals.

$$ {\updelta}_{es}=\updelta {\mathrm{B}}_e+{\updelta \mathrm{W}}_{es} $$
(8)

where e and s represent the earthquake and the station, respectively. The between-event residual (δBe) means the residual for different earthquakes e; the within-event residual (δWes) means the residual at station s for the earthquake e.

The total residuals δes are calculated in the previous analysis, as shown in Fig. 7b. The between-event residual δBe is calculated by choosing recordings with the distance Rjb within 80 km. The reason is that when the distance is beyond 80 km, crustal structure can have a significant effect on ground motion (Abrahamson et al. 2014). The between-event residual δBe is the average deviation between the chosen recordings and the median of the predicted values from the BSSA14 model. The δWes represents the degree of misfit between the observed value at station s and the median prediction for the specific earthquake e. To compare the source, path, and site effect of Changning earthquake with those of earthquakes with similar magnitude (Mw ~ 6) in the same region, the Kangding earthquake, Ludian earthquake, Jinggu earthquake, and Changning aftershock are compared (Hu et al. 2015, Hu et al. 2016, and Xu et al. 2019). As shown in Fig. 8, these four earthquakes are plotted on the map. As shown in Fig. 8, records for distance Rjb within 80 km are used to calculate the between-event residuals.

Fig. 8
figure 8

a Rjb versus earthquakes in the same region and b geological background of Southwest China

Full size image

The parameters and geometries of the fault planes for the Kangding earthquake, Ludian earthquake, and Jinggu earthquake are shown in Table 4.

Table 4 Parameters of the selected earthquakes at the same region
Full size table

The epicenter location and focal depth were provided by the CENC, and the MW, strike, dip, and, slip values are adopted from the Global Centroid-Moment-Tensor (GCMT) project. The δBe values of the five earthquakes for different periods are shown in Fig. 9.

Fig. 9
figure 9

Between-event residuals versus period. The between-event residuals are calculated in terms of the BSSA14 model for the Kangding earthquake, Ludian earthquake, Jinggu earthquake, Changning main shock, and Changning aftershock

Full size image

As shown in Fig. 9, the between-event residuals of PGA and Sa of Changning main shock are greater than zero for periods over 0.6 s. This means that the source effects are strong in the intermediate and long periods while it is weak in the short periods. As regards the Changning aftershock, the between-event residuals of PGA and Sa are greater than zero for periods over 0.5 s. Compared with the average values of global shallow crustal earthquakes, the source effects are strong in the intermediate and long periods while it is weak in the short periods. These results also indicate that the source effect of Changning main shock and aftershock is stronger than that of the BSSA14 model with the same magnitude of global shallow crustal earthquakes in the intermediate and long period. The source effects of the Ludian, Jinggu, and Kangding earthquakes are all weaker than that of Changning main shock, aftershock, and these from BSSA14 model with the same magnitude of global shallow crustal earthquakes.

As shown in Eq. 8, the within-event residual (δWes) can be calculated by subtracting the value of between-event residual (δBe) from the total residual (δes) in terms of BSSA14 model.

$$ {\updelta \mathrm{W}}_{es}=\Delta {\mathrm{C}}_3\left({R}_{\mathrm{jb}}-{R}_{ref}\right)+{\updelta \mathrm{W}}_R $$
(9)

To study the relationship between the within-event residual (δWes) and Rjb, the form of BSSA14 (Boore et al. 2014) model is adopted. In Eq. 9, the ΔC3 is an adjustment coefficient of inelastic attenuation, δWR is the approximate mean of the within-event residual (δWes) values at closest distances and Rref = 1 km. To ensure the reliability of the regression result, the ground motion recordings in the distance of Rjb = 40–400 km are adopted as the ground motion recordings within Rjb < 40 km are very few. The within-event residual (δWes) versus Rjb for PGA and Sa at the period of 0.5, 2.0, and 5.0 s is shown by the green points in Fig. 10.

Fig. 10
figure 10

Within-event residual for PGA and Sa versus Rjb based on BSSA14 model. The red fitted curves of δWes versus Rjb. The point with Rjb = 0 is plotted on the vertical axis. a PGA (peak ground acceleration), b T=0.5 s (response spectrum value at perod 0.5 s ), c T=2.0 s (response spectrum value at perod 2.0 s ), d T=5.0 s (response spectrum value at perod 5.0 s)

Full size image

The parameter ΔC3 can be regarded as a quantitative representation of inelastic attenuation, where ΔC3 > 0 means weak inelastic attenuation and ΔC3 < 0 means strong inelastic attenuation (Al Atik and Abrahamson 2010; Ren et al. 2018). As shown in Fig. 10, ΔC3 values for PGA and Sa at the periods of 0.5 s are greater than zero while ΔC3 values for Sa at the periods of 2.0 and 5.0 s are less than zero. It indicates that the inelastic attenuation for PGA and Sa at the periods of 0.5 s is weak, while inelastic attenuation for Sa at the periods of 2.0 and 5.0 s is strong. In addition, the values of ΔC3 for Sa at period of T = 0.01–5.0 s are shown in Fig. 11.

Fig. 11
figure 11

ΔC3 calculated from the linear regression between within-event residual (δWes) and Rjb at the period of T = 0.01–5.0 s from the BSSA14 model

Full size image

As shown in Fig. 11, for Kangding earthquake, the values of ΔC3 at period of T < 3.0 s are greater than zero. This means that the inelastic attenuation of Kangding earthquake is weak. The values of ΔC3 are much similar between Ludian and Jinggu earthquake while the values of ΔC3 are much different between the Changning earthquake and Jinggu earthquake. For the Jinggu earthquake, the values of ΔC3 during periods of T < 5.0 s are less than zero mostly. This result indicates that the inelastic attenuation of the Jinggu earthquake is very strong. However, as for Changning earthquake, the values of ΔC3 during periods of T < 0.5 s are greater than zero. This result indicates that the inelastic attenuation of the Changning earthquake is weak during periods of T < 0.5 s. The values of ΔC3 at period of T > 0.5 s are less than zero. This result indicates that the inelastic attenuation of the Changning earthquake is strong at periods of T > 0.5 s. The Changning aftershock has the similar trend as the Changning earthquake. There are many reasons causing different inelastic attenuations. As is shown in Fig. 8, the epicenter of Changning earthquake and Kangding earthquake is in the Sichuan province. However, the epicenter of Jinggu earthquake and Ludian earthquake is in Yunnan province. Geological conditions of the two provinces are very different leading to the seismic waves traveling through different geological contexts. For each earthquake, the sampled paths are different. That may cause different inelastic attenuations.

5 Response spectra characteristics

Seven sets of strong motions with Rjb < 100 km are recorded in the most serious damaged areas of the Changning earthquake. The response spectra of the seven sets of recordings are compared with the design spectrum, as shown in Fig. 12. The horizontal spectral accelerations are defined as the geometric mean of the spectral accelerations of the EW and NS components. The seismic design intensities of some counties near the epicenter are shown in Table 5 (China Ministry of Construction 2010).

Fig. 12
figure 12

Comparison of horizontal spectral accelerations with 5% damping ratio between the Changning earthquake and Chinese seismic design spectra

Full size image
Table 5 Seismic design intensities near Changning County
Full size table

Figure 12 shows that the spectral accelerations at Joyner-Boore distances of less than 50 km are larger than the seismic design spectra (China Ministry of Construction 2010). The Chinese seismic design spectrum is divided into four sections. The first section is straight line when period T = 0 s, the Sa = 0.45αmax and when the period T = 0.1 s and the Sa = η2αmax. The second section is a flat line for periods 0.1 s < T < Tg and Sa = η2αmax. The third section is segment of a curve where Tg < T < 5Tg, and \( \mathrm{Sa}={\left(\frac{T_g}{T}\right)}^r{\upeta}_2{\alpha}_{max} \). The last section is also segment of a curve where 5Tg < T, and Sa = (η20.2r − η1(T − 5Tg))αmax. Herein, the damping ratio is 0.05, the η2 is 1, η1 is 0.02, and r is 0.9. For seismic design level of frequently occurred earthquakes, the αmax is 0.04 at the intensity of 6 and αmax is 0.08 at the intensity of 7. From Fig. 12, the predominant periods of acceleration response spectrum (Sa) of the seven records are from 0.1 to 1.0 s. However, the natural periods of buildings in the severely stricken area are mainly from 0.3 to 1.0 s. These values mean that the predominant periods of the ground motions in the Changning earthquake are consistent with the natural periods of the local buildings; due to the resonance effects, this similarity leads to catastrophic engineering damage. However, when the period exceeds 3 s, the spectral accelerations become very small.

6 Arias intensity characteristics

In addition to the parameters directly related to the ground motion amplitude, increasing attention has been paid to the parameters related to the energy of ground motion. Researchers have used the Arias intensity in a variety of engineering applications (Jibson and Keefer 1993; Harp and Wilson 1995). The Arias intensity (Arias 1970) is a ground motion intensity measure proportional to the integral of the absolute value of the acceleration squared over the significant duration of the signal. The equation for the Arias intensity is as follows:

$$ {I}_{\mathrm{A}}=\frac{\pi }{2\mathrm{g}}{\int}_0^{T_{\mathrm{d}}}{a}^2(t) dt $$
(10)

where g represents the gravitational acceleration, Td represents the duration of the ground motion, and a(t) represents the acceleration time history. In order to compare the observed values of Arias intensity of Changning earthquake with that of the same magnitude, the predicted values of CB12 model (Campbell and Bozorgnia 2012) are adopted as shown in Fig. 1. CB12 model is developed using the strong ground motion database that composed of earthquakes from all over the world with magnitudes between 4.3 and 7.9 (Campbell and Bozorgnia 2010). This model is commonly used in some researcher on the Arias intensity.

The observed values of the Arias intensity of Changning earthquake are compared with the predicted values from CB12 model in Fig. 13. Most of the Arias intensity is larger than the predicted values of CB12 model, and most of the residuals are larger than zero. Especially, the Arias intensity is higher than CB12 prediction at distances larger than 100 km. The Arias intensity is a ground motion intensity measure proportional to the integral of the absolute value of the acceleration squared over the significant duration of the ground motion signal. The total residuals of Arias intensity of Changning earthquake show a clear amplification at distance around 150 km. Large-amplitude Moho reflections have been reported to produce strong shaking from shallow earthquakes in the epicentral distances around 150 km. With the long epicentral distance, the observed large values of as intensity are most likely to be the wave reflections from the Moho discontinuity. These phenomena may cause the energy of the ground motion for the Changning earthquake to be larger than those for earthquakes with the same magnitude at distances larger than 100 km. Such ground motions are more likely to cause serious damage.

Fig. 13
figure 13

Observed values of Arias intensity of Changning earthquake compared with the predicted values of CB12 model and the residuals. The solid line represents the predicted values of CB12 where the values of Mw = 5.8, VS30 = 370 m/s. The dotted lines are the standard deviation of CB12 model. The green solid points represent the observed values of ground motion. Residuals are calculated based on the real values of Mw 5.8 Changning earthquake and the VS30 for each site

Full size image

7 Duration characteristics

Duration is one of the important parameters of ground motions in structural seismic design. There are more than 40 definitions (Bommer and Martinez-Pereira 2000; Bommer and Stanfford 2009) for duration, among which the significant duration (DSR) is one of the most commonly used. In this study, the significant duration DSR (5–75%) and DSR (5–95%) are selected to investigate the duration characteristics of the ground motions. The DSR of Changning earthquake are shown in Fig. 14. The values of DSR are calculated by the geometrical mean of two horizontal components. The empirical equation (AS16 model) for the prediction of significant duration of ground motion is used in active crustal regions (Afshari and Stewart 2016). Ren et al. (2018) applied the AS16 model in analyzing the significant duration of ground motion of Mw 6.6 Lushan earthquake and Mw 6.5 Jiuzhaigou earthquake in Sichuan, China.

Fig. 14
figure 14

a Observed DSR (5–75%) and DSR (5–95%) of ground motion compared with the predicted values from AS16 model. The solid line represents the predicted values from AS16. The dotted lines are the standard deviation from AS16 model. The green solid points represent the observed values of ground motion. b Residuals versus Rrup. Residuals are calculated based on the real values of Mw = 5.8, VS30 for each site and ZTOR = 0 km

Full size image

The observed horizontal DSR (5–75%) and DSR (5–95%) are compared with the predicted values from AS16 model in Fig. 14. The observed values are mostly consistent with the predicted values for DSR (5–75%) and DSR (5–95%). As shown in Fig. 14b, residuals are calculated using Mw = 5.8, VS30 for each site and ZTOR = 0 km. For DSR (5–95%), the residuals are very small and near zero. For DSR (5–75%), most of the residuals are lower than zero at the distance of 200 to 300 km. These results indicate that the DSR (5–95%) and DSR (5–75%) of Changning earthquake are similar to those for earthquakes with the same magnitude.

The within-event residuals (δWes) are shown in Fig. 15. The form of the fitted curve between the within-event residual (δWes) and Rrup is the same as Eq. 9. The values of ΔC3 are approximately equal to zero. These results indicate that the path effect of Changning earthquake on DSR is similar to that of the AS16 model with the same magnitude.

Fig. 15
figure 15

Within-event residuals of DSR (5–95%) and DSR (5–75%) versus Rrup. The fitted curves of δWes and Rrup are plotted in red

Full size image

8 Conclusions

To understand the characteristics of the Mw 5.8 Changning earthquake, based on 58 sets of three-component acceleration data recorded by strong-motion stations in Sichuan Province, the characteristics of these ground motions are analyzed by considering amplitudes, spectra, Arias intensity, and durations through regression and residual analyses. The following conclusions are obtained.

  1. 1.

    The observed horizontal PGAs, PGVs, and Sa are compared with the predicted values from BSSA14 model and the total residuals are calculated. The residuals of the Changning earthquake are basically greater than zero. These results indicate that the values of PGV, PGA, and Sa are larger than those of global shallow crustal earthquakes with the same magnitude from the BSSA14 model. Especially for PGV, larger values of PGV may cause serious damage of structures.

  2. 2.

    The between-event residuals of the Changning earthquake are calculated based on the BSSA14 model. The between-event residuals of PGA and Sa are greater than zero except for periods from 0.01 to 0.6 s. These results indicate that the source effect of Changning earthquake is stronger in the long periods than that of the BSSA14 model of the same magnitude. The within-event residuals are also analyzed. The values of ΔC3 at periods of T < 0.5 s are greater than zero, which indicates that the inelastic attenuation of the Changning earthquake is weak at these periods. The values of ΔC3 at periods of T > 0.5 s are less than zero, which indicates that inelastic attenuation of the Changning earthquake is strong at these periods.

  3. 3.

    The observed values of Arias intensity are compared with the predicted values from the CB12 model. The result indicates that the observed values of the Arias intensity of Changning earthquake are larger than the predicted values from CB12 model, which implies that the energy of the ground motion of the Changning earthquake is larger than those of earthquakes with the same magnitude. The observed values of DSR (5–75%) and DSR (5–95%) are similar to the predicted values from the AS16 model.