1 Introduction

Many seismological observations have revealed that heterogeneity in the earth’s crust can cause the scattering of seismic waves, which can carry a considerable amount of geological structural information. The scattered seismic wavefield can be used to study inhomogeneities in the crust and lithosphere (Aki 1969, 1973; Wu and Aki 1985, 1988; Flatter and Wu 1988; Korn 1990, 1993, 1997; Sato and Fehler 1998; Sato 1984, 1989; Saito et al. 2002). Heterogeneity can be divided into large-scale and small-scale inhomogeneities (Sato 1984, 1989; Saito et al. 2002), according to the relationship between seismic wave length and the scale of heterogeneities. Large-scale inhomogeneities can be described using traditional structural parameters (e.g., seismic velocity, conductivity, and density), but small-scale inhomogeneities are described using the parameters σ and a, where σ is the velocity fluctuation ratio and a is the correlation length of a heterogeneity. For Gaussian or exponential heterogeneous media, the degree of heterogeneity can be described using the power spectral density function (PSDF). In a Gaussian heterogeneous media (\( p(m)={\sigma}^2\sqrt{\pi^3}{\alpha}^3{e}^{-{m}^2{\alpha}^2/4} \), where m is wave length), a higher value of σ means a stronger inhomogeneity in the lithospheric medium, and a higher value of a means a larger-scale inhomogeneity (Sato 1984, 1989; Saito et al. 2002). Precise values for σ and a, which are not decoupled, cannot be obtained directly (Sato 1984, 1989; Saito et al. 2002). For years seismologists have been trying to deduce precise values for σ and a, by using methods such as seismic array observation (Wu and Aki 1988) or modeling teleseismic P coda envelope (Korn 1997). The teleseismic fluctuation wavefield method (TFWM) is currently accepted as an accurate means of evaluating values for σ and a (Ritter et al. 1998; Ritter and Rothert 2000).

The teleseismic P-wavefield recorded at local seismic stations contains important information concerning the conditions encountered along a seismic wave path. Teleseismic waves follow paths that are similar, except for the travel path below seismic stations. Because the teleseismic wave comes from the same source and travels a closely similar path, variations in the observed wavefield among the stations are caused by differences in the geological structures beneath the seismic stations (Ritter et al. 1998; Ritter and Rothert 2000). An observed wavefield can be divided into two elements: the average wavefield and scattering wavefield. The average wavefield reflects the “similarities” in structures along the path traveled by a seismic wave, while the scattering wavefield reflects the “differences” in the medium below the seismic stations. Structures in the crust and upper mantle below such observatories can therefore be obtained by analyzing the differences between the scattering and the average wavefields. This is known as the teleseismic fluctuation wavefield method (TFWM) (Ritter et al. 1998; Ritter and Rothert 2000; Mach 1969; Langston 1989), which was widely used in seismic array studies in the past, but is now used to study inhomogeneities in the lithosphere. Mach (1969) was the first to carry out a systematic study on the teleseismic P-wavefield using data from the LASA (Large Aperture Seismic Array). Based on the teleseismic P-wavefield records of LASA and other sub-seismic arrays, he discovered a discontinuity in the crust from two seismic arrays. Aki (1973) reported that the inhomogeneous stratified media below the LASA is about 60 km thick, with a velocity fluctuation ratio of about 4%. Langston (1989), Korn (1997), and Wagner and Langston (1992) verified the validity of the TFWM by studying inhomogeneities in the lithospheric medium through numerical simulation. Ritter et al. (1998) and Ritter and Rothert (2000) studied the structural parameters of the medium in the crust and mantle in different regions using TFWM and thereby acquired the velocity fluctuating ratio and length of heterogeneities. Korn (1993, 1997) and Hock et al. (2004) explored the inhomogeneity of the lithospheric medium in Central and Northern Europe.

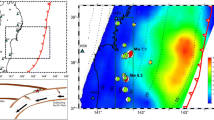
The eastern edge of the Qinghai-Tibet Plateau lies in the frontal zone of the collision between the Indian Plate and the Eurasian Plate and is part of the intersection between the Qinghai-Tibet Plateau and the Yangtze Block (Fig.1). Due to its geographical location and complicated and intensive tectonic movements, the eastern edge of the Qinghai-Tibet Plateau has unique advantages for studying the collisional process of the Indian Plate and the Eurasian Plate and the deep dynamic processes occurring within the Qinghai-Tibet Plateau and the Yangtze Block. Many scholars have studied the deep structures at the eastern edge of the Qinghai-Tibet Plateau and its adjacent regions; deep seismic wide-angle reflection and refraction results have demonstrated that the structure and properties of the Sichuan-Qinghai Block and the Mid-Sichuan Block are significantly different. The lithosphere of the Mid-Sichuan Block exhibits characteristics such as high seismic velocity and stability, while the Sichuan-Qinghai Block is of a low seismic velocity, weak, and easily broken lithospheric medium. In the Sichuan-Qinghai Block, a low seismic velocity layer is apparent in the middle crust (Lu et al. 2009; Liu et al. 1989; Wang et al. 2003a, b; Jia and Zhang 2008). The results of seismic tomography demonstrate significant low-velocity anomalies in both the middle and lower crust of this region, and most strong earthquakes occur at the boundary where high-velocity anomalies convert to low-velocity anomalies (Li et al. 2009; Wu et al. 2009; Lei et al. 2009, 2014; Lei and Zhao 2016). The results of electromagnetic sounding reveal that there is a large-scale, low-resistivity body under the Sichuan-Yunnan Diamond Block, which presents the characteristics of transverse partition and lateral heterogeneity (Wang et al. 2009). Q-value tomography results show that the lateral heterogeneity of the crustal medium is strong and there is a significant difference in the value of Q between the Sichuan-Yunnan and the Mid-Sichuan Blocks, the former with significantly high attenuation and the latter with lower attenuation (Su et al. 2006; Ma et al. 2007; Zhou et al. 2008).

Fig. 1
figure 1

Map of major tectonics and seismic stations (thick lines are main fault belts, thin lines are secondary faults, triangles are stations, solid arrows mean the direction of incoming wave, black hollow arrows mean the flux direction of lower crustal materials, and black line is the seismic wide-angle refraction profile). F1, Longmenshan fault zone; F2, Xianshuihe fault zone; F3, Anninghe fault zone. Block I, Sichuan-Qinghai Block; block II, Sichuan-Yunnan Diamond Block; block III, Mid-Sichuan Block (map is plotted by the generic mapping tools using ETOPO1 Global Relief Model)

Full size image

Previous studies have shown that the crustal medium in the area shows strong lateral heterogeneity, but currently the results only qualitatively describe the phenomenon of medium heterogeneity. The degree of heterogeneity has not yet been quantitatively studied, especially the lateral differences between the Sichuan-Yunnan Block, the Mid-Sichuan Block, and the Sichuan-Qinghai Block. In this paper, the inhomogeneity parameters (σ and a) of the crust are evaluated quantitatively using the TFWM method, and its variation characteristics and geodynamic significance are further analyzed.

2 Method

Scattered seismic waves are generated when a seismic wave propagates through an inhomogeneous medium. The seismic wavefield can be divided into the average wavefield, which reflects the large-scale structural information of the homogeneous medium and the scattering wavefield, which reflects the structural information of the inhomogeneous medium. The seismic wavefield at any point in an inhomogeneous medium (r) can be expressed as (Ritter et al. 1998; Ritter and Rothert 2000):

$$ {U}_{\mathrm{t}}\left(\boldsymbol{r},t\right)=\left\langle U\left(\boldsymbol{r},t\right)\right\rangle +{U}_{\mathrm{f}}\left(\boldsymbol{r},t\right) $$
(1)

where Ut(r, t), ⟨U(r, t)⟩, and Uf(r, t) are total wavefield, coherent wavefield (average wavefield), and the fluctuation wavefield (scattered wavefield), respectively, for r(x, y, z) at time t. The angular brackets mean space (statistical) averaging. Therefore, the turbulence intensity of a fluctuation wavefield can be described by the dimensionless parameter ε (Ritter et al. 1998, Ritter and Rothert 2000):

$$ \varepsilon =\frac{\left|{U}_f\left(\boldsymbol{r},t\right)\right|}{\left|\left\langle {U}_t\left(\boldsymbol{r},t\right)\right\rangle \right|} $$
(2)

If we assume that dissipation of the anelastic energy is negligible, then the coherent part of the wavefield is dampened only by scattering. The conservation of energy can be expressed in terms of intensity:

$$ {I}_{\mathrm{t}}={I}_{\mathrm{c}}+{I}_{\mathrm{f}} $$
(3)

where It, Ic, and If are the intensities of the total wavefield, the coherent wavefield, and the fluctuation wavefield, respectively. Since Ic = |⟨U⟩|2 and If = |Uf|2, then Eq. (2) can be rewritten as

$$ \left\langle {\epsilon}^2\right\rangle =\frac{{\left|{U}_{\mathrm{f}}\right|}^2}{{\left|\left\langle U\right\rangle \right|}^2}=\frac{I_{\mathrm{f}}}{I_{\mathrm{c}}}=\frac{I_{\mathrm{t}}}{I_{\mathrm{c}}}-1 $$
(4)

It can be seen from Eqs. (2), (3), and (4) that if ⟨ϵ3⟩ ≪ 1 (where Icis higher than If), then the medium has a relatively weak inhomogeneity, while if ⟨ϵ3⟩ ≫ 1 (where If is higher than Ic), then the medium has a relatively strong inhomogeneity. Therefore, Eq. (4) can be used to analyze and estimate the inhomogeneity in medium of the crust and the upper mantle.

For Gaussian or exponential random media, the relationship between ⟨ε2⟩ and the inhomogeneity parameters of the medium (c, σ, α, and L) (Ritter et al. 1998) is

$$ \ln \left(\left\langle {\varepsilon}^2\right\rangle +1\right)=\frac{8{\pi}^2{\sigma}^2\alpha L}{c^2}{f}^2=\gamma {f}^2 $$
(5)

where c is the mean P-wave velocity in the medium, a is the correlation length of heterogeneities, L is the travel path of the seismic wave ray, and σ is the average velocity fluctuation ratio. From Eq. (5), we can see that ln(⟨ε2⟩ + 1) exhibits positive correlation with the squared frequency. Therefore, the coefficient γ is determined by calculating the least-squares fit of ln(⟨ε2⟩ + 1) in the frequency domain for various teleseismic recordings. γ is proportional to the seismic wave scattering strength (σ2α) and can be related to the parameters L and c. In addition, Eq. (5) allows for testing the validity of the assumptions used in our approach because the frequency dependence ln(⟨ε2⟩ + 1)~f2 must be observed. In the area studied, the thickness of the scattering layer (L) and the P-wave velocity (c) of the medium can be obtained from previous research results using methods such as deep seismic sounding or tomography. If \( \frac{L}{c^2} \) is known, the value of σ2α and its variation range can be determined from Eq. (5).

3 Tectonic setting

The main tectonic units in the southern Longmenshan fault zone (F1) and its adjacent regions are the Songpan-Ganzi fold belt and the Yangtze Blocks (Fig. 1). The northeast-trending F1 is an important tectonic boundary. To the west of F1, an assemblage of epi-metamorphic Paleozoic and Mesozoic Triassic strata of the Songpan-Ganzi fold belt can be found, which extends eastward as thrusting nappes, forming Paleozoic and Mesozoic stable neritic facies and the terrestrial sedimentary formations of the Yangtze Block (Deng et al. 1994; Li et al. 2011). The Yangtze Block has a relatively stable sedimentary environment that formed during the Neopaleozoic era with a thick, unmetamorphosed sedimentary layer. Folding began during the Yanshan and Himalayan movements. The Xianshuihe fault zone (F2) is a sinistral strike-slip fault zone formed during intensive Quaternary movement. Over the past 100 years, a series of strong earthquakes have occurred in the region. The Anninghe fault zone (F3) is a regional fracture that formed during the Presinian period which is characterized by steep-angle subduction, multi-phase magmatic intrusion, and extrusion. It extends to the south into Yunnan and connects with the Xiaojiang fracture, generating intensive north-south neotectonic movements. F1, F2, and F3 (Fig.1) comprise the main tectonic pattern at the eastern edge of the Qinghai-Tibet Plateau and the adjacent regions, dividing the region into the Sichuan-Qinghai Block (zone I), the Sichuan-Yunnan Diamond Block (zone II), and the Mid-Sichuan Block (zone III).

4 Data and data processing

For this study, data from 139 earthquakes recorded by 70 seismic stations in the study region from January 2007 to December 2010 were collected. Data used for the study is required to fulfill the following four criteria (Ritter et al. 1998; Ritter and Rothert 2000): (1) the epicentral distance must be larger than 70° in order to acquire the vertical P-wavefield; (2) the focal depth must be larger than 70 km in order to avoid pP seismic phases in the P coda; (3) the waveform of the first P onset should be relatively simple to allow easy discrimination between the primary wave front and the following coda; and (4) at least 10 recordings should be available to obtain a fair statistic in determining the mean field. Meanwhile, to avoid interference from other teleseismic phases, the velocity spectrum of every seismic event was analyzed. The “velocity amplitude-time domain” records were converted into “slowness-time domain” (slowness variation range 3.5 s/°~7.5 s/°; step length 0.2 s/°). Seismic events from other seismic phases within the first 20 s of the P-wave tail were eliminated according to the “slowness-time domain” seismic phase distribution range. This selection left the 13 events listed in Table 1. The 70 seismic stations were divided into three groups according to the geological blocks and their spatial position with 15 seismic stations in zone I and 25 and 30 seismic stations in zone II and in zone III, respectively. The waveforms were aligned at the first P arrivals, and a fourth-order Butterworth bandpass filter from 0.2 to 6.0 Hz was applied. Next, the P-wavefields were stacked and averaged to acquire the mean wavefield. The fluctuation field for each seismic station was gained by subtracting the mean wavefield from the original wavefield. Thirdly, the amplitude spectra of the mean wavefield and the fluctuation wavefield were obtained using Fourier transformation and were then stacked and averaged. Finally, the scattering strength was determined by the ratio of the amplitude spectra of the fluctuation field and the mean wavefield. The coefficient γ was determined by calculating a least-squares fit of ln(⟨ε2⟩ + 1) in the frequency domain.

Table 1 Parameters of teleseismic event
Full size table

Figures 2, 3, and 4 are examples from an M7.3 earthquake in 2011 that illustrate the differences between the scattered wavefield in zones I, II, and III. Figures 2a, 3a, and 4a show the typical original wavefields of zones I, II and III, with the associated fluctuation wavefields in Figs. 2b, 3b, and 4b. It can be seen from the first traces (stack wavefield) in Figs. 2a, 3a, and 4a that the signal to noise ratio (SNR) is significantly higher than that of other traces, the high-frequency signal caused by scattering is stacked effectively, and the main phases are strengthened. Comparing the original wavefields in Figs. 2, 3, and 4, it is difficult to find obvious differences between zones I, II, and III; differences were obvious when comparing the fluctuation wavefield, both in the frequency and the seismic phases. These differences in the fluctuation wavefields indicate that there are significant differences in the structure of the medium beneath the seismic stations. For example, the fluctuation wavefields recorded by the XJI, RTA, WCH, and GZA stations are different between the time periods of 10 s and 15 s in Fig. 2b. Although the RTA and the GZA observations are less than 120 km apart, the frequency spectrum and seismic phases of the fluctuation wavefields are significantly different (Fig. 2b).

Fig. 2
figure 2

Average and fluctuation wavefields of zone I (a average wavefield; b fluctuation wavefield) (amplitudes are normalized and filtered from 0.2 to 6 Hz)

Full size image
Fig. 3
figure 3

Average and fluctuation wavefields of zone II (a average wavefield; b fluctuation wavefield) (amplitudes are normalized and filtered from 0.2 to 6 Hz)

Full size image
Fig. 4
figure 4

Average and fluctuation wavefields of zone III (a average wavefield; b fluctuation wavefield) (amplitudes are normalized and filtered from 0.2 to 6 Hz)

Full size image

The amplitude spectra of the mean wavefield (black line) and the fluctuation wavefield (dot line) for the study areas are shown in Fig. 5a, b, and c, respectively. The frequency-dependent energy intensity of the mean wavefield and the fluctuation wavefield are different in zones I, II, and III. The transition frequency is defined as the transition from a dominating mean wavefield to a dominating fluctuation wavefield. For example, the transition frequency is 0.61 Hz, 0.42 Hz, and 0.55 Hz in zones I, II, and III, respectively. For the same incident wave, if the medium is the homogeneous, the transition frequency must be the same in different regions. However, the transition frequencies in zones I, II, and III are different; this observation also reveals the different characteristics of the crustal medium beneath the stations.

Fig. 5
figure 5

Amplitude spectra of mean wavefield (black line) and fluctuation wavefield (dot line) in the study area (a zone I; b zone II; c zone III). f indicates the transition frequency which gives the transition from a dominating mean wavefield to a dominating fluctuation wavefield

Full size image

The seismic scattering intensities of the fluctuation wavefield in zones I, II, and III are shown in Fig. 6. The cutoff frequency is the intensity of the fluctuation wavefield which does not change for higher frequencies. When the frequency (low frequency) is less than the cutoff frequency, the energy of the fluctuation wavefield is exponentially related to the square of frequency, and when the frequency (high frequency) is larger than the cutoff frequency, the energy of the fluctuation wavefield does not change with increase of frequency. The relationships between the energy of the fluctuation wavefield and the frequency can also be seen from Eq. (5).

Fig. 6
figure 6

Seismic scattering intensity of the fluctuation wavefield in zones I, II, and III. The cutoff frequencies are indicated

Full size image

The intensity of the fluctuation wavefield and the cutoff frequencies are different for the different zones. The cutoff frequencies are 1.25 Hz, 1.2 Hz, and 1.61 Hz for zones I, II, and III, respectively. The ln(⟨ε2⟩ + 1)~f2 can be fitted in the frequency domain through the least-squares method. The fitting coefficient γ are 1.50 Hz−2, 0.97 Hz−2, and 0.99 Hz−2 in zones I, II, and III, respectively. Figure 7 shows the fitting curve of ln(⟨ε2⟩ + 1) and f for the M7.0 teleseismic event on September 3, 2011. The cutoff frequencies of the fluctuation wavefields and the fitting coefficients γ are different in zones I, II, and III, which reveal the difference in the crustal heterogeneity beneath the stations (Table 1).

Fig. 7
figure 7

Quadratic LSQ fitting curve of ln(〈ε2〉 + 1) and cutoff frequencies

Full size image

5 Results

The calculated values of γ and the associated confidence intervals determined by the TMFW method are based on the 13 teleseismic events in Table 1. From Table 1, we can see that there are some differences in γ for different seismic events, but the variational trend of γ is consistent in zones I, II, and III. Most of the high values of γ are in zone I, and most of the low values are in zone III, with mid-values in zone II. The average value of γ can therefore be arranged in order from the largest to smallest occurring zones I, II, and III.

It can be seen from Eq. (5) that the velocity fluctuation ratio (σ) is negatively correlated with the correlation length of heterogeneity (α). If γ is known, σ2α can be estimated. For a given region, the scattering layer thickness (L), average P-wave velocity (c), and the \( \frac{L}{c^2} \) of the study area are listed in Table 2 (Liu et al. 1989; Wang et al. 2002), and the range of the velocity fluctuation ratios are given as Aki’s result (Aki 1973); therefore, α and its range can be estimated.

Table 2 Parameters of scattering layer thickness, average velocity, and L/C−2 in the study area
Full size table

According to Eq. (4), when ln(⟨ε2⟩) < 1, the seismic wavefield is dominated by the mean wavefield, and the scale of heterogeneity is large. If ln(⟨ε2⟩) > 1, the seismic wavefield is dominated by the fluctuation wavefield, and the scale of heterogeneity is comparatively small (Sato 1984, 1989; Sato and Fehler 1998; Saito et al. 2002; Ritter et al. 1998, Ritter and Rothert 2000). Therefore, the transition frequency, as in the conversion point between the dominance of fluctuation wavefield and the dominance of mean wavefield, is a key parameter for evaluating the scale of inhomogeneity. According to the relationship between frequency, wavelength, and velocity (c = λf), when values for the transition frequency (f) and average velocity (c) are available, the correlation length of heterogeneities in the upper and the lower crust can be estimated. The transition frequencies of zones I, II, and III are 0.61 Hz, 0.42 Hz, and 0.55 Hz, respectively (Fig. 5). The correlation lengths and the velocity fluctuation ratio of heterogeneities in the upper crust and the lower crust in zones I, II, and III are listed in Table 3.

Table 3 Parameters of scattering layer thickness, average velocity, and L/c−2 in study area
Full size table

The values and confidence intervals of σ and α in the crust are shown in Fig. 8. Figure 8a portrays the upper crust and Fig. 8b the lower crust. The variation trend of σ and α in the upper and lower crust are similar; the biggest value of σ is in zone I and the smallest in zone II. The biggest value of α is in zone III, and the smallest in zone I.

Fig. 8
figure 8

The values and ranges of σ and α in zones I, II, and III (a upper crust, b lower crust)

Full size image

By comparing σ and α in the upper and the lower crust in zones I, II, and III, it becomes clear that σ and α in the upper and lower crust are similar (Fig. 8). By comparing σ and α in the upper and the lower crust in zones I, II, and III, it becomes clear that σ and α in the upper and lower crust are similar (Fig. 8). The results for σ and α in the upper and lower crust are almost the same in zone I, with σ at approximately 5.1% and α at about 10 km. This means that the degree of heterogeneity in the upper crust is almost the same. The values for σ and α are about 3.6% and 14 km in the upper crust and about 3.8% and 17 km in the lower crust in zone II, respectively, which means that the degree of heterogeneity in the lower crust is slightly bigger than that of the upper crust. In zone III, the σ and α of upper crust are 5.1% and 10.7 km. The σ and α of lower crust are 4.9% and 11.8 km. This means that the degree of heterogeneity in the upper crust is slight than that of the lower crust. Figure 8 mainly indicates a difference between zone II compared with zones I and III, especially when taking into account the ranges of σ and α.

6 Discussion and conclusion

The Qinghai-Tibet Plateau is the most intense area of modern tectonic movement on the earth. The collision between the Indian Plate and the Eurasian Plate caused the Qinghai-Tibet Plateau to rise sharply. The thickness of the crust of the Tibetan Plateau was obviously thickened, with its internal temperature gradually increased. At the same time, under the action of pushing pressure and gravity, the material in the lower crust of plateau moves in all directions, and the east flow of plateau material appeared because of the restriction of cold and hard rigid body (Clack and Royden 2000). During the eastward movement, due to the blockage of the strong Mid-Sichuan Block in the east, the plateau material was mainly divided into two parts, one part moved to the northeast, forming the Sichuan-Qinghai Block, while the other part flowed to the southeast, forming the Sichuan-Yunnan Diamond Block (Clack and Royden 2000; Zhu and Zhang 2009). The direction of black hollow arrows in Fig. 1 is the direction of lower crustal material flow.

Figure 9 shows the seismic wide-angle reflection and refraction profile across the Sichuan-Yunnan Diamond Block (zone II), Sichuan-Qinghai Block (zone I), and Mid-Sichuan Block (zone III), starting from Zhubali (ZBL) in Batang County and ending at Zizhong (ZZ) in Zigong County. The location of the survey line can be seen in Fig. 1.

Fig. 9
figure 9

Two-dimensional crustal velocity structure of ZBL-ZZ seismic profile (Wang et al. 2003a, b) (the gray solid line, dotted line, wide dotted line, and arrow represent P-wave velocity contour, fault structure, ductile shear zone, and migration direction of crustal material, respectively, and the number is the P-wave velocity)

Full size image

It can be seen from Fig. 9 that there are obvious differences in the thickness of the crust in zones I, II, and III and the crustal medium presents strong lateral velocity heterogeneity. Material flowing eastward in the lower crust is blocked by the Mid-Sichuan Block (zone III), and hot material rises along the Longmenshan fault zone (F1), resulting in a large amount of deep material hoarding in the zone I (the area between F1 and F2), which has also produced several strong earthquakes in this region including the Wenchuan 8.0 earthquake in 2008. The reasons for the heterogeneity of crustal material in zone I that is stronger than zones II and III are the migration and accumulation of deep material together with the occurrence of numerous strong earthquakes.

The Mid-Sichuan Block belongs to the Yangtze craton, which has a stable sedimentary environment since the late Paleozoic. And only during the Yanshan movement and Himalayan movement did the folding movement occur in varying degrees (Wang et al. 2003a, b). The results of wide-angle reflection and refraction show that there are two sets of fault systems in the lithosphere of the Mid-Sichuan Block (Cai et al. 2008); the first is the shallow fault system dominated by the brittle shear zone of the crust surface, while the other is the ductile shear zone cutting the Moho interface or the crust-mantle transition zone called the crust-mantle ductile shear zone. The ductile shear zone of crust and mantle in the study area belongs to the ductile shear zone of extruded crust and mantle. In the Mid-Sichuan Block, there are a series of NW trending fault structures in the upper crust (Fig. 9) and a series of NE trending crust-mantle ductile shear zones in the bottom area of the lower crust (Cai et al. 2008). At the same time, the research found that the NW trending crust-mantle ductile shear zone passes through zone III along Yibin, Zigong, and Chengdu (Fan et al. 2016), which may be one of the reasons that the medium inhomogeneity parameters in zone III are larger than zone II.

It can be seen from Fig. 8 that the error range of medium heterogeneity parameter overlaps. Compared with the errors caused by data processing and calculation (e.g., the size of the fitting error of γ; the cutting frequency errors of the mean and fluctuation wavefields), the errors caused by the crustal model error and the uneven distribution of stations, etc. are more serious. In general, the range of variation in the inhomogeneity parameters is consistent with previous results. The σ of the crustal medium is less than 7% and can reach 10% (Aki 1973; Korn 1990) where the tectonic movement is severe.