1 Introduction

Two-dimensional materials have shown high potential for the realization of nano-devices in the near future. Reducing the thickness of materials down to a mono (or few) atomic layer has drawn enormous interest because they could reveal unusual trends that are distinct from their bulk counterparts, e.g., Quantum spin Hall effect, 2D ferroelectricity, magnetism, and superconductivity [1,2,3,4,5,6] Motivated by the incredible improvement of graphene, other 2D materials have been a noticeable research field of concern. Graphene, the first successfully exfoliated essential material in 2D limit with the honeycomb lattice, possesses linear band dispersion crossing at the K-point in the 1st Brillouin zone (BZ), generating the Dirac Fermions. The two-dimensional dichalcogenide materials have attracted concentration for the last few decades due to their various application such as spintronics, electronic sensors, memory devices, and field-effect transistors [7, 8]. Many stimulating 2D materials like hexagonal boron nitride (h-BN) and dichalcogenides have been studied experimentally by various researchers [9,10,11,12].

Various computational studies have been presented to examine the nature of two-dimensional dichalcogenides, the chromium-containing ternary tritellurides CrSiTe3 and CrGeTe3, MnPX3 ternary chalcogenides, and CrX3 trihalides. The vanadium-based dichalcogenides VX2 (X = S, Se) were first recommended and reported for their strain-tunable ferromagnetic phase [13]. The chromium-trihalides CrX3 (X = F, Cl, Br, I) [13,14,15,16,17,18,19] are a new class of semiconducting ferromagnetic materials with a high Curie temperature (TC < 100 K). Attempts have been made to transform 2D materials into magnetic by straining, doping, or finding inherently magnetic 2D materials. Previous research was focused mainly on doping the non-magnetic 2D materials along with transition magnetic metals, e.g., Co functionalized graphene [20].

Density functional theory (DFT) studies have grouped TM trichalcogenides with the general formula MnCX3 (X = Se Te). Bulk compounds in this family have already been known [19, 21,22,23], but recently mono- and few layers of these compounds have been successfully exfoliated [16, 18, 20, 24,25,26,27,28,29,30,31,32,33,34]. One major lead of the MnCX3 family is that it has a very wide range of chemical diversity as well as structural complexity. Compounds in the MnCX3 family display interesting properties such as half-metallicity or semiconducting coupled with ferromagnetic (FM) and antiferromagnetic (AFM) order [7, 8, 16, 18,19,20, 23,24,25,26,27,28,29,30,31,32,33,34,35].

Keeping in view the aforementioned theoretical and experimental extraordinary methods, the biaxial strain is the main parameter for the phase transition. Excited from these methods here in this study, we emphasize the electronic and magnetic properties of monolayer MnAX3, as well as the mutual coupling amongst the strain and magnetism, which are thoroughly examined using density-functional theory (DFT). The transition from FM to AFM is observed by applying strain on these monolayers. To confirm the AFM stability after applying biaxial as well as uniaxial strain, we calculated various configurations of AFM, i.e., Neel antiferromagnetic (nAFM), zigzag antiferromagnetic (zAFM), striped antiferromagnetic (sAFM), and ferromagnetic (FM). We investigate the electronic structures improve when the magnetic phases change from ferromagnetic to antiferromagnetic. Our results show a robust mutuality between magnetism and structural properties in MnCX3 materials, owing to an amazingly strong reliance on exchange interaction forces on the strain. Our calculations demonstrate that the race between antiferromagnetic and ferromagnetic order can be significantly increased by strain engineering since these materials include transition metals and thus have strong dependence. The goal of this study is to provide an understanding into expected materials-property trends and to study the viability of engineering magnetic properties in these materials employing biaxial as well as uniaxial strain.

2 Computational Methods

All the calculations are carried out by density functional theory (DFT) executed in the Vienna Ab-initio Simulation Package (VASP) [36]. The generalized gradient approximation (GGA) with the parameterization scheme of Perdew-Burke-Ernzerhof (PBE) is applied for the electron exchange–correlation processes, while the electron–ion interactions are processed by the projector augmented wave (PAW) method [37]. Hubbard model is applied to comprise the contribution of the on-site strong interactions of the localized d electrons of the Mn (U = 4 eV) atoms. The cutoff energy of 500 eV is selected, for the plane-wave expansion of the electronic eigenfunctions, for the monolayer MCX3. The total energy of the structure and force criterion for the atomic relaxation are chosen as 10−5 eV and 0.01 respectively, so that the structures fully become relaxed. It should be noticed that for the phonon calculations, we have considered EDIFF = 10−7 eV in order to minimize the error to a maximum possible extent. The periodic images of monolayers of MCX3 are separated by 20 Aͦ to bypass the interlayer interactions K-point sampling with a 7 × 7 × 1 mesh is used for the integration of the Brillouin zone (BZ). The displacement step size is selected as 0.015 Aͦ using four displacements for each ion in the x and y directions. Phonon calculations are performed using the finite displacement method as implemented in the phonopy program [38].

3 Result and Discussion

3.1 Structural Properties

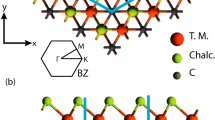
We predict two new members of the MnCX3 family MnCTe3 and MnCSe3 monolayers, whose bulk structures have been discovered in past experiments [16, 20, 39,40,41]. The space group of these two recently predicted structures is P-31 M. Therefore, the addition of these two members will expand and broaden the scope of this family. The unit cell of MnCTe3 and MnCSe3 is shown with green color in Fig. 1.

Fig. 1
figure 1

Top a and side b views of crystal structure of MnCX3 (X = Te, Se) compounds. Green box represents the unit cell, where two transition metal atoms assemble in a honeycomb structure

Full size image

The two Mn atoms in the unit cell have sixfold coordination with Se/Te atoms, creating octahedra, whereas the carbon atoms have threefold coordination with the Se/Te atoms. The relaxed lattice parameters for MnCTe3 and MnCSe3 monolayers are noted as a = b = 6.633 Å, a = b = 6.126 Å, and α = 120˚. The lattice parameters and structure thickness are linked to the dimension of the chalcogen atoms, since the length of C–C dimers expands. Moreover, the bond lengths in MnCTe3 regarding Mn–Te and Mn–Mn are 2.86 Å 3.83 Å respectively, whereas the Mn–Te–Mn bond angle is 84.04°. The Mn–Se bond length (2.65 Å) in MnCSe3 is shorter due to the smaller radius of Se compared to Te atom. Due to the smaller Se atomic size, the C–C dimer size is also reduced. As a result, the Mn–Mn bond length (3.53 Å) gets shorten. However, the Mn–Se–Mn bond angle is slightly reduced.

3.2 Magnetic Properties

We explore the ground-state (GS) magnetic ordering of the MnCX3 (X = Te, Se) by comparing their GS energies. The GS of the MnCTe3 and MnCSe3 are −49.68 eV and −54.19 eV for FM while −48.95 eV and −51.47 eV for AFM case respectively. We also calculate different configurations of AFM, i.e., Neel (nAFM) −97.903 eV, zigzag AFM (zAFM), −97.900 eV and stripy AFM (sAFM) −98.6437 eV, and ferromagnetic (FM) −98.6949 eV, which show that FM state is more stable than the AFM. The difference between the ground-state energy of the antiferromagnetic (AFM) and ferromagnetic (FM) order (EAFM – EFM) reveals that both systems energetically favor FM ordering. We tested different values for the on-site Coulomb interactions to evaluate the GS energies. After computing the GS energies, we realized that the band gap converge is at around U = 4 eV. Therefore, for the rest of the calculations, we adopt U = 3 eV for the strength of the on-site Coulomb interaction. The formal valences of the atoms are Mn2+, C4+, Te−2, and Se−2. According to Hund’s rule, Mn2+ with a 3d5 electronic configuration reveals a high spin state. The magnetic moments are developed largely at the localized Mn atom sites in the ferromagnetic configuration. In the FM state, every Mn atom provides 4.335 μB, whereas, in the AFM state, the two Mn atoms in the unit cell participate ± 4.219 μB. Magnetism requires two key parameters: (1) local magnetic moment, (2) spins-coupling. Here, Te and Se act as a mediator among Mn–Mn coupling which leads to superexchange interaction.

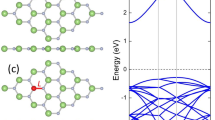
Our results demonstrate that the ferromagnetism persists in the monolayer layer of MnCX3 (X = Se, Te). In a 2D MnCX3 crystal, the significantly larger bond-length between the Mn–Mn magnetic atoms omits the possibility of direct exchange. Therefore, the exchange interactions among the metal atoms are thus largely facilitated by indirect exchange interactions. The carbon atom weakly hybridizes with the transition-metal atoms as can be clearly seen from the PDOS in Fig. 2a, c. However, the d-orbitals of the Mn considerably hybridize with chalcogen atoms (Se, Te). The chalcogen atoms carry tiny negative magnetic moments and they couple antiferromagnetically with their surrounding Mn atoms. Thus, this indirect coupling encases the superexchange interaction.

Fig. 2
figure 2

Schematic interpretations of different magnetic ordering in MnCX3 compounds. a Ferromagnetic, b Néel antiferromagnetic, c stripy antiferromagnetic, and d zigzag antiferromagnetic

Full size image

3.3 Electronic Properties

To investigate the electronic properties of the MnCTe3 and MnCSe3 monolayers, we calculate the spin-polarized band structures and partial density of states (PDOS). The band structures as well as the PDOS of the MnCTe3 and MnCSe3 reveal that both the systems possess half-metallic behaviors in their ground states which can be clearly seen in Fig. 3. The spin-up channel conducts as it crosses the Fermi level, while the spin-down does not conduct. The spin-down channels MnCTe3 and MnCSe3 remain insulating with finite gaps (1.78 eV and 1.049 eV) respectively. In addition to Mn-t2g states, the band structures of the former and latter are fully spin-polarized at the Fermi level by the Te-p and Se-p orbitals respectively. Moreover, PDOS depicts that both systems possess a large spin splitting gap which makes the half metallicity robust against external perturbation. The large spin-splitting gaps (1.78 eV for MnCSe3 and 1.049 eV for MnCTe3) make them promising materials for spintronic applications since they can provide a hundred percent spin-polarized carriers. This gap between spin-up and spin-down channels is located around the fermi level. Thus, 2D MCX3 compounds gain half-metallic character due to exchange splitting around the fermi level. Importantly, the spin-splitting gap can be notably enhanced or suppressed by applying biaxial or uniaxial strain. Interesting features of the band structures are the presence of the Dirac points which is not observed in other transition metal trichalcogenides.

Fig. 3
figure 3

(Color online) PDOS of monolayer a MnCTe3 and c MnCSe3. The corresponding contribution of the atoms is depicted with different colors. In the PDOS plots, the negative and positive parts represent the majority and minority spin channels. The Fermi level (EF) is fixed at zero. Band structure of b MnCTe3 and d MnCSe3. Moreover, the blue- and red-colored lines represent the bands of majority and minority spin bands

Full size image

3.4 Phonon Dispersions and Molecular Dynamics Simulations

After proving structural stability, we performed phonon dispersion calculations, see Fig. 4. Phonon spectra of the MnCX3 monolayers are computed to validate the dynamic stability of MnCSe3 and MnCTe3 monolayers. The maximum frequency of MnCTe3 is smaller compared to that of the MnCSe3 monolayer because Te is heavier than Se. The lack of soft phonon modes in the first Brillion zones calculated through high symmetry points for the monolayer MnCSe3 and MnCTe3 is the indication for their dynamic stability, in analogy to monolayer W2C, WS, WSe, MoC, WC, and many others [42,43,44,45]. First, three modes with relatively smaller frequencies are the acoustic modes whereas the rest with higher frequencies are the optical modes. Each mode is because of specific lattice vibration. There are three branches of the acoustic modes, longitudinal (LA), transverse (TA), and out-of-plane (ZA). The LA and TA branches show linear while the ZA shows a quadratic behavior neat to the gamma point which is a characteristic of the free-standing single layers, claimed as a result of the point group symmetry [46, 47]. Our findings are consistent with the earlier reported phonon band dispersions for other stable monolayers [44,45,46].

Fig. 4
figure 4

Phonon band dispersions for monolayer a MnCTe3 and b MnCSe3, respectively

Full size image

We further study the thermodynamic stability of monolayers MnCTe3 and MnCSe3 at 300 K by performing the ab initio molecular dynamics simulations with a time step of 1 fs for 7.5 ps (Fig. 5). We observed that the energy fluctuations with time are very small. Also, the atoms of the lattice vibrate from its lattice site and reconstruct the structure. It shows that both these structures are stable at room temperature.

Fig. 5
figure 5

Ab initio molecular dynamic simulations at 300 K for 7.5 pc with a time step of 1 fs for a MnCTe3 and b MnCSe3, respectively

Full size image

3.5 Strain-Induced Magnetic Phase Transition

2D materials are very delicate due to their thin nature and therefore essentially show a decent response to external stimuli, like strain, pressure, and doping. Motivated by such feature, we subjected both the monolayers of MnCTe3 and MnCSe3 to external strains which may allow to tune and enhance their magnetic and electronic properties. To know the mechanism of the phase transitions caused by the strain, we examine the dependence of magnetic properties against strain variations. The local magnetic moment appears on Mn atoms in MnCTe3 and MnCSe3. At the ground state, the two Mn atoms in the unit cell reside at an optimized distance dMn-Mn. The superexchange interaction tends to favor FM order between the local magnetic moments of the Mn atom. However, we explore that both the systems are quite sensitive to the external strain. The strain ε can be defined as:

$$\upvarepsilon =\frac{\left(a-{a}_{0}\right)}{a}\times 100$$
(1)

where a0 and a are the lattice parameter of the system with and without strain respectively. We assume that the energy difference between FM and AFM by including the contribution of the second and the third nearest neighbors. Therefore, the exchange energy due to the contribution of the first nearest neighbor can be written as:

$${E}_{\mathrm{FM}}-{E}_{\mathrm{AFM}}=-6J{\left|\overrightarrow{S}\right|}^{2}$$
(2)

where S is the spin and J is the exchange parameter. If EFM − EAFM is known, then the exchange parameter J can be computed via Eq. (2) from the energy difference calculation. The Currie temperature with the available value of J can be calculated by the mean-field expression:

$${T}_{\mathrm{c}}=\frac{3J}{2{K}_{B}}$$
(3)

where Tc and Kb represent the Currie temperature and Boltzmann constant. Eq. 3 shows that the Curries temperature can be increased by increasing the exchange energy.

For a clearer picture, we plot the exchange energy (EAFM-EFM) against externally applied strain in Fig. 6, which depicts that the FM states, regarding both the systems, are robust against tensile strain. Importantly, the stability of the ground state of the FM state increases with increasing tensile strain. However, its stability decreases with compressive strain and EAFM-EFM switches its sign at some value, where magnetic phase transition takes place from FM to AFM order. The direct exchange interaction varies with the distance between two local moments as ≈1/d5Mn–Mn [46] and it promotes antiferromagnetism in a system. With tensile strain, the two nearest magnetic Mn atoms move away from each other. As a result, the direct exchange reduces drastically whereas the superexchange also reduces but it is not affected significantly. The net effect enhances the FM order in both systems. By contrast, in compressive strain, the nearest magnetic atoms get closer and closer to each other. Therefore, a direct exchange is enhanced drastically while superexchange does not increase at that much pace. At some significant compressive strain, the direct exchange completely dominates and the systems go under magnetic phase transition from FM to stripy AFM (sAFM) state. In particular, the critical values of strain for MnCTe3 and MnCSe3 are −3% and −1% respectively. Our analysis shows that the superexchange dominates for tensile strain. For the compressive strain, direct exchange and superexchange complete each other; however, the direct exchange dominates beyond a particular value and brings phase transition in both systems. It is important to mention that a similar result was reported by Zheng et al. for CrI3 under compressive strain [48]. Moreover, the compressive strain also influences the electronic structure and alters the half-metallic state of MnCTe3 and MnCSe3 at the critical value of strain as shown in Fig. 7a–f as well as from half-metallic to semiconductor state. Additionally, by increasing the compressive strain, i.e., from −3 to −7%, the strain does not significantly change the bandgap. The strain effects on band gaps give a handy method to control the bandgap by design via epitaxy. For both these systems, strains −3%, −5%, and −7%; the VBM; and the CBM of the total density of states (TDOS) TDOS are mainly dominated by the Mn-d, Te-p, and Se-p orbitals. The contribution of the C atom is very small to DOS, so we neglect in the partial density of states. From Fig. 7, one can see a significant hybridization between the Te-p, Se-p, and Mn-d states. We believe that MnCTe3 and MnCSe3 are promising materials for spintronic devices since they depict ferro- and antiferromagnetism and show many interesting electronic behaviors like half metallicity semiconducting state.

Fig. 6
figure 6

Energy difference between FM and AFM phases for a MnCTe3 and b MnCSe3

Full size image
Fig. 7
figure 7

TDOS and partial density of states of a–c MnCTe3 and d − f MnCSe3 with −3%, −5%, and − 7% strains, respectively

Full size image

4 Conclusions

In this paper, we accomplished comprehensive first-principle calculations in order to investigate the structural, magnetic, and electronic properties of the MnCX3 (X = Se, Te) to broaden the scope of this family for the realization of future spintronics applications. Firstly, we verified their dynamical stability by evaluating the phonon dispersions. We did not find a negative band in the phonon dispersion which clearly depicts their dynamic stability. We further confirmed their thermodynamic stability by performing the ab initio molecular dynamic simulations. The small fluctuations with time in the energies guarantee its thermal stability. Our results indicate that van der Waal 2D MnCX3 (X = Se, Te) favors the ferromagnetic phase in the monolayer limit. We notice that the magnetic moment hinge largely depends on the transition metal atoms. The band structures of both the member inherent half-metallic nature with respect to the majority spin channel. The PDOS depicts that the Mn-d contributes around the Fermi level. Moreover, we have analyzed the impact of biaxial as well as uniaxial strain and the impact of strain on the magnetic and electronic properties. Our results indicate that the magnetic ordering can be manipulated by strain engineering because it substantially sets a competing environment between FM and AFM order. By analyzing the effects of the strain, we found that FM order gets more stable with tensile train for both species regarded MnCX3. However, the systems MnCTe3 and MnCSe3 undergo a magnetic phase transition (from FM to AFM order) upon applying compressive strain of 3% and 1% respectively. The AFM ordering is getting more and more stable with increasing compressive strain. The compressive strain greatly affects the electronic structures of the 2D monolayer MnCTe3 and MnCSe3. The half-metallic states transform into semiconducting at particular compressive strain. The intrinsic half-metallic character and the sensitivity of the exchange coupling of these systems to external agents such as strain make them incredible room for new functionalities in magnetic 2D materials. Based on our calculations, we conclude that monolayers MnCTe3 and MnCSe3 are exciting candidate materials for 2D spintronics.