1 Introduction

The search for new sources of cold in refrigeration systems to avoid any toxic risk of gas and overcome energy problems has yielded an important demand for new technology such as the magnetocaloric effect (MCE). By ensuring the demand of energy consumption and ecological efficiency, magnetic refrigeration is a new track to reduce the environmental risk compared with those based on the traditional refrigeration technique which relies mainly on conventional compression and expansion techniques [1,2,3,4].

Nowadays, perovskite manganite oxides with their major properties and applications are recommended as a promising field of scientific research exhibiting a dual feature of electric and magnetic characteristics [5]. These multiferroic properties underline the high impact of microstructural properties on the magnetocaloric effect interpreted in the framework of Zener’s theory [6, 7]. In fact, the mixed valence state of manganese (Mn3+/Mn4+) of these materials presents the dominant role to alternate the magnetic phase from a ferromagnetic (FM) to an antiferromagnetic (PM) behavior governed by the double exchange (DE) and super exchange (SE) mechanisms, respectively [8].

Exceptional perovskite-type hole-doped manganite (La1 − xSrxMnO3, LSMO) [9] ceramics exhibit an interesting sensitivity to temperature and applied field properties as well as potential technological applications in magnetic reading heads, hyperthermia and catalytic oxidation with high performance around the FM-PM phase transition [10,11,12]. Indeed the properties of this manganite can be tuned by an appropriate substitution of the divalent cation Sr2+ by a monovalent ion such as (Li, Na, K) which causes the oxidation of Mn3+ to Mn4+ ion to give rise to the double exchange interactions Mn3+-O2−-Mn4+ which are the origin of the coexistence of large magnetoresistance and magnetocaloric effect as reported by many research groups. The obtained mixed valence oxides generally exhibit a ferromagnetic-metallic to a paramagnetic-insulation transition. Nevertheless, the strontium-doped lanthanum manganite has a well-defined critical temperature of transition into a ferromagnetic state (TC = 377 K) [13], which is the highest Curie point among manganites of LaMnO3 type. Therefore, in order for a material to be a good candidate for industrial or domestic cooling power technology at room temperature, it is necessary to reduce its Curie temperature by taking into account the modulation of the relative ratio Mn3+/Mn4+ [14,15,16]. This can be achieved by the substitution of manganese with a non magnetic ion which destroys the FM interactions and enhances the nonmetallic character in the material [17, 18]. However, new investigation in this field modification at the B site has attracted surging attention owing to their important effect on the hybridization of the valence states between the oxygen and the B site ion.

This work aims to investigate the physical phenomena governing the TC temperature evolution and to control the performance of the parent compound under the effect of simultaneous doping on the Sr sites and Mn sites which may bring more complexity and unexpected randomization in the system. The obtained results proved that a strong FM-PM phase transition coupled with Curie temperature TC occurs near room temperature and shows a large magnetocaloric effect with a value of ΔSmax = 1.98 J/kg K under a magnetic field of 2 T for the La0.7Sr0.25Na0.05Mn1 − xAl0.05O3 indicating it can be a promising candidate for magnetic refrigeration at room temperature. In fact, we report on the microstructural properties of La0.7Sr0.25Na0.05Mn1 − xAlxO3 polycrystalline samples and their impact on the measurement and prediction of magnetization using a phenomenological model.

2 Experimental Details

Many synthesis procedures such as conventional ceramic or coprecipitation method are not suitable for advanced and technological applications, as these methods produce particles of large size, faulty homogeneity, and often-secondary phases. One key development that serves best to exemplify this fact is the use of the sol-gel method which has recently emerged as a versatile technique. The major advantage of this technique is to produce a ceramic form at lower annealing temperature that has a good control over the particle size formation and their uniform distribution. This technique provides high-quality homogeneous fine-sized particles with better morphology, narrowly distributed in size [19]. Using the commercial metal nitrate as a starting material, La0.7Sr0.25Na0.05Mn1 − xAlxO3 (LSNMAlx) samples were prepared by polymerization complex (PC) sol-gel technique. After slow evaporation to obtain sol-gel and converting the metal nitrate solution into citrate, ethylene glycol was added to the solution under stirring and heated between 140 and 190 °C to get a gel. Further heating treatment of this solution led to the formation of a dry porous mass which was calcined in air at 600 °C for 12 h until powder was obtained. The obtained powder was pressed into circular pellets which were sintered in air at 900° for 15 h. The behavior and the microstructural properties of the grains were characterized at room temperature by scanning electron microscopy (SEM) on a JSM-6400 apparatus under 25 KV. The structural properties, such as phase purity and homogeneity, were investigated using X-ray diffraction (XRD) with an XPERT-PRO diffractometer and a graphite monochromatized radiation (λCukα = 1.54 Å). The data collected in the range of 0 ≤ 2θ ≤ 100 were analyzed by the FULLPROF software based on the Rietveld code [20]. The isothermal magnetization (M) vs. magnetic field (μ0H) ranging from 0 to 5 T at different temperatures (T) was measured by a magnetometer with a superconducting coil in a magnetic field of 0.5 T and corrected by a standard procedure from low-field DC magnetization measurements.

3 Results and Discussion

3.1 Structural Properties and Morphological Characterization

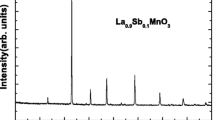
The main panel of Fig. 1 shows the XRD patterns of (LSNMAl0.05) samples at room temperature. A clear, narrow, sharp, and intense peak provides a unique structural phase with a high crystalline nature of the prepared sample. Using the final file of refinement, all peaks were indexed on the basis of a rhombohedral structure in the R-3c space group (no. 167), in which the (La, Sr, Na) atoms were at 6a (0, 0, 1/4) positions, (Mn, Al) at 6b (0, 0, 0), and O at 18e (x, 0, 1/4). Detailed results of all refinement and the structural parameters are summarized in Table 1. One of the clearest remarks from this table is that the structural parameters decreased with an increase of the substitution level, suggesting that the insertion of the Al-doping element into the basic compound can be explained by the small ionic size of Al3+ (0.535 Å) compared to that of Mn3+ (0.645 Å) [21]. However, introducing aluminum (Al) into the basic ceramics creates an MnO6 octahedron tilting and assures a continuous distortion from the ideal cubic structure. The internal “chemical” pressures are reflected by the variation of the structural parameters, which directly explains the double exchange mechanism and magnetism in perovskite. A theoretical estimation of the tolerance factor was calculated using the following equation [22]:

$$ {t}_G=\frac{r_{\mathrm{A}}+{r}_{\mathrm{O}}}{\sqrt{2\left({r}_{\mathrm{B}}+{r}_{\mathrm{O}}\right)}} $$
(1)

where rA, rB, and rO are the ionic radii of the A, B, and O site atoms in ABO3, respectively.

Fig. 1
figure 1

Rietveld refinement result (open symbols) and X-ray diffraction pattern (solid lines) for La0.7Sr0.25Na0.05Mn0.95Al0.05O3 sample collected at room temperature

Full size image
Table 1 Results of Rietveld refinements, determined from XRD patterns for La0.7Sr0.25Na0.05Mn1 − xAlxO3 (LSNMAlx) (x = 0.0 and x = 0.05)
Full size table

The value of Goldschmidt’s tolerance factor in the region 0.75 < tG < 1.06 confirms a stable perovskite structure. In fact, this factor can reveal the limit distance of the motion of the atoms from the ideal arrangement in the perovskite structure. In our study, the value of Goldschmidt’s factor of LSNMAlx was extracted from Shannon’s ionic radii and was found to be 0.978 and 0.982 for x = 0.0 and x = 0.05, respectively, which improves the stability of the perovskite structure. The physical behavior of materials is directly related to the crystal structure as well as to its microstructure.

3.2 Magnetic Behaviors

Figure 2 shows the variation of the field-cooled magnetization vs. temperature at μ0H = 0.05 T for the La0.7Sr0.25Na0.05Mn1 − xAlxO3 (LSNMAlx) samples. Upon increasing the temperature, one can see that all studied compounds present a (PM-FM) transition which broadens gradually with the increase of Al concentration. By manipulating the dependence of dM/dT with temperature, the Curie temperature TC values were fixed at their minimum and were found to be 348 K for LSNMAl0.0 and 297 K for LSNMAl0.05 (inset of Fig. 2), indicating that the chemical pressure induced by the nonmagnetic Al at Mn site directly affects the magnetic ordering temperature [23, 25]. However, the insertion of Al provides a considerable modification in the valence state of Mn ions and is expected to break some of the Mn3+-O2−-Mn4+ network. These particular behaviors can lead to the presence of antiferromagnetic interactions between Al and Mn ions and cause a reduction of the magnetic interaction [26]. In addition, the competition between the two distinct mixed phase states (FM and AFM interactions) is strengthened in the FM exchange phase and a short-range FM interaction known as cluster spin glass state is, therefore, expected to govern the magnetic proprieties in the Al-doped samples, which has a direct impact on the double exchange [27]. More recently, it has been reported that the magnetic behavior in the ceramics characterized by two magnetic contributions related to the paramagnetic interaction of the particle surface differs from that detected in the core which exhibits a spin arrangement. Generally, the high magnetic disorders in the shell dominate the magnetic interaction of the compound and hide the dead magnetic layer effect described as spin glass-like arrangement. However, Hueso et al. [28] and V.M. Andrade et al. [29] have analyzed the magnetic transition in perovskites and assumed that the inner cores and the disordered shell always cover the conventional first- and second-order magnetic transition, respectively. However, this interplay of the interaction features hides the effect of the first-order transition and reveals that particle size plays an important role in reducing the Curie temperature and broadening the behavior of the second-order transition, although both transition natures should be present simultaneously. Vasseur et al. [30] showed a proportional variation of the grain size with TC in the La0.75Sr0.25MnO3 compound related to the effect of the surface layer, which is consistent with H. Baaziz et al. [31] results. Meanwhile, they assumed that grain boundaries and the strong Jahn-Teller (JT) distortion can induce a strain effect in the grain and provide a decrease of the Curie temperature with increasing grain size. However, the effects of crystallite size of manganite on its magnetic properties are not fully explored. In our study, increasing the Al-doping rate reduced the magnetization and TC, which is similar to the variation of the average grain size but the smaller size of aluminum cannot be the prominent parameter. It is evident that the electronic configuration of Al3+ in the absence of d electrons governs this property and tends to break the whole propagation in the manganese-oxygen lattice. Therefore, the behavior of the magnetic property in our samples may be explained by the super exchange (SE) mechanism and the crystallite size effect.

Fig. 2
figure 2

Left axes: variation of the magnetization vs. temperature for La0.7Sr0.25Na0.05Mn1 − xAlxO3 (x = 0.0 and x = 0.05) sample at 0.05 T. Right axes: the temperature dependent of the inverse susceptibility and the solid line is the fitting result following the Curie Weiss law. Inset: plot of dM/dT curve as a function of temperature

Full size image

To understand the magnetic interaction in the PM state (T ≥ TC), we present in Fig. 2 the variation of temperature with the inverse static magnetic susceptibility χ−1 measured at μ0H = 0.05 T (the so-called Curie-Weiss plot). Generally, the paramagnetic susceptibilities should obey the Curie-Weiss law, i.e., χ = C/T − θCW, where C is the molar Curie constant and θCW is the Weiss-Curie temperature. The following parameters were extracted by linearly extrapolating the data to the Curie-Weiss law in the whole PM temperature range. In the statistical theory of paramagnetism as brought forward by Langevin, the experimental effective paramagnetic moments μeff were calculated following the relations given by

$$ {\mu}_{\mathrm{eff}}=\sqrt{\frac{3{k}_{\mathrm{B}}}{\mu_{\mathrm{B}}^2{N}_{\mathrm{A}}}C} $$
(2)

where μB = 9.274.10−21 emu is the Bohr-magneton, NA = 6.023.1023 mol−1 is the number of Avogadro, and kB = 1.38016.10−16 erg K−1 is the Boltzmann constant.

By suppressing the orbital momentum in Mn3+ and Mn4+, the theoretical paramagnetic effective moment (\( {\mu}_{\mathrm{eff}}^{\mathrm{theo}} \)) was written as \( g\sqrt{S\left(S+1\right)}\kern0.22em {\mu}_{\mathrm{B}} \) where g = 2 is the gyromagnetic factor and S is the spin of the cation. According to the La0.7Sr0.25Na0.05Mn1 − xAlxO3 polycrystalline sample, we calculated (\( {\mu}_{\mathrm{eff}}^{\mathrm{theo}} \)) using the following relation

$$ {\upmu}_{\mathrm{eff}}^{\mathrm{cal}}=\sqrt{0.65.{\left[{\upmu}_{\mathrm{eff}}^{\mathrm{th}}\left({\mathrm{Mn}}^{3+}\right)\right]}^2+\left(0.35-x\right){\left[{\upmu}_{\mathrm{eff}}^{\mathrm{th}}\left({\mathrm{Mn}}^{4+}\right)\right]}^2} $$
(3)

with \( {\mu}_{\mathrm{eff}}^{\mathrm{th}}\left({\mathrm{Mn}}^{3+}\right)=4.9{\mu}_{\mathrm{B}} \) and \( {\mu}_{\mathrm{eff}}^{\mathrm{th}}\left({\mathrm{Mn}}^{4+}\right)=3.87{\mu}_{\mathrm{B}} \) [32].

From the linear fit at high temperature, the evaluated μeff is 4.71 μB (x = 0.0) and 4.48 μB (x = 0.05), which is a little higher than the theoretical \( {\mu}_{\mathrm{eff}}^{\mathrm{theo}} \) 4.56 μB (x = 0.0) and 4.31 μB (x = 0.05). The divergence between the experimental and the theoretical values gives additional evidence on the effect of short-range FM exchange [33, 34]. Moreover, the extracted value of θCW is slightly higher than that of TC (θCW > TC) due to the presence of short-range interactions above TC and a magnetic inhomogeneity in the ceramic. This fact could explain the effect of aluminum on the magnetic properties such as the decrease of the ferromagnetic interactions [35].

3.3 Theoretical Considerations

Magnetocaloric effect (MCE) defined as the variation of temperature in an adiabatic process of magnetic materials obtained by the magnetic entropy change ΔSM with the effect of an external magnetic field has been extensively investigated over the last few decades in order to determine its parameters, especially its entropy change ( ΔSM), full width at half maximum (δTFWHM), change in specific heat (ΔCP,H), and relative cooling power (RCP). These parameters are usually determined through isothermal M(H) magnetization curves using theoretical thermodynamic equations and the well-known Maxwell-Weiss relation. In the present work, based on the molecular field theory of ferromagnetism [36], we adopted the Hamad model [37] to calculate these parameters. According to this model, the variation of M vs. temperature and TC is described by the following equation:

$$ M\;\left(T,H\right)=\left(\frac{M_{\mathrm{i}}-{M}_{\mathrm{f}}}{2}\right)\times \left[\tan h\kern0.24em \left(A\kern0.24em \left({T}_{\mathrm{C}}-T\right)\right)\right]+ BT+C $$
(4)

where

  • Mi/Mf is the initial/final value of magnetization at magnetic transition (Fig. 3).

  • B is the magnetization sensitivity dM/dT at a ferromagnetic state before transition.

  • \( {S}_{\mathrm{C}}=\frac{\mathrm{dM}}{\mathrm{dT}}\left|{}_{T={T}_{\mathrm{C}}}\right. \) is the magnetization sensitivity dM/dT at Curie temperature TC.

  • \( A=\left(\frac{2\kern0.5em \left(B-\frac{\mathrm{dM}}{\mathrm{dT}}\left|{}_{T={T}_{\mathrm{C}}}\right.\right)}{M_{\mathrm{i}}-{M}_{\mathrm{f}}}\right) \);

  • \( C=\left(\frac{M_{\mathrm{i}}+{M}_{\mathrm{f}}}{2}\right)-{BT}_{\mathrm{C}} \)

Fig. 3
figure 3

Temperature dependence of magnetization in constant applied magnetic field

Full size image

Differentiating Eq. (4) gives

$$ \frac{\mathrm{dM}}{\mathrm{dT}}=-A\left(\frac{M_{\mathrm{i}}-{M}_{\mathrm{f}}}{2}\right)\sec {h}^2\Big(A\left({T}_{\mathrm{C}}-T\right)+B $$
(5)

Therefore, for a magnetic system using the abovementioned formula, we can deduce the variation of the ΔSM (T) vs μ0H from 0 to the final value μ0Hmax as follows:

$$ \Delta {S}_M={\mu}_0{H}_{\mathrm{max}}\left[-A\kern0.24em \left(\frac{M_{\mathrm{i}}-{M}_{\mathrm{f}}}{2}\right)\kern0.24em \sec {h}^2\left(A\;\left({T}_{\mathrm{C}}-T\right)\right)+B\right] $$
(6)

As a result from Eq. (6), the maximum value of ΔSM can be calculated as follows:

$$ \Delta {S}_{\mathrm{max}}={\mu}_0{H}_{\mathrm{max}}\left[-A\kern0.24em \left(\frac{M_{\mathrm{i}}-{M}_{\mathrm{f}}}{2}\right)+B\right] $$
(7)

Furthermore, δTFWHM was calculated as follows:

$$ \delta {T}_{\mathrm{FWHM}}=\frac{2}{A}\cos {h}^{-1}\;{\left(\frac{2A\;\left({M}_{\mathrm{i}}-{M}_{\mathrm{f}}\right)}{A\kern0.24em \left({M}_{\mathrm{i}}-{M}_{\mathrm{f}}\right)+2B}\right)}^{1/2} $$
(8)

Another parameter which should be analyzed to evaluate the performance and refrigeration capacity of these compounds is the RCP defined as follows [38].

$$ \mathrm{RCP}=-\Delta {S}_{\mathrm{max}}\;\delta {T}_{\mathrm{FWHM}}={\mu}_0{H}_{\mathrm{max}}\left({M}_{\mathrm{i}}-{M}_{\mathrm{f}}-\frac{2B}{A}\right)\times \cos {h}^{-1}{\left(\frac{2A\kern0.24em \Big({M}_{\mathrm{i}}-{M}_{\mathrm{f}}}{A\kern0.24em \left({M}_{\mathrm{i}}-{M}_{\mathrm{f}}\right)+2B}\right)}^{1/2} $$
(9)

Another key parameter expected from the magnetic contribution added to the entropy change in the compounds for the evaluation of MCE is the heat capacity ΔCP,H which can be calculated by the following expression [39]:

$$ \Delta {C}_{P,H}=T\frac{\delta \Delta {S}_M}{\delta T} $$
(10)

From Eqs. (6) and (10), the heat capacity can be calculated as follows:

$$ \Delta {\mathrm{C}}_{\mathrm{p},\mathrm{H}}=-{\mathrm{T}\mathrm{A}}^2\left(\mathrm{Mi}-\mathrm{Mf}\right)\sec {\mathrm{h}}^2\left[\mathrm{A}\left({\mathrm{T}}_{\mathrm{C}}-\mathrm{T}\right)\right]\;\tan \mathrm{h}\left[\mathrm{A}\left({\mathrm{T}}_{\mathrm{C}}-\mathrm{T}\right)\right]{\upmu}_0{\mathrm{H}}_{\mathrm{max}} $$
(11)

Using this phenomenological model, all parameters evaluated under magnetic field variation can be simply calculated for LSNMAlx.

3.4 Simulation and Discussion

Briefly, the phase transition temperature TC and the initial/final (Mi/Mf) results of magnetization at magnetic phase transition were estimated by the present data of (M vs. T) and the A and C values were calculated from the values of (dM/dT) in the ferromagnetic region (B) and Curie temperature TC (SC). Figure 4 presents the thermo-magnetization curves under several μ0H from 1 to 5 T for the samples. As expected, on decreasing temperature, we can see clearly that the experimental data curves M(T) showed a PM-FM magnetic transition without any detected anomalies. Moreover, the decrease of the applied magnetic field μ0H reduced the magnetization and TC shifted from 348 to 297 K with the effect of aluminum. This behavior could be explained in the framework of the fluctuations of the magnetic moments interaction [40]. Still in Fig. 4, the symbols and the line represent the experimental data and the model’s prediction by the estimated parameter, respectively, collected in Table 2. It is clear that the agreement between the theoretical and experimental data is found to be very adequate.

Fig. 4
figure 4

Magnetization versus temperature for the La0.7Sr0.25Na0.05Mn1 − xAlxO3 (x = 0.0 and x = 0.05). The solid lines are modeled results and symbols represent experimental data

Full size image
Table 2 Model parameters for La0.7Sr0.25Na0.05Mn1 − xAlxO3 (LSNMAlx) (x = 0.0 and x = 0.05) samples in different applied magnetic fields
Full size table

Figure 5 presents the temperature dependence of the numerical prediction results of ΔSM data at several μ0H for LSNMAlx samples. It should be noted that around its TC, the magnitude of ΔSmax rose with increasing μ0H and decreased by the Al-doping effect from 4.92 J/kg K to 3.84 J/kg K at μ0H = 5 T for LSNMAl0.0 and LSNMAl0.05, respectively. The most important results imply that the LSNMAl0.05 compound with TC = 297 K could be a practical refrigerant material in household magnetic-refrigeration technology. In fact, Zener’s model [6] is strongly recommended to explain this property of the large magnetocaloric effect in manganites. Moreover, Guo et al. [41, 42] explain the large value of ΔSM by the stronger spin-lattice coupling detected by a simultaneous variation of structural distortion and the magnetic transitions. For practical applications, the cooling efficiency was also evaluated by RCP parameter [43]:

$$ RCP=\Delta {S}_{\mathrm{max}}\kern0.5em \delta {T}_{\mathrm{FWHM}} $$
(12)
Fig. 5
figure 5

Magnetic entropy change (ΔSM) of La0.7Sr0.25Na0.05Mn0.95Al0.05O3 sample as a function of temperature upon different magnetic field intervals (μ0ΔH)

Full size image

Compared to the conventional refrigerant materials, the obtained high value of the RCP proves that our compound LSNMAlx could be used in the field of magnetic refrigeration (Table 3). The values of all parameters involved in magnetic refrigeration for LSNMAlx calculated using the proposed phenomenological model are listed in Table 3.

Table 3 Comparison of reported values of the maximum magnetic entropy change (|ΔSmax|) and RCP values for various manganites and the two Gd and Gd5Ge2Si2 materials
Full size table

Figure 6 illustrates the specific heat change (ΔCp) as a function of temperature at various magnetic fields extracted using Eq. (11). It is clear that around the phase transition, the specific heat change undergoes a sharp variation from a negative value (ΔCP ≺ 0) to a positive value (ΔCP ≻ 0) below and above TC, respectively [44], which strongly affects the total specific heat in LSNMAlx. Moreover, both extrema below and above TC of (ΔCp) for these ceramics are extracted and collected in Table 3.

Fig. 6
figure 6

Heat capacity changes (ΔCp) as function of temperature for La0.7Sr0.25Na0.05Mn1 − xAlxO3 (x = 0.0 and x = 0.05) in different applied magnetic field variations

Full size image

This model presents a new method to estimate and calculate many factors and important measured parameters using the thermo-magnetization value under several magnetic fields in a limited processing time without any additional computational effort. Generally, magnetic and magnetocaloric results in manganite oxides present some limitations related to the presence of the FM clusters and the short-range FM interaction [45]. With the effect of magnetic field, the FM clusters grow in size when approaching TC, which broadens the FM-PM transition.

4 Conclusion

We have reported in this work the effect of aluminum on the structural and magnetic properties of La0.7Sr0.25Na0.05Mn1 − xAlxO3 (LSNMAlx) (x = 0.0 and x = 0.05) and investigated its correlation. XRD analysis study indicates a rhombohedral system with an R-3c space group. Magnetic measurements provide a second-order PM-FM transition. Theoretical model was used to extract the value of many magnetocaloric parameters from the thermo-magnetization variation. As already mentioned, our samples are characterized by a large magnetocaloric effect with a value of ΔSmax = 2.52 J/kg K under μ0H = 2 T, which is close to other results reported for magnetic refrigerants. Our compounds with their efficient magnetic properties at room temperature could be used in the field of magnetic refrigeration as alternative candidates for traditional magnetic refrigerants. Al doping led to a small reduction in the magnetocaloric parameter values such as entropy change and RCP, indicating a major role of aluminum on the magnetic and magnetocaloric properties. Moreover, Al doping creates an antiferromagnetic super exchange interaction and gives rise to a complex behavior of magnetic phase.