Conductivity in Cuprates Arises from Two Different Sources: One-Electron Exchange and Disproportionation

Abstract

Simulation of the resistivity in the normal state of doped La_2−x Sr _x CuO₄ has been performed using a hopping model based on Marcus theory. The results are in substantial agreement with experimental results. At oxidative doping, Cu(III) sites are formed and electron mobility possible due to hopping: Cu(III)Cu(II) → Cu(II)Cu(III) (one-electron exchange). In the underdoped, non-metallic region, the resistivity (ρ) decreases from almost insulation at T = 0 to a minimum at about T = 100 K. ρ then increases more than linearly with T (∼T ^3/2) in the region 100 < T < 500 K. A photo-induced metal-metal (MM) charge transfer transition at 2 eV 2Cu(II) + h ν→ Cu(I) + Cu(III) is responsible for the strong absorption in the visible spectrum of La₂CuO₄. The down-shift of spectral density with doping (x) in La_2−x Sr _x CuO₄ depends on the appearance of Cu(III) sites which makes optical as well as thermal one-electron exchange transitions possible with lower energy. Disproportionation occurs spontaneously for x > 0.06, opening up for electron pair formation. Configuration interaction between two-electron states of low chemical potential, but strong vibrational coupling, gives rise to the superconductor and pseudogaps. Data from photo-induced conductivity and absorption spectra are used in the simulation, which gives results in good agreement with experiments. Possible explanations for Raman and MIR absorption suggest themselves.

1 Introduction

The slow advent of a consistent theory for cuprate superconductivity (SC) has to a large extent been caused by a failure to realize the importance of structural dependence on the number of electrons at a site in a crystal with localized electronic structure. In this paper, such couplings have been included using the Marcus model [1–5]. Another reason for lack of progress is that conductivity has been incorrectly identified with ligand-metal (LM) charge transfer (CT). Conductivity is related to metal-metal (MM) CT between adjacent, equivalent sites in different oxidation states, in the present case the three oxidation states of copper Cu(I), Cu(II), and Cu(III) [6]. The neglect of negative terms in the expression for Hubbard-U [7] made it impossible for a long time to explain U < 0 [8] and why spectral density at 2 eV is moved to lower energies (<0.8 eV) after doping [9]. Finally, the electronic configuration interaction (CI) between the charged and spin-coupled states, which is a necessary condition for a superconducting (SC) phase [10], has not been widely recognized.

Hubbard-U, for example in CuO or La₂CuO₄, can be defined phenomenologically as the free-energy difference between the spin-coupled ground state and a CT state, where an electron has moved from one site in a crystal to the next. U refers either to adiabatic motion between free energy minima (U _ad) or excitation at the fixed ground state geometry (U _vert). Adiabatic U _ad is considerably smaller than U _vert. U _vert can be obtained from the optical conductivity spectrum [9].

Attractive Cu(III) sites appear after doping (x > 0), and the Cu(II)/Cu(III) transitions in the upper-left corner in Fig. 1 become possible [(1)]. This explains the transfer of spectral density to energies below 1 eV. For x < 0.055 in La_2−x Sr _x CuO₄, the stable phase is spin-coupled with x additional Cu(III) sites. Increased doping leads to a negative U state. For x > 0.055, the “charged state” with alternating Cu(I)/Cu(III) sites + x additional Cu(III) charges is lower in energy than the spin-coupled state [8]. The SC phase appears in the doping range 0.055 < x < 0.26. In this range, the ground state wave function is a quantum mechanical mix of the spin-coupled and charged wave functions [10].

Fig. 1

Four different possibilities for MMCT excitation in the CuO₂ plane (left picture). The two excitations on the left upper corner are due to one-electron exchange. In the lower left corner, the disproportionation transition at 2 eV in undoped La₂CuO₄ is shown. In the lower right corner, the same transition close to a hole is shown. The final results are indicated in the right figure

The resistivity (ρ) in La$_{\mathrm {2-}_{x}}$Sr _x CuO₄ has been measured by Takagi et al. for x-values up to x = 0.34 from T = 0 to T = 1000 K [11]. For dopings increasing from x = 0 to x = 0.05, the resistivity has a minimum at T _min ≈ 100 K. For T → 0 and x = 0, ρ tends to large values (see Section 7). If T > T _min, T increases as T ^3/2, but above 600 K, linearly in T [11].

At a low doping level, the conductivity increases proportional to doping, and the mechanism is likely of self-exchange-type:

$$ \text{Cu(II)} + \text{Cu(III)} \leftrightarrow \text{Cu(III)} + \text{Cu(II)} ({\Delta} G_{\mathrm{0}}=0) $$

(1)

Corresponding optical CT reaction may be written (Fig. 1, upper left corner):

$$ \text{Cu(II)} + \text{Cu(III)} + \mathrm{h} \nu \leftrightarrow \text{Cu(III)} + \text{Cu(II)} $$

(2)

Equations 1 and 2 describe transfer of one single electron (or spin). Cu(III) sites with unoccupied 3 d(x ²− y ²)-orbitals in the Cu3d-subshell (Zhang-Rice singlets) are clearly observable in “stripes” [12]. Heikes and Johnston studied conductivity in doped transition metal oxides, for example CuO doped to Li _x Cu_(1−x)O [13]. Li ⁺is the dopant and replaces some Cu(II) sites whereby other Cu(II) sites are oxidized to Cu(III) sites. At x = 0.2 in CuO, the conductivity is caused mainly by self-exchange Cu(II)/Cu(III). The activation energy is 0.087 eV (2 kcal/mol; for x = 0.02 [13]). It is reasonable to interpret the absorption in La_2−x Sr _x CuO₄ (≈0.13 eV) [14] as due to (2). The activation energy in (1) is then 1/4 ⋅0.13 in the Marcus model (≈0.035 eV), in La₂CuO$_{\mathrm {4+}_{y}}$, consistent with the experimental resistivity minimum for underdoped cuprates [11] (see below).

The results of Heikes and Johnston [13] support the electron exchange hopping mechanism (1) originally suggested by De Boer and Verwey for NiO [15] and discussed by Mott and Peierls [16]. The other mechanism is the disproportionation suggested by Mott [7] (see below). In other words, the doping results by Heikes and Johnston support two different mechanisms for conductivity: for x = 0, disproportionation, and for x > 0 also electron exchange.

Pekar was the first one to point out that electrons do not always move freely in solids, but as “polarons” [17]. In a later paper, Landau and Pekar pointed out the “internal contradiction” that ions are not fixed at lattice sites but are in a motion, coupled to the motion of the electrons in localized systems such as the cuprates [18]. In the present paper, the internal contradiction is properly accounted for using the Marcus-Hush-Sutin model [1–3].

For x = 0 in CuO, the activation energy is 0.43 eV > > 0.087 eV (10 kcal/mol in ref. [13]) and therefore notdue to a mechanism where_{ΔG 0} > 0 (thermal disproportionation):

$$ \text{2Cu(II)} \to \text{Cu(I)} + \text{Cu(III)}^{\mathrm{\thinspace \thinspace \thinspace }}({\Delta} G_{\mathrm{0}}=U_{\text{ad}}) $$

(3)

Corresponding optical disproportionation:

$$ 2\text{Cu(II)} + \mathrm{h}\nu \to \text{Cu(I)} + \text{Cu(III)}^{\mathrm{\thinspace \thinspace \thinspace }} $$

(4)

changes the spin-coupled state to a charged state, without changing the spin of the system (Fig. 1, lower part). Equation 4 is the MMCT transfer transition at h ν = 2.0 eV [19].

In the optimally doped system, there is a minimum in the far infrared optical conductivity at about 300 cm ⁻¹ in YBa₂Cu₃ O _6.95 [20–23] and La_2−x Sr _x CuO₄ [9], probably due to the SC gap. For 800>$\tilde {{\nu }}$>300 cm ⁻¹, the absorption is due to (4) since it cannot be due to (2), which is independent of doping and at 0.135 eV (∼ 1100 cm ⁻¹) [14].

After doping, MMCT transitions appear at lower energies (Fig. 1, lower right corner) due to the nearby hole. This decrease is seen in the spectrum of La_2−x Sr _x CuO₄ [9]. Continued lowering leads to CI between spin-coupled and charged state [13, 24].

As will be discussed below, we also find conductivity due to electron pair hopping of the following type with activation energy in the 0.5 eV region:

$$ \text{Cu(I)} + \text{Cu(III)} \to \text{Cu(III)} + \text{Cu(I)} $$

(5)

This mechanism contributes of course in the SC region, but also in the under- and overdoped regions outside the SC region. The pseudogap (see below) involving two-electron states will be of importance for high temperatures. In the overdoped region, there are very few Cu(II) sites and conductivity will be mainly due to coherent and incoherent two-electron transfer (ET).

Creation of Cu(III) sites is called “hole doping”. In “electron doping” Cu(I), sites are created. The same model may be used as will be commented on later.

2 Electron Transfer Between Sites

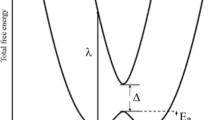
ET rate depends on bond-length fluctuations caused by the varying number of electrons [1–3] in a local system. The Marcus model is based on the free energy potential surface (PES) of the Born-Oppenheimer approximation. It follows from the model that there are activation barriers up to one fourth of the vertical excitation energy λ [1]. The nuclear and electronic motions are coupled via structural fluctuations.

The Marcus model describes ET between two molecules (M + M ⁻), two sites in a crystal or polymer, or two ions in a solvent. PES should not be mixed up with potentials for individual electrons. The x-axis (Fig. 2) is a collective reaction coordinate for the nuclear positions, one where the CuO bond-length deceases at one site and increases at another. h ν in (2) corresponds to a vertical excitation (λ). The avoided crossing is treated using the Landau-Zener method [3, 25]. The electrons are coupled to nuclear coordinates by breathing and half-breathing modes. In a cuprate, the most relevant vibrations are found between 400 and 800 cm ⁻¹.It follows from Fig. 2 that if the coupling | H ₁₂| = Δ/2 is large, the barrier is eliminated. We refer to ref. [3] for a detailed derivation. The ratio | H ₁₂|/ λ determines whether the activation barrier disappears and the system becomes delocalized [2, 4].

Fig. 2

Potential free energy surfaces in the Marcus model for one-electron transfer; λ is reorganization energy, Δ = 2 H ₁₂ is coupling, and E _a activation energy. (n,n + 1) etc. refers to site orbital occupation

At a Cu(III) site, the antibonding molecular Cu-3 d(x ² − y ²)-O2p orbital is empty. At a Cu(II) site, the same orbital is occupied by one electron. The CuO bond in the CuO₂ plane is therefore larger by about 0.1 Å. Due to this difference in bond-length, the electron life time is quite large (ps-ns range), and the conductivity low in CuO and cuprates in the normal state. The greater the difference in bond-length between the two valence states, the more the two parabolas are separated along the x-axis (Fig. 2) and the larger the activation barrier and deeper the trapping.

Conductivity due to ET hinges on the parameters in Fig. 2. The electron is localized where the antibonding is the least and the bond lengths the largest. The energy is further lowered by polarization of the medium. In a mixed-valence crystal, the system oscillates between the two minima with a rate equal to the electron exchange rate. In an electric field directed between donor and acceptor, there is a net free energy difference ΔG ^𝜃for conductivity. If the barriers (Figs. 2, 3, and 4) are below the vibrational energy, the system may be regarded as delocalized and itinerant with metallic conductivity.

Fig. 3

Potential energy surfaces for electron pair transfer; U _ad <0

Fig. 4

Potential energy surfaces for the cuprate ground state; U _ad >0

λ is the vertical excitation energy from the Cu ²⁺/Cu ³⁺ to the Cu ³⁺/Cu ²⁺ energy surfaces (Fig. 2). For example in the Fe ²⁺/Fe ³⁺ mixed valence system, λ corresponds to 12 000 cm ⁻¹, just below the visible region [3]. In the case of a cuprate, there are four rather than six bonds, and hence, we may expect λ to correspond to 8000 cm ⁻¹ or about 1 eV, which is also in the IR region. Increased coupling H ₁₂ tends to eliminate the barrier and form a system with ordinary metallic conductivity.

Figures 3 and 4 show how to apply the Marcus model to electron pairtransfer. The outer, local minima refer to two electrons being at one of the sites and the central minimum to one electron on each sub-system, in our case Cu(II) sites.The disproportionation energy in (3) is equivalent to adiabatic Hubbard-U (U _ad). Figures 3 and 4 make it clear that there is a vertical Hubbard-U, seen as a wide and strong absorption in a spectrum (around 2 eV). The vibrational breathing or half breathing modes are coupled to the CuO bond-length coordinates along the x-axis, in its turn coupled to disproportionation. Figure 3 shows disproportionation (U _ad < 0), while Fig. 4 shows the case typical for cuprates with U _ad > 0. A major difference to the traditional Marcus case for one-electron exchange is that we need the Hubbard-U parameter for the difference in total free energy between the charged state and the spin-coupled state. This Hubbard-U parameter can become negative by oxidative or reductive doping [8].

3 Mobility in the Marcus Model

To obtain the conductivity, we will use a model for hopping where each step is an ET transfer step in Marcus theory [1–3]. The latter model has been used extensively for transition metal systems and all experience suggests that complete vibrational relaxation takes place in ET step even in the fastest ET reactions. In the spin-coupled and charged phase, we may also assume that there is no interaction between the transferring electrons. We may therefore use a model of Drude type.

With hopping a distance and hop probability k, the average drift velocity is

$$ v_{d}=a\cdot k \quad k=(k_{+} -k_{-}) $$

(6)

We may think of this as a one-dimensional motion in the direction of an electric field$\vec {{E}}$. The hop probability in the direction of the field k ₊ is different from the probability against the field, k ₋. In a continuous system, we may think of the drift velocity (v _d ) as the velocity of a fully accelerated particle with mobility μ:

$$ v_{d}=\mu \vec{{E}} $$

(7)

The conductivity σ is directly related to the mobility through

$$ \sigma=nev_{d}/E=ne\mu=J/E $$

(8)

where n is the number of charge carriers per volume unit, e the charge of the electron, and J = nev _d the current density.

Electron mobility (v _d ) is given in cm ²/Vs. The current in the conductor is I = J⋅A, where A is the cross section surface area. In a conductor of length ℓ

$$ R=\frac{\rho \cdot \ell}{A} $$

(9)

where R is the resistance. The resistivity (ρ) is inverted conductivity (σ). According to (7), the conductivity may be written as

$$ \sigma=1/\rho=J/E=I/\text{EA} $$

(10)

From (7–10) follows:

$$ IR=\frac{\rho \ell \mathrm{I} }{A}=E \ell =V $$

(11)

I = JA is thus the current (in Ampère) and V the voltage (in Volts). Equation 10 is Ohms law.

In hopping conductivity, the electrons leap step-wise from a lattice point to another. Small changes of geometry when the number of electrons at a site changes cause activation energy and resistance. In the Marcus model, the height of the barrier will be different for forward (k ₊) and backward (k ₋) transfer.

In the Marcus model (Fig. 2), the electron exchange is between two sites and is fully symmetrical (ΔG ^𝜃= 0), as long as the field is equal to zero. When the electric field is switched on, the parabola acting with the field is moved down compared to the other one, in such a way that the height of the barrier is decreased.

The height of the barrier for forward (E ₊) and backward transfer (E ₋) in the presence of a field E can be expressed as [5]

$$ E_{\pm } =\frac{\lambda }{4}\left( {1\pm \frac{eEa}{\lambda }} \right)^{2}=\frac{\lambda }{4}\pm \frac{eEa}{2}+\frac{\left( {eEa} \right)^{2}}{4\lambda } $$

(12)

The rate of ET between the two molecules is:

$$ k_{\pm } =\nu_{n} \kappa \cdot \exp \left( {-\frac{E_{\pm } }{k_{B} T}} \right) $$

(13)

ν _n is the frequency for the vibrational mode that is coupled to till ET (we assume one unique mode). T is the temperature and k _B the Boltzmann constant. Corresponding modes induce ET. In the case of metal complexes, the relevant mode is the breathing or half-breathing mode at 500–600 cm ⁻¹.

We thus calculate the difference between the forward and backward rates for ET. If E is small, the third term in (12) may be neglected, and we obtain after Taylor expansion:

$$\begin{array}{@{}rcl@{}} k_{+} -k_{-} &=&\nu_{n} \kappa \left[ {\exp \left( {-\frac{E_{+} }{k_{B} T}} \right)-\exp \left( {-\frac{E_{-} }{k_{B} T}} \right)} \right]\\ &\approx& \nu_{n} \kappa \cdot \frac{eEa}{k_{B} T}\cdot \exp \left( {-\frac{\lambda }{4k_{B} T}} \right) \end{array} $$

(14)

κ is called the electronic factor and is equal to [3]

$$ \kappa =2\left[ {\frac{1-\exp \left( {-\nu_{el} /2\nu_{n} } \right)}{2-\exp \left( {-\nu_{el} /2\nu_{n} } \right)}} \right]; \quad \nu_{el} =\frac{{\Delta}^{2}}{4\pi \hslash }\left( {\frac{\pi^{3}}{\lambda k_{B} T}} \right)^{1/2} $$

(15)

ν _el is called the “electronic frequency”, while ν _n is the nuclear frequency. κ and ν _el will be derived below.

According (9), (11), and (14) the total current can be expressed as

$$ \sigma =\frac{J}{E}=\nu_{n} \kappa \cdot \frac{ne^{2}a^{2}}{k_{B} T}\cdot \exp \left( {-\frac{\lambda }{4k_{B} T}} \right) $$

(16)

provided that Δ is small.

In the case ν _el < < ν _n , we obtain κ = ν _el/ ν _n in (15). If this is inserted in (29), we obtain a conductivity proportional to the square of the coupling (Δ²), independent of the nuclear frequency ν _n

$$ \sigma =\frac{J}{E}=\frac{ne^{2}a^{2}}{k_{B} T}\cdot \frac{{\Delta}^{2}}{4\pi \mathrm{h} }\left( {\frac{\pi^{3}}{\lambda k_{B} T}} \right)^{1/2}\cdot \exp \left( {-\frac{\lambda }{4k_{B} T}} \right) $$

(17)

where n is the concentration of carriers.

The result in (17) is shown in Fig. 5. We notice that the same equation is used both in the activated region up to T ≈ 200 K, as in the higher temperature region where the conductivity is decreased for increased temperature, as for a metal.

Fig. 5

Calculated conductivity according to (9). Applies to underdoped cuprate as a function of temperature in the case of localized carriers

For the case ν _el > > ν _n , we may set κ = 1 in (15) and obtain

$$ \sigma =\frac{J}{E}=\nu_{n} \frac{ne^{2}a^{2}}{k_{B} T}\exp \left( {-\frac{E_{a} }{k_{B} T}} \right) $$

(18)

In the case when the activation energy tends to zero and hence the exponential may be replaced by unity, σ is proportional to 1/T in (18), reminding about the Einstein relation for diffusion [26].

In a crystalline ET-system, the conductivity is first increasing as a function of absolute temperature to a maximum and then decreases with temperature as in the case of a metal. Bloch conduction may be regarded as a limit value for a disappearing barrier. In the latter case, we are talking about Hush-Reimers delocalization [27], where delocalization happens if λ < 2| H ₁₂|(U < 2| H ₁₂|).

Using ρ = 1/ σ, we may calculate a minimum (ρ _min) in

$$ \rho =T^{m}\exp \left( {\frac{E_{a} }{k_{B} T}} \right) $$

(19)

$$ \text{for } T_{\min } =\frac{1}{m}\cdot \frac{E_{a} }{k_{B}} $$

(20)

m is the power of T in the expression for the conductivity. m = 3/2 in the present case if the Marcus model holds, as in (17). For low temperatures, the Marcus model needs updating (see below, Section 7). In the case of semi-conductors, m = 0, and hence, there is no minimum. In the plain Einstein case [26], m = 1, and in the case of (17) above, m = 3/2. In the case of electron pair transfer, there are two successive Landau-Zener avoided crossings (Figs. 3 and 4), and hence, m = 2. The existence of a minimum in the results of Takagi et al. [11] is ample proof that the activation is not due to a semi-conductor gap.

This temperature-independent minimum of resistivity in the underdoped region is thus derived from one-electron Cu(II)/Cu(III) exchange and has nothing to do with disproportionation and electron pair transfer. As we approach the SC region, there is a change to a phase with ρ = 0 and electron pair transfer in the ground state.

The conductivity in an infinite ET-system is the product of carrier mobility and carrier concentration (n). In the case ν _n > > ν _el:

$$ \sigma =n\cdot \text{const}.\cdot \frac{{\Delta}^{2}}{4\pi \mathrm{h}}\left( {\frac{\pi^{3}}{\lambda k_{B} }} \right)^{1/2}\cdot \left( {\frac{1}{T}} \right)^{3/2}\exp \left( {-\frac{\lambda }{4k_{B} T}} \right) $$

(21)

The activation energy is λ/4 and the resistivity (ρ = 1/ σ)

$$ \rho =\text{const}.^{-1}\cdot \frac{1}{n}\cdot \frac{4\pi \mathrm{h} }{{\Delta}^{2}}\cdot \left( {\frac{\lambda k_{B} }{\pi^{3}}} \right)\cdot T^{3/2}\exp \left( {\frac{\lambda }{4k_{B} T}} \right) $$

(22)

In the low-doping region, we may associate the carrier concentration with the molar fraction of Cu(III) carriers, thus n∼p = x.

For the case when ν _e > > ν _n , we may use (18) and derive

$$ \rho =\nu_{n}^{-1}\text{const.}^{-1}\cdot \frac{1}{p}\cdot T\exp \left( {\frac{E_{a} }{k_{B} T}} \right) $$

(23)

There are thus two different cases depending on the ratio between coupling Δ and reorganization energy λ. This also affects E _a directly since one may derive, if |Δ|< < λ [3]

$$ E_{a}=\frac{\lambda }{4}\cdot \left( {1-\frac{\Delta }{\lambda }} \right)^{2} $$

(24)

E _a = λ/4 for Δ = 0 and E _a = 0 for λ = Δ. Except for short distances between the interacting sites, we have, however, |Δ|< < λ. In that case the activation energy depends only on λ and is equal to λ/4. If |Δ| = λ, on the other hand, the barrier disappears (E _a = 0):

$$ \rho =\nu_{n}^{-1}\text{const.}^{-1}\cdot \frac{1}{p}\cdot T $$

(25)

Equation 25 holds only in the case of very strong coupling. This may be compared to the Einstein case when ρ∼T [26]. In the Einstein case, there is only a 1/T in (14) since the electrons are always hopping if the barrier is overcome. This is the case in (25) too. If the particles move fast, however, there is a slow-down originating from the Landau probability for hopping rate. In reality, electrons follow quantum mechanics, however, and have to collect probability for the hopping event. Therefore, the nuclei should move slowly, and therefore, there is an additional factor T ^−1/2in (17).

4 One-Electron Exchange in the Underdoped Case

Oxidative doping of a cuprate leads to a Cu(II)/Cu(III) mixed-valence system and possible exchange of electrons, and hence conductivity. The conductivity is activated like in semiconductors, but due to structural relaxation rather than a band gap. Activation due to structural relaxation [m = 3/2 (rather than m = 0) in (20)] leads to a minimum in the resistivity as a function of temperature. Simulation based on (23–24) is shown in Fig. 6. The visible agreement with the results of Takagi et al. [11] below 400 K suggests that one-electron exchange is in operation.

Fig. 6

Calculated resistivity for La_2−x Sr _x CuO₄ with x = 0.04. Full-drawn curve shows the contribution from one-electron exchange alone. In the dashed curve, the contribution to conductivity from the pseudogap has been added. The activation energy has been set to 0.175 eV

In Fig. 6, activation energy is 0.035 eV [14], which corresponds to Cu(III)/Cu(II) exchange, since there is a photo-conductivity peak at 4 × 0.035 = 0.14 eV [14]. The coupling parameter between two Cu ions, through an oxygen ion, has quite arbitrarily been chosen as H ₁₂ = 0.0065 eV which gives the gap Δ = 0.013 eV. We obtain the full-drawn curve in Fig. 6. Incidentally, the activation energy for the Hall factor is also 0.035 eV [14]. The Einstein diffusion model [26] for non-interacting particles is thus invalid in this region. Ando et al. [28] have plotted the experimental resistivity from zero to 240 K and found a T ² behaviour (rather than T ^3/2). It is unclear whether this disagreement with (17) is significant.

Above T = 400 K the resistivity bends down (dashed line), signaling a novel conductivity mechanism, probably due to the pseudogap (see Section 5). The pseudogap has been determined from NMR spectra via a characteristic temperature T* and the Knight shift [29]. Due to an odd number of electrons, the Cu(II) sites and surrounding oxygen sites are spin polarized. The number of Cu(II) sites is decreasing with increased doping and disappears for T > T _C. The electronic states forming the pseudogap will be discussed in the next section.

For T → 0 the resistivity of the Marcus model tends to infinity. The reason is that the nuclei move classically in this model. The nuclear motion has to be treated quantum mechanically, as will be discussed in Section 6.

The resistivity minimum and the value of the resistivity proportional to 1/p according to (22, 25) are in agreement with the experiments [11] (Fig. 7).

Fig. 7

Calculated resistivity as a function of temperature (T) for two different low-doping cases

Since the SC gap has nothing to do with one-electron exchange, it cannot be treated within the same simulation. SC depends on CI between the charged state and the spin-coupled states [10, 26]. SC appears when the charged state has lowered its energy sufficiently (because of doping) to have the largest quantum weight in the ground state. The SC of this mixed state has been discussed in earlier publications [10, 24].

We conclude that (1) is an important conductivity mechanism where single electrons (spins) are transferred. In the case of electron doping Cu(I), sites are created and the reaction corresponding to (1) is exchanged between Cu(I) and Cu(II):

$$ \text{Cu(II)} + \text{Cu(I)} \leftrightarrow \text{Cu(I)} + \text{Cu(II)}\quad({\Delta} G_{\mathrm{0}}=0) $$

(26)

Equation 3 is the same in both cases. Next, we will consider another type of transfer, (5), where charge, but not spin, is transferred (Fig. 1, lower right corner).

5 Contribution from Disproportionation. Pseudogap

In a local system, Cooper pairing is replaced by disproportionation (3). The phonons are coupled to the electron motion as is evident by the shifts of the nuclear coordinates. After sufficient doping, the Hubbard free energy gap develops into a SC gap and a pseudogap [8, 19]. In the SC phase, excitation from the SC ground state destroys SC. Thermal excitation across the pseudogap contributes to conductivity. In the simulations of the previous section, the pseudogap has been included in a simple way by adding an activation energy to fit the experimental curve. A rather good fitting is obtained (the dashed curve in Fig. 6) with E _a ’ = 0.2 eV, a value taken from Fig. 7 of ref. [9] (appropriate for x = 0.1).

The wave function for a two-site model (Fig. 8) may be written (ab + ba)( α β−β α), where α β−β α is the spin singlet function. a and b are active (highest occupied) spatial orbitals: Cu3 d(x ²−y ²) mixed with O2p(x) and O2p(y), on sites A and B, respectively. This is well known in the chemistry of copper and has been confirmed to hold also for cuprates. The charged state uses the same “active” orbitals to form aa and bb, i.e. site paired wave functions. In an asymmetric form, we may write the CT transition as ab →aa, emphasizing CT from b to a. The corresponding symmetric, projected functions aa + bb and aa − bb both have the spin function (α β−β α) [10]. This type of wave function (aa or bb) forms an excited state but becomes energetically available by doping [8] (Fig. 8).When SC appears, the two upper states have moved down in energy and interact with the spin-coupled ground state [8, 10, 24]. The two holes in a pair of Cu(II) ions are related by the same type of wave function as the two electrons in the H ₂ molecule [10] (except that in H ₂, aa and bb are unstable). The extended system has been treated in ref. [24].

Fig. 8

SC gap and pseudogap in La_2−x Sr _x CuO₄. SG superconducting gap, PG pseudogap

For x = 0.07 La$_{\mathrm {2-}_{x}}$Sr _x CuO₄, the resistivity goes to zero at T = 0 and the SC dome. The two symmetric states in Fig. 8 mix (ab + ba) and (aa + bb). The new SC phase is due to interaction between the spin-coupled phase and the charged phase [10, 24]. The two states are both states with paired electrons and the new conducting ground state wave function is then also paired. Contrary to the self-exchange process in the previous section, the number of electrons involved in the excitation is even. The excitations, marked out in Fig. 8, are allowed as long as spin is conserved (S = 0).

The SC gap is opened by interaction between aa + bb and ab + ba in the SC region. When the temperature has increased above T _C, the aa −bb level is well occupied and transitions to the higher spin-coupled state possible.

There is a clear distinction between orbital or band gaps on one hand, and total energy gaps on the other. The connection between band gaps and total energy gaps, measured experimentally, is not at all clear. A measured gap is always a total energy gap. For example the Hubbard gap has to be defined as the total energy gap to the lowest MMCT state and has nothing to do with any “ligand field gap” or LMCT gap. Only interaction between ground state and MMCT state leads to conductivity. It is impossible to describe the local Hubbard gap in any form of Bloch model.

The spin-coupled ground state is the type of ground state seen in all Mott insulators, which can be said to be due to correlation between the two electrons in the original sense of Löwdin [30] (cf. hydrogen molecule). SC appears in the ground state, due to CI between the spin-coupled state and the charged state Cu ⁺, Cu ³⁺. The latter two states are also localized, but the final CI-state may be delocalized, if the final CI is strong. Hush-Reimers delocalization [27] means that a PES becomes flat between two total energy minima in the Marcus model. This leads to vibrational mode transfer [31]. “Correlation energy” is the error when calculating energy and wave function using Hartree-Fock or DFT, rather than a physical effect. The final SC state cannot be a single configuration state.

If the interpretation in Fig. 8 is correct, the temperature has to be high enough to populate the aa −bb before the pseudogap can be seen in the spectrum. This appears to agree with the state ordering in ARPES spectra [32].

For temperatures T > T _C, the resistivity raises more than linearly in the overdoped region. At these doping levels and temperatures, there are mainly Cu(I) and Cu(III) sites available, since the disproportionated state forms the ground state (Fig. 8 to the right). Electron pair exchange of the type in (5) is possible, however.

Sutin et al. derived the T ^−1/2 factor in the rate of ET reactions [3], due to the increased kinetic energy of the electron, typical for a Landau-Zener avoided crossing [25]. The factor T ⁻¹ arises from (14). Its appearance can be traced back to Einstein [26]. A T ^3/2 factor thus appears for the resistivity in the underdoped region, when conductivity is caused by ET. This visibly agrees with the experiments [11] and T _min, if the activation energy is obtained from the absorption spectrum.

Similarly, the resistivity increases with T as T ² in the overdoped region [33–36]. Here, conductivity should be caused by electron pair transfer, since there are no Cu(II) ions available. The rate should then be quadratic in T, since there are two consecutive avoided crossings (Figs. 3 and 4) and a T ^1/2 for each of them [and in addition the Einstein factor T due to (14)]. Thus, this type of exchange leads to a T ² behaviour for the increase of resistivity as long as coherence remains in the ground state. Other possible mechanisms are scattering mechanisms leading to ρ∼T ⁵ for small T. [37]. In the SC region for temperatures above T _C, there will first be T ² dependence of the resistivity, then linear Einstein behaviour when coherence is lost.

6 Behaviour of Resistivity as T → 0

The 1/T-like behaviour of ρ for T → 0 involves more drama than Figs. 6 and 7 reveal. Ando, Boebinger et al. [38–40] have studied the behaviour of resistivity when the temperature tends to zero, by eliminating SC by alternating magnetic fields. Resistivity appears and can be measured. It turns to a finite value as T → 0. The trend is consistent with the resistivity in the underdoped region, which also tends to finite values as T → 0. However, the Marcus result tends to ∞ for T → 0 [(22)]. In the Marcus model, the nuclei move classically, and hence for low temperatures, the system must be thermally excited across the barrier to obtain conductivity. In reality, there is conductivity at T = 0, caused by nuclear tunneling (Fig. 9). The Jortner model may be used to treat this problem [41–43].

Fig. 9

Quantum nuclear tunneling versus classical activated motion

According to (22), the logarithm of the conductivity tends to

$$ \ln \rho =-\ln \sigma \sim \frac{3}{2}\ln \left( T \right)+\frac{\lambda }{4k_{B} }\frac{1}{T}\sim \frac{\lambda }{4k_{B} }\frac{1}{T}\quad (T \to 0) $$

(27)

The last step is because ln(T) is negligible compared to 1/T as T → 0. This behaviour holds only in the classical limit of nuclear motion, however. In the present case, a number of publications show that the resistivity tends to a finite value as T → 0 [38–40]. Theoretically, there are corrections that arise due to the Born-Oppenheimer approximation, since quantum mechanically, the nuclei may tunnel through the barrier.

In the Jortner model [41–43], the Fermi golden rule is used to derive the probability per second that a system in an electronic state m and vibrational levels w will make a transition to another electronic state n with vibrational levels v as

$$ W_{nv} =\frac{\pi}{2}{\Delta}^{2}\sum\limits_{m,w}\left|\langle\chi_{nv}|\chi_{mw}\rangle\right|^{2}\delta (\varepsilon_{nv}-\varepsilon_{mw}) $$

(28)

Δ is the electronic coupling matrix element that we have defined earlier. The Marcus model permits the system to reach the right parabola only if there is energy enough to pass the barrier. In the Jortner model, the right parabola can be reached also by tunneling. In particular for T = 0 from the lowest vibrational state, {n0} is the final vibronic state, i.e. the lowest vibrational state (v = 0) in the electronic state n represented by the right parabola. The precursor states {mv} are the vibronic states of the left parabola. The probabilities are obtained by assuming a Boltzmann distribution over the vibrational levels v in the left parabola

$$k=\frac{1}{Z}\sum\limits_{n,v} {\exp \left( {-\frac{\varepsilon_{nv} }{k_{B} T}} \right)W_{nv} } $$

$$ =\frac{\pi }{2}\frac{{\Delta}^{2}}{Z}\sum\limits_{n,v} \sum\limits_{m.w}\exp \left( -\frac{\varepsilon_{nv} }{k_{B} T} \right)\left|\langle \chi_{nv}|\chi_{mw}\rangle\right|^{2} \delta (\varepsilon_{nv}-\varepsilon_{mw}) $$

(29)

Z is the partition function

$$ Z=\sum\limits_{n,v} {\exp \left( {-\frac{\varepsilon_{nv} }{k_{B} T}} \right)_{nv} } $$

(30)

Clearly if the temperature tends to zero, only the lowest vibrational state {0v}can make a small but non-zero contribution to the reaction rate k. log k is then a linear function of 1/T with the slope −ε ₁₀/ k _B. The slope is zero, since we are in the lowest vibrational state. For higher temperatures, there are contributions from the other vibrational states. Finally, the slope will be −E _a / k _B as in the classical case. The final rate often resembles the function T ^−1/3. T ^−1/3 behaviour goes against experimental results in the present case, however, since the limit value as T → 0 is less than infinity. The Jortner model [41–43] represents the correct physics for very low temperatures, replacing the T ^−1/3-variable range hopping model by a model where ρ is finite at T = 0.

7 Possible Explanations of Raman and MIR Absorption for Cuprates

All cuprates, hole or electron doped [44, 45], appear to have a MMCT at 1.5–2 eV, almost independent of structure around the copper(II) ions, not counting the always present four oxygen atoms in the plane [46]. Hubbard-U is thus well defined and almost the same for all cuprates. In YBa₂Cu₃ O _{6 + x} , U has been measured up to 5 eV [47, 48]. There is another sharp and strong absorption at 4 eV, apparently due to O2p →Cu3d, where the O2p orbitals are strongly mixed with Cu3d. Normally (in aqueous solution), these transitions are forbidden but become allowed when different Cu sites are involved. (This mixing with O2p of course also occurs in the MMCT transition at ≈2 eV.) The LM transition between pure O2p and Cu3d orbitals appears at ≈3 eV.

The Raman spectra of La₂CuO₄, particularly the strong absorption at 3000 cm ⁻¹ [49], was studied by Lyons et al. and later by Tokura, Onose et al. for a number of hole doped and electron doped cuprates [46, 50, 51]. Perkins et al. [52] and Grüninger et al. [53, 54] have studied the MIR absorption at about 0.4 eV, equivalent to about 3000 cm ⁻¹. Remarkably enough, the Raman and MIR absorptions are at the same energy. In the doped cuprates, the Raman absorption hangs on until SC is achieved and there is no longer any dependence on the nuclear coordinates [19, 49–51]. MIR absorption occurs as long as there is disproportionation.

Tokhura, Onose et al. have studied resistivity in the electron doped Nd$_{\mathrm {2-}_{x}}$Ce _x CuO₄ and found approximately the same pattern as in La$_{\mathrm {2-}_{x}}$Sr _x CuO₄ [46, 49–51]. The MMCT absorption peaks in other undoped cuprates are found at 1.5–2 eV as for La₂CuO₄. [9]. Clearly, the properties are due to the CuO₂ plane and the four ligands of each copper atom [46, 49–51].

The theory used here suggests a direct coupling between Raman and MIR, which would explain the same absorption energy. The conductivity spectrum for La₂CuO₄ shows vibrational resolution up to about 1000 cm ⁻¹ (Fig. 10). In a normal vibrational spectrum, only the lowest transition for each symmetry appears, due to selection rules. In the gap between the lower and upper PES in Figs. 2 and 3, which appears at the 5th vibrational level in Fig. 10 (marked U _cross), the symmetry leading to the selection rule is obviously broken since Cu(I)/Cu(III) states are mixed into the Cu(II)/Cu(II) state. This explains the first of the transitions at about 0.4 eV of the MIR spectrum. Assuming that U _ad = 0, the MIR absorption should then occur at 1/4U which is in rough agreement with the experiments.

Fig. 10

Intersecting Cu(I)/Cu(II) and Cu(I)/Cu(III) potential curves

The modes of the vibrational levels in the Marcus diagram are all of the breathing or half-breathing type, allowed in the Raman spectrum. Due to the loss of symmetry in the gap level, the electron motion becomes strongly coupled to the vibrations, making the absorption allowed, and explaining the equal energies. The explanation lies in the crossing of the two parabolas in Fig. 10 and the vibronic level marked as U _cross. Both MIR absorption and Raman absorption occur for the some higher vibrational levels, but with less intensity.

It is interesting that the given explanation is possible only if the “internal contradiction” pointed out by Landau and Pekar [18] is taken into account. Many properties depend on the nuclear coordinates in Fig. 10 and cannot be explained if the x-axis dependence is left out. In the conducting or superconducting systems, there is no longer any x dependence because of delocalization and this explains why the strong Raman absorption at 0.4 eV disappears [51].U _ad cannot be too large if Fig. 10 is going to exist at all as a basis for the explanation. A small U _ad requires that three oxidation states are possible with similar geometry and with a low free energy for disproportionation [55, 56].

Heikes and Johnston also studied conductivity in doped nickel oxide Li _x Ni_(1−x)O [13]. Li ⁺is the dopant and replaces some Ni(II) sites whereby other Ni(II) sites are oxidized to Ni(III) sites [13]. The corresponding doped cuprate, La_2−x Sr _x NiO₄, is isostructural with La_2−x Sr _x CuO₄. By doping (x > 0), Ni ³⁺ sites are created, which explains conductivity [57]. Since Hubbard-U is considerably larger for the nickelate than for the cuprate, the scenario is different, however. Apparently, U _ad cannot be brought to zero in this case to make SC possible. Raman and MIR absorption remain and there is one-electron exchange conductivity of the same kind as for the cuprates. The MIR absorption also exist [57–60].

8 Discussion

La₂CuO₄ and CuO are both systems with localized electron structure and U > 0. The ground state wave function cannot be formed from one-electron Bloch functions. Instead, each site is best described using the local ligand field model. To describe conductivity, it is necessary to consider hopping between sites. In both La₂CuO₄ and CuO, the MMCT transitions cover a large part of the visible region [6, 9]. The ultimate reason for the large width is difference in equilibrium geometry before and after CT. In NiO on the other hand, the charge transfer spectrum appears completely in the UV region. The colour is the same as in aqueous Ni(II) solutions and is due to ligand field transitions. There is no SC in any Ni oxide or in nickelates.

After doping to La_2−x Sr _x CuO₄, a mixed valence spin system is formed with Cu(III) sites among the Cu(II) sites, closely related to the appearance of stripes [12]. The appearance of Cu(III) sites decreases U _ad and increases the interaction between the spin-coupled ground state and the Cu(I)-Cu(III) charged state. At a certain doping level, there is a spontaneous disproportionation of Cu(II) to a Cu(I)-Cu(III) (charged) system. There are thus two different “charged states”, the striped (spin) state with Cu(II) and Cu(III) sites and the charged state with Cu(I) and Cu(III) sites. The corresponding phases interact and form a new SC phase [4].

Conductivity appears as one-electron hopping or two-electron singlet pair hopping. If disproportionation of Cu(II) becomes exergonically possible, the available electronic states at low energy make SC possible. The SC gap and the pseudogap are formed [61]. Bose-Einstein statistics is followed and the system may become SC. In the slightly doped cuprate or copper(II)oxide systems, a mixed valence state of type Cu(III)/Cu(II) is present. One-electron transitions are the only ones available and the statistics of Fermi-Dirac type.

The peak intensity maximum at 0.135 eV (≈1100 cm ⁻¹) [14] is very likely due to one-electron transfer [19], i.e. λ for the one-electron exchange reaction. This is consistent with the well-resolved data for YBa₂Cu₃ O ₇ [20-23,47,48].

We find two physically different mechanisms for conductivity in the limit of delocalization: ordinary metallic conductivity or SC. The remarkable fact that cuprates, oxidatively or reductively doped, are important superconductors is after all understandable. It may be traced back to the occurrence of three different oxidation states for copper, Cu(I), Cu(II), and Cu(III), with approximately the same free energy [55, 56].