Introduction

White-collar crimes often have extensive consequences for victims, stakeholders as well as society as a whole. However, it is often problematic to define and measure these types of crimes or to quantify the effects (Friedrichs 2010). Bankruptcy fraud is one particular sub-form of white-collar crime, committed within the framework of a (formal) business activity. In Sweden, offenders have committed dishonesty or carelessness towards creditors, favoritism to (certain) creditors, or accounting fraud. An insolvent firm has therefore exploited an economic opportunity in order to gain some form of financial or business advantage (Alalehto and Larsson 2009; Delaney 1992; Friedrichs 2010). A substantial number of white-collar crimes takes place within the small business sector (Croall 1989; Korsell 2015), and this is also true in a historical perspective—for example, a majority of the people convicted for bankruptcy fraud in early twentieth century Sweden were small-scale entrepreneurs.

The understanding of how white-collar crimes would affect other agents and interests is incomplete. All other things being equal, it could be expected that the trend of bankruptcy frauds has a positive relationship with the bankruptcy trend: if bankruptcies decrease (increase), bankruptcy frauds should also decrease (increase). This interpretation suggests that variations in bankruptcies ‘cause’ variations in bankruptcy frauds. In the present article, we reverse this view, hypothesizing that the economic system—and agents within this system—would be affected by this form of economic crime. Drawing on recent research in the criminology and economics literatures, we develop a framework for an analysis of the diffusion of bankruptcy frauds to other economic agents. Empirically, we investigate the potential effect of bankruptcy frauds on economic activity—more specifically, on the bankruptcy volume. Our case concerns Sweden and the period of analysis is long, stretching from 1830 to 2010.

The bankruptcy system has been regarded as a cleansing mechanism that sorts out inefficient firms from the market (e.g., Miller 1991). However, this may not always be the case; it can also be conceived as a financial institution. As firms themselves can file for bankruptcy, the bankruptcy system can be used to redistribute assets and evade payment of debts and obligations. The aim of this particular type of bankruptcy is usually to continue the business within the framework of an entirely new firm. The bankruptcy clears the firm of debt, while the costs are taken by the taxpayers and by creditors with unprivileged claims—usually other firms. This is usually not a legal violation, but rather a strategic means for reconstructing a business, or for making a profit (Akerlof et al. 1993; Delaney 1992). Bankruptcies in general would also have potentially damaging effects on other economic agents. Economists have developed models on the consequences of critical events in the economy: interlinkages between firms would have potential domino effects. Failure of fulfilling debt commitments may lead to ‘bankruptcy chains’—a bankruptcy spreads to other firms, which may create a vicious cycle of bankruptcies (Gatti et al. 2006, 2009).

Since bankruptcy frauds are integrated in the bankruptcy system, interlinkages and networks in the economy represent a source of diffusion of both bankruptcies and of bankruptcy frauds. According to the criminology literature, bankruptcy frauds have potential diffusion effects that are analogous to the effects of bankruptcies and ‘strategic bankruptcies’: a bankruptcy fraud committed by one firm may ruin other small businesses, such as suppliers and creditors (e.g., Alvesalo and Virta 2010; Croall 2004a). In essence, ‘bankruptcy for profit’ and criminal behavior amongst both large, established businesses (e.g., Akerlof et al. 1993; Levi 2008a; Pontell 2005) and by small businesses and entrepreneurs (Baumol 1990; Desai and Acs 2007; Gottschalk and Smith 2011), if reaching a cumulative level, would thus disturb the mechanism for entry and exit in the economy.

In the present study, we show that it is possible to generate long, comprehensive series of measurements of white-collar crime—in the present case, bankruptcy frauds. We use unique aggregate time-series, derived from several historical and contemporary sources. Methodologically, we apply the recently developed cointegrating nonlinear autoregressive distributed lag (NARDL) model. This model makes it possible to investigate whether the dependent variable, the bankruptcy volume, reacts asymmetrically to increases and decreases in bankruptcy frauds, both in the short and the long run. Consequently, the effects of the independent variable, as it rises, could be different to the effects as it falls. When there is asymmetry, standard linear models may produce misleading conclusions (Shin et al. 2011).

The relationship between crimes and economic variables is an expanding field of research. Empirical studies suggest that crime would have detrimental effects on economic activity (e.g., Carboni and Detotto 2016; Detotto and Otranto 2010) and that variations in crime would even have an asymmetric impact on the economy (Goulas and Zervoyianni 2015). In line with these recent efforts, along with the literatures on bankruptcy diffusion and white-collar crime, the main research question in this article is whether it is possible to identify a relationship between bankruptcy frauds and the volume of bankruptcies. Research in both criminology and economics (e.g., Bushway et al. 2012; Krüger 2011) furthermore maintains that crimes co-vary with economic fluctuations, and economists also regularly assert that the business cycle would affect the development of bankruptcies (e.g., Hol 2007). Therefore, a supplementary question in our article concerns whether there is a long-run relationship among macroeconomic fluctuations, bankruptcy frauds and the development of the volume of bankruptcies.

To the best of our knowledge, the methodological approach of our study and the particular type of data that we employ has only to a little extent been used in previous analyses of white-collar crimes. Box et al. (2018) use Swedish bankruptcy fraud data across nearly two centuries, assuming that the effects from frauds on bankruptcies are symmetric. Furthermore, Alalehto and Larsson (2009) utilize some of the same historical sources, but for a considerably shorter period (1864–1912). Our results can be summarized as follows. We find no relationship between macroeconomic change and the volume of bankruptcy frauds. However, variation in the business cycle and, more importantly, changes in the annual volume of bankruptcy frauds revealed an asymmetric (causal) effect on the volume of bankruptcies. In particular, our results show an asymmetric diffusion effect from economic frauds to the bankruptcy system: increases in the bankruptcy fraud volume had a positive and significant effect on the volume of bankruptcies. However, decreases in the volume of frauds had no significant effect.

Research Framework

Networks, Interlinkages and Bankruptcy Diffusion

Several literatures assert that households, firms and financial institutions are connected through networks—social or economic, personal or impersonal. Economic agents—e.g., banks, suppliers and contractors—are generally connected through debts and claims. In financial economics, interlinkages between banks are seen as a cause of financial spillover and ‘contagion.’ When one region suffers a bank crisis, other regions suffer a loss since their claims on the region in crisis fall in value. This is a spillover effect—if strong enough, it can induce a crisis in adjacent regions (Allen and Gale 2000). Economists have also recently developed models on network economies. Specifically, Gatti et al. (2006, 2009) build a model on the credit interlinkages between firms and banks. In their model, macroeconomic cycles are outcomes of a complex interaction between firms and banks with heterogeneous conditions at the micro level. Here, the corporate sector consists of ‘downstream firms’ and ‘upstream firms’. The latter supply intermediate inputs to the downstream firms, which are pure borrowers from both banks and upstream firms. Upstream firms are lenders and supply trade credit to the borrowing downstream firms, but upstream firms are also borrowers from banks. Banks are pure lenders to both down- and upstream firms. Thus, the activities and fates of upstream firms are largely determined by the production of downstream firms. This implies that an unexpected shock in the economy would affect the credit relationship between down- and upstream firms; if the shock is substantial, borrowers may not be able to fulfill debt commitments—the default of one agent will thus cause the default of another or other agents. In turn, the number of links between agents implies a high probability of bankruptcy diffusion (Gatti et al. 2009).

Interlinkages between economic agents are also acknowledged in other areas of the economic sciences. In labor economics, spillover effects from business closures have been found to affect the labor market (e.g., Gathmann et al. 2014). Similarly, business scholars acknowledge interlinkages between firms in a market economy: bankruptcies and defaults have been identified as potentially critical events for a business relationship and the connected businesses in various forms of credit interlinkages or other business networks (e.g., Fors 2008; Ooghe and De Prijcker 2008). Consequently, while business failures may be outcomes of several different factors—e.g., inadequate management, changing industry conditions, or macroeconomic variation—they could also be an outcome of a domino effect caused by the failures of debtors or customers (Wu 2010). In sum, several literatures support the notion that corporate defaults and business failures would have effects on economic activity through interlinkages.

Crimes and Economic Activity

What is the relation between crimes and economic activity? One emergent field of research in the economic sciences addresses the link between economic variables and crimes: recent results maintain that there is a causal effect going from economic crimes to economic activity at the macro level. For example, in the case of Italy, Detotto and Pulina (2013; see also Detotto and Otranto 2010; Carboni and Detotto 2016) conclude that crimes generally have a negative effect on the legal side of the economy, thus reducing the employment rate. In particular, violence crimes have a crowding-out effect on economic development. A similar effect is maintained for other crimes, such as corruption and terrorism (Eckstein and Tsiddon 2004; Lauridsen 2009). In country panel analyses, Goulas and Zervoyianni (2013, 2015) assert that the effect of crime is asymmetric: during booms and expansions, crimes are not as detrimental to the economy as they are during recessions. During recessions, the negative effect is significantly stronger since the strain on public-sector resources is larger since it becomes more difficult to obtain additional resources for combatting and preventing crime. Furthermore, a high crime level will produce a perception of instability and will negatively affect savings and thus growth. Finally, increased crime is likely to induce individuals to work less and there will therefore be fewer available labor resources. These findings lead to the conclusion that both the level of crime and changes in the crime level (or in crime rates) would have causal effects on economic activity, but in the other causal direction.

Linkages between fluctuations in crime rates, or the level of crimes, and economic cycles are well-established in both criminology and economics. Crimes are thought to be dependent on the state of the economy, and it would be remarkable if crimes were completely immune to the general economic conditions. Empirical studies have found that the effect of real economic activity on crimes differs between different types of crimes. Property crimes, violence crimes and sex crimes are normally countercyclical (Cook and Zarkin 1985; Bushway et al. 2012). The opposite is true for economic crimes due to the highly significant increase in opportunities of these types of crime during economic expansions and booms; as opposed to theft and violence crimes, white-collar crimes and frauds display a pro-cyclical sensitivity to the business cycle—in times of affluence, economic crimes and frauds would generally increase (Bushway et al. 2010, 2012; Detotto and Otranto 2012; Krüger 2011; Povel et al. 2007).

The Effects of (White-Collar) Crime and Bankruptcy Fraud

Bankruptcy fraud normally translates into an economic crime that is committed in a small business; Korsell (2015: 91) establishes that “the majority of those convicted of economic crime are more likely to belong to a class of small businessmen dressed in overalls than that of managing directors.” Detecting and substantiating offences committed by small firms is normally easier than crimes higher up the corporate ladder. Many times, however, there are no clear victims of economic crime. Rather, this is a classic intelligence crime, as opposed to crimes where there is a clear physical victim to report the crime. The incidence of economic crime is therefore to a great extent dependent on society’s control mechanisms (Baard et al. 2010; Korsell 2015; Levi 2008a, b).

The study of diffusion of illegal practices and frauds among offenders has a long history in ‘white-collar criminology’, in that respect, research has more been targeting white-collar offenders, investigating if the status of offenders is a defining feature of white-collar crime, or, alternatively, focusing on issues of regulation and punishment (Croall 2001; see also Baker and Faulkner 2003). Baker and Faulkner (2003, 2004) propose a typology of the diffusion of fraud: essentially, diffusion among offenders could come about either through social networks or through impersonal methods. In the first case, new offenders learn about techniques from other offenders; in the second, new offenders learn the techniques from observation and from ‘society’. For instance, in an empirical study closely related to the theme of the present article, Alalehto and Larsson (2009) analyze the relationship between the industrialization process in Sweden and the aggregate development of bankruptcy frauds from 1864 to 1912, testing the established criminology hypothesis (Coleman 1998; Robb 1992) that white-collar crimes intensify with the industrialization process. Alalehto and Larsson (2009) consequently investigate fraud diffusion among offenders. However, diffusion of fraud among victims such as investors, creditors, and suppliers has been more neglected in research. Therefore, it is possible to distinguish networks from impersonal methods when it comes to fraud diffusion among victims. In the first case, victims have ties with offenders or are influenced to invest; in the second, they are influenced through direct contact or through the market mechanism (Baker and Faulkner 2003).

In that respect, criminologists assert that social and economic networks can be a major source of fraud diffusion. However, white-collar crime has been a less researched field despite the fact that the losses from economic crimes may be several times higher than the losses from other types of crime, even if losses from the former often are hard to estimate (e.g., Levi and Burrows 2008). Most research on white-collar crimes has consisted of case-studies or cross-sectional investigations, and empirical data on economic crimes is often lacking (Alalehto 2015; Alvesalo and Virta 2010; Friedrichs 2010; Korsell 2015; Levi and Burrows 2008). The literature asserts that frauds have the potential to ruin other small business owners since their claims on the insolvent party are lost due to unlawful behavior. In spite of this, the understanding of how white-collar crimes would affect other agents and interests is incomplete (Baker and Faulkner 2003; Croall 2004a; Korsell 2015). The Nordic criminology literature has recently discussed the wider effects of white-collar crimes and economic frauds: a business that cooperates with an unreliable partner, or is economically linked to another firm, can become a victim of various credit, ordering and payment frauds, or debtor’s crimes (bankruptcy frauds). Consequently, the impact of economic crime should be understood in a wider perspective. A discussion that only strictly concentrates on the quantity of economic damages runs the risk of concealing the overall impact of criminal activities. Examples of other victims are, e.g., employees, consumers, the environment, and other firms and the market (see Alvesalo and Virta 2010).

Concluding and summarizing several streams of research on (white-collar) crime and the economy, we find that the criminology literature has generated hypotheses on the potential effects of economic crimes, even though empirical knowledge of this relationship is generally lacking. The present article sets out from these assumptions. Furthermore, previously generated assumptions and typologies of white-collar offenders and victims in criminology are analogous to the principal idea of bankruptcy diffusion in the economics and business literatures: one agent’s default—or fraudulent behavior—has the potential to spill over to other agents. In line with the ‘bankruptcy diffusion perspective’ (e.g., Gatti et al. 2009) and research on the relationship between crime and economic variables (e.g., Carboni and Detotto 2016), we address these questions by investigating the link between bankruptcy frauds and bankruptcies in Sweden over an extended period of time. We specifically test the following previously generated assumptions: (a) that the volume of bankruptcy frauds is affected by macroeconomic change; (b) that the bankruptcy volume is affected by macroeconomic change, and—the central question in this article—(c) that bankruptcy frauds would have a propensity to diffuse to other economic activities and agents.

Methodological Considerations

As in several other Western societies, modern bankruptcy laws were gradually introduced from the mid-nineteenth century in Sweden (Gratzer 2008; Mann 2002; Tuula 2001). As for the regulation of bankrupand bankruptcy procedures, the Bankruptcy code from 1818 was succeeded by new codes in 1862 and 1921. According to Tuula (2001), neither of these reforms were ‘radical’—several aspects of former laws remained or were modified in the new laws; reforms mainly concerned procedural matters. In 1987, the legal framework that is still effective was introduced. In the Bankruptcy code of 1987, the code of 1921 has—similar to former reforms—remained unchanged in several instances (Mellqvist and Welamson 2017; Swedish Government 2010). Furthermore, a significant change in the law on corporate reconstruction—equivalent to Chapter 11 in the United States—became effective from 1996 with the purpose of lowering the volume of bankruptcies and rescuing insolvent firms. However, it appears that the reform in the mid-1990s had no substantial effects on the bankruptcy frequency (Karlsson-Tuula 2006, 2011). As pointed out by Alalehto and Larsson (2009), the definition of bankruptcy fraud has remained essentially intact in Sweden ever since the early 19th century. While both penalties and legal procedures have changed over time, the offence has essentially been defined as dishonesty, carelessness or favoritism towards creditors (see also Karlsson-Tuula 2011; Swedish Government 1996). Since 1986, this offence is formally labeled ‘Crimes against creditors’, committed towards all existing and, in some cases, foreseeable creditors (one example is accounting fraud). The term ‘creditor’ includes all parties with an interest in an individual bankruptcy: private persons, corporations, banks and financial institutions, as well as the government. Historically, bankruptcy fraud has been regulated in several codes: in the Bankruptcy code, in the Penal code, and in the Commercial code and the three codes have overlapped in an intricate way. Carelessness was introduced in the early 19th century in the Bankruptcy code of 1818, and carelessness and fraudulent behavior towards creditors were also introduced in the Penal code of 1864 (Rydin 1888). This code remained until 1942, when a reform introduced five special debtor’s crimes (bankruptcy frauds): dishonesty to creditors; grave such dishonesty; carelessness towards creditors; favoritism to creditors, and bookkeeping (accounting) crimes. Crimes against creditors is still today defined according to the Penal code of 1942 (Swedish Government 1996).

In comparison to all economic crimes, bankruptcy frauds are comparatively few and correspond to around two to three percent in Sweden. Bankruptcy fraud is therefore a sub-component of the overall phenomenon of white-collar crime, and the latter lacks a clear definition in the literature (see, for example, Friedrichs 2010: 5–8; Levi 2008b). Our study uses long, annual aggregate series on bankruptcy frauds, which we use as a representation for white-collar crime over longer periods. Indeed, the nature of our empirical data makes us unable to take analyze several important questions in the (white-collar) criminology literature (such as the volume of losses from frauds). Furthermore, it could naturally be discussed whether bankruptcy fraud is a valid or even appropriate indicator for white-collar crimes; to begin with, the motivation to defraud can be defined as heterogeneous: in his seminal study, Levi (2008b [originally 1981]) suggests a threefold typology. The first is ‘pre-planned frauds’ where the business scheme is set up from the start as a way of defrauding victims (e.g., individuals, other firms, the public). The second is ‘intermediate frauds’ where individuals start out by obeying laws and regulations but intentionally turn to fraud at a later stage. The third type is ‘slippery-slope frauds.’ Here, deceptions intensify, commonly while trying to rescue an insolvent business that, in practice, is doomed to fail. Due to the nature of the data in this article—discussed in detail, below—we are neither able to empirically separate nor identify various types of motivations. Correspondingly, and following both Levi (2008a, b) and others, we admit that the nature of (bankruptcy) frauds and white collar crimes changes over time. The types of techniques and organization have changed, often in accordance with technological change (such as the Internet; see e.g. Levi and Burrows 2008; Lindström 2002). Consequently, several of the problems that are included in the indicators and data that we use in the present study cannot be solved.

Bankruptcy Frauds as a Representation of White-Collar Crime

Is it possible to use bankruptcy frauds as a representation of white-collar offences? We maintain that it is an acceptable representation and—at least if we are interested in longer changes in crimes related to white-collar offences (in Sweden)—perhaps the only available indicator. In our study, it is not possible to discern nor to disaggregate the bankruptcy fraud data on different sub-types of offences. Rather, and in line with previous research on longer changes in white-collar crime behavior in Sweden (Alalehto and Larsson 2009), the present article is forced to accept the categorization of criminals according to the Swedish courts. The criterion is thus adapted to the nature of the offences given by the Penal code. However (and as also pointed out by Alalehto and Larsson 2009), both the Penal code and the Bankruptcy code in Sweden have historically been closely related in intention to the concept of white-collar crime that is used even today.

Overall, economic and white-collar crime is often discussed as a modern phenomenon. It is obvious that recent technological innovations such as computer technologies, big data mining on the Internet, etc., have radically changed the possibilities for criminals; and many contemporary examples of economic crime were not possible to commit in earlier periods of history, such as VAT-related frauds, insider trading, and cartel building (Levi 2008b; Lindström 2002). From a long-term context in general—and in the Swedish context in particular—bankruptcy frauds could be viewed as an acceptable representation for white-collar crimes. Despite the fact that it is not a main crime category in empirical research, the offence is nonetheless of importance for authorities’ detection of suspected fraud in business activity, particularly when it comes to insolvency. The advantage of using bankruptcy frauds is that the detection risk (at least theoretically) is at its highest in the context of a bankruptcy filing. The bankruptcy trustee is responsible for the bankrupt business; if an offense is detected it must be reported to a public prosecutor. The data on bankruptcy frauds covers a long period and consists of unbroken observations; in comparison to alternative indicators on white-collar crime, it has a good validity. Therefore, like Alalehto and Larsson (2009), we maintain that our series on bankruptcy frauds constitute an essential and relevant representation of white-collar crime.

It is also important to acknowledge that not only the methods and techniques for frauds change over longer periods but also that the (social) composition of bankruptcies in general has changed. During the period of study, bankruptcies transformed from personal (i.e., individual) bankruptcies to corporate bankruptcies, and this is also the case for the social composition of bankruptcy frauds. However, over the entire period, an absolute majority of the bankruptcies concern business activity, in particular small business activity. Overall, the majority of all new firms that are created each year will exit within a short period of time—and most of them are small firms.Footnote 1 This is also true in a historical perspective: as an example, between 1914 and 1917, an absolute majority of all registered bankruptcies in Sweden (nearly 85 percent) were personal bankruptcies. In that time and age, very few bankruptcies were represented by formal business organizations, such as joint-stock companies or partnerships. However, the lion’s share of personal bankruptcies in the early twentieth century was, in fact, related to small business activities, consisting of master craftsmen, journeymen, tradesmen, small-scale merchants and traveling salesmen (Statistics Sweden 1923). Consequently, in both a historical and contemporary perspective, the overwhelming share of registered bankruptcies relates to small business activity. In that respect, we believe that our empirical data comes close to the notion of the most ‘common’ white-collar crime and its typical ‘victim’—in both cases, the small business (Croall 2004a, 2004b; Korsell 2015).

Data Considerations

Our study uses official statistics on bankruptcy frauds (and bankruptcies). However, crime data reported in official statistics, the popular press and in research are often incomplete and/or misleading. Reported frauds only represent a minority of the total amount of reported economic, or white-collar crimes. Moreover, it is usually more difficult to prove crimes against creditors, particularly if the bookkeeping records are incomplete or missing, and bankruptcy investigators often lack resources for more extensive investigations (Korsell 2003). Economic crimes have not been systematically studied by historians and our knowledge is still very fragmented. More systematic analyses of the extent to which economic crime was noticed by authorities during the 19th century in Sweden is still lacking (Lindström 2004); in addition, Swedish printed historical statistics are largely restricted to traditional criminality—that is, violence and theft crimes—and it is generally difficult to identify economic crimes or corporate crimes (von Hofer 2011). Economic crime in particular has unrecorded numbers which are said to be much larger than other criminal offenses, partly because of the absence of victims that may notify the offences to an authority, partly due to the fact that an economic crime is a reconnaissance crime. This crime is usually detected by the authorities through intelligence, reconnaissance and control. The detection risk is therefore totally dependent on the authorities’ efforts and their willingness to combat crimes; crime statistics do therefore not give any satisfactory basis for assessing the extent of economic and white-collar crime or its impact on the economic development. The number of detected crimes is to some extent related to the control and supervision activities of society. Even the risk of being detected affects the volume of crime (for discussions, see Dahlbäck 1978; Friedrichs 2010; Karstedt and Bussman 1999, Levi 2008a, b; Swedish Government 2008).

As for bankruptcy frauds, it is very plausible that the true number is higher than the official statistics which we employ in the present study. The first empirical study on bankruptcy frauds in Sweden was made by Kedner (1975), finding that around 30–40% of the firms with a dividend to creditors were reported to the public prosecution authority as bankruptcy frauds. The Swedish Enforcement Authority (KFM) found in 2009 that notifications for fraud were made in 35 percent of all bankruptcies (KFM 2010); Magnusson (1999) found that for 75 percent of the bankrupt firms in Sweden in 1983, there was suspicion of crime. Similar results are found in other countries: Liebl (1988) and Weyand (1997) estimated that between 80 and 90 percent of all German bankruptcies were related to crime, and investigations on criminal bankruptcies in Norway during the 1980s and 1990s report figures that vary between 56 and 70% (Langli 2001). These investigations indicate that bankruptcy frauds are likely to be severely under-represented in official statistics and that the exact numbers are unknown. Despite this, other longitudinal series on different types of white-collar crimes are not available (Alalehto and Larsson 2009).

In our own study, we utilize two main annual time series that relate to the bankruptcy phenomenon: one series on the aggregate volume of bankruptcy frauds and one series on the aggregate registered volume of bankruptcies (1830–2010). Our data is both historical and contemporaneous, derived from archives as well as from several printed and electronic sources.Footnote 2 Our dataset on bankruptcies and frauds consists of count data; other studies more often attempt to use rates. However, in the present case, it would be very difficult to find a suitable population or series for creating rates. For example, and as discussed above, the social composition of bankruptcies and bankruptcy frauds changes over time—from personal to corporate (units). Longer consistent series over enterprising do not exist and we believe a count analysis to be the most appropriate one in the present case.Footnote 3

As noted, we use this aggregate bankruptcy volume series as an indicator for other agents and for economic activity; this dependent variable is calculated by subtracting the registered bankruptcy fraud volume from the registered bankruptcy volume (counts). This is done for the following reasons: for any calendar year, the total stock of bankruptcies will always entail a certain number of bankruptcy frauds—that is, each bankruptcy fraud is also a bankruptcy event, meaning that a fraud is counted twice in the statistics. In our data, the average share of bankruptcy frauds in relation to all registered bankruptcies for the whole observation period is 5.2%; however, it varies substantially and this figure generally increases over time. This is why we use the net bankruptcy volume as the dependent variable.

Furthermore, it is unlikely that bankruptcy frauds per se would have any significant or measurable impact on the aggregate economy. As noted, bankruptcy frauds represent a small fraction of all crimes committed in Sweden, particularly from a historical point of view. For example, in our data, the total number of bankruptcy frauds in the mid-1800s amounted to around 20 per year while, at the same time, there were approximately 1500 bankruptcies per year. During that period of time, however, around 40,000 individuals were sentenced for criminal offences of all types (von Hofer 2011). In the early 2000s, the number of registered bankruptcy frauds was, on average, 900 per year while the total number of bankruptcies varied between 7000 and 8000 annually (and the number of individuals sentenced for all types of crime in the early 2000s exceeded 400,000). It would be naïve to assume that changes in the mere frequency (count) of bankruptcy frauds would significantly affect the aggregate economic output. However, from a diffusion perspective, increases in the stock of fraudulent bankruptcies could potentially diffuse to other agents in the economic system (Alvesalo and Virta 2010; Baker and Faulkner 2003; Croall 2004a; Gatti et al. 2006).

In this article, we attempt to quantify the potential effects of crimes by studying how net changes in frauds are related to changes in the bankruptcy frequency. Available data enables us to address the potential relationship among crimes, bankruptcies and macroeconomic change. In the spirit of Bushway et al. (2012), we here take on a more ‘humble’ task; the one of measuring the net effect of bankruptcy frauds—and of macroeconomic variation—on the bankruptcy volume. In the following analysis, we employ long historical series on the Swedish Gross Domestic Product (GDP; Schön and Krantz 2012) as an indicator for macroeconomic variation. The link between economic fluctuations and bankruptcies constitutes a secondary aim of our article; we do not specifically elaborate on how and to what extent various business cycles would differ from each other or have different effects on the dependent variable. A number of studies have attempted to analyze the aggregate relationship between crimes and the business cycle or macroeconomic variation in general, using both non-parametric (Cook and Zarkin 1985; Bushway et al. 2012; see also Bushway et al. 2010) and parametric approaches (e.g., Krüger 2011). In the present case, we merely acknowledge that past research has found linkages between different forms of crimes and macroeconomic variation. Using economic variation is also important for another reason since macro fluctuations, ex ante, are likely to affect the volume (or the rate) of bankruptcies (e.g., Hol 2007; Lane and Schary 1989; Levy and Bar-Niv 1987).

Bankruptcies and Bankruptcy Frauds, 1830–2010

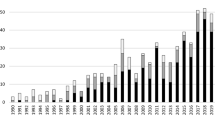
The aggregated series on bankruptcies and bankruptcy frauds in Sweden from 1830 to 2010 are reported in Fig. 1. As can be observed, the development in the total bankruptcy volume has varied substantially over time, with a low and moderately stable level from 1830 up to the late 1850s. From here to the first half of the 1920s, there was a trend of a general increase in bankruptcies (although with a substantial variation). As noticed, variations in bankruptcies may be partially caused by business cycle changes (e.g., Hol 2007) and it is likely that the industrialization process and the emergence of a modern capitalist society in Sweden from the late 1800s gradually made the bankruptcy frequency co-vary more systematically with the business cycle. For instance, the lowest observed count in bankruptcies in 1873 coincides with an economic boom, and the highest value (in 1868) seems to be synchronized with a deep recession; similarly, the bankruptcy peaks in 1921, 1933 and 1991 correspond to severe macroeconomic crises in Sweden during the twentieth century.

Fig. 1
figure 1

Registered bankruptcies and bankruptcy frauds in Sweden, 1830–2010

Full size image

As can be observed, there was a fall in the bankruptcy trend from the mid-1920s up to end of World War II; the remainder of the observation period witnesses a significant absolute increase in the bankruptcy volume. Even so, it can also be observed that the volume of bankruptcies was relatively low and stable between c.1945 and c.1965. This may be an outcome of regulations of the economy during the war and the prosperous post-war period, during which the Swedish economy grew substantially. From the mid-1960s, the number of bankruptcies increased significantly; in a comparative perspective, the years from the mid-1980s to 2010 show the highest historical levels (even if the trend is generally negative from 1992 and onwards). It is highly likely that the changes in the bankruptcy volume reflect macro-economic change; for instance, the peak in 1992 is likely to be an outcome of the crises in the financial and real estate markets in the early 1990s (Lönnborg et al. 2003).

The trend of bankruptcy frauds is generally positively increasing between 1830 and 2010, but with a considerable variation (Fig. 1; see also von Hofer 2011). How can this be explained? It is reasonable to assume that the industrialization process, the increased use of the joint-stock company as an economic form of organization—which de-personalizes the economic risk—as well as the expansion of the market economy have led to an increase in the bankruptcy frequency and thus to an increase in bankruptcy frauds (Alalehto and Larsson 2009). Furthermore, Swedish criminologists have noted that the general crime rate may increasingly have started to co-vary with the capitalist business cycles from the second half of the 19th century (von Hofer and Tham 2000). The development of bankruptcy frauds is somewhat different from registered bankruptcies, however. The fraud volume remained comparatively low—approximately 10 registered frauds per year—up to the mid-1800s. From then, the number of frauds varied around 40 per annum, but took off from the late 1940s and the early 1950s. As has been noted, the bankruptcy volume had a similar take-off, but approximately 20 years later. Assuming a constant tendency to commit crime (and a constant share of public resources for investigations of crimes), we would therefore expect the trend of bankruptcy frauds to follow the bankruptcy trend; however, our data reveals deviations from this assumption. The picture is complicated by the strong fluctuations of peaks and troughs in bankruptcy frauds during the 1960s and 1970s, as well as by the dramatic increase in the number of bankruptcies at the beginning of the 1990s. Therefore, different periods display differences in the relationship between bankruptcies and bankruptcy frauds.

How can the changes in bankruptcy frauds over time be explained? It is an unresolved question among criminologists as regards the extent to which changes in the crime rate or crime volume reflect genuine changes in criminal behavior, or if they are principally an outcome of changes in clearance rates. Our own bankruptcy frauds series have distinct similarities to trends in other Swedish crime data: convictions for theft offences in Sweden generally fell from the early 19th century and onwards. However, after World War II, theft convictions increased substantially. Overall, the principal trend for convictions in 20th century Sweden has followed the form of an S-curve: a slowly increasing trend that rises more steeply in the 1950s, reaching a more stable level at the end of the century (von Hofer and Tham 2000). For the 1900–2000 period, bankruptcy frauds show the same pattern with a ‘levelling-off’ from the 1990s. However, it can also be observed that in the new millennium, the volume has increased even more; the data in this article reveals that the overall bankruptcy trend since the 1990s has generally fallen while the bankruptcy fraud volume has generally increased. Overall, we are here thus able to observe some trends in the two series, as well as fluctuations in those series. Do these fluctuations co-vary, and is it possible to identify a relationship?

Model and Testing Methodology

As noted above, we employ two series that relate to bankruptcies: the volume (counts) of registered bankruptcy frauds and the net bankruptcy volume (total volume of bankruptcies minus the volume of frauds) between 1830 and 2010, as well as data on GPD per capita growth (Schön and Krantz 2012) for the same period. The cointegration technique makes it possible to deal with nonstationarity as well as to separate long-run equilibrium relationships from short-run equilibrium relationships. In this study, we focus on whether macroeconomic variation, and—in particular—whether the volume of bankruptcy frauds has an influence on the bankruptcy volume in both the long and short run. When using the total registered bankruptcy volume as the dependent variable, preliminary cointegration tests of the long-run causal relationship revealed that we were unable to find a long-run relationship. However, it can be recalled that the registered stock of bankruptcies always consists of a share of bankruptcy frauds—the latter are counted twice in the statistics. Using the net bankruptcy volume as the dependent variable (registered bankruptcies minus bankruptcy frauds) in our preliminary tests, which we simply call Bankruptcies, B, we were able to find a cointegration relationship. Consequently, throughout the remaining analysis, we employ B as the dependent variable.

Our analysis is carried out under the framework of the nonlinear autoregressive distributed lag (NARDL) model developed by Shin et al. (2011). NARDL is an extension of the autoregressive distributed lag (ARDL) model developed by Pesaran, Shin and Smith (2001). Since the ARDL model only allows for symmetric relationships, it can be regarded as a special case of NARDL. The NARDL framework presents several advantages. First of all, the approach is robust to endogeneity; similar to the ARDL approach, Shin et al. (2011) argue that NARDL with a properly selected lags order is robust to endogeneity. Second, similarly to the ARDL approach, NARDL requires no prior information concerning stationarity of the variables involved. For a study of asymmetric responses, we must make the transformation of variables into their partial sums. These partial sums are, obviously, not stationary. The NARDL framework therefore provides a platform for studying the equilibrium condition in which we are interested. Third, NARDL is more reliable in terms of possible structural changes and policy regime shifts across time periods. We have long time series in our study and this advantage should therefore not be neglected. Despite the fact that the NARDL approach has been developed relatively recently, there are many applications: Eberhardt and Presbitero (2013) find some evidence for a nonlinear relationship between debt and long-run growth across countries. In addition, Garz (2013) investigates the potential link between negative economic news coverage and pessimism in German unemployment expectations, finding that the quantitative dominance of negative over positive news causes an asymmetric reaction in unemployment expectations, which promotes pessimism. Furthermore, Verheyen (2013) analyzes EMU exports to the U.S., and finds that exports respond more strongly to depreciations than to appreciations.

Equilibrium Conditions

For allowing asymmetric influences, we can capture some degrees of non-linearity, which are characterized via the partial sums of positive and negative changes associated with the variables considered. Since real GDP growth, GGDP, and the logarithm of the volume of bankruptcy frauds, lnBF, will be explanatory variables, we define the partial sums of them

$$GGDP_{t}^{ + } = \mathop \sum \limits_{i = 1}^{t} \hbox{max} \left( {\Delta GGDP_{i} ,0} \right)$$
$$GGDP_{t}^{ - } = \mathop \sum \limits_{i = 1}^{t} \hbox{min} \left( {\Delta GGDP_{i} ,0} \right)$$
$$\ln BF_{t}^{ + } = \mathop \sum \limits_{i = 1}^{t} \hbox{max} \left( {\Delta \ln BF_{i} ,0} \right)$$
$$\ln BF_{t}^{ - } = \mathop \sum \limits_{i = 1}^{t} \hbox{min} \left( {\Delta \ln BF_{i} ,0} \right)$$

Note that \(\Delta GGDP\) denotes changes in GDP growth, and \(\Delta \ln BF\) represents the growth rate of bankruptcy frauds. It can be observed that if these changes are positive, these developments would be added to the corresponding positive sums, respectively. Consequently, GGDP + t and \(\ln BF_{t}^{ + }\) are monotonically increasing functions. Similarly, since only negative changes will be added to the negative partial sums, GGDP − t and \(\ln BF_{t}^{ - }\) are monotonically decreasing functions. Accordingly, the partial sums can be regarded as stochastic trends of the original, since the original series can be decomposed into these two trends: GGDPt = GGDP0 + GGDP + t  + GGDP − t and \(\ln BF_{t} = \ln BF_{0} + BF_{t}^{ + } + BF_{t}^{ - }\), respectively. We formulate two long-run equilibrium conditions according to our two exercises and start with the simple one: bankruptcy frauds, BF, in relation to real GDP growth:

$$\ln BF = \alpha_{0} + L_{GGDP}^{ + } GGDP^{ + } + L_{GGDP}^{ - } GGDP^{ - } + v_{t}$$
(1)

Unlike the symmetric case (ARDL), the impacts of real GDP growth are separated via two stochastic trends. The long-run coefficient \(L_{GGDP}^{ + }\) captures the influence of positive changes in real GDP growth; a one percentage point increase in real GDP growth would lead the bankruptcy frauds to change \(L_{GGDP}^{ + } *100\%\). Similarly, the long-run coefficient, \(L_{GGDP}^{ - }\), refers to \(L_{GGDP}^{ - } *100\%\) changes in the bankruptcy frauds, when there is a one percentage point reduction in real GDP growth. The key feature of asymmetry is that these two long-run coefficients are allowed to be different. Note that the time trend is not included in (1). This NARDL setting is different from the symmetric case, since real GDP growth is not subjected to any time trend; here, the time trend is not useful since the two stochastic trends of GDP growth, GGDP+ and GGDP−, take care of the role played by the time trend in the ARDL model. Our second long-run equilibrium condition is bankruptcies, B, in relation to both bankruptcy frauds and real GDP growth:

$$\ln B = \alpha_{0} + L_{GGDP}^{ + } GGDP^{ + } + L_{GGDP}^{ - } GGDP^{ - } + L_{BF}^{ + } BF^{ + } + L_{BF}^{ - } BF^{ - } + v_{t}$$
(2)

Similar to the previous condition, the long-run coefficients \(L_{GGDP}^{ + }\) and \(L_{GGDP}^{ - }\) in (2) capture the influence of positive and negative changes in real GDP growth, respectively. Analogously, the long-run coefficients, L + BF and L − BF , describe the impacts of bankruptcy frauds. Note that these stochastic trends are in terms of logarithms, meaning that a one-percent increase in bankruptcy frauds would lead to L + BF  % changes in bankruptcies, and a one-percent decrease in bankruptcy frauds would cause L − BF  % changes in bankruptcies. Once more, the symmetries are characterized by possible differences between \(L_{GGDP}^{ + }\) and \(L_{GGDP}^{ - }\), and, \(L_{BF}^{ + }\) and \(L_{BF}^{ - }\), respectively.

Short-Run Adjustments

The short-run adjustments are defined as the first differences of the variables involved in (1) and (2). Following the conventional error correction model (ECM), we also model the short-run adjustments by including responses to disequilibrium. Disequilibrium is the feature when the long-run residuals vt are not zero in the short run due to short-run transitory shocks. It is important to consider whether short-run adjustments would respond to contribute to eliminate the disequilibrium. Formally, short-run adjustments associated with (1) and (2) are formulated as:

$$\Delta \ln BF_{t} = \,\alpha_{1} \left( {\ln BF_{t - 1} - L_{GGDP}^{ + } GGDP_{t - 1}^{ + } - L_{GGDP}^{ - } GGDP_{t - 1}^{ - } - \alpha_{0} } \right) + \mathop \sum \limits_{i = 1}^{p} \beta_{i} \Delta \ln BF_{t - i} + \mathop \sum \limits_{i = 0}^{q1} \theta_{j}^{GGDP + } \Delta GGDP_{t - i}^{ + } + \mathop \sum \limits_{i = 0}^{q2} \theta_{j}^{GGDP - } \Delta GGDP_{t - i}^{ - } + u_{t}$$
(3)

and

$$\Delta \ln B_{t} =\, \alpha_{1} \left( {\ln B_{t - 1} - L_{GGDP}^{ + } GGDP_{t - 1}^{ + } - L_{GGDP}^{ - } GGDP_{t - 1}^{ - } - L_{BF}^{ + } BF_{t - 1}^{ + } - L_{BF}^{ - } BF_{t - 1}^{ - } - \alpha_{0} } \right) + \mathop \sum \limits_{i = 1}^{p} \beta_{i} \Delta \ln B_{t - i} + \mathop \sum \limits_{i = 0}^{q1} \theta_{j}^{GGDP + } \Delta GGDP_{t - i}^{ + } + \mathop \sum \limits_{i = 0}^{q2} \theta_{j}^{GGDP - } \Delta GGDP_{t - i}^{ - } + \mathop \sum \limits_{j = 0}^{q3} \theta_{j}^{BF + } \Delta BF_{t - j}^{ + } + \mathop \sum \limits_{j = 0}^{q4} \theta_{j}^{BF - } \Delta BF_{t - j}^{ - } + u_{t}$$
(4)

As revealed in (3) and (4), the short-run adjustments can roughly be divided into two sources. The first component is associated with the terms in parenthesis, which characterize disequilibrium in a previous period, t − 1. A significantly negative adjustment coefficient α1 would indicate the short-run adjustments in a correct direction to eliminate a possible occurrence of disequilibrium. Using our second exercise as an example, a positive disequilibrium, vt−1 > 0, would imply that lnB was higher than the level implied by the equilibrium condition (4). Therefore, we would expect lnB to adjust downwards in the following periods, namely \(\Delta \ln B_{t} < 0.\) This is characterized by a negative coefficient α1. The magnitude of α1 governs the speed of adjustment; the higher the value of α1, the faster the return to equilibrium. If α1 is not significant, the short-run adjustments are irrelevant to the equilibrium condition—in that case we would also conclude that there is no real causal relationship in the long run. The remaining component relates to responses of the dependent variable to its own historical changes governed by βi, and responses to changes in positive and negative trends governed by θ i+ j and θ i− j , for i = GGDP and BF. It should be noted that we also allow for asymmetric short-run responses.

Testing Methodology

The present study aims at identifying the long-run equilibrium conditions (1) and (2) by estimating the coefficients in (3) and (4), respectively. The bounds test (Pesaran et al. 2001) is adopted to identify the existence equilibrium conditions. To implement this test, we estimate the following equations corresponding to (3) and (4), respectively:

$$\Delta \ln BF_{t} =\, \alpha_{0}^{'} + \alpha_{1} \ln BF_{t - 1} + \alpha_{GGDP}^{ + } GGDP_{t - 1}^{ + } + \alpha_{GGDP}^{ - } GGDP_{t - 1}^{ - } + \mathop \sum \limits_{i = 1}^{p} \beta_{i} \Delta \ln BF_{t - i} + \mathop \sum \limits_{i = 0}^{q1} \theta_{j}^{GGDP + } \Delta GGDP_{t - i}^{ + } + \mathop \sum \limits_{i = 0}^{q2} \theta_{j}^{GGDP - } \Delta GGDP_{t - i}^{ - } + u_{t}$$
(5)

and

$$\Delta\ln B_{t} =\, \alpha_{0}^{'} + \alpha_{1} \ln B_{t - 1} + \alpha_{GGDP}^{ + } GGDP_{t - 1}^{ + } + \alpha_{GGDP}^{ - } GGDP_{t - 1}^{ - } + \alpha_{BF}^{ + } \ln BF_{t - 1}^{ + } + \alpha_{BF}^{ - } \ln BF_{t - 1}^{ - } + \mathop \sum \limits_{i = 1}^{p} \beta_{i} \Delta \ln B_{t - i} + \mathop \sum \limits_{i = 0}^{q1} \theta_{j}^{GGDP + } \Delta GGDP_{t - i}^{ + } + \mathop \sum \limits_{i = 0}^{q2} \theta_{j}^{GGDP - } \Delta GGDP_{t - i}^{ - } + \mathop \sum \limits_{j = 0}^{q3} \theta_{j}^{BF + } \Delta BF_{t - j}^{ + } + \mathop \sum \limits_{j = 0}^{q4} \theta_{j}^{BF - } \Delta BF_{t - j}^{ - } + u_{t}$$
(6)

The long-run coefficients can be identified according to:

$$L_{GGDP}^{ + } = {{ - \alpha_{GGDP}^{ + } } \mathord{\left/ {\vphantom {{ - \alpha_{GGDP}^{ + } } {\alpha_{1} }}} \right. \kern-0pt} {\alpha_{1} }}$$
$$L_{GGDP}^{ - } = {{ - \alpha_{GGDP}^{ - } } \mathord{\left/ {\vphantom {{ - \alpha_{GGDP}^{ - } } {\alpha_{1} }}} \right. \kern-0pt} {\alpha_{1} }}$$
$$L_{BF}^{ + } = {{ - \alpha_{BF}^{ + } } \mathord{\left/ {\vphantom {{ - \alpha_{BF}^{ + } } {\alpha_{1} }}} \right. \kern-0pt} {\alpha_{1} }}$$
$$L_{BF}^{ + } = {{ - \alpha_{BF}^{ - } } \mathord{\left/ {\vphantom {{ - \alpha_{BF}^{ - } } {\alpha_{1} }}} \right. \kern-0pt} {\alpha_{1} }}$$

(5) and (6) are estimated with OLS. However, since the distributions of estimated coefficients in (5) and (6) are non-Gaussian, standard t- and F-tests are not valid here. The bounds test affirms rejecting the null of no co-integration when the F-statistics from the null test concerning, \(\alpha_{1} = {\alpha_{GGDP}^{ + } } = {\alpha_{GGDP}^{ - } } = 0\) in (5), and, \(\alpha_{1} = {\alpha_{GGDP}^{ + } } = {\alpha_{GGDP}^{ - } } = {\alpha_{BF}^{ + } } = {\alpha_{BF}^{ - } } = 0\)in (6) exceed the upper bounds provided by Pesaran et al. (2001). The upper bounds are sensitive to the number of independent variables involved. However, according to Shin et al. (2011), the partial sums are not really two variables; the number of independent variables in (5) should be something between 1 and 2; in (6) it should be between 2 and 4. As suggested by Shin et al. (2011), the conclusion from relatively few independent variables should be regarded as cautious and conservative—the null of no co-integration would be relatively harder to reject. In contrast, it is comparatively easier to reject the null when using more independent variables. In our study, we shall report both.

It is important to note that, in the ARDL/NARDL framework, the bounds test is only valid with serially uncorrelated residuals. Appropriate numbers of lags, p and qs, as proved in Pesaran et al. (2001), can make u serially uncorrelated, unless the model is misspecified. As an estimating strategy, we first determine the ps and qs according to the criterion of AIC. Then, we carry out the Breusch–Godfrey autocorrelation test. If u is serially correlated, we extend ps or/and qs. Furthermore, we carry out more diagnostic tests: the Breusch-Pagan’s heteroscedasticity, the Ramsey functional form, autoregressive conditional heteroscedasticity (ARCH), and the cumulative sum of the recursive residual (CUSUM) and CUSUM square (CUSUMSQ) for testing the stability of the parameters, which are tests based on the 95% confidence band. Shin et al. (2011) note that for satisfying all requirements listed above, rather large ps or/and qs are needed in general. In order to save the degrees of freedom, Shin et al. (2011) suggest adopting a stepwise selection of the short-run lags. In this paper, we shall follow this approach for keeping individual short-run lags according to the p-values.

As the distinct feature of NARDL, it is important to identify asymmetries. For testing long-run asymmetries, we first adopt the standard Wald tests to test H0: L + GGDP  = L − GGDP , for GDP growth, and H0: L + BF  = L − BF , for bankruptcy frauds. Shin et al. (2011) note that the Wald statistics follow the Chi square distribution with one degree of freedom. The Wald test for short-run asymmetries is less complicated and more straightforward. Short-run asymmetries are defined as H0: ∑  q1 i=0 θ GGDP+ j  = ∑  q2 i=0 θ GGDP− j , for GDP growth, and H0: ∑  q3 j=0 θ BF+ j  = ∑  q4 j=0 θ BF− j , for bankruptcy frauds, with selected lags. Shin et al. (2011) point out that these Wald statistics are following the Chi square distribution with one degree of freedom.

Results

Bankruptcy Frauds and Macroeconomic Variation

The result for our first exercise is reported in Table 1. The maximum of the lags for both p and qs are set as 12. According to the stepwise exercise, the remaining lags are reported in the table. The estimation result is reported in the first column in Table 1, which mainly consists of two panels: the upper panel contains the point estimates of coefficients; the lower panel shows bounds, diagnostic, and asymmetric tests. We start with the lower panel. The diagnostic tests hint at possible specification errors of ARCH, nonstable parameter according to CUSUM and CUSUMSQ.

Table 1 Bankruptcy frauds and GDP growth
Full size table

Despite these specification errors, we take a look at the bound test. The F-value is about 1.51, which is lower than the critical values irrespective of the number of independent variables considered. Thus, we fail to identify a long-run equilibrium condition between bankruptcy frauds and real GDP growth, even if specification errors were to be ignored. This finding implies that we are unable to establish that bankruptcy frauds were responsive to variations in the macro economy. For a robustness test, we further repeat the exercises in two sub-sample periods, separated by the year 1933 even though the Chow break point test cannot reject the null of 1933 not being a break year; this analytical procedure is largely consistent with our second exercise (see next section). The specification errors remain in both sub-samples and we remain confirmed with not being able to identify a long-run relation between bankruptcy frauds and GDP growth.

The Effect of Bankruptcy Frauds

The result for our second exercise is reported in Table 2. The maximum of the lags for both p and q is also set as 12. According to the stepwise exercise, the remaining lags are reported in the table. The result of (4) based on the whole sample is reported in the first column in Table 2. Once more, we start with the lower panel. All diagnostic tests are passed (no heteroscedasticity can only be rejected at 10%).

Table 2 Bankruptcy frauds, GDP growth and bankruptcies
Full size table

The F-statistic for the bounds test is 6.56. Even if we take the most conservative view by considering the case of two independent variables, we can still reject the null of the no-cointegration hypothesis at 1% (the upper bound at 1% is 5.00). Thus, we are able to identify the long-run equilibrium specified in (2).

For an interpretation of the long-run relation (2), we move to the upper panel of the table. Concerning the impacts due to GDP growth, we first note that long-run coefficients are all significant. \(L_{GGDP}^{ + }\) is about − 0.24, indicating that a one-percentage point positive growth in real GDP would lead to a 24% reduction in bankruptcies. On the other hand, \(L_{GGDP}^{ - }\) is about − 0.21, significant at 5%. Consequently, a one percentage point negative GDP growth would lead to a relatively smaller reduction in the bankruptcies, around 21 percent. Using a numerical example to illustrate this: generally, a 24 percent loss in bankruptcies would be a result of the real GDP growth rate changing from 2 to 3%. However, bankruptcies would ‘only’ increase by about 21 percent if the growth rate were to change from 3 to 2%. Applying the Wald test, we find that the difference of \(L_{GGDP}^{ + }\) and \(L_{GGDP}^{ - }\) is merely significant at 10 percent, as indicated by the Wald test statistic, W GGDP LR , being 3.11. This result does not only reveal a finding on whether the business cycle affects the bankruptcy volume (e.g., Hol 2007; Levy and Bar-Niv 1987); more importantly, it shows that the impacts are symmetric, even if the magnitude of decreases in bankruptcy generated by economic booms seems to be larger than that of increases in bankruptcy during recessions.

Concerning the potential diffusion or spillover effects from bankruptcy frauds to bankruptcies, our results show that the long-run coefficient L + BF is about 0.58. This implies that a one-percent increase in bankruptcy frauds would cause an increase in the stock of bankruptcies by 0.58%. This marginal diffusion effect is statistically significant: when frauds boost, it would have negative influences on other economic agents, thus driving more firms out of business than would otherwise be the case. Thus, a substantial increase in bankruptcy frauds, such as during the second half of the mid-1960s or in the 2004–2008 period (Fig. 1), would have a significant impact on the volume of bankruptcies. According to these results, bankruptcy frauds have the propensity to diffuse and therefore the propensity to affect economic activity. The explanation seems intuitive and easily understandable (however, we have an alternative explanation, discussed below). On the other hand, when the volume of bankruptcy frauds—for any reason—is reduced, the marginal diffusion effect becomes less visible. The long-run coefficient L − BF is about 0.20; however, as can be observed in Table 2, it is not significant. In other words, reductions in the volume of bankruptcy frauds would not lead to significant changes in the volume of bankruptcies. The Wald statistic with symmetry null hypothesis, L + BF  = L − BF , is 2.58 and is not significant. The contradiction might be due to the lower power of the Wald test.

For short-term adjustments, our results reveal that the adjustment coefficient α1 is about − 0.13 and highly significant. This indicates that the volume of bankruptcies would adjust towards eliminating the disequilibrium; this can be interpreted as bankruptcies indeed being caused by both macroeconomic factors and bankruptcy frauds. The speed of adjustment is at 13%, at which disequilibrium would be eliminated annually; in other words, it would take more than 7 years to eliminate the disequilibrium. The remaining sources for the short-run adjustments are less interesting. Nevertheless, we can note some persistency of the short-run adjustments of the bankruptcy. β1 is 0.28 and highly significant. Thus, short-run adjustments made in the previous period would be persistent to the current period.

We also carry out the robustness tests by re-estimating the NARDL model into two sub-samples separated by the year of 1933. The crucial methodological consideration here is to create two sub-samples with roughly equal sizes. There are two major exogenous events around that historical period of time: the Great Depression—affecting Sweden particularly hard in 1932/1933, and World War II (1939–1945). However, the Chow break point test cannot reject that the null of years 1939–1945 is not break years—hence, it seems that World War II does not represent a structural break. The Chow break point test can reject that the null of 1933 is not a break year, and we decide to use 1933 to construct two sub-samples. The results are reported in the second and third columns in Table 2.

In the first sub-sample, 1830–1933, all diagnostic tests can be passed. The F-statistic for the bounds test is 7.27. As the whole sample, we may reject the null of the no-cointegration-hypothesis. Interestingly, in this period, only GDP growth is important for explaining bankruptcies. The impacts of GDP growth are symmetric at 0.09: a one percentage-point increase in GDP growth would lead to a 9 percent reduction in the volume of bankruptcies. On the other hand, bankruptcy frauds play no role in explaining changes in bankruptcies. The impacts of frauds are mainly from the short-run adjustments of θ BF+0 and θ BF+1 .

In the second sub-sample, 1934–2010, we can pass all the diagnostic tests (while the Breusch–Godfrey autocorrelation and FF tests are significant at 10%). The F-statistic for the bounds test is highly significant at 10.17. As in the two previous exercises, we may reject the null of the no-cointegration hypothesis. In this sub-period, GDP growth becomes less important. As in the case of the whole sample (1830–2010), increases in bankruptcy frauds would lead to increases in bankruptcies, but at a higher magnitude: 0.73 in comparison to 0.58. Similarly, negative developments in bankruptcy frauds would not have any significant impact on the volume of bankruptcies. The Wald asymmetric test towards bankruptcy frauds is significant. Thus, we confirm asymmetric responses from frauds on bankruptcies.

How could these asymmetries be interpreted in a meaningful way? It is highly plausible that changes in policy and legislation over time, which we do not investigate here, have substantial effects on variations in both bankruptcies and bankruptcy frauds. Furthermore, our analysis (Table 2) also includes the effect of the GDP growth rate; evidently, and in line with past research results, the magnitude and influence of the business cycle would have a pervasive and, conceivably, considerably stronger influence on the bankruptcy volume than would changes in bankruptcy frauds. Furthermore, this result may be due to the identified nonlinearity relationship: as can be observed, a 1% increase in fraudulent bankruptcies would have a greater (significant) impact on the total number of bankruptcies than would an equivalent reduction in bankruptcy frauds (which was non-significant). Imaginably, fraudulent bankruptcies can cause both poorly-performing firms (or ‘marginal’ firms) and well-performing firms to fail. It is likely that when the fraudulent bankruptcies increase, more well-performing firms will be affected by the intensifications of frauds. If, on average, the latter category of firms are generally more involved in networks and interlinkages, the failures of these firms could trigger even more firms to fail. Therefore, increases in fraudulent bankruptcies would generally lead to significant intensifications in the number of bankruptcies. However, when the number of bankruptcy frauds is reduced, this decrease would have a smaller impact on economic activity: poor-performing firms would be prone to fail anyway, and fewer well-performing firms would default when fraudulent bankruptcies decrease. Our results indicate that this reduction is small and insignificant and even if this assumption is fairly logical, it is more or less speculative—yet, the positive effect of increases in the number of bankruptcy frauds on the volume of bankruptcies that we have found indicates that previously generated hypotheses in the economics and criminology literatures on bankruptcy and fraud diffusion deserve further research attention.

Discussion and Conclusions

As has been shown in this study, the volume of bankruptcy frauds has diffused substantially over time in Sweden—particularly from the second half of the twentieth century, reaching historically high levels in the new millennium. In line with the literature on white-collar crime, we have assumed that changes in the propensity to commit bankruptcy fraud will affect other agents—or, in other words, victims. Our results are consistent with earlier analyses of the link between frauds and bankruptcies; however, these have only allowed for symmetric responses (Box et al. 2018). In this article, we found an asymmetric relationship between changes in bankruptcy frauds and the bankruptcy volume in Sweden over an extended period of analysis. Increases in frauds revealed a significant and positive effect on the bankruptcy volume while decreases in frauds had no observable effect. As can be recalled, a secondary aim with our study—as well as an important control factor in the analysis—has been to investigate the extent to which bankruptcy frauds and bankruptcies vary with macroeconomic changes.

We have used the aggregate on bankruptcy frauds in Sweden as a representation of the incidence and variation of white-collar crime over a long period of time. Similar to other attempts to study white-collar and/or economic crimes, we have only been able to employ data that captures some aspects, or fragments, of the phenomenon (Alalehto and Larsson 2009; Friedrichs 2010; Levi 2008a, b). We are aware of the fact that it is not a perfect measure. However, we would like to claim that the considerable advantage of our empirical data is that we observe longer patterns of variation over time. Shorter observation periods would be less capable of studying this relationship. Both criminologists and economists have asked if there is a link between (economic) crimes and macroeconomic variation; furthermore, they have asked whether there exists a relationship between variations in bankruptcies and economic change. In contrast to previous results (Bushway et al. 2010; Detotto and Otranto 2012; Krüger 2011), we could not find any evidence for the assumption that macroeconomic variation would affect the propensity to commit bankruptcy fraud—at least, we found no evidence of a long-run relationship. Future research with the specific purpose of analyzing this particular link, using more advanced and developed methods (e.g., Bushway et al. 2012; Krüger 2011), might of course generate other results. However, we found that the dependent variable in our analysis—the (net) bankruptcy volume—was affected by macroeconomic change, and this result is in line with previous findings (Hol 2007; Levy and Bar-Niv 1987). More importantly, our results reveal that the main hypothesis in our article—that bankruptcy frauds would be a potential source of diffusion—receives support: net increases in frauds increased the net bankruptcy volume.

Since we utilize aggregate time series, it is obvious that we have been unable to study both individual bankruptcy events and individual bankruptcy fraud events. Therefore, it has not been possible to identify, or count (the number of), potential interlinkages between individual agents/events. Similarly, we have been unable to investigate whether such a linkage exists at all; to view all bankruptcy events during a specific year as a ‘victim’ would be overly simplistic. Correspondingly, the nature of our data has not allowed for a measurement of neither the size/scale of individual observation units, nor of the ‘magnitude’ or size of individual bankruptcy frauds (such as financial losses related to each fraud event). Consequently, it is highly plausible that the number of interlinkages as well as the heterogeneous nature of bankrupt agents/fraudulent agents—given that they exist—have very different effects on ‘victims.’ This implies that the effect of a bankruptcy fraud committed by a small firm where the financial losses of the creditor(s) are insignificant, most likely differs from situations where the losses are substantial to the creditor. In the latter case, the risk for bankruptcy is almost certainly considerably higher. Naturally, it could also be discussed whether huge corporate scandals and crimes (such as Lehman Brothers) should be counted as a single fraud.

However, our results give some empirical support for previously generated hypotheses in criminology and in the economic sciences: firms and other agents are connected through (credit) networks; particularly fast increases or shocks in the economy have the potential to produce avalanches of failures (Allen and Gale 2000; Gatti et al. 2006, 2009; Ooghe and De Prijcker 2008; Wu 2010). Thus, the presence of interlinkages is a source of bankruptcy diffusion. In the present article, this type of ‘shock’ has been represented by changes in the propensity to commit bankruptcy fraud (and our results indicate that the fraud volume was unaffected by macroeconomic variation), while the economic system corresponds to the bankruptcy volume. The notion of bankruptcy diffusion is closely related to hypotheses on victimization in white-collar criminology. While the diffusion of (white-collar) illegal practices and frauds among offenders has been a common theme, the diffusion of frauds among victims has received less attention (Baker and Faulkner 2004; Croall 2001). Once more, since we have no access to micro-level data, we cannot conclusively determine exactly how, or to what extent, bankruptcy frauds have diffused to victims in Sweden over these 180 years.

However, recent discussions and empirical findings in criminology suggest that there is a case for assuming that stakeholders and other agents are affected by white-collar crimes. It is likely that bankruptcy frauds would have an impact on both individuals and other organizations; one such impact would be that other firms may risk being driven out of business (Alvesalo and Virta 2010; Croall 2004a). Using the volume of registered bankruptcies over 180 years as a representation of economic agents, we have found some aggregate empirical support for this hypothesis. The methodological approach of our study is, to the best of our knowledge, novel. As discussed above, our approach and the nature of our empirical data have some limitations but we believe that our framework has several advantages—in particular, our approach facilitates the testing of previously generated conceptions and hypotheses in research that specifically focuses on the relationship between (economic) crimes, the economy, and the diffusion of (economic and white-collar) crime—among both offenders and victims. This article has shown one potential avenue for future research; one such route would be to test whether the results for Sweden also apply to other societies.