Acoustic Response of Reference Notches: Derivation of Acceptance Criteria for Automated Ultrasonic Testing Based on the Correlation Between Defect Quality and Effective Defect Size

Abstract

This paper presents a detailed study of the acoustic response of artificially manufactured notches, which are established reference defects in common standards for ultrasonic testing (UT). Measurements were performed with standard tubes manufactured for the commissioning of automated UT machines. Included reference notches are at the inner and outer tube surface and have different lengths and orientations (longitudinal, oblique and transverse). From the acoustic reflection profile, i.e. the measured defect amplitude along the notch axis, the effective defect length and the defect homogeneity are introduced as measured quantities of the reference defect quality. The large data sample of 320 evaluated notch profiles gives insight to the statistics of the achieved reference defect quality. Key approach of the analysis is the correlation between both measured quantities. It reveals a universal behaviour, which can be described by a sigmoidal function converging for high quality defects towards the theoretical limits. Based on the obtained parametrization it is possible to define criterions for the required defect quality and the test speed as function of the specified repeatability. This solves the current dilemma how to distinguish between variations due to the reference quality from those related to the testing machine. Furthermore, the presented measurement procedure can be used for a reference certification, which complements existing standards for the ultrasonic system and the probes.

1 Introduction

Automated ultrasonic testing (UT) machines enable geometry measurements and a non-destructive defect inspection, both on the surface and in the volume of the material [1, 2]. The evaluation of test results is based on a comparison relative to those of artificial defects in a reference piece, which are manufactured according to the applied standards. Therefore, the UT-system must be adjusted on given reference standards before the inspection of the production material. Afterwards a verification must be performed, which is re-checked after a certain number of test cycles and at the end of the tested lot [3, 4].

Notches represent a typical reference defect with a one-dimensional extension. They are used in most common standards related to surface crack testing [3,4,5,6,7,8,9]. Length, position and orientation of the reference notch depend on the manufacturing process of the material, e.g. the applied rolling process in a tube production. With the designed test speed of the UT-system, the notch is sampled at least once across the nominal defect length. Assuming an ideal reflection behaviour of the reference defect it is thus ensured that the maximum response is measured and variations in the repeatability runs reflect the precision of the testing machine. However, in a previous work [10] it was demonstrated that the defect quality has an impact on the results: With decreasing quality of the reference defect, (i) the measured repeatability is degraded, (ii) there are complex patterns of the probability distribution for the measured amplitudes in the repeatability runs far away from a Gaussian behaviour thus leading to (iii) an asymmetric position of the mean value between the maximum and minimum value of the measurement series.

Due to the increasing demands on the repeatability and the throughput of testing machines, the impact of the reference quality becomes relevant for the evaluation of the machine performance [10, 11]. However, dedicated studies on the acoustic characterization of reference defects are scarce [12,13,14]. Specifications on the defect quality are restricted to mechanical tolerances and just in a few cases the acoustic response is included to some extent [8, 9]. In this work, the defect homogeneity and the effective defect length are introduced as a quantitative measure for the quality of the reference notches. The extracted value depends on the applied threshold which reflects the required repeatability of the UT machine. After a short introduction to main measurement procedures (Chapter 2), the definition of the quality parameters is given in Chapter 3 and theoretical limits for both are discussed in Chapter 4. In Chapter 5, experimental results of a high-statistical data sample are presented. Plotting the effective defect size as a function of the defect homogeneity, it is possible to obtain a global parametrization. It is used to extract limits on the notch quality for a required repeatability and to introduce a reduction factor for notches with lower quality.

2 Measurement Procedures

2.1 Adjustment

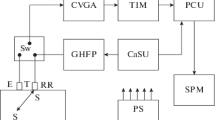
Reference defects are used to set up the UT system. Figure 1 illustrates the sensitivity adjustment on a notch manufactured at the surface of a tube or bar. Therefore, a grid of measurement points in the defect area with an adequate resolution is needed. The shot distance both in longitudinal direction ($\Delta\text{x}$) and at the circumference ($\Delta\text{y}$) must be significantly smaller than the notch length and the sound field width. For each grid point (${\text{x}}_{\text{i}}\boldsymbol{ },\boldsymbol{ }{\text{y}}_{\text{j}}$) the corresponding amplitude (${\text{A}}_{\text{ij}}$) is measured. The maximum of all values is compared to a given target value (${\text{A}}_{\text{TGT}}$). The resulting scaling factor is applied as gain correction (${\Delta}$dB).

Fig. 1

Illustration of the adjustment procedure on a reference defect

To avoid any missing detection of the reference defect in repeatability runs, the target value must exceed the event threshold (${\text{A}}_{\text{THR}}$), which is defined as trigger for the flaw indication. The minimum ratio between the target and the threshold value is given by the required repeatability (${\text{R}}_{0}$) of the UT system, which corresponds to the maximum tolerable amplitude variation in the repeatability runs. Typically, this ratio is given in decibel (dB).

2.2 Verification

After the adjustment procedure the amplitude measurement is repeated with the same grid size in order to confirm the applied gain correction. Again, the amplitude matrix (${\text{A}}_{\text{ij}}^{*}$) for each grid point is measured. The deviation of the maximum value from the target value can be expressed as ratio (${\text{R}}_{\text{V}}$) in decibel.

${\text{R}}_{\text{V}}$ is linked to the relative error ($\Delta\text{A/A}$) of the amplitude measurement. If a large data sample is available, this error can be extracted by statistical methods. Assuming a Gaussian behavior, the relative error is given by the standard deviation (${\sigma}$) of the frequency count of ${\text{R}}_{\text{V}}$. Obviously, the error of the amplitude measurement must be significantly smaller than the required repeatability, i.e. ${\sigma}\left({\text{R}}_{\text{V}}\right)<{\text{R}}_{0}$.

2.3 Repeatability Runs

Repeatability runs correspond to a series of test cycles with the same reference material after the adjustment and verification. They are performed under production conditions with higher test speed to evaluate the intrinsic accuracy of the testing machine. With the defined test speed, the reference defect is sampled at least once across its effective length assuming an ideal reflection behavior. The measured repeatability (${\text{R}}_{\text{A}}$) is defined as the ratio between the minimum (${\text{A}}_{\text{min}}$) and the maximum amplitude (${\text{A}}_{\text{max}}$) of the measurement series for the same reference defect.

The acceptance criterion is then defined by ${\text{R}}_{{\text{A}}} \leq {\text{ R}}_{0}$.

3 Characterization of Reference Defects

3.1 Reflection Profile

The reflection behaviour can be visualized by a C-Scan representation, which is in this case a 2D colour-coded plot of the maximum measured amplitudes. In case of 1D extended reference defects such as notches, there are two independent reflection profiles corresponding to the two opposing sound entry directions. Figure 3 illustrates the extraction of a reflection profile for one notch side. It corresponds to the projected amplitude distribution (${\text{P}}$) of the maximum defect echo along the defect axis (${x^{\prime}}$).

$$ {\text{P}}(x_{m}^{\prime } ) = \mathop {\max }\limits_{{\text{n}}} \left\{ {A^{*} \left( {x_{m}^{\prime } {\text{ }},{\text{ }}y_{n}^{\prime } } \right)} \right\} $$

(1)

The coordinate transformation is given by:

$$ x^{\prime}_{{{\text{m(i,j)}}}} = {\text{x}}_{{\text{i}}} \cdot {\text{cos}}\upphi - {\text{y}}_{{\text{j}}} \cdot {\text{sin}}\upphi $$

(2)

$$ y^{\prime}_{{{\text{n(i,j)}}}} = {\text{x}}_{{\text{i}}} \cdot {\text{sin}}\upphi + {\text{y}}_{{\text{j}}} \cdot {\text{cos}}\upphi $$

(3)

where ${\phi }$ represents the defect angle as defined in Fig. 1. To obtain a unique distance between two sample points ($\Delta\text{d}$), the interval size on the defect axis ($\Delta{x^{\prime}}$) is set to the intrinsic resolution of the measurement grid, i.e.$\Delta{x^{\prime}}=\Delta\text{x}=\Delta\text{y}=\Delta\text{d}$. This results in the following discretization:

$$ {\text{P}}_{{\text{k}}} \left( {\Delta {{x^{\prime}}}_{{\text{k}}} } \right) = \mathop {{\text{max}}}\limits_{{{\text{k~}} \le {\text{m < k + 1}}}} {{P(x^{\prime}}}_{{\text{m}}} {\text{)}} $$

(4)

where ${\text{k}}$ is an integer number and $\Delta{{\text{x}}{^{\prime}}}_{\text{k}}={\text{k}}{\cdot}{\Delta}{\cdot}\text{d}$.

3.2 Effective Defect Length

If the defect is larger than the sound field width, its size can be determined by the coherent range of the reflection profile with flaw amplitudes above a given threshold [15]. From here on, the respective length for a given threshold level (${\text{A}}_{\text{THR}}$) will expressed as effective length (${\text{L}}_{\text{Rx}}$). ${\text{R}}_{\text{x}}$ indicates the dB offset of the profile maximum (${\text{P}}_{\text{max}}$) with respect to the threshold level.

$${\text{R}}_{\text{x}}=\text{20}{\cdot}{\text{log}}\left(\frac{{\text{P}}_{\text{max}}}{{\text{A}}_{\text{THR}}}\right)$$

(5)

Commonly the reflector size is defined by the Full Width at Half Maximum (FWHM) method, which is correlated to a threshold of -6 dB with respect to the maximum [15]. Assuming an ideal reference defect, the FWHM (${\text{L}}_{\text{6dB}}$) is slightly larger than the nominal manufactured length (${\text{L}}_{\text{nom}}$) due to the extension of the sound field, i.e.${ \, {\text{L}}}_{\text{6dB}}\gtrsim {\text{L}}_{\text{nom}}$. For the same reason the effective length becomes smaller with increasing threshold (see Fig. 2).

Fig. 2

Effective defect length across the defect axis (x’) with respect to different threshold levels for an ideal reflection behaviour (left) and in case of a reference defect with a deteriorated quality (right). The amplitude is expressed in a relative Screen Height (%SH)

$$\text{FWHM = }{\text{L}}_{\text{6dB}}>{\text{L}}_{\text{5dB}}>{\text{L}}_{\text{4dB}}>{\text{L}}_{\text{3dB}}>{\text{L}}_{\text{2dB}}>{\text{L}}_{\text{1dB}}$$

(6)

To improve the resolution of the discretization ($\Delta\text{d}$), a linear interpolation is done between the first data point below (${\text{P}}_{\text{m}}$ or ${\text{P}}_{\text{n+1}}$) and above (${\text{P}}_{\text{m+1}}$ or ${\text{P}}_{\text{n}}$) the threshold. Indices refer to the position in the reflection profile with m < n being integer numbers. The respective intersection of the linear interpolation with the threshold at the rising (${\text{a}}_{\text{Rx}}$) and the falling edge (${\text{b}}_{\text{Rx}}$) is given by:

$${\text{a}}_{\text{Rx}}=\left(\text{m + }\frac{{\text{A}}_{\text{THR}}-{\text{P}}_{\text{m}}}{{\text{P}}_{\text{m+1}}-{\text{P}}_{\text{m}}}\right) \Delta\text{d}$$

(7)

$${\text{b}}_{\text{Rx}}=\left(\text{n + }\frac{{\text{P}}_{\text{n}} -{\text{A}}_{\text{THR}}}{{\text{P}}_{\text{n}}-{\text{P}}_{\text{n+1}}}\right) \Delta\text{d}$$

(8)

and the effective length (${{L^{\prime}}}_{{\text{R}}_{\text{x}}})$ for an ideal reflector results in

$${\text{L}}_{\text{Rx}}={\text{b}}_{\text{Rx}}-{\text{a}}_{\text{Rx}}$$

(9)

As shown in Fig. 2, inhomogeneities of the reflection profile decrease the effective length of the reference defect. In this case it is then defined as the sum of all profile sections (${\text{l}}_{\text{i}}$) above the respective threshold within the FWHM range. Consequently, this definition only applies for threshold levels above the 6 dB threshold. The section lengths result from a linear interpolation according to Eqs. (7)–(9) providing intersections ${\text{a}}_{\text{i}}$ and ${\text{b}}_{\text{i}}$ with the threshold at the rising and the falling edge, respectively.

$${\text{L}}_{\text{Rx}}=\sum_{\text{i}}{{\text{l}}}_{\text{i}}=\text{(}{b}_{1}-{\text{a}}_{1}) + \dots +\text{(}{b}_{\text{i}}-{\text{a}}_{\text{i}}) $$

(10)

with

$${\text{a}}_{\text{6dB}}\le {\text{a}}_{1}<{\text{b}}_{1}<\dots <{\text{a}}_{\text{i}}<{\text{b}}_{\text{i}}\le {\text{b}}_{\text{6dB}}$$

(11)

3.3 Defect Profile Homogeneity

The defect profile homogeneity (DPH) will be introduced as quantitative measurand for the quality of the manufactured defect. It is defined by the area ratio of the measured notch profile above the 6 dB threshold at half maximum, divided by the underlying rectangular formed by the FWHM of the notch, the maximum of the profile (${\text{P}}_{\text{max}}$) as upper and the 6 dB threshold, i.e. $\frac{1}{{2}} {\text{P}}_{\text{max}}$ as lower limit. An illustration is given in Fig. 3. In this study, the discretized form was used for the calculation. It is given by:

$${\text{DPH}}=\frac{\sum_{\text{i=m}}^{\text{n}}\left({\text{P}}_{\text{i}}-\frac{1}{{2}} {\text{P}}_{\text{max}}\right)}{ \frac{1}{{2}} {\text{P}}_{\text{max}} \left({1}+{\text{n}}-{\text{m}}\right)}$$

(12)

where m, n and i are integer numbers with the following relation

Fig. 3

Extraction of the reflection profile from C-scan data and definition of the defect profile homogeneity (DPH) as a quantitative measurement of the reference quality

$$\frac{{\text{a}}_{\text{6dB}}}{\Delta\text{d}}\le {\text{m}}\le {\text{i}}\le {\text{n}}\le \frac{{\text{b}}_{\text{6dB}}}{\Delta\text{d}}$$

(13)

In ideal case, the homogeneity is close to 100% and only influenced by the rising and falling edge, both related to the sound field of the probe. Any deteriorations due to the notch profile further decrease the percentage thus allowing a quantification of the notch quality.

4 Theoretical Description

This chapter contains a discussion of the theoretical limits for the effective length and the defect homogeneity as defined in Chapter 3. In good approximation, the projection profile of a refence defect results from the convolution of the sound field profile with the shape of the defect. In ideal case they can be described by a Gaussian and a rectangular function with the nominal defect length (${\text{L}}_{\text{nom}}$), respectively. The sound field width (SFW) is defined by the FWHM of the sound field profile. Depending on the ratio between the nominal defect length and the sound field width (${\text{L}}_{\text{nom}}/\mathrm{SFW}$), the obtained shape of the profile can be divided into three different regimes.

• (I) If the nominal defect length is smaller than the sound field width, the resulting profile is again close to a Gaussian shape but with an increased width.

• (II) In the intermediate region ($1.0<{\text{L}}_{\text{nom}}/\mathrm{SFW}\lesssim 2.2$), the resulting profile is not only wider but also deviates more and more from a Gaussian shape.

• (III) If the ratio further increases (${\text{L}}_{\text{nom}}/\mathrm{SFW}>2.2$), the shape of the rising and falling edges do not change anymore but a plateau is forming in the centre part.

An example for each region is shown in Fig. 4. The transition points between the different regimes are determined by the shape of the rising and falling edge of the convoluted profile. It can be approximated by an exponential power distribution (EPD), which is parametrized by location μ, scale σ’ and shape β and includes the Gamma function ${\Gamma(1/\beta)}$ for normalization [4].

Fig. 4

Reflection profile (red, thick line) obtained by the convolution of a Gaussian sound field (dotted blue line) with a rectangular defect (full blue line) for different ratios between the nominal defect length (L_nom) and the sound field width (SFW). The dashed grey line indicates the fit results for the rising edge based on an exponential power distribution as given in Eq. (14) (Color figure online)

$$ {\text{EPD(x)}} = \frac{\beta }{{2\sigma ^{\prime}\Gamma \left( {\frac{1}{\beta }} \right)}}{\text{exp}}\left[ { - \left( {\frac{{\left| {{\text{x}} - \mu } \right|}}{{\sigma ^{\prime}}}} \right)^{\beta } } \right] $$

(14)

For β = 2, Eq. (14) converges to a Gaussian. The FWHM of the EPD is given by:

$$ {\text{FWHM }}_{{{\text{EPD}}}} = {\text{2}} \cdot \sigma ^{\prime} \cdot \sqrt[\beta ]{{{\text{ln}}\left( 2 \right)}} $$

(15)

Figure 5 shows the fit parameters as function of the ratio between the nominal defect length and sound field width $\left({\text{L}}_{\text{nom}}/{\text{SFW}}\right)$. With increasing ratio, the shape parameter β rises from two to three and the EPD is enlarging up to a factor of 2.28 compared to the sound field width.

Fig. 5

Fit results for the approximation of the rising and falling edge according to Eq. (14) as a function of the ratio between the nominal defect length (L_nom) and the sound field width (SFW). The crossover between the regimes is indicated by the dashed blue lines (Color figure online)

Based on the fit results it is possible to calculate theoretical limits for the effective length. If the ratio stays below 2.2, the FWHM of the profile (${\text{L}}_{\text{6dB}}$), is equal to the FWHM of the EPD.

$${\text{L}}_{\text{6dB}}={\text{FWHM }}_{\text{EPD}} ;{\text{if}} \left({\text{L}}_{\text{nom}}/{\text{SFW}}\right) \le \text{2.2}$$

(16)

Otherwise the width of the rectangular center part must be added:

$${\text{L}}_{\text{6dB}}={\text{FWHM }}_{\text{EPD}} +\left({\text{L}}_{\text{nom}}-\text{2.2}\bullet {\text{SFW}}\right) ;{\text{if}} \left({\text{L}}_{\text{nom}}/{\text{SFW}}\right)>\text{2.2}$$

(17)

Calculated results based on Eqs. (16) and (17) are summarized in Fig. 6. As shown at left, the FWHM of the profile is always larger than the nominal defect length. However, the deviation is rapidly dropping to a permille range. The diagram to the right plots the effective length for higher thresholds relative to the 6 dB length. In region I (nominal defect length ≤ sound field width), it spreads from around 40% for ${\text{R}}_{\text{x}}$ = 1 dB to more than 90% for ${\text{R}}_{\text{x}}$ = 5 dB. For larger defects the rectangular center part is formed and becomes more and more dominant. Because the deviation results only from the profile edges, the spreading for different thresholds is decreased and the overall values are higher.

Fig. 6

Theoretical limits for an ideal reference notch plotted as a function of the ratio between the nominal defect size (L_nom) and the sound field width (SFW). Left: Relative deviation for the FWHM of the profile (L_6dB) with respect to the nominal defect length (L_nom). Right: Effective defect lengths for different threshold levels (L_Rx) relative to the FWHM of the profile. The ratio drops with decreasing Rx. The crossover between the regimes is indicated by the dashed blue lines (Color figure online)

As for the effective length, theoretical limits on the defect homogeneity can be calculated assuming that in ideal case impacts are related only to the sound beam profile shaping the profile edges. The area of the profile for the DPH calculation is directly linked to the integral of the EPD. If the ratio $\left({\text{L}}_{\text{nom}}/{\text{SFW}}\right)$ is above 2.2, the rectangular area in the center part must be added. Equation (12) can be thus re-formed as follows:

$${\text{DPH}}=\frac{{\int }_{{a^{\prime}}}^{{b^{\prime}}} \left[{\text{EPD}}\left({\text{x}}\right)- \, \frac{1}{{2}}\text{ EPD}\left({\mu}\right)\right]\text{ dx}+\frac{1}{{2}}\text{ EPD}\left({\mu}\right)\bullet \left[{\text{L}}_{\text{6dB}} -{{\text{FWHM}} }_{\text{EPD}}\right]}{ \, \frac{1}{{2}}\text{ EPD}\left({\mu}\right)\bullet {\text{L}}_{\text{6dB}}}$$

(18)

The integration limits for Eq. (18) are ${{a^{\prime}}} = \mu - \frac{1}{2}{\text{FWHM }}_{{{\text{EPD}}}}$ and ${{b^{\prime}}} = \mu + \frac{1}{2}{\text{FWHM }}_{{{\text{EPD}}}}$. According to Eq. (16), the second summand is zero if $\left({\text{L}}_{\text{nom}}/{\text{SFW}}\right)\le 2. 2$.

Theoretical limits on the DPH according to Eq. (18) are plotted in Fig. 7. The lowest value around 62% is obtained for a Gaussian profile. In region II, where the shape factor β constantly changes from 2 to 3, this value increases to 71%. For larger defects in region III $\left({\text{L}}_{\text{nom}}/{\text{SFW}}>2.2\right)$ there is a further increase related to the impact of the plateau, which is forming in center part of the profile. The DPH value rises from 85 to 95% if the nominal defect length is a factor of 3 and 10 larger than the sound field width, respectively.

Fig. 7

Maximum defect homogeneity (DPH_max) assuming an ideal reflection behaviour of a rectangular shaped defect as a function of the ratio between the nominal defect size (L_nom) and the sound field width (SFW). The crossover between the regimes is indicated by the dashed blue lines (Color figure online)

As illustrated in Fig. 8, perturbations of the defect shape have an impact on the reflection profile. If the maximum length of the remaining undisturbed part (L_R) is larger than the sound field width (SFW), any deterioration will decrease the DPH value with respect to the ideal case. For smaller fractions of (${\text{L}}_{\text{R}}/{\text{SFW}}$), deviations from the ideal profile shape are getting less while the maximum amplitude is dropping down. Due to the rescaling effect, extracted DPH values can be even slightly higher with respect to the ideal case.

Fig. 8

Impact of an asymmetric (left) and symmetric (right) perturbation for different sound field widths (SFW). The upper row shows (i) the beam profile (dotted grey), (ii) the nominal (blue) and (iii) the perturbated defect shape (yellow) where L_R indicates the largest undisturbed length. The corresponding convolutions are shown in the lower row. With decreasing ratio SFW/L_R, the disturbed profiles (dotted line) have lower amplitudes. For direct comparison it is rescaled (full line), which is indicated by the arrow in case of larger shifts. The ratio of the obtained DPH values for the disturbed (II) and ideal (I) reflection profile are listed at the bottom (Color figure online)

5 Measurement and Results

The studies were performed with four reference standard tubes manufactured for a typical commissioning procedure. They are 8 m long, have a diameter between 114 and 273 mm and a wall thickness relative to the diameter ranging from 5.5 to 7.5%. In all cases, notches both at the inner and outer tube surface served as reference defects. In total 64 longitudinal notches, 64 transverse notches and 32 notches with obliquities between 11° and 45° were analysed. As the two sound directions for the flaw detection are independent, this corresponds to the evaluation of 320 notch profiles. The notch length was either ½ inch (12.7 mm) or 1 inch (25.4 mm) with a depth of either 5% or 10% of the wall thickness.

All measurements were done at a test stand with a roller conveyor and a linear scanner unit using a 3 MHz matrix probe [17]. In this way it was possible to adjust all incident angles electronically thus avoiding any additional mechanical setting that would decrease the comparability of results. The measurement of each profile was repeated six times in order to reduce the systematic error.

Figure 9 shows the frequency distribution for the relative deviation of the maximum amplitudes with respect to the target value, which were obtained in the verification and were calculated according to Eq. (3). It can be fitted with a Gaussian having the centre position (${{\bar{R}}}_{{\text{V}}}$) as expected close to zero (${{\bar{R}}}_{{\text{V}}} =$ 0.03 dB) and a standard deviation $\left( {\sigma {\text{FR}}_{{\text{V}}} } \right)$ of 0.2 dB. The latter represents the accuracy of the amplitude measurement, i.e. $\Delta\text{A}/{\text{A}}={\sigma}\left({\text{R}}_{\text{V}}\right)$. As required, this is significantly smaller than the maximum threshold level applied in the analysis, which is 1 dB below the maximum: $\Delta\text{A}/{\text{A}}<\text{min}({\text{R}}_{\text{x}})=$ 1 dB.

Fig. 9

Histogram of the relative deviation (R_V) of the maximum amplitudes of the verification run compared to the target value. The fitted Gaussian is shown in grey, the centre position as dashed line in orange (mean value) (Color figure online)

In Fig. 10, the relative frequency of the measured values for the 6 dB length and the homogeneity is plotted separately for the different notch types. For longitudinal and oblique notches, the average 6 dB length is slightly smaller than the nominal length. The respective deviation of 1.0 mm and 1.2 mm can be explained by the manufactured notch shape at the edges. For the transverse notches there is a split between the inner and outer defects. In average both have larger deviations of + 2.0 mm and − 2.2 mm, respectively. Most probable reason here is the adjustment of the notch manufacturing process to the tube bending. A similar trend is observed for the DPH distributions. The best result is obtained for the longitudinal notches with an average of 76%, for oblique and transverse notches it further decreases from 72 to 68%, respectively.

Fig. 10

Histograms of the measured profile lengths (L_6dB) with respect to the nominal defect length (L_nom), at left, and the of the defect homogeneity (DPH), at right, for the different defect types: a longitudinal notches, b oblique notches and c transverse notches. The grey line indicates the average value. In case of transverse notches there are two separate length distributions for the inner and outer defects

Examples of profiles with the highest quality are shown in Fig. 11. DPH values above 80% are reached for all flaw types and the variations at the plateau stay below 1 dB. The slope of the profile edges can be fitted according to Eq. (14) thus allowing the extraction of the sound field width. Results deliver a value of around 3.75 mm for all flaw types, which is a factor of 3.4 and 6.7 smaller than the nominal defect length of 1 inch and ½ inch, respectively. Referring to Fig. 6, this correlates to a theoretical limit on the DPH of around 86% for half-inch and 93% for one-inch defects. Figure 12 contains selected examples of notch profiles with lower DPH values. Compared to Fig. 11 it turns out that variations only stay within 1 dB in case of the highest defect quality. For DPH values < 80% the effective 1 dB length is already affected.

Fig. 11

Examples of profiles with the best homogeneity for a longitudinal notches, b oblique notches and c transverse notches. Red circles are measured values, the red line shows the data fit based on the convolution of the rectangular defect profile (blue line) and a Gaussian sound field (dotted line) with a FWHM of 3.75 mm as best approximation of the profile edges. The vertical green line at 0.89 indicates the 1 dB threshold level (Color figure online)

Fig. 12

Selected profiles with lower quality. Grey circles are measured values, the red line shows the convolution of the rectangular defect profile (blue line) with a Gaussian sound field (dotted line) with a FWHM of 3.75 mm obtained as best fit for the most homogenous profiles (see Fig. 11). The vertical green line at 0.89 indicates the 1 dB threshold level (Color figure online)

The overall summary of the measured results is compiled in Fig. 13. It shows the effective length for a given threshold relative to the 6 dB length as a function of the defect homogeneity.

Fig. 13

Ratio of the effective length for different threshold levels and the 6 dB length in dependence of the defect homogeneity. Symbols are related to the average value of the measurement series for one notch side, error lines show minimum and maximum values. Theoretical limits (TL) deduced from Eqs. (17) and (18) are given by the dark yellow lines. The red line shows the best fit to the lower boundary of the data points according to Eq. (19) (Color figure online)

Each data point corresponds to the values of one notch side. The light orange lines indicate the theoretical limits for one-inch notches assuming the extracted sound field width of 3.75 mm. As expected, the measured effective length converges to these limits in case of a high defect quality. The decrease at lower DPH values is changing gradually from a rather smooth decline at low thresholds to a strong fall-off within a small DPH range at high threshold levels. The overall behaviour can be described by a sigmoidal function of the form:

$$ {\text{y}} = {\text{C}}_{1} + \frac{{{\text{C}}_{2} - {\text{C}}_{1} }}{{{\text{ 1}} + 10^{{\left( {{\text{X}}_{0} - {\text{x}}} \right) \cdot {\text{S}}}} }} $$

(19)

where S is slope, X₀ is the centre, C₁ and C₂ are the lower and upper asymptote, respectively. The variance of the effective length for similar DPH values finally depends on the specific shape of the notch profile. However, for practical use the impact of the worst-case scenario is the most important. Therefore, the fit describes the lower boundary shown as red line in the diagrams.

The parametrisation can be used to define a modus operandi for reference defects of deteriorated quality. Repeatability runs must be performed under production conditions to demonstrate the reliability of the system. The test speed refers to an ideal profile with a plateau in the centre part, whose length is close to the nominal defect length. In a first step, a minimum acceptable effective length (L_min) must be specified and agreed between the parties. Typically, it is related to the aperture size and the available overlap of the test helix. To ensure that deteriorations stay above a given threshold, it is then possible to specify the minimum defect homogeneity (DPH_min). It corresponds to that DPH value of the fit for which L_min is reached. Extracted values for different threshold levels are listed in Table 1. Obviously, the applied threshold level must be higher than the corresponding one for the repeatability to access the real performance of the testing machine.

Table 1 Matrix of minimum DPH values required for repeatability runs with full test speed applying different thresholds (R_x) and different criteria concerning the minimum effective defect length (L_min) with respect to the nominal defect length (L_nom)

Normally, reference defects with values below DPH_min would be excluded from the evaluation. In this case the re-manufacturing of new reference is required which is costly and, in most cases, very difficult within the given time limits. Therefore, the introduction of a speed reduction factor for the repeatability runs offers an interesting alternative. It allows to still use deteriorated defects but with a lower test speed. Figure 14 illustrates the speed reduction factor for different threshold levels, which is deduced from the given fit results illustrated in Fig. 13.

Fig. 14

Speed reduction factors (f_red) for different threshold levels (R_x) deduced from the sigmoidal data fit according of Eq. (19) and shown in Fig. 13. Results for different acceptance criteria concerning the minimum effective defect length (L_min) with respect to the nominal length (L_nom). Dashed lines show the minimum DPH values (see Table 1) for full production speed, if in range. Arrows indicate that for lower values a reduced speed is required

6 Conclusions

With the increasing demands on the precision of testing machines, the quality of the reference defects plays an important role [10, 11]. This works introduces the effective defect length and the defect homogeneity as quality parameters for a quantitative characterization. They are deduced from the acoustic reflection profile. Based on the given definitions, theoretical limits for reference notches are discussed and combined with test results of manufactured notches in standard reference tubes used for commissioning. The measurements were done on a test stand, which provides a robust and reliable tool to perform such studies with an independent system of high accuracy [17]. It can cope with larger reference pieces of up to 8 m length and diameters up to 650 mm, which are typically too large for standard lab systems.

For the detailed analysis a large data sample was available. Cumulative results for different notch orientations (longitudinal, oblique and transverse) give a first insight to the overall statistics of the manufacturing process with respect to the achieved quality. Most powerful approach of this study is the combination of both quality parameters, i.e. the plot of the effective length as a function of the defect homogeneity. It reveals a universal behaviour, which is independent of the tube diameter, the notch position (inside or outside tube surface) and the orientation. This correlation can be parametrized by a sigmoidal function. The fit data serve as basis for the definition of limits on the defect quality for repeatability measurements of testing machines. Moreover, a speed reduction factor can be deduced for deteriorated references, which allows its use without the costly and time-consuming re-manufacturing of new references. Both aspects will facilitate the commissioning and audits significantly.

Finally, the presented concept can be extended from 1D profiles of notches to side-drilled holes or an 2D analysis of references such as flat bottom holes. Moreover, it applies for the characterization of natural defects. The overall procedure can be used for a reference certification, which complements existing standards for the UT system [18] and the probes [19].