Skip to main content
SpringerLink
Log in

Using Interpolation with Nonlocal Autoregressive Modeling for Defect Detection in Welded Objects

  • Published:
Journal of Nondestructive Evaluation Aims and scope Submit manuscript

Abstract

X-rays and gamma rays are used in industrial radiography to detect internal defects and different structures of the test object. The radiography interpreters must be able to evaluate and interpret the radiography images as accurately as possible. To improve the operator’s image perception and interpretation, the quality of radiographs can be enhanced by different image processing methods. In this study, the sparse representation method with a nonlocal autoregressive model (NAM) based on a sparse representation model (SRM) algorithm was implemented to improve the defect detection capabilities. The technique relies on generating a regularized and smoothed image, which is then subtracted from the original image to reconstruct the high contrast image. The algorithm was successfully applied to different radiography images. Improved defect detection was achieved while preserving the fine details and the main information of the images. For the enhanced images of samples in this study, figures of merits were found between 83 and 98% for the different defects and regions of interests in the reconstructed radiographs by the NAM–SRM algorithms. These figures of merit were between 67 and 89% in the original radiographs, respectively. The results show that the reconstructed images by NARM–SRM algorithms have better visualization and also the defect regions are very clear to the original radiographs. Regarding computing time, the proposed method is faster than the other four chosen iterative methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Vilar, R., Zapata, J., Ruiz, R.: An automatic system of classification of weld defects in radiographic images. NDT&E Int. 42, 467–476 (2009)

    Article  Google Scholar 

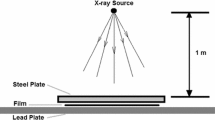
  2. International Atomic Energy Agency (IAEA): Radiation Safety in Industrial Radiography: Specific Safety Guide, p. 104. IAEA, Vienna (2011)

    Google Scholar 

  3. Mgonja, C.T.: Evaluation on use of industrial radiography for weld joints inspection in Tanzania. Int. J. Mech. Eng. Technol. 8(5), 65–74 (2017)

    Google Scholar 

  4. Mery, D.: Computer Vision for X-ray Testing. Springer, New York (2015)

    Book  Google Scholar 

  5. Harara, W.: Low cost digital radiography system for weld joints and castings testing. Russ. J. Nondestruct. Test. 46(8), 618–625 (2010). https://doi.org/10.1134/S1061830910080115

    Article  Google Scholar 

  6. Martz, H.E., Logan, C.M., Schneberk, D.J., Shull, P.J.: X-ray Imaging: Fundamentals, Industrial Techniques and Applications. CRC Press, London (2016)

    Book  Google Scholar 

  7. Michael, K.T.: The application of quantitative data analysis for the assessment of flat panel x-ray detectors in digital radiography as part of a quality assurance program. Biomed. Phys. Eng. Express 3(3), 035004 (2017)

    Article  Google Scholar 

  8. Mumford, D., Shah, J.: Optimal approximation by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 42, 577–685 (1989)

    Article  MathSciNet  Google Scholar 

  9. Keller, W.J., Pessiki, S.: Enhancing radiographic imaging of cementitious materials in composite structures with photon attenuating inclusions. Res. Nondestruct. Eval. 30(4), 231–251 (2019)

    Article  Google Scholar 

  10. Movafeghi, A.: Using empirical mode decomposition and a fuzzy algorithm for the analysis of weld defect images. Insight 57(1), 35–39 (2015). https://doi.org/10.1784/insi.2014.57.1.35

    Article  Google Scholar 

  11. Movafeghi, A., Yahaghi, E., Mohammadzadeh, N.: Defect detection improvement of digitised radiographs by principal component analysis with local pixel grouping. J. Nondestruct. Eval. (2015). https://doi.org/10.1007/s10921-015-0290-z

    Article  Google Scholar 

  12. Yang, J., Wright, J., Huang, T., Ma, Y.: Image super-resolution via sparse representation. IEEE Trans. Image Process. 19, 2861–2873 (2010)

    Article  MathSciNet  Google Scholar 

  13. Li, X., Orchard, M.T.: New edge-directed interpolation. IEEE Trans. Image Process. 10(10), 1521–1527 (2001)

    Article  Google Scholar 

  14. Zhang, X., Wu, X.: Image interpolation by adaptive 2-d autoregressive modeling and soft-decision estimation. IEEE Trans. Image Process. 17(6), 887–896 (2008)

    Article  MathSciNet  Google Scholar 

  15. Mallat, S., Yu, G.: Super-resolution with sparse mixing estimators. IEEE Trans. Image Process. 19(11), 2889–2900 (2010)

    Article  MathSciNet  Google Scholar 

  16. Dong, W., Zhang, L., Lukac, R., Shi, G.: Sparse representation based image interpolation with nonlocal autoregressive modeling. IEEE Trans. Image Process. 22(4), 1382–1394 (2013)

    Article  MathSciNet  Google Scholar 

  17. Trefethen, L.N., Bau III, D.: Numerical Linear Algebra, vol. 50. SIAM, Philadelphia (1997)

    Book  Google Scholar 

  18. Saad, Y.: Iterative Methods for Sparse Linear Systems, vol. 82. SIAM, Philadelphia (2003)

    Book  Google Scholar 

  19. Dong, W., Zhang, L., Shi, G., Wu, X.: Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization. IEEE Trans. Image Process. 20(7), 1838–1857 (2011)

    Article  MathSciNet  Google Scholar 

  20. Wang, Y., Yang, J., Yin, W., Zhang, Y.: A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 1(3), 248–272 (2008)

    Article  MathSciNet  Google Scholar 

  21. Lin, Z., Chen, M., Ma, Y.: The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv (2012). https://doi.org/10.1016/j.jsb.2012.10.010

    Article  Google Scholar 

  22. Mairal, J., Bach, F., Ponce, J., Sapiro, G., Zisserman, A.: Non-local sparse models for image restoration. In: IEEE International Conference on Computer Vision, Tokyo, Japan (2009)

  23. Buades, A., Coll, B., Morel, J.M.: A non-local algorithm for image denoising. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2005)

  24. Mery, D., Riffo, V., Zscherpel, U., Mondragón, G., Lillo, I., Zuccar, I., Lobel, H., Carrasco, M.: GDXray: the database of X-ray images for nondestructive testing. J Nondestruct Eval 34, 42 (2015). https://doi.org/10.1007/s10921-015-0315-7

    Article  Google Scholar 

  25. ISO 17636-1: Non-destructive Testing of Welds—Radiographic Testing—Part 1: X- and Gamma-Ray Techniques with Film. International Organization for Standardization, Geneva (2013)

    Google Scholar 

  26. ISO 14096-2: Non-destructive Testing—Qualification of Radiographic Film Digitisation Systems—Part 2: Minimum Requirement. International Organization for Standardization, Geneva (2005)

    Google Scholar 

  27. Wang, Z., Bovik, A.C., Sheikh, H.R., Simoncelli, E.P.: Image quality assessment: from error measurement to structural similarity. IEEE Trans. Image Process. 3(4), 600–612 (2004)

    Article  Google Scholar 

  28. Mirzapour, M., Yahaghi, E., Movafeghi, A.: Comparison of four iterative methods for improving the contrast of the radiography images. Phys. Scr. 94, 035001 (2019)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Reactor and Nuclear Safety Research School, Nuclear Science & Technology Research Institute (NSTRI), Tehran, Iran

    Amir Movafeghi

  2. Department of Mathematics, Faculty of Basic Sciences, Bu-Ali Sina University, Hamedan, Iran

    Mahdi Mirzapour

  3. Department of Physics, Imam Khomeini International University, Qazvin, Iran

    Effat Yahaghi

Authors
  1. Amir Movafeghi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mahdi Mirzapour
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Effat Yahaghi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Amir Movafeghi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Movafeghi, A., Mirzapour, M. & Yahaghi, E. Using Interpolation with Nonlocal Autoregressive Modeling for Defect Detection in Welded Objects. J Nondestruct Eval 39, 60 (2020). https://doi.org/10.1007/s10921-020-00704-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10921-020-00704-2

Keywords

Search

Navigation