1 Introduction

Nondestructive evaluation (NDE) techniques used on concrete structures can facilitate structural inspections, improve quality control, and support the sustainable use of resources [1]. Measurements based on vibrations and acoustic waves are frequently used to assess the mechanical properties in these structures. Such measurements are typically categorized based on their operating frequency, with ultrasonic methods as a major group. As a complement to the predominant use of ultrasonic reflection imaging approaches, we present a Lamb wave phase velocity imaging technique based on a full wave field response. Compared to ultrasonic approaches, this technique operates in a lower frequency regime and with a wider frequency content.

Ultrasonic testing allows the interior of a concrete construction element to be examined and visualized in the form of an reflection image [2, 3]. In this process, internal objects and anomalies such as defects appear as points or regions with deviating color. Techniques such as synthetic aperture focusing have made ultrasonic testing an effective, widely used, and powerful NDE approach for concrete structures. Recent progress has been made with this type of testing. One example is the development of wireless apertures that enable flexible data acquisition over larger areas compared to handheld devices [4]. However, for structures with heavy reinforcement or coarse aggregates, scattering and attenuation are challenges that may hinder the evaluation and reduce the ability to create a reflection image [3,4,5,6]. Since scattering and attenuation are related to the wavelength and number of cycles along the path of the ultrasonic pulse, this may particularly be a problem for high frequencies or thick structures [5].

To reduce the influence from scattering and attenuation, an alternative approach is to operate at a lower frequency regime, which leads to the usage of a longer spatial wavelength. This can, for instance, be achieved using a mechanical impactor as an input pulse source instead of an ultrasonic transducer. Based on this concept, the impact-echo (IE) method is a common and established technique for testing concrete structures [7]. In this method, an impact is applied to the surface using, for example, a hammer or a steel ball to generate a transient pulse with broadband frequency content. Ideally, the structural response to this transient excitation is dominated by a reverberating mode with a distinct frequency dependent on the material properties and geometry; i.e., the procedure corresponds to a general resonance test. Faults and anomalies can be detected by analyzing and monitoring the relative variation of the response along the surface. This procedure can be further extended with automatic data acquisition [8] and air-coupled sensors [9, 10] to generate a frequency image showing the relative variation of the response over a surface [8, 9].

There has been an improved understanding of the mechanism in IE testing over time. Whereas early studies interpreted the resonance mode as a discrete pulse with multiple reflections between the structural interfaces [7], more recent studies link the reverberating mode to the general theory of Lamb waves [11]. By showing that the resonance mode in IE testing corresponds to the first symmetric zero-group velocity (S1-ZGV) Lamb mode [11, 12], an important relationship to Lamb waves can be established. With this relationship determined at the outset and using the theoretical basis of Lamb wave theory, ongoing developments have advanced techniques that combine evaluation of the S1-ZGV Lamb mode frequency with propagating surface waves [13,14,15,16,17]. Such techniques, which use both propagating and nonpropagating modes with an analysis based on Lamb wave theory, enable a direct quantitative estimation of plate thickness and material velocity in absolute values; this differs from the original IE method that requires either a calibration sample or correction factor to provide the corresponding result [17]. In addition to quantitative estimations, the Lamb wave interpretation also facilitates the improved detectability and accuracy of the S1-ZGV frequency [18, 19] and enables an evaluation of Poisson’s ratio [20] from the characteristics of the S1-ZGV Lamb mode shape.

Clearly, the results in the literature demonstrate the potential for using Lamb waves in the NDE of plate-like concrete structures. At present, these techniques are still mainly based on an evaluation at multiple discrete points [7, 8] or, in some cases, along line arrays with equidistant impact (signal) spacing [15]. Naturally, there is no prerequisite or limitation that only these two types of geometrical domains (point and line) can be used; other layouts have been observed in related applications such as geophysical investigations with surface waves [21] and Lamb wave testing of aluminum plates [22]. Thus, to improve the verification of the spatial distribution of results in the testing of plate-like concrete structures, a prospective methodology is to perform a Lamb wave analysis with a two-dimensional (2D) surface considered in both the data collection and the data evaluation [23]. To the authors’ best knowledge, no examples of such an analysis with Lamb waves in the testing of plate-like concrete structures have been reported in the literature. This highlights the need for further investigations and serves as the motivation for the present study.

In this study, we demonstrate and describe a new technique for Lamb wave phase velocity imaging analysis of plate-like concrete structures. This technique can be interpreted as an adoption and implementation of local wavenumber analysis [24] or short space Fourier transform [25] for the application of plate-like concrete structures. The technique is based on a full wave field dataset collected over a surface using an impact hammer and an accelerometer. In contrast to previous studies of concrete plates, which measured stationary modes at multiple discrete points over a surface, the novel aspect of this technique is that it evaluates propagating waves in multiple 2D subdomains (2D arrays); the 2D arrays enable an improved spatial resolution in the evaluation in the lateral plane of the plate. Flexibility in terms of operating frequency is obtained since the impact source creates a response with wide-frequency bandwidth. As a result, further developments of the presented technique have potential for the evaluation of large structures in which scattering and attenuation may present issues when using ultrasonic approaches. The aim of this study is therefore twofold: one, to provide a detailed description about the implementation of the 2D array technique, and two, to illustrate the flexibility and potential of the technique by means of a practical measurement as illustrating example. It is emphasized that the presented technique does not represent a substitute technique that replaces ultrasonic approaches; the general usage of lower frequency (longer wavelength) to avoid scattering implies a reduced local sensitivity for damage compared to ultrasonic approaches. Thus, the presented technique should be considered as an alternative and complementary technique in relation to ultrasonic approaches for concrete structures.

The paper is organized as follows. In Sect. 2, we present a practical measurement as an illustrating example for the presented technique. Data processing and implementation of the technique are presented and explained in Sect. 3. First, data from a line array are processed in a conventional analysis of surface waves; this analysis is based on a 2D Fourier transform for which a discrete implementation is explained. Then, a transformation technique that converts data to a radial-offset domain is presented. The transformation allows the analysis of the data from the 2D arrays; as example, we analyze the phase velocity for the A0 Lamb mode and present the results in a polar and image plot. Finally, concluding remarks are provided in Sect. 4.

Fig. 1
figure 1

a Sketch of measurement domain and b overview of measurement equipment

Full size image

2 Method and Measurement

We perform a measurement on a newly cast concrete slab that serves as the foundation and ground for a future school building. The entire slab (building) is approximately rectangular in shape with length 60 m and width 17 m. No joints appear within the extent of these outer boundaries; i.e., the slab is cast in a continuous assembly. The slab has a uniform nominal thickness of 0.12 m, except along the walls and bases of columns the thickness is increased to enhance the load-carrying capacity. More specifically, the measurement data in this study are acquired inside a rectangle with length 4 m and width 1.8 m. This rectangle is shown and highlighted in green in Fig. 1a. In turn, this rectangle is located in the center of a room with length 8.1 m and width 6 m, shown in Fig. 1a. The nominal thickness of the slab in the room follows the uniform standard value of 0.12 m, except along the top, left, and bottom edges of the room (gray color in Fig. 1a) where the thickness is increased to 0.32 m to support the load from the inner walls. Along the right edge of the room, which also is at the edge of the slab (gold color in Fig. 1a) and the outer wall, the nominal thickness is increased to 0.5 m. Except at this right edge of the room (slab edge), the distances to the outside edges of the slab are a minimum of 9 m. Thus, the location of the measurement ensures low influence from reflections caused by free slab edges. Moreover, since a newly cast plate is studied, it is expected that the slab will have uniform material properties and thickness and will be free of anomalies and defects. The measurement location is selected in order to create a controlled and reliable test environment that facilitates the development of new processing techniques without introducing excessive uncertainties.

Measurement data are collected with portable equipment consisting of a triaxial accelerometer (PCB model 356A15), impact hammer (PCB model 086C03), signal conditioners (PCB model 480b21), data acquisition card (NI USB-6251 BNC), and laptop computer. An overview of the equipment is shown in Fig. 1b. The collected data are composed of the vibration responses recorded by the accelerometer due to impacts made with the hammer. Responses from 1040 impacts are recorded at positions shown in Fig. 2a as black dots. The accelerometer remains at a fixed position during the measurement, and it is marked with a blue diamond in the center of the measurement domain shown by the green rectangle in Fig. 2a, b. Figure 2a, b also show the orientation of the xyz-domain assigned to the measurement. For the direction parallel to the x-axis, the impact points appear at x-coordinates from ± 0.05 m to ± 2 m with offset intervals of 0.05 m between the points; note that no impact points appear along the line x = 0. For the direction parallel to the y-axis, impact points appear at y-coordinates from − 0.9 m to + 0.9 m with offset intervals of 0.15 m between the points; a coarser sampling interval is used in this direction to reduce the number of impact points (i.e. reduce the amount of time required for recording the data). Figure 2b shows a photograph of the slab taken during the measurement. This figure depicts the rectangle (green color), the accelerometer (blue diamond), the coordinate system (yellow dotted lines), and the edge of the rectangular domain (yellow solid lines). For brevity, the 1040 impact points are not highlighted in Fig. 2b.

Fig. 2
figure 2

a Measurement domain and associated coordinate system and b photograph from measurement with illustration of coordinate system and practical execution

Full size image

Planning and organization are important in the collection of a large number of impact responses. In our case, we divide the 1040 points into 26 lines, each containing 40 impact points. Figure 2b shows an example of a line that is illustrated with yellow dashed markings. Along the line, 40 impacts are performed from left to right, covering a distance of \(40\times 0.05=2\) m. This corresponds to half of the rectangular domain length of 4 m. The 0.05 m offset distance between each point along the x-direction is maintained with guidance from the carpenter’s ruler placed adjacent to the line; see Fig. 2b. The process is then continued by marking a new line, for instance with a chalk line as used here, and thereafter collecting of a new set of 40 impacts. The described procedure is repeated 26 times in total, thus producing the 1040 impact points. Accordingly, it can be observed that the overall process corresponds to a series of measurements that are similar to those used in a multichannel analysis of surface waves (MASW) [26]. In the current measurement, each line requires approximately 5 min working time to mark the line and perform the impacts. Thus, 2–3 h of effective working time are required to collect the complete dataset of 1040 impacts. It should be mentioned that a major part of this effective working time is spent on marking the appropriate location of the lines; typically, the impacts themselves are easily performed in a short amount of time.

For studies of vibrating systems, the coupling condition of the accelerometer is a crucial issue. In this study, the accelerometer is mounted with glue at the center of the rectangular domain (Fig. 2a, b, blue diamond marker) and it is kept in this position throughout the entire course of the measurement. This ensures a consistent coupling condition at the receiving end of the measurement system for all 1040 impacts, and it means that measurement uncertainty, except for electrical noise, is mainly generated at the sending end due to the potential variation in the coupling condition of the hammer impacts. In addition to generating the vibrations in the plate, the impact hammer also works as a triggering device; thus, reciprocity can be used. In more detail, reciprocity generally states that the response of a linear elastic system measured by an accelerometer at location A due to an impact applied at location B is equal to the response measured from the reciprocal arrangement, with the impact applied at location A and the accelerometer at location B. As a result, we are able to obtain a dataset containing the full wave field response from a transient point source excitation at the position of the accelerometer (Fig. 2a, b, blue diamond) recorded with 1040 sensors located at the impact points (Fig. 2a, black dots). Note that an important condition required for usage of reciprocity in this case is a well-defined, consistent and repeatable impact source (in this case a modal hammer). In the following, this dataset is further studied and analyzed.

3 Data Processing and Results

The data acquisition card operates at the sampling frequency \(f_s =200\) kHz and a recording length of 20 ms, i.e., a recording length of 4000 samples. With the use of reciprocity, the collected dataset represents the full wave field response due to a point source excitation recorded with an array consisting of 1040 sensors. In the following, the aim is to demonstrate potential processing schemes relevant for this dataset by providing an explanation and details regarding the implementation of these schemes. The 1040 sensors are analyzed by dividing them into subsets of smaller groups. Accordingly, the groups can be interpreted as synthetic sensor arrays created by the geometrical shape that defines the group.

For this measurement, since a triaxial accelerometer is used, each sensor records three individual signals: the acceleration response in the x-, y-, and z-directions. Thus, the dataset contains 3120 signals in total. In the following analysis, both the surface normal response (z-direction) and the surface in-plane responses (x- and y-directions) are considered. However, note that the presented analysis is not dependent on all components being measured; the adopted methodology is also applicable for data recorded with a conventional single-axis accelerometer, which typically measures the surface normal component (z-direction).

3.1 Line Array

An array defined by a line enables the study of a wave field in both space and time. In geophysical applications, this is often referred to as multichannel analysis of surface waves (MASW) [26], and similar approaches using this very general type of array are also used to test metal plates [27] and plate-like concrete structures [15]. Typically, for most applications, the arrays are characterized by uniform spatial sensor spacing along a line. In the case of this study, we create the array by selecting sensors along the positive x-axis; see Fig. 3a in which the blue diamond markers indicate the positions of the sensors and the red cross indicates the location of the transient point source excitation (from reciprocity). The array shown in Fig. 3a consists of 40 sensors located every 0.05 m along the positive x-axis over the range \(x=0.05\) m to \(x=2\) m. For this line array case, we consider the signals containing the surface in-plane (x-direction) acceleration response and the surface normal (z-direction) acceleration response. Thus, the signals containing the acceleration response in the y-direction (transversal surface in-plane response) are ignored and not considered in the following analysis.

Fig. 3
figure 3

a Measurement domain and line array shown with blue diamond markers, b time-domain low-pass filtered surface in-plane acceleration response and wave mode labels, c frequency-phase velocity correlation image and Lamb mode labels (Color figure online)

Full size image

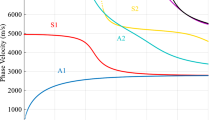
Data corresponding to the surface in-plane (x-direction) acceleration response recorded with the array in Fig. 3a are shown in Fig. 3b. For improved readability, the presented time domain data are low-pass filtered to reduce the frequency content above 30 kHz. Figure 3b shows the time history, up to 2 ms, of the signals that represent the surface in-plane acceleration response for all sensors in the array as a function of the x-coordinate of the sensors. This type of plot, sometimes referred to as a wiggle plot or seismic record, allows an initial analysis of the data in both time and space. Note that all signals are normalized and gained (amplified) to improve readability. In Fig. 3b, the longitudinal wave can be identified (see marking with arrow). After a time of approximately 1 ms, a stationary mode is observed. This mode corresponds to the S1-ZGV Lamb mode (see marking with ellipse), i.e., the reverberating mode typically analyzed in IE measurements of plates. Between the longitudinal wave and the S1-ZGV Lamb mode, a propagating surface wave can also be noticed (see marking with arrow).

Although the visualization of the data in Fig. 3b possibly allows estimations of both velocity (slope in Fig. 3b) and frequency (periodicity in Fig. 3b), these estimations may be challenging since the recorded wave field consists of multimodal and dispersive Lamb waves that are present simultaneously over a wide frequency range. For this reason, estimations that are more robust are generally obtained by transforming the data to the frequency domain in both time and space. This can be achieved using a 2D Fourier transform, as given by [28]:

$$\begin{aligned}&S\left( {k,f} \right) =\mathop \int \limits _{-\infty }^{+\infty } \mathop \int \limits _{-\infty }^{+\infty } s\left( {x,t} \right) e^{-2\pi i\left( {ft-kx} \right) }dx dt\end{aligned}$$
(1)

where S is the measured response as a function of spatial frequency (wave number) k and temporal frequency f, and s is the recorded vibration as a function of space x and time t. By using a discrete implementation (see Sect. 3.2) of this transform and the relation \(V=f/k\), where V is the phase velocity, the surface in-plane acceleration response is transformed to the frequency-phase velocity domain. The same transformation is also performed for the surface normal acceleration response. Then, a superposition of the transformed surface in-plane and surface normal responses is created and shown in Fig. 3c; for this case the superposition improves the resolution compared to the opposite case of using each component individually. Basically, Fig. 3c shows the correlation for different combinations of frequencies f and phase velocities V for the data recorded by the array. The dark color indicates strong correlation, whereas the light color indicates weak correlation. In Fig. 3c, the two fundamental Lamb modes A0 and S0 can be identified (see markings). In addition, the part of the S1 Lamb mode curve related to the S1-ZGV Lamb mode can also be observed. This type of correlation image can be used to track the dispersive properties of the measured wave field. In other words, a Lamb wave dispersion analysis can be performed and used to evaluate the elastic properties and thickness of the plate [27]. Note that this type of analysis is independent of a priori information about the structure; compared with, for instance, the conventional IE technique [7], no empirical correction factors or calibration values are required [17].

3.2 Two-Dimensional Discrete Fourier Transform

Since no analytical expressions exist for the measured response, the expression in Eq. 1 must be numerically evaluated to create the correlation image in Fig. 3c. The literature provides examples of implementing such evaluations [26, 28,29,30,31,32]. Although the format of implementation varies in the literature, the aim of estimating the spectral content in time and space is common. In this study, we adopt a discrete implementation described in a matrix format, since the matrix format is easily modified for arrays with nonuniform sensor spacing. Moreover, this format can be directly implemented in codes such as MATLAB. Here, the line array given by the blue diamond markers in Fig. 3a is used as an illustrating example. However, it is emphasized that the implementation is general and applicable to other line arrays as well.

Let \({\varvec{s}}\left[ n \right] \) be a row vector containing the signal recorded by a sensor:

$$\begin{aligned} {\varvec{s}}\left[ n \right] =\left[ {{\begin{array}{cccc} {s\left[ 1 \right] }&{} {s\left[ 2 \right] }&{} \cdots &{} {s\left[ N \right] } \\ \end{array} }} \right] \end{aligned}$$
(2)

The index \(n=1, 2, \ldots N\) refers to each discrete sample of the signal in time. In this case, the vector \({\varvec{s}}[n]\) contains \(N=4000\) discrete samples s recorded at time intervals \(1/f_s \), where \(f_s =200\) kHz is the temporal sampling frequency. The spatial array consists of sensors that are numbered with index \(m=1, 2, \ldots M\). For the array studied here (blue diamond markers in Fig. 3a), the number of sensors is \(M=40\). The sensors are located at the coordinates given by \(x_m =m \cdot 0.05\), where 0.05 is the spatial sampling interval along the x-axis. The y-coordinates are for all sensors \(y_m =0\). An M-by-N matrix \({\varvec{S}}\) containing the signals \({\varvec{s}}_m \) for all sensors \(m=1, 2, \ldots M\) in the array is defined by

$$\begin{aligned} {\varvec{S}}= \left[ {{\begin{array}{l} {{\varvec{s}}_1 } \\ {{\varvec{s}}_2 } \\ \vdots \\ {{\varvec{s}}_M } \\ \end{array} }} \right] \end{aligned}$$
(3)

In this case, the signal \({\varvec{s}}_1 \) corresponds to the sensor located closest to the point source location (red cross at \(x=y=0\) in Fig. 3a), and \({\varvec{s}}_M = {\varvec{s}}_{40} \) corresponds to the sensor located farthest away from the point source. That is, the sensor signals in matrix \({\varvec{S}}\) are sorted according to ascending distance from the point source according to ascending x-coordinates.

For the discrete Fourier transform in the time domain, a complex and discrete test function is defined by

$$\begin{aligned} \theta _f \left[ n \right] =e^{-2\pi i f_{test} n/f_s } \end{aligned}$$
(4)

The test function \(\theta _f \) describes a complex harmonic oscillation with frequency \(f_{test} \). The subscript f indicates that the function is associated with frequency in the time domain. The term \(n/f_s \) can be interpreted as the time variable along which the function is periodic. By calculating the test function for \(n=1, 2, \ldots N\), i.e., for the same length and time as the signals \({\varvec{s}}_m \), a test vector is created by

$$\begin{aligned} {\varvec{\theta }}_f = \left[ {{\begin{array}{l} {\theta _f [ 1 ]} \\ {\theta _f [ 2 ]} \\ \vdots \\ {\theta _f [ N ]} \\ \end{array} }} \right] \end{aligned}$$
(5)

Then, the discrete Fourier transform in the time domain is formulated as

$$\begin{aligned} {\varvec{s}}_f ={\varvec{S\theta }} _f \end{aligned}$$
(6)

The resulting column vector \({\varvec{s}}_f \) with length M contains complex numbers that are related to both the amplitude and phase of the spectral content for each sensor signal \({\varvec{s}}_m \) at the test frequency \(f_{test} \).

For the discrete Fourier transform in the space domain, a new complex and discrete test function is defined as

$$\begin{aligned} \theta _{f-V} \left[ {x_m } \right] = e^{2\pi i f_{test} /V_{test} x_m } \end{aligned}$$
(7)

The test function \(\theta _{f-V} \) describes a complex harmonic oscillation defined by the test frequency \(f_{test} \) and the test phase velocity \(V_{test} \). The subscript \(f-V\) indicates that the function is associated with frequency in time and the phase velocity. As a result, the function is defined by frequency in the space domain given by a test wave number \(k_{test} =f_{test} /V_{test} \). This means that the function \(\theta _{f-V} \) is periodic along the spatial x-axis of the array. The test function is calculated for the x-coordinates of each sensor to create a new test vector:

$$\begin{aligned} {\varvec{\theta }} _{f-V} =\left[ {{\begin{array}{l} {\theta _{f-V} \left[ {x_1 } \right] } \\ {\theta _{f-V} \left[ {x_2 } \right] } \\ \vdots \\ {\theta _{f-V} \left[ {x_M } \right] } \\ \end{array} }} \right] \end{aligned}$$
(8)

The discrete Fourier transform in space domain is then given by

$$\begin{aligned} s_{f-V} =({\varvec{s}}_f \oslash \hbox {abs}\left( {{\varvec{s}}_f } \right) )^{{\varvec{T}}}{\varvec{\theta }} _{f-V} \end{aligned}$$
(9)

where \(\oslash \) is an element-wise division (Hadamard division) and \(\hbox {abs}\left( {{\varvec{s}}_f } \right) \) is the absolute value of each element in the vector \({\varvec{s}}_f \). Here, the element-wise division with the absolute values of the elements in \({\varvec{s}}_f \) is used as a normalizing operation that removes the dependency on the amplitude of the wave field. Thus, this discrete Fourier transform in the space domain corresponds to an analysis of the phase angles of the complex elements in vector \({\varvec{s}}_f \). This means that the magnitude of the resulting transformation given by \(s_{f-V} \) represents a measure of the correlation showing the extent to which a wave mode with frequency \(f_{test} \) and phase velocity \(V_{test} \) exists in the recorded wave field. The subscript \(f-V\) is used to symbolize the association with both frequency f and phase velocity V. In the implementation presented here, \(s_{f-V} \) represents a complex scalar value. Thus, for the creation of a correlation image as presented in Fig. 3c, the above steps may be repeated over a range of combinations of test frequencies \(f_{test} \) and test phase velocities \(V_{test} \).

In this example, the correlation image in Fig. 3c is created by calculating \(s_{f-V} \) for both the surface in-plane (x-direction) and the surface normal (z-direction) responses. The transformed responses are then combined in the correlation image to \(\left( {|s_{f-V, \mathrm{in-plane}} \left| {+|s_{f-V, \mathrm{normal}} } \right| } \right) ^{2}\). The parenthesis is squared to facilitate the contrast of the correlation image, i.e., the power of the parenthesis acts as a modulating gain. Here, note that although the surface in-plane component and the surface normal component of Lamb modes in general are different in both phase and magnitude along the propagation axis, the frequency and phase velocity of a Lamb mode is the same for both components. For this example, an improved correlation image quality is obtained by the usage of two components instead of one component.

3.3 Radial Offset Domain Transformation

By assuming cylindrical spreading of the wave field due to a point source, the processing scheme for a line array can be extended to include 2D arrays created by groups of sensors defined by a surface. Practically, this can be realized by transforming the recorded data to a radial offset domain. In the radial offset domain, the locations of the sensors are defined by a spatial radial coordinate r that measures the distance from the sensor to the source location (from reciprocity: red cross in Fig. 3a, b). Naturally, the radial coordinate \(r_m \) for a sensor m is given by

$$\begin{aligned} r_m = \sqrt{x_m^2 +y_m^2 } \end{aligned}$$
(10)

where \(x_m \) and \(y_m \) are the coordinates for the sensor m in the xy-plane. In other words, the radial offset domain represents a polar domain with a radial axis r directed outward from the center of the domain located at \(x=y=0\) (the location of the transient source from reciprocity).

In the radial offset domain, two acceleration responses are used: the surface normal response (z-direction) and the surface in-plane response (r-direction). Note that the z-axis in the radial offset domain is the same as the z-axis in the initial xyz-domain displayed in Fig. 2. For this reason, no action is needed for the signals containing the surface normal response (z-direction); this response is only dependent on one physical channel (axis) of the accelerometer. However, to obtain the surface in-plane response (r-direction) in the radial offset domain, a simple transformation of the initially recorded data is required since this response is dependent on two physical channels (axes) of the accelerometer. Accordingly, the surface in-plane acceleration response (r-direction) signal \({\varvec{s}}_{m, in{\text {-}}plane} \) for a sensor m can be obtained by

$$\begin{aligned} {\varvec{s}}_{m, in{\text {-}}plane} =\left( {{\varvec{s}}_{m,x} x_m + {\varvec{s}}_{m,y} y_m } \right) /r_m \end{aligned}$$
(11)

where \({\varvec{s}}_{m,x} \) and \({\varvec{s}}_{m,y} \) are the signals containing the surface in-plane acceleration response in the x- and y-directions for the sensor m, respectively. That is, \({\varvec{s}}_{m, in{\text {-}}plane} \) is obtained by projecting the acceleration response in the x- and y-direction onto the polar radial r-direction.

To proceed and further develop the study, the described transformation technique is applied to the collected dataset. An example of the output from this transformation is presented in Fig. 4, which shows the normalized surface in-plane (\(\hbox {r}\)-direction) acceleration response (Fig. 4b) and the normalized surface normal (\(\hbox {z}\)-direction) acceleration response (Fig. 4c) for the sensors marked with blue diamonds (Fig. 4a). For improved readability, the presented time-domain data are low-pass filtered to reduce the frequency content above 30 kHz. The selected sensors in Fig. 4a represent 14 sensors located at the radial offset distance \(\hbox {r}=1.7\pm 0.01\) m, i.e., at approximately the same radial offset distance \(\hbox {r}\) from the point source (red cross in Fig. 4a). In both Fig. 4b, c, the signals from the 14 sensors show similar behavior. The consistency among the signals, showing the first arrival of the longitudinal wave around 0.9 ms and a surface wave around 1.2 ms, indicates that the plate under investigation is homogenous. Moreover, this consistency also implies a reliable and robust triggering in the time domain for each sensor. After around 1.7 ms, the signals are no longer consistent. This is related to the exposure of the sensors to different amounts of scattering and reflections; thus, we anticipate the reduced consistency as a function of time, as observed here.

Fig. 4
figure 4

a Measurement domain and sensors shown with blue diamonds, b corresponding time-domain low-pass filtered acceleration response for surface in-plane direction and c surface normal direction (Color figure online)

Full size image

3.4 2D Array

By assuming a relatively constant material and plate thickness within a limited surface region, a 2D array defined by a group of sensors can be evaluated as a line array in the radial offset domain using a similar approach to that described in Sect. 3.2. This is done by adopting the transformation technique described in Sect. 3.3. One example of this evaluation is illustrated with the 2D array shown as blue markers in Fig. 5a. This 2D array is defined by the surface of a rectangle with a width of 0.3 m and a slope of \(25^{\circ }\) (Fig. 5a). The 2D array contains 85 sensors, and the data collected by these sensors are further studied in the radial offset domain. The surface in-plane acceleration response (r-direction) as function of time and space is shown in Fig. 5b. For improved readability, the presented time-domain data are low-pass filtered to reduce the frequency content above 30 kHz. In Fig. 5b, the longitudinal wave and the S1-ZGV Lamb mode can be observed; the data show major similarities with Fig. 3b.

The data are transformed to the frequency-phase velocity domain, and the results from this transformation are displayed in Fig. 5c. The processing technique required to create this correlation image is principally the same as that described in Sect. 3.2. However, since the data are analyzed in the radial offset domain, the coordinate variable \(x_m \) is replaced with the radial coordinate variable \(r_m \). As a result, the test function for the discrete Fourier transform in the space domain takes a slightly different form, according to

$$\begin{aligned} \theta _{f-V} \left[ {r_m } \right] = e^{2\pi i f_{test} /V_{test} r_m } \end{aligned}$$
(12)

The corresponding test vector is created by

$$\begin{aligned} {\varvec{\theta }}_{f-V} =\left[ {{\begin{array}{l} {\theta _{f-V} \left[ {r_1 } \right] } \\ {\theta _{f-V} \left[ {r_2 } \right] } \\ \vdots \\ {\theta _{f-V} \left[ {r_M } \right] } \\ \end{array} }} \right] \end{aligned}$$
(13)

where \(r_m \) are the radial coordinates for the sensors. This means that the test vector \({\varvec{\theta }} _{f-V} \) now represents a complex harmonic vector that is periodic along the radial axis r. Both the surface in-plane response (r-direction) and the surface normal response (z-direction) are calculated and used to create the correlation image in Fig. 5c according to \(\left( {|s_{f-V, \text {in}{\text {-}}\text {plane}} \left| {+|s_{f-V, \text {normal}} } \right| } \right) ^{2}\). Major similarity between the correlation image for this 2D array (Fig. 5c) and the correlation image for the line array (Fig. 3c) is observed. This similarity ensures validity and strengthens the feasibility of using 2D arrays in evaluations performed in the radial offset domain. The similarity also verifies, to some extent, that the plate is homogenous within the measurement domain. This result is expected since a newly cast plate is studied; the test location is intentionally selected to ensure an environment with few uncertainties.

Fig. 5
figure 5

a Measurement domain and rectangular 2D array shown with blue diamond markers, b time-domain low-pass filtered surface in-plane acceleration response, c frequency-phase velocity correlation image and estimated velocity for A0 Lamb mode at 6 kHz

Full size image

3.5 Variation of Phase Velocity: Polar Angle and 2D Imaging

The dispersive properties of Lamb modes in a plate are defined by the material properties and thickness. If a variation in the material or thickness is present in the lateral plane of the plate, then a variation in the dispersion is also present. The homogeneity of a plate can be assessed by measuring the phase velocity of Lamb modes at different locations on the plate. For a complete assessment, the analysis may be focused on the full frequency range of the dispersive wave field. However, this may be an elaborate task, at least for an initial assessment of a measurement object. It is therefore reasonable to select one or a few modes at a narrow range of frequencies for the initial analysis of homogeneity. As such example, in the following part of this study, we select the A0 Lamb mode at the frequency 6 kHz; see the marking with a red cross in Fig. 5c. This Lamb mode is selected since its mode shape is present through the entire thickness of the plate. The phase velocity of the mode is therefore dependent on both the material properties along the complete cross-sectional thickness as well as on the dimension of the thickness itself; i.e., the mode is not sensitive to potential local surface material inhomogeneities.

Using the test phase velocity that maximizes the correlation image amplitude at 6 kHz in Fig. 5c, the phase velocity for the A0 Lamb mode is estimated to be 1.86 km/s; see the marking with a red cross in Fig. 5c. The corresponding wavelength is therefore \(\lambda =V/f\approx 0.3\, \hbox {m}\). Thus, considering the nominal plate thickness of 0.12 m, this mode can be considered as a robust selection suitable for an initial assessment of the general homogeneity of the plate. The estimated phase velocity is representative of the surface region covered by the 2D array displayed with blue diamond markers in Fig. 5a. That is, the estimate represents a type of spatial average of the phase velocity for the mode within the surface region given by the 2D array; the 2D array can be interpreted as a spatial averaging operator dependent on the surface size and shape in relation to the wavelength of the mode.

Figure 6a shows the estimated phase velocity for the A0 Lamb mode at 6 kHz as a function of the polar angle of the 2D array in steps of \(5^{\circ }\). This result is obtained by a stepwise rotation of the 2D array in Fig. 5a around the measurement and a corresponding estimation of the phase velocity at each step. Results show little variation in the estimated phase velocity; the minimum, mean, and maximum phase velocities are 1793, 1849, and 1911 m/s, respectively. That is, the variation is typically within ± 3% of the mean phase velocity, and an almost consistent phase velocity for the A0 Lamb mode is observed. The minor variation of phase velocity may be attributed slight variation in plate thickness due to unevenness or inclination of the underlying styrofoam blocks. Thus, results from this initial assessment show that the plate is essentially homogenous within the measurement domain. This is expected since a newly cast plate is studied.

Fig. 6
figure 6

a Estimated phase velocity for the A0 Lamb mode at 6 kHz as a function of polar angle for the rectangular 2D array; b envelope for normalized absolute values of the array window functions in frequency (wave number) domain shown as gray shading; blue line corresponds to rectangular 2D array in Fig. 5a (Color figure online)

Full size image

When performing a frequency analysis with discrete Fourier transforms, the topic of sampling is an important matter. In this example, where the phase velocity is estimated as a function of the angle of the 2D array, constant and uniform sampling is used in the time domain. However, this is not the case for sampling in the space domain, since each angle (step of \(5^{\circ })\) is associated with one particular 2D array and set of sensors. This means that the number of sensors, as well as their interrelating locations in the radial offset (space) domain, will vary among the different 2D arrays (angles). For this reason, it is of interest to evaluate the influence from the characteristics of each 2D array (angle).

From a signal-processing point of view, a general array corresponds to a spatial window function that is used to sample the wave field [33]. The sampling in the radial offset (space) domain represents a multiplication of the spatial array window function and the physical wave field. According to the convolution theorem, multiplication in the space domain corresponds to convolution in the frequency (wave number) domain. Thus, the measurement (sampling) corresponds to a convolution between the discrete Fourier transform of the array window function and the true wave field in the frequency domain. Owing to this, the resolution of the estimated phase velocity (wave number) is dependent on the discrete Fourier transform of the array window function. In this example, the array window is defined by a discrete rectangular function with unit value at the locations of the sensor positions and zero value elsewhere. This means that the spatial discrete Fourier transform of the array window function, at a test wave number \(k_{test} =f_{test} /V_{test} \), is obtained by a summation of the complex components in the test vector \({\varvec{\theta }} _{f-V} \) [29]. By repeating this calculation for a range of test wave numbers \(k_{test} \), the spatial Fourier transform of the array window function is obtained.

For the 2D array shown with blue diamond markers in Fig. 5a, the absolute value of the spatial Fourier transform for the array window function is shown in Fig. 6b with a blue solid line. The gray shading in Fig. 6b represents the envelope corresponding to all 2D arrays that are used to create Fig. 6a; that is, all absolute values of the spatial Fourier transforms for the array window functions are contained within the boundaries of this gray shaded envelope. Note that the magnitude of the window functions are normalized in Fig. 6b. In the evaluation of the spatial Fourier transforms of window functions, two aspects are considered. The first aspect concerns the width of the main lobe at the wave number \(k=0\), which determines the resolution of the estimated frequency (wave number). A narrowing of this width increases the resolution and a broadening reduces the resolution. In Fig. 6b, the envelope exhibits some spread. From a manual inspection (not displayed here) of the data analysis of the 2D arrays with the greatest main lobe width, we can see that reliable estimations of the phase velocity are obtained even for these 2D arrays. In particular, we verify that we can obtain correlation images (as in Fig. 5c) with sufficient resolution and similarity compared with those created from the other 2D arrays with a narrower main lobe width. In other words, we perform a manual analysis and verification (not displayed here) of the data from the 2D arrays with the greatest main lobe width to ensure reliability in the evaluation. The second aspect concerns the locations of the highest side lobes, at \(k= \pm 7\,\mathrm{m}^{-1}\) in Fig. 6b, which provide information about potential aliasing. For the mean phase velocity of \(V= 1849~m/s\) at the frequency \(f=6\,\mathrm{kHz}\), the corresponding wave number is \(k=f/V=6000/1849\approx 3.2\,\mathrm{m}^{-1}\). This means that the side lobes appear at \(k=3.2\pm 7\,\mathrm{m}^{-1}\). For the phase velocity, this corresponds to approximately \(V= -1600\,\mathrm{m/s}\) and \(V= 600\,\mathrm{m/s}\). Consequently, since the A0 Lamb mode is a single dominating mode at the investigation frequency (6 kHz), the effect from aliasing from these side lobes does not represent an issue in this example. To summarize, by considering these two aspects, we verify that the result presented in Fig. 6a is based on a reliable sampling in space. This type of verification is central in all types of frequency analyses, but is especially important for the cases, as here, where nonuniform sampling is used.

Fig. 7
figure 7

a Measurement domain and circular 2D array shown with blue diamond markers; b envelope for normalized absolute values of the array window functions in frequency (wave number) domain shown as gray shading; blue line corresponds to circular 2D array in the top-left subfigure; c estimated phase velocity for the A0 Lamb mode at 6 kHz as function of 2D array center coordinate (Color figure online)

Full size image

The study of the variation in phase velocity in Fig. 6a is made by rotating a 2D array with a rectangular shape. However, the rectangular shape represents only one among many possible shapes. For instance, a possible alternative is a 2D array defined by a circular surface. Figure 7a shows an example of a 2D array defined by a circle with radius 0.45 m, and this type of 2D array is further explored in the following. Compared with the rectangular 2D array in Fig. 5a, with one end fixed at the source location, Fig. 7a shows that the position of a 2D array with a circular shape can be changed more freely within the measurement domain given by the green rectangle. Here, we sweep the circular 2D array within a rectangular grid space defined by 40 points along the x-axis and 20 points along the y-axis. Following the same principle as previously described, an estimation of the phase velocity for the A0 Lamb mode at 6 kHz is made at each grid point. Accordingly, this provides an estimate of the phase velocity over a 2D grid surface. The result from this evaluation is shown in Fig. 7c as a phase velocity image with color corresponding to the estimated phase velocity. Note that the color of each pixel is representative of the estimated phase velocity within the complete surface covered by the corresponding 2D array. In other words, the pixel color does not represent a pointwise phase velocity estimation, since the 2D array has an averaging (smoothing) influence; i.e. increased size of the 2D array leads to increased averaging (smoothing). The minimum, mean, and maximum phase velocities are 1771 m/s, 1840 m/s, and 1910 m/s, respectively. Thus, also for this evaluation, an almost consistent phase velocity for the A0 Lamb mode is observed in the phase velocity image. Similar to the result in Fig. 6a, the phase velocity image in Fig. 7c further confirms that a condition of material homogeneity and plate thickness is present in the measurement domain. Again, this result is expected since a newly cast and ideally homogenous plate is studied.

Similar to the evaluation based on a rotating 2D array, this evaluation is also associated with nonuniform sampling in the space domain. For the circular 2D array shown in Fig. 7a, the spatial Fourier transform of the corresponding array window function is shown with a solid blue line in Fig. 7b. The gray shading corresponds to the envelope of the spatial Fourier transforms of all array window functions. As previously, we verify the robustness of the estimation by monitoring the correlation image quality for the 2D arrays with the greatest main lobe. Again, since the A0 Lamb mode is a single dominating mode, the effect from aliasing due to side lobes does not present an issue in this case. Yet, for detailed and further investigations of an object, the implementation of a sampling criterion that discards estimates obtained from arrays with insufficient spectral resolution and performance may provide an approach for handling the sampling and ensuring consistent reliability of the results.

4 Concluding Remarks

With a full wave field dataset as the basis, we demonstrate and describe the implementation of a processing technique that enables a Lamb wave analysis in the frequency-phase velocity domain. Through the transformation of data into the radial offset domain, the initial technique is extended to include 2D arrays defined by 2D surfaces such as rectangles or circles. An analysis of the phase velocity as a function of polar angle is performed for 2D arrays with a rectangular shape, and a 2D phase velocity imaging analysis is performed for the 2D array with a circular shape. Naturally, other 2D array layouts are possible although they are not discussed here.

Results from the analysis of the phase velocity variation for the A0 Lamb mode at 6 kHz show a consistent phase velocity with little variation and a mean value around 1850 m/s. This means that the investigated plate is, as expected, essentially homogenous with little variation in the material properties and thickness within the measurement domain. Although not shown in this study it is likely that variations in material properties and plate thickness in the lateral plane of the plate, i.e. variations in phase velocity, can be detected as deviations in the estimated phase velocity [24]. Thus, this type of analysis is an example of an initial assessment of material condition and plate thickness for an unknown testing object. That is, one practical application of the technique is to use it as a tool for identifying potential locations and regions for further investigations. For most 2D arrays in this study, we used nonuniform sampling in the space domain. It is shown that a spectral estimation can also be performed under this sampling condition. Nevertheless, to ensure reliable results, the effect from the sampling condition should be evaluated.

The presented technique is demonstrated on one specific plate. Naturally, for further developments, it is important to investigate the application on other test objects as well as to understand its sensitivity to defects and anomalies. It is reasonable that the literature on guided wave applications in other fields may be useful for this task. Concerning the practicality of the measurements, it is expected that, with modern developments in fields such as wireless protocols, positioning systems, digital image processing, and augmented reality, the effort of collecting a full wave field dataset over a measurement domain, as in this study, can be minimized. More specifically, the bottleneck of this technique is the time required for marking the location of the impacts. Once this issue is addressed by the implementation of techniques for automatically determination of the location of impacts at arbitrary positions, it is expected that measurements can be performed with high efficiency and with only a little amount of time required.

To summarize, from a general viewpoint we are able to show that a Lamb wave phase velocity imaging analysis of concrete plates can be performed with essentially the same simple equipment as that used for the IE method [7]. This highlights the very general characteristic of the utilized full wave field response, that a substantial number of evaluation methodologies are likely possible. Compared to ultrasonic transducers, transient impact sources are not limited to a narrow band of operating frequency; on the contrary, energy over a wide range of frequencies is generated and fed into a full wave field response. For this reason, techniques based on transient impact sources (full wave field) are important in cases where scattering and attenuation issues limit the use of ultrasonic techniques. In view of the need to inspect infrastructure constructions of large dimensions with potentially heavily reinforcement and coarse aggregates, we believe full wave field approaches, such as the one presented, represent a valuable and qualified complement to ultrasonic techniques. Here, it is emphasized that full wave field approaches operating in the frequency range below ultrasonic techniques, say 10–20 kHz, do not provide a substitute for ultrasonic techniques; our opinion is that optimal NDE is obtained by combining information from several techniques. That said, we hope that future full wave field approaches are considered equally qualified as ultrasonic techniques, and that this study provides a step toward a more developed and unified evaluation approach for concrete structures that utilize as many techniques (carriers of information) as reasonably possible.