Abstract
We develop flux globalization based well-balanced central-upwind schemes for hydrodynamic equations with general free energy. The proposed schemes are well-balanced in the sense that they are capable of exactly preserving quite complicated steady-state solutions and also exactly capturing traveling waves, even when vacuum regions are present. In order to accurately track interfaces of the vacuum regions and near vacuum parts of the solution, we use the technique introduced in Chertock et al. (J Sci Comput 90:Paper No. 9, 2022) and design a hybrid approach: inside the no vacuum regions, we use the flux globalization based well-balanced central-upwind scheme, while elsewhere we implement the central-upwind scheme similar to the one proposed in Bollermann et al. (J Sci Comput 56:267–290, 2013) in the context of wet/dry fronts in the shallow water equations. The advantages of the proposed schemes are demonstrated on a number of challenging numerical examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The goal of this paper is to develop a highly accurate, robust and well-balanced (WB) finite-volume method for the one-dimensional (1-D) hydrodynamic equations with general free energy. The studied system reads as
where x is the spatial variable, t is the time, \(\rho =\rho (x,t)\) is the density, \(u=u(x,t)\) is the velocity, \(m(x,t)=\rho (x,t)u(x,t)\) is the momentum, \(P(\rho )\) is the pressure satisfying \(P(0)=0\) and \(P'(\rho )\ge 0\) for \(\rho \ge 0\) (typically, \(P(\rho )=\sigma \rho ^\nu \) with positive parameters \(\sigma \) and \(\nu \), which will be specified in numerical examples), and \(\gamma \ge 0\) is the damping coefficient. The potential term H(x, t) on the right-hands side (RHS) of (1.1) may contain the external field V as well as the interaction potential W (both V and W are assumed to be continuous), and in general it takes the following form:
Finally, \(\psi (x)\) is a nonnegative symmetric smooth function called the communication function in the Cucker–Smale model [2, 22] describing collective behavior of systems due to alignment [9]. Other applications of the system (1.1) and (1.2) include the Keller–Segel model of chemotaxis [5] and generalized Euler–Poisson systems [10]; it also arises in modeling of a wide variety of physical problems such as colloidal suspensions and polymers [24, 27, 28], relaxation dynamics of microscopic films [47] and capillary prewetting [48].
The system (1.1) and (1.2) is a hyperbolic system of balance laws. It is well-known that such systems may admit nonsmooth solutions even the initial data are smooth. This makes the development of numerical methods for (1.1) and (1.2) a challenging task. In addition, a good numerical method should be able to accurately respect a delicate balance between the flux and source terms in the second equation of (1.1). In particular, one is interested in developing WB numerical schemes, which are capable of preserving (some of) steady states of the studied system. The WB property is important as many of the physically relevant solutions of (1.1) and (1.2) are, in fact, small perturbations of the corresponding steady states.
In general, smooth steady-state solutions of (1.1) and (1.2) satisfy the following time-independent equations:
where the function \(\Pi (\rho )\) is such that
When \(m\ne 0\) and thus \(\rho \ne 0\), the steady states (1.3) can be rewritten in terms of the equilibrium variables m and E:
where
We note that there is a free-energy functional
associated with the system (1.1) and (1.2), and its variation with respect to the density \(\rho \) is
In the case when \(u\equiv 0\), the steady-state (1.3) can be written as
where the constant can vary on different connected components of \(\textrm{supp}(\rho )\).
When the damping coefficient \(\gamma =0\) and \(V(x)\equiv 0\) in (1.2), then another particular solution a good numerical scheme should be able to capture exactly is a traveling wave satisfying
where \(\rho _0(x)=\rho (x,0)\) is the initial datum.
It should be observed that if \(\,\Pi (\rho )=\frac{g}{2}\rho ^2\,\) with \(\rho \) being a water depth and g being the acceleration due to gravity, \(H(x)=V(x)\) with V(x) representing the bottom topography, \(\gamma =0\), and \(\psi \equiv 0\), then the system (1.1) and (1.2) becomes the Saint–Venant system of shallow water equations. In the past decades, many WB schemes for the Saint–Venant system have been developed. Some of them are capable of preserving still-water (“lake-at-rest”) steady-states only (see, e.g., [1, 3, 4, 25, 31, 37, 43]) and others can preserve moving-water equilibria as well (see, e.g., [15, 17, 18, 21, 39, 42, 46]). We also refer the reader to recent review papers on WB schemes for shallow water models [14, 33, 45].
First- and second-order WB schemes for the system (1.1) and (1.2) have been recently developed in [12]. These schemes are capable of exactly preserving motionless steady states (1.9) only and their WB property hinges on a special approximation of the discrete free energy functional and a special treatment of the source terms. High-order extensions of the schemes from [12] have been introduced in [7].
In this paper, we develop a WB scheme which is capable of exactly preserving general steady states (1.3) (including motionless steady states (1.9)) as well as accurately capturing traveling waves (1.10) at the discrete level. Our scheme is based on the flux globalization approach, which was introduced in [13, 20, 23, 26, 40] and has recently been applied to a variety of hyperbolic systems of balance laws in [6, 17, 19, 21, 34, 35]. We incorporate the source terms of the momentum equation into its flux and rewrite (1.1) in the following equivalent form:
where
is a global flux with
where \({\widehat{x}}\) is an arbitrary number. Notice that both steady states (1.5) and (1.9) can be written as
The system (1.11)–(1.13) is quasi-conservative and thus it can be solved in a rather straightforward way using a Riemann-problem-solver-free numerical method designed for hyperbolic systems of conservation laws. We follow [6, 17, 19,20,21, 34, 35] and use the semi-discrete finite-volume central-upwind (CU) scheme. More precisely, we use the technique recently introduced in [34] and design a new quadrature rule to approximate the global term given by (1.13). This allows us to develop a WB scheme capable of preserving both \(K\equiv \textrm{Const}\) and \(E\equiv \textrm{Const}\) (or (1.9) if the vacuum areas where \(\rho =0\) are present, which, according to [12], may occur when the parameter \(\nu >1\)), which are equivalent in the continuous case, but not equivalent in the discrete case. As demonstrated in [6, 34], preserving both discrete version of the steady states helps to preserve a wider variety of physically relevant steady states and thus to improve the stability property of the resulting scheme.
In addition, our new flux globalization based WB CU is able to accurately capture interfaces of the vacuum regions and near vacuum (\(\rho \approx 0\)) parts of the solution. This is achieved by following a hybrid approach recently introduced in [21]: inside the no vacuum regions, we use the flux globalization based CU scheme, while elsewhere we implement the CU scheme similar to the one proposed in [3] in the context of wet/dry fronts in the shallow water equations. The latter scheme is based on a special subcell finite-volume reconstruction of the equilibrium variable \(\zeta \) and a proper approximation of the source terms appearing on the RHS of (1.1). We prove that the resulting hybrid scheme is capable of exactly preserving the steady states (1.9) even in the presence of vacuum regions. We emphasize that the flux globalization based WB CU scheme from [6, 34] used inside the no vacuum regions is different from the one used in [21] and this makes it easier to treat the vacuum region interface and thus to design a reliable and robust hybrid scheme.
In order to stress the major differences between the proposed flux globalization based WB CU schemes and the existing WB CU schemes, we would like to emphasize the following two points. First, unlike the WB CU scheme from [21], our new scheme is capable of preserving both \(K\equiv \textrm{Const}\) and \(E\equiv \textrm{Const}\) discrete steady states. Second, unlike the WB CU schemes from [6, 34], our new scheme relies on a hybrid approach, which helps to capture the interfaces of the vacuum regions and near vacuum regions and thus to accurately capture solutions that contain such regions.
We finally turn our attention to traveling wave solutions (1.10). We proceed as in [32] and develop a moving framework approach. To this end, we modify the studied system (1.1) by adding a linear advection terms \(-u^*\rho _x\) and \(-u^*m_x\) to the left-hand side (LHS) of the \(\rho \)- and m- equations, respectively:
Here, \(u^*\) is a constant, which will be varied at every time step of the numerical discretization. Obviously, solutions of (1.14) are obtained from the corresponding solutions of (1.1) by the change of variables \(x\rightarrow x-u^*t\). The constant \(u^*\), however, provides us with an additional degree of freedom, which we choose in such a way that the traveling wave (1.10) reduces to motionless steady states in the introduced moving framework. We then apply the new flux globalization based WB CU scheme to the system (1.14).
The rest of the paper is organized as follows. In Sect. 2, we introduce a hybrid flux globalization based WB CU schemes. In Sect. 3, we test the proposed schemes on a variety of numerical examples and demonstrate their ability to compute numerical solutions of several models described by the hydrodynamic equations (1.1) and (1.2) in an accurate and robust manner.
2 Hybrid Flux Globalization Based WB CU Schemes
In this section, we introduce a hybrid flux globalization based WB CU scheme. To this end, we will discretize the system (1.11)–(1.13) in the no vacuum regions only, while elsewhere we will numerically solve the original system (1.1) and (1.2).
The computational domain is split into the finite-volume cells \(C_j=[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}]\) of size \(\Delta x\) centered at \(x_j=\big (x_{j-\frac{1}{2}}+x_{j+\frac{1}{2}}\big )/2\) with \(j=1,\ldots ,N\). We assume that at a certain time level t, the cell averages,

are available. Note that  like most of the index quantities below depends on t, but we omit this dependence for the sake of brevity. Following the approach proposed in [37] in the context of the Saint–Venant system with nonflat bottom topography, we replace the potential function H(x) defined in (1.2) with its continuous piecewise linear approximation
like most of the index quantities below depends on t, but we omit this dependence for the sake of brevity. Following the approach proposed in [37] in the context of the Saint–Venant system with nonflat bottom topography, we replace the potential function H(x) defined in (1.2) with its continuous piecewise linear approximation
where \(H_{j+\frac{1}{2}}:=H(x_{j+\frac{1}{2}})\), and the convolution integral in the computation of \(H(x_{j+\frac{1}{2}})\) is computed using the midpoint rule:

Here, \(V_{j+\frac{1}{2}}:=V(x_{j+\frac{1}{2}})\) and \(W_{i,{j+\frac{1}{2}}}:=W({x_i-x_{j+\frac{1}{2}}})\) in the case the interaction potential W is smooth, or \(W_{i,{j+\frac{1}{2}}}\) is an average value of W over the interval of length \(\Delta x\) centered at \(x_i-x_{j+\frac{1}{2}}\) in the case of general locally integrable potentials W. We then introduce the following notations:
As indicated in [7, 12], when \(\nu =1\), that is, in the isothermal case with \(P(\rho )=\sigma \rho \), the density does not develop vacuum regions during the temporal evolution, while when \(\nu >1\), vacuum regions can be generated. Therefore, in the case when \(\nu >1\), we identify the vacuum and no vacuum regions using the following definition.
Definition 2.1
We say that the cell \(C_j\) at time t is:
(i) vacuum if

where \(\varepsilon \) is a small positive number chosen in such a way that the magnitude of density present in the cell \(C_j\) can be considered as negligibly small according to the scales of the studied problem (in the numerical examples reported in Sect. 3, we have chosen \(\varepsilon =10^{-12}\));
(ii) semi-vacuum if

(iii) no vacuum if neither (2.4) nor (2.5) is satisfied.
Based on this definition, the computational domain may contain vacuum and/or near vacuum regions. In Fig. 1, we present a typical case of the steady state (1.9), which contains vacuum and no vacuum regions. This steady state will be referred to as a combined “vacuum–no vacuum” steady states. We assume that the cells are numbered as follows: cells \(C_{j_\ell },\ldots ,C_{j_r}\) are no vacuum, while cells \(C_j\) with \(j<j_\ell \) and \(j>j_r\) are either semi-vacuum or fully vacuum. Inside the no vacuum regions, \(\zeta _j\equiv \textrm{Const}\), while this is not, in general, true in the semi-vacuum and vacuum cells; see Fig. 1 and Sect. 2.2, where we design a special piecewise linear reconstruction of \(\zeta \), which preserves the steady states (1.9).
2.1 Flux Globalization Based WB CU Scheme in No Vacuum Regions
In this section, we introduce the flux globalization based WB CU scheme, which is a modified version of the scheme first developed in [34] and then extended in [6] to several shallow water models. We emphasize that this scheme is only implemented inside the no vacuum regions, which correspond to the cells \(C_{j_\ell +1},\ldots ,C_{j_r-1}\) in the setting shown in Fig. 1.
In the flux globalization based WB CU scheme the cell averages are evolved in time using the following semi-discretzation:

where \(\varvec{{{\mathcal {K}}}}_{j+\frac{1}{2}}=\left( {{\mathcal {K}}}^{(1)}_{j+\frac{1}{2}},\mathcal{K}^{(2)}_{j+\frac{1}{2}}\right) ^\top \) are the CU numerical fluxes from [36]:
Here, \(K_{j+\frac{1}{2}}^\pm \) are the one-sided point values of the global flux function (1.12), which are given by
where \({\varvec{U}}_{j+\frac{1}{2}}^\pm =\big (\rho _{j+\frac{1}{2}}^\pm ,m_{j+\frac{1}{2}}^\pm \big )^\top \) are the left/right-sided point values at the cell interface \(x=x_{j+\frac{1}{2}}\), which will be computed later. In (2.7), \(a^\pm _{j+\frac{1}{2}}\) are the one-sided local propagation speeds, which can be estimated using the eigenvalues of the Jacobian of the original system (1.1). The simplest estimate is
where \(u=m/\rho \) should be computed using a proper desingularization procedure. In the numerical experiments presented in Sect. 3, we have used
with the desingularization parameter \(\tau =10^{-6}\). For alternative desingularizations introduced in the context of shallow water models, we refer the reader, for instance, to [33, 37].
In order to apply the flux globalization based WB CU scheme from [6, 34], we begin with computing the point values of the equilibrium variable E at \(x=x_j\) out of the available cell averages  and
and  . We use formulae (1.6) and (1.7), and obtain
. We use formulae (1.6) and (1.7), and obtain

As it was done in [6], we first rewrite the expression of Q in (1.6) in a recursive way and then apply the trapezoidal rule to evaluate the global integral term \(Q_j\). Namely, we set
where

In order to use formula (2.11), we provide the starting value \(Q_{j_\ell }\), which is computed by taking \(\widehat{x}=x_{j_\ell -\frac{1}{2}}\) and applying the trapezoidal rule so that
where \(u_{j_\ell -\frac{1}{2}}\) and thus \(\Psi _{j_\ell -\frac{1}{2}}:=\Psi (x_{j_\ell -\frac{1}{2}})\) are determined based on the prescribed boundary conditions.
Equipped with  and \(\{E_j\}\), we obtain second-order piecewise linear reconstructions
and \(\{E_j\}\), we obtain second-order piecewise linear reconstructions

which are used to compute the one-sided point values \(m_{j+\frac{1}{2}}^\pm \) and \(E_{j+\frac{1}{2}}^\pm \) at the cell interfaces \(x=x_{j+\frac{1}{2}}\):

In (2.14) and (2.15), \((m_x)_j\) and \((E_x)_j\) are the slopes which should be computed using a nonlinear limiter to ensure a non-oscillatory nature of the piecewise linear reconstruction. In the numerical experiments reported in Sect. 3, we have used the generalized minmod limiter [38, 41, 44]

with \(\theta =1.3\), and the minmod function given by
After obtaining the left- and right-sided values \(m_{j+\frac{1}{2}}^\pm \) and \(E_{j+\frac{1}{2}}^\pm \), we compute the corresponding values of \(\rho \) by numerically solving the following nonlinear equations:
for \(\rho _{j+\frac{1}{2}}^+\) and \(\rho _{j+\frac{1}{2}}^-\), respectively. Here, \(Q_{j+\frac{1}{2}}\) is computed using the definition (1.6) and the midpoint quadrature, which result in
Details on solving the nonlinear equations in (2.17) are provided in Appendix 1.
Equipped with the reconstructed one-sided point values \(\rho _{j+\frac{1}{2}}^\pm \) and \(m_{j+\frac{1}{2}}^\pm \), we then follow the method in [6, 34] to compute \(R_{j+\frac{1}{2}}\):
However, there is a major difference between the computation in (2.18) and similar computations in [6, 34], where R was not assumed to be continuous at \(x=x_{j+\frac{1}{2}}\) and two values \(R_{j+\frac{1}{2}}^\pm \) were considered there. The difference between \(R_{j+\frac{1}{2}}^+\) and \(R_{j+\frac{1}{2}}^-\) was attributed to a jump in H at \(x=x_{j+\frac{1}{2}}\), which is not the case in this paper as H is assumed to be continuous, which justifies the use of the continuous piecewise linear interpolant in (2.1). In order to make the scheme WB, one needs to design a WB quadrature for \(B_j\) in (2.18). To this end, we first notice that the steady states of (1.11)–(1.13) satisfy
which is derived using (1.4), (1.6), and (1.7). We then follow the method introduced in [6, 34] and rewrite (2.19) in the following matrix form:
where
Next, we integrate (2.20) over the cell \(C_j\) to obtain
and then applying the trapezoidal rule to the last integral on the right results in
Finally, we substitute (2.20) and (2.21) into (2.22) and end up with
where \(P_{j+\frac{1}{2}}^-=P\big (\rho _{j+\frac{1}{2}}^-\big )\) and \(P_{j-\frac{1}{2}}^+=P\big (\rho _{j-\frac{1}{2}}^+\big )\).
At the end, we compute \(K_{j+\frac{1}{2}}^\pm \) using (2.8) and write down the semi-discrete flux globalization based WB CU scheme (2.6) and (2.7) inside the no vacuum regions:

where \({{\mathcal {K}}}^{(1)}_{j+\frac{1}{2}}\) and \({{\mathcal {K}}}^{(2)}_{j+\frac{1}{2}}\) are given by (2.7).
We now prove that in the no vacuum case, the flux globalization based WB CU scheme (2.24), (2.7) is WB in the sense that it is capable of exactly preserving the steady states (1.9) and (1.5).
Theorem 2.2
If there are no vacuum regions, that is, if  for all j and the discrete data are at a steady state, namely, if either
for all j and the discrete data are at a steady state, namely, if either

or

where \(E_j\) and \(u_j\) are given by (2.10), then the RHS of (2.24) will vanish. This implies that the designed flux globalization based scheme is WB.
Proof
If (2.25) is satisfied, then  and \(E_j\) given by (2.10) reduces to \(\zeta _j\) given by (1.8). We therefore only prove that the scheme is WB provided (2.26) is satisfied. As we perform the piecewise linear reconstruction (2.14), (2.16), we immediately conclude that in this case
and \(E_j\) given by (2.10) reduces to \(\zeta _j\) given by (1.8). We therefore only prove that the scheme is WB provided (2.26) is satisfied. As we perform the piecewise linear reconstruction (2.14), (2.16), we immediately conclude that in this case
Thus the nonlinear equations in (2.17) for \(\rho _{j+\frac{1}{2}}^+\) and \(\rho _{j+\frac{1}{2}}^-\) are identical and hence
Next, from (2.23), (2.27), and (2.28) we conclude that
We then use (2.8), (2.27), and (2.28) to compute
so that \(K_{j+\frac{1}{2}}^+-K_{j+\frac{1}{2}}^-=0\), and also, taking into account that \(u_{j\pm \frac{1}{2}}={\widehat{m}}/\rho _{j\pm \frac{1}{2}}\), we obtain
Finally, we substitute (2.27), (2.28), and (2.30) into (2.7) and (2.24) to obtain  and
and  for all j. This completes the proof of the theorem. \(\square \)
for all j. This completes the proof of the theorem. \(\square \)
Remark 2.3
In order to use (2.20)–(2.22) to derive a WB quadrature for \(B_j\) in (2.18), one needs to guarantee \(M(\varvec{U})\) is an invertible matrix, which is true for \(\rho >0\). However, in the presence of semi-vacuum and vacuum regions, where \(\rho \approx 0\), one cannot use (2.20)–(2.22) to compute \(B_j\), as the equilibrium variable E is not necessarily constant on the entire domain at the steady state. We therefore design a hybrid approach in Sect. 2.2.
Remark 2.4
As in [7, 12], we assume that H is continuous and only consider smooth steady states of several models, which can be described by the hydrodynamic equations with free energy. We note that if \(P(\rho )=\frac{g}{2}\rho ^2\) with \(\rho \) being a water depth and g being the acceleration due to gravity, \(H(x)=V(x)\) with V(x) representing the bottom topography, \(\gamma =0\), and \(\psi \equiv 0\), the studied system reduces to the Saint–Venant system of shallow water equations, which admits interesting discontinuous steady states. A possible way to design a scheme capable of exactly preserving some of the discontinuous steady states is by incorporating the path-conservative technique into the flux globalization approach (this has been done in [6, 34]).
2.2 WB CU Scheme in the Semi-Vacuum and Vacuum Regions
Unfortunately, the flux globalization based WB CU scheme described in Sect. 2.1 does not apply in the case when vacuum regions are present. This is attributed to the fact that E defined in (1.6) is constant at steady states in the no vacuum regions only. We therefore develop a special WB CU scheme for vacuum and/or semi-vacuum regions. First, we note that when \(\nu =1\), there are no vacuum regions, and therefore we only consider the case of \(\nu >1\), in which
Our goal is to design a WB scheme capable of preserving the steady states (1.9) with vacuum regions, similar to those sketched in Fig. 1. The scheme will be designed for the original studied system (1.1) and (1.2), which we rewrite in a vector form as
with
where \(\Psi \) is defined by (1.7). The semi-discretization of (2.32) and (2.33) results in the following system of time-dependent ODEs:

where \(\varvec{{{\mathcal {F}}}}_{j+\frac{1}{2}}\) are the numerical fluxes to be specified,  , and
, and

which needs to be computed using a special WB quadrature.
We follow the approach introduced in [3, 21] and proceed as follows. For simplicity of presentation, we will consider a special “vacuum–no vacuum” setting sketched in Fig. 1. A generalization for a general combination of vacuum and no vacuum regions will be quite obvious. First of all, in the semi-vacuum cells, we define the following continuous piecewise linear function:
where \(x_j^*\) is the location of the vacuum/no vacuum interface in the cell \(C_j\). Here, we assume that \({\widetilde{H}}'(x)<0\) in \(C_j\) as in Fig. 2 (left). The case \({\widetilde{H}}'(x)>0\), which corresponds to Fig. 2 (right), is treated in a similar symmetric way. As a result, using the definitions (1.8) and (2.31), the density function \(\rho _j(x)\) in the cell \(C_j\) has the following form:
The values \(x_j^*\) and \({\widehat{\zeta }}_j\) can be determined using the mass conservation requirement, which gives

where \(\Delta x_j^*:=x_{j+\frac{1}{2}}-x_j^*\). It then follows from (2.36) that

see Fig. 2 (left). From Fig. 1, it is clear that (2.37) is valid for \(j=j_\ell -1\). However, for \(j=j_r+1\), \((H_x)_{j_r+1}>0\) and thus we have

there; see Fig. 2 (right).
Equipped with the values \({\widehat{\zeta }}_{j_\ell -1}\) and \({\widehat{\zeta }}_{j_r+1}\), we proceed as in [21] and use the following piecewise linear reconstruction in the semi-vacuum and vacuum cells \(C_j\) with \(j\le j_\ell -1\) or \(j\ge j_r+1\) as well as in the no vacuum cells and \(C_{j_\ell }\) and \(C_{j_r}\), which have semi-vacuum or vacuum neighbors. Given  and
and  in those cells, we first compute the values
in those cells, we first compute the values  and
and  (the latter computation needs to be desingularized using a formula similar to (2.9)) and then perform the piecewise linear reconstruction (2.14)–(2.16) but applied to \(\zeta \) and u rather than E and m. This results in the one-sided point values, which we denote by \({\widetilde{\zeta }}_{j+\frac{1}{2}}^{\,\pm }\) and \(u_{j+\frac{1}{2}}^\pm \). Then, from formulae (1.8) and (2.31) we obtain \({\widetilde{\rho }}_{j+\frac{1}{2}}^{\,\pm }=\big [\frac{\nu -1}{\sigma \nu }({\widetilde{\zeta }}_{j+\frac{1}{2}}^{\,\pm }-H_{j+\frac{1}{2}})\big ]^{\frac{1}{\nu -1}}\). These point values of \(\rho \), however, may be unreliable and thus they should be modified before being used in the numerical flux evaluation. We proceed according to following algorithm.
(the latter computation needs to be desingularized using a formula similar to (2.9)) and then perform the piecewise linear reconstruction (2.14)–(2.16) but applied to \(\zeta \) and u rather than E and m. This results in the one-sided point values, which we denote by \({\widetilde{\zeta }}_{j+\frac{1}{2}}^{\,\pm }\) and \(u_{j+\frac{1}{2}}^\pm \). Then, from formulae (1.8) and (2.31) we obtain \({\widetilde{\rho }}_{j+\frac{1}{2}}^{\,\pm }=\big [\frac{\nu -1}{\sigma \nu }({\widetilde{\zeta }}_{j+\frac{1}{2}}^{\,\pm }-H_{j+\frac{1}{2}})\big ]^{\frac{1}{\nu -1}}\). These point values of \(\rho \), however, may be unreliable and thus they should be modified before being used in the numerical flux evaluation. We proceed according to following algorithm.
Algorithm 1
(Modified Reconstruction of \(\rho _{j+\frac{1}{2}}^\pm \))
-
Case 1 (
 and
and  ): Vacuum does not occur.
): Vacuum does not occur.-
Case 1A \((\,\widetilde{\zeta }_{j-\frac{1}{2}}^{\,+}\ge H_{j-\frac{1}{2}}\) and \(\,\widetilde{\zeta }_{j+\frac{1}{2}}^{\,-}\ge H_{j+\frac{1}{2}}):\) No correction is needed and we set
$$\begin{aligned} \rho _{j+\frac{1}{2}}^\pm =\,\widetilde{\rho }_{j+\frac{1}{2}}^{\,\pm }. \end{aligned}$$ -
Case 1B \((\,\widetilde{\zeta }_{j-\frac{1}{2}}^{\,+}<H_{j-\frac{1}{2}}\) or \(\,\widetilde{\zeta }_{j+\frac{1}{2}}^{\,-}<H_{j+\frac{1}{2}}):\) We make the following corrections:
if \(\,\widetilde{\zeta }_{j+\frac{1}{2}}^{\,-}<H_{j+\frac{1}{2}}\), then we set

if \(\,\widetilde{\zeta }_{j-\frac{1}{2}}^{\,+}<H_{j-\frac{1}{2}}\), then we set

-
-
Case 2 (
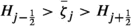 ): Semi-vacuum as in Fig. 2 (left).
): Semi-vacuum as in Fig. 2 (left).-
Case 2A (the neighboring cell \(C_{j+1}\) satisfies Case 1A): We set
$$\begin{aligned} \zeta _{j+\frac{1}{2}}^-=\zeta _{j+\frac{1}{2}}^+\quad \text{ and }\quad \rho _{j+\frac{1}{2}}^-= \left[ \frac{\nu -1}{\sigma \nu }\left( \zeta _{j+\frac{1}{2}}^--H_{j+\frac{1}{2}}\right) \right] ^{\frac{1}{\nu -1}}. \end{aligned}$$-
Case 2A1 (
 ): We set
): We set  .
. -
Case 2A2 (
 ): We set \(\rho _{j-\frac{1}{2}}^+=0\).
): We set \(\rho _{j-\frac{1}{2}}^+=0\).
-
-
Case 2B (the neighboring cell \(C_{j+1}\) does not satisfy Case 1A): In this case, the semi-vacuum cell \(C_{j+1}\) does not have a reliable reconstructed linear piece of \(\zeta \); see Fig. 3. We therefore perform the piecewise linear reconstructions (2.14)–(2.16) applied to the variable \(\rho \) to obtain

We note that this part is a modification of the algorithm in [21, §3.1]. The robustness of the new approach is demosntrated in the numerical examples reported in Sect. 3.
-
-
Case 3 (
 ): Semi-vacuum cell as in Fig. 2 (right).
): Semi-vacuum cell as in Fig. 2 (right).This case is analogous to Case 2.
Sketch of Case 2B in Algorithm 1
Equipped with the one-sided point values \(\rho _{j+\frac{1}{2}}^\pm \) and \(u_{j+\frac{1}{2}}^\pm \), we obtain \(m_{j+\frac{1}{2}}^\pm =\rho _{j+\frac{1}{2}}^\pm u_{j+\frac{1}{2}}^\pm \), and then following the approach in [3, §4], we write down the CU numerical fluxes in (2.34):
where
In order to make the resulting scheme WB, we approximate the cell average of the source term (2.35) using the following WB (see the proof of Theorem 2.6 below) quadrature:

where

In order to preserve the aforementioned combined “vacuum–no vacuum” steady states, we develop a hybrid approach: inside the no vacuum regions, namely, in the cells \(C_{j_\ell +1},\ldots ,C_{j_r-1}\) as plotted in Fig. 1, we use the flux globalization based WB CU scheme (Sect. 2.1) for the equivalent system (1.11)–(1.13). Outside of these regions, we utilize the CU scheme (Sect. 2.2) for the original system (1.1) and (1.2). The resulting hybrid scheme is WB provided the one-sided reconstructed point values coincide at the interfaces between these areas (these interfaces are marked by the red dashed line in Fig. 1). If the discrete data satisfy (1.9), we immediately have \(m_{j_{\ell }+\frac{1}{2}}^-=m_{j_{\ell }+\frac{1}{2}}^+=0\) and \(m_{j_r-\frac{1}{2}}^-=m_{j_r-\frac{1}{2}}^+=0\), which imply \(E_{j_{\ell }+\frac{1}{2}}^\pm =\zeta _{j_{\ell }+\frac{1}{2}}^\pm \) and \(E_{j_r-\frac{1}{2}}^\pm =\zeta _{j_r-\frac{1}{2}}^\pm \), and hence \(\rho _{j_{\ell }+\frac{1}{2}}^-=\rho _{j_{\ell }+\frac{1}{2}}^+\) and \(\rho _{j_r-\frac{1}{2}}^-=\rho _{j_r-\frac{1}{2}}^+\).
Remark 2.5
Due to the presence of vacuum regions, one needs to ensure that the proposed hybrid scheme has the positivity-preserving property. We achieve this goal with the help of the “draining time step” technique, which was introduced in [4].
We now prove that the use of the numerical fluxes (2.38) and (2.39) and the source terms approximation (2.40)–(2.41) leads to a WB scheme in the vacuum and semi-vacuum regions.
Theorem 2.6
Assume that the discrete data are at a combined “vacuum–no vacuum” steady state, namely, the discrete data satisfy the following relations:

for all \(j\,(\)see Fig. 1), where \(\zeta ^*\) is a constant. Then, the proposed CU scheme (2.34), (2.38)–(2.41) is WB.
Proof
In order to prove this theorem, we need to show that the RHS of (2.34) vanishes for \(j\le j_\ell \) and \(j\ge j_r\) as long as the data satisfy (2.42).
First, we note that in the vacuum cells \(C_j\) (\(j<j_\ell -1\) or \(j>j_r+1\)) the RHS of (2.34) vanishes since in those cells  and
and  .
.
We then note that in all of the considered cells, \(m_{j+\frac{1}{2}}^\pm =u_{j+\frac{1}{2}}^\pm =0\) and \(\Psi _j=0\), and hence (2.38) and (2.39) reduce to
Next, we consider the first no vacuum cell \(C_{j_\ell }\) (the last no vacuum cell \(C_{j_r}\) is treated similarly), in which \(\zeta _{j_{\ell }-\frac{1}{2}}^\pm =\zeta _{j_{\ell }+\frac{1}{2}}^\pm =\zeta ^*\), and hence using Algorithm 1 we obtain that \(\rho _{j_{\ell }-\frac{1}{2}}^\pm =\rho _{j_{\ell }-\frac{1}{2}}\) and \(\rho _{j_{\ell }+\frac{1}{2}}^\pm =\rho _{j_{\ell }+\frac{1}{2}}\). This implies
At the same time, the source term approximation (2.40)–(2.41) becomes

where
which can be substituted into (2.45) to obtain

We then use (2.44) and (2.46) to verify that the RHS of (2.34) vanishes.
Finally we consider the semi-vacuum cell \(C_{j_\ell -1}\) (the cell \(C_{j_r+1}\) is treated similarly), where \(\rho _{j_\ell -\frac{3}{2}}^\pm =0\) and \(\rho _{j_\ell -\frac{1}{2}}^\pm =\rho _{j_\ell -\frac{1}{2}}\), which is substituted into (2.43) to obtain
At the same time, the source term approximation (2.40)–(2.41) becomes

Therefore, according to (2.34), (2.38)–(2.41), in order to complete the proof of the theorem, we need to show that

Indeed, since \({\widehat{\zeta }}_{j_\ell -1}=\zeta _{j_{\ell }-\frac{1}{2}}^-=\zeta ^*\), and since

we obtain by equating the RHS of (2.50) and (2.51) and then using (2.52) that

Finally, we substitute (2.52) into (2.48) and obtain (2.49). This completes the proof of the theorem. \(\square \)
Remark 2.7
As shown in Theorems 2.2 and 2.6, the proposed CU scheme is designed to exactly preserve particular discrete versions of the steady states (2.25), (2.26), and (2.42). This is due to the fact that in (2.2), (2.11), (2.12), and (2.13), we have used particular quadratures to approximate the point values used in the evaluation of the discrete steady states to be preserved. Therefore, when the WB property is experimentally verified, the initial data should be prepared so that they will satisfy the corresponding discrete steady states. This will be further explained in Examples 4 and 10.
2.3 Capturing Traveling Waves
In this section, we consider the system (1.1) and (1.2) with \(\gamma =0\) and \(V(x)\equiv 0\) and we are concerned with improving the quality of the resolution of computed traveling wave solutions (1.10). To this end, we modify the hybrid flux globalization based WB CU scheme presented in Sects. 2.1 and 2.2 by applying the moving framework approach from [32]. To this end, we numerically solve the modified system (1.14), which can be rewritten as
Here,
where \(u^*\) is a constant being computed at every time step in the following way:
In order to apply the flux globalization approach to the system (2.53), we first incorporate the source terms into the flux and end up with the following quasi-conservative system:
where
is a global flux with the global variable
We then use the flux globalization based WB CU scheme presented in Sect. 2.1 to numerically solve the system (2.56)–(2.58) from a certain time level t to the next time level \(t+\Delta t\), where \(\Delta t\) is an adaptive time step being computed by (3.2) below. Once the numerical solutions  and
and  are obtained, we shift all spatial grid mesh cells \(C_j\) centered at \(x_j\) to the new locations centered at \(x_j+u^*\Delta t\), and prescribe the obtained solutions on the shifted cells. Finally, we compute the velocities \(u_j={\mathfrak {u}}_j+u^*\) by (2.54), and this completes one time step of the resulting method.
are obtained, we shift all spatial grid mesh cells \(C_j\) centered at \(x_j\) to the new locations centered at \(x_j+u^*\Delta t\), and prescribe the obtained solutions on the shifted cells. Finally, we compute the velocities \(u_j={\mathfrak {u}}_j+u^*\) by (2.54), and this completes one time step of the resulting method.
We note that the traveling wave solutions (1.10) corresponds to the motionless steady-state solution of (2.56)–(2.58):
As the flux globalization based WB CU scheme proposed in Sect. 2.1 is capable of preserving these steady states, it is also capable of exactly capturing the traveling waves (1.10). This makes our scheme superior to its counterparts in [7, 12], where the magnitude of traveling waves was affected by numerical diffusion.
Remark 2.8
In this section, no vacuum or semi-vacuum cells are taken into account. When vacuum or semi-vacuum regions emerge, we will use the WB CU schemes introduced in Sect. 2.2 to numerically solve the system (2.53) in those areas. In addition, we will compute \(u^*\) using a modified version of (2.55), which takes into account no vacuum velocity values only. For instance, in the situation that corresponds to the “vacuum–no vacuum” setting sketched in Fig. 1, we will take
Notice that since the proposed hybrid flux globalization based WB CU schemes are able to preserve the combined “vacuum–no vacuum” steady states, the traveling wave solutions with vacuum or semi-vacuum regions can also be captured exactly.
3 Numerical Examples
In this section, we demonstrate the performance of the proposed hybrid flux globalization based WB CU scheme on a number of numerical examples. In all of them, unless specified differently, we set \(\sigma =1\) and use the homogeneous Neumann boundary conditions for \(\rho \) and homogeneous Dirichlet boundary conditions for m, namely, we use the following ghost cell values:

Furthermore, the damping coefficient \(\gamma =0\) in Examples 4, 5, 8, and 9, while the linear damping term is present in the rest of the numerical examples: \(\gamma =0.001\) in Example 1, \(\gamma =1\) in Examples 2, 3, and 7 (Test 1–4), \(\gamma =0.05\) in Example 7 (Test 5), and \(\gamma =0.01\) in Examples 6 and 10. The communication function \(\psi (x)\equiv 0\) in Examples 2, 3, 7, and 9, while the Cucker–Smale damping term with
is used in Examples 1, 4–6, 8, and 10.
We have integrated the ODE systems (2.6) and (2.34) using the three-stage third-order strong stability preserving (SSP) Runge-Kutta method (see, e.g., [29, 30]) with a time step computed at every time level using the CFL number 1/2, namely, by taking
3.1 Example 1: Accuracy Test
In the first example, which is a modification of an accuracy test used in [6, 18], we verify the experimental rate of convergence. To this end, we take \(P(\rho )=\rho ^2\), \(V(x)=\sin ^2(\pi x)\), \(W(x)\equiv 0\), and the following initial data:
prescribed in the computational domain [0, 1] subject to the 1-periodic boundary conditions. We compute the solutions at the final time \(t=0.1\) by the proposed hybrid WB CU scheme on a sequence of uniform meshes with \(\Delta x=1/100\), 1/200, 1/400, 1/800, and 1/1600 and obtain the reference solution using the same scheme but on a much finer uniform mesh with \(\Delta x=1/12800\). We then calculate the \(L^1\)-errors and the experimental rates of convergence for both \(\rho \) and m. The obtained results are summarized in Table 1. As one can clearly see, the proposed scheme achieves the expected second order of accuracy.
3.2 Well-Balanced Property Validation: Motionless Steady States
In this section, we study three numerical examples. We first consider two examples taken from [12], in which the initial data correspond to the motionless steady states (1.9), the external field \(V(x)=\frac{1}{2}x^2\) and the interaction potential \(W(x)\equiv 0\). We then consider an example with the initial condition satisfying (1.9) at the continuous level only and with the external field \(V(x)\equiv 0\) and the interaction potential \(W(x)=\frac{1}{2}x^2\).
3.2.1 Example 2: Motionless Steady State Without Vacuum Regions
In the second example, we take \(P(\rho )=\rho \) and the following initial conditions:
It is easy to verify that this initial setting satisfies the steady-state condition (1.9) and its discrete version (2.25).
We use \(N=100\) uniform cells in the computational domain \(\Omega =[-5,5]\) and run the simulations until the final time \(t=20\). The discrete \(L^1\)- and \(L^\infty \)-errors are reported in Table 2. As one can see, both the proposed hybrid flux globalization based WB CU scheme and the scheme developed in [12], which will be referred to as the CKPS scheme from here on, can preserve the steady-state solution within the machine error.
3.2.2 Example 3: Motionless Steady State with Vacuum Regions and Its Small Perturbation
In the third example, we take \(P(\rho )=\rho ^2\), which supports the vacuum regions. We consider the following initial conditions:
prescribed in the computational domain \([-5,5]\). We first run the simulations with \(N=100\) uniform cells until the final time \(t=20\) and compute the discrete \(L^1\)- and \(L^\infty \)-errors, reported in Table 3. As one can see, both the hybrid flux globalization based WB CU scheme and the CKPS scheme are capable of preserving the steady state even in the presence of vacuum regions.
We then test the ability of the proposed scheme to capture small perturbations of steady states. To this end, we modify \(\rho (x,0)\) in the initial data in (3.4) by adding a small perturbation. The modified initial condition is
We compute the numerical solutions at three different times \(t=0.5\), 2.5 and 4 using both coarse and fine uniform meshes with \(N=100\) and \(N=1000\). The differences \(\rho (x,t)-\rho _{\textrm{eq}}(x)\) are plotted in Fig. 4, where the results computed by the hybrid flux globalization based WB CU scheme and the CKPS scheme from [12] are compared with those computed using the CU scheme from [36], which is non-well-balanced (NWB) when directly applied to the studied system (1.1) and (1.2). As one can see in the top row of Fig. 4, when the coarse mesh is used, the solutions computed by the WB CU and CKPS schemes are very similar, whereas the solution computed by the NWB CU scheme is very different. When the mesh is refined (see the bottom row of Fig. 4), they seem to converge to the same solution and we can see that the initial perturbation first splits into two waves propagating in the opposite directions, which later merge into one wave due to the influence of the potential term. This suggests that the use of a NWB scheme leads to the appearance of nonphysical waves (which are large when the mesh is coarse and are still visible in the fine NWB solution at the early time \(t=0.5\)) and emphasizes the importance of the WB property possessed by the proposed flux globalization based WB CU scheme. In addition, both the WB CU and CKPS schemes are capable of exactly preserving the motionless steady states (1.9) and hence their results are very close on both the coarse and fine meshes.
3.2.3 Example 4: Convergence to Motionless Steady State
In the fourth example, we consider the same pressure function, the same initial conditions (3.3) as in Example 2, but different \(V(x)\equiv 0\) and \(W(x)=\frac{1}{2}x^2\). Our goal is to show that it is essential to prepare discrete steady-state data in order to verify the WB property of studied schemes. We first take the initial cell averages

which are not at a discrete steady state as they do not satisfy (2.25). We then use the proposed hybrid WB CU and CKPS schemes to compute the numerical solutions until the final time \(t=10\) on \(N=200\) uniform cells. The obtained discrete \(L^1\)- and \(L^\infty \)-errors, that is, the norms of the differences  and
and  are reported in Table 4. As one can clearly see, neither of the two studied schemes can preserve the steady state within the machine error since the initial data are not prepared and the values \(\zeta _j\) are not initially constant.
are reported in Table 4. As one can clearly see, neither of the two studied schemes can preserve the steady state within the machine error since the initial data are not prepared and the values \(\zeta _j\) are not initially constant.
It should be pointed out that it is a nontrivial task to construct prepared initial conditions mentioned in Remark 2.7. We therefore run the simulations again with the same initial data (3.5) but until a longer time \(t=60\) and report the differences  and
and  in Table 5. As one can see, the errors in \(\rho \) are about the same as at the time \(t=10\), while the errors in m decay to the machine error.
in Table 5. As one can see, the errors in \(\rho \) are about the same as at the time \(t=10\), while the errors in m decay to the machine error.
In addition, at every time step we compute the \(L^1\)-norm of the differences in \(\rho \) and m between the current solution and the solution at the previous time step. From the obtained results shown in Fig. 5 (left and middle), one can clearly see that by the final time the discrete steady states have been already reached by both of the two studied schemes. In Fig. 5 (right), we plot the obtained discrete steady-state densities, which are almost the same. Finally, we use these discrete densities, which can be considered as “prepared” steady-state densities, and  as initial data and repeat the simulation until the final time \(t=10\) to test the WB property of the studied schemes. As expected, both of them can exactly preserve the discrete steady state (2.25) within the machine error; see Table 6, where we compute the differences between the numerical solutions at the final time \(t=10\) and the “prepared” initial data, and compare them with the results reported in Tables 4 and 5.
as initial data and repeat the simulation until the final time \(t=10\) to test the WB property of the studied schemes. As expected, both of them can exactly preserve the discrete steady state (2.25) within the machine error; see Table 6, where we compute the differences between the numerical solutions at the final time \(t=10\) and the “prepared” initial data, and compare them with the results reported in Tables 4 and 5.
3.3 Applications to Various Free Energy Models
In this section, we apply the proposed hybrid flux globalization based WB CU scheme to a variety of models with different choices of the free energy. For most of these models analytical results are limited. The examples considered in this section are taken from [7, 12].
3.3.1 Example 5: Model with the Cucker–Smale Damping Term and Attractive Potential
In the fifth example, we consider the model with the Cucker–Smale damping term, no linear damping and attractive potential (\(H(x)=V(x)=\frac{1}{2}x^2\)). We take \(P(\rho )=\rho \) and consider the following initial data:
prescribed in the computational domain \(\Omega =[-5,5]\). We compute the numerical solutions at two intermediate times \(t=0.7\) and 2, and a large final time \(t=15\) using \(N=50\), 200, and 1000 uniform cells and plot the obtained results (\(\rho \), m, and \(\zeta \)) in Fig. 6. Our coarse mesh (\(N=50\)) results seem to be in a good agreement with those reported in [12, Example 3.2], where a finer mesh with \(N=200\) was used. When we refine the mesh the solution becomes much shaper as it develops kinks in \(\rho \) and \(\zeta \), and a jump discontinuity in m at \(x=0\) at an intermediate time \(t=2\). One can also observe some kinks at a smaller time \(t=0.7\). This type of the solution behavior may be attributed to the lack of linear damping term. Finally, by the very large final time \(t=15\), the solution has almost converged to the steady state with \(m\equiv 0\), \(\zeta \equiv \textrm{Const}\).
3.3.2 Example 6: Model with the Cucker–Smale Damping Term and Attractive Kernel
In the sixth example, we consider the same pressure function and the same initial conditions as in Example 5, but we now take \(H(x)=W(x)*\rho \) with the interaction potential \(W(x)=\frac{1}{2}x^2\). We compute the numerical solutions at two intermediate times \(t=2.5\) and 5, and a large final time \(t=75\) using \(N=200\) uniform cells and plot the obtained results in Fig. 7 (top row). Since the presence of linear damping term (although with a small coefficient), the results, especially the density and momentum fields, have quite smaller oscillations than those observed in Example 5.
Compared with the results reported in [12, Example 3.3], our numerical solution seems to faster converge to the steady state; compare the solutions at \(t=5\) in Fig. 7 and [12, Figure 3]. In order to numerically investigate whether the faster convergence results are correct, we refine the mesh and repeat the computation using \(N=1000\) uniform cells. The results are reported in Fig. 7 (bottom row), where one can see that our fine mesh solution is very close to our coarse mesh solution. This suggests that the convergence dynamics computed by the proposed hybrid flux globalization based WB CU scheme is quite accurate.
3.3.3 Example 7: Hydrodynamic Generalization of the Keller–Segel System
In the seventh example, we consider the hydrodynamic extension of the Keller–Segel model proposed in [16] and takes into account the inertia of the biological entities. In this model, the potential \(H(x)=W(x)*\rho \) and we consider different kernels W and different pressure functions \(P(\rho )=\sigma \rho ^\nu \). In Tests 1–4, we use the homogeneous kernels \(W(x)=|x|^{\alpha }/\alpha \), where \(\alpha >-1\) as introduced in [8], where by convention we set \(W(x)=\ln |x|\) for \(\alpha =0\). In Test 5, we use the Morse-type potential as in [11] with \(W(x)=-e^{-|x|^2/2}/2\pi \). For the studied generalized Keller–Segel model there are three possible regimes depending on \(\alpha \) and \(\nu \) (see [8]): diffusion dominated \((\nu >1-\alpha )\), balanced \((\nu =1-\alpha )\) in which a critical mass separates self-similar and blow-up behavior, and aggregation-dominated \((\nu <1-\alpha )\) regimes.
Test 1 We first take \(W(x)=2\sqrt{|x|}\) and \(P(\rho )=\rho ^{\frac{3}{2}}\), which correspond to the diffusion-dominated regime. We consider the following initial conditions:
prescribed in the computational domain \(\Omega =[-8,8]\). We compute the numerical solution at two intermediate times \(t=3.7\) and 11, and a large final time \(t=70\) using \(N=200\) uniform cells and plot the obtained results (\(\rho \), m, and \(\zeta \)) in Fig. 8. As one can see, the solution approaches to a compactly supported steady state. As expected, at the steady state the variation of the free energy with respect to the density \(\rho \) has a constant value only within the support of the density. We note that our results are in good agreement with those reported in [12, Example 3.8] though as in Example 6 our solution seems to converge to the steady state somewhat faster; see the solution at time \(t=11\) in Fig. 8 and [12, Figure 8].
Test 2 We then take a singular interaction potential \(W(x)=\ln |x|\) and \(P(\rho )=3\rho ^{\frac{5}{2}}\) (this setting also corresponds to the diffusion-dominated regime). The initial data,
are prescribed in the computational domain \(\Omega =[-8,8]\). We compute the numerical solution at times \(t=10\), 20, and a large final time \(t=250\) using \(N=200\) uniform cells and plot the obtained results (\(\rho \), m, and \(\zeta \)) in Fig. 9. We observe that the final compactly-supported density profiles have slightly different shapes due to the balances between the attraction from the local kernel W(x) and the repulsion caused by the diffusion of the pressure \(P(\rho )\). Comparing the obtained results with their counterparts reported in [7, Figure 3.9], we observe that the solution computed by our scheme converges to the steady state much faster. As one can see, at \(t=10\) the density component of our solution is closer to the steady-state density profile while the momentum is larger than the one reported in [7, Figure 3.9], which indicates faster convergence. At a later time \(t=20\), our solution is already almost at the steady state, which once again indicates much faster convergence. These results are confirmed by the mesh refinement study not reported here for the sake of brevity.
Test 3 Next, we take the same singular interaction potential \(W(x)=\ln |x|\), but the linear pressure \(P(\rho )=\rho \). This scenario corresponds to the balanced regime, and there is a critical mass separating the global-in-time from the finite-time blowup solutions. We consider the following initial data:
where \(M_0\) is the total mass of the system. We take \(M_0=0.1\), which is relatively small and is expected to lead to the global-in-time solution.
We set the computational domain \(\Omega =[-8,8]\) and use \(N=200\) uniform cells to compute the numerical solutions at times \(t=5\), 15, and 60. The obtained results (\(\rho \), m, and \(\zeta \)) are shown in Fig. 10, where the numerical solution is clearly global-in-time and diffusion-dominated. By the time \(t=60\), the solution is already almost at discrete steady state, which is unlike the steady density reported in [7, Figure 3.7(a)] is not uniform. This can be clearly seen in Fig. 11, where we plot the numerical solution at even larger time \(t=200\) using \(N=200\) and 1000 uniform cells—these solutions are already at the discrete steady state and the density is clearly nonuniform.
Test 4 For the next simulation, we select a larger total mass \(M_0=3\) while keeping the same other settings as in Test 3. In this case, the total mass is above the critical one and the solution (\(\rho \)) is expected to blow up within a finite time as supported by our numerical results presented in Figs. 12–14. First, in Fig. 12, we show that the solutions computed using three different meshes with \(N=51\), 201, and 801 uniform cells at times \(t=3\), 6, and 7.5. One can observe the aggregation phenomenon as the mass concentrates near \(x=0\). One can also see that the obtained solutions have not reached the discrete steady state as both m and \(\zeta \) are far from being uniform at \(t=7.5\). We note that though qualitatively \(\rho \) in Fig. 12 behaves similarly to the density reported in [7, Figure 3.8], the aggregation in our simulations seems to occur faster and by the time \(t=7.5\) our solution is already close to the blowup as the maximum of \(\rho \) grows roughly by a factor of 4 at every mesh refinement (notice that when \(\delta \)-functions are represented using the finite-volume uniform cell approximation their magnitude are expected to be proportional to \(1/\Delta x\)).
We then perform a careful numerical blowup investigation. We begin with computing the behavior of the maximum of \(\rho \) as a function of time using four consecutive meshes with \(N=51\), 201, 801, and 3201. The obtained results are reported in Fig. 13 (left), where one can clearly see that the maxima of all of the four discrete solutions keep to increase. In order to more accurately predict the blowup time, we also plot the ratio \(||\rho ^{4N-3}||_\infty /||\rho ^N||_\infty \) as well as the maximum and minimum of m as functions of time for different N in the middle and right panels of Fig. 13. The \(||\rho ^{4N-3}||_\infty /||\rho ^N||_\infty \) curves clearly approach 4 but the blowup time cannot be predicted with a high accuracy just from this graph. We note that at post-blowup times the computed solution may lose its symmetry and may exhibit a nonregular behavior. Indeed, we can see this in Fig. 13 (left) as the maximum of \(\rho \) computed on the finest mesh with \(N=3201\) starts oscillating after about \(t=14\), which means that the blowup has already occurred by then. As an additional blowup indicator, we consider the behavior of the maximum and minimum of m for different N as function of time; see Fig. 13 (right). In fact, the maximum and minimum curves are supposed to be symmetric with respect to the line \(m=0\). One can see that this is the case at pre-blowup times, but after the blowup occurs the symmetry is lost and the magnitude of m starts increasing. This gives us an indication that the blowup time is about \(t=10\). Finally, in Fig. 14, we show \(\rho \) computed at the time \(t=10\) using \(N=51\), 201, and 801 uniform cells, and the blowup can be clearly seen in this figure.
Test 5 In the final test, we consider a Morse-type potential \(W(x)=-e^{-|x|^2/2}/\sqrt{2\pi }\), for which the attraction between two bumps of density separated at a considerable distance is quite weak. However, when enough time has passed and the bumps get closer, they merge in an exponentially fast pace due to the convexity of the Gaussian potential, and a new equilibrium is reached with just one bump. The interesting fact about this system is therefore the existence of two timescales: the time to get the bumps of density close enough, which could be very slow, and the time to merge the bumps, which is exponentially fast in time.
In order to verify that the proposed hybrid flux globalization based WB CU scheme can capture this type of solution behavior, we use the setting from [12, Example 3.8 with Morse-type potential] and consider the initial density containing three bumps. In particular, the initial data,
are prescribed in the computational domain \(\Omega =[-8,12]\). We take the pressure function \(P(\rho )=\rho ^3\) and compute the numerical solutions using \(N=200\) uniform cells at times \(t=100\) and 270, and a large final time \(t=3000\). The obtained results are depicted in Fig. 15. As one can see, first the two central bumps of density merge after some time, and then the third bump, with less mass, starts getting closer until it also blends. Notice that compared with the results reported in [12, Figure 10] the evolution process is substantially faster in our computations. This can also be seen in the evolution of \(\zeta \), whose initial profile is very complicated, but eventually it converges to a simple steady state with constant value on the compact support of \(\rho \). One can observe that unlike the solution reported in [12, Figure 10(c)], \(\zeta \) is already near its steady state at the time \(t=270\).
3.4 Traveling Wave
In this section, we demonstrate the ability of the hybrid flux globalization based WB CU scheme to accurately capture a traveling wave and its small perturbation.
3.4.1 Example 8: Traveling Wave and Its Small Perturbation
In the eighth example, we first demonstrate that the proposed hybrid flux globalization based WB CU scheme can capture the traveling wave solution (1.10) exactly. We take \(W(x)=\frac{1}{2}x^2\) and \(P(\rho )=\rho \). Our goal is to capture the traveling wave solution given by
We prescribe the initial data  and \(u_j(0)\equiv 0.2\) on the interval \([-5,5]\). We run the simulation using \(N=200\) uniform cells until the final time \(t=30\). The obtained results are plotted in Fig. 16. As one can see, the exact density profile is simply advected to the right with the constant velocity u, and \(\zeta \) is also kept constant. This is confirmed by the \(L^1\)- and \(L^\infty \)-errors reported in Table 7, where one can clearly see that the proposed hybrid WB CU scheme is capable of accurately capturing the traveling wave within the machine error. Notice that the computational domain translates in time as explained in Sect. 2.3, and at the final time \(t=30\) the domain is [1, 11]. We also point out that the CKPS scheme fails to maintain constant u and \(\zeta \); see [12, Example 3.5].
and \(u_j(0)\equiv 0.2\) on the interval \([-5,5]\). We run the simulation using \(N=200\) uniform cells until the final time \(t=30\). The obtained results are plotted in Fig. 16. As one can see, the exact density profile is simply advected to the right with the constant velocity u, and \(\zeta \) is also kept constant. This is confirmed by the \(L^1\)- and \(L^\infty \)-errors reported in Table 7, where one can clearly see that the proposed hybrid WB CU scheme is capable of accurately capturing the traveling wave within the machine error. Notice that the computational domain translates in time as explained in Sect. 2.3, and at the final time \(t=30\) the domain is [1, 11]. We also point out that the CKPS scheme fails to maintain constant u and \(\zeta \); see [12, Example 3.5].
We then use the same initial velocity while add a small perturbation of size \(10^{-3}\) in the interval \([-2.25,-2]\) to the initial discrete density profile as it was done in Example 4, and compute the numerical solutions by the hybrid flux globalization based WB CU scheme and the NWB CU scheme at three different times \(t=0.5\), 1.5, and 3 using both \(N=100\) and 1000 uniform cells. The differences between the computed and background densities are plotted in Fig. 17. As one can clearly see, the hybrid flux globalization based WB CU scheme is capable of capturing the small perturbation without generating unphysical waves both on the coarse and fine meshes. At the same time, the NWB CU scheme produces large unphysical waves when the coarse mesh is used. Even though the magnitude of these waves significantly reduces when the mesh is refined, the advantage of the proposed hybrid flux globalization based WB CU scheme over its simpler counterpart seems to be obvious.
Example 8: The difference between the computed and the background densities computed at times \(t=0.5\) (left column), \(t=1.5\) (middle column), and \(t=3.0\) (right column) using the hybrid flux globalization based WB CU and NWB CU schemes with \(N=100\) (top row) and 1000 (bottom row) uniform cells
3.5 Well-Balanced Property Validation: Moving Steady States
In this section, our goal is to demonstrate that the proposed hybrid flux globalization based WB CU scheme is capable of exactly preserving the moving steady states (1.5) with \(\widehat{m}\ne 0\) and accurately capturing their small perturbation. We would like to point out that in the two examples considered in this section (Examples 9 and 10), we only test by the proposed hybrid WB CU scheme and do not compare it with the CKPS scheme, since the latter scheme cannot preserve moving steady states.
3.5.1 Example 9: Simple Moving Steady State
In the ninth example, we take \(P(\rho )=2\rho ^{\frac{3}{2}}\), \(W(x)\equiv 0\), and
The initial data are given in terms of m and E:
which are prescribed in the computational domain \([-2,2]\) and satisfy (1.5). Clearly, the corresponding discrete initial data,  and \(E_j(0)\equiv 20\), satisfy (2.26). The initial values
and \(E_j(0)\equiv 20\), satisfy (2.26). The initial values  can then be obtained by numerically solving equations (2.10), which, since in this example \(\gamma =0\) and \(W(x)=\psi (x)\equiv 0\), reduce to the following algebraic equations:
can then be obtained by numerically solving equations (2.10), which, since in this example \(\gamma =0\) and \(W(x)=\psi (x)\equiv 0\), reduce to the following algebraic equations:

We first set the free boundary conditions and apply the proposed WB CU scheme to compute the solution at \(t=10\), 30, and 50 using \(N=400\) uniform cells and observe that the errors in both m and E, that is, the norms of the differences  and \(\{E_j(t)-E_j(0)\}_{j=1}^N\) remain very small in this long-time simulations; see Table 8.
and \(\{E_j(t)-E_j(0)\}_{j=1}^N\) remain very small in this long-time simulations; see Table 8.
We then modify the initial data by adding a small perturbation of size \(10^{-3}\) to the cell averages of the steady-state density in the interval \([-0.1,0.1]\) and compute the numerical solutions on two uniform meshes with \(N=400\) and 4000 cells at three times \(t=0.05\), 0.1, and 0.2. The differences \(\rho (x,t)-\rho _{\textrm{eq}}(x)\), where \(\rho _{\textrm{eq}}(x)\) is the background steady-state density, are plotted in Fig. 18, where one can clearly see that the proposed hybrid flux globalization based WB CU scheme accurately captures small perturbations of the studied steady state.
3.5.2 Example 10: Convergence to Moving Steady State
First, we would like to point out that when \(\psi (x)\ne 0\) and either \(\gamma \ne 0\) or \(W(x)\ne 0\), it is hard to analytically obtain the steady-state solutions as it was done in a simpler case in Example 9. Therefore, in the final example, we proceed as in Example 4, namely, we first study the convergence towards a moving steady state.
We take \(\gamma =0.01\), \(P(\rho )=\rho ^{\frac{5}{2}}\), \(W(x)=xe^{-10x^2}\), and
We consider the following initial data:
which are prescribed in the computational domain \([-2,2]\), and set the following Dirichlet boundary conditions:
We compute the numerical solution by the hybrid flux globalization based WB CU scheme using \(N=100\) uniform cells until the final time \(t=150\). By this time, the solution converges to a moving steady state as can be clearly seen in Fig. 19.
We then use the obtained discrete steady-state solutions plotted in Fig. 19 as initial data and run the simulations until the final time \(t=5\). We compute the discrete \(L^1\)- and \(L^\infty \)-errors in m and E, and report the results in Table 9. As one can see, the errors are very small.
Finally, we add a small perturbation to the density of the obtained discrete steady-state solution, which we denote by \(\rho _\textrm{eq}(x)\), and consider the following initial data:
subject to the homogeneous Neumann boundary conditions. We compute the numerical solutions by the hybrid flux globalization based WB CU scheme at times \(t=0.01\), 0.05, and 0.1 using \(N=100\) and 500 uniform cells and plot the obtained results in Fig. 20. As one can observe, both the low- and high-resolution results are oscillation-free and the propagating perturbation is well captured by the proposed scheme.
Data availability
The data that support the findings of this study and FORTRAN codes developed by the authors and used to obtain all of the presented numerical results are available from the corresponding author upon reasonable request.
References
Audusse, E., Bouchut, F., Bristeau, M.-O., Klein, R., Perthame, B.: A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 25, 2050–2065 (2004)
Barbaro, A.B.T., Cañizo, J.A., Carrillo, J.A., Degond, P.: Phase transitions in a kinetic flocking model of Cucker–Smale type. Multiscale Model. Simul. 14, 1063–1088 (2016)
Bollermann, A., Chen, G., Kurganov, A., Noelle, S.: A well-balanced reconstruction of wet/dry fronts for the shallow water equations. J. Sci. Comput. 56, 267–290 (2013)
Bollermann, A., Noelle, S., Lukáčová-Medvidová, M.: Finite volume evolution Galerkin methods for the shallow water equations with dry beds. Commun. Comput. Phys. 10, 371–404 (2011)
Calvez, V., Carrillo, J.A., Hoffmann, F.: Equilibria of homogeneous functionals in the fair-competition regime. Nonlinear Anal. 159, 85–128 (2017)
Cao, Y., Kurganov, A., Liu, Y., Xin, R.: Flux globalization based well-balanced path-conservative central-upwind schemes for shallow water models. J. Sci. Comput. 92. Paper No. 69 (2022)
Carrillo, J.A., Castro, M.J., Kalliadasis, S., Perez, S.P.: High-order well-balanced finite-volume schemes for hydrodynamic equations with nonlocal free energy. SIAM J. Sci. Comput. 43, A828–A858 (2021)
Carrillo, J.A., Chertock, A., Huang, Y.: A finite-volume method for nonlinear nonlocal equations with a gradient flow structure. Commun. Comput. Phys. 17, 233–258 (2015)
Carrillo, J.A., Choi, Y.-P., Tadmor, E., Tan, C.: Critical thresholds in 1D Euler equations with non-local forces. Math. Models Methods Appl. Sci. 26, 185–206 (2016)
Carrillo, J.A., Choi, Y.-P., Zatorska, E.: On the pressureless damped Euler–Poisson equations with quadratic confinement: critical thresholds and large-time behavior. Math. Models Methods Appl. Sci. 26, 2311–2340 (2016)
Carrillo, J.A., Huang, Y., Martin, S.: Explicit flock solutions for Quasi–Morse potentials. Eur. J. Appl. Math. 25, 553–578 (2014)
Carrillo, J.A., Kalliadasis, S., Perez, S.P., Shu, C.-W.: Well-balanced finite-volume schemes for hydrodynamic equations with general free energy. Multiscale Model. Simul. 18, 502–541 (2020)
Caselles, V., Donat, R., Haro, G.: Flux-gradient and source-term balancing for certain high resolution shock-capturing schemes. Comput. Fluids 38, 16–36 (2009)
Castro, M.J., Morales de Luna, T., Parés, C.: Well-balanced schemes and path-conservative numerical methods. In: Xing, Y. (ed.) Handbook of Numerical Methods for Hyperbolic Problems, vol. 18 of Handbook of Numerical Analysis, pp. 131–175. Elsevier, Amsterdam (2017)
Castro, M.J., Pardo Milanés, A., Parés, C.: Well-balanced numerical schemes based on a generalized hydrostatic reconstruction technique. Math. Models Methods Appl. Sci. 17, 2055–2113 (2007)
Chavanis, P.H., Sire, C.: Kinetic and hydrodynamic models of chemotactic aggregation. Phys. A 384, 199–222 (2007)
Cheng, Y., Chertock, A., Herty, M., Kurganov, A., Wu, T.: A new approach for designing moving-water equilibria preserving schemes for the shallow water equations. J. Sci. Comput. 80, 538–554 (2019)
Cheng, Y., Kurganov, A.: Moving-water equilibria preserving central-upwind schemes for the shallow water equations. Commun. Math. Sci. 14, 1643–1663 (2016)
Chertock, A., Cui, S., Kurganov, A., Özcan, ŞN., Tadmor, E.: Well-balanced schemes for the Euler equations with gravitation: conservative formulation using global fluxes. J. Comput. Phys. 358, 36–52 (2018)
Chertock, A., Herty, M., Özcan, Ş.N.: Well-balanced central-upwind schemes for \(2\,\times \,2\) systems of balance laws. In: Klingenberg, C., Westdickenberg, M. (eds.) Theory, Numerics and Applications of Hyperbolic Problems I, vol. 236 of Springer Proceedings in Mathematics & Statistics, pp. 345–361. Springer, Berlin (2018)
Chertock, A., Kurganov, A., Liu, X., Liu, Y., Wu, T.: Well-balancing via flux globalization: applications to shallow water equations with wet/dry fronts. J. Sci. Comput. 90. Paper No. 9 (2022)
Cucker, F., Smale, S.: Emergent behavior in flocks. IEEE Trans. Autom. Control 52, 852–862 (2007)
Donat, D., Martinez-Gavara, A.: Hybrid second order schemes for scalar balance laws. J. Sci. Comput. 48, 52–69 (2011)
Durán-Olivencia, M.A., Goddard, B.D., Kalliadasis, S.: Dynamical density functional theory for orientable colloids including inertia and hydrodynamic interactions. J. Stat. Phys. 164, 785–809 (2016)
Fjordholm, U.S., Mishra, S., Tadmor, E.: Well-balanced and energy stable schemes for the shallow water equations with discontinuous topography. J. Comput. Phys. 230, 5587–5609 (2011)
Gascón, L., Corderán, J.M.: Construction of second-order TVD schemes for nonhomogeneous hyperbolic conservation laws. J. Comput. Phys. 172, 261–297 (2001)
Goddard, B.D., Nold, A., Savva, N., Pavliotis, G.A., Kalliadasis, S.: General dynamical density functional theory for classical fluids. Phys. Rev. Lett. 109, 120603 (2012)
Goddard, B.D., Pavliotis, G.A., Kalliadasis, S.: The overdamped limit of dynamic density functional theory: rigorous results. Multiscale Model. Simul. 10, 633–663 (2012)
Gottlieb, S., Ketcheson, D., Shu, C.-W.: Strong Stability Preserving Runge–Kutta and Multistep Time Discretizations. World Scientific Publishing Co Pte. Ltd., Hackensack (2011)
Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability-preserving high-order time discretization methods. SIAM Rev. 43, 89–112 (2001)
Jin, S., Wen, X.: Two interface-type numerical methods for computing hyperbolic systems with geometrical source terms having concentrations. SIAM J. Sci. Comput. 26, 2079–2101 (2005)
Kliakhandler, I., Kurganov, A.: Quasi-Lagrangian acceleration of Eulerian methods. Commun. Comput. Phys. 6, 743–757 (2009)
Kurganov, A.: Finite-volume schemes for shallow-water equations. Acta Numer. 27, 289–351 (2018)
Kurganov, A., Liu, Y., Xin, R.: Well-balanced path-conservative central-upwind schemes based on flux globalization. J. Comput. Phys. 474, Paper No. 111773 (2023)
Kurganov, A., Liu, Y., Zeitlin, V.: A well-balanced central-upwind scheme for the thermal rotating shallow water equations. J. Comput. Phys. 411, Paper No. 109414 (2020)
Kurganov, A., Noelle, S., Petrova, G.: Semi-discrete central-upwind schemes for hyperbolic conservation laws and Hamilton–Jacobi equations. SIAM J. Sci. Comput. 23, 707–740 (2001)
Kurganov, A., Petrova, G.: A second-order well-balanced positivity preserving central-upwind scheme for the Saint–Venant system. Commun. Math. Sci. 5, 133–160 (2007)
Lie, K.-A., Noelle, S.: On the artificial compression method for second-order nonoscillatory central difference schemes for systems of conservation laws. SIAM J. Sci. Comput. 24, 1157–1174 (2003)
Liu, X., Chen, X., Jin, S., Kurganov, A., Yu, H.: Moving-water equilibria preserving partial relaxation scheme for the Saint–Venant system. SIAM J. Sci. Comput. 42, A2206–A2229 (2020)
Martinez-Gavara, A., Donat, R.: A hybrid second order scheme for shallow water flows. J. Sci. Comput. 48, 241–257 (2011)
Nessyahu, H., Tadmor, E.: Nonoscillatory central differencing for hyperbolic conservation laws. J. Comput. Phys. 87, 408–463 (1990)
Noelle, S., Xing, Y., Shu, C.-W.: High-order well-balanced finite volume WENO schemes for shallow water equation with moving water. J. Comput. Phys. 226, 29–58 (2007)
Ricchiuto, M.: An explicit residual based approach for shallow water flows. J. Comput. Phys. 280, 306–344 (2015)
Sweby, P.K.: High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Anal. 21, 995–1011 (1984)
Xing, Y.: Numerical methods for the nonlinear shallow water equations. In: Abgrall, R., Shu, C.-W. (eds.) Handbook of Numerical Methods for Hyperbolic Problems, vol. 18 of Handbook of Numerical Analysis, pp. 361–384. Elsevier, Amsterdam (2017)
Xing, Y., Shu, C.-W.: A survey of high order schemes for the shallow water equations. J. Math. Study 47, 221–249 (2014)
Yatsyshin, P., Savva, N., Kalliadasis, S.: Spectral methods for the equations of classical density-functional theory: relaxation dynamics of microscopic films. J. Chem. Phys. 136, 124113 (2012)
Yatsyshin, P., Savva, N., Kalliadasis, S.: Geometry-induced phase transition in fluids: capillary prewetting. Phys. Rev. E 87, 020402 (2013)
Funding
Open access funding provided by University of Zurich The work of A. Kurganov was supported in part by NSFC Grants 12111530004 and 12171226, and by the fund of the Guangdong Provincial Key Laboratory of Computational Science and Material Design (No. 2019B030301001). The work of Y. Liu was supported in part by SNF Grants 200020_204917 and FZEB-0-166980.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Solving the Nonlinear Algebraic Equations in (2.17)
A Solving the Nonlinear Algebraic Equations in (2.17)
In this appendix, we describe how to solve the nonlinear equations in (2.17) using Newton’s method.
We first rewrite (2.17) as
Given the point values \(H_{j+\frac{1}{2}}\), \(Q_{j+\frac{1}{2}}\) and the one-sided point values \(m_{j+\frac{1}{2}}^\pm \), \(E_{j+\frac{1}{2}}^\pm \), we numerically solve equations (A.1) and (A.2) for \(\rho ^+_{j+\frac{1}{2}}\) and \(\rho ^-_{j+\frac{1}{2}}\), respectively, following the lines of [34]. Here, we describe how to solve (A.1) only and the solution of (A.2) can be obtained in a similar way.
If \(m_{j+\frac{1}{2}}^+=0\), then (A.1) admits a unique positive solution
Otherwise, the solution of (A.1) may not be unique. A physically relevant solution will then be chosen using the Mach number, which is defined as

(when we solve (A.2), the Mach number will be given by  ). It is easy to check that if \({{\mathcal {M}}}_{j+\frac{1}{2}}^+=1\), which corresponds to the sonic case, then the function \(\Phi (\rho )\) vanishes precisely at the point of its local minimum \(\rho _0^+\), namely, at
). It is easy to check that if \({{\mathcal {M}}}_{j+\frac{1}{2}}^+=1\), which corresponds to the sonic case, then the function \(\Phi (\rho )\) vanishes precisely at the point of its local minimum \(\rho _0^+\), namely, at
If \({{\mathcal {M}}}_{j+\frac{1}{2}}^+>1\) (\({{\mathcal {M}}}_{j+\frac{1}{2}}^+<1\)), that is, in the supersonic (subsonic) case, we use Newton’s method to obtain the numerical solutions of (A.1). To this end, one needs to have a proper initial guess \(\rho ^*\). We look for \(\rho ^*\) in the domain where \(\Phi (\rho )\) is convex, that is, in
Moreover, if \({{\mathcal {M}}}_{j+\frac{1}{2}}^+>1\), then we need to take \(\rho ^*<\rho _0^+\). Thus, one can take
and if \(\nu \ge 2\), we must ensure that \(\Phi (\rho ^*)>0\). If \(\mathcal{M}_{j+\frac{1}{2}}^+<1\), then we need to take \(\rho ^*>\rho _0^+\) and to ensure that \(\Phi (\rho ^*)>0\).
Finally, we provide the reader with the detailed algorithm for finding a proper initial guess \(\rho ^*\).
Algorithm A.1
( Selecting \(\rho ^*\))
Choose \(\delta >0\), \(\lambda _1\in (0,1)\) and \(\lambda _2>1\).
-
If \(\mathcal{M}_{j+\frac{1}{2}}^+>1\) (supersonic case), then:
-
1. If \(\nu =1\), take \(\rho ^*=\rho ^+_1\);
-
2. If \(1<\nu <2\), take \(\rho ^*=\rho ^+_2\);
-
3. If \(\nu \ge 2\), then:
-
Step I. Set
 ;
; -
Step II. Compute \(\Phi (\rho ^*)\);
-
Step III. If \(\Phi (\rho ^*)<\delta \), then set \(\rho ^*=\lambda _1\rho ^*\) and go back to Step II.
-
-
-
If \(\mathcal{M}_{j+\frac{1}{2}}^+<1\) (subsonic case), then:
-
Step I. Set
 ;
; -
Step II. Compute \(\Phi (\rho ^*)\);
-
Step III. If \(\Phi (\rho ^*)<\delta \), set \(\rho ^*=\lambda _2\rho ^*\) and go back to Step II.
-
Remark A.1
In all of our numerical experiments, we have used \(\delta =10^{-4}\), \(\lambda _1=0.9\) and \(\lambda _2=1.1\).
Remark A.2
When Eq. (A.2) is solved,  in Step I of Algorithm 1 should be replaced with
in Step I of Algorithm 1 should be replaced with  .
.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, X., Kurganov, A. & Liu, Y. Flux Globalization Based Well-Balanced Central-Upwind Schemes for Hydrodynamic Equations with General Free Energy. J Sci Comput 95, 95 (2023). https://doi.org/10.1007/s10915-023-02221-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-023-02221-6
Keywords
- Hydrodynamic equations with general free energy
- Well-balanced schemes
- Flux globalization
- Central-upwind schemes
- Vacuum regions




 and
and  ): Vacuum does not occur.
): Vacuum does not occur.

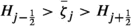 ): Semi-vacuum as in Fig.
): Semi-vacuum as in Fig.  ): We set
): We set  .
. ): We set
): We set 
 ): Semi-vacuum cell as in Fig.
): Semi-vacuum cell as in Fig. 

















 ;
; ;
;