Skip to main content
SpringerLink
Log in

Bound-preserving Flux Limiting for High-Order Explicit Runge–Kutta Time Discretizations of Hyperbolic Conservation Laws

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

We introduce a general framework for enforcing local or global maximum principles in high-order space-time discretizations of a scalar hyperbolic conservation law. We begin with sufficient conditions for a space discretization to be bound preserving (BP) and satisfy a semi-discrete maximum principle. Next, we propose a global monolithic convex (GMC) flux limiter which has the structure of a flux-corrected transport (FCT) algorithm but is applicable to spatial semi-discretizations and ensures the BP property of the fully discrete scheme for strong stability preserving (SSP) Runge–Kutta time discretizations. To circumvent the order barrier for SSP time integrators, we constrain the intermediate stages and/or the final stage of a general high-order RK method using GMC-type limiters. In this work, our theoretical and numerical studies are restricted to explicit schemes which are provably BP for sufficiently small time steps. The new GMC limiting framework offers the possibility of relaxing the bounds of inequality constraints to achieve higher accuracy at the cost of more stringent time step restrictions. The ability of the presented limiters to recognize undershoots/overshoots, as well as smooth solutions, is verified numerically for three representative RK methods combined with weighted essentially nonoscillatory (WENO) finite volume space discretizations of linear and nonlinear test problems in 1D. In this context, we enforce global bounds and prove preservation of accuracy for the linear advection equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data Availability

The code to reproduce the datasets (in all tables) is available at https://github.com/manuel-quezada/BP_Lim_for_RK_Methods.

References

  1. Boris, J.P., Book, D.L.: Flux-corrected transport: I. SHASTA, a fluid transport algorithm that works. J. Comput. Phys. 11, 38–69 (1973)

    Article  Google Scholar 

  2. Zalesak, S.T.: Fully multidimensional flux-corrected transport algorithms for fluids. J. Comput. Phys. 31, 335–362 (1979)

    Article  MathSciNet  Google Scholar 

  3. Harten, A.: High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 49, 357–393 (1983)

    Article  MathSciNet  Google Scholar 

  4. Harten, A.: On a class of high resolution total-variation-stable finite-difference-schemes. SIAM J. Numer. Anal. 21, 1–23 (1984)

    Article  MathSciNet  Google Scholar 

  5. Gottlieb, S., Ketcheson, D., Shu, C.-W.: Strong Stability Preserving Runge-Kutta and Multistep Time Discretizations. World Scientific, Singapore (2011)

    Book  Google Scholar 

  6. Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability-preserving high-order time discretization methods. SIAM Rev. 43, 89–112 (2001)

  7. Zhang, X., Shu, C.-W.: Maximum-principle-satisfying and positivity-preserving high-order schemes for conservation laws: survey and new developments. Proc. Royal Soc. A: Math. Phys. Eng. Sci. 467, 2752–2776 (2011)

  8. Hundsdorfer, W., Ketcheson, D.I., Savostianov, I.: Error analysis of explicit partitioned Runge–Kutta schemes for conservation laws. J. Sci. Comput. 63, 633–653 (2015)

  9. Ketcheson, D.I., MacDonald, C.B., Ruuth, S.J.: Spatially partitioned embedded Runge–Kutta methods. SIAM J. Numer. Anal. 51, 2887–2910 (2013)

  10. Kuzmin, D., Quezada de Luna, M., Kees, C.: A partition of unity approach to adaptivity and limiting in continuous finite element methods. Computers Math. Appl. 78, 944–957 (2019)

  11. Arbogast, T., Huang, C.-S., Zhao, X., King, D.N.: A third order, implicit, finite volume, adaptive Runge-Kutta WENO scheme for advection-diffusion equations. Computer Methods Appl. Mech. Engrg. 368, 113155 (2020)

  12. Duraisamy, K., Baeder, K., Liu, J.-G.: Concepts and application of time-limiters to high resolution schemes. J. of Sci. Comput. 19, 139–162 (2003)

    Article  MathSciNet  Google Scholar 

  13. Feng, D., Neuweiler, I., Nackenhorst, U., Wick, T.: A time-space flux-corrected transport finite element formulation for solving multi-dimensional advection-diffusion-reaction equations. J. Comput. Phys. 396, 31–53 (2019)

  14. Lee, J.-L., Bleck, R., MacDonald, A.E.: A multistep flux-corrected transport scheme. J. Comput. Phys. 229, 9284–9298 (2010)

    Article  Google Scholar 

  15. Lohmann, C., Kuzmin, D., Shadid, J.N., Mabuza, S.: Flux-corrected transport algorithms for continuous Galerkin methods based on high order Bernstein finite elements. J. Comput. Phys. 344, 151–186 (2017)

    Article  MathSciNet  Google Scholar 

  16. Xiong, T., Qiu, J.-M., Zhengfu, X.: High order maximum-principle-preserving discontinuous Galerkin method for convection-diffusion equations. SIAM J. Sci. Comput. 37(2), A583–A608 (2015)

    Article  MathSciNet  Google Scholar 

  17. Yang, P., Xiong, T., Qiu, J.-M., Zhengfu, X.: High order maximum principle preserving finite volume method for convection-dominated problems. J. of Sci. Comput. 67(2), 795–820 (2016)

    Article  MathSciNet  Google Scholar 

  18. Xiong, T., Qiu, J.M., Xu, Z.: A parametrized maximum principle preserving flux limiter for finite difference RK-WENO schemes with applications in incompressible flows. J. Comput. Phys. 252, 310–331 (2013)

    Article  MathSciNet  Google Scholar 

  19. Zhengfu, X.: Parametrized maximum principle preserving flux limiters for high order schemes solving hyperbolic conservation laws: one-dimensional scalar problem. Math. Comput. 83–289, 2213–2238 (2014)

    MathSciNet  MATH  Google Scholar 

  20. Kuzmin, D.: Monolithic convex limiting for continuous finite element discretizations of hyperbolic conservation laws. Comput. Methods Appl. Mech. Engrg. 361, 112804 (2020)

    Article  MathSciNet  Google Scholar 

  21. Anderson, R., Dobrev, V., Kolev, T., Kuzmin, D., Quezada de Luna, M., Rieben, R., Tomov, V.: High-order local maximum principle preserving (MPP) discontinuous Galerkin finite element method for the transport equation. J. Comput. Phys. 334, 102–124 (2017)

    Article  MathSciNet  Google Scholar 

  22. Hajduk, H.: Monolithic convex limiting in discontinuous Galerkin discretizations of hyperbolic conservation laws. Preprint arXiv:2007.01212 [math.NA] (2020)

  23. Kuzmin, D., Hajduk, H., Rupp, A.: Limiter-based entropy stabilization of semi-discrete and fully discrete schemes for nonlinear hyperbolic problems. Preprint arXiv:2107.11283 [math.NA], July (2021)

  24. Kuzmin, D., Quezada de Luna, M.: Entropy conservation property and entropy stabilization of high-order continuous Galerkin approximations to scalar conservation laws. Computers Fluids 213, 104742 (2020)

    Article  MathSciNet  Google Scholar 

  25. LeVeque, R.J.: Finite Volume Methods for Hyperbolic Problems. Cambridge University Press, Cambridge (2002)

    Book  Google Scholar 

  26. Guermond, J.-L., Popov, B.: Invariant domains and first-order continuous finite element approximation for hyperbolic systems. SIAM J. Numer. Anal. 54, 2466–2489 (2016)

    Article  MathSciNet  Google Scholar 

  27. Hu, X.Y., Adams, N.A., Shu, C.-W.: Positivity-preserving method for high-order conservative schemes solving compressible Euler equations. J. Comput. Phys. 242, 169–180 (2013)

    Article  MathSciNet  Google Scholar 

  28. Zhang, X., Shu, C.-W.: On positivity-preserving high order discontinuous Galerkin schemes for compressible Euler equations on rectangular meshes. J. Comput. Phys. 229, 8918–8934 (2010)

    Article  MathSciNet  Google Scholar 

  29. Deimling, K.: Ordinary Differential Equations in Banach Spaces, vol. 596. Springer, Berlin (2006)

    MATH  Google Scholar 

  30. Blanchini, F.: Set invariance in control. Automatica 35(11), 1747–1767 (1999)

    Article  MathSciNet  Google Scholar 

  31. Horváth, Z.: Invariant cones and polyhedra for dynamical systems. In: In Proceeding of the International Conference in Memoriam Gyula Farkas, pp. 65–74 (2005)

  32. Jameson, A.: Computational algorithms for aerodynamic analysis and design. Appl. Numer. Math. 13, 383–422 (1993)

    Article  MathSciNet  Google Scholar 

  33. Jameson, A.: Positive schemes and shock modelling for compressible flows. Int. J. Numer. Methods Fluids 20, 743–776 (1995)

    Article  MathSciNet  Google Scholar 

  34. Cotter, C.J., Kuzmin, D.: Embedded discontinuous Galerkin transport schemes with localised limiters. J. Comput. Phys. 311, 363–373 (2016)

    Article  MathSciNet  Google Scholar 

  35. Guermond, J.-L., Nazarov, M., Popov, B., Tomas, I.: Second-order invariant domain preserving approximation of the Euler equations using convex limiting. SIAM J. Sci. Comput. 40, A3211–A3239 (2018)

    Article  MathSciNet  Google Scholar 

  36. Kuzmin, D.: A new perspective on flux and slope limiting in discontinuous Galerkin methods for hyperbolic conservation laws. Comput. Methods Appl. Mech. Engrg. 373, 113569 (2021)

    Article  MathSciNet  Google Scholar 

  37. Hairer, E., Norsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I: Nonstiff Problems, 2nd edn. Springer, Berlin (1993)

    MATH  Google Scholar 

  38. Barth, T., Jespersen, D.C.: The design and application of upwind schemes on unstructured meshes. AIAA Paper, 89-0366 (1989)

  39. Shu, C.-W.: High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. 51, 82–126 (2009)

    Article  MathSciNet  Google Scholar 

  40. Guermond, J.-L., Pasquetti, R., Popov, B.: Entropy viscosity method for nonlinear conservation laws. J. Comput. Phys. 230, 4248–4267 (2011)

    Article  MathSciNet  Google Scholar 

  41. Kurganov, A., Tadmor, E.: New high-resolution central schemes for nonlinear conservation laws and convection-diffusion equations. J. Comput. Phys. 160, 241–282 (2000)

    Article  MathSciNet  Google Scholar 

  42. Kurganov, A., Petrova, G., Popov, B.: Adaptive semidiscrete central-upwind schemes for nonconvex hyperbolic conservation laws. SIAM J. Sci. Comput. 29, 2381–2401 (2007)

    Article  MathSciNet  Google Scholar 

  43. Ern, A., Guermond, J.-L.: Weighting the edge stabilization. SIAM J. Numer. Anal. 51, 1655–1677 (2013)

    Article  MathSciNet  Google Scholar 

  44. Kuzmin, D.: Entropy stabilization and property-preserving limiters for \(P_1\) discontinuous Galerkin discretizations of scalar hyperbolic problems. J. Numer. Math. (2020). https://doi.org/10.1515/jnma-2020-0056

    Article  Google Scholar 

  45. Kuzmin, D., Quezada de Luna, M.: Algebraic entropy fixes and convex limiting for continuous finite element discretizations of scalar hyperbolic conservation laws. Comput. Methods Appl. Mech. Engrg. 372, 113370 (2020)

    Article  MathSciNet  Google Scholar 

  46. Lohmann, C.: Physics-Compatible Finite Element Methods for Scalar and Tensorial Advection Problems. Springer Spektrum, Berlin (2019)

    Book  Google Scholar 

  47. Kraaijevanger, J.F.B.M.: Contractivity of Runge–Kutta methods. BIT 31, 482–528 (1991)

    Article  MathSciNet  Google Scholar 

  48. Spiteri, R.J., Ruuth, S.J.: A new class of optimal high-order strong stability-preserving time discretization methods. SIAM J. Numer. Anal. 40, 469–491 (2002)

    Article  MathSciNet  Google Scholar 

  49. Butcher, J.C.: On Runge–Kutta processes of high order. J. Australian Math. Soc. 4–2, 179–194 (1964)

    Article  MathSciNet  Google Scholar 

Download references

Funding

The work of Dmitri Kuzmin and Johanna Grüll was supported by the German Research Association (DFG) under Grant KU 1530/23-1. The work of Manuel Quezada de Luna and David I. Ketcheson was funded by King Abdullah University of Science and Technology (KAUST) in Thuwal, Saudi Arabia.

Author information

Authors and Affiliations

  1. Institute of Applied Mathematics (LS III), TU Dortmund University, Vogelpothsweg 87, D-44227, Dortmund, Germany

    Dmitri Kuzmin & Johanna Grüll

  2. King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia

    Manuel Quezada de Luna & David I. Ketcheson

Authors
  1. Dmitri Kuzmin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Manuel Quezada de Luna
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. David I. Ketcheson
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Johanna Grüll
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Manuel Quezada de Luna.

Ethics declarations

Conflict of interest

The authors declare that they have no known conflicts of interest, competing interests or personal relationships that could have appeared to influence the work reported in this paper.

Code Availability

The code to reproduce the numerical experiments is available at https://github.com/manuel-quezada/BP_Lim_for_RK_Methods.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A. High-Order Baseline RK Methods

Appendix A. High-Order Baseline RK Methods

In this appendix, we provide details of the three high-order explicit baseline RK methods for solving

$$\begin{aligned} \frac{\mathrm d u_i}{\mathrm d t} = F_i({\hat{u}}):=-\frac{1}{|K_i|}\sum _{j\in {\mathcal {N}}_i}|S_{ij}|H_{ij}({\hat{u}}). \end{aligned}$$
(A.1)

1.1 Appendix A.1. Fourth-Order Strong Stability Preserving (SSP54) RK Method

The SSP-RK time integrator that we consider in this work is the 4th-order method proposed in [47, 48]. The Butcher form of its intermediate stages is as follows:

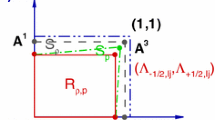
$$\begin{aligned}&y^{(1)} = u^n + 0.391752226571890\varDelta t F(u^n), \\&\quad y^{(2)} = 0.444370493651235u^n + 0.555629506348765 y^{(1)}\\&\qquad \quad +0.368410593050371\varDelta t F(y^{(1)}), \\&\quad y^{(3)} = 0.620101851488403 u^n + 0.379898148511597 y^{(2)}\\&\qquad \quad + 0.251891774271694\varDelta tF(y^{(2)}), \\&\quad y^{(4)} = 0.178079954393132 u^n + 0.821920045606868 y^{(3)}\\&\qquad \quad + 0.544974750228521 \varDelta t F(y^{(3)}), \\&\quad y^{(5)} = 0.517231671970585 y^{(2)} + 0.096059710526147 y^{(3)} \\&\qquad \quad + 0.063692468666290 \varDelta t F(y^{(3)}) \\&\quad + 0.386708617503269 y^{(4)} + 0.226007483236906 \varDelta t F(y^{(4)}). \end{aligned}$$

Note that each stage is a convex combination of Euler steps. Therefore, if \(F(\cdot )\) is a BP spatial discretization and \(u^n\) is BP, then each stage is BP under appropriate time step restrictions. The RK update is given by \(u^{n+1} = y^{(5)}\). Hence, if the stages are BP, \(u^{n+1}\) is BP and no extra limiting is needed.

1.2 Appendix A.2. Fifth-Order Extrapolated Euler (ExE-RK5) RK Method

The Butcher tableau of the 5th-order extrapolated Euler RK method is given by

$$\begin{aligned} \begin{array}{c|ccccccccccc} 0 &{} 0 &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ 1/2 &{} 1/2 &{} 0 &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ 1/3 &{} 1/3 &{} 0 &{} 0 &{} &{} &{} &{} &{} &{} &{} &{} \\ 2/3 &{} 1/3 &{} 0 &{} 1/3 &{} 0 &{} &{} &{} &{} &{} &{} &{} \\ 1/4 &{} 1/4 &{} 0 &{} 0 &{} 0 &{} 0 &{} &{} &{} &{} &{} &{} \\ 1/2 &{} 1/4 &{} 0 &{} 0 &{} 0 &{} 1/4 &{} 0 &{} &{} &{} &{} &{} \\ 3/4 &{} 1/4 &{} 0 &{} 0 &{} 0 &{} 1/4 &{} 1/4 &{} 0 &{} &{} &{} &{} \\ 1/5 &{} 1/5 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} &{} &{} \\ 2/5 &{} 1/5 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1/5 &{} 0 &{} &{} \\ 3/5 &{} 1/5 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1/5 &{} 1/5 &{} 0 &{} \\ 4/5 &{} 1/5 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1/5 &{} 1/5 &{} 1/5 &{} 0 \\ \hline &{} 0 &{} -4/3 &{} 27/4 &{} 27/4 &{} -32/3 &{} -32/3 &{} -32/3 &{} 125/24 &{} 125/24 &{} 125/24 &{} 125/24. \\ \end{array} \end{aligned}$$
(A.2)

The intermediate stages (written in Shu-Osher and Butcher form) are as follows:

$$\begin{aligned} y^{(1)}&= u^n\approx & {} u(t^n), \\ y^{(2)}&= y^{(1)} + \frac{1}{2} \varDelta t F(y^{(1)})\approx & {} u(t^n+\varDelta t/2), \\ y^{(3)}&= y^{(1)} + \frac{1}{3} \varDelta t F(y^{(1)})\approx & {} u(t^n+\varDelta t/3), \\ y^{(4)}&= y^{(3)} + \frac{1}{3} \varDelta t F(y^{(3)}) = y^{(1)}+\frac{\varDelta t}{3} [F(y^{(1)}) + F(y^{(3)})]\approx & {} u(t^n+2\varDelta t/3), \\ y^{(5)}&= y^{(1)} + \frac{1}{4} \varDelta t F(y^{(1)})\approx & {} u(t^n+\varDelta t/4), \\ y^{(6)}&= y^{(5)} + \frac{1}{4} \varDelta t F(y^{(5)}) = y^{(1)}+\frac{\varDelta t}{4} [F(y^{(1)}) + F(y^{(5)})]\approx & {} u(t^n+\varDelta t/2), \\ y^{(7)}&= y^{(6)} + \frac{1}{4} \varDelta t F(y^{(6)}) = y^{(1)}+\frac{\varDelta t}{4} [F(y^{(1)}) + F(y^{(5)}) + F(y^{(6)})]\approx & {} u(t^n+3\varDelta t/4), \\ y^{(8)}&= y^{(1)} + \frac{1}{5} \varDelta t F(y^{(1)})\approx & {} u(t^n+\varDelta t/5), \\ y^{(9)}&= y^{(8)} + \frac{1}{5} \varDelta t F(y^{(8)}) = y^{(1)}+\frac{\varDelta t}{5} [F(y^{(1)}) + F(y^{(8)})]\approx & {} u(t^n+2\varDelta t/5), \\ y^{(10)}&= y^{(9)} + \frac{1}{5} \varDelta t F(y^{(9)}) = y^{(1)}+\frac{\varDelta t}{5} [F(y^{(1)}) + F(y^{(8)}) + F(y^{(9)})]\approx & {} u(t^n+3\varDelta t/5), \\ y^{(11)}&= y^{(10)} + \frac{1}{5} \varDelta t F(y^{(10)}) = y^{(1)}+\frac{\varDelta t}{5} [F(y^{(1)}) + F(y^{(8)}) + F(y^{(9)}) + F(y^{(10)})]\approx & {} u(t^n+4\varDelta t/5). \end{aligned}$$

Note that if \(F(\cdot )\) is a BP spatial discretization and \( u^n\) is BP, then each stage of this ExE-RK method is BP under appropriate time step restrictions. The approximations \(y^{(1)}\), \(y^{(2)}\), \(y^{(3)}\), \(y^{(5)}\), and \(y^{(8)}\) are BP because they correspond to forward Euler updates of \(u^n\). The remaining stages are BP since \(y^{(m)}\) is a forward Euler update of a BP approximation \(y^{(r)}\) for some \(r\in \{1,\ldots ,m-1\}\).

The Aitken–Neville interpolation yields the temporally 5th-order approximation

$$\begin{aligned} u^\mathrm{RK} =&\frac{1}{24}\left[ y^{(1)}+\varDelta t F(y^{(1)})\right] -\frac{8}{3}\left[ y^{(2)}+\frac{1}{2}\varDelta t F(y^{(2)})\right] +\frac{81}{4}\left[ y^{(4)}+\frac{1}{3}\varDelta t F(y^{(4)})\right] \\&-\frac{128}{3}\left[ y^{(7)}+\frac{1}{4}\varDelta t F(y^{(7)})\right] +\frac{625}{24}\left[ y^{(11)}+\frac{1}{5}\varDelta t F(y^{(11)})\right] . \end{aligned}$$

Note that this Euler extrapolation method combines \(S=5\) first-order approximations of \(u^{n+1}\). Since this combination is not convex, \(u^\mathrm{RK}\) is not necessarily BP even if \(y^{(1)},\ldots ,y^{(11)}\) are BP. To enforce the BP property of the final solution, we perform flux limiting using the Butcher form representation

$$\begin{aligned} u^\mathrm{RK}&= u^n + \varDelta t \Big [ -\frac{4}{3}F(y^{(2)}) + \frac{27}{4}F(y^{(3)}) + \frac{27}{4}F(y^{(4)}) - \frac{32}{3}F(y^{(5)}) - \frac{32}{3}F(y^{(6)}) \nonumber \\&\quad -\frac{32}{3}F(y^{(7)})+ \frac{125}{24}F(y^{(8)}) + \frac{125}{24}F(y^{(9)}) + \frac{125}{24}F(y^{(10)} + \frac{125}{24}F(y^{(11)}) \Big ]. \end{aligned}$$
(A.3)

1.3 Appendix A.3. Sixth-Order (RK76) RK Method

This 6th-order RK method, proposed in [49], consists of seven stages and has the Butcher tableau

$$\begin{aligned} \begin{array}{c|ccccccc} 0 &{} 0 &{} &{} &{} &{} &{} &{} \\ 1/3 &{} 1/3 &{} 0 &{} &{} &{} &{} &{} \\ 2/3 &{} 0 &{} 2/3 &{} 0 &{} &{} &{} &{} \\ 1/3 &{} 1/12 &{} 1/3 &{} -1/12 &{} 0 &{} &{} &{} \\ 1/2 &{} -1/16 &{} 9/8 &{} -3/16 &{} -3/8 &{} 0 &{} &{} \\ 1/2 &{} 0 &{} 9/8 &{} -3/8 &{} -3/4 &{} 1/2 &{} 0 &{} \\ 1 &{} 9/44 &{} -9/11 &{} 63/44 &{} 18/11 &{} 0 &{} -16/11 &{} 0\\ \hline &{} 11/120 &{} 0 &{} 27/40 &{} 27/40 &{} -4/15 &{} -4/15 &{} 11/120. \end{array} \end{aligned}$$
(A.4)

The intermediate stages of this method are not Euler steps. If we require them to be BP, the numerical fluxes \(H_{ij}\) should be constrained using the limiters from Sect. 3.3 in each stage. The BP property of the final solution \(u^\mathrm{RK}\) can be enforced similarly using the limiter from Sect. 3.2.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kuzmin, D., Quezada de Luna, M., Ketcheson, D.I. et al. Bound-preserving Flux Limiting for High-Order Explicit Runge–Kutta Time Discretizations of Hyperbolic Conservation Laws. J Sci Comput 91, 21 (2022). https://doi.org/10.1007/s10915-022-01784-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-022-01784-0

Keywords

Search

Navigation