Skip to main content
SpringerLink
Log in

Implicit Multistage Two-Derivative Discontinuous Galerkin Schemes for Viscous Conservation Laws

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

In this paper we apply implicit two-derivative multistage time integrators to conservation laws in one and two dimensions. The one dimensional solver discretizes space with the classical discontinuous Galerkin method, and the two dimensional solver uses a hybridized discontinuous Galerkin spatial discretization for efficiency. We propose methods that permit us to construct implicit solvers using each of these spatial discretizations, wherein a chief difficulty is how to handle the higher derivatives in time. The end result is that the multiderivative time integrator allows us to obtain high-order accuracy in time while keeping the number of implicit stages at a minimum. We show numerical results validating and comparing methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Alexander, R.: Diagonally implicit Runge–Kutta methods for stiff O.D.E’.s. SIAM J. Numer. Anal. 14, 1006–1021 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  2. Arnold, D.N., Brezzi, F., Cockburn, B., Marini, L.D.: Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39, 1749–1779 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  3. Banks, J., Henshaw, W.: Upwind schemes for the wave equation in second-order form. J. Comput. Phys. 231, 5854–5889 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  4. Cash, J.: Diagonally implicit Runge–Kutta formulae with error estimates. J. Inst. Math. Its Appl. 24, 293–301 (1979)

    Article  MATH  Google Scholar 

  5. Causley, M.F., Cho, H., Christlieb, A.J., Seal, D.: Method of lines transpose: high order L-stable O(N) schemes for parabolic equations using successive convolution. arXiv preprint arXiv:1508.03105 (2015)

  6. Chen, Y., Cockburn, B., Dong, B.: Superconvergent HDG methods for linear, stationary, third-order equations in one-space dimension. Math. Comput. doi:10.1090/mcom/3091 (2016)

  7. Christlieb, A.J., Feng, X., Seal, D.C., Tang, Q.: A high-order positivity-preserving single-stage single-step method for the ideal magnetohydrodynamic equations. arXiv preprint arXiv:1509.09208 (2015)

  8. Christlieb, A.J., Gottlieb, S., Grant, Z., Seal, D.C.: Explicit strong stability preserving multistage two-derivative time-stepping schemes. J. Sci. Comput. (2016). doi:10.1007/s10915-016-0164-2

  9. Cockburn, B., Dong, B., Guzmán, J.: A hybridizable and superconvergent discontinuous Galerkin method for biharmonic problems. J. Sci. Comput. 40(1), 141–187 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Cockburn, B., Gopalakrishnan, J.: A characterization of hybridized mixed methods for second order elliptic problems. SIAM J. Numer. Anal. 42, 283–301 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  11. Cockburn, B., Hou, S., Shu, C.W.: The Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws IV: the multidimensional case. Math. Comput. 54, 545–581 (1990)

    MathSciNet  MATH  Google Scholar 

  12. Cockburn, B., Lin, S.Y.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws III: one dimensional systems. J. Comput. Phys. 84, 90–113 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  13. Cockburn, B., Shu, C.W.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws II: general framework. Math. Comput. 52, 411–435 (1988)

    MathSciNet  MATH  Google Scholar 

  14. Cockburn, B., Shu, C.W.: The Runge–Kutta local projection \({P}^1\)-discontinuous Galerkin finite element method for scalar conservation laws. RAIRO Math Model. Numer. Anal. 25, 337–361 (1991)

    MathSciNet  MATH  Google Scholar 

  15. Cockburn, B., Shu, C.W.: The Runge–Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. Math. Comput. 141, 199–224 (1998)

    MathSciNet  MATH  Google Scholar 

  16. Donéa, J.: A Taylor-Galerkin method for convective transport problems. In: NumericalMethods in Laminar and Turbulent Flow (Seattle, Wash., 1983), pp. 941–950. Pineridge, Swansea (1983)

  17. Donéa, J., Giuliani, S., Halleux, J.P.: Taylor–Galerkin methods for the wave equation. In: Numerical Methods for Nonlinear Problems, vol. 2 (Barcelona, 1984), pp. 813–825. Pineridge, Swansea (1984)

  18. Dumbser, M.: Arbitrary High order Schemes for the Solution of Hyperbolic Conservtion Laws in Complex Domains. Shaker Verlag, Aachen (2005)

    Google Scholar 

  19. Dumbser, M., Munz, C.D.: Building blocks for arbitrary high order discontinuous Galerkin schemes. J. Sci. Comput. 27(1–3), 215–230 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  20. Dyson, R.: Technique for very high order nonlinear simulation and validation. J. Comput. Acoust. 10, 211–229 (2002)

  21. Guo, W., Qiu, J.M., Qiu, J.: A new Lax–Wendroff discontinuous Galerkin method with superconvergence. J. Sci. Comput. 65(1), 299–326 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Hairer, E., Nørsett, S.P., Wanner, G.: Solving ordinary differential equations I. Springer Series in Computational Mathematics, vol. 8. Springer Berlin Heidelberg (1987)

  23. Hairer, E., Wanner, G.: Multistep-multistage-multiderivative methods of ordinary differential equations. Computing (Arch. Elektron. Rechnen) 11(3), 287–303 (1973)

    MathSciNet  MATH  Google Scholar 

  24. Hairer, E., Wanner, G.: Solving ordinary differential equations II. Springer Series in Computational Mathematics, vol. 14. Springer Berlin Heidelberg (1991)

  25. Harten, A., Enquist, B., Osher, S., Chakravarthy, S.R.: Uniformly high order accurate essentially non-oscillatory schemes III. J. Comput. Phys. 71, 231–303 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  26. Henshaw, W.: A high-order accurate parallel solver for Maxwell’s equations on overlapping grids. SIAM J. Sci. Comput. 28(5), 1730–1765 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  27. Henshaw, W., Kreiss, H.O., Reyna, L.: A fourth-order-accurate difference approximation for the incompressible Navier–Stokes equations. Comput. Fluids 23(4), 575–593 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  28. Hopf, E.: The partial differential equation \(u_t + uu_x = \mu u_{xx}\). Commun. Pure Appl. Math. 3, 201–230 (1950)

    Article  MathSciNet  MATH  Google Scholar 

  29. Jaust, A., Schütz, J.: A temporally adaptive hybridized discontinuous Galerkin method for time-dependent compressible flows. Comput. Fluids 98, 177–185 (2014)

    Article  MathSciNet  Google Scholar 

  30. Jaust, A., Schütz, J., Seal, D.: Multiderivative time-integrators for the hybridized discontinuous Galerkin method. In: Proceedings to YIC GACM 2015 (2015)

  31. Jiang, G.S., Shu, C.W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126(1), 202–228 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  32. Jiang, Y., Shu, C.W., Zhang, M.: An alternative formulation of finite difference weighted ENO schemes with Lax–Wendroff time discretization for conservation laws. SIAM J. Sci. Comput. 35(2), A1137–A1160 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  33. Lax, P., Wendroff, B.: Systems of conservation laws. Commun. Pure Appl. Math. 13(2), 217–237 (1960)

    Article  MathSciNet  MATH  Google Scholar 

  34. Nguyen, N.C., Peraire, J., Cockburn, B.: An implicit high-order hybridizable discontinuous Galerkin method for linear convection–diffusion equations. J. Comput. Phys. 228, 3232–3254 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  35. Nguyen, N.C., Peraire, J., Cockburn, B.: An implicit high-order hybridizable discontinuous Galerkin method for nonlinear convection–diffusion equations. J. Comput. Phys. 228, 8841–8855 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  36. Nguyen, N.C., Peraire, J., Cockburn, B.: High-order implicit hybridizable discontinuous Galerkin methods for acoustics and elastodynamics. J. Comput. Phys. 230, 3695–3718 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  37. Nguyen-Ba, T., Nguyen-Thu, H., Giordano, T., Vaillancourt, R.: One-step strong–stability–preserving Hermite–Birkhoff–Taylor methods. Sci. J. Riga Tech. Univ. 45, 95–104 (2010)

    MATH  Google Scholar 

  38. Qiu, J.: Development and comparison of numerical fluxes for LWDG methods. Numer. Math. Theory Methods Appl. 1(4), 435–459 (2008)

    MathSciNet  MATH  Google Scholar 

  39. Qiu, J., Dumbser, M., Shu, C.W.: The discontinuous Galerkin method with Lax–Wendroff type time discretizations. Comput. Methods Appl. Mech. Eng. 194(42–44), 4528–4543 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  40. Qiu, J., Shu, C.W.: Finite difference WENO schemes with Lax-Wendroff-type time discretizations. SIAM J. Sci. Comput. 24(6), 2185–2198 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  41. Reed, W., Hill, T.: Triangular mesh methods for the neutron transport equation. Tech. rep, Los Alamos Scientific Laboratory (1973)

  42. Schütz, J., May, G.: A hybrid mixed method for the compressible Navier–Stokes equations. J. Comput. Phys. 240, 58–75 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  43. Seal, D.C., Güçlü, Y., Christlieb, A.J.: High-order multiderivative time integrators for hyperbolic conservation laws. J. Sci. Comput. 60(1), 101–140 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  44. Seal, D.C., Tang, Q., Xu, Z., Christlieb, A.J.: An explicit high-order single-stage single-step positivity-preserving finite difference WENO method for the compressible Euler equations. J. Sci. Comput. arXiv preprint arXiv:1411.0328 (2014)

  45. Tan, S., Shu, C.W.: Inverse Lax–Wendroff procedure for numerical boundary conditions of conservation laws. J. Comput. Phys. 229(21), 8144–8166 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  46. Tan, S., Shu, C.W., Ning, J.: Efficient implementation of high order inverse Lax–Wendroff boundary treatment for conservation laws. J. Comput. Phys. 231, 2510–2527 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  47. Tsai, A., Chan, R., Wang, S.: Two-derivative Runge–Kutta methods for PDEs using a novel discretization approach. Numer. Algorithms 65, 687–703 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  48. Xu, Y., Shu, C.W.: Local discontinuous Galerkin methods for high-order time-dependent partial differential equations. Commun. Comput. Phys. 7(1), 1–46 (2010)

    MathSciNet  Google Scholar 

Download references

Acknowledgments

We would like to thank the anonymous reviewers for their helpful comments and suggestions to improve the quality of this work.

Author information

Authors and Affiliations

  1. Vakgroep wiskunde en statistiek, Hasselt University, Agoralaan Gebouw D, 3590, Diepenbeek, Belgium

    Alexander Jaust & Jochen Schütz

  2. Department of Mathematics, United States Naval Academy, 121 Blake Road, Annapolis, MD, 21402, USA

    David C. Seal

Authors
  1. Alexander Jaust
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jochen Schütz
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. David C. Seal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alexander Jaust.

Tabulated results

Tabulated results

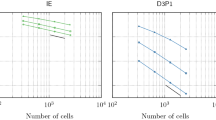
In this section we present complete error tables for the data presented summarily throughout the paper (Tables 1, 2, 3, 4, 5, 6, 7 and 8).

Table 1 Numerical results for the heat equation
Full size table
Table 2 Numerical results for the convection equation
Full size table
Table 3 Numerical results for the convection–diffusion equation with smooth initial condition
Full size table
Table 4 Results for the convection–diffusion equation
Full size table
Table 5 Numerical results for Burgers equation
Full size table
Table 6 Numerical results for the linear coupled advection equation
Full size table
Table 7 Numerical results for the linear coupled advection equation
Full size table
Table 8 Numerical results for the Euler equations
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jaust, A., Schütz, J. & Seal, D.C. Implicit Multistage Two-Derivative Discontinuous Galerkin Schemes for Viscous Conservation Laws. J Sci Comput 69, 866–891 (2016). https://doi.org/10.1007/s10915-016-0221-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-016-0221-x

Keywords

Search

Navigation