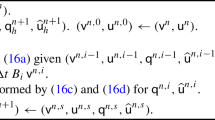Modified Non-linear Weights for Fifth-Order Weighted Essentially Non-oscillatory Schemes

Abstract

This paper is concerned with fifth-order weighted essentially non-oscillatory (WENO) scheme with a new smoothness indicator. As the so-called WENO-JS scheme (Jiang and Shu in J Comput Phys 126:202–228, 1996) provides the third-order accuracy at critical points where the first and third order derivatives do not becomes zero simultaneously, several fifth-order WENO scheme have been developed through modifying the known smoothness indicators of WENO-JS. Recently a smoothness indicator based on $L^1$-norm has been proposed by Ha et al. (J Comput Phys 232:68–86, 2013) (denoted by WENO-NS). The aim of this paper is twofold. Firstly, we further improve the smoothness indicator of WENO-NS and secondly, using this measurement, we suggest new nonlinear weights by simplifying WENO-NS weights. The proposed WENO scheme provides the fifth-order accuracy, even at critical points. Some numerical experiments are provided to demonstrate that the present scheme performs better than other WENO schemes of the same order.

1 Introduction

The essentially non-oscillatory (ENO) schemes [11, 12, 21, 22] and the weighted ENO (WENO) schemes [14, 16, 20] have become effective methods for approximating solutions to systems of hyperbolic conservation laws. The ENO schemes utilize a local adaptive stencil to obtain information from smooth regions so that they can prevent spurious oscillations near discontinuities, while achieving high order accuracy in smooth regions. The WENO schemes are constructed to use all the candidate stencils instead of using only one of the candidate stencils. The key point in WENO schemes is a convex combination of lower order fluxes associated with each candidate stencil to compute the numerical fluxes to yield higher order accuracy in smooth region. In that way, the WENO schemes [16] obtain $(r+1)$th order of accuracy from the rth order ENO methods with r stencils of r points in the smooth regions, while in regions near discontinuities these methods behave similarly to the ENO methods. In [14], Jiang and Shu introduced the WENO-JS scheme with a new smoothness indicator using the sum of the $L^2$-norms of all the derivatives of r local interpolating polynomials, to achieve $(2r-1)$th order from the stencils of the rth order ENO schemes for $r=2,3$.

The WENO-JS scheme has become a quite successful methodology for solving problems with strong discontinuities and complicated smooth solutions in computational fluid dynamics. However, WENO-JS is too dissipative to solve problems with lots of structures in the smooth part of the solution, such as direct numerical simulation of turbulent flows. In particular, Henrick et al. [13] noticed that the fifth-order WENO-JS scheme fails to yield the maximum convergence order of the scheme at critical points where the first derivative vanishes but the third order derivative does not. In order to amend this drawback, an improved fifth-order WENO method (called WENO-M) [13] has been suggested by incorporating a mapping procedure to maintain the nonlinear weights of the convex combination of stencils as near as possible to the linear weights of fifth order accuracy except for discontinuities. Later, Borges, Carmona, Costa, and Don designed another fifth-order WENO scheme [5] (called WENO-Z) by adding a new smoothness indicator which is obtained by a linear combination of the classical smoothness indicator of WENO-JS. Compared to the WENO-JS scheme, the WENO-M and WENO-Z schemes generate the maximum rate of accuracy at smooth regions including critical points and decrease the numerical dissipation with sharper results. The WENO-M and WENO-Z schemes are devised through a novel utilization of the known smoothness indicators of WENO-JS. Very recently, another version of a smoothness indicator based on $L^1$-norm has been proposed in [10]. This WENO scheme (WENO-NS) has the fifth order accuracy and yields an improved behavior in compared to other fifth-order WENO schemes, but finding optimal internal parameters in WENO-NS weights is rather complicated. Higher than fifth order WENO schemes [3, 6, 8] and efficient shock capturing methods [1, 4, 7, 17, 18, 27] have been developed by several researchers.

The aim of this study is to further improve the WENO-NS scheme. We first modify the smoothness indicator of WENO-NS and then introduce a new the nonlinear weights through simplifying the ones of WENO-NS. The motivation for this study is based on the observation that the given three substencils for a fifth-order WENO scheme may provide unbalanced contribution to the evaluation point. Thus, our main idea is to make a balanced tradeoff among the substencils. We see that this modification yields better results than the WENO-NS as well as other fifth-order schemes. A simple analysis verifies that the resulting WENO (called WENO-P) scheme has the fifth-order accuracy, even at critical points. Some numerical experiments are conducted to demonstrate the performance of the new scheme. The proposed scheme is as simple to implement as the classical WENO or WENO-Z schemes but yields better approximations at almost the same computational cost.

The outline of this paper is given as follows. We present, in Sect. 2, a brief description of WENO reconstructions. Section 3 introduces a new measurement which estimates smoothness of a local solution in the construction of a fifth-order WENO scheme. Some numerical results are provided in Sect. 4 to demonstrate advantages of the proposed WENO scheme. Finally, concluding remarks are given in Sect. 5.

2 WENO Schemes

We consider a numerical solution of hyperbolic conservation laws

$$\begin{aligned} q_t + f(q)_x = 0, \quad x \in \mathbb {R},\quad t\ge 0, \end{aligned}$$

(2.1)

where $q = (q_1,\ldots , q_m)$ is a conserved quantity and f(q) is the flux. In order to discuss WENO reconstruction for (2.1), we introduce the following notation. Let $\{I_j\}$ be a partition of a spatial domain with the jth cell $I_j= [x_{j-1/2},x_{j+1/2}]$. Let $x_j$ denote the center of the cell $I_j$ and $x_{j\pm 1/2}$ indicate the cell boundaries. The function value at the node $x_j$ is denoted by $f_j:=f(x_j)$. Throughout of this paper, we assume that the set $\{x_{j+1/2}\}_j$ is uniformly gridded and denote by $\Delta x = x_{j+1/2}-x_{j-1/2}$ the size of $I_j$.

2.1 Numerical Flux

The one-dimensional hyperbolic conservation laws in (2.1) can be approximated by the semi-discrete form:

$$\begin{aligned} \frac{d q_j}{d t} = - \frac{\partial f}{\partial x} \Big |_{x =x_j}, \end{aligned}$$

(2.2)

where $q_j(t)$ is the numerical approximation to the point value $q(x_j , t)$. The conservation property of the spatial discretization is obtained by defining a function h implicitly through the following equation (see Lemma 2.1 of [22]),

$$\begin{aligned} f(q(x))= \frac{1}{\Delta x} \int ^{x+\Delta x/2}_{x-\Delta x/2} h(\xi )d\xi , \end{aligned}$$

(2.3)

such that the spatial derivative in (2.2) is exactly represented as a conservative finite difference formula at the cell boundaries. A conservative finite difference formulation looks for numerical flux ${\hat{f}}$ approximating h at the cell boundaries such that it approximates $h(x_{j\pm 1/2})$ with higher accuracy. Accordingly, the approximation to the spatial derivative $\frac{\partial f}{\partial x}$ at $x=x_j$ will take the conservative form

$$\begin{aligned} \frac{\partial f}{\partial x} \Big |_{x =x_j} \approx \frac{{\hat{f}}_{j+1/2} - {\hat{f}}_{j-1/2}}{\Delta x}. \end{aligned}$$

(2.4)

In the construction of the numerical flux ${\hat{f}}$, the primary concern is the order of approximation occurred in the approximation to the spatial derivative (2.4) since it determines the order at which the overall scheme converges in space. It is also of importance for the numerical flux ${\hat{f}}_{j\pm 1/2}$ to have a suitable convergence order to $h(x_{j\pm 1/2})$. It plays an important role as a criterion for the admissibility of non-linear weights for non-oscillatory interpolations.

2.2 Fifth-Order WENO Scheme

The WENO schemes are designed as high resolution schemes for hyperbolic problems. A fifth-order WENO scheme uses a five-point stencil. To approximate solutions near shocks without spurious oscillations, the five-point stencil is subdivided into three candidate substencils ${\mathcal S}_0 (j), {\mathcal S}_1 (j)$ and ${\mathcal S}_2 (j)$. For each cell $I_j$, the corresponding stencil is denoted by

$$\begin{aligned} {\mathcal S}_{k} (j) := \{x_{j+k-2},\, x_{j+k-1},\, x_{j+k}\}, \quad k= 0,1,2. \end{aligned}$$

(2.5)

In each substencil ${\mathcal S}_{k} (j)$, a local numerical flux $\hat{f}^{k}(x)$ is constructed as a second degree polynomial such that it approximates the value h(x) with a third-order accuracy at the cell boundary $x=x_{j+1/2}$. Then these numerical fluxes $\hat{f}_{j+1/2}^{k}$ ($k=0,1,2$) are combined in a weighted average to define a fifth-order WENO approximation to the value $h(x_{j+ 1/2})$ in smooth regions, that is,

$$\begin{aligned} \hat{f}_{j+ 1/2} := \sum _{k=0}^2 \omega _k \hat{f}^{k}_{j+ 1/2}, \end{aligned}$$

(2.6)

where $\omega _k$ is the weight associated with the substencil ${\mathcal S}_k$ and $\omega _0 + \omega _1 + \omega _2 =1$. To calculate $\hat{f}_{j-1/2}$, the stencil for $\hat{f}_{j+1/2}$ is translated to the left by one grid spacing so that it enables the approximation to derivatives in (2.4) to maintain the fifth-order approximation accuracy.

The success of a WENO scheme indeed depends on the construction of the nonlinear weights $\omega _k$. A fundamental requirement for $\omega _k$ is that the weights can remove effectively the contribution of stencils which contain discontinuous data, while retaining the fifth order accuracy in smooth areas. For this purpose, we need to take the smoothness of the local solution $\hat{f}^{k}_{j+ 1/2}$ on ${\mathcal S}_{k}(j)$ into account of weights $\omega _k$. Letting $\beta _k$ be smoothness indicators for $\hat{f}^{k}_{j+ 1/2}$, the nonlinear weights $\omega _k$ are typically defined by

$$\begin{aligned} \omega _k = \frac{\alpha _k}{\sum ^{2}_{\ell =0} \alpha _\ell } \quad \text {and }\quad \alpha _k = \frac{d_k}{(\epsilon + \beta _k)^2},~\quad k=0,1,2, \end{aligned}$$

(2.7)

where $0< \epsilon \ll 1$ is employed to avoid the denominator becoming zero, and where the coefficients $d_k$ are the so-called ideal weights given by

$$\begin{aligned} d_0= 1/10,\quad d_1= 3/5, \quad d_2= 3/10. \end{aligned}$$

(2.8)

A sufficient condition for a final WENO scheme to have the fifth-order accuracy (even at critical points) is that the non-linear weights $\omega _k$ converge to the ideal weights $d_k$ with the following rate (e.g., see [5, 13]):

$$\begin{aligned} \omega ^\pm _k - d_k = {\mathcal O}(\Delta x^3), \end{aligned}$$

(2.9)

where superscripts ‘$+$’ and ‘$-$’ on $\omega _k$ correspond to their use in either $\hat{f}^k_{j+1/2}$ and $\hat{f}^k_{j-1/2}$ respectively. It is worthwhile to note that the condition (2.9) can be weakened for WENO-JS to $\omega ^\pm _k - d_k = g(x_{j+1/2}){\mathcal O}(\Delta x^2) + {\mathcal O}(\Delta x^3)$ for a locally Lipschitz continuous function g under a suitable condition of $\epsilon$ in (2.7) [2].

3 New WENO Scheme

3.1 Smoothness Indicator

In [14], Jiang and Shu introduced a fifth-order WENO scheme (called WENO-JS) along with the smoothness indicators

$$\begin{aligned} \beta _k = \sum ^{2}_{\ell =1} \int ^{x_{j+1/2}}_{x_{j-1/2}} \Delta x^{2\ell -1} \Biggl (\frac{d^\ell }{dx^\ell }\hat{f}^{k}\Biggr )^2dx, \quad \text {for }\;k=0,1,2. \end{aligned}$$

(3.1)

which estimate the regularities of the local solutions. However, as noticed by Henrick et al. [13], the WENO-JS scheme yields only third order accuracy around critical points where the first derivative of f becomes zero and third derivative does not vanish, if the value $\epsilon$ in (2.7) is significantly small, (e.g., $\epsilon = 10^{-40}$). In order to overcome this limitation, Henrick et al. [13] suggested an improved fifth-order WENO method (called WENO-M). They devised a map combining the ideal weights and the smoothness indicators of WENO-JS to ensure the optimal convergence order at critical points. Later, Borges et al. [5] introduced the WENO-Z scheme by involving a global smoothness measurement into the non-linear weights of the WENO-JS. Very recently, in [10], Ha et al. developed a new version of fifth-order WENO scheme (called WENO-NS).

Unlike other WENO schemes based on (3.1), the WENO-NS incorporates a new type of smoothness indicator based on $L^1$-norm. It measures the regularity of the solution on each three-point substencil ${\mathcal S}_k(j)$ by estimating the approximate magnitude of its derivatives. Specifically, the smoothness indicator $\beta _k$ in [10] over the stencil ${\mathcal S}_k(j)$ is of the form

$$\begin{aligned} \beta _k (\xi ):= \xi \left| D_{1,k}f\right| + \left| D_{2,k}f\right| , \quad \xi \in (0, 1], \end{aligned}$$

(3.2)

where $D_{n,k}$ are defined by

$$\begin{aligned} D_{1,k}f&: =(1-k)f_{j-2+k} +(2k-3)f_{j-1+k}+ (2-k)f_{j+k}, \nonumber \\ D_{2,k}f&: = f_{j-2+k}-2f_{j-1+k} +f_{j+k}. \end{aligned}$$

(3.3)

In fact, the operators $D_{n,k}$ can be regarded as a generalized undivided difference such that $D_{n,k}f$ approximate the derivative $\Delta x^n f^{(n)}$ at the point $x_{j+1/2}$ with the following accuracy:

$$\begin{aligned} D_{n,k}f =\frac{d^n f}{dx^n}(x_{j+1/2})\Delta x^n + {\mathcal O}(\Delta x^3). \end{aligned}$$

(3.4)

The number $\xi$ in (3.2) is employed to balance the tradeoff between the accuracies around the smooth and singular areas. The parameter $\xi$ may be chosen depending on the local data feature, but to save computational costs, we suggest to use a fixed value of $\xi$. Having performed some numerical experiments, a good choice of $\xi$ would be in the range [0.1, 0.5]; we recommend $\xi =0.4$ for Euler equations and $\xi = 0.1$ for linear advection equation including jump discontinuities. The robustness of the choice of $\xi$ will be discussed later in Sect. 3.4 with quantitative assessment.

An advantage of using the above smoothness indicator is that $D_{1,k} f$ in (3.2) approximates $\frac{df}{dx}$ with higher accuracy. The second term in (3.2) is the same as the ones of the WENO-JS, but the proposed method uses the absolute values, while the WENO-JS uses the squared ones. Using the technique of Taylor expansion and applying the relation (3.4), we indeed have the following expressions

$$\begin{aligned} \beta _0&= \xi \left| { f_{j+1/2}'}{\Delta x}- \frac{23}{24}{f_{j+1/2}''' }\,{\Delta x}^3 \right| +\left| f_{j+1/2}''{\Delta x}^2 - \frac{3}{2} f_{j+1/2}'''{\Delta x}^3 \right| + {\mathcal O}(\Delta x^{4}), \nonumber \\ \beta _1&={\xi } \left| f_{j+1/2}' {\Delta x} + \frac{1}{24} f_{j+1/2}'''{\Delta x}^3\right| + \left| f_{j+1/2}''{\Delta x}^2 -\frac{1}{2} f_{j+1/2}''' {\Delta x}^3 \right| + {\mathcal O}(\Delta x^{4}) , \nonumber \\ \beta _2&= \xi \left| f_{j+1/2}'{\Delta x} +\frac{1}{24} f_{j+1/2}''' {\Delta x}^3\right| + \left| f_{j+1/2}'' {\Delta x}^2 + \frac{1}{2} f_{j+1/2}'''{\Delta x}^3 \right| + {\mathcal O}(\Delta x^{4}). \end{aligned}$$

(3.5)

For the computation of the numerical flux ${\hat{f}}$ at $x_{j-1/2}$, the stencil is shifted to the left by one grid spacing. Also, the above Eq. (3.5) is applied to $f_{j-1/2}$ in a symmetric way. The readers are referred to the article [10] for more details.

3.2 A New Nonlinear Weight

In this section, we provide a new fifth order WENO which improves the WENO-NS in [10]. To this end, our task is twofold. First, we modify the smoothness indicators of WENO-NS. Secondly, we suggest new nonlinear weights by simplifying the previous WENO-NS weights. Our motivation for this study is that the given three substencils ${\mathcal S}_0(j), {\mathcal S}_1(j)$ and ${\mathcal S}_2(j)$ may provide unbalanced contribution to the evaluation point. The two substencils ${\mathcal S}_1(j)$ and ${\mathcal S}_2(j)$ are symmetric with respect to the point $x_{j+1/2}$. However, owing to the existence of the substencil ${\mathcal S}_0(j)$, the interpolation process may be over influenced from the left substencils. For instance, as we see in (3.5), $\beta _k$’s are dominated by the factor $\Delta x |f^{\prime }_{j+1/2}|$. Then, when evaluating numerical fluxes at $x_{j+1/2}$, the WENO interpolation is affected more strongly by two stencils (associated with $d_0=1/10$ and $d_1 = 3/5$) rather than the other stencil (associated with $d=3/10$), resulting in biased contribution to the evaluation point. In this view point, we give weights to the three substencils to make their balanced contributions. Our approach is to employ adjusted smoothness indicators defined as follows

$$\begin{aligned} \tilde{\beta }_0 =\beta _0,\quad \tilde{\beta }_1 = (1 + \delta ) \beta _1,\quad \tilde{\beta }_2 = (1 - \delta ) \beta _2, \end{aligned}$$

where $\delta >0$ is a parameter for balancing the contribution of substencils. We will see later that the number $\delta = 0.05$ is a good choice among several alternatives for the parameter $\delta$. Then the new WENO weights are defined through the following process. First let $\zeta$ be a global higher order smoothness measurement defined by

$$\begin{aligned} \zeta = (\beta _0 -\beta _2)^2. \end{aligned}$$

(3.6)

Then the final WENO (denoted by WENO-P) weights are defined to be of the form

$$\begin{aligned} \omega _k =\frac{\alpha ^P_k}{\sum _{\ell =0}^2 \alpha ^P_\ell }, \quad \alpha _k^P = d_k\left( 1 + \frac{\zeta }{(\epsilon +\tilde{\beta }_k)^2}\right) , \end{aligned}$$

(3.7)

where $0< \epsilon \ll 1$ is a small number (e.g., $\epsilon =10^{-40}$) chosen to make the denominator become non-zero.

Remark 3.1

When constructing the global smoothness measurement, the WENO-NS uses an additional contribution term which measures the solution smoothness on the stencil ${\mathcal S}_1(j)$ [10]. However, instead of using this measurement, the proposed method adjusts the contribution of each substencil. It simplifies the construction of nonlinear weights of WENO-P and saves the computation costs. Although the number $\delta$ is chosen empirically, our numerical experiments reveal that it yields more accurate results compared to other combinations. Furthermore, it is necessary to remark that the numerical flux ${\hat{f}}_{j-1/2}$ is computed by shifting the stencils of ${\hat{f}}_{j+1/2}$ to the left by one grid spacing. Thus, the same weight $\alpha _k^P$ (and hence, $\omega _k$) are applied to the corresponding substencils.

In order for the final WENO scheme to have the fifth-order convergence rate, we verify that the nonlinear weights $\omega _k$ satisfy the following sufficient condition

$$\begin{aligned} \omega _k - d_k = {\mathcal O}(\Delta x^3). \end{aligned}$$

(3.8)

The proof for this convergence rate is similar to the case in [10]. However, in order for this paper to be self-contained, we briefly sketch the proof. For this purpose, we put $\epsilon =0$ for the following estimate and find from (3.5) that $\zeta$ is of the form

$$\begin{aligned} \zeta =\Delta x^6 \left( A + {\mathcal O}(\Delta x^2)\right) \end{aligned}$$

(3.9)

even at critical points where the first derivative is zero, but the second derivative is not. Then, due to the fact $\tilde{\beta }_k= {\mathcal O}(\Delta x)$ at non-critical points, the condition (3.8) holds immediately. Consequently, the WENO-P has the fifth-order convergence order. Next, consider the critical points where $f^{\prime }_{j+1/2} = 0$ and $f^{\prime \prime }_{j+1/2} \not =0$. Since $\tilde{\beta }_k= |f^{\prime \prime }_{j+1/2}| \Delta x ^2(1+ {\mathcal O}(\Delta x))$, there is a constant $C>0$ independent of k such that

$$\begin{aligned} 1+ \frac{\zeta }{\tilde{\beta }_k^2}&= 1+ C\Delta x^2 + {\mathcal O}(\Delta x^3) \\&= C_{\Delta x}\Biggl (1+ \frac{{\mathcal O}(\Delta x^3)}{1+ C\Delta x^2}\Biggr ) = C_{\Delta x}\big (1+ {\mathcal O}(\Delta x^3)\big ) \end{aligned}$$

with $C_{\Delta x}=(1+ C\Delta x^2) >0$. Therefore, substituting this into (3.7), the conditions (3.8) are also satisfied for the new weights $\omega _k$. It ensures that the suggested WENO-P has the fifth convergence order, even at critical points where the first derivative is zero but the second derivative is not zero.

3.3 Convergence of the WENO-P

In this section, we test the approximation order of the suggested WENO-P scheme on the linear equation

$$\begin{aligned} q_t + q_x = 0, \quad -1\le x \le 1, \quad t \ge 0, \end{aligned}$$

(3.10)

with two initial data

$$\begin{aligned} q_0(x) = \sin (\pi x) \quad \text {and} \quad q_0(x) = \sin \left( \pi x - \frac{1}{\pi }\sin \pi x \right) . \end{aligned}$$

(3.11)

Fig. 1

$L^\infty$ error plots of WENO schemes for the linear equation (3.10) with periodic boundary conditions and two initial data $\sin (\pi x)$ (left) and $\sin \bigl (\pi x - \displaystyle {\frac{\sin \pi x}{\pi }}\bigr )$ (right)

The WENO-P scheme with the Lax–Friedrichs flux splitting is implemented with $\xi = 0.1$ in (3.3). We especially make use of the fourth order non-TVD Runge–Kutta methods for the time step as $\Delta t \sim (\Delta x)^{5/4}$ to be effectively fifth-order. Figure 1 shows the convergence behaviors of the $L^\infty$ errors of several WENO schemes at $t=2$. The errors of WENO schemes except WENO-JS converge to the error obtained with ideal weights. It means that all the fifth-order WENO schemes provide almost the same results at high resolutions. However, at low resolutions, the proposed non-linear weights stand rather away from the ideal weights. As a result, it may behave less accurate at smooth regions on coarse meshes, but it yields improved results at regions with discontinuities or steep gradients. Furthermore, due to the balanced contribution of three substencils, the discontinuities are smeared less by WENO-P than by other WENO schemes. The proposed non-linear weights behave as a tradeoff to get high accuracy around discontinuities.

Fig. 2

a Comparison of the analytical solution with the numerical solutions of the linear advection Eq. (3.10) with WENO-JS, WENO-Z, WENO-NS and WENO-P at $t=40$ using $\Delta x = 0.01$. b Closer-up in the region $x \in [-0.15,0.15]$. c The behavior of the several values of $\delta$ in Eq. (3.7) in the region $x \in [-0.005,0.04]$

3.4 Behaviors of the New Smoothness Indicators

We now discuss how the parameter $\delta$ in (3.7) affects the construction of numerical fluxes. The performance of the proposed schemes is compared with other choices of $\delta$ as well as other fifth-order WENO schemes. Specifically, we test it with the linear advection Eq. (3.10) with

$$\begin{aligned} q_0 (x) = {\left\{ \begin{array}{ll} -\sin (\pi x) -\frac{1}{2}x^3 &{}\quad \text {if }\;-1 \le x < 0 , \\ -\sin (\pi x) - \frac{1}{2}x^3 +1 &{}\quad \text {if }\;0 \le x \le 1 , \\ \end{array}\right. } \end{aligned}$$

(3.12)

which is a piecewise sine function with a jump discontinuity at $x=0$. We solve it up to $t = 40$ to see the behaviors of the WENO schemes at the jump discontinuity. Numerical results are presented and compared, visually and by using some quantitative measurement (local $L^1$-errors near discontinuity). As shown in Fig. 2 and Table 1, there are significant improvements near discontinuity with the proposed scheme using $\delta =0.05$, yielding better results than the other $\delta$ values. So, here after, all the computations are carried out with $\delta =0.05$. More quantitative evaluations will be given in Sect. 4.1 (see Tables 3, 4). In addition, local $L^1$-errors of the WENO-NS and WENO-P schemes in Table 2 for different choices of $\xi$, in which the robustness of the parameter $\xi$ can be observed.

4 Numerical Results

In this section we assess the performance of the proposed scheme with several selected test problems. Its performance will be compared with the WENO-JS, WENO-Z, and WENO-NS schemes. The presentation of this section begins with the solution of the advection equation, followed by the solutions of one and two dimensional Euler equations.

4.1 Scalar Test Problems

In order to observe the shock capturing ability of the WENO-P scheme we test it for one dimensional scalar advection equations with two initial data. The results of the proposed scheme are compared to those of WENO-NS, WENO-Z and the classic WENO-JS. For the time-stepping, the third order TVD Runge–Kutta schemes [22] are used.

Example 4.1

(1 D scalar problem) Let us first consider the one-dimensional linear advection equation

$$\begin{aligned} q_t + q_x = 0, \quad -1\le x \le 1, \quad t \ge 0, \end{aligned}$$

(4.1)

with

$$\begin{aligned} q(x,0) = q_0(x). \end{aligned}$$

Table 1 Local $L^1$ errors on the region $[-0.15,0.15]$ (near discontinuity) at $t=40$ of the linear advection Eq. (3.10) with the initial condition (3.12) for different choices of $\delta$

Table 2 Local $L^1$ errors on the region $[-0.15,0.15]$ (near discontinuity) at $t=40$ of the linear advection Eq. (3.10) with the initial condition (3.12) for different choices of $\xi$

(i) Let the initial condition be given by

$$\begin{aligned} q(x,0) = {\left\{ \begin{array}{ll} 1 &{} \quad \text {if }\;-\frac{1}{2} \le x < \frac{1}{2} , \\ 0 &{} \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(4.2)

We use $\xi =0.1$ in Eq. (3.2) and solve the advection Eq. (4.1) until the time $t = 40$ to illustrate the behaviors of schemes at the jump discontinuities after a long time. The computed results are given in Fig. 3. We see that the result of WENO-P is closer to the analytic solution than those of the other fifth-order WENO schemes. Moreover, according to different resolutions, local $L^1$-errors (near discontinuities) of fifth order WENO schemes are displayed in Table 3 with different choices of $\delta$, in which the robustness and advantages of the proposed scheme can be observed.

(ii) Consider the linear advection Eq. (4.1) with another initial condition given by

$$\begin{aligned} q_0(x) = {\left\{ \begin{array}{ll} -x \sin \left( \frac{3 \pi }{2}x^2\right) , &{}\quad \text {if }\;-1 \le x \le -\frac{1}{3}, \\ |\sin (2 \pi x)|, &{}\quad \text {if }\;-\frac{1}{3} < x \le \frac{1}{3}, \\ 2x - 1 - \frac{1}{6}\sin (3 \pi x), &{}\quad \text {if }\;\frac{1}{3} \le x \le 1. \end{array}\right. } \end{aligned}$$

(4.3)

The solution of this problem contains contact discontinuities, corner singularities and smooth areas. We solve the equation up to $t = 41$. The numerical results are provided in Fig. 4. Comparison of the results demonstrates the advantages of the proposed scheme to approximate the exact solution near discontinuities. As in the previous example, local $L^1$-errors (near discontinuities) of fifth order WENO schemes are displayed in Table 4 with different choices of $\delta$. The robustness of the choice of the parameter $\delta$ is clearly observed.

Fig. 3

Comparison between the exact solution and the numerical solutions of the linear advection Eq. (4.1) with WENO-JS, WENO-Z, WENO-NS and WENO-P at $t=40$ using $\Delta x = 0.01$

Table 3 Local $L^1$ errors on the region [0.35, 0.65] (near discontinuity) at $t=40$ of the linear advection Eq. (4.1) with the initial condition (4.2) for different choices of $\delta$, using several WENO schemes and WENO-P

Fig. 4

Comparison between the exact solution and the numerical solutions of the linear advection equation with the initial condition (4.3) using WENO-JS, WENO-Z, WENO-NS and WENO-P at $t=41$. Here, $\Delta x = 0.01$

4.2 Euler Systems

Now we consider the numerical solutions of one and two dimensional gas dynamic Euler equations. In the following examples we set $\xi = 0.4$ in (3.2).

4.2.1 1D Euler Systems

Consider the one-dimensional Euler gas dynamic equations given as

$$\begin{aligned} U_t + F(U)_x = 0 \end{aligned}$$

(4.4)

with

$$\begin{aligned} U=(\rho , \rho u , E)^T,\quad F(U)=(\rho u,\rho u^2+p,u(E+p))^T. \end{aligned}$$

The pressure p and total energy E is defined by

$$\begin{aligned} p = (\gamma - 1) \left( E- \frac{1}{2} \rho u^2\right) , \end{aligned}$$

where $\rho$ and u are the density profile and velocity component, respectively, and $\gamma$ is the ratio of specific heats. The eigenvalues of Jacobian matrix $A(U) = \partial F/\partial U$ can be written as follows:

$$\begin{aligned} \lambda _1(q) = u- c, \quad \lambda _2(q) = u, \quad \lambda _3(q) = u + c, \end{aligned}$$

where $c= \sqrt{\gamma p/ \rho }$ is the sound speed. The characteristic decomposition with Roe’s approximation is used at the cell faces and the Lax–Friedrichs formulation is used for the numerical fluxes to generalize the WENO schemes to 1D Euler systems.

Table 4 Local $L^1$ errors on the regions $[-0.15,0.15]\cup [-0.8167, -0.5167] \cup [0.5167,0.8167]$ (near discontinuities) at time $t=41$ of the linear advection Eq. (4.1) with the initial condition (4.3) for different choices of $\delta$, using several WENO schemes and WENO-P with varied $\delta$

Fig. 5

Numerical solutions of the shock-density entropy interacting of Shu–Osher [22] with WENO-JS, WENO-Z, WENO-NS and WENO-P at $t =1.8$ with a $k = 5$ and $\Delta x = 0.04$, b $k = 10$ and $\Delta x = 0.02$ and c $k = 15$ and $\Delta x = 0.0125$ in Eq. (4.5)

Fig. 6

Numerical solutions of Lax problem [15] at $t=1.3$ ($\Delta x = 0.05$) using WENO-JS, WENO-Z, WENO-NS, and WENO-P. a Density profile and the local enlarge plots of the contact wave of density and b pressure profile

Fig. 7

Numerical solutions of Sod problem [23] at $t=0.2$ ($\Delta x = 0.005$) using WENO-JS, WENO-Z, WENO-NS and WENO-P. a Density profile and the local enlarge plots of the contact wave of density and b pressure

Fig. 8

Density profiles of 2D problems [19] at $t = 0.8$ using $\Delta x = \Delta y = 1/400$: a WENO-JS, b WENO-Z, c WENO-NS and d WENO-P

Fig. 9

Density Profiles of 2D problems [19] at $t = 0.8$ using $\Delta x = \Delta y = 1/800$: a WENO-JS, b WENO-Z, c WENO-NS and d WENO-P

Example 4.2

(i) Shu–Osher problem in one dimensional Euler equation [22]. The Shu–Osher problem used to probe the stability and accuracy of the shock-capturing method. We compute the 1-D Euler equation with the following initial conditions

$$\begin{aligned} (\rho , u, p) = {\left\{ \begin{array}{ll} (3.857143,2.629369,10.33333) &{}\quad \text {if }\;-5 \le x < -4, \\ (1+ 0.2 \sin (kx),0,1) &{}\quad \text {if }\;-4 \le x \le 5, \end{array}\right. } \end{aligned}$$

(4.5)

where k is the wave number of the entropy wave.

We solve this equation up to time $t = 1.8$. In this problem, a shock-wave propagating to the right (Mach 3) interacts with a perturbed density disturbance. The density perturbation going through the shock wave generates oscillations that are progressing into smaller amplitude shocks. The reference solution has been computed on a fine grid of 3201 grid using the fifth-order WENO-JS scheme [14]. Figure 5 shows numerical results of all schemes with different wave numbers k in (4.5). The fifth order WENO-P scheme produces solutions of comparable or better accuracy than the other schemes for the given wave numbers and meshes.

(ii) For the Lax problem [15], the initial condition is given by

$$\begin{aligned} (\rho , u, p) = {\left\{ \begin{array}{ll} (0.445,0.698,3.528) &{}\quad \text {if }\; -5 \le x < 0, \\ (0.500,0.000,0.571) &{}\quad \text {if }\; 0 \le x \le 5 \end{array}\right. } \end{aligned}$$

(4.6)

and the final time is $t = 1.3$. We set heat of specific ratio $\gamma =1.4$. The density profile and pressure of the Lax problem are shown in Fig. 6. The WENO-P scheme performs reasonably well and better than WENO-JS but yields similar results as WENO-Z and WENO-NS.

(iii) The initial data of the Sod problem [23] are given by

$$\begin{aligned} (\rho , u, p) = {\left\{ \begin{array}{ll} (1.000,0.750,1.000) &{}\quad \text {if }\;0 \le x < 0.5, \\ (0.125,0.000,0.100) &{}\quad \text {if }\;0.5 \le x \le 1, \end{array}\right. } \end{aligned}$$

with $\gamma =1.4$. We compute the equation until $t = 0.2$. The simulated density and pressure field are shown in Fig. 7. The performance of WENO-P are nearly the same as WENO-NS and WENO-Z but yields better than WENO-JS. The exact Riemann solver presented in Toro [24] is used here.

4.2.2 2D Euler Systems

In this subsection we apply the proposed scheme to 2D problem for 2D gas dynamics, Rayleigh–Taylor instability and Double Mach reflection of a strong shock in Cartesian coordinates. The governing 2D compressible Euler equation is given by

$$\begin{aligned} U_t + F(U)_x + G(U)_y = 0, \end{aligned}$$

(4.7)

where

$$\begin{aligned} U= & {} (\rho , \rho u , \rho v , E)^T, \\ F(U)= & {} (\rho u, p + \rho u^2 , \rho uv , u(E+p))^T, \\ G(U)= & {} (\rho v,\rho vu, p + \rho v^2, v(E+p))^T. \end{aligned}$$

The total energy E and pressure p is defined by

$$\begin{aligned} p= & {} (\gamma -1)\left( E - \frac{1}{2} \rho (u^2 +v^2)\right) , \end{aligned}$$

where $\gamma$ is the specific heat ratio. Here $\rho , u, v$ are density, x-wise-velocity components and y-wise-velocity components, respectively. The 2D Euler problem is solved in a dimension-by-dimension fashion with proposed scheme together with the third Runge–Kutta methods [22].

Example 4.3

(2D Problem for 2D gas dynamics) The first test 2D Riemann problem, introduced by [19], is solved on the rectangular domain $[0,1] \times [0,1].$ The 2D Riemann problem is defined by initial constant states in each quadrant which is divided by lines $x=0.8$ and $y=0.8$ on the square:

$$\begin{aligned} (\rho , u , v, p) = {\left\{ \begin{array}{ll} (1.5, 0, 0, 1.5) &{}\quad \text {if }\;0.8\le x\le 1, 0.8\le y\le 1, \\ (0.5323, 1.206, 0, 0.3)&{}\quad \text {if }\;0\le x< 0.8, 0.8\le y\le 1, \\ (0.138, 1.206, 1.206, 0.029) &{}\quad \text {if }\;0\le x < 0.8, 0\le y < 0.8,\\ (0.5323, 0, 1.206, 0.3)&{}\quad \text {if }\;0.8 <x\le 1, 0 \le y< 0.8 \end{array}\right. } \end{aligned}$$

and Dirichlet boundary conditions.

We take the heat specific ratio $\gamma = 1.4$. We display the numerical results of WENO-P with other WENO schemes in Figs. 8 and 9. An examination of these results reveals that WENO-P (d) yields a better resolution of the complex structure appearing in other WENO schemes.

Example 4.4

(Two-dimensional Rayleigh–Taylor instability) Taylor instability happens on an interface between two fluids of different densities when an acceleration is directed from heavier fluid to lighter fluid. This problem has been simulated extensively in the literature (e.g., [9, 26]). The computational domain is $[0,1/4] \times [0,1]$ and the initial conditions are

$$\begin{aligned} (\rho , u , v, p) = {\left\{ \begin{array}{ll} (2, 0, -0.025 a \cos (8 \pi x) , 2y+1) &{}\quad \text {if }\;0 \le y < 0.5, \\ (1, 0, -0.025 a \cos (8 \pi x) , y+\frac{3}{2})&{}\quad \text {if }\;0.5 \le y < 1, \end{array}\right. } \end{aligned}$$

with the sound speed $a = \sqrt{\gamma p/\rho }$ and the ratio of specific heats $\gamma = 5/3$. The gravitational effect is introduced by adding $\rho$ and $\rho v$ to the right hand side of third equation and fourth equation, respectively, of the 2 dimensional Euler equation. Reflective boundary conditions are imposed for the left and right boundaries, and

$$\begin{aligned} (\rho , u , v, p) = {\left\{ \begin{array}{ll} (2, 0, 0, 2.5) &{}\quad \text {top boundary}, \\ (1, 0, 0, 1)&{}\quad \text {bottom boundary}. \end{array}\right. } \end{aligned}$$

The final simulation time is $t=1.95$. The density contour plotted in Fig. 10 shows that the WENO-P scheme obtains more complex structures than the other schemes.

Fig. 10

Density profiles of Rayleigh–Taylor instability at $t = 1.95$ using $\Delta x = \Delta y = 1/500$: a WENO-JS, b WENO-Z, c WENO-NS and d WENO-P

Fig. 11

Double Mach reflection of a strong shock [25] at $t = 0.2$ using $\Delta x= \Delta y =1/400$ with WENO-JS, WENO-Z, WENO-NS, and WENO-P from the top to the bottom

Fig. 12

Zoom on $[2,2.8] \times [0,0.6]$ of the Double Mach reflection of a strong shock [25] at $t = 0.2$. WENO-JS, WENO-Z, WENO-NS, and WENO-P from the top to the bottom. First column $\Delta x = \Delta y = 1/100$, second column $\Delta x = \Delta y = 1/200$, third column $\Delta x = \Delta y = 1/400$

Example 4.5

(Double Mach reflection of a strong shock [25]) The final test considered in this paper is the two dimensional double Mach reflection of a shock off an oblique surface which describes the reflection of a planar Mach shock in air hitting a wedge. This test is widely used to verify the performance of numerical methods. We calculate this test problem on $[0, 4] \times [0, 1]$ and display the results in $[0, 3] \times [0, 1]$ as customary. Initially a right-moving Mach 10 shock is imposed and the shock front makes an angle of $60^{\circ }$ with the x-axis at $x = \frac{1}{6}$. The region from $x = 0$ to $x = \frac{1}{6}$ along the bottom boundary is assigned values for the initial post-shock flow and reflecting boundary condition is taken for the rest. The left hand boundary is assigned values for the initial post-shock flow. For the right-hand boundary at $x=4$, all gradients are set to zero. The top boundary of the problem is set to describe the exact motion of the Mach 10 shock. See [25] for a detailed description of this problem. We solve it up to time $t=0.2$ using $\Delta x = \Delta y = 1/400$ with $\gamma =1.4$. The numerical results of the WENO-P scheme are compared with WENO-JS, WENO-Z and WENO-NS in Fig. 11. Figure 12 shows the details at the Mach stem of the density variable at the final time with several grid points. It can be clearly seen that WENO-P and WENO-NS resolve better the instabilities around the Mach stem.

5 Conclusion

In this paper, we introduce a modified fifth-order WENO scheme to approximate solutions of nonlinear hyperbolic conservation laws. The motivation for this study is that the given three substencils for a fifth-order WENO scheme may provide unbalanced contributions to the evaluation point. Thus, in order to overcome this problem, we employ a parameter to make balancing the contribution of substencils. Numerical experiments show that the proposed WENO scheme yields better approximations than other fifth-order schemes at the treatment of numerical solutions including discontinuities. The computational cost of WENO-P is almost the same as WENO-Z and WENO-JS and more efficient than WENO-NS. The choice of parameter for balancing the contribution of substencils depends on the organization of substencils. In the near future, we will further investigate it for higher order WENO schemes.