Spectral Method for Fourth-Order Problems on Quadrilaterals

Abstract

In this paper, we investigate the spectral method for fourth-order problems defined on quadrilaterals. Some results on the Legendre irrational orthogonal approximations are established, which play important roles in the related spectral method on quadrilaterals. As examples of applications, we provide spectral schemes for a model problem with various boundary conditions. The spectral accuracy of suggested algorithms are proved. Numerical results demonstrate the effectiveness of suggested algorithms, and confirm the analysis well. The approximation results and techniques developed in this paper are also applicable to other fourth-order problems defined on quadrilaterals.

Appendix

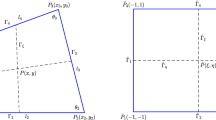
This appendix is devoted to the lifting technique. The edges $L_i$ of domain $\Omega$ are as follows (see Fig. 1),

$$\begin{aligned} L_i:\,l_i(x,y)=a_i x+b_i y+c_i=0,\qquad 1\le i\le 4. \end{aligned}$$

(A.1)

Let $l_{i+4}(x,y)=l_i(x,y),~i=1,2,3,4$. We could rewrite the equations corresponding to the edges as $x=x_i(y)$ for $L_i,i=1,3$, and $y=y_i(x)$ for $L_i,i=2,4$. Clearly,

$$\begin{aligned} \frac{dx_i}{dy}=-\frac{b_i}{a_i}\,\mathrm{for }\,i=1,3,\qquad \frac{dy_i}{dx}=-\frac{a_i}{b_i} \,\mathrm{for}\,i=2,4. \end{aligned}$$

(A.2)

We denote the normal vector of edges $L_i$ by $n_i=(\cos \alpha _i,\cos \beta _i)^T,~1\le i\le 4$. Besides, $Q_i$ stand for the four corners of domain $\Omega$ as in Fig. 1.

Our aim is to design the lifting function $v_b(x,y)$ such that

$$\begin{aligned} v_b(x,y)|_{L_i}= & {} v_b(x_i(y),y) = g_i(y),\qquad \partial _{n_i} v_b(x,y)|_{L_i}=h_i(y),\qquad i=1,3, \nonumber \\ v_b(x,y)|_{L_i}= & {} v_b(x,y_i(x))=g_i(x),\qquad \partial _{n_i} v_b(x,y)|_{L_i}=h_i(x),\qquad i=2,4, \end{aligned}$$

(A.3)

where $g_i(y),h_i(y) (i=1,3)$ and $g_i(x),h_i(x)(i=2,4)$ are given functions. In addition, the functions $g_i(y)$ and $g_i(x)$ fulfill certain consistent conditions ensuring the continuity of $v_b(x,y)$ at the corners of domain.

In the forthcoming discussions, we introduce the following polynomials,

$$\begin{aligned} s_i(x,y)= & {} \displaystyle \prod _{1\le j\le 4,j\ne i}(a_j x+b_j y+c_j)^2=\displaystyle \frac{l_1^2(x,y)l_2^2(x,y)l_3^2(x,y)l_4^2(x,y)}{l_i^2(x,y)}, \nonumber \\ t_i(x,y)= & {} (a_i x+b_i y+c_i)s_i(x,y)=l_i(x,y)s_i(x,y),\qquad i=1,2,3,4. \end{aligned}$$

(A.4)

It can be checked that

$$\begin{aligned} \partial _n s_i(x,y)\ne & {} 0,\quad s_i(x,y)\ne 0,\quad \partial _n t_i(x,y)\ne 0,\quad t_i(x,y)=0,\quad \,\mathrm{on}\,L_i,\,i=1,2,3,4, \nonumber \\ \partial _n s_i(x,y)= & {} s_i(x,y)=\partial _n t_i(x,y)=t_i(x,y)=0,\quad \mathrm{~on~}\cup ^{4}_{j=1,j\ne i}L_j, \end{aligned}$$

(A.5)

We also introduce the following polynomials,

$$\begin{aligned} \sigma _{i1}(x,y)= & {} l^2_{i+2}(x,y)l^2_{i+3}(x,y),\qquad \sigma _{i2}(x,y)=l_{i+1}(x,y)\sigma _{i1}(x,y), \nonumber \\ \sigma _{i3}(x,y)= & {} l_{i}(x,y)\sigma _{i1}(x,y),\,\,\,\quad \qquad \sigma _{i4}(x,y)=l_{i}(x,y)l_{i+1}(x,y)\sigma _{i1}(x,y), \nonumber \\ i= & {} 1,2,3,4. \end{aligned}$$

(A.6)

It can be verified that

$$\begin{aligned} \sigma _{12}(x,y)|_{L_2}= & {} \sigma _{13}(x,y)|_{L_1}=\sigma _{14}(x,y)|_{L_1\cup L_2}=0, \nonumber \\ \partial _n \sigma _{1j}(x,y)|_{L_3\cup L_4}= & {} \sigma _{1j}(x,y)|_{L_3\cup L_4}=0,\quad 1\le j\le 4. \end{aligned}$$

(A.7)

We can also verify that $\sigma _{ij}(x,y),2\le i,j\le 4$ have the same properties. Accordingly, we design the desired lifting function $v_b(x,y)$ satisfying (A.3) as follows,

$$\begin{aligned} v_b(x,y)= & {} \widetilde{g}_1(y)s_1(x,y)+\widetilde{h}_1(y)t_1(x,y) +\widetilde{g}_2(x)s_2(x,y)+\widetilde{h}_2(x)t_2(x,y) \nonumber \\&+\,\widetilde{g}_3(y)s_3(x,y)+\widetilde{h}_3(y)t_3(x,y) \nonumber \\&+\,\widetilde{g}_4(x)s_4(x,y)+\widetilde{h}_4(x)t_4(x,y)+\displaystyle \sum ^4_{i,j=1}p_{ij}\sigma _{ij}(x,y), \end{aligned}$$

(A.8)

where $\widetilde{g}_i,\widetilde{h}_i$ and $p_{ij}, 1\le i,j\le 4$ are undetermined functions and constants. We shall construct those undetermined quantities properly in the following four steps.

Step 1 According to (A.3), we use (A.5) and (A.7) to derive that

$$\begin{aligned} v_b(x,y)|_{L_1}= & {} \widetilde{g}_1(y)s_1(x_1(y),y)+p_{11}\sigma _{11}(x_1(y),y)+p_{12}\sigma _{12}(x_1(y),y) \nonumber \\&+\,p_{41}\sigma _{41}(x_1(y),y)+p_{43}\sigma _{43}(x_1(y),y)=g_1(y), \nonumber \\ v_b(x,y)|_{L_2}= & {} \widetilde{g}_2(x)s_2(x,y_2(x))+p_{21}\sigma _{21}(x,y_2(x))+p_{22}\sigma _{22}(x,y_2(x)) \nonumber \\&+\,p_{11}\sigma _{11}(x,y_2(x))+p_{13}\sigma _{13}(x,y_2(x))=g_2(x),\qquad \mathrm {etc.} \end{aligned}$$

(A.9)

Furthermore, the corner $Q_1=L_1\cap L_2$. Thus we know from (A.5) and (A.7) that

$$\begin{aligned} s_1(x_1(y),y)= & {} s_2(x,y_2(x))=\sigma _{12}(x_1(y),y)=\sigma _{13}(x,y_2(x)) \\= & {} \sigma _{21}(x,y_2(x))=\sigma _{22}(x,y_2(x))=\sigma _{41}(x_1(y),y)\\= & {} \sigma _{43}(x_1(y),y)=0, \qquad \,\mathrm{at} \,Q_1. \end{aligned}$$

Therefore

$$\begin{aligned} v_b(x,y)|_{Q_1}=p_{11}\sigma _{11}(x,y)|_{Q_1}=g_1(y)|_{Q_1}=g_2(x)|_{Q_1}. \end{aligned}$$

In other words,

$$\begin{aligned} p_{11}=\frac{g_1(y)|_{Q_1}}{\sigma _{11}(x,y)|_{Q_1}}=\frac{g_2(x)|_{Q_1}}{\sigma _{11}(x,y)|_{Q_1}}. \end{aligned}$$

(A.10)

Due to the continuity of $v_b(x,y)$, we have $g_1(y)|_{Q_1}=g_2(x)|_{Q_1}$. Thereby, the above expression is meaningful and so determines the constant $p_{11}$. In the same manner, we can calculate the constants $p_{i1},\,i=2,3,4$.

Step 2 For simplicity, let $\partial _x s_1(x_1(y),y)=\partial _x s_1(x,y)|_{x=x_1(y)}$, etc. By differentiating the two equations of (A.9), we derive that

$$\begin{aligned} \partial _y(v_b(x_1(y),y))= & {} \partial _y\widetilde{g}_1(y)s_1(x_1(y),y) +\widetilde{g}_1(y)(\partial _xs_1(x_1(y),y)\frac{dx_1}{dy}+\partial _y s_1(x_1(y),y)) \nonumber \\&+\,p_{11}(\partial _x\sigma _{11}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{11}(x_1(y),y)) \nonumber \\&+\,p_{12}(\partial _x\sigma _{12}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{12}(x_1(y),y)) \nonumber \\&+\,p_{41}(\partial _x\sigma _{41}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{41}(x_1(y),y)) \nonumber \\&+\,p_{43}(\partial _x\sigma _{43}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{43}(x_1(y),y))=\partial _yg_1(y), \nonumber \\ \partial _x(v_b(x,y_2(x)))= & {} \partial _x\widetilde{g}_2(x)s_2(x,y_2(x)) +\widetilde{g}_2(x) \left( \partial _xs_2(x,y_2(x))+\partial _ys_2(x,y_2(x))\frac{dy_2}{dx}\right) \nonumber \\&+\,p_{21} \left( \partial _x\sigma _{21}(x,y_2(x))+\partial _y\sigma _{21}(x,y_2(x))\frac{dy_2}{dx}\right) \nonumber \\&+\,p_{22}\left( \partial _x\sigma _{22}(x,y_2(x))+\partial _y\sigma _{22}(x,y_2(x))\frac{dy_2}{dx}\right) \nonumber \\&+\,p_{11}\left( \partial _x\sigma _{11}(x,y_2(x))+\partial _y\sigma _{11}(x,y_2(x))\frac{dy_2}{dx}\right) \nonumber \\&+\,p_{13}\left( \partial _x\sigma _{13}(x,y_2(x))+\partial _y\sigma _{13}(x,y_2(x))\frac{dy_2}{dx}\right) =\partial _xg_2(x). \end{aligned}$$

(A.11)

Moreover, we know from (A.5) and (A.7) that at the corner $Q_1$,

$$\begin{aligned} s_1(x_1(y),y)= & {} \partial _x s_1(x_1(y),y)=\partial _y s_1(x_1(y),y)=0 \\ s_2(x,y_2(x))= & {} \partial _x s_2(x,y_2(x))=\partial _y s_2(x,y_2(x))=0, \\ \partial _x\sigma _{41}(x_1(y),y)= & {} \partial _y\sigma _{41}(x_1(y),y)=\partial _x\sigma _{43}(x_1(y),y)=\partial _y\sigma _{43}(x_1(y),y)=0, \\ \partial _x\sigma _{21}(x,y_2(x))= & {} \partial _y\sigma _{21}(x,y_2(x))=\partial _x\sigma _{22}(x,y_2(x))=\partial _y\sigma _{22}(x,y_2(x))=0. \end{aligned}$$

Therefore

$$\begin{aligned} \partial _yv_b(x_1(y),y)|_{Q_1}= & {} p_{11}(\partial _x\sigma _{11}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{11}(x_1(y),y))|_{Q_1} \nonumber \\&+\,p_{12}(\partial _x\sigma _{12}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{12}(x_1(y),y))|_{Q_1}=\partial _yg_1(y)|_{Q_1}, \nonumber \\ \partial _xv_b(x,y_2(x))|_{Q_1}= & {} p_{11}(\partial _x\sigma _{11}(x,y_2(x))+\partial _y\sigma _{11}(x,y_2(x))\frac{dy_2}{dx})|_{Q_1} \nonumber \\&+\,p_{13}(\partial _x\sigma _{13}(x,y_2(x))+\partial _y\sigma _{13}(x,y_2(x))\frac{dy_2}{dx})|_{Q_1} \nonumber \\= & {} \partial _xg_2(x)|_{Q_1}. \end{aligned}$$

(A.12)

Consequently,

$$\begin{aligned} p_{12}= & {} \displaystyle \frac{\partial _yg_1(y)|_{Q_1}-p_{11}(\partial _x\sigma _{11}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{11}(x_1(y),y))|_{Q_1}}{(\partial _x\sigma _{12}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{12}(x_1(y),y))|_{Q_1}}, \nonumber \\ p_{13}= & {} \displaystyle \frac{\partial _xg_2(x)|_{Q_1}-p_{11}(\partial _x\sigma _{11}(x,y_2(x))+\partial _y\sigma _{11}(x,y_2(x))\frac{dy_2}{dx})|_{Q_1}}{(\partial _x\sigma _{13}(x,y_2(x))+\partial _y\sigma _{13}(x,y_2(x))\frac{dy_2}{dx})|_{Q_1}}. \end{aligned}$$

(A.13)

These expressions with (A.10) determine the constants $p_{12}$ and $p_{13}$. We can calculate the $p_{i2}$ and $p_{i3},~i=2,3,4$ in the same way.

Furthermore, we obtain from the first equation of (A.9) that

$$\begin{aligned}&\widetilde{g}_1(y)\nonumber \\&\quad =\displaystyle \frac{g_1(y)-p_{11}\sigma _{11}(x_1(y),y)-p_{12}\sigma _{12}(x_1(y),y) -p_{41}\sigma _{41}(x_1(y),y)-p_{43}\sigma _{43}(x_1(y),y)}{s_1(x_1(y),y)}. \end{aligned}$$

(A.14)

Since $p_{ij},\,1\le i\le 4,1\le j\le 3$ are given already by (A.10) and (A.13), the above expressions determine the functions $\widetilde{g}_1(y)$. We also can determine the functions $\widetilde{g}_2(x),\widetilde{g}_3(y)$ and $\widetilde{g}_4(x)$.

Step 3 According to (A.3), we use (A.5) and (A.7) to derive that

$$\begin{aligned} h_1(y)= & {} \partial _{n_1}u(x,y)|_{L_1}=\partial _xu(x_1(y),y)\cos \alpha _1+\partial _yu(x_1(y),y)\cos \beta _1,\\ h_2(x)= & {} \partial _{n_2}u(x,y)|_{L_2}=\partial _xu(x,y_2(x))\cos \alpha _2+\partial _yu(x,y_2(x))\cos \beta _2. \end{aligned}$$

Then, we have

$$\begin{aligned} \partial _yh_1(y)|_{Q_1}= & {} (\partial ^2_xu(x,y)\frac{d x_1}{d y}+\partial _{xy}u(x,y))|_{Q_1}\cos \alpha _1 +(\partial _{xy}u(x,y)\frac{d x_1}{d y} \nonumber \\&+\,\partial ^2_yu(x,y))|_{Q_1}\cos \beta _1, \nonumber \\ \partial _xh_2(x)|_{Q_1}= & {} \left( \partial ^2_xu(x,y)+\partial _{xy}u(x,y)\frac{dy_2}{dx}\right) |_{Q_1}\cos \alpha _2 \nonumber \\&+\,\left( \partial _{xy}u(x,y)+\partial ^2_yu(x,y)\frac{dy_2}{dx}\right) |_{Q_1}\cos \beta _2. \end{aligned}$$

(A.15)

Moreover, due to $g_1(y)=u(x_1(y),y),~g_4=u(x,y_4(x))$ and (A.4), we find that

$$\begin{aligned} \partial ^2_yg_1(y)|_{Q_1}= & {} \partial ^2_xu(x,y)|_{Q_1}\left( \frac{dx_1}{dy}\right) ^2 +2\partial _{xy}u(x,y)|_{Q_1}\frac{d x_1}{d y}+\partial ^2_yu(x,y)|_{Q_1}, \nonumber \\ \partial ^2_xg_2(x)|_{Q_1}= & {} \partial ^2_xu(x,y)|_{Q_1}+2\partial _{xy}u(x,y)|_{Q_1}\frac{dy_2}{dx} +\partial ^2_yu(x,y)|_{Q_1}\left( \frac{dy_2}{dx}\right) ^2. \end{aligned}$$

(A.16)

From the first equation of (A.15) and (A.16), we have

$$\begin{aligned} A_{Q_1}= & {} \left( \left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2-1\right) \partial _yh_1(y)|_{Q_1} \nonumber \\&+\,\left( \cos \beta _1-\frac{dx_1}{dy}\left( \frac{dy_4}{dx}\right) ^2\cos \alpha _1\right) \partial ^2_yg_1(y)|_{Q_1} \nonumber \\&+\,\left( \frac{dx_1}{dy}\cos \alpha _1-\left( \frac{dx_1}{dy}\right) ^2\cos \beta _1\right) \partial ^2_xg_4(x)|_{Q_1}, \nonumber \\ B_{Q_1}= & {} \left( \cos \alpha _1+\frac{dx_1}{dy}\cos \beta _1\right) \left( \left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2-1\right) \nonumber \\&+\,2\frac{dx_1}{dy}\frac{dy_4}{dx}\cos \alpha _1+2\frac{dx_1}{dy}\cos \beta _1 \nonumber \\&-\,2\left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2\cos \alpha _1 -2\left( \frac{dx_1}{dy}\right) ^2\frac{dy_4}{dx}\cos \beta _1. \nonumber \\ \partial _{xy}u(x,y)|_{Q_1}= & {} \frac{A_{Q_1}}{B_{Q_1}}. \end{aligned}$$

(A.17)

From the second equation of (A.15) and (A.16), we have

$$\begin{aligned} C_{Q_1}= & {} \left( \left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2-1\right) \partial _yh_4(y)|_{Q_1} \nonumber \\&+\,\left( \frac{dy_4}{dx}\cos \beta _4-\left( \frac{dy_4}{dx}\right) ^2\cos \alpha _4\right) \partial ^2_yg_1(y)|_{Q_1} \nonumber \\&+\,\left( \cos \alpha _4-\left( \frac{dx_1}{dy}\right) ^2\frac{dy_4}{dx}\cos \beta _4\right) \partial ^2_xg_4(x)|_{Q_1}, \nonumber \\ D_{Q_1}= & {} \left( \frac{dy_4}{dx}\cos \alpha _4+\cos \beta _4\right) \left( \left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2-1\right) \nonumber \\&+\,2\frac{dy_4}{dx}\cos \alpha _4+2\frac{dx_1}{dy}\frac{dy_4}{dx}\cos \beta _4 \nonumber \\&-\,2\frac{dx_1}{dy}\left( \frac{dy_4}{dx}\right) ^2\cos \alpha _4 -2\left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2\cos \beta _4. \nonumber \\ \partial _{xy}u(x,y)|_{Q_1}= & {} \frac{C_{Q_1}}{D_{Q_1}}. \end{aligned}$$

(A.18)

Then, we obtain the compatibility conditions as $\partial _{xy}u(x,y)|_{Q_1}=\frac{A_{Q_1}}{B_{Q_1}}=\frac{C_{Q_1}}{D_{Q_1}}$.

Next, by differentiating the (A.8) twice, we derive that

$$\begin{aligned} \partial _{xy}v(x,y)= & {} \partial _y\widetilde{g}_1(y)\partial _xs_1(x,y)+\widetilde{g}_1(y)\partial _{xy}s_1(x,y) +\partial _y\widetilde{h}_1(y)\partial _xt_1(x,y) \\&+\,\widetilde{h}_1(y)\partial _{xy}t_1(x,y) +\partial _x\widetilde{g}_2(x)\partial _ys_2(x,y)+\widetilde{g}_2(x)\partial _{xy}s_2(x,y)\\&+\,\partial _x\widetilde{h}_2(x)\partial _yt_2(x,y)+\widetilde{h}_2(x)\partial _{xy}t_2(x,y)+\partial _y\widetilde{g}_3(y)\partial _xs_3(x,y)\\&+\,\widetilde{g}_3(y)\partial _{xy}s_3(x,y) +\partial _y\widetilde{h}_3(y)\partial _xt_3(x,y)+\widetilde{h}_3(y)\partial _{xy}t_3(x,y)\\&+\,\partial _x\widetilde{g}_4(x)\partial _ys_4(x,y)+\widetilde{g}_4(x)\partial _{xy}s_4(x,y) +\partial _x\widetilde{h}_4(x)\partial _yt_4(x,y)\\&+\,\widetilde{h}_4(x)\partial _{xy}t_4(x,y) +\sum ^4_{i,j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y). \end{aligned}$$

Moreover, we know form (A.5) and (A.7) that

$$\begin{aligned} \partial _xs_i(x,y)|_{Q_1}= & {} \partial _xt_i(x,y)|_{Q_1} = \partial _{xy}t_i(x,y)|_{Q_1}=\partial _{xy}\sigma _{i4}(x,y)|_{Q_1}=0,\qquad 1\le i\le 4, \\ \partial _{xy}s_3(x,y)|_{Q_1}= & {} \partial _{xy}s_4(x,y)|_{Q_1}=0. \end{aligned}$$

Therefore,

$$\begin{aligned} \partial _{xy}u(x,y)|_{Q_1}= & {} \partial _{xy}v(x,y)|_{Q_1} \\= & {} \widetilde{g}_1(y)\partial _{xy}s_1(x,y)|_{Q_1}+\widetilde{g}_2(x)\partial _{xy}s_2(x,y)|_{Q_1} +\displaystyle \sum ^4_{i=1}\displaystyle \sum ^3_{j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y)|_{Q_1}. \end{aligned}$$

Consequently,

$$\begin{aligned} p_{14} = \frac{\partial _{xy}u(x,y)|_{Q_1} -(\widetilde{g}_1(y)\partial _{xy}s_1(x,y) +\widetilde{g}_2(x)\partial _{xy}s_2(x,y) +\sum \nolimits ^4_{i=1}\sum \nolimits ^3_{j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y))|_{Q_1}}{\partial _{xy}\sigma _4(x,y)|_{Q_1}}. \end{aligned}$$

(A.19)

In the same manner, we can determine the constants $p_{i4},~1\le i\le 4$.

Step 4 According to (A.3), we use (A.5) and (A.7) to derive that

$$\begin{aligned} \partial _nv_b(x,y)|_{L_1}= & {} \partial _n(\widetilde{g}_1(y)s_1(x,y) +\widetilde{h}_1(y)t_1(x,y)+\displaystyle \sum ^4_{i,j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y))|_{L_1} \nonumber \\= & {} h_1(y). \end{aligned}$$

(A.20)

Moreover, with the aid of (A.5), we deduce that

$$\begin{aligned} \partial _n(\widetilde{h}_1(y)t_1(x,y))|_{L_1}= & {} (\widetilde{h}_1(y)\partial _xt_1(x,y)\cos \alpha _1+\partial _y\widetilde{h}_1(y)t_1(x,y)\cos \beta _1\\&+\,\widetilde{h}_1(y)\partial _yt_1(x,y)\cos \beta _1)|_{L_1} \\= & {} \widetilde{h}_1(y)(\partial _xt_1(x,y)\cos \alpha _1+\partial _yt_1(x,y)\cos \beta _1)|_{L_1}\\= & {} \widetilde{h}_1(y)\partial _nt_1(x,y)|_{L_1}. \end{aligned}$$

By substituting the above equality into (A.20), we obtain

$$\begin{aligned} \widetilde{h}_1(y)=\frac{h_1(y)-\partial _n(\widetilde{g}_1(y)s_1(x,y))|_{L_1} -\left( \displaystyle \sum \nolimits ^4_{i,j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y)\right) |_{L_1}}{\partial _nt_1(x,y)|_{L_1}}, \end{aligned}$$

(A.21)

which determines the function $\widetilde{h}_1(y)$.

In the same way, we can determine the functions $\widetilde{h}_2(x),\,\widetilde{h}_3(y)$ and $\widetilde{h}_4(x)$.

Finally, a combination of (A.10), (A.13), (A.14), (A.19) and (A.21) leads to the desired lifting function (A.8).

Remark 5.1

We can construct the lifting function for the boundary condition corresponding to the mixed inhomogeneous boundary value problems of fourth order.