Skip to main content
SpringerLink
Log in

How Many Numerical Eigenvalues Can We Trust?

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

When using finite element and finite difference methods to approximate eigenvalues of 2mth-order elliptic problems, the number of reliable numerical eigenvalues can be estimated in terms of the total degrees of freedom \(N\) in resulting discrete systems. The truth is worse than what we used to believe in that the percentage of reliable eigenvalues decreases with an increased \(N\), even though the number of reliable eigenvalues increases with \(N\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Babuška, I., Osborn, J.E.: Eigenvalue problems. In: Ciarlet, P.G., Lions, J.L. (eds.) Handbook of Numerical Analysis, Vol. II, Finite Element Methods (Part I), pp. 641–787. North Holland, Amsterdam (1991)

    Google Scholar 

  2. Kac, M.: Can one hear the shape of a drum? Am. Math. Mon. 73, 1–23 (1966)

    Article  MATH  Google Scholar 

  3. Levine, H.A., Protter, M.H.: Unrestricted lower bounds for eigenvalues of classes of elliptic equations and systems of equations with applications to problems in elasticity. Math. Methods Appl. Sci. 7, 1–13 (1985)

    Article  MathSciNet  Google Scholar 

  4. Li, P., Yau, S.T.: On the Schrödinger equation and the eigenvalue problem. Comm. Math. Phys. 88, 309–318 (1983)

    Article  MATH  MathSciNet  Google Scholar 

  5. Lin, Q., Xie, H., Xu, J.: Lower bounds of the discretization error for piecewise polynomials. Math. Comp. 88(285), 1–13 (2014)

  6. Pleijel, A.: On the eigenvalues and eigenfunctions of elastic plates. Comm. Pure Appl. Math. 3, 1–10 (1950)

    Article  MATH  MathSciNet  Google Scholar 

  7. Polya, G.: On the eigenvalues of vibrating membranes. Proc. London Math. Soc. 11, 419–433 (1961)

    Article  MATH  MathSciNet  Google Scholar 

  8. Protter, M.H.: Can one hear the shape of a drum? Revisited. SIAM Rev. 29–2, 185–197 (1987)

    Article  MathSciNet  Google Scholar 

  9. Strang, G., Fix, G.J.: An Analysis of the Finite Element Method. Prentice-Hall, Englewood Cliffs (1973)

    MATH  Google Scholar 

  10. Weideman, J.A.C., Trefethen, L.N.: The eigenvalues of second-order spectral differentiation matrices. SIAM J. Numer. Anal. 25–6, 1279–1298 (1988)

    Article  MathSciNet  Google Scholar 

  11. Weyl, H.: Über die asymptotische verteilung der Eigenwerte. Gott Nach. 1911, 110–117 (1911)

Download references

Acknowledgments

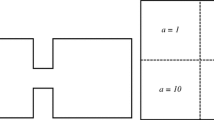
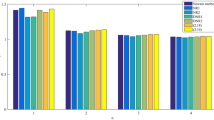
The author would like to thank Professor Huiyuan Li for producing the two graphs in the paper.

Author information

Authors and Affiliations

  1. Beijing Computational Science Research Center, Beijing, 100084, China

    Zhimin Zhang

  2. Department of Mathematics, Wayne State University, Detroit, MI, 48202, USA

    Zhimin Zhang

Authors
  1. Zhimin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhimin Zhang.

Additional information

This work is supported in part by the National Natural Science Foundation of China under Grants 11471031 and 91430216, and the US National Science Foundation through Grants DMS-1115530 and DMS-1419040.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Z. How Many Numerical Eigenvalues Can We Trust?. J Sci Comput 65, 455–466 (2015). https://doi.org/10.1007/s10915-014-9971-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-014-9971-5

Keywords

Mathematics Subject Classification

Search

Navigation