Skip to main content
SpringerLink
Log in

Numerical approach for time-fractional Burgers’ equation via a combination of Adams–Moulton and linearized technique

  • Original Paper
  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

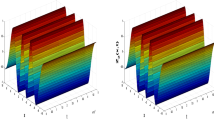
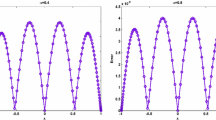
Abstract

Recently, fractional derivatives have become increasingly important for describing phenomena occurring in science and engineering fields. In this paper, we consider a numerical method for solving the fractional Burgers’ equations (FBEs), a vital topic in fractional partial differential equations. Due to the difficulty of the fractional derivatives, the nonlinear FBEs are linearized through the Rubin–Graves linearization scheme combined with the implicit the third-order Adams–Moulton scheme. Additionally, in the spatial direction of the FBEs, the fourth-order central finite difference scheme is used to obtain more accurate solutions. The convergence of the proposed scheme is theoretically and numerically analyzed. Also, the efficiency is demonstrated through several numerical experiments and compared with that of existing methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Availability of data and materials

Data sharing is not applicable to this article as no data sets were generated or analyzed during the current study.

References

  1. R.L. Bagley, P.J. Torvik, A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 27, 201–210 (1983). https://doi.org/10.1122/1.549724

    Article  CAS  Google Scholar 

  2. D.A. Benson, S.W. Wheatcraft, M.M. Meerschaert, Application of a fractional advection-dispersion equation. Water Resour. Res. 36, 1403–1412 (2000). https://doi.org/10.1029/2000WR900031

    Article  Google Scholar 

  3. R. Choudhary, S. Singh, D. Kumar, A second-order numerical scheme for the time-fractional partial differential equations with a time delay. Comput. Appl. Math. 41(3), 114 (2022). https://doi.org/10.1007/s40314-022-01810-9

    Article  Google Scholar 

  4. A.D. Fitt, A.R.H. Goodwin, K.A. Ronaldson, W.A. Wakeham, A fractional differential equation for a MEMS viscometer used in the oil industry. J. Comput. Appl. Math. 229, 373–381 (2009). https://doi.org/10.1016/j.cam.2008.04.018

    Article  Google Scholar 

  5. M. Oeser, S. Freitag, Modeling of materials with fading memory using neural networks. Int. J. Numer. Methods Eng. 78, 843–862 (2009). https://doi.org/10.1002/nme.2518

    Article  Google Scholar 

  6. S. Bu, A collocation methods based on the quadratic quadrature technique for fractional differential equation. AIMS Math. 7(1), 804–820 (2022). https://doi.org/10.3934/math.2022048

    Article  Google Scholar 

  7. Y. Jeon, S. Bu, Improved numerical approach for Bagley-Torvik equation using fractional integral formula and Adams-Moulton method. J. Comput. Nonlinear Dyn. (to be appeared) (2024)

  8. W. Deng, Smoothness and stability of the solutions for nonlinear fractional differential equations. Nonlinear Anal.: Theory Math. Appl. 72(3–4), 1768–1777 (2010). https://doi.org/10.1016/j.na.2009.09.018

    Article  Google Scholar 

  9. K. Diethelm, N.J. Ford, A.D. Freed, Detailed error analysis for a fractional Adams method. Numer. Algorithms 36(1), 31–52 (2004). https://doi.org/10.1023/B:NUMA.0000027736.85078.be

    Article  Google Scholar 

  10. C. Lubich, Discretized fractional calculus. SIAM J. Math. Anal. 17, 704–719 (1986). https://doi.org/10.1137/0517050

    Article  Google Scholar 

  11. I. Podlubny, Fractional Differential Equations (Academic Press, San Diego, 1999)

    Google Scholar 

  12. F. Mainardi, The fundamental solutions for the fractional diffusion-wave equation. Appl. Math. Lett. 9(6), 23–28 (1996)

    Article  Google Scholar 

  13. R. Metzler, J. Klafter, Boundary value problems for fractional diffusion equations. Physica A 278, 107–125 (2000)

    Article  CAS  Google Scholar 

  14. Q. Wang, Numerical solutions for fractional KdV-Burgers’ equation by Adomian decomposition method. Appl. Math. Comput. 182(2), 1048–1055 (2006)

    Google Scholar 

  15. R. Jiwari, A Haar wavelet quasilinearization approach for numerical simulation of Burgers’ equation. Comput. Phys. Commun. 183, 2413–2423 (2012)

    Article  CAS  Google Scholar 

  16. F. Pitolli, A fractional B-spline collocation method for the numerical solution of fractional Predator-Prey models. Fractal Fract. 2, 13 (2018)

    Article  Google Scholar 

  17. M. Yaseen, M. Abbas, T. Nazir, D. Baleanu, A finite difference scheme based on cubic trigonometric B-splines for a time fractional diffusion wave equation. Adv. Differ. Equ. 2017, 274 (2017)

    Article  Google Scholar 

  18. V.D. Djordjevica, T.M. Atanackovic, Similarity solutions to the nonlinear heat conduction and Burgers/Korteweg de Vries fractional equations. J. Comput. Appl. Math. 222(2), 701–714 (2008)

    Article  Google Scholar 

  19. J.J. Keller, Propagation of simple nonlinear waves in gas-filled tubes with friction. Z. Angew. Math. Phys. 32, 170–181 (1981)

    Article  Google Scholar 

  20. N. Sugimoto, Generalized Burgers’ equation and fractional calculus, nonlinear wave motion. Pitman Monogr. Surv. Pure Appl.: Longman Sci. Tech. Harlow 43, 162–179 (1989)

    Google Scholar 

  21. Z. Asgari, S.M. Hosseini, Efficient numerical schemes for the solution of generalized time fractional burgers type equations. Numer. Algorithms 77, 763–792 (2018)

    Article  Google Scholar 

  22. L. Chen, S.J. Lü, T. Xu, Fourier spectral approximation for time fractional burgers equation with nonsmooth solutions. Appl. Numer. Math. 169, 164–178 (2021)

    Article  Google Scholar 

  23. M.S. Rawashdeh, A reliable method for the space-time fractional burgers and time-fractional Cahn-Allen equations via the FRDTM. Adv. Differ. Equ. (99) (2017)

  24. R. Shokhanda, P. Goswami, Solution of generalized fractional burgers equation with a nonlinear term. Int. J. Appl. Comput. Math 8(235) (2022)

  25. D. Li, M. Zhang, M. Ran, A linear finite difference scheme for generalized time fractional Burgers’ equation. Appl. Math. Model. 40(11–12), 6069–6081 (2016). https://doi.org/10.1016/j.apm.2016.01.043

    Article  Google Scholar 

  26. F. Liu, C. Yang, K. Burrage, Numerical method and analytical technique of the modified anomalous subdiffusion equation with a nonlinear source term. J. Comput. Appl. Math. 231(1), 160–176 (2009). https://doi.org/10.1016/j.cam.2009.02.013

    Article  Google Scholar 

  27. Y. Xu, O. Agrawal, Numerical solutions and analysis of diffusion for new generalized fractional Burgers’ equation. Fract. Calc. Appl. Anal. 16(3), 709–736 (2013). https://doi.org/10.2478/s13540-013-0045-4

    Article  Google Scholar 

  28. K.E. Atkinson, An Introduction to Numerical Analysis (Wiley, New York, 1991)

    Google Scholar 

  29. V. Mukundan, A. Awasthi, Linearized implicit numerical method for Burgers’ equation. Nonlinear Eng. Model. Appl. 5(4), 219–234 (2016). https://doi.org/10.1515/nleng-2016-0031

    Article  Google Scholar 

  30. P.C. Jain, D.N. Holla, Numerical solutions of coupled Burgers’ equation. Int. J. Non-Linear Mech. 13(4), 213–222 (1978). https://doi.org/10.1016/0020-7462(78)90024-0

    Article  Google Scholar 

  31. R. Garrappa, Numerical solution of fractional differential equations: a survey and a software tutorial. Mathematics 6(2), 1 (2018). https://doi.org/10.3390/math6020016

    Article  Google Scholar 

  32. S. Bu, Y. Jeon, Higher order predictor-corrector methods with an enhanced predictor for fractional differential equations. Math. Comput. Simul. (to be appeared) (2023)

  33. Y. Yan, K. Pal, N.J. Ford, Higher order numerical methods for solving fractional differential equations. BIT Numer. Math. 54 (2014)

  34. S.G. Rubin, R.A. Graves Jr., Viscous flow solutions with a cubic spline approximation. Comput. fluids 3(1), 1–36 (1975)

    Article  Google Scholar 

  35. B.K. Singh, M. Gupta, Trigonometric tension B-spline collocation approximations for time fractional Burgers’ equation. J. Ocean Eng. Sci. (in press) (2022)

  36. A. Esen, O. Tasbozan, Numerical solution of time fractional Burgers’ equation by cubic B-spline finite elements. Mediterr. J. Math. 13, 1325–1337 (2016)

    Article  Google Scholar 

  37. M. Onal, A. Esen, A Crank-Nicolson approximation for the time fractional Burgers’ equation. Appl. Math. Nonlinear Sci. 5(2), 177–184 (2020)

    Article  Google Scholar 

  38. M. Yaseen, M. Abbas, An efficient cubic trigonometric B-spline collocation scheme for the time-fractional telegraph equation. Int. J. Comput. Math. 97(3) (2020)

  39. T.S. El-Danaf, A.R. Hadhoud, Parametric spline functions for the solution of the one time fractional Burgers’ equation. Appl. Math. Model. 36 (2012)

Download references

Funding

The first author Jeon and the corresponding author Bu were supported by basic science research program through the National Research Foundation of Korea (NRF) funded by the Korea government (MSIT) (Grant Number RS-2023-00237912) and (Grant Number NRF-2022R1A2C1004588), respectively.

Author information

Authors and Affiliations

  1. Mechatronics Research Center, Hongik University, Sejong, 30016, Republic of Korea

    Yonghyeon Jeon

  2. Department of Liberal Arts, Hongik University, Sejong, 30016, Republic of Korea

    Sunyoung Bu

Authors
  1. Yonghyeon Jeon
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sunyoung Bu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

This is a joint work in all respects.

Corresponding author

Correspondence to Sunyoung Bu.

Ethics declarations

Competing interest

The authors declare that they have no competing interests.

Ethics approval

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jeon, Y., Bu, S. Numerical approach for time-fractional Burgers’ equation via a combination of Adams–Moulton and linearized technique. J Math Chem 62, 1189–1208 (2024). https://doi.org/10.1007/s10910-024-01589-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10910-024-01589-6

Keywords

Search

Navigation