1 Introduction

The process of aging and its effects on various measurable biological features have been extensively studied in recent years [1]. Considerable effort has been put into establishing the concept and markers of biological aging which is designed to incorporate the general deterioration of multiple biological functions [2,3,4]. Specifically, the relationship between chronological age and DNA methylation has been rigorously investigated [5, 6] with multiple predictive models (deemed “epigenetic clocks”) presented [7,8,9,10,11,12,13,14,15] that aim to estimate the chronological age by observing DNA methylation levels in various genomic positions.

DNA methylation is one of the epigenetic changes affecting the genome, through the process of which the nucleotide sequence of the DNA remains intact, while methyl groups are attached to the molecule, almost exclusively in CpG dinucleotide contexts. These in turn have a profound influence on chromatin structure, i.e., on the way the DNA is wrapped around histone molecules for compaction. Methylated genomic regions tend to be tightly packed, their accessibility during biological processes limited. Thus, DNA methylation has a direct regulatory role by influencing the transcription of affected genes.

One of the simplest techniques for predicting an outcome from a set of independent variables is linear regression, during which a line is fitted to the data in many dimensions that minimizes an appropriately defined loss function or prediction error. In many cases, model training suffers greatly from overfitting whenever the number of independent variables greatly exceeds the number of available observations. To counteract this issue, the general practice is to add regularization terms to the loss function that ensure that even in the case of many independent parameters, most model coefficients remain close to zero. L1-regularization applies a penalty term proportional to the sum of absolute coefficient values, while L2-regularization uses the sum of squared coefficient values as penalty.

Most of the best-known age predictors work on the principle of training a penalized multiple linear regression model that linearly combines L1 and L2 penalties (elastic net model) on a suitable set of methylation data (training dataset) and using the thus obtained regression coefficients to predict chronological age on an independent cohort (test dataset). The main difference between the approaches is not a methodological one, but rather the technical issue of data selection.

It has been previously demonstrated that epigenomic patterns and peculiarities largely depend on the type of tissue being analyzed [13], thus many epigenetic clocks focus on generating a predictive model optimized for a specific tissue type with very high accuracy [7,8,9,10, 12, 13, 15]. On the other hand, Horvath [14] has shown that it is also feasible to build a multi-tissue predictor which can estimate chronological age in samples with a wide variety of sources with surprising precision.

Besides the question of tissue of origin, the exact details of data acquisition cannot be overlooked either. Most of the publicly available methylation datasets were generated by one of the three Illumina platforms: Illumina Infinium HumanMethylation27 BeadChip (27 K), Illumina Infinium HumanMethylation450 BeadChip (450 K) or Illumina Infinium HumanMethylationEPIC BeadChip (EPIC). All the platforms measure DNA methylation with single-site resolution throughout the genome with the main difference being the number of CpG sites (or probes) investigated. The 27 K array provides information about 27,578, the 450 K array about 485,512 and the EPIC array about 866,836 CpG sites. However, even though with ever newer technologies incrementally more information is available about the samples, there are only 24,677 CpG sites that are explored by all three platforms. Thus, epigenetic clocks trained on datasets evaluated on specific platforms [7, 13,14,15] might suffer from a substantial loss of accuracy when tested on samples analyzed with a different instrument, especially if the methylation values of the covariates included in the model are missing from the data. This subject was partly addressed by McEwen et al. (2018) [16] on a relatively small cohort of samples analyzed on both 450 K and EPIC platforms, who found that DNA methylation age (DNAm age) predicted by the Horvath pan-tissue clock [14] and chronological age had a Pearson-correlation coefficient in the range of r = 0.86–0.87 and r = 0.84–0.86 for the 450 K and EPIC data, respectively (depending on preprocessing methods). This is a notable decrease in precision compared to the result (r = 0.96) obtained for the test dataset in Horvath [14] which contained 27 K and 450 K data.

Given that, by design of the penalized regression approach, all elastic net-based epigenetic clocks contain a couple hundred CpG sites at most, they disregard the better part of the methylation information available even if the EPIC platform was used for assessment. Also, CpG sites included in the various models as covariates (clock CpGs) rarely overlap between clocks. Consequently, it is reasonable to assume that limiting model training to the 24,677 CpG sites overlapping all three platforms and selecting a subset of these for chronological age prediction would still yield sufficient results and could provide a model which can be straightforwardly adapted to any Illumina dataset without further modifications.

Therefore, we aimed to create a revised version of the original Horvath pan-tissue epigenetic clock by reproducing the original pipeline of model selection on a training dataset which includes most of the original training data from [14] but that has also been expanded with EPIC methylation data obtained from multiple source tissues. We compared model performance on a test set that contains both a large part of the original test data from [14] and additional publicly available EPIC datasets.

2 Materials and methods

2.1 DNA methylation datasets used for training and testing

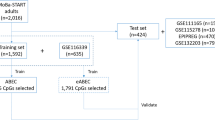
The methylation datasets used in this study contained only normal (non-cancerous) samples and were obtained either from the NCBI Gene Expression Omnibus (GEO) [17] or the NCI Genomic Data Commons (GDC) data portal [18]. GEO study accession numbers of the investigated datasets are listed in Supplementary file 1 along with additional summarizing statistics. The GDC data portal principally stores data from cancer cases, but for many patients normal, non-cancerous tissue samples are also available serving mostly as a reference for comparison in various bioinformatical pipelines. Whenever available, the methylation data for these samples were downloaded using the GDC Data Transfer Tool. The details of these studies can also be found in Supplementary file 1.

Altogether the training and testing datasets contained 5964 and 4369 samples respectively.

Downloaded datasets contained DNA methylation information in the form of a single β-value for each investigated CpG site of each sample which ranges from 0 (completely unmethylated) to 1 (completely methylated) [19]. On many datasets, various normalization steps were performed prior to submission to the relevant data portal.

2.2 Data preprocessing

In the case of datasets downloaded from GEO, samples were filtered to only contain ones that were non-cancerous and were not affected by known methylation altering diseases. Similarly to Horvath [14], mean intra-cohort correlation was calculated for each sample of each dataset and samples with a value of less than 0.9 were discarded to get rid of technical artefacts. Samples with a maximum methylation β-value of less than 0.96 were also filtered out for the same reason. All samples for which no chronological age information was available were excluded.

27 K and 450 K GEO datasets were split into training and test sets according to the categorization defined by Horvath [14]. EPIC datasets and all data obtained from the GDC data portal were grouped into training and test sets by adhering to the heuristic criteria of distributing samples of various (1) chronological ages, (2) source tissues and (3) measurement platforms homogenously among the two datasets. Details of training and test set data are available in Supplementary file 1.

All further investigations were limited to the 24,677 CpG sites that overlap across all platforms. The training data was additionally examined to identify sites with missing values in at least 90% of the samples of any given dataset. Probes that were thus missing from most samples in multiple datasets were also excluded from downstream analysis, resulting in a total of 21,255 investigated probes (see Supplementary file 2).

Both the Illumina 450 K and EPIC platforms simultaneously use two different types of chemical assays (Infinium type I and type II probes) to measure DNAm levels which results in distinctly different β-value distributions across different probe types within a single sample. For this reason, it is generally advisable to perform some type of normalization on the raw data to obtain comparable results. One of the widely used techniques is Beta Mixture Quantile dilation (BMIQ) [20] that rescales the β-values of type II probes so that their distribution is similar to that of type I ones. Given however that the 27 K assay only contains type II probes, the above described overlapping CpGs consequently belong to the type II category, rendering the problem of probe-type normalization obsolete in our specific case.

In spite of this, Horvath [14] found that it can be beneficial to normalize the β-values of the datasets to a gold standard distribution acquired by averaging the β-values of the largest dataset of the training data. In our analysis, we refrained from performing this step. The rationale behind this adjustment is that normalization both takes a lot of time and results in artificially similar datasets, hence we were hoping to create a prediction model that is easy and fast to run even on a large number of samples and that generalizes well to data of various origins.

The only further preprocessing step is performed as a safety measure on samples that contain methylation values that are lower than 0 or higher than 1, which are simply rescaled to the (0,1) range. This step is generally not necessary as β-values by definition should conform to this criterion, but we implemented it in order to avoid possible error messages when running the below models in less-controlled settings.

2.3 Age predictor models used in the analysis

Essentially, we intended to use the same framework for model building as Horvath [14] to simply construct a revised and updated epigenetic clock that can be used on all types of methylation data. To this end, we employed the cv.glmnet() function of the glmnet R package and trained our models with tenfold cross-validation with the “alpha” parameter fixed at 0.5, while varying “lambda” to achieve the lowest MSE (mean squared error) among tested models. Methylation β-values were used as independent variables and the following transformation of chronological age as the dependent variable:

$$F(age) = \left\{\begin{array}{c}log(age+1)-log({age}_{\mathrm{adult}}+1), if age\le {age}_{\mathrm{adult}}\\ (age-{age}_{\mathrm{adult}})/({age}_{\mathrm{adult}}+1), if age >{age}_{\mathrm{adult}}\end{array}\right.$$

with \({age}_{\mathrm{adult}}=20\) throughout the analysis.

Three different models were built this way: “elasticNet (239)” was trained on all training data and resulted in 239 CpG sites with a non-zero coefficient; “filtered H (272)” was trained on those 308 CpG sites of the original Horvath pan-tissue clock that overlapped the initial set of 21,255 investigated probes and resulted in 272 sites with non-zero coefficients; and “retrained H (308)” which was simply fit to the dataset without cross-validation and contained all the 308 CpG sites of the original Horvath pan-tissue clock that overlapped the initial set of 21,255 investigated probes (Supplementary file 2).

The predictions of a fourth model, the original Horvath pan-tissue clock is also analyzed below, referred to as the “original H (336)” model, given that out of the 354 CpG sites of the original predictor, only 336 are present in EPIC data (Supplementary file 2). Testing was performed by simply setting the coefficients of the missing probes to zero.

2.4 Measures of model accuracy

Model accuracy was assessed by calculating the two measures defined in Horvath [14]: the Pearson-correlation coefficient (r) between chronological age and predicted DNAm age; and median absolute error (MAE), the median value of the absolute differences between chronological age and predicted DNAm age. For example, a median absolute error of 4 years means that the DNAm age predicted by the given model differs by 4 years or less from the actual chronological age for 50% of the samples. In some cases, the 90th percentile of absolute errors is also displayed to characterize the absolute error distribution in more detail.

3 Results

3.1 Training accuracy of different models

Even though accuracy on the training dataset is not a reliable measure of model generalizability, it is a useful guide to uncover if it is even possible to establish a linear relationship between CpG site methylation values and chronological age. Figure 1 contains the predicted DNAm age and respective chronological age values for the training dataset in case of the three above defined models and also for the “original H (336)” model. Given that the first three models (panels A-C) were specifically optimized on this dataset, their superior performance is expected compared to the “original H (336)” model (panel D). The performance of the “original H (336)” model was assessed on the training dataset extended with the 28 CpG sites contained in the original model that do overlap all three platforms but were previously filtered out due to many missing values (see Supplementary file 2). The efficacy of the “original H (336)” model suffers most in the case of EPIC array datasets, in line with basic intuition. Discrepancies between chronological and predicted age for 27 K and 450 K data can be attributed to the fact that only 336 of the original 354 clock CpGs are among the ones overlapping all platforms. Nevertheless, the results show that it is possible to achieve higher accuracy than what the original model is able to provide in a dataset extended with EPIC data by the simple reoptimization of either the selected sites or their coefficients.

Fig. 1
figure 1

Predicted DNAm age in the function of actual chronological age for the samples of the training set in case of the four tested models (A “elasticNet (239)”, B “filtered H (272)”, C “retrained H (308)”, D “original H (336)”) colored by Illumina platform. The first three models were trained on this dataset, while the last one was used as is. The vertical axis is identical for all panels (r Pearson-correlation coefficient, MAE median absolute error; black diagonal lines are at a 45-degree angle)

Full size image

3.2 Test accuracy of different models

The more meaningful results of testing the models on an independent dataset are displayed on Fig. 2. The two panels show the same data colored by the type of dataset (A) or the applied prediction model (B). The overall performance measures of the three models introduced in the study ranged between r = 0.917–0.921 and MAE = 3.60–3.85. The same metrics for the “original H (336)” model on the whole testset were r = 0.880 and MAE = 5.13. It is apparent that all tested models perform best on 27 K and 450 K datasets downloaded from GEO. Even the “original H (336)” model has high correlation and low median absolute error for these datasets, given that these were part of the original testing data of Horvath [14] and the Horvath pan-tissue epigenetic clock was specifically trained on 27 K and 450 K datasets. The three models trained on datasets containing EPIC array data perform well on EPIC array test sets (r = 0.89–0.90; MAE = 3.54–4.51 years), while the “original H (336)” model has remarkably lower accuracy (r = 0.83; MAE = 6.09 years). Interestingly, all models suffer from a notable decrease in performance on test data downloaded from the GDC data portal, with “filtered H (272)” and “retrained H (308)” models providing the highest accuracy in terms of both correlation and MAE. The general trend of diminished power for GDC data might be due to the fact, that non-cancerous samples stored on the portal are usually surgical resections of the normal tissue surrounding the tumor that might still contain a low concentration of tumor cells which can influence the methylation landscape of the whole sample in an unforeseen manner.

Fig. 2
figure 2

Accuracy (Pearson-correlation between predicted and chronological age vs. median absolute error) of the investigated models in the test dataset. Points are colored either by data type (A) or the model used for prediction (B). An ideal model would result in a correlation of 1 and a median absolute error of 0 years, thus points nearest to the upper left corner of the graphs provide the best results for the given data type/model combination

Full size image

In common applications, when the precise estimation of the chronological age is of utmost importance, the distribution of absolute errors provides a better understanding of model performance than the correlation between predicted and chronological age. Therefore, we plotted the absolute error distribution for the four models on Fig. 3 with their main statistical properties highlighted in case of the whole dataset (A) and specifically for EPIC samples (B). It is apparent that both globally and for EPIC samples only the “filtered H (272)” model provides the most accurate results, and the “original H (336)” model has the lowest performance.

Fig. 3
figure 3

Absolute error distribution in the test dataset for the investigated models for the whole dataset (A) and for EPIC samples only (B). The filled curves show the estimated normalized probability density function of the data, the vertical axes are identical for all graphs

Full size image

3.3 CpG sites highly associated with chronological age

Given that 95 of the 239 CpG sites selected automatically out of 21,255 in the “elasticNet (239)” model overlap with the CpG clock sites of the original Horvath pan-tissue epigenetic clock, we found it worth investigating if there were any specific CpG probes present in all four models with high absolute coefficient and consistent sign. Figure 4 shows the coefficients of the probes overlapping in the three trained models and the original Horvath pan-tissue clock. In all three cases, there is high correlation between the coefficient values of the models, suggesting that the selected probes have an inherent association with biological age and were not simply selected as a technical peculiarity of the elastic net model fitting approach. The five CpGs that appeared with consistently high absolute coefficients in all four models were cg00864867, cg06993413, cg14424579, cg16241714 and cg22736354. All of them had a positive coefficient value in all four models, implying that these sites tend to be hypermethylated in the elderly and hypomethylated in younger people. They are located on genes PAWR (PRKC Apoptosis WT1 Regulator), DPP8 (Dipeptidyl peptidase 8), AGBL5 (Cytosolic carboxypeptidase-like protein 5), CEBPD (CCAAT/enhancer-binding protein delta) and NHLRC1 (E3 ubiquitin-protein ligase NHLRC1) respectively, all of which are involved in either apoptosis, autophagy, various metabolic processes, transcription or cell differentiation according to the Gene Ontology (GO) database [21, 22].

Fig. 4
figure 4

Relationship between trained model coefficients (A. “elasticNet (239)” B. “filtered H (272)” C. “retrained H (308)”) and the “original H (336)” model coefficients. CpG sites with an absolute coefficient larger than 1.5 in either of the two displayed models are labelled with their CpG IDs. CpG sites that appear in all four models with the same sign and have an absolute coefficient that is larger than 1.5 in at least one of the models are highlighted with a grey border. (N: number of overlapping probes between the two models; r: Pearson-correlation coefficient between model coefficient values; grey diagonal lines are at a 45-degree angle)

Full size image

4 Discussion

We present three epigenetic clock models based on a large cohort of multi-tissue, multi-platform methylation data that are straightforward extensions of the original Horvath pan-tissue epigenetic clock, but which can be applied with high accuracy on EPIC array data as well. Two out of the three models were specifically designed to include only a subset of the clock CpGs defined by Horvath [14] to make them easily adaptable to previous pipelines where raw data might already be filtered to this probeset.

Out of the three models, the best performance on the test set was achieved with an elastic net model limited to the 308 original clock CpGs which overlap all three of the 27 K, 450 K and EPIC methylation platforms and that had a total of 272 non-zero covariates (“filtered H (272)”). All three introduced models outperformed the original Horvath pan-tissue epigenetic clock, especially on EPIC array data. This result can be attributed to the fact that the original model was trained exclusively on 27 K and 450 K data and more than a dozen of its covariates are inherently missing from EPIC array datasets.

Previous results [15] suggest that even better accuracy can be achieved with models trained on datasets of specific tissue types whenever the test dataset is also originated from the same tissue source, although this tradeoff between performance and generalizability is an expected characteristic of any machine learning approach.

We also found that an elastic net model trained on all the CpG sites overlapping all three methylation platforms included 239 CpGs with non-zero coefficients of which about 40% overlapped with the clock CpGs of the original Horvath clock. This suggests that these sites have a strong association with biological aging irrespective of tissue source or measurement platform. Five of these appeared with high absolute coefficients in all tested models and were located on genes with known impact on various aging-related cellular pathways. These results imply that the tested epigenetic clock models not only fit well to the training and testing datasets, but that they also capture and track the manifestations of true biological processes, and thus can be potentially applied to further independent data with reasonable accuracy.