Theory of transcription bursting: stochasticity in the transcription rates

Abstract

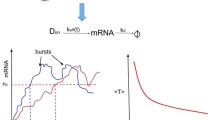
Transcription bursting creates variation among the individuals of a given population. Bursting emerges as the consequence of turning on and off the transcription process randomly. There are at least three sub-processes involved in the bursting phenomenon with different timescale regimes viz. flipping across the on–off state channels, microscopic transcription elongation events and the mesoscopic transcription dynamics along with the mRNA recycling. We demonstrate that when the flipping dynamics is coupled with the microscopic elongation events, then the distribution of the resultant transcription rates will be over-dispersed. This in turn reflects as the transcription bursting with over-dispersed non-Poisson type distribution of mRNA numbers. We further show that there exist optimum flipping rates (α_C, β_C) at which the stationary state Fano factor and variance associated with the mRNA numbers attain maxima. These optimum points are connected via $\alpha_{C} = \sqrt {\beta_{C} \left( {\beta_{C} + \gamma_{r} } \right)}$. Here α is the rate of flipping from the on-state to the off-state, β is the rate of flipping from the off-state to the on-state and γ_r is the decay rate of mRNA. When α = β = χ with zero rate in the off-state channel, then there exist optimum flipping rates at which the non-stationary Fano factor and variance attain maxima. Here $\chi_{C,v} \simeq {{3k_{r}^{ + } } \mathord{\left/ {\vphantom {{3k_{r}^{ + } } {2\left( {1 + k_{r}^{ + } t} \right)}}} \right. \kern-0pt} {2\left( {1 + k_{r}^{ + } t} \right)}}$ (here $k_{r}^{ + }$ is the rate of transcription purely through the on-state elongation channel) is the optimum flipping rate at which the variance of mRNA attains a maximum and $\chi_{C,\kappa } \simeq {{1.72} \mathord{\left/ {\vphantom {{1.72} t}} \right. \kern-0pt} t}$ is the optimum flipping rate at which the Fano factor attains a maximum. Close observation of the transcription mechanism reveals that the RNA polymerase performs several rounds of stall-continue type dynamics before generating a complete mRNA. Based on this observation, we model the transcription event as a stochastic trajectory of the transcription machinery across these on–off state elongation channels. Each mRNA transcript follows different trajectory. The total time taken by a given trajectory is the first passage time (FPT). Inverse of this FPT is the resultant transcription rate associated with the particular mRNA. Therefore, the time required to generate a given mRNA transcript will be a random variable. For a stall-continue type dynamics of RNA polymerase, we show that the overall average transcription rate can be expressed as $k_{r} \simeq h_{\infty }^{ + } k_{r}^{ + }$ where $k_{r}^{ + } \simeq {{\lambda_{r}^{ + } } \mathord{\left/ {\vphantom {{\lambda_{r}^{ + } } L}} \right. \kern-0pt} L}$, λ⁺_r is the microscopic transcription elongation rate in the on-state channel and L is the length of a complete mRNA transcript and h⁺_∞  = [β/(α + β)] is the stationary state probability of finding the transcription machinery in the on-state channel.

Appendices

Appendix 1

Consider the following backward type coupled master equations along with the boundary conditions (Eq. 39 along with Eq. 37 of the main text) corresponding to the second moments of the first passage times (FPTs) required to generate a complete mRNA transcript starting from an arbitrary n size of mRNA [41, 43].

$$ \lambda_{r}^{ + } R_{n + 1}^{ + } - \lambda_{r}^{ + } R_{n}^{ + } - \alpha R_{n}^{ + } + \beta R_{n}^{ - } = - 2T_{n}^{ + } ; \, \lambda_{r}^{ - } R_{n + 1}^{ - } - \lambda_{r}^{ - } R_{n}^{ - } + \alpha R_{n}^{ + } - \beta R_{n}^{ - } = - 2T_{n}^{ - } ; \, R_{L}^{ \pm } = 0 $$

(80)

In this equation, the first moments of the FPTs are defined as follows (as described in Eq. 37 of the main text).

$$ \begin{aligned} T_{n}^{ + } & = {{\left( {\alpha \lambda_{r}^{ - } \left[ {\beta \left( {L - n} \right) + \lambda_{r}^{ - } \left( {1 - W^{ - L + n} } \right)} \right] + \beta^{2} \left( {L - n} \right)\lambda_{r}^{ + } } \right)} \mathord{\left/ {\vphantom {{\left( {\alpha \lambda_{r}^{ - } \left[ {\beta \left( {L - n} \right) + \lambda_{r}^{ - } \left( {1 - W^{ - L + n} } \right)} \right] + \beta^{2} \left( {L - n} \right)\lambda_{r}^{ + } } \right)} {y^{2} }}} \right. \kern-0pt} {y^{2} }} \\ T_{n}^{ - } & = {{\left( {\left[ {L - n} \right]y - \lambda_{r}^{ - } \lambda_{r}^{ + } \alpha \left( {1 - W^{ - L + n} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\left[ {L - n} \right]y - \lambda_{r}^{ - } \lambda_{r}^{ + } \alpha \left( {1 - W^{ - L + n} } \right)} \right)} {y^{2} }}} \right. \kern-0pt} {y^{2} }} \, \\ T_{n} & = {{\left( {\left[ {L - n} \right]y - \lambda_{r}^{ - } \lambda_{r}^{ + } \alpha \left( {1 - W^{ - L + n} } \right) + \alpha \lambda_{r}^{ - } \left[ {\beta \left( {L - n} \right) + \lambda_{r}^{ - } \left( {1 - W^{ - L + n} } \right)} \right] + \beta^{2} \left( {L - n} \right)\lambda_{r}^{ + } } \right)} \mathord{\left/ {\vphantom {{\left( {\left[ {L - n} \right]y - \lambda_{r}^{ - } \lambda_{r}^{ + } \alpha \left( {1 - W^{ - L + n} } \right) + \alpha \lambda_{r}^{ - } \left[ {\beta \left( {L - n} \right) + \lambda_{r}^{ - } \left( {1 - W^{ - L + n} } \right)} \right] + \beta^{2} \left( {L - n} \right)\lambda_{r}^{ + } } \right)} {y^{2} }}} \right. \kern-0pt} {y^{2} }} \\ T_{n} & = T_{n}^{ + } + T_{n}^{ - } ; \, y = \left[ {\alpha \lambda_{r}^{ - } + \beta \lambda_{r}^{ + } } \right]; \, W = \left( {1 + {\beta \mathord{\left/ {\vphantom {\beta {\lambda_{r}^{ - } + {\alpha \mathord{\left/ {\vphantom {\alpha {\lambda_{r}^{ + } }}} \right. \kern-0pt} {\lambda_{r}^{ + } }}}}} \right. \kern-0pt} {\lambda_{r}^{ - } + {\alpha \mathord{\left/ {\vphantom {\alpha {\lambda_{r}^{ + } }}} \right. \kern-0pt} {\lambda_{r}^{ + } }}}}} \right) \\ \end{aligned} $$

(81)

The set of difference Eq. (80) is exactly solvable using standard summing technique [41] and the final expression corresponding to the variance (v_T), Fano factor (κ_T) and coefficient of variation (μ_T) of FPTs associated with the generation of a complete mRNA transcript of length L starting from n = 0 can be written as follows.

$$ \begin{aligned} R_{n} & = R_{n}^{ + } + R_{n}^{ - } ; \, R_{0} = R_{0}^{ + } + R_{0}^{ - } \\ \eta_{T} & = T_{0} = {{\left( {Ly - \lambda_{r}^{ - } \lambda_{r}^{ + } \alpha \left( {1 - W^{ - L} } \right) + \alpha \lambda_{r}^{ - } \left[ {\beta L + \lambda_{r}^{ - } \left( {1 - W^{ - L} } \right)} \right] + \beta^{2} L\lambda_{r}^{ + } } \right)} \mathord{\left/ {\vphantom {{\left( {Ly - \lambda_{r}^{ - } \lambda_{r}^{ + } \alpha \left( {1 - W^{ - L} } \right) + \alpha \lambda_{r}^{ - } \left[ {\beta L + \lambda_{r}^{ - } \left( {1 - W^{ - L} } \right)} \right] + \beta^{2} L\lambda_{r}^{ + } } \right)} {y^{2} }}} \right. \kern-0pt} {y^{2} }} \\ v_{T} & = R_{0} - T_{0}^{2} = \frac{{W^{ - 2L} \left( {\begin{array}{*{20}l} {\alpha^{2} \lambda_{r}^{ + } A_{1} + \alpha^{3} \lambda_{r}^{ - } A_{2} } \hfill \\ { + \alpha^{4} L\left[ {\lambda_{r}^{ - } } \right]^{2} W^{L} \left( {2\beta \lambda_{r}^{ - } W^{L} + 3\beta \lambda_{r}^{ + } W^{L} + \lambda_{r}^{ - } \lambda_{r}^{ + } \left( {W^{L} - 2} \right) + 2\left[ {\lambda_{r}^{ - } } \right]^{2} } \right)} \hfill \\ { + \alpha^{5} L\left[ {\lambda_{r}^{ - } } \right]^{3} W^{2L} + \alpha \beta \left[ {\lambda_{r}^{ + } } \right]^{2} W^{L} A_{3} + \beta^{4} L\left[ {\lambda_{r}^{ + } } \right]^{3} (\beta + \lambda_{r}^{ - } )W^{2L} } \hfill \\ \end{array} } \right)}}{{(\alpha \lambda_{r}^{ - } + \beta \lambda_{r}^{ + } )^{4} (\alpha \lambda_{r}^{ - } + \lambda_{r}^{ + } (\beta + \lambda_{r}^{ - } ))}} \\ \kappa_{T} & = \left( {{{v_{T} } \mathord{\left/ {\vphantom {{v_{T} } {\eta_{T} }}} \right. \kern-0pt} {\eta_{T} }}} \right); \, \mu_{T} = \left( {{{v_{T} } \mathord{\left/ {\vphantom {{v_{T} } {\eta_{T}^{2} }}} \right. \kern-0pt} {\eta_{T}^{2} }}} \right) \\ \end{aligned} $$

(82)

Here y and W are defined as in Eq. (81) and various other terms A₁, A₂ and A₃ in Eq. (82) are defined as follows.

$$ A_{1} = \left( {\begin{array}{*{20}l} {\beta^{2} L\lambda_{r}^{ - } W^{L} \left( {\left[ {\lambda_{r}^{ - } } \right]^{2} \left( {5W^{L} + 4} \right) - 2\lambda_{r}^{ - } \lambda_{r}^{ + } \left( {2W^{L} + 1} \right) + \left[ {\lambda_{r}^{ + } } \right]^{2} \left( {5W^{L} - 2} \right)} \right)} \hfill \\ { + \beta^{3} LW^{2L} \left( {3\left[ {\lambda_{r}^{ - } } \right]^{2} + 6\lambda_{r}^{ - } \lambda_{r}^{ + } + \left[ {\lambda_{r}^{ + } } \right]^{2} } \right)} \hfill \\ { + \beta \left[ {\lambda_{r}^{ - } } \right]^{2} \left( {4W^{L} + (2L - 3)W^{2L} - 1} \right)(\lambda_{r}^{ - } - \lambda_{r}^{ + } )^{2} + \left[ {\lambda_{r}^{ - } } \right]^{3} \left( {W^{2L} - 1} \right)(\lambda_{r}^{ - } - \lambda_{r}^{ + } )^{2} } \hfill \\ \end{array} } \right) $$

(83)

$$ A_{2} = \left( {\begin{array}{*{20}l} {\left[ {\lambda_{r}^{ - } } \right]^{2} \left( {\beta^{2} LW^{2L} - 2\beta L\lambda_{r}^{ + } \left( {W^{L} - 1} \right)W^{L} + \left[ {\lambda_{r}^{ + } } \right]^{2} \left( { - 2LW^{L} + W^{2L} - 1} \right)} \right)} \hfill \\ { + 3\beta^{2} L\left[ {\lambda_{r}^{ + } } \right]^{2} W^{2L} + 2\left[ {\lambda_{r}^{ - } } \right]^{3} \left( {\beta L\left( {W^{L} + 1} \right)W^{L} + 2L\lambda_{r}^{ + } W^{L} - \lambda_{r}^{ + } W^{2L} + \lambda_{r}^{ + } } \right)} \hfill \\ { + 2\beta L\lambda_{r}^{ - } \lambda_{r}^{ + } W^{L} \left( {3\beta W^{L} + 2\lambda_{r}^{ + } \left( {W^{L} - 1} \right)} \right) + \left[ {\lambda_{r}^{ - } } \right]^{4} \left( { - 2LW^{L} + W^{2L} - 1} \right)} \hfill \\ \end{array} } \right) $$

(84)

$$ A_{3} = \left( {\begin{array}{*{20}l} {2\beta^{2} L\left( {\left[ {\lambda_{r}^{ - } } \right]^{2} \left( {2W^{L} + 1} \right) - \lambda_{r}^{ - } \lambda_{r}^{ + } \left( {W^{L} + 1} \right) + \left[ {\lambda_{r}^{ + } } \right]^{2} W^{L} } \right)} \hfill \\ {{\mkern 1mu} {\mkern 1mu} + \beta^{3} LW^{L} (3\lambda_{r}^{ - } + 2\lambda_{r}^{ + } ) + 2\beta \lambda_{r}^{ - } \left( {LW^{L} - 2W^{L} + L + 2} \right)(\lambda_{r}^{ - } - \lambda_{r}^{ + } )^{2} } \hfill \\ {{\mkern 1mu} {\mkern 1mu} - 4\left[ {\lambda_{r}^{ - } } \right]^{2} \left( {W^{L} - 1} \right)(\lambda_{r}^{ - } - \lambda_{r}^{ + } )^{2} } \hfill \\ \end{array} } \right) $$

(85)

In Eqs. (83)–(85), W is defined as in Eq. (81). When α = β = χ, then the expression corresponding to the variance of FPTs given in Eq. (82) simplifies to the following form.

$$ \begin{aligned} \eta_{T} & = {{\left( {L\left[ {\lambda_{r}^{ - } + \lambda_{r}^{ + } } \right] - \lambda_{r}^{ - } \lambda_{r}^{ + } \left( {1 - Y^{ - L} } \right) + \lambda_{r}^{ - } \left[ {\chi L + \lambda_{r}^{ - } \left( {1 - Y^{ - L} } \right)} \right] + \chi L\lambda_{r}^{ + } } \right)} \mathord{\left/ {\vphantom {{\left( {L\left[ {\lambda_{r}^{ - } + \lambda_{r}^{ + } } \right] - \lambda_{r}^{ - } \lambda_{r}^{ + } \left( {1 - Y^{ - L} } \right) + \lambda_{r}^{ - } \left[ {\chi L + \lambda_{r}^{ - } \left( {1 - Y^{ - L} } \right)} \right] + \chi L\lambda_{r}^{ + } } \right)} {\left[ {\lambda_{r}^{ - } + \lambda_{r}^{ + } } \right]^{2} }}} \right. \kern-0pt} {\left[ {\lambda_{r}^{ - } + \lambda_{r}^{ + } } \right]^{2} }} \\ v_{T} & = \frac{{Y^{ - 2L} \left( {\begin{array}{*{20}l} {2\chi^{2} LY^{L} (\lambda_{r}^{ - } + \lambda_{r}^{ + } )^{2} B_{1} + 4\chi^{3} LY^{2L} (\lambda_{r}^{ - } + \lambda_{r}^{ + } )^{3} } \hfill \\ { + \chi \lambda_{r}^{ - } (\lambda_{r}^{ - } - \lambda_{r}^{ + } )^{2} (\lambda_{r}^{ - } + \lambda_{r}^{ + } )B_{2} + \left[ {\lambda_{r}^{ - } } \right]^{2} \lambda_{r}^{ + } \left( {Y^{L} - 1} \right)(\lambda_{r}^{ - } - \lambda_{r}^{ + } )^{2} B_{3} } \hfill \\ \end{array} } \right)}}{{\chi^{2} (\lambda_{r}^{ - } + \lambda_{r}^{ + } )^{4} (\chi (\lambda_{r}^{ - } + \lambda_{r}^{ + } ) + \lambda_{r}^{ - } \lambda_{r}^{ + } )}} \\ \kappa_{T} & = \left( {{{v_{T} } \mathord{\left/ {\vphantom {{v_{T} } {\eta_{T} }}} \right. \kern-0pt} {\eta_{T} }}} \right); \, \mu_{T} = \left( {{{v_{T} } \mathord{\left/ {\vphantom {{v_{T} } {\eta_{T}^{2} }}} \right. \kern-0pt} {\eta_{T}^{2} }}} \right) \\ \end{aligned} $$

(86)

The terms Y, B₁, B₂ and B₃ in Eq. (86) are defined as follows.

$$ \begin{aligned} Y & = \left( {1 + {\chi \mathord{\left/ {\vphantom {\chi {\lambda_{r}^{ - } + {\chi \mathord{\left/ {\vphantom {\chi {\lambda_{r}^{ + } }}} \right. \kern-0pt} {\lambda_{r}^{ + } }}}}} \right. \kern-0pt} {\lambda_{r}^{ - } + {\chi \mathord{\left/ {\vphantom {\chi {\lambda_{r}^{ + } }}} \right. \kern-0pt} {\lambda_{r}^{ + } }}}}} \right); \, B_{1} = \left( {\left[ {\lambda_{r}^{ - } } \right]^{2} \left( {Y^{L} + 2} \right) + \left[ {\lambda_{r}^{ + } } \right]^{2} Y^{L} - 2\lambda_{r}^{ - } \lambda_{r}^{ + } } \right) \\ B_{2} & = \left( {\lambda_{r}^{ - } \left( { - 2LY^{L} + Y^{2L} - 1} \right) + 2\lambda_{r}^{ + } \left( {LY^{L} - 2Y^{L} + L + 2} \right)Y^{L} } \right) \\ B_{3} & = \left( {\lambda_{r}^{ - } Y^{L} - 4\lambda_{r}^{ + } Y^{L} + \lambda_{r}^{ - } } \right) \\ \end{aligned} $$

(87)

Numerical analysis of Eq. (86) reveals the existence of maximum v_T, κ_T and μ_T at the optimum flipping rate χ_C,T which is demonstrated in Fig. 8b, d. Equation (81) clearly suggest that when the microscopic transcription elongation rate associated with the off-state channel is close to zero i.e. λ⁻_r  → 0 then the overall average transcription rate scales with the on–off flipping rates as k_r = [1/T₀] ≃ k⁺_r [β/(α + β)] where k⁺_r  = λ⁺_r /L is the overall transcription rate of the pure on-state channel and λ⁺_r is the elongation rate of the on-state channel.

Appendix 2

Let us consider the uncoupled on–off state transcription elongation channels. When there is no flipping across the on and off state channels, then Eq. (1) will be uncoupled as follows.

$$ \partial_{t} u_{m,t}^{ \pm } = k_{r}^{ \pm } u_{m - 1,t}^{ \pm } + \gamma_{r} \left( {m + 1} \right)u_{m + 1,t}^{ \pm } - \left( {k_{r}^{ \pm } + \gamma_{r} m} \right)u_{m,t}^{ \pm } ; \, u_{m,0}^{ \pm } = \delta \left( m \right) $$

(88)

Here u^±_m,t is the probability of finding m number of mRNAs at time t in the respective independent transcription channels. Upon defining the generating functions as G^±_s,t  = ∑^∞_m=0 s^mu^±_m,t one can transform Eq. (89) into the following partial differential equations.

$$ \partial_{t} G_{s,t}^{ \pm } = k_{r}^{ \pm } \left( {s - 1} \right)G_{s,t}^{ \pm } + \gamma_{r} \left( {1 - s} \right)\partial_{s} G_{s,t}^{ \pm } ; \, G_{s,0}^{ \pm } = 1 $$

(89)

Upon solving Eq. (89) for the for the appropriate boundary conditions one finds the expression for the generating functions as follows.

$$ G_{s,t}^{ \pm } = \exp \left( {{{k_{r}^{ \pm } \left( {s - 1} \right)\left( {1 - \exp \left( { - \gamma_{r} t} \right)} \right)} \mathord{\left/ {\vphantom {{k_{r}^{ \pm } \left( {s - 1} \right)\left( {1 - \exp \left( { - \gamma_{r} t} \right)} \right)} {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right) $$

(90)

Using this generating function one can derive various statistical properties of the mRNA number fluctuations corresponding to on–off channels as follows.

$$ \begin{aligned} \eta_{m,t}^{ \pm } & = \lim_{s \to 1} \partial_{s} G_{s,t}^{ \pm } = {{k_{r}^{ \pm } \left( {1 - \exp \left( { - \gamma_{r} t} \right)} \right)} \mathord{\left/ {\vphantom {{k_{r}^{ \pm } \left( {1 - \exp \left( { - \gamma_{r} t} \right)} \right)} {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }} \\ v_{m,t}^{ \pm } & = \lim_{s \to 1} \partial_{s}^{2} G_{s,t}^{ \pm } + \eta_{m,t} - \eta_{m,t}^{2} = {{k_{r}^{ \pm } \left( {1 - \exp \left( { - \gamma_{r} t} \right)} \right)} \mathord{\left/ {\vphantom {{k_{r}^{ \pm } \left( {1 - \exp \left( { - \gamma_{r} t} \right)} \right)} {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }} \\ \kappa_{m,t}^{ \pm } & = 1; \, \mu_{m,t}^{ \pm } = \left( {{{k_{r}^{ \pm } \left( {1 - \exp \left( { - \gamma_{r} t} \right)} \right)} \mathord{\left/ {\vphantom {{k_{r}^{ \pm } \left( {1 - \exp \left( { - \gamma_{r} t} \right)} \right)} {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)^{ - 1} \\ \end{aligned} $$

(91)

Upon expanding the generating function into a Macularin series with respect to variable s and then setting s = 1, one finally obtains the probability density functions as follows.

$$ u_{m,t}^{ \pm } = \left( {\left( {{{k_{r}^{ \pm } } \mathord{\left/ {\vphantom {{k_{r}^{ \pm } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)\left[ {1 - \exp \left( { - \gamma_{r} t} \right)} \right]} \right)^{m} {{\exp \left( { - \left( {{{k_{r}^{ \pm } } \mathord{\left/ {\vphantom {{k_{r}^{ \pm } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)\left[ {1 - \exp \left( { - \gamma_{r} t} \right)} \right]} \right)} \mathord{\left/ {\vphantom {{\exp \left( { - \left( {{{k_{r}^{ \pm } } \mathord{\left/ {\vphantom {{k_{r}^{ \pm } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)\left[ {1 - \exp \left( { - \gamma_{r} t} \right)} \right]} \right)} {m!}}} \right. \kern-0pt} {m!}} $$

(92)

Using Eq. (92) one can directly obtain the steady state probability density functions as follows.

$$ u_{m,\infty }^{ \pm } = \left( {{{k_{r}^{ \pm } } \mathord{\left/ {\vphantom {{k_{r}^{ \pm } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)^{m} {{\exp \left( { - {{k_{r}^{ \pm } } \mathord{\left/ {\vphantom {{k_{r}^{ \pm } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)} \mathord{\left/ {\vphantom {{\exp \left( { - {{k_{r}^{ \pm } } \mathord{\left/ {\vphantom {{k_{r}^{ \pm } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)} {m!}}} \right. \kern-0pt} {m!}} $$

(93)

When the on–off state flipping is uncoupled from the transcription elongation, then the flipping dynamics can be described by the following set of coupled differential equations.

$$ \partial_{t} \left[ {\begin{array}{*{20}c} {h_{t}^{ + } } \\ {h_{t}^{ - } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \alpha } & \beta \\ \alpha & { - \beta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {h_{t}^{ + } } \\ {h_{t}^{ - } } \\ \end{array} } \right]; \, \left[ {\begin{array}{*{20}c} {h_{0}^{ + } } \\ {h_{0}^{ - } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right] $$

(94)

Here we have the normalization condition h⁺_t  + h⁻_t  = 1. Upon solving Eq. (94) with the appropriate initial conditions, one obtains the expression for the time dependent probability h^±_t of finding the transcription state in the respective on–off channels as follows.

$$ \left[ {\begin{array}{*{20}c} {h_{t}^{ + } } \\ {h_{t}^{ - } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {{\beta \mathord{\left/ {\vphantom {\beta {\left( {\alpha + \beta } \right)}}} \right. \kern-0pt} {\left( {\alpha + \beta } \right)}}} \right] - \left[ {{\alpha \mathord{\left/ {\vphantom {\alpha {\left( {\alpha + \beta } \right)}}} \right. \kern-0pt} {\left( {\alpha + \beta } \right)}}} \right]\exp \left( { - \left( {\alpha + \beta } \right)t} \right)} \\ {\left[ {{\alpha \mathord{\left/ {\vphantom {\alpha {\left( {\alpha + \beta } \right)}}} \right. \kern-0pt} {\left( {\alpha + \beta } \right)}}} \right]\left( {1 - \exp \left( { - \left( {\alpha + \beta } \right)t} \right)} \right)} \\ \end{array} } \right]; \, \left[ {\begin{array}{*{20}c} {h_{\infty }^{ + } } \\ {h_{\infty }^{ - } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\beta \mathord{\left/ {\vphantom {\beta {\left( {\alpha + \beta } \right)}}} \right. \kern-0pt} {\left( {\alpha + \beta } \right)}}} \\ {{\alpha \mathord{\left/ {\vphantom {\alpha {\left( {\alpha + \beta } \right)}}} \right. \kern-0pt} {\left( {\alpha + \beta } \right)}}} \\ \end{array} } \right] $$

(95)

Upon combining Eq. (92) with Eq. (95), one can derive p^±_m,t  ≃ u^±_m,t h^±_t , which is the probability of finding m number of mRNAs in the respective on–off state channels. Explicitly one can write the following expression.

$$ p_{m,t} \simeq u_{m,t}^{ + } h_{t}^{ + } + u_{m,t}^{ - } h_{t}^{ - } = h_{t}^{ + } \left( {\varphi_{t}^{ + } } \right)^{m} {{\exp \left( { - \varphi_{t}^{ + } } \right)} \mathord{\left/ {\vphantom {{\exp \left( { - \varphi_{t}^{ + } } \right)} {m!}}} \right. \kern-0pt} {m!}} + h_{t}^{ - } \left( {\varphi_{t}^{ - } } \right)^{m} {{\exp \left( { - \varphi_{t}^{ + } } \right)} \mathord{\left/ {\vphantom {{\exp \left( { - \varphi_{t}^{ + } } \right)} {m!}}} \right. \kern-0pt} {m!}} $$

(96)

In this equation, we have defined the function φ^±_t  = (k^±_r /γ_r)[1 − exp (− γ_rt)]. When the timescale associated with the on–off state flipping dynamics is much lower than the timescale associated with the mRNA synthesis and decay dynamics so that (α + β) ≫ γ_r, then Eq. 96 reduces to p_m,t ≃ u⁺_m,t h⁺_∞  + u⁻_m,t h⁻_∞ . Under complete steady state conditions p_m,∞ ≃ u⁺_m,∞ h⁺_∞  + u⁻_m,∞ h⁻_∞ and one obtains the following bimodal Poisson type expression.

$$ p_{m,\infty } \simeq {{\left[ {\left( {{{k_{r}^{ + } } \mathord{\left/ {\vphantom {{k_{r}^{ + } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)^{m} \beta \exp \left( { - {{k_{r}^{ + } } \mathord{\left/ {\vphantom {{k_{r}^{ + } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right) + \left( {{{k_{r}^{ - } } \mathord{\left/ {\vphantom {{k_{r}^{ - } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)^{m} \alpha \exp \left( { - {{k_{r}^{ - } } \mathord{\left/ {\vphantom {{k_{r}^{ - } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {{{k_{r}^{ + } } \mathord{\left/ {\vphantom {{k_{r}^{ + } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)^{m} \beta \exp \left( { - {{k_{r}^{ + } } \mathord{\left/ {\vphantom {{k_{r}^{ + } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right) + \left( {{{k_{r}^{ - } } \mathord{\left/ {\vphantom {{k_{r}^{ - } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)^{m} \alpha \exp \left( { - {{k_{r}^{ - } } \mathord{\left/ {\vphantom {{k_{r}^{ - } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)} \right]} {\left( {\alpha + \beta } \right)m!}}} \right. \kern-0pt} {\left( {\alpha + \beta } \right)m!}} $$

(97)

When the transcription rate associated with the off-state channel tends toward zero, then one recovers the Poisson density function with zero spike [17] as follows.

$$ \lim_{{k_{r}^{ - } \to 0}} p_{m,\infty } \simeq \left[ {{\alpha \mathord{\left/ {\vphantom {\alpha {\left( {\alpha + \beta } \right)}}} \right. \kern-0pt} {\left( {\alpha + \beta } \right)}}} \right] + {{\left( {{{k_{r}^{ + } } \mathord{\left/ {\vphantom {{k_{r}^{ + } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)^{m} \beta \exp \left( { - {{k_{r}^{ + } } \mathord{\left/ {\vphantom {{k_{r}^{ + } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)} \mathord{\left/ {\vphantom {{\left( {{{k_{r}^{ + } } \mathord{\left/ {\vphantom {{k_{r}^{ + } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)^{m} \beta \exp \left( { - {{k_{r}^{ + } } \mathord{\left/ {\vphantom {{k_{r}^{ + } } {\gamma_{r} }}} \right. \kern-0pt} {\gamma_{r} }}} \right)} {\left( {\alpha + \beta } \right)m!}}} \right. \kern-0pt} {\left( {\alpha + \beta } \right)m!}} $$

(98)