Skip to main content
SpringerLink
Log in

Analysis of the approximate slow invariant manifold method for reactive flow equations

  • Original Paper
  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

Abstract

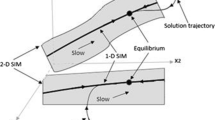
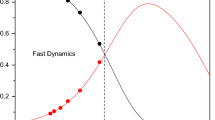
The Approximate Slow Invariant Manifold method of Singh, Powers and Paolucci is a useful method for addressing model reduction in systems of reactive flow equations. It exploits separations of time scales between slow and fast species, and it generalizes the Intrinsic Low-Dimensional Manifold method, which was developed for model reduction in the context of reaction kinetics, to systems with diffusive and active transport. In this article, we present a mathematical analysis of the Approximate Slow Invariant Manifold method in the context of systems of reaction–diffusion equations with slow and fast reaction kinetics. Beginning with systems of two species (one slow and one fast), and then treating general systems with multiple slow and fast species, we explicitly determine the accuracy of the Approximate Slow Invariant Manifold method. We find that it is correct up to and including the terms of first order in the small parameter that measures the separation of the kinetics time scales, and that it captures many of the terms at second order, as well. Our analysis includes precise statements of the errors at second order, and we find that these are proportional to the slow components of the reaction–diffusion equation, as well as to the curvature of the critical manifold. We illustrate the results analytically on two prototypical examples, the Michaelis–Menten–Henri model with diffusion of the slow species and the Davis–Skodje model in which both the slow and fast species diffuse.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E. Benoit, M. Brons, M. Desroches, M. Krupa, Extending the zero-derivative principle for slow-fast dynamical systems. Zeit. Angew. Math. Phys. 66, 2255–2270 (2015)

    Article  Google Scholar 

  2. V. Bykov, U. Maas, The extension of the ILDM concept to reaction-diffusion manifolds. Combust. Theor. Model. 11, 839–862 (2007)

    Article  CAS  Google Scholar 

  3. M. Davis, Low-dimensional manifolds in reaction–diffusion equations. Part 1. Fundamental aspects. J. Phys. Chem. A 110, 5235–5256 (2006)

    Article  CAS  Google Scholar 

  4. M. Davis, Low-dimensional manifolds in reaction-diffusion equations. Part 2. Numerical analysis and method development. J. Phys. Chem. A 110, 5257–5272 (2006)

    Article  CAS  Google Scholar 

  5. M.J. Davis, R.T. Skodje, Geometric investigation of low-dimensional manifolds in systems approaching equilibrium. J. Chem. Phys. 111, 859–874 (1999)

    Article  CAS  Google Scholar 

  6. L. Edelstein-Keshet, Mathematical Models in Biology (SIAM, Philadelphia, 2005)

    Book  Google Scholar 

  7. N. Fenichel, Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 31, 53–98 (1979)

    Article  Google Scholar 

  8. A.N. Gorban, I.V. Karlin, Thermodynamic parameterization. Phys. A. 190, 393–404 (1992)

    Article  Google Scholar 

  9. A.N. Gorban, I.V. Karlin, Method of invariant manifolds for chemical kinetics. Chem. Eng. Sci. 58, 4751–4768 (2003)

    Article  CAS  Google Scholar 

  10. C.W. Gear, T.J. Kaper, I.G. Kevrekidis, A. Zagaris, Projecting to a slow manifold: Singularly perturbed systems and legacy codes. SIAM J. Appl. Dyn. Syst. 4, 711–732 (2005)

    Article  Google Scholar 

  11. A.N. Gorban, I.V. Karlin, AYu. Zinovyev, Invariant grids for reaction kinetics. Phys. A. 333, 106–154 (2004)

    Article  CAS  Google Scholar 

  12. A. Goeke, S. Walcher, E. Zerz, Quasi-Steady State - Intuition. Perturbation theory and algorithmic algebra, International workshop on computer algebra in scientific computing, vol. 9301 (Springer, Cham, 2015), pp. 135–151

  13. M. Hadjinicolaou, D.A. Goussis, Asymptotic solution of stiff PDEs with the CSP method: The reaction diffusion equation. SIAM J. Sci. Comput. 20, 781–810 (1998)

    Article  Google Scholar 

  14. F. Heineken, H. Tsuchiya, R. Aris, On the mathematical status of the pseudo-steady-state hypothesis of biochemical kinetics. Math. Biosci. 1, 95–113 (1967)

    Article  Google Scholar 

  15. H.M. Hardin, A. Zagaris, K. Krab, H.V. Westerhoff, Simplified yet highly accurate enzyme kinetics for cases of low substrate concentrations. FEBS J. 276, 5491–5506 (2009)

    Article  Google Scholar 

  16. K.M. Hangos, Engineering model reduction and entropy-based Lyapunov functions in chemical reaction kinetics. Entropy 12(4), 772–797 (2010)

    Article  CAS  Google Scholar 

  17. H.G. Kaper, T.J. Kaper, Asymptotic analysis of two reduction methods for systems of the chemical reactions. Physica D. 165, 66–93 (2002)

    Article  CAS  Google Scholar 

  18. H.G. Kaper, T.J. Kaper, A. Zagaris, Geometry of the computational singular perturbation method. Math. Model. Nat. Phenom. 10(3), 16–30 (2015)

    Article  Google Scholar 

  19. D. Lebiedz, Entropy-related extremum principles for model reduction of dissipative dynamical systems. Entropy 12, 706–719 (2010)

    Article  CAS  Google Scholar 

  20. S.H. Lam, D.A. Goussis, Understanding complex chemical kinetics with computational singular perturbation, In: Proceedings of the 22nd International symposium on combustion, The University of Washington, Seattle, WA, August 14–19, 1988, The Combustion Institute, Pittsburgh, 931–941 (1988)

  21. S.H. Lam, D.A. Goussis, The CSP method for simplifying kinetics. Int. J. Chem. Kinet. 26, 461–486 (1994)

    Article  CAS  Google Scholar 

  22. G. Li, A.S. Tomlin, H. Rabitz, Determination of approximate lumping schemes by a singular perturbation method. J. Chem. Phys. 99(5), 3562–3574 (1993)

    Article  CAS  Google Scholar 

  23. L. Michaelis, M.L. Menten, Die Kinetik der Invertinwirkung. Biochem. Z. 49, 333–369 (1913)

    CAS  Google Scholar 

  24. U. Maas, Coupling of chemical reaction with flow and molecular transport. Appl. Math. 3, 249–266 (1995)

    Google Scholar 

  25. U. Maas, Mathematical modeling of the coupling of chemical kinetics with laminar and turbulent transport processes. In: K.J. Bathe (Ed.) Proceedings of the first MIT conference on computational fluid and solid mechanics, vol. 2, (Elsevier, Amsterdam, 2001), pp. 1304–1308

  26. U. Maas, S.B. Pope, Simplifying chemical kinetics: intrinsic low-dimensional manifolds in composition space. Combust. Flame. 88, 239–264 (1992)

    Article  CAS  Google Scholar 

  27. U. Maas, S.B. Pope, Laminar flame calculations using simplified chemical kinetics based on intrinsic low-dimensional manifolds. In: 25th International symposium on combustion, (Combustion Institute, Pittsburgh, 1994), pp. 13–49

  28. J.D. Mengers, J.M. Powers, One-dimensional slow invariant manifolds for fully coupled reaction and micro-scale diffusion. SIAM J. Appl. Dyn. Syst. 12, 560–595 (2013)

    Article  Google Scholar 

  29. B.O. Palsson, Systems Biology: Simulation of Dynamic Network States (Cambridge University Press, Cambridge, 2011)

    Book  Google Scholar 

  30. B.O. Palsson, E.N. Lightfoot, Mathematical modeling of dynamics and control in metabolic networks, I: On Michaelis–Menten kinetics. J. Theoret. Biol. 111, 273–302 (1984)

    Article  CAS  Google Scholar 

  31. M.R. Roussel, S.J. Fraser, Geometry of the steady-state approximation: Perturbation and accelerated convergence methods. J. Chem. Phys. 93, 1072–1081 (1990)

    Article  CAS  Google Scholar 

  32. V.G. Romanovski, M. Mencinger, B. Fercec, Investigation of center manifolds of three-dimensional systems using computer algebra. Program. Comput. Softw. 39(2), 67–73 (2013)

    Article  Google Scholar 

  33. V.G. Romanovski, D. Shafer, The Center and Cyclicity Problems: A Computational Algebra Approach (Springer, New York, 2009)

    Google Scholar 

  34. M. Stiefenhofer, Quasi-steady-state approximation for chemical reaction networks. J. Math. Biol. 36, 593–609 (1998)

    Article  Google Scholar 

  35. S. Singh, J.M. Powers, S. Paolucci, On slow manifolds of chemically reactive systems. J. Chem. Phys. 117, 1482–1496 (2002)

    Article  CAS  Google Scholar 

  36. S. Singh, Y. Rastigejev, S. Paolucci, J.M. Powers, Viscous detonation in \(\text{ H }_2-\text{ O }_2-\text{ Ar } \) using intrinsic low-dimensional manifolds and wavelet adaptive multilevel representation. Combust. Theor. Model. 5, 163–184 (2001)

    Article  CAS  Google Scholar 

  37. L.A. Segel, M. Slemrod, The quasi-steady-state assumption: A case study in perturbation. SIAM Rev. 31, 446–477 (1989)

    Article  Google Scholar 

  38. L. Szili, J. Toth, Necessary condition of the turing instability. Phys. Rev. E 48, 183 (1993)

    Article  CAS  Google Scholar 

  39. A.M. Turing, The chemical basis of morphogenesis. Phil. Trans. Roy. Soc. Lond. B. 237, 37–72 (1952)

    Article  Google Scholar 

  40. T. Turányi, A.S. Tomlin, M.J. Pilling, On the error of the quasi-steady-state approximation. J. Phys. Chem. 97, 163–172 (1993)

    Article  Google Scholar 

  41. K. Uldall Kristiansen, M. Brons, J. Starke, An iterative method for the approximation of fibers in slow-fast systems. SIAM J. Appl. Dyn. Syst. 13, 861–900 (2014)

    Article  Google Scholar 

  42. S. Vajda, P. Valko, T. Turányi, Principal component analysis of chemical kinetics. Int. J. Chem. Kinet. 17, 55–81 (1985)

    Article  CAS  Google Scholar 

  43. B. Yang, S.B. Pope, An investigation of the accuracy of manifold methods and splitting schemes in the computational implementation of combustion chemistry. Combust. Flame. 112, 16–32 (1998)

    Article  CAS  Google Scholar 

  44. A.N. Yannacopoulos, A.S. Tomlin, J. Brindley, J.H. Merkin, M.J. Pilling, The use of algebraic sets in the approximation of inertial manifolds and lumping in chemical kinetic system. Physica D. 83, 421–449 (1995)

    Article  CAS  Google Scholar 

  45. A. Zagaris, C. Vandekerckhove, C.W. Gear, I.G. Kevrekidis, T.J. Kaper, Stability and stabilization of the constrained runs schemes for equation-free projection to a slow manifold. Dis. Cont. Dyn. Syst. 32, 2759–2803 (2012)

    Article  Google Scholar 

Download references

Acknowledgements

The research of X.W. and T.J.K. was partially supported by NSF-DMS 1109587. The authors thank Arjen Doelman for a useful conversation.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Boston University, Boston, MA, 02215, USA

    Xiaoxuan Wu & Tasso J. Kaper

Authors
  1. Xiaoxuan Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tasso J. Kaper
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tasso J. Kaper.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, X., Kaper, T.J. Analysis of the approximate slow invariant manifold method for reactive flow equations. J Math Chem 55, 1725–1754 (2017). https://doi.org/10.1007/s10910-017-0756-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10910-017-0756-6

Keywords

Search

Navigation